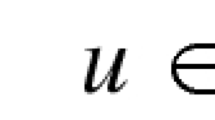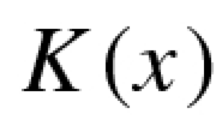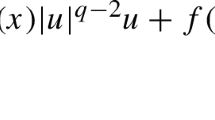Abstract
We consider the boundary value problem

where \(\Omega \subset \mathbb {R}^{N}\), \(N \ge 2\), is a bounded domain with smooth boundary. We assume \(c,\, h \in L^q(\Omega )\) for some \(q > \max \{N/p,1\}\) with \(c \gneqq 0\) and \(\mu \in L^{\infty }(\Omega )\). We prove existence and uniqueness results in the coercive case \( \lambda \le 0\) and existence and multiplicity results in the non-coercive case \( \lambda >0\). Also, considering stronger assumptions on the coefficients, we clarify the structure of the set of solutions in the non-coercive case.



Similar content being viewed by others
References
Abdel Hamid, H., Bidaut-Veron, M.F.: On the connection between two quasilinear elliptic problems with source terms of order 0 or 1. Commun. Contemp. Math. 12(5), 727–788 (2010)
Abdellaoui, B., Dall’Aglio, A., Peral, I.: Some remarks on elliptic problems with critical growth in the gradient. J. Differ. Equ. 222(1), 21–62 (2006)
Abdellaoui, B., Peral, I.: Existence and nonexistence results for quasilinear elliptic equations involving the \(p\)-Laplacian with a critical potential. Ann. Mat. Pura Appl. (4) 182(3), 247–270 (2003)
Abdellaoui, B., Peral, I., Primo, A.: Elliptic problems with a Hardy potential and critical growth in the gradient: non-resonance and blow-up results. J. Differ. Equ. 239(2), 386–416 (2007)
Allegretto, W., Huang, Y.X.: A Picone’s identity for the \(p\)-Laplacian and applications. Nonlinear Anal. 32(7), 819–830 (1998)
Ambrosetti, A., Brezis, H., Cerami, G.: Combined effects of concave and convex nonlinearities in some elliptic problems. J. Funct. Anal. 122(2), 519–543 (1994)
Arcoya, D., De Coster, C., Jeanjean, L., Tanaka, K.: Remarks on the uniqueness for quasilinear elliptic equations with quadratic growth conditions. J. Math. Anal. Appl. 420(1), 772–780 (2014)
Arcoya, D., De Coster, C., Jeanjean, L., Tanaka, K.: Continuum of solutions for an elliptic problem with critical growth in the gradient. J. Funct. Anal. 268(8), 2298–2335 (2015)
Boccardo, L., Murat, F., Puel, J.-P.: Existence de solutions faibles pour des équations elliptiques quasi-linéaires à croissance quadratique. In: Nonlinear Partial Differential Equations and Their Applications. Collège de France Seminar, vol. 4 (Paris, 1981/1982), volume 84 of Res. Notes in Math., pp 19–73. Pitman, Boston (1983)
Boccardo, L., Murat, F., Puel, J.-P.: Quelques propriétés des opérateurs elliptiques quasi linéaires. C. R. Acad. Sci. Paris Sér. I Math. 307(14), 749–752 (1988)
Boccardo, L., Murat, F., Puel, J.-P.: \(L^\infty \) estimate for some nonlinear elliptic partial differential equations and application to an existence result. SIAM J. Math. Anal. 23(2), 326–333 (1992)
Chang, K.C.: A variant mountain pass lemma. Sci. Sin. Ser. A 26(12), 1241–1255 (1983)
Chang, K.C.: Variational methods and sub- and supersolutions. Sci. Sin. Ser. A 26(12), 1256–1265 (1983)
Cuesta, M.: Existence results for quasilinear problems via ordered sub- and supersolutions. Ann. Fac. Sci. Toulouse Math. (6) 6(4), 591–608 (1997)
Cuesta, M., Takác, P.: A strong comparison principle for positive solutions of degenerate elliptic equations. Differ. Integral Equ. 13(4–6), 721–746 (2000)
Dall’Aglio, A., Giachetti, D., Puel, J.-P.: Nonlinear elliptic equations with natural growth in general domains. Ann. Mat. Pura Appl. (4) 181(4), 407–426 (2002)
De Coster, C., Jeanjean, L.: Multiplicity results in the non-coercive case for an elliptic problem with critical growth in the gradient. J. Differ. Equ. 262(10), 5231–5270 (2017)
de Figueiredo, D.G., Gossez, J.-P., Ramos Quoirin, H., Ubilla, P.: Elliptic equations involving the \(p\)-laplacian and a gradient term having natural growth. ArXiv e-prints (2017)
de Figueiredo, D.G., Gossez, J.-P., Ubilla, P.: Local “superlinearity” and “sublinearity” for the \(p\)-Laplacian. J. Funct. Anal. 257(3), 721–752 (2009)
de Figueiredo, D.G., Solimini, S.: A variational approach to superlinear elliptic problems. Commun. Partial Differ. Equ. 9(7), 699–717 (1984)
DiBenedetto, E.: \(C^{1+\alpha }\) local regularity of weak solutions of degenerate elliptic equations. Nonlinear Anal. 7(8), 827–850 (1983)
Dinca, G., Jebelean, P., Mawhin, J.: Variational and topological methods for Dirichlet problems with \(p\)-Laplacian. Port. Math. (N.S.) 58(3), 339–378 (2001)
Ekeland, I.: Convexity Methods in Hamiltonian Mechanics, Volume 19 of Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)]. Springer, Berlin (1990)
Ferone, V., Murat, F.: Nonlinear problems having natural growth in the gradient: an existence result when the source terms are small. Nonlinear Anal. 42(7, Ser. A: Theory Methods), 1309–1326 (2000)
Ghoussoub, N.: Duality and Perturbation Methods in Critical Point Theory, Volume 107 of Cambridge Tracts in Mathematics. Cambridge University Press, Cambridge (1993)
Godoy, T., Gossez, J.-P., Paczka, S.: On the antimaximum principle for the \(p\)-Laplacian with indefinite weight. Nonlinear Anal. 51(3), 449–467 (2002)
Iturriaga, L., Lorca, S., Ubilla, P.: A quasilinear problem without the Ambrosetti-Rabinowitz-type condition. Proc. R. Soc. Edinburgh Sect. A 140(2), 391–398 (2010)
Iturriaga, L., Souto, M.A., Ubilla, P.: Quasilinear problems involving changing-sign nonlinearities without an Ambrosetti–Rabinowitz-type condition. Proc. Edinb. Math. Soc. (2) 57(3), 755–762 (2014)
Jeanjean, L.: On the existence of bounded Palais–Smale sequences and application to a Landesman-Lazer-type problem set on \({ R}^N\). Proc. R. Soc. Edinb. Sect. A 129(4), 787–809 (1999)
Jeanjean, L., Ramos Quoirin, H.: Multiple solutions for an indefinite elliptic problem with critical growth in the gradient. Proc. Am. Math. Soc. 144(2), 575–586 (2016)
Jeanjean, L., Sirakov, B.: Existence and multiplicity for elliptic problems with quadratic growth in the gradient. Commun. Partial Differ. Equ. 38(2), 244–264 (2013)
Ladyzhenskaya, O.A., Ural’tseva, N.N.: Linear and quasilinear elliptic equations. Translated from the Russian by Scripta Technica, Inc. Translation editor: Leon Ehrenpreis. Academic Press, New York, London (1968)
Leonori, T., Porretta, A., Riey, G.: Comparison principles for \(p\)-Laplace equations with lower order terms. Ann. Mat. Pura Appl. (4) 196(3), 877–903 (2017)
Li, G., Yang, C.: The existence of a nontrivial solution to a nonlinear elliptic boundary value problem of \(p\)-Laplacian type without the Ambrosetti-Rabinowitz condition. Nonlinear Anal. 72(12), 4602–4613 (2010)
Lieberman, G.M.: Boundary regularity for solutions of degenerate elliptic equations. Nonlinear Anal. 12(11), 1203–1219 (1988)
Lucia, M., Prashanth, S.: Strong comparison principle for solutions of quasilinear equations. Proc. Am. Math. Soc. 132(4), 1005–1011 (2004)
Peral, I.: Multiplicity of solutions for the p-laplacian. Lecture Notes of the Second School of Nonlinear Functional Analysis and Applications to Differential Equations (1997)
Porretta, A.: On the comparison principle for \(p\)-Laplace type operators with first order terms. In: On the Notions of Solution to Nonlinear Elliptic Problems: Results and Developments, Volume 23 of Quad. Mat., pp. 459–497. Dept. Math., Seconda Univ. Napoli, Caserta (2008)
Pucci, P., Serrin, J.: The Maximum Principle, Volume 73 of Progress in Nonlinear Differential Equations and their Applications, vol. 73. Birkhäuser Verlag, Basel (2007)
Vázquez, J.L.: A strong maximum principle for some quasilinear elliptic equations. Appl. Math. Optim. 12(3), 191–202 (1984)
Acknowledgements
The authors thank warmly L. Jeanjean for his help improving the presentation of the results.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by P. Rabinowitz.
Appendix A: Sufficient condition
Appendix A: Sufficient condition
Lemma A.1
Given \(f \in L^r(\Omega )\), \(r > \max \{ N/p,1\}\) if \(p\not =N\) and \(1<r<\infty \) if \(p=N\), let us consider
for an arbitrary \(u \in W_0^{1,p}(\Omega )\). It follows that:
-
(i)
If \(1< p < N\) and \(\Vert f^{+}\Vert _{N/p} < S_N\), \(E_f(u)\) is an equivalent norm in \(W_0^{1,p}(\Omega )\).
-
(ii)
If \(p = N\) and \(\Vert f^{+}\Vert _{r} < S_{N,r}\), \(E_f(u)\) is an equivalent norm in \(W_0^{1,p}(\Omega )\).
-
(iii)
If \(p > N\) and \(\Vert f^{+}\Vert _1 < S_N\), \(E_f(u)\) is an equivalent norm in \(W_0^{1,p}(\Omega )\).
where, for \(p \ne N\), \(S_N\) denotes the optimal constant in the Sobolev inequality, i.e.
and, for \(p = N\),
Proof
We give the proof for \(1< p < N\). The other cases can be done in the same way. First of all, by applying Hölder and Sobolev’s inequalities, observe that, for any \(h \in L^{\frac{N}{p}}(\Omega )\), it follows that
On the one hand, by using this inequality, observe that
On the other hand, following the same argument, we obtain that
with \(A > 0\) since \(\Vert f^{+}\Vert _{\frac{N}{p}} < S_N\). The result follows. \(\square \)
As an immediate Corollary, we have a sufficient condition to ensure that \(m_p > 0\).
Corollary A.2
Recall that \(m_p\) is defined by (1.1). Under the assumptions (\(A_{1}\)), it follows that:
-
(i)
If \(1< p < N\), then \(\Vert h^{+}\Vert _{N/p} < \left( \frac{p-1}{\mu } \right) ^{p-1} S_N\) implies \(m_p > 0\).
-
(ii)
If \(p = N\), then \(\Vert h^{+}\Vert _q < \left( \frac{p-1}{\mu } \right) ^{p-1} S_{N,q}\) implies \(m_p > 0\).
-
(iii)
If \(p > N\), then \(\Vert h^{+}\Vert _1 < \left( \frac{p-1}{\mu } \right) ^{p-1} S_N\) implies \(m_p > 0\).
Rights and permissions
About this article
Cite this article
De Coster, C., Fernández, A.J. Existence and multiplicity for elliptic p-Laplacian problems with critical growth in the gradient. Calc. Var. 57, 89 (2018). https://doi.org/10.1007/s00526-018-1346-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00526-018-1346-6