Abstract
We study output reference tracking of systems with high relative degree via output feedback only; this is, tracking where the output derivatives are unknown. To this end, we prove that the conjunction of the funnel pre-compensator with a minimum phase system of arbitrary relative degree yields a system of the same relative degree which is minimum phase as well. The error between the original system’s output and the pre-compensator’s output evolves within a prescribed performance funnel; moreover, the derivatives of the funnel pre-compensator’s output are known explicitly. Therefore, output reference tracking with prescribed transient behaviour of the tracking error is possible without knowledge of the derivatives of the original system’s output; via funnel control schemes for instance.
Similar content being viewed by others

1 Nomenclature
Throughout the present article, we use the following notation, where \(I \subseteq \mathbb {R}\) denotes an interval
- \(\mathbb {N}\):
-
the set of positive integers,
- \(\mathbb {R}_{\ge 0}\), \(\mathbb {C}_-\):
-
the sets \(:= [0, \infty )\), \(\left\{ \, \mu \in \mathbb {C}\, \left| \, \text {Re}(\mu ) < 0 \right. \right\} \), respectively,
- \(A \in \mathbb {R}^{n \times m}\):
-
the matrix A is in the set of real \(n \times m\) matrices,
- \({{\,\mathrm{\mathbf {Gl}}\,}}_n(\mathbb {R})\):
-
the group of invertible matrices in \(\mathbb {R}^{n \times n}\),
- \(A > 0\):
-
\(:= \iff x^\top A x > 0\) for all \(x \in \mathbb {R}^n \setminus \{0\}\), the matrix \(A \in \mathbb {R}^{n \times n}\) is positive definite
- \(\sigma (A)\):
-
 ,
, - \(\lambda _{\mathrm{max}}(A), \lambda _{\mathrm{min}}(A) \):
-
the largest and the smallest eigenvalue of a matrix \(A \in \mathbb {R}^{n \times n}\) with \(\sigma (A) \subseteq \mathbb {R}\), respectively,
- \(\Vert x \Vert \):
-
\(:=\sqrt{x^\top x} \) Euclidean norm of \(x \in \mathbb {R}^n\),
- \(\Vert A \Vert \):
-
\(:= \max _{\Vert x\Vert =1} \Vert Ax\Vert \) spectral norm of \(A \in \mathbb {R}^{m \times n}\),
- \({\mathcal {L}}_{\mathrm{loc}}^\infty (I \rightarrow \mathbb {R}^p)\):
-
set of locally essentially bounded functions \( f: I \rightarrow \mathbb {R}^p\) ,
- \({\mathcal {L}}^\infty (I \rightarrow \mathbb {R}^p)\):
-
set of essentially bounded functions \( f: I \rightarrow \mathbb {R}^p\) ,
- \(\Vert f \Vert _{\infty } \):
-
\(:= {{\,\mathrm{\mathrm ess\,sup}\,}}_{t \in I} \Vert f(t)\Vert \) norm of \(f \in {\mathcal {L}}^\infty (I \rightarrow \mathbb {R}^p)\) ,
- \({\mathcal {W}}^{k,\infty }(I \rightarrow \mathbb {R}^p)\):
-
set of k-times weakly differentiable functions \( f : I \rightarrow \mathbb {R}^p\) such that \(f,\ldots ,f^{(k)} \in {\mathcal {L}}^\infty (I \rightarrow \mathbb {R}^p)\),
- \({\mathcal {C}}^k( I \rightarrow \mathbb {R}^p) \):
-
set of k-times continuously differentiable functions \(f : I \rightarrow \mathbb {R}^p\), \({\mathcal {C}}(I\rightarrow \mathbb {R}^p) = {\mathcal {C}}^0(I\rightarrow \mathbb {R}^p)\),
- \(f|_{J}\):
-
the restriction of \(f : I \rightarrow \mathbb {R}^n\) to \(J \subseteq I\), I an interval, a. a. almost all.
For later use, we recall the Kronecker product of two matrices \(L \in \mathbb {R}^{l \times m}\) and \(K = \left( k_{ij} \right) _{i=1,\ldots ,k;j=1,\ldots ,n } \in \mathbb {R}^{k \times n}\)
2 Introduction
In the present article, we elaborate on the so called funnel pre-compensator, first proposed in [13]. The funnel pre-compensator is a simple adaptive dynamical system of high-gain type which receives signals from a certain class of signals specified later, and has an output which approximates the input signal in the sense that the error between the input signal and the pre-compensator’s output evolves within a prescribed performance funnel; moreover, the derivatives of the pre-compensator’s output are known explicitly. Comparing the preprint [11] and the work [13], it is clear that the funnel pre-compensator was inspired by the concept of high-gain observers (mainly inspired by the adaptive high-gain observer proposed in [16]); for detailed literature on high-gain observers see [21, 35, 41, 43] and the survey [34] as well as the references therein, respectively. For a discussion and detailed comparison of some properties of high-gain observers and the funnel pre-compensator, see [13].
Although there is plenty of properly working high-gain-based feedback controller with prescribed error performance, for funnel control schemes, see, e.g. [10, 28], the recent work [8] or the construction of a bang-bang funnel controller cf. [37], and for prescribed performance controller see [1, 2], all suffer from the problem that the output signal’s derivatives (funnel control) or the full state (prescribed performance controller) have to be available to the control scheme. For funnel control this means, if the output’s derivatives are not available from measurement, the output measurement has to be differentiated which is an ill-posed problem, see, e.g. [24, Sec. 1.4.4]. Prominent ideas in the literature to handle this topic are so called backstepping procedures, see, e.g. [29, 30] in conjunction with an input filter. However, the backstepping procedure typically involves high powers of a “large-valued" gain function, which causes numerical issues and leads to impractical performances, see [24, Sec. 4.4.3]. Another approach to solve an arbitrary good transient and steady-state response problem for linear minimum phase systems with arbitrary relative degree is presented in [39]. The proposed controller involves an internal compensator scheme of LTI type which allows to achieve an arbitrary small error within an arbitrary short time receiving the systems’s output and the reference signal only. Although this control scheme has a number of advantageous features such as noise tolerance and applicability to systems with unknown relative degree to name but two (see also the survey [25]), it is an adaptive scheme with a monotonically non-decreasing gain and involves a (piecewise constant) switching function where the switching times are determined in a two-phase scheme of rather high complexity. In the works [19, 20], approaches to realize output tracking with prescribed error behaviour via output feedback only are presented. In [19] single-input single-output systems of known arbitrary relative degree with bounded input bounded state stable internal dynamics are under consideration. The control scheme involves higher derivatives of the output which are approximated via a high-gain observer. With this, tracking via output feedback can be realized. However, in this setting knowledge of the control coefficient is required and hence the particular control scheme is—in contrast to standard funnel control schemes—not model free. In [20] an extension of the prescribed performance controller [2] is used to achieve output tracking with prescribed error performance of unknown nonlinear multi-input multi-output systems with known vector relative degree. A high-gain observer scheme is used to make the required derivatives available. Since the control schemes in [19, 20] involve high-gain observers both suffer from the problem of proper initializing, i.e. the high-gain parameters are to be predetermined appropriately; however, it is not clear how to choose these parameters appropriately in advance. In [38], an output feedback funnel control scheme is developed which achieves output tracking with prescribed transient behaviour for a class of nonlinear single-input single-output systems where the nonlinearity is a function of time and the output variable only. In particular, the problem of choosing parameters appropriately in advance is circumvented.
As mentioned above, the derivatives of the pre-compensator’s output are known explicitly, and hence the aforesaid gives rise to the idea that the funnel pre-compensator scheme proposed in [13] can help resolving the long-standing problem of adaptive feedback control with prescribed error performance of nonlinear systems with relative degree higher than one with unknown output derivatives. In order to resolve this problem, in the present article we prove that the application of a cascade of funnel pre-compensators to a minimum phase system of arbitrary relative degree yields a system of the same relative degree, which is minimum phase as well. In particular, the derivatives of the pre-compensator’s output are known explicitly. Therefore, output reference tracking with prescribed transient behaviour using well known funnel control schemes for systems of arbitrary (possibly high) relative degree, as for instance from [10] or the recent work [8], is possible without knowledge of the system’s output derivatives. In particular, the tracking error between the original system’s output and the desired reference trajectory evolves within a prescribed performance funnel. For systems of relative degree two, this was shown in [13] and this result was used for funnel control in [12], but for arbitrary relative degree \(r\in \mathbb {N}\) this remained an open problem which we solve in the present paper.
Before we recall and investigate the funnel pre-compensator introduced in [13], we highlight that, contrary to most approaches, the funnel pre-compensator does not necessarily receive signals u and y which are input and output of a dynamical system or a corresponding plant, but, defining \({\mathcal {L}}{\mathcal {W}}_{m}^{r,\infty } := {\mathcal {L}}_{\mathrm{loc}}^\infty (\mathbb {R}_{\ge 0}\rightarrow \mathbb {R}^m) \times {\mathcal {W}}_\mathrm{loc}^{r,\infty }(\mathbb {R}_{\ge 0}\rightarrow \mathbb {R}^{m}) \), we consider signals u and y belonging to the large set

We emphasize that it is not assumed to know the matrix valued function \(\varGamma \). Only knowledge of the signals u and y and the number \( r \in \mathbb {N}\) is assumed. It is self-evident that the signals u and y can be input and output of a corresponding plant, respectively; for an example see [13]; however, the signal set \({\mathcal {P}}_r\) allows for a much larger class of dynamical systems, cf. [10] and the works [7, 28].
The present article is organized as follows. In Sect. 2, we recall the concept of the funnel pre-compensator first introduced in [13], and recapitulate the respective results we will work with. Section 3 contains the main result of the present article. After introducing the system class under consideration in Sect. 3.1 and establishing the set of feasible design parameters of the pre-compensator in Sect. 3.2, in Sect. 3.3 we state that the application of a cascade of funnel pre-compensators to a minimum phase system with arbitrary relative degree \(r \in \mathbb {N}\) leads to a system of same relative degree which is minimum phase as well, and moreover, the first \(r-1\) derivatives of the pre-compensator’s output are known explicitly; this is, in Sect. 3.3 we present the extension of [13, Thm. 2] to arbitrary relative degree. The proof of this result is relegated to the Appendix. In Sect. 4, we turn towards an application of the funnel pre-compensator, namely output tracking via output feedback only. We show that with the aid of the funnel pre-compensator output tracking with prescribed transient behaviour of the tracking error with unknown output derivatives is possible via funnel control techniques. In Sect. 5, we provide numerical simulations illustrating the findings from Sect. 4.
3 The funnel pre-compensator
In order to incorporate the main result of the present article into the context of the funnel pre-compensator proposed in [13], we briefly recall the respective results. The funnel pre-compensator is a pre-compensator of high-gain type in the spirit of funnel control; for details concerning funnel control see the works [10, 27, 28], the recent work [8] and the references therein, respectively. The funnel pre-compensator (1) is a dynamical system receiving signals \({(u,y) \in {\mathcal {P}}_r}\), for some \(r \in \mathbb {N}\), and giving z as an output, the first derivative of the latter is known exactly.
The error between the signals y and z, namely \(e := y-z\), evolves within a prescribed performance funnel
The situation is depicted in Fig. 1. The shape of the performance funnel is determined by the funnel functions, which belong to the following set

Note that the boundary of the performance funnel is given by the reciprocal of the funnel functions, namely by \(1/\varphi \). We highlight two important properties of the funnel functions \(\varphi \in \varPhi _r\). First, we allow \(\varphi (0) = 0\) which means that the boundary has a pole at \(t=0\). This will be important in the context of funnel control, where initial conditions of the form \(\varphi (0) \Vert e(0)\Vert <1\) occur, which are satisfied trivially for \(\varphi (0)=0\). Second, we do not require monotonically increasing funnel functions, see Fig. 1b. Although in most situations one will choose the funnel functions in such a manner that the funnel boundary is monotonically decreasing, there may occur situations where widening the funnel boundary over some time interval is beneficial, e.g. if the signal y is changing strongly or in the presence of (periodic) disturbances.
We recall the funnel pre-compensator \(FP : {\mathcal {P}}_r \rightarrow {\mathcal {P}}_{r} \) proposed in [13], defined for \((u,\xi ) \in {\mathcal {P}}_{r}\) and \(\varphi \in \varPhi _1\) via
where
and \({\tilde{\varGamma }} \in \mathbb {R}^{m \times m}\), \(a := (a_1,\ldots ,a_r)\), \(p := (p_1,\ldots ,p_r)\) and \(\varphi \) are design parameters to be determined later in Sect. 3.2
At this stage, we bring back to mind the result [13, Prop. 1] concerning the feasibility of the funnel pre-compensator. It guarantees transient behaviour of the error between the signal y and the pre-compensator state \(z_1\); and the derivative \(\dot{z}_1\) is known exactly. However, the higher derivatives of the pre-compensator’s output, namely \(\ddot{z},\ldots , z^{(r-1)}\) which explicitly depend on \(\dot{y}, \ldots , y^{(r-1)}\), do not approximate the higher derivatives of y in the sense that (since \(\dot{y},\ldots , y^{(r-1)}\) are unknown) transient behaviour of the errors \(e_i := y^{(i-1)} - z_i\), \(i=2,\ldots ,r\) cannot be achieved. This motivates a successive application of the funnel pre-compensator, resulting in a cascade of funnel pre-compensators as proposed in [13]. This means, we apply funnel pre-compensators in a row to the preceding system, which is already a funnel pre-compensator, i.e. for \(i \in \mathbb {N}\) we have \(FP : {\mathcal {P}}_r \rightarrow {\mathcal {P}}_{r}, (u,z_{i-1,1}) \mapsto (u,z_{i,1})\), the situation is depicted in Fig. 2.
This cascade achieves an approximation \(z := z_{r-1,1}\) of the signal y with transient behaviour of the error \(y-z\), and furthermore, the higher derivatives of the funnel pre-compensator’s output, namely \(\dot{z},\ldots ,z^{(r-1)}\) are known explicitly. Applying the pre-compensator \(r-1\) times, we obtain for \(\varphi _1, \varphi \in \varPhi _r\)
where, except of the first, all pre-compensators in the cascade have the same funnel function \(\varphi \), and all have the same gain matrix \({\tilde{\varGamma }}\); \(\varphi _1, \varphi \in \varPhi _r\), and \({a,p>0}\) are given by the corresponding matrices A, P, Q satisfying (A.1), to be introduced in Sect. 3.2. For such a cascade of funnel pre-compensators [13, Thm. 1] states that it yields a system with output \(z := z_{r-1,1}\) such that the error \(e := y - z\) evolves within a prescribed performance funnel, and moreover, the derivatives \(\dot{z}, \ldots , z^{(r-1)}\) are known explicitly. An explicit representation of \(z^{(j)}\) and its dependency on the states \(z_{i,j}\) are discussed in detail in [13, Rem. 3]. Figure 3 gives a picture of the dependence of \(z^{(j)}\) on the states \(z_{i,j}\).
Dependence of the derivatives \(z^{(j)}\) on the intermediate pre-compensator states. The figure is based on the respective figure in [13]
At the first glance, the expression for \(z^{(j)}\) in [13, Rem. 3] looks lengthy and awkward to handle. However, we highlight that with the aid of the given formula in [13, Rem. 3] the computation of all required derivatives of z can be performed completely algorithmically.
4 Main result: application of the funnel pre-compensator to minimum phase systems
In this section, we face the open question formulated in [13, Rem. 4], namely if the interconnection of a minimum phase system with a cascade of funnel pre-compensators yields a minimum phase system for relative degree larger than three. A careful inspection reveals that the proof of [13, Thm. 2] is incomplete as regards the boundedness of \(h_1, h_2\) in the case \(r=3\); this is, however, resolved in the present article. We show that for arbitrary \(r \in \mathbb {N}\) the interconnection of a cascade of \(r-1\) funnel pre-compensators with a minimum phase system with relative degree r yields a system of the same relative degree which is minimum phase as well, and the first \(r-1\) derivatives of the interconnection’s output, this is, the funnel pre-compensator’s output z, are known explicitly.
4.1 System class
We recall the system class under investigation in [13]. First, we introduce the following class of operators.
Definition 3.1
If for \(\sigma > 0\) and \(n,q \in \mathbb {N}\) the operator \(T: {\mathcal {C}}([-\sigma ,\infty ) \rightarrow \mathbb {R}^{n}) \rightarrow {\mathcal {L}}_{\mathrm{loc}}^\infty (\mathbb {R}_{\ge 0}\rightarrow \mathbb {R}^q)\) has the following properties
-
(a)
T maps bounded trajectories to bounded trajectories, i.e. for all \(c_1 > 0\), there exists \(c_2>0\) such that for all \(\xi \in {\mathcal {C}}([-\sigma ,\infty ) \rightarrow \mathbb {R}^n)\),
$$\begin{aligned} \sup _{t \in [-\sigma ,\infty )} \Vert \xi (t) \Vert \le c_1 \ \Rightarrow \ \sup _{t \in [0,\infty )} \Vert T(\xi )(t) \Vert \le c_2, \end{aligned}$$ -
(b)
T is causal, i.e. for all \(t \ge 0\) and all \(\zeta , \xi \in {\mathcal {C}}([-\sigma ,\infty ) \rightarrow \mathbb {R}^n)\),
$$\begin{aligned} \zeta |_{[-\sigma ,t)} = \xi |_{[-\sigma ,t)} \ \Rightarrow \ T(\zeta )|_{[0,t)} \overset{a.a.}{=} T(\xi )|_{[0,t)}, \end{aligned}$$ -
(c)
T is locally Lipschitz continuous in the following sense: for all \(t \ge 0 \) and all \(\xi \in {\mathcal {C}}([-\sigma ,t] \rightarrow \mathbb {R}^n)\) there exist \(\Delta , \delta , c > 0\) such that for all \(\zeta _1, \zeta _2 \in {\mathcal {C}}([-\sigma ,\infty ) \rightarrow \mathbb {R}^n)\) with \(\zeta _1|_{[-\sigma ,t]} = \xi \), \(\zeta _2|_{[-\sigma ,t]} = \xi \) and \(\Vert \zeta _1(s) - \xi (t)\Vert < \delta \), \(\Vert \zeta _2(s) - \xi (t)\Vert < \delta \) for all \(s \in [t,t+\Delta ]\) we have
$$\begin{aligned} {{\,\mathrm{\mathrm ess\,sup}\,}}_{s \in [t,t+\Delta ]}\Vert T(\zeta _1)(s) - T(\zeta _2)(s) \Vert \le c \ \mathrm {sup}_{s \in [t,t+\Delta ]} \Vert \zeta _1(s) - \zeta _2(s)\Vert , \end{aligned}$$
then we say the operator T belongs to the operator class \({\mathcal {T}}_\sigma ^{n,q}\).
With this, we introduce the system class \({\mathcal {N}}^{m,r}\) which is the same class of systems under consideration in [13], namely (multi-input multi-output) systems with stable internal dynamics, and the system’s input and output have the same dimension.
Definition 3.2
For a system
where \(\tau > 0\) is the “memory" of the system, i.e. an initial trajectory is given, \(r \in \mathbb {N}\) is the relative degree, and for \(p \in \mathbb {N}\) the “disturbance" satisfies \(d \in {\mathcal {L}}^\infty (\mathbb {R}_{\ge 0}\rightarrow \mathbb {R}^p)\), for \(q \in \mathbb {N}\) we have \(f \in {\mathcal {C}}(\mathbb {R}^p \times \mathbb {R}^q \rightarrow \mathbb {R}^m)\), the high gain matrix \(\varGamma \) is symmetric and sign definite (w.l.o.g. we assume \(0<\varGamma = \varGamma ^\top \in \mathbb {R}^{m \times m}\)), and the operator T belongs to the class \({\mathcal {T}}^{rm,q}_\tau \), we say system (3) belongs to the class \({\mathcal {N}}^{m,r}\), and we write
The function \(u:\mathbb {R}_{\ge 0}\rightarrow \mathbb {R}^m\) is called input, the function \(y : \mathbb {R}_{\ge 0}\rightarrow \mathbb {R}^m\) output of system (3), respectively. Note that the input and the output have the same dimension. Condition (a) in Definition 3.1 resembles a minimum phase property, more precise, an input to state stability of the internal dynamics of system (3), where from the viewpoint of the internal dynamics the system’s output and its derivatives act as inputs.
For fixed input \(u \in {\mathcal {L}}^\infty (\mathbb {R}_{\ge 0}\rightarrow \mathbb {R}^m)\) a function \(y \in {\mathcal {C}}^{r-1}([-\tau ,\omega ) \rightarrow \mathbb {R}^m)\) is called solution of (3) on an interval \([-\tau ,\omega )\), where \(\omega \in (0,\infty ]\), if \(y|_{[-\tau ,0]} = y^0\) and \(y^{(r-1)}|_{[0,\omega )}\) is weakly differentiable and satisfies (3) for almost all \(t \in [0,\omega )\). A solution y is called maximal solution, if it has no right extension that is also a solution.
Remark 3.3
An important subclass of (3) are linear systems of the form
where u denotes the input, and y the output of the system, respectively; further we have the system matrix \( A \in \mathbb {R}^{n \times n}\), the input distribution matrix \( B \in \mathbb {R}^{n \times m}\) and the linear output measurement \( C : \mathbb {R}^{n} \rightarrow \mathbb {R}^m\), this is, \( C \in \mathbb {R}^{m \times n}\) for \(m \le n\), and \({{\,\mathrm{\mathrm rk}\,}}C = {{\,\mathrm{\mathrm rk}\,}}B = m\); note that the dimensions of the input and the output are equal. Let
Note that \({\mathcal {W}}^{r-1,\infty }(\mathbb {R}_{\ge 0}\rightarrow \mathbb {R}^n) \subset {\mathcal {D}}(\mathbb {R}_{\ge 0}\rightarrow \mathbb {R}^n)\). Now, if
then—straightly following the derivations and calculations in [31, Thm. 3]—with
and the operator
the change of coordinates
transforms system (4) into Byrnes–Isidori form
with output
where
and the high-gain matrix \(\varGamma \) is given in (5). The last differential equation in (6a) describes the internal dynamics of system (4). We associate the (linear) integral operator
with the internal dynamics in (6a) and obtain for \({H(\cdot ) := e^{Q \cdot } [0, I_{n-rm}] U x^0}\) and \(D(t) := e^{Qt} \left( d_\eta (0) + \int _0^{t} e^{-Qs} d_\eta (s) \, \text { d}s\right) \) the internal state
With this and (6) we find that (4) is equivalent to the functional differential equation
where \(f(v,w) = v + w\) for \(v,w \in \mathbb {R}^m\), and the operator J satisfies conditions (b),(c) of Definition 3.1. The minimum phase property (condition (a)) for linear systems and its various equivalent conditions have been studied extensively, see, e.g. [3, 18, 44]. Here, we restrict ourself to mention the equivalence between system (4) being minimum phase, i.e. \(\sigma (Q) \subseteq \mathbb {C}_-\), and having asymptotically stable zero dynamics (see, e.g. [31]), where the latter means (cf. [30, 32])
Note that for \(\sigma (Q) \subseteq \mathbb {C}_-\), we have \(D \in {\mathcal {L}}^\infty (\mathbb {R}_{\ge 0}\rightarrow \mathbb {R}^m)\). Therefore, if system (4) has relative degree \(r \in \mathbb {N}\) as in (5) and satisfies (8) it is contained in the system class \({\mathcal {N}}^{m,r}\). Note that if the commonly used assumption is satisfied that the disturbance does not affect the integrator chain but enters the system on the input’s level (cf. [4, 5]), i.e.
then \({\mathcal {D}}(\mathbb {R}_{\ge 0}\rightarrow \mathbb {R}^n) = {\mathcal {L}}^\infty (\mathbb {R}_{\ge 0}\rightarrow \mathbb {R}^n)\); in this case we have \((\xi ^\top , \eta ^\top )^\top = Ux\) and \((d_r^\top , d_\eta ^\top )^\top = [(CA^{r-1})^\top , N^\top ]^\top d\).
We conclude this subsection with the preceding remark and turn towards the funnel pre-compensator’s design parameters.
4.2 The pre-compensator’s design parameters
We introduce the set of feasible design parameters for the funnel pre-compensator. For \(a = (a_1,\ldots ,a_{r})^\top \in \mathbb {R}^r\), \(p = (p_1,\ldots ,p_r)^\top \in \mathbb {R}^r\) we set
where (A.1) – (A.4) denote the following properties.
- (A.1):
-
The numbers \(a_{i}\) are such that \(a_i > 0\) for all \(i=1,\ldots ,r\), and
$$\begin{aligned} A := \begin{bmatrix} -a_1 &{} 1 &{} &{}\\ \vdots &{} &{} \ddots &{} \\ -a_{r-1} &{} &{} &{} 1 \\ -a_{r} &{} &{} &{}0 \end{bmatrix} \in \mathbb {R}^{r \times r} \end{aligned}$$is Hurwitz, i.e. \(\sigma (A) \subseteq \mathbb {C}_-\). Furthermore, let \(P = {\left[ {\begin{matrix} P_1 &{} P_{2} \\ P_{2}^\top &{} P_{4} \end{matrix}}\right] } > 0\), with \( P_1 \in \mathbb {R}\), \( P_{2} \in \mathbb {R}^{1 \times (r-1)}\), \( P_{4} \in \mathbb {R}^{(r-1) \times (r-1)}\) be the solution of
$$\begin{aligned} A^\top P + P A + Q = 0 \end{aligned}$$for some \(Q \in \mathbb {R}^{r \times r}\) with \(Q = Q^\top > 0\); then p is defined as
$$\begin{aligned} \begin{pmatrix} p_{1 }\\ \vdots \\ p_{r} \end{pmatrix} := P^{-1}\begin{pmatrix} P_1 - P_{2} P_{4}^{-1} P_{2}^\top \\ 0 \\ \vdots \\ 0 \end{pmatrix} = \begin{pmatrix} 1 \\ - P_{4}^{-1} P_{2}^\top \end{pmatrix}. \end{aligned}$$ - A.2:
-
The funnel functions \(\varphi _1, \varphi \in \varPhi _r\) from (2) satisfy
$$\begin{aligned} \exists \, \rho >1 \ \forall \, t\ge 0: \ \varphi (t) = \rho \, \varphi _1(t). \end{aligned}$$ - A.3:
-
The matrix \({\tilde{\varGamma }}\) from (2) is symmetric and sign definite (w.l.o.g. we assume \({\tilde{\varGamma }} > 0\)) and moreover, for \(\varGamma = \varGamma ^\top > 0\) from (3) we have
$$\begin{aligned} {\varGamma {\tilde{\varGamma }}^{-1} = \left( \varGamma {\tilde{\varGamma }}^{-1} \right) ^\top > 0}. \end{aligned}$$ - A.4:
-
For \(\varGamma \) from (3), \({\tilde{\varGamma }}\) from (2) and \(\rho \) from (A.2) the matrix \(G := I_m - \varGamma {\tilde{\varGamma }}^{-1}\) satisfies
$$\begin{aligned} \Vert G\Vert < \min \left\{ \frac{\rho - 1}{r-2} , \, \frac{\rho }{4\rho ^2 (\rho +1)^{r-2} -1} \right\} . \end{aligned}$$
If conditions (A.1) – (A.4) hold we write \((a,p,\varphi ,\varphi _1,\rho ,{\tilde{\varGamma }}) \in \Sigma \). Condition (A.2) means that the first funnel which limits the error \(y-z_{1,1}\) is somewhat tighter than the others; property (A.3) in particular asks for regularity of the matrix product \(\varGamma {\tilde{\varGamma }}^{-1}\), and (A.4) ensures that the matrix \({\tilde{\varGamma }}\) is “not too different" from matrix \(\varGamma \).
Remark 3.4
At the first glance, there are a lot of parameters to be chosen appropriately satisfying (A.1). However, consider the polynomial \((s+s_0)^r\), which has all its roots in \(\mathbb {C}_-\) for \(s_0 > 0\). Then, with
we obtain
this is, the matrix A is Hurwitz. Moreover, the simple choice \(Q = I_m\) is always feasible; and the matrix P is completely determined by the choice of A and Q. Therefore, since the constants \(p_1,\ldots ,p_r\) are given via the Lyapunov matrix P, all parameters required to satisfy (A.1) can be determined by choosing the real number \({s_0 > 0}\).
4.3 The funnel pre-compensator applied to minimum phase systems
In this section, we show that the conjunction of a system (3) with a cascade of funnel pre-compensators as in (2) leads to a minimum phase system. To this end, we prove the extension of [13, Thm. 2] for arbitrary relative degree \(r \in \mathbb {N}\).
We show that the minimum phase property of system (3), modelled by property (a) of Definition 3.1, is preserved by the conjunction of system (3) with the cascade of funnel pre-compensators (2). To this end, we require that the operator T satisfies a stronger condition.
Definition 3.5
For \(r,m \in \mathbb {N}\), \(n = rm\) and \(1\le k \le r\), we define the operator class \({\mathcal {T}}^{n,q}_{\sigma ,k} := \left\{ \, T \in {\mathcal {T}}^{n,q}_\sigma \, \left| \, T~\text {satisfies}~({a'_k}) \right. \right\} \subseteq {\mathcal {T}}^{n,q}_\sigma \) (equality if \(k=r\)), where
- (\({a'_k}\)):
-
for all \(c_1 > 0\) there exists \(c_2 > 0\) such that for all \(\xi _1,\ldots ,\xi _r \in {\mathcal {C}}([-\sigma ,\infty ) \rightarrow \mathbb {R}^m)\)
$$\begin{aligned}&\sup _{t \in [-\tau ,\infty )} \left\| \left( \xi _1(t)^\top ,\ldots ,\xi _{k}(t)^\top \right) \right\| \le c_1 \ \Rightarrow \ \sup _{t \in [0,\infty )} \Vert T(\xi _1,\ldots ,\xi _r)(t) \Vert \le c_2. \end{aligned}$$
Now, the stronger condition on the operator T, namely boundedness whenever the first component of its input is bounded, reads \(T \in {\mathcal {T}}^{{rm},q}_{\sigma ,1}\), this is, T is bounded whenever \(y: \mathbb {R}_{\ge 0}\rightarrow \mathbb {R}^{m}\) is bounded. Furthermore, we set
Remark 3.6
The somewhat arcane condition \(T \in {\mathcal {T}}^{rm,q}_{\sigma ,1}\) reflects the intuition that in order to have the conjunction of the system with the funnel pre-compensator being a minimum phase system, we must be able to conclude from the available information (only the output y) that the internal dynamics stay bounded. Note that this, however, does not mean that the operator T does not act on the output signal’s derivatives but on y only, see Example 5.2.
Remark 3.7
We highlight that, if for Q in (6a) we have \(\sigma (Q) \subseteq \mathbb {C}_-\), this is, if condition (8) is satisfied, the operator defined in (7) is contained in \({\mathcal {T}}^{rm,q}_{\sigma ,1}\). This means, the class of linear minimum phase systems which satisfy (5) is encompassed by the system class \( {\mathcal {N}}^{m,r}_1\). Moreover, \({\mathcal {N}}^{m,r}_1\) encompasses systems of the following form
where for \(rm \le n \in \mathbb {N}\) the function \(f: \mathbb {R}_{\ge 0}\times \mathbb {R}^{rm} \times \mathbb {R}^{n-rm} \rightarrow \mathbb {R}^{m}\) is locally Lipschitz in \((\xi ,\eta ) \in \mathbb {R}^{rm} \times \mathbb {R}^{n-rm}\), and piecewise continuous and bounded in t; \({g: \mathbb {R}^{n-rm} \times \mathbb {R}^{m} \rightarrow \mathbb {R}^{n-rm}}\) is such that for \(\xi _1 \in {\mathcal {L}}^{\infty }(\mathbb {R}_{\ge 0}\rightarrow \mathbb {R}^m)\) the corresponding ODE has a bounded solution (see, e.g. [36, Thm. 4.3]); and \(\varGamma \in {{\,\mathrm{\mathbf {Gl}}\,}}_m(\mathbb {R})\) is symmetric and sign definite. Therefore, with constant input parameter a subclass of the class of systems under consideration in [19] is contained in \( {\mathcal {N}}^{1,r}_1 \subset {\mathcal {N}}^{m,r}_1\). Moreover, the class \({\mathcal {N}}^{m,r}_1\) encompasses the system class under consideration in [30]. In [17, Cor. 5.7] explicit criteria on the parameters a, b of nonlinear systems of the form \(\dot{x}(t) = a(x(t)) + b(x(t)) u(t)\) are given such that it can be transformed into a system (9).
We present a version of [13, Thm. 2] (in particular without the restriction \({r \in \{ 2,3 \}}\)), and hereinafter prove it.
Theorem 3.8
Consider a system (3) with \((d,f,T,\varGamma ) \in {\mathcal {N}}^{m,r}_1\) (note that \(T \in {\mathcal {T}}^{rm,q}_{\tau ,1}\), \(q \in \mathbb {N}\)) and \(y^0 \in {\mathcal {W}}^{r-1,\infty }([-\tau ,0] \rightarrow \mathbb {R}^m)\). Further consider the cascade of funnel pre-compensators defined by (2) with \((a,p, \varphi ,\varphi _1,\rho , {\tilde{\varGamma }} ) \in \Sigma \) and assume the initial conditions
are satisfied. Then, for \({\bar{q}} = rm(r-1)+r\), there exist \({\tilde{d}} \in {\mathcal {L}}^\infty ( \mathbb {R}_{\ge 0}\rightarrow \mathbb {R}^r\)), \({\tilde{F}} \in {\mathcal {C}}( \mathbb {R}^r \times \mathbb {R}^{{\bar{q}}} \rightarrow \mathbb {R}^m)\) and an operator \({\tilde{T}} : {\mathcal {C}}([-\tau ,\infty ) \rightarrow \mathbb {R}^{rm}) \rightarrow {\mathcal {L}}_{\mathrm{loc}}^\infty (\mathbb {R}_{\ge 0}\rightarrow \mathbb {R}^{{\bar{q}}})\) with
such that the conjunction of (2) and (3) with input u and output \(z : = z_{r-1,1}\) can be equivalently written as
with respective initial conditions.
Since the proof is quite long and partly technical we present a sketch of it here; the proof itself is relegated to the Appendix and is subdivided in three main steps. In the first step, we recall the transformations given in [13, pp. 4759–4760] which allow to analyse the error dynamics of two successive pre-compensators. The second step is the main part of the proof consisting of preparatory work to show that there exists an operator \({\tilde{T}} \in {\mathcal {T}}^{rm,{\bar{q}}}_\tau \) such that the conjunction of a minimum phase system (3) with a cascade of funnel pre-compensators (2) can be written as in (11); the functions \({\tilde{d}}\) and \({\tilde{F}}\) are then given naturally. We define an operator \({\tilde{T}}\) mapping the pre-compensator’s output z and its derivatives to the state of the overall auxiliary error-system (17) and the respective gain functions. In order to show that \({\tilde{T}}\) satisfies condition (a) in Definition 3.1 we establish boundedness of the solution of the auxiliary system (17) and the respective gain functions. Here, step two splits into two parts. First, using \(T \in {\mathcal {T}}^{rm,q}_{\tau ,1}\)—more specifically we use that \(T(y,\ldots ,y^{(r-1)})\) is bounded whenever y is bounded—we may define an overall system of errors of two successive pre-compensators, namely system (21) for \(i=3,\ldots ,r-1\)
where the error states \(w_{i,j}\) stem from the transformations in Step 1 and the compact states \(w_i, {\bar{w}}\) are defined at the beginning of Step 2a; \(B_1, B_2, B_i\) are bounded functions. For this overall error-system (21), we find a Lyapunov function, which in combination with Grönwall’s lemma allows us to deduce boundedness of the error states \(w_i\). In the second part of step two, which is the most technical part of the proof, we show that the gain functions \(h_i\) are bounded. This demands particular accuracy since the functions \(h_i\) may introduce singularities. Due to the shape of the gain functions, namely \(h(t) = \left( 1 - \varphi (t)^2\Vert x(t)\Vert ^2 \right) ^{-1}\) boundedness is equivalent to the existence of \(\nu > 0\) such that \(\Vert x(t)\Vert \le \varphi (t)^{-1} - \nu \), which is commonly utilized in the standard funnel control proofs, cf. [10, pp. 350–351]. However, unlike the standard funnel case, the dynamics under consideration involve the previous gain function, respectively, and the first equation involves the last gain function; to see this, we recall (29) for \(i=2,\ldots ,r-1\)
where \(x_i\) are auxiliary states defined in Step 2b; \(b_1,b_i\) are bounded functions. It turns out that this loop structure demands some technical derivations and requires accurate estimations of the involved expressions. Exploiting properties (A.1) – (A.4) of the design parameters we can show by contradiction that there exist \(\kappa _i > 0\) such that \(\Vert x_i(t)\Vert \le \varphi (t)^{-1} - \kappa _i\) for all \(i=2,\ldots ,r-1\) (and \(\Vert x(t)_1\Vert \le \varphi _1(t)^{-1} - \kappa _1\)), respectively, which implies boundedness of all gain functions \(h_i\). In step three, we summarize the previously established results to deduce \({\tilde{T}} \in {\mathcal {T}}^{rm,{\bar{q}}}_{\tau }\). Then, the functions \({\tilde{d}}\) and \({\tilde{F}}\) arise naturally in equation (55). Together, we may conclude that the conjunction of a minimum phase system (3), where \((d,f,T,\varGamma ) \in {\mathcal {N}}^{m,r}_1\), with a cascade of funnel pre-compensators (2), where \((a,p,\varphi ,\varphi _1,\rho , {\tilde{\varGamma }}) \in \Sigma \), can be equivalently written as a minimum phase system (11) with \(({\tilde{d}}, {\tilde{F}}, {\tilde{T}}, {\tilde{\varGamma }}) \in {\mathcal {N}}^{m,r}\).
As a direct consequence of the pre-compensator’s design, namely to be of funnel type, we have the following result.
Corollary 3.9
We use the notation and assumptions from Theorem 3.8. Then, for any \(u \in {\mathcal {L}}_\mathrm{loc}^\infty (\mathbb {R}_{\ge 0}\rightarrow \mathbb {R}^m)\) and any solution of (2), (3) with initial conditions (10) we have
Proof
The prescribed transient behaviour (12) follows directly from an iterative application of [13, Prop. 1]. \(\square \)
Remark 3.10
A careful inspection of the proof of Theorem 3.8 reveals that conditions (A.2) – (A.4) on the design parameters are sufficient but far from necessary. Condition (A.4) on the norm of the matrix \({G = I_m - \varGamma {\tilde{\varGamma }}^{-1}}\) can be interpreted as a “small gain condition" as conjectured in [13, Rem. 4]; roughly speaking it means “choose the matrix \({\tilde{\varGamma }}\) close enough to the matrix \(\varGamma \)". Examining the proof shows that this condition plays a crucial role in the estimations (26) and (43); however, it allows for various reformulations and small changes which still are sufficient to prove the theorem; especially, the condition \(\Vert G\Vert < \rho /(4\rho ^2(\rho +1)^{r-2} -1)\) has many varieties—we cannot claim having found the weakest. If \(\varGamma \) is known, the simple choice \({\tilde{\varGamma }} = \varGamma \) is feasible and the proof simplifies significantly; moreover, in this case (A.3) & (A.4) are satisfied at once. However, in general the matrix \(\varGamma \) is not (or only partially) known and hence verification of conditions (A.3) and (A.4) causes problems. In such general cases methods for parameter identification can be useful. For linear systems of type (4) there is plenty of literature on system identification, see for instance [15, 40], and the recent work [45] where under the assumptions of controllability and persistently exciting inputs system identification is performed; in [46] the estimated parameters result from a least square problem. Note that although the system identification in [45, 46] is developed for time-discrete linear systems the results can be applied to time-continuous linear systems to some extend, see, e.g. [15, Sec. 1]. In [23], parameter identification for nonlinear systems is studied, where under a identifiability condition and with the aid of a high-gain observer system parameters are identified. In [22], an extended high-gain observer is introduced to identify the state and the unknown parameters dynamically; and in the recent (rather technical) work [33], parameter identification via an adaption scheme for nonlinear systems is proposed and an error bound between the nominal and the estimated parameter is given. However, the approaches [22, 23, 33] involve the system equations and hence the parameter identification is not model free. Nevertheless, if a model is available an extension of [33, Prop. 2.1] to matrix valued parameters may yield error bounds such that the stronger version of (A.4)
can ensured to be satisfied.
Remark 3.11
If the first \(k \le r-1\), derivatives of the output signal y(t) are known, the funnel pre-compensator can be applied to \(y^{(k)}(t)\). Then, the condition \(T \in {\mathcal {T}}^{{rm},q}_{\sigma ,1}\) in Theorem 3.8 becomes the relaxed condition \(T \in {\mathcal {T}}^{{rm},q}_{\sigma ,k}\). Moreover, the error bound tightens and we have
Remark 3.12
Although the funnel pre-compensator introduced in [13] may take signals y and u with different dimensions, the system class \({\mathcal {N}}^{m,r}\) under consideration is restricted to systems where the input and output have the same dimension; this comes into play when applying control schemes to the conjunction of a minimum phase system with a cascade of funnel pre-compensators, see Sect. 4. However, a careful inspection of the proof of Theorem 3.8 yields that an extension of Theorem 3.8 to systems with different input (\(u :\mathbb {R}_{\ge 0}\rightarrow \mathbb {R}^m\)) and output (\(y: \mathbb {R}_{\ge 0}\rightarrow \mathbb {R}^p\)) dimensions is possible, if \(m > p\). In the case \(m < p\) (less inputs than outputs) with \({{\,\mathrm{\mathrm rk}\,}}\varGamma = {{\,\mathrm{\mathrm rk}\,}}{\tilde{\varGamma }} = m\) one would require the matrix product \(\varGamma {\tilde{\varGamma }}^\dagger \in \mathbb {R}^{p \times p}\) (\({\tilde{\varGamma }}^\dagger \) denotes a pseudoinverse of \({\tilde{\varGamma }}\)) to be strictly positive definite; however, since \({{\,\mathrm{\mathrm rk}\,}}(\varGamma {\tilde{\varGamma }}^\dagger ) \le \min \{ m,p \} < p\) only positive semi-definiteness can be demanded which is not sufficient. If \( m > p\) (more inputs than outputs) the proof of Theorem 3.8 can be adapted such that the statement is still true in the following two cases:
-
(i)
Known \(m-p\) entries of the input are set to zero, w.l.o.g. the last \(m-p\). Therefore, \(\varGamma u(t) = \varGamma _p (u_1(t), \ldots , u_p(t))^\top \), where \(\varGamma _p = \varGamma _p^\top \in \mathbb {R}^{p \times p}\) and sign definiteness is required. Then, conditions (A.3) & (A.4) have to be satisfied for \(\varGamma _p\) and \({\tilde{\varGamma }}_p\).
-
(ii)
The system itself ignores known \(m-p\) entries of the input (w.l.o.g. the last \(m-p\)), i.e. \(\varGamma = [\varGamma _p, 0]\), where \(\varGamma _p = \varGamma _p^\top \in \mathbb {R}^{p \times p} \) and sign definiteness is required. Then, \(\varGamma u(t) = \varGamma _p (u_1(t),\ldots ,u_p(t))^\top \). Choosing \({\tilde{\varGamma }} = [{\tilde{\varGamma }}_p, 0]\) with \({\tilde{\varGamma }}_p = {\tilde{\varGamma }}_p^\top > 0\), conditions (A.3) & (A.4) have to be satisfied for \(\varGamma _p\) and \({\tilde{\varGamma }}_p\).
In both cases, the respective transformations in Step 1 of the proof are feasible and the proof of Theorem 3.8 can be done with corresponding matrices \(\varGamma _p\) and \({\tilde{\varGamma }}_p\).
5 Output feedback control
In this section, we discuss the combination of the funnel pre-compensator with feedback control schemes. Theorem 3.8 yields that the conjunction of a minimum phase system (3) with a cascade of funnel pre-compensators (2) is again a minimum phase system and hence amenable to funnel control; for funnel control schemes for systems with higher relative degree see, e.g. [10, 30] and the recent work [8]. We show that the combination of the funnel pre-compensator with a funnel control scheme achieves output tracking with prescribed transient behaviour of the tracking error via output feedback only. This resolves the long-standing open problem that for the application of funnel controller to systems with higher relative degree the derivatives of the output are required to be known.
Compared to the control scheme in [10]—involving high derivatives of virtual error variables which need to be calculated before implementation—the control scheme from [8] is much easier to implement. Therefore, along with other benefits (see Remark 4.5 below) we recall the funnel control scheme from [8, Thm. 1.9]. For \(e(t) := z(t) - y_\mathrm{ref}(t) \in \mathbb {R}^m\) define \(\mathbf{e }(t) := (e^{(0)}(t)^\top ,\ldots ,e^{(r-1)}(t)^\top )^\top \in \mathbb {R}^{rm} \), this is, the instant error vector between the signal z and the reference signal \(y_{\mathrm{ref}}\) and their derivatives, respectively. Next, the control parameters are chosen. The funnel function \(\phi \) belongs to the set
where \(\text {AC}_{\mathrm{loc}}(\mathbb {R}_{\ge 0}\rightarrow \mathbb {R})\) denotes the set of locally absolutely continuous functions \(f:\mathbb {R}_{\ge 0}\rightarrow \mathbb {R}\); \(N \in {\mathcal {C}}(\mathbb {R}_{\ge 0}\rightarrow \mathbb {R})\) is a surjection, \(\alpha \in {\mathcal {C}}^1([0,1), [1,\infty ))\) is a bijection, and for \({\mathcal {B}}:= \left\{ \, w \in \mathbb {R}^m\, \left| \, \Vert w\Vert < 1 \right. \right\} \) the function \({\gamma : {\mathcal {B}}\rightarrow \mathbb {R}^m, \ w \mapsto \alpha (\Vert w\Vert ^2)w}\) is defined. Further, recursively the maps \(\rho _k : {\mathcal {D}}_k \rightarrow {\mathcal {B}}\), \(k=1,\ldots ,r\) are defined as follows
Then, the funnel control scheme from [8, Sec. 1.4, Eqt. (9)] is given by
Remark 4.1
Since by (A.3) we have \({\tilde{\varGamma }} > 0\) according to [8, Rem. 1.8.(b)] the simple choice \(N(s) = -s\) is feasible. Moreover, similar to the gain functions \(h_i\) in (2) we may choose \(\alpha (s) = 1/(1-s)\) by which the control scheme is given by
Now, if the reference trajectory satisfies
we have the following result.
Corollary 4.2
Consider a system (3) with \((d,f,T,\varGamma ) \in {\mathcal {N}}^{m,r}_1\) and \(y^0 \in {\mathcal {W}}^{r-1,\infty }([-\tau ,0] \rightarrow \mathbb {R}^m)\) in conjunction with a cascade of funnel pre-compensators (2) with \((a,p,\varphi ,\varphi _1,\rho ,{\tilde{\varGamma }}) \in \Sigma \). Furthermore, assume the initial conditions (10) in Theorem 3.8 are satisfied. Moreover, let \(\phi \in \varPhi _{\mathrm{FC}}\) and assume that for the pre-compensator’s output \(z := z_{r-1,1}\) the funnel control initial value constraint
is satisfied. Then, if (15) is satisfied, the funnel controller (13), with input \(z = z_{r-1,1}\) from (2), applied to system (3) yields an initial-value problem, which has a solution, and every solution can be extended to a maximal solution \((y,\zeta ): [-\tau ,\omega ) \rightarrow \mathbb {R}^{m} \times \mathbb {R}^{rm(r-1)}\), where \(\omega \in (0,\infty ]\) and \(\zeta =(z_{1,1}^\top ,\ldots ,z_{r-1,r}^\top )^\top \in \mathbb {R}^{m(r-1)r}\), and the maximal solution has the properties
-
i)
the solution is global, this is \(\omega = \infty \),
-
ii)
the input u, the compensator states \(\zeta \), the pre-compensator gain functions \(h_1,\ldots ,h_{r-1}\), and the original system’s output and its derivatives \(y,\dot{y},\ldots ,y^{(r-1)}\) are bounded, this is, for all \(i=1,\ldots ,r-1\) we have \(u \in {\mathcal {L}}^\infty (\mathbb {R}_{\ge 0}\rightarrow \mathbb {R}^m)\), \(\zeta \in {\mathcal {L}}^\infty (\mathbb {R}_{\ge 0}\rightarrow \mathbb {R}^{m(r-1)r})\), \(h_i \in {\mathcal {L}}^\infty (\mathbb {R}_{\ge 0}\rightarrow \mathbb {R})\), \(y \in {\mathcal {W}}^{r, \infty }(\mathbb {R}_{\ge 0}\rightarrow \mathbb {R}^m)\),
-
iii)
the errors evolve in their respective performance funnels, this is
$$\begin{aligned} \begin{aligned} \exists \, \varepsilon _1> 0 \ \forall \, t> 0: \&\Vert y(t) - z_{1,1}(t) \Vert< \varphi _1(t)^{-1} - \varepsilon _1 , \\ \forall \, i=2,\ldots ,r-1 \ \exists \, \varepsilon _i> 0 \ \forall \, t> 0: \&\Vert z_{i-1,1}(t) - z_{i,1}(t) \Vert< \varphi (t)^{-1} - \varepsilon _i , \\ \exists \, \beta> 0 \ \forall \, t > 0: \&\Vert z(t) - y_{\mathrm{ref}}(t) \Vert < \phi (t)^{-1} - \beta . \end{aligned} \end{aligned}$$
In particular, with \(\varepsilon := \sum _{i=1}^{r-1} \varepsilon _i\), the tracking error \(y - y_{\mathrm{ref}}\) evolves within a prescribed funnel, this is
Proof
Theorem 3.8 yields that a system (3) with \((d,f,T,\varGamma ) \in {\mathcal {N}}^{m,r}_1\) in conjunction with a cascade of funnel pre-compensators (2) with \((a,p,\varphi ,\varphi _1,\rho ,{\tilde{\varGamma }}) \in \Sigma \) results in a minimum phase system with \(({\tilde{d}}, {\tilde{F}}, {\tilde{T}}, {\tilde{\varGamma }}) \in {\mathcal {N}}^{m,r}\), and the respective aspects of assertions \( ii)~ \& ~iii)\), namely concerning \(\zeta , h_i\), are true; hence, the conjunction belongs to the system class under consideration in [8]. Then, [8, Thm. 1.9] is applicable and yields the remaining aspects of assertions \(i)-iii)\). Furthermore, the transient behaviour of the tracking error \(y-y_\mathrm{ref}\) is a direct consequence of iii). \(\square \)
Remark 4.3
Recalling Remark 3.7, we highlight that Corollary 4.2 guarantees for a large class of systems output tracking with prescribed transient behaviour of the tracking error via output feedback only; note that this result applies to single-input, single-output systems as well as to multi-input, multi-output systems. The controller proposed in [20] as well achieves output tracking with prescribed performance of the error via output feedback for minimum phase multi-input, multi-output systems of arbitrary relative degree; in particular, this controller as well as the control scheme (13) is applicable to linear minimum phase systems. However, as it involves a high-gain observer structure, the controller from [20] suffers from the problem of proper initializing, i.e. some parameters have to be chosen large enough in advance, however, it is not clear how large. Contrary, conditions (A.1)–(A.4) explicitly determine the set \(\Sigma \) of feasible design parameters of the funnel pre-compensator. This resolves a long-standing problem in the field of high-gain-based output feedback control with prescribed transient behaviour.
Remark 4.4
An application of the funnel pre-compensator to linear non-minimum phase system under consideration in [4] allows output feedback tracking for a certain class of linear non-minimum phase systems with the controller scheme proposed in [4, Sec. 3]. However, in combination with the funnel pre-compensator the bound of the tracking error discussed in [4, Sec. 4] is not valid any more. For deeper insights regarding output tracking of linear non-minimum phase systems see [4].
Remark 4.5
We highlight two important aspects. First, according to [8, Sec. 1.4], in particular [8, Rem. 1.7 (c)] tracking of a given reference is also possible, if the number of the available derivatives of the reference signal is smaller than the relative degree. This means the following. Let \({\hat{r}} \) be the number of derivatives of the reference signal \(y_{\mathrm{ref}}\) available for the feedback controller. Then, with the control scheme (13) output tracking with prescribed transient behaviour of the tracking error is possible in the case \({\hat{r}} < r\). Second, in the case \({\hat{r}} = r\) exact asymptotic tracking can be achieved, see [8, Rem. 1.7 (f)]. In the present context, this means \(\lim _{t \rightarrow \infty } (z(t)-y_{\mathrm{ref}}(t)) = 0\), however, \(\lim _{t \rightarrow \infty } (y(t) - z(t)) = 0\) cannot be guaranteed since \(\varphi \in \varPhi _r\). Note that, while the second aspect is of limited practical interest (see also [8, Sec. 1.1]), the first aspect allows, for instance, target tracking of a given “smooth" trajectory, the derivatives of which are as unknown as the derivatives of the system.
Remark 4.6
Remark 3.11 applies also for output tracking, i.e. if the first \({k \le r-1}\) derivatives of the output signal y(t) are known, the pre-compensator takes the signal \(y^{(k)}(t)\) which results in a tighter funnel boundary of the tracking error \({y - y_{\mathrm{ref}}}\). Moreover, in this case we only require \(T \in {\mathcal {T}}^{{rm},q}_{\sigma ,k}\), this is, the funnel pre-compensator is applied to systems with \((d,f,T,\varGamma ) \in {\mathcal {N}}^{m,r}_k\).
6 Simulations
In this section, we provide simulations of the funnel pre-compensator and its applications. First, we consider the pure functionality of the funnel pre-compensator applied to signals \((u,y) \in {\mathcal {P}}_r\). Second, we simulate output tracking via funnel control. To this end, we apply a funnel control scheme to the conjunction of a cascade of funnel pre-compensators with a minimum phase system.
Example 5.1
We give an illustrative example how the funnel pre-compensator works. Moreover, we qualitatively compare the influence of the pre-compensator’s parameters to its performance. We choose the signals
and, since \((u,y) \in {\mathcal {C}}^\infty (\mathbb {R}_{\ge 0}\rightarrow \mathbb {R}) \times {\mathcal {C}}^\infty (\mathbb {R}_{\ge 0}\rightarrow \mathbb {R})\), we choose to simulate the application of the cascade of funnel pre-compensators (2) for the case \(r=3\). For the funnel pre-compensator we initially choose a Hurwitz polynomial, i.e. a polynomial whose roots have strict negative real part, by which the matrix \(A \in \mathbb {R}^{3 \times 3}\) from (A.1) is determined via the polynomial’s coefficients, cf. Remark 3.4. Since it turned out that the parameters \(a_i\) influence the pre-compensator’s performance the most we compare three sets of these parameters. To this end, we choose the Hurwitz polynomials
by which we obtain corresponding matrices
which means \(a_1 = 3\), \(a_2 = 3\), \(a_3 = 1\), \(b_1 = 9\), \(b_2 = 27\), \(b_3 = 27\), and \(c_1 = 15\), \(c_2 = 75\), \(c_3 = 125\). Choosing \(Q := I_3\) the respective Lyapunov matrix \(P_i\), \({i\in \{A,B,C\}}\) is given as
from which \(p_1^a = 1\), \(p_2^a = 2/3\), \(p_3^a = 1/3\) , \(p_1^b = 1\), \(p_2^b = 1037/481\), \(p_3^b = 1787/711\), and \(p_1^c = 1\), \(p_2^c = 1383/391\), \(p_3^c = 2230/333\). Further, we choose the funnel function \(\varphi (t) = (e^{-2t} + 0.05)^{-1}\), and \(\varphi _1(t) = \varphi (t)/\rho \) for \(\rho = 1.5\). Finally, we choose \(z_{i,j}(0) = 0\) for all \(i=1,2\), \(j=1,2,3\) by which the conditions on the initial values in [13, Thm. 1] are satisfied. We run the simulation over the time interval 0–10 s. The outcome is depicted in Fig. 4.
Figure 4a shows the signal y and the pre-compensator’s output \(z_A, z_B, z_C\), respectively. The “quality" of the approximation depends strongly on the choice of the parameters \(a_i\) satisfying (A.1). While in the first case the signal y and \(z_A\) differ quite much, in the second case the approximation is much better, and in the third case the signal y and the output \(z_C\) are almost identical which means that the approximation of the given signal by the funnel pre-compensator is pretty good. Figure 4b shows the error between the signal y and the pre-compensator’s output, respectively. Here, the aforesaid crystallizes from the viewpoint of errors, which are quite different. However, we highlight that in all three cases the error evolves within the prescribed funnel boundaries and hence all approximations \(z_A, z_B, z_C\) of the signal y are at least as good as a “predetermined quality". The simulation has been performed in Matlab (solver: ode23tb).
Next, we apply the funnel control scheme (14) to the conjunction of a cascade of funnel pre-compensators (2) with a minimum phase system (3) to achieve output tracking with prescribed transient behaviour of the tracking error via output feedback only, i.e. we illustrate an application of Corollary 4.2. We emphasize that the funnel pre-compensator receives only the measurement of the output signal y of the system under consideration. Then, the applied controller (14) takes the pre-compensator’s output z and its derivatives which are known explicitly.
Example 5.2
Since the application of the funnel pre-compensator to the standard illustrative example mass on a car system from [42] was already discussed in detail in [13, Sec. 5.1], and the application of the controller (13) to this particular example was elaborated in [8, Sec. 3.1], we consider the following artificial, in particular, nonlinear multi-input multi-output ODE of relative degree \(r=3\) with \(m=2\) and initial conditions \(y|_{[-\tau ,0]} \equiv 0 \in \mathbb {R}^2\) for some \(\tau >0\),
where
and for \(d = (d_1,d_2)^\top \), \(\xi _{i} = (\xi _{i,1},\xi _{i,2})^\top \), \(i=1,2,3\)
whereby the internal dynamics are bounded-input bounded-state stable and the associated operator T belongs to the class \({\mathcal {T}}^{6,3}_{\tau ,1}\). The disturbance is chosen as \(d : \mathbb {R}_{\ge 0}\rightarrow \mathbb {R}^2\), \( t \mapsto (0.2 \sin (5t) + 0.2 \cos (7t), \, 0.25 \sin (9t) + 0.2 \cos (3t))^\top \) by which \(d \in {\mathcal {L}}^\infty (\mathbb {R}_{\ge 0}\rightarrow \mathbb {R})\) and hence \((d,f,T,\varGamma ) \in {\mathcal {N}}^{2,3}_1\). For the funnel pre-compensator, we choose the Hurwitz polynomial \((s+s_0)^3\) with \(s_0 = 7\) and \(Q = I_3\) to determine matrices A and P satisfying (A.1) and obtain the respective parameters \(a_1 = 21\), \(a_2 = 147\), \(a_3 = 343\) and \(p_1 = 1\), \(p_2 = 1180/241\), \(p_3 = 1742/135\). We choose the pre-compensator’s funnel function \(\varphi (t) = (e^{-3t} + 0.05 )^{-1}\), and for \({\tilde{\varGamma }} = 2 \cdot I_2\) with \(\rho = 1.1\) conditions (A.3) & (A.4) are satisfied. We stress that \(\varGamma \) and \({\tilde{\varGamma }}\) are quite different; while \(\varGamma \) distributes both input signals \((u_1,u_2)\) to both output directions \((y_1,y_2)\), \({\tilde{\varGamma }}\) only allocates the input signal \(u_i\) to output direction \(y_i\), \(i=1,2\). Next, we choose the controller’s funnel function \(\phi _{\mathrm{FC}}(t) = (2e^{-t} + 0.05 )^{-1}\). Then, with \(z_{i,j}(0) = 0\), \(i=1,2\), \(j=1,2,3\) the assumptions on the initial values from Corollary 4.2 are satisfied. Further, we choose the reference trajectory as \(y_{\mathrm{ref}}: \mathbb {R}_{\ge 0}\rightarrow \mathbb {R}^2\), \(t \mapsto (e^{-(t-5)^2}, \, \sin (t) )^\top \). We simulate the output tracking over a time interval 0–10 s. In order to illustrate the funnel pre-compensator’s contribution, we compare the two cases, first, if the derivatives of the output of system (16) are available to the controller and second, if not. The outcomes of the simulations are depicted in Fig. 5, where the output’s subscript \(\mathrm FC\) (\(y_{\mathrm{FC}}\)) denotes the case when the derivatives of the system are available, i.e. the funnel pre-compensator is not necessary and hence not present; and the subscript \(\mathrm FPC\) (\(y_{\mathrm{FPC}}\)) indicates the situation when the system’s output is approximated by the pre-compensator and the derivatives of the latter are handed over to the controller.
Output reference tracking of the nonlinear multi-input multi-output minimum phase system (16) via output feedback
Figure 5a shows the tracking error between the system’s output \(y_i\) and the reference trajectory \(y_\mathrm{ref,i}\), \(i=1,2\), in both cases, respectively. Note that in the case when the derivatives of the system’s output are available the error evolves within the funnel boundaries defined by \(1/\phi _{FC}\) as expectable from the results in [8, Thm. 1.9]. We emphasize that in the second case (the derivatives of the system’s output are not available) the transient behaviour of the tracking error can be guaranteed to evolve within the boundaries \( (\rho + r-2)/\varphi + 1/\phi _{\mathrm{FC}} = {(\rho +1)/\varphi + 1/\phi _{\mathrm{FC}}}\), where \(r=3\) and \(\rho =1.1\) in this particular example. Moreover, we can observe that even in the latter case the error evolves within the boundaries of \(1/\phi _{\mathrm{PC}}\). Figure 5b shows the control input \(u_i\), \(i=1,2\), generated by (14), respectively. Both signals show oscillations which arise from the influence of the disturbance d, i.e. the controller compensates the disturbance’s affect to the system. Analogously to the approximation performance discussed in the previous Example 5.1, the tracking performance (and so the input signal u) strongly depends on the choice of the pre-compensator’s parameters, this is, on the choice of A (for fixed \(Q = I_m\)) and can be improved with larger values of \(s_0\). The simulations have been performed in Matlab (solver: ode45, rel. tol: \(10^{-6}\), abs. tol: \(10^{-6}\)).
7 Conclusion
In the present article, we showed that the conjunction of the funnel pre-compensator with a minimum phase system of arbitrary relative degree results in a minimum phase system of the same relative degree. This resolves the open question raised in [13] where the funnel pre-compensator was introduced and the aforesaid was proven for the special case of relative degree two. Using the fact that the derivatives of the pre-compensator’s output are known explicitly, we showed that output reference tracking with prescribed transient behaviour using funnel-based feedback control schemes is possible with output feedback only. In particular, output tracking with unknown output derivatives is possible for the class of linear minimum phase systems (4); moreover, for a class of linear non-minimum phase systems (single-input, single-output systems as well as multi-input, multi-output systems). Since the investigations in the recent works [9] and [6] show applicability of existing control techniques to nonlinear non-minimum phase systems, we are confident that an integration of the funnel pre-compensator into this particular context will also be fruitful.
Now, in future research we will investigate the extension of the present results to a larger class of systems, in particular, systems with \((d,f,T,\varGamma ) \in {\mathcal {N}}^{m,r}\) will be focused; furthermore, systems which are not linear affine in the control term will be investigated.
References
Bechlioulis CP, Rovithakis GA (2009) Adaptive control with guaranteed transient and steady state tracking error bounds for strict feedback systems. Automatica 45(2):532–538
Bechlioulis CP, Rovithakis GA (2014) A low-complexity global approximation-free control scheme with prescribed performance for unknown pure feedback systems. Automatica 50(4):1217–1226
Berger T (2014) On differential-algebraic control systems. Ph.D. thesis, Institut für Mathematik, Technische Universität Ilmenau, Universitätsverlag Ilmenau, Germany . https://www.db-thueringen.de/receive/dbt_mods_00023107
Berger T (2020) Tracking with prescribed performance for linear non-minimum phase systems. Automatica 115:10899. https://doi.org/10.1016/j.automatica.2020.108909
Berger T (2021) Fault-tolerant funnel control for uncertain linear systems. IEEE Trans Autom Control 66(9):4349–4356. https://doi.org/10.1109/tac.2020.3030759
Berger T, Drücker S, Lanza L, Reis T, Seifried R (2021) Tracking control for underactuated non-minimum phase multibody systems. Nonlinear Dyn 104(4):3671–3699. https://doi.org/10.1007/s11071-021-06458-4
Berger T, Ilchmann A, Reis T (2014) Funnel control for nonlinear functional differential-algebraic systems. In: Proceedings of the MTNS 2014. Groningen, pp 46–53
Berger T, Ilchmann A, Ryan EP (2021) Funnel control of nonlinear systems. Math Control Signals Systems 33(1):151–194. https://doi.org/10.1007/s00498-021-00277-z
Berger T, Lanza L (2020) Output tracking for a non-minimum phase robotic manipulator. Submitted for publication. https://arxiv.org/abs/2001.07535
Berger T, Lê HH, Reis T (2018) Funnel control for nonlinear systems with known strict relative degree. Automatica 87:345–357. https://doi.org/10.1016/j.automatica.2017.10.017
Berger T, Reis T (2016) The funnel observer . Universität Hamburg, Hamburger Beiträge zur Angewandten Mathematik 2016-03
Berger T, Reis T (2018) Funnel control via funnel pre-compensator for minimum phase systems with relative degree two. IEEE Trans Autom Control 63(7):2264–2271. https://doi.org/10.1109/TAC.2017.2761020
Berger T, Reis T (2018) The funnel pre-compensator. Int J Robust Nonlinear Control 28(16):4747–4771. https://doi.org/10.1002/rnc.4281
Bernstein DS (2009) Matrix mathematics: theory, facts, and formulas, 2nd edn. Princeton University Press, Princeton, Oxford
Bingulac S, Sinha NK (1990) On the identification of continuous-time multivariable systems from samples of input–output data. Math Comput Model 14:203–208. https://doi.org/10.1016/0895-7177(90)90176-n
Bullinger E, Ilchmann A, Allgöwer F (1998) A simple adaptive observer for nonlinear systems. In: Huijberts HJC (ed) Proceedings of the IFAC symposium nonlinear control systems design, NOLCOS98. Pergamon, Enschede, pp 806–811
Byrnes CI, Isidori A (1991) Asymptotic stabilization of minimum phase nonlinear systems. IEEE Trans Autom Control 36(10):1122–1137
Byrnes CI, Willems JC (1984) Adaptive stabilization of multivariable linear systems. In: Proceedings of the 23rd IEEE conference decision control, pp 1574–1577
Chowdhury D, Khalil HK (2019) Funnel control for nonlinear systems with arbitrary relative degree using high-gain observers. Automatica 105:107–116. https://doi.org/10.1016/j.automatica.2019.03.012
Dimanidis IS, Bechlioulis CP, Rovithakis GA (2020) Output feedback approximation-free prescribed performance tracking control for uncertain MIMO nonlinear systems. IEEE Trans Autom Control 65(12):5058–5069. https://doi.org/10.1109/tac.2020.2970003
Esfandiari F, Khalil HK (1987) Observer-based design of uncertain systems: recovering state feedback robustness under matching conditions. In: Proceedings of allerton conference, Monticello, pp 97–106
Farza M, Menard T, Ltaief A, Maatoug T, M’Saad M, Koubaa Y (2015) Extended high gain observer design for state and parameter estimation. In: 2015 4th international conference on systems and control (ICSC). IEEE. https://doi.org/10.1109/icosc.2015.7153303
Floret-Pontet F, Lamnabhi-Lagarrigue F (2002) Parameter identification and state estimation for continuous-time nonlinear systems. In: Proceedings of the 2002 American control conference (IEEE Cat. No.CH37301). American automatic control council. https://doi.org/10.1109/acc.2002.1024836
Hackl CM (2012) Contributions to high-gain adaptive control in mechatronics. Ph.D. thesis, Fakultät für Elektrotechnik und Informationstechnik, TU München
Ilchmann A (1991) Non-identifier-based adaptive control of dynamical systems: a survey. IMA J. Math. Control Inf. 8(4):321–366
Ilchmann A (2013) Decentralized tracking of interconnected systems. In: Hüper K, Trumpf J (eds) Mathematical system theory-Festschrift in Honor of Uwe Helmke on the Occasion of his Sixtieth Birthday. CreateSpace, pp 229–245
Ilchmann A, Ryan EP (2008) High-gain control without identification: a survey. GAMM Mitt. 31(1):115–125
Ilchmann A, Ryan EP, Sangwin CJ (2002) Tracking with prescribed transient behaviour. ESAIM Control Optim. Calc. Var. 7:471–493
Ilchmann A, Ryan EP, Townsend P (2006) Tracking control with prescribed transient behaviour for systems of known relative degree. Syst. Control Lett. 55(5):396–406
Ilchmann A, Ryan EP, Townsend P (2007) Tracking with prescribed transient behavior for nonlinear systems of known relative degree. SIAM J. Control Optim. 46(1):210–230
Ilchmann A, Wirth F (2013) On minimum phase. Automatisierungstechnik 12:805–817
Isidori A (1995) Nonlinear control systems, 3rd edn. Communications and control engineering series. Springer, Berlin
Kaltenbacher B, Nguyen TTN (2021) A model reference adaptive system approach for nonlinear online parameter identification. Inverse Prob 37(5):055006. https://doi.org/10.1088/1361-6420/abf164
Khalil HK, Praly L (2014) High-gain observers in nonlinear feedback control. Int. J. Robust Nonlinear Control 24:993–1015
Khalil HK, Saberi A (1987) Adaptive stabilization of a class of nonlinear systems using high-gain feedback. IEEE Trans Autom Control 32:1031–1035
Lanza L (2021) Internal dynamics of multibody systems. Syst Control Lett. 152:104931. https://doi.org/10.1016/j.sysconle.2021.104931
Liberzon D, Trenn S (2013) The bang-bang funnel controller for uncertain nonlinear systems with arbitrary relative degree. IEEE Trans Autom Control 58(12):3126–3141
Liu YH, Su CY, Li H (2021) Adaptive output feedback funnel control of uncertain nonlinear systems with arbitrary relative degree. IEEE Trans Autom Control 66(6):2854–2860. https://doi.org/10.1109/tac.2020.3012027
Miller DE, Davison EJ (1991) An adaptive controller which provides an arbitrarily good transient and steady-state response. IEEE Trans Autom Control 36(1):68–81
Rao GP, Sivakumar L (1982) Order and parameter identification in continuous linear systems via walsh functions. Proc IEEE 70(7):764–766. https://doi.org/10.1109/proc.1982.12385
Saberi A, Sannuti P (1990) Observer design for loop transfer recovery and for uncertain dynamical systems. IEEE Trans Autom Control 35(8):878–897
Seifried R, Blajer W (2013) Analysis of servo-constraint problems for underactuated multibody systems. Mech Sci 4:113–129
Tornambè A (1988) Use of asymptotic observers having high gains in the state and parameter estimation. In: Proceedings of the 27th IEEE conference decision control, Austin, Texas, pp 1791–1794
Trentelman HL, Stoorvogel AA, Hautus MLJ (2001) Control theory for linear systems. Communications and control engineering. Springer, London. https://doi.org/10.1007/978-1-4471-0339-4
van Waarde HJ, Persis CD, Camlibel MK, Tesi P (2020) Willems’ fundamental lemma for state-space systems and its extension to multiple datasets. IEEE Control Syst Lett 4(3):602–607. https://doi.org/10.1109/lcsys.2020.2986991
Zheng Y, Li N (2021) Non-asymptotic identification of linear dynamical systems using multiple trajectories. IEEE Control Syst Lett 5(5):1693–1698. https://doi.org/10.1109/lcsys.2020.3042924
Acknowledgements
I am deeply indebted to Thomas Berger (University of Paderborn) for excellent mentoring, many fruitful discussions, helpful advices and corrections.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was supported by the German Research Foundation (Deutsche Forschungsgemeinschaft) via the Grant BE 6263/1-1.
Appendix
Appendix
Proof of Theorem 3.8
Since the special case \(r=2\) was already proven in [13, Thm. 2], we concentrate on the case \(r \ge 3\). Therefore, in the following let \(r \ge 3\). The proof is subdivided in three steps.
Step 1: We briefly present the transformations performed in [13, p. 4758–4760]. We consider the error dynamics of two successive systems. Set \(v_{i,j}(\cdot ) := z_{i-1,j}(\cdot ) - z_{i,j}(\cdot )\) for \(i=2,\ldots ,r-1\) and \(j=1,\ldots ,r\). Then,
In order to investigate the dynamics of \(v_{1,1}\), we define \(e_{1,j}(\cdot ) := y^{(j-1)}(\cdot ) - z_{1,j}(\cdot )\) for \(j=1,\ldots ,r-1\), and \(e_{1,r}(\cdot ) := y^{(r-1)}(\cdot ) - \varGamma {\tilde{\varGamma }}^{-1} z_{1,r}(\cdot )\). Then, we obtain
Now, we set \(v_{1,1}(\cdot ) := e_{1,1}(\cdot )\), and define \(\tilde{v}(\cdot ) := \sum _{i=1}^{r-1} v_{i,1}(\cdot )\) and \(v_{1,j}(\cdot ) := e_{1,j}(\cdot ) - \sum _{k=1}^{j-1} R_{r-j+k+1} \tilde{v}^{(k-1)}(\cdot )\) for \(j=2,\ldots ,r\). Then, we obtain
We record some useful observations
the following relation for \(z_{1,r}\)
and
Therefore, we have
Now, for \(G: = I - \varGamma {\tilde{\varGamma }}^{-1}\) and \(j=1,\ldots ,r-1\) we define \(w_{i,j}(\cdot ) := v_{i,j}(\cdot )\) for \(i=2,\ldots ,r-1\) and \(j=1,\ldots ,r\), and \(w_{1,r}(\cdot ) := v_{1,r}(\cdot )\). Further, for \(j=1,\ldots ,r\) we set
Next, we investigate the dynamics of \(w_{i,j}\). We set \(\tilde{w}(\cdot ) := \sum _{i=2}^{r-1} w_{i,1}(\cdot )\), and obtain, for \(i=1\)
for \(i=2\)
and for \(i=3,\ldots ,r-1\) we find
Step 2: For \({\bar{q}} = rm(r-1) + r\) we define the operator \({\tilde{T}} : {\mathcal {C}}([-\tau ,\infty ) \rightarrow \mathbb {R}^{rm}) \rightarrow {\mathcal {L}}_\mathrm{loc}^\infty (\mathbb {R}_{\ge 0}\rightarrow \mathbb {R}^{{\bar{q}}})\) as the solution operator of (17) in the following sense: for \(\xi _1,\ldots ,\xi _r \in {\mathcal {C}}([0,\infty ) \rightarrow \mathbb {R}^m)\) let \(w_{i,j} : [0,\omega ) \rightarrow \mathbb {R}^m\), \(\omega \in (0,\infty ]\) be the unique maximal solution of (17), with \(z= \xi _1, \dot{z} = \xi _2, \ldots , z^{(r-1)} = \xi _r \), and with suitable initial values \(w_{i,j}(0)\) according to the transformations. Then, we define for \(t \in [0,\omega )\)
Note, that in (17a) the terms \(y,\dot{y},\ldots , y^{(r-1)}\) can be expressed in terms of \(w_{i,j}\) and \(z,\dot{z},\ldots , z^{(r-1)}\) using \(y^{(i)} = z^{(i)} + w_{1,1}^{(i)} + \varGamma {\tilde{\varGamma }}^{-1} {\tilde{w}}^{(i)}\) and the equations (17). Now, for
where \({\tilde{\zeta }}(\cdot ) := \sum _{i=2}^{r-1}\zeta _{i,1}(\cdot )\), we have \((t,w_{1,1}(t),\ldots ,w_{r-1,r}(t)) \in {\mathcal {D}}\) for all \(t \in [0,\omega )\). Furthermore, the closure of the graph of the solution \((w_{1,1},\ldots ,w_{r-1,r})\) of (17) is not a compact subset of \({\mathcal {D}}\).
Next, we show \({\tilde{T}} \in {\mathcal {T}}^{rm,{\bar{q}}}_{\tau }\); first we show that property (a) from Definition 3.1 is satisfied. To this end, we assume that \(z,\dot{z},\ldots , z^{(r-1)}\) are bounded on \([0,\omega )\). As the solution evolves in \({\mathcal {D}}\), \(w_{1,1}- G {\tilde{w}}, w_{2,1},\ldots ,w_{r-1,1}\) are bounded. Thus, \(y = z + w_{1,1} + \varGamma {\tilde{\varGamma }}^{-1} {\tilde{w}}\) is bounded and hence \(T\left( y,\dot{y},\ldots , y^{(r-1)}\right) \) is bounded via \(T \in {\mathcal {T}}^{rm,q}_{\tau ,1}\), and therefore \(f\left( d(\cdot ),T\left( y,\dot{y},\ldots , y^{(r-1)}\right) (\cdot )\right) \) is bounded on \([0,\omega )\).
Step 2a: We show \(w_{i,j} \in {\mathcal {L}}^\infty ([0,\omega ) \rightarrow \mathbb {R}^m)\) for \(i=1,\ldots ,r-1\) and \(j=1,\ldots ,r\). We set \(w_i := (w_{i,1}^\top ,\ldots ,w_{i,r}^\top )^\top \in \mathbb {R}^{rm}\) for \(i=1,\ldots ,r-1\) and \({\bar{w}} := w_{1,1} - G {\tilde{w}}\). For corresponding matrices A, Q, P from satisfying (A.1), using the Kronecker matrix product, we define
Then, using [14, Fact 7.4.34], we have \(\sigma ({\hat{A}}) = \sigma (A)\), \(\sigma ({\hat{P}}) = \sigma (P)\) and \(\sigma ({\hat{Q}}) = \sigma (Q)\), and
Furthermore, for \(p_1,\ldots ,p_r\) from (A.1), setting \({\bar{P}} := (p_1,\ldots ,p_{r})^\top \otimes I_m\) we have
where \({\tilde{p}} := P_1 - P_2 P_4^{-1} P_2^\top > 0\). Then, we may rewrite (17) as
for \(i=3,\ldots ,r-1\) and suitable bounded functions \(B_1, B_2, B_i \in {\mathcal {L}}^\infty ([0,\omega ) \rightarrow \mathbb {R}^{rm})\), respectively.
Seeking a suitable Lyapunov function for the overall system (21), we define with \( {\hat{P}}\) from (18)
which is possible since (A.3) is satisfied by assumption. Observe \(P_1 = P_1^\top > 0\) and, recalling \({\hat{P}} \bar{P} = [{\tilde{p}} I_m,0,\ldots ,0]^\top \in \mathbb {R}^{rm \times m}\) via (20), we have
Since for all \(M \in \mathbb {R}^{m \times m}\) we have \({\hat{A}} (I_r \otimes M) = (I_r \otimes M) {\hat{A}}\), \({\hat{A}}^\top (I_r \otimes M) = (I_r \otimes M) {\hat{A}}^\top \) we obtain
and respective for \({\hat{P}}_1 {\hat{A}}\). Therefore,
where \({\hat{Q}}_1 = {\hat{Q}}_1^\top \) by (A.3), and \({\hat{Q}}_1 > 0\) via (19) and (A.3). We define
and set \(w := (w_1^\top ,\ldots ,w_{r-1}^\top )^\top \in \mathbb {R}^{m r(r-1)}\).
Now, we consider the Lyapunov function candidate
and study its evolution along the solution trajectories of the respective differential equations (21). We fix \(\theta \in (0,\omega )\) and note that \(w_i \in {\mathcal {L}}^\infty ([0,\theta ) \rightarrow \mathbb {R}^{rm})\) for all \(i=1,\ldots ,r-1\). Using (22) and (23), we obtain for \(t \in [\theta , \omega )\)
where \(\lambda _{\mathrm{min}}({\hat{Q}}), \lambda _{\mathrm{min}}({\hat{Q}}_1)\) denotes the smallest eigenvalue of \({\hat{Q}}\) and \({\hat{Q}}_1\), respectively.
In order to proceed with the estimation of each term in (24), we record the following observation. Due to (A.2) we have for \(i=2,\ldots ,r-2\) and \(t \in [\theta ,\omega )\)
We recall \({\bar{w}}(\cdot ) = w_{1,1}(\cdot ) - G{\tilde{w}}(\cdot )\) and observe \(\Vert w_{2,1}(t)\Vert < \varphi (t)^{-1}\) and \(\Vert {\tilde{w}}(t) \Vert < \sum _{i=2}^{r-1}\varphi (t)^{-1} = (r-2) \varphi (t)^{-1}\) for \(t \in [\theta ,\omega )\). Therefore, we obtain for \(t \in [\theta , \omega )\)
We set
Then, using \(2ab \le 2a^2 + \tfrac{1}{2}b^2\) for \(a,b \in \mathbb {R}\), we may estimate (24) with the aid of (25) and (26) for \(t \in [\theta ,\omega )\)
where \(\mu := \tfrac{\min \{\lambda _{\mathrm{min}}({\hat{Q}}), \lambda _\mathrm{min}({\hat{Q}}_1)\}}{\lambda _{\mathrm{max}}({\mathcal {P}})} = \tfrac{\min \{\lambda _{\mathrm{min}}({\hat{Q}}), \lambda _{\mathrm{min}}({\hat{Q}}_1)\}}{\max \{\lambda _{\mathrm{max}}({\hat{P}}),\lambda _{\mathrm{max}}(P_1)\}}> 0\). With the aid of Grönwall’s lemma we obtain
and therefore,
Inequality (27) implies \(w \in {\mathcal {L}}^\infty \left( [\theta ,\omega ) \rightarrow \mathbb {R}^{rm(r-1)}\right) \) and hence we have \(w_i \in {\mathcal {L}}^\infty ([0,\omega ) \rightarrow \mathbb {R}^{rm})\) for all \(i=1,\ldots ,r-1\). In particular, we obtain \({\bar{w}} \in {\mathcal {L}}^\infty ([0,\omega ) \rightarrow \mathbb {R}^m)\).
Step 2b: We show \(h_i \in {\mathcal {L}}^\infty ([0,\omega ) \rightarrow \mathbb {R})\), for all \(i=1,\ldots ,r-1\). For the sake of better legibility we set \(x_1(\cdot ) := {\bar{w}}(\cdot )\) and \(x_i(\cdot ) := w_{i,1}(\cdot )\) for \(i=2,\ldots ,r-1\). Observing \(- \varGamma {\tilde{\varGamma }}^{-1} - G = -\varGamma {\tilde{\varGamma }}^{-1} - (I- \varGamma {\tilde{\varGamma }}^{-1}) = -I_m\), and setting \({\tilde{w}}_2(\cdot ) := \sum _{i=2}^{r-1} w_{i,2}(\cdot )\) we obtain via (17)
Since \(p_1 =1\), using (17) and (28) we have for \(t \in [0,\omega )\) and \(i=2,\ldots ,r-1\)
for suitable functions \(b_i \in {\mathcal {L}}^\infty ([0,\omega ) \rightarrow \mathbb {R}^m)\), \(i=1,\ldots ,r-1\), respectively. We observe that in (29) for all \(i=2,\ldots ,r-1\) the \(i^\mathrm{th}\) differential equation depends on the preceding gain function \(h_{i-1}\), respectively, and the first differential equation depends on the last gain function \(h_{r-1}\). Therefore, we cannot apply standard funnel argumentation to show boundedness of the gain functions, cf. [28, p. 484–485], [26, p. 241–242] or [10, p. 350–351]. However, on closer examination of the respective proofs in the aforementioned references we may retain the following. Due to the shape of the gain function \(h_i\), boundedness of \(h_i\) on \([0,\omega )\) is equivalent to the existence of \({\nu _i > 0}\) such that for all \(t \in [0,\omega )\) we have \({\varphi (t)^{-1} - \Vert x_i(t)\Vert \ge \nu _i}\), \(i=2,\ldots ,r-1\) (\({\varphi _1(t)^{-1} - \Vert x_1(t)\Vert \ge \nu _1}\)), respectively. Moreover, via the loop structure in (29) it suffices to show boundedness of one gain function, which implies boundedness of all remaining.
We define \(\psi _1(\cdot ) := \varphi _1(\cdot )^{-1}\), \(\psi (\cdot ) := \varphi (\cdot )^{-1}\), set \(\lambda _1 := \inf _{s \in (0,\omega )} \psi _1(s) > 0\) and \(\lambda := \inf _{s \in (0,\omega )} \psi (s) > 0\), and fix \(\beta \in (0,\omega )\). Since \(\liminf _{t \rightarrow \infty } \varphi (t) > 0\) and \({\dot{\varphi }}(\cdot )\) is bounded, we have that \(\tfrac{\text { d}}{\text { d}t}\psi |_{[\beta , \infty )}(\cdot )\) is bounded, and respective for \(\tfrac{\text { d}}{\text { d}t}\psi _1|_{[\beta , \infty )}(\cdot )\). Thus, there exists a Lipschitz bound \(L > 0\) of \(\psi |_{[\beta ,\infty )}(\cdot )\), and \(L_1\) of \(\psi _{1}|_{[\beta ,\infty )}(\cdot )\). For \(\rho >1\) as in (A.2) we fix \(\delta > 0\) as
and define
With this we choose
small enough such that for \(\Delta _1, \, \Delta > 0\) from (31)
Note that \(L_1, L\) are well defined since \(\Delta _1, \, \Delta > 0\) and \(\rho > \Vert G\Vert \). Further, since \(\rho > 1\) we choose \({\hat{\delta }} \) such that
With this we define
Note that these definitions imply \(\kappa _{r-1}< \kappa _{r-2}< \cdots< \kappa _2 < \kappa _1\). We show that for all \(t \in [0,\omega )\) we have \(\psi _1(t) - \Vert x_1(t)\Vert \ge \kappa _1\) and \(\psi (t) - \Vert x_i(t)\Vert \ge \kappa _i\) for all \(i=2,\ldots ,r-1\); which is true on \((0,\beta ]\) by definition of \(\kappa \). We set
where the infimum of the empty set is infinity as usual. Seeking a contradiction, we suppose that \(t_0^\ell < \infty \) for some \(\ell \in \{1,\ldots ,r-1\}\). Then, either
or
If (35b) is true, we decrease \({\hat{\delta }}\) and obtain \(t_0^1 < t_0^{r-1}\); therefore without loss of generality, we may assume that (35a) is true. We set \(t_0 := t_0^\ell \), i.e. \(t_0\) denotes the moment of the very first complete excess of \(\kappa _\ell \), and distinguish three cases, namely either \(\ell = 1\), or \(\ell =2\), or \(3 \le \ell \le r-1\).
If \(\ell = 1\) there may occur two possible cases, namely either
or
First, we draw our attention to case (36a) and observe
and thus, using (A.2),
Then, due to the definition of \(t_0\), there exists \( t_1 \in (t_0, \omega )\) such that \(\psi _1( t_1) - \Vert x_1 ( t_1) \Vert < \kappa _1\), and
Thus, we readily deduce the following relations for \(t \in [t_0, t_1]\)
We consider the first equation in (29) for \(t \in [t_0, t_1]\)
Via condition (A.2) and relation (37) we obtain for \(t \in [t_0, t_1]\)
Hence, using the estimation above and the relations from (38) we estimate the first equation in (29) for \(t \in [t_0, t_1]\)
From this we calculate
and therefore,
a contradiction. Now, we consider the case (36b) where by \(t_0 = t_0^1 < t_0^{r-1}\)
This, together with the definition of \(t_0\) implies the existence of \(t_1 \in (t_0,t_0^{r-1})\) such that
from which we obtain for \(t \in [t_0,t_1]\)
and therefore,
the last inequality via
where we used \(\kappa _1 < \tfrac{\lambda _1}{\rho +1}\) in the last step. Furthermore, recalling \(h_{r-1}\) and using the definition of \(\kappa _1\) and \( \kappa _{r-1}\) we deduce for \(t \in [t_0,t_1]\)
and hence for \(t \in [t_0,t_1]\) we have
We consider the first equation in (29) for \(t \in [t_0, t_1]\) and obtain
Noting that by definition of \(\kappa _1,\kappa _{r-1}\) we have \(\kappa _1 - \rho \kappa _{r-1} = \kappa \, \left( 1 - \tfrac{\delta ^{r-2} {\hat{\delta }}}{2 \rho } \right) > 0\), we estimate for \(t \in [t_0,t_1]\)
Therefore, we find for \(t \in [t_0,t_1]\)
To sum up, with (38), (42) and (43), and the calculations above we obtain for \({t\in [t_0,t_1]}\)
Then, similar to (39) we deduce a contradiction. Therefore, in both cases (36a) and (36b), and for \(t \in [\beta , \omega )\) we have \(\psi _1(t) - x_1(t) \ge \kappa _1\). Moreover, for \(t \in [0,\beta )\) we have \(\psi _1(t) - \Vert x_1(t)\Vert \ge \kappa _1\) by definition of \( \kappa \), and hence \(h_1 \in {\mathcal {L}}^{\infty }([0,\omega ) \rightarrow \mathbb {R})\). Then, successively we obtain \(h_i \in {\mathcal {L}}^\infty ([0,\omega ) \rightarrow \mathbb {R})\) for all remaining \(i \in \{2,\ldots ,r-1\}\).
If \(\ell = 2\) we have, because \(t_0 = t_0^2 < t_0^1\) by (35a)
and, invoking the definition of \(t_0 = t_0^2\) there exists \( t_1 \in (t_0,t_0^1)\) such that for \({t \in [t_0,t_1]}\)
So we readily conclude for \(t \in [t_0, t_1]\)
and analogously to (42) we find
and furthermore, using (44) and estimation (45a), we have for \(t \in [t_0,t_1]\)
Note that (46) implies \(\Vert x_1(t)\Vert < \rho \Vert x_2(t)\Vert \) for \(t \in [t_0, t_1]\). We consider equation (29) for \(i=2\) and \(t \in [t_0, t_1]\) and obtain
Thanks to (30) and (34), we have
Hence, using the property (A.2) and the relations from (45) we obtain for \(t \in [ t_0, t_1]\)
With this, using (45a) we estimate (47) for \(t \in [ t_0, t_1]\)
Then, similar to (39) a contradiction arises. Therefore, for all \(t \in [\beta , \omega )\) we have \(\psi (t) - x_2(t) \ge \kappa _2\). Moreover, for \(t \in [0,\beta )\) we have \(\psi (t) - \Vert x_2(t)\Vert \ge \kappa _2\) by definition of \( \kappa \). Hence \(h_2 \in {\mathcal {L}}^{\infty }([0,\omega ) \rightarrow \mathbb {R})\). Then, successively we obtain \(h_i \in {\mathcal {L}}^\infty ([0,\omega ) \rightarrow \mathbb {R})\) for all remaining \({i \in \{1,\ldots ,r-1\}\setminus \{2\}}\).
If \(3 \le \ell \le r-1\) we have, because \(t_0 = t_0^{\ell } < t_0^{\ell -1}\) by (35a)
Then, by invoking the definition of \(t_0 = t_0^{\ell }\) there exists \( t_1 \in (t_0,t_0^{\ell -1})\) such that
As before, we deduce for \(t \in [t_0, t_1]\)
similar to (42) we obtain
and, using (49) and (50a), we have for \(t \in [t_0, t_1]\)
Note that (51) implies \(\Vert x_\ell (t)\Vert > \Vert x_{\ell -1}(t)\Vert \) for \(t \in [t_0, t_1]\). We consider equation (29) for \(i=\ell \) and \(t \in [t_0, t_1]\) and obtain
Recording
and using (50) we estimate
With this and using (50a), we estimate (52) for \(t \in [ t_0, t_1]\)
As before, a contradiction arises from analogous calculations as in (39). Therefore, for all \(t \in [\beta , \omega )\) we have \(\psi (t) - \Vert x_\ell (t)\Vert \ge \kappa _\ell \). Moreover, for \(t \in [0,\beta )\) we have \({\psi (t) - \Vert x_\ell (t)\Vert \ge \kappa _\ell }\) by definition of \( \kappa \), and hence \(h_\ell \in {\mathcal {L}}^{\infty }([0,\omega ) \rightarrow \mathbb {R})\). Then, successively we obtain \(h_i \in {\mathcal {L}}^\infty ([0,\omega ) \rightarrow \mathbb {R})\) for all remaining \(i \in \{1,\ldots ,r-1\}\setminus \{\ell \}\).
Step 3: We show \(\omega = \infty \) and \({\tilde{T}} \in {\mathcal {T}}^{rm,{\bar{q}}}_\tau \). Seeking a contradiction we assume \(\omega < \infty \). Then, since \(h_i\) and \(w_{i,j}\) for \(i=1,\ldots ,r-1\) and \(j=1,\ldots ,r\) are bounded via the previous steps, it follows that the graph of the solution of (17) is a compact subset of \({\mathcal {D}}\), a contradiction. Thus, \({\omega = \infty }\). Therefore, the operator \({\tilde{T}}\) is well defined and satisfies condition (a) of Definition 3.1 by the previous calculations. Moreover, property (b) of Definition 3.1 is satisfied. Further, note that \(\tilde{T}\) is defined via the solution of (17), which depends linearly on \(z,\dot{z}, \ldots , z^{(r-1)}\), \(T \in {\mathcal {T}}^{n,q}_{\tau ,1}\), and since \(f \in {\mathcal {C}}(\mathbb {R}^r \times \mathbb {R}^{m(r-1)r} \rightarrow \mathbb {R}^m)\) its integral is locally Lipschitz continuous. Therefore, the operator \({\tilde{T}}\) satisfies (c) of Definition 3.1 and hence \({\tilde{T}} \in {\mathcal {T}}^{rm,\bar{q}}_\tau \).
Finally, we observe that the higher derivatives of z can be calculated via a successive application of the cascade’s equations (2) and result in
and hence, with \(z_{r-1,r+1}(t) := {\tilde{\varGamma }} u(t)\) the results above allow us to write the conjunction of (2) and (3) with input u and output \(z = z_{r-1,1}\) as
where \({\tilde{F}} \in {\mathcal {C}}(\mathbb {R}^r \times \mathbb {R}^{{\bar{q}}} \rightarrow \mathbb {R}^m)\), \(\tilde{d}(t) := (\varphi (t), {\dot{\varphi }}(t), \ldots , \varphi ^{(r-1)}(t) )^\top \in {\mathcal {L}}^{\infty }(\mathbb {R}_{\ge 0}\rightarrow \mathbb {R}^r)\) and \({\tilde{T}} \in {\mathcal {T}}^{rm, \bar{q}}_\tau \). Therefore, \(({\tilde{d}}, {\tilde{F}}, {\tilde{T}}, {\tilde{\varGamma }}) \in {\mathcal {N}}^{m,r}\) which completes the proof. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lanza, L. Output feedback control with prescribed performance via funnel pre-compensator. Math. Control Signals Syst. 34, 715–758 (2022). https://doi.org/10.1007/s00498-022-00322-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00498-022-00322-5


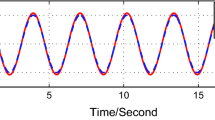
 ,
,



