Path Refinement in Weighted Regions

Abstract

In this paper, we study the weighted region problem (WRP) which is to compute a shortest path in a weighted partitioning of a plane. Recent results show that WRP is not solvable in any algebraic computation model over the rational numbers. Therefore, it is unlikely that WRP can be solved in polynomial time. Research has thus focused on determining approximate solutions for WRP. Approximate solutions for WRP typically show qualitatively different behaviors. We first formulate two qualitative criteria for weighted shortest paths. Then, we show how to produce a path that is quantitatively close-to-optimal and qualitatively satisfactory. More precisely, we propose an algorithm to transform any given approximate linear path into a linear path with the same (or shorter) weighted length for which we can prove that it satisfies the required qualitative criteria. This algorithm has a linear time complexity in the size of the given path. At the end, we explain our experiments on some triangular irregular networks (TINs) from Earth’s terrain. The results show that using the proposed algorithm, on average, 51% in query time and 69% in memory usage could be saved, in comparison with the existing method.

Appendices

Appendices

1.1 An Example that Causes Quadratic Running Time for the Naïve Backtracking Approach

Fig. 19

The directed red polygonal chain shows the sub-path from $x_{i+1}$ to $x_{k_3}$ in the original input path. The corner $x_{k_1}$ is the first corner in this sub-path that is disobeying the CNR. The naïve approach replaces the sub-path from $x_{i+1}$ to $x_{k_1}$ by the orange polygonal chain whose first segment is the only segment from the forward chain. After that replacement, the naïve algorithm continues and finds the corner $x_{k_2}$ that disobeys CNR. The algorithm replaces the sub-path from $x_{i+2}$ to $x_{k_2}$ by the blue polygonal chain. If the replacement happens n/2 times and the number of corners between $x_{i+1}$ and $x_{k_1}$ is n/2, then the total time complexity is quadratic in the size of the input path. In this example, the corner $x_{k_3}$ also disobeys CNR after replacing the sub-path from $x_{i+2}$ to $x_{k_2}$ by the blue polygonal chain. The green polygonal curve shows the final replacement of the sub-path from $x_{i+1}$ to $x_{k_3}$ (Color figure online)

1.2 Local Refinement is Unbounded

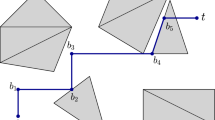
It is possible to apply the refinement algorithm on the path alternatively from s to t and from t to s. Every time, the length of the path may decrease. Here, we construct an example showing that any local refinement of corners of the path could be repeated many times (unbounded in terms of input size) and every time the length of the path decreases. In Fig. 20, three triangles are drawn, $\Delta _1$, $\Delta _2$ and $\Delta _3$. The input path to the refinement algorithm starts at $x_i$ and ends at $x_{i+3}$, $\Pi =[s=x_i,x_{i+1},x_{i+2},x_{i+3}=t]$ (the red solid polygonal chain in Fig. 20). The sub-path $[x_{i+1},x_{i+2},x_{i+3}]$ disobeys CNR. Therefore, $x_{i+2}$ will be translated to the intersection point of $N({x_{i+1}},{e_{i+2}})$ (the dashed line in Fig. 20) and $e_{i+2}$. Then, the first run of the refinement algorithm is over. Now, the second run traverses $\Pi$ in a reverse order from $x_{i+3}$ to $x_{i}$. In the second run, the sub-path $[x_{i+2},x_{i+1},x_{i}]$ disobeys CNR. Therefore, $x_{i+1}$ will be translated to the intersection point of $N({x_{i+2}},{e_{i+1}})$ (the dotted line in Fig. 20) and $e_{i+1}$. Then, in the next run from $x_{i}$ to $x_{i+3}$, again the sub-path $[x_{i+1},x_{i+2},x_{i+3}]$ disobeys CNR. This pattern could be repeated as it is a function of the geometric properties of the triangles.

This example could be generalized for any local refinement rules that guarantee reduction in the length of the path. We define a local rule to be a rule that takes $k<L$ corners of the input path into account, where L is the size of the path. We discuss when $k=3$. In order to generalize it for a larger k, it is enough to divide $\Delta _2$ in Fig. 20 into k smaller triangles, by k edges through the corner of the triangulation v and assign the weight $\infty$ to all the new triangles.

Fig. 20

The constructed example for showing that the local refinement may take arbitrary number of steps to converge

Suppose $\mathcal {L}$ is a set of local rules that takes 3 corners, $[x_{i},x_{i+1},x_{i+2}]$, of the input path into account. $\mathcal {L}$ refines the sup-path $[x_{i},x_{i+1},x_{i+2}]$ and makes it closer to the local optimum path from $x_{i}$ to $x_{i+2}$ (to make it shorter). Since $w_2$ is an arbitrary large number, $\mathcal {L}$ translates $x_{i+1}$ to be closer to the intersection point of $N({x_{i+2}},{e_{i+1}})$ and $e_{i+1}$ (because $w_2$ is very expensive). Then, in the next step, $\mathcal {L}$ refines the sup-path $[x_{i+1},x_{i+2},x_{i+3}]$ and makes it closer to the local optimum path from $x_{i+1}$ to $x_{i+3}$. Since $w_2$ is $\infty$, $\mathcal {L}$ translates $x_{i+2}$ to be closer to the intersection point of $N({x_{i+1}},{e_{i+2}})$ and $e_{i+2}$. These two translations could be arbitrary small. They depend on the geometric properties (i.e., the angles and length of edges) of the triangles. Therefore, the number of times that the refinement by $\mathcal {L}$ could improve the path length is unbounded.