Skip to main content
SpringerLink
Log in

Free and forced vibration analysis of moderately thick orthotropic plates in thermal environment and resting on elastic supports

  • Original
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

Abstract

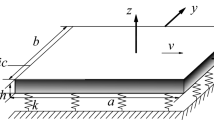
This paper investigates the free and forced vibration of moderately thick orthotropic plates under thermal environment and resting on elastic supports. Three kinds of elastic supports, namely non-homogeneous elastic foundations, point elastic supports and line elastic supports, are considered in the present study. The first-order shear deformation theory is employed to formulate the strain and kinetic energy functions of the structures, and then the stiffness and mass matrices can be obtained by applying the Hamilton’s principle. The modified Fourier method is adopted to solve the dynamic problems of moderately thick orthotropic plates with different combinations of temperature variations, elastic supports and boundary conditions. The accuracy and reliability of the proposed formulation are validated by comparing the obtained results with the finite element method results. Finally, the effects of some key parameters including temperature variation and stiffness values of the elastic supports on the modal and dynamic characteristics of the plates are analyzed in detail. In views of the versatility of the developed method, it offers an efficient tool for the structural analysis of moderately thick orthotropic plates under thermal environment and resting on elastic supports.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17

Similar content being viewed by others

References

  1. Laura, P.A.A., Gutierrez, R.H.: Transverse vibrations of rectangular plates on inhomogeneous foundations, part I: Rayleigh–Ritz method. J. Sound. Vib. 101(3), 307–315 (1985)

    Article  Google Scholar 

  2. Horenberg, J.A.G., Kerstens, J.G.M.: Transverse vibrations of rectangular plates on inhomogeneous foundations, part II: modal constraint method. J. Sound. Vib. 101(3), 317–324 (1985)

    Article  Google Scholar 

  3. Ju, F., Lee, H.P., Lee, K.H.: Free vibration of plates with stepped variations in thickness on non-homogeneous elastic foundations. J. Sound. Vib. 183(3), 533–545 (1995)

    Article  MATH  Google Scholar 

  4. Xiang, Y.: Vibration of rectangular Mindlin plates resting on non-homogenous elastic foundations. Int. J. Mech. Sci. 45(6), 1229–1244 (2003)

    Article  MATH  Google Scholar 

  5. Motaghian, S., Mofid, M., Akin, J.E.: On the free vibration response of rectangular plates, partially supported on elastic foundation. Appl. Math. Model. 36(9), 4473–4482 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  6. Jahromi, H.N., Aghdam, M.M., Fallah, A.: Free vibration analysis of Mindlin plates partially resting on Pasternak foundation. Int. J. Mech. Sci. 75(4), 1–7 (2013)

    Article  Google Scholar 

  7. Thinh, T.I., Nguyen, M.C., Ninh, D.G.: Dynamic stiffness formulation for vibration analysis of thick composite plates resting on non-homogenous foundations. Compos. Struct. 108(1), 684–695 (2014)

    Article  Google Scholar 

  8. Fallah, A., Aghdam, M.M., Kargarnovin, M.H.: Free vibration analysis of moderately thick functionally graded plates on elastic foundation using the extended Kantorovich method. Arch. Appl. Mech. 83(2), 1–15 (2013)

    Article  MATH  Google Scholar 

  9. Huang, M., Sakiyama, T., Matsuda, H., Morita, C.: Free vibration analysis of stepped rectangular plates resting on non-homogeneous elastic foundations. Eng. Anal. Bound. Elem. 50(66), 180–187 (2015)

    Article  MathSciNet  Google Scholar 

  10. Dehghan, M., Nejad, M., Moosaie, A.: An effective combination of finite element and differential quadrature method for analyzing of plates partially resting on elastic foundation. Eng. Solid. Mech. 4(4), 201–218 (2016)

    Article  Google Scholar 

  11. Wu, Z., Wang, J., Ren, X.: Effects of hygro-thermo-mechanical loading on composite plate resting on elastic foundation. Arch. Appl. Mech. 85(12), 1825–1846 (2015)

    Article  Google Scholar 

  12. Kim, C.S., Dickinson, S.M.: The flexural vibration of rectangular plates with point supports. J. Sound. Vib. 117(2), 249–261 (1987)

    Article  Google Scholar 

  13. Bhat, R.B.: Vibration of rectangular plates on point and line supports using characteristic orthogonal polynomials in the Rayleigh–Ritz method. J. Sound. Vib. 149(1), 170–172 (1991)

    Article  Google Scholar 

  14. Cheung, Y.K., Zhou, D.: Vibrations of rectangular plates with elastic intermediate line-supports and edge constraints. Thin. Wall. Struct. 37(4), 305–331 (2000)

    Article  Google Scholar 

  15. Lee, L.T., Lee, D.C.: Free vibration of rectangular plates on elastic point supports with the application of a new type of admissible function. Comput. Struct. 65(2), 149–156 (1997)

    Article  MATH  Google Scholar 

  16. Zhao, Y.B., Wei, G.W., Xiang, Y.: Plate vibration under irregular internal supports. Int. J. Solids Struct. 39(5), 1361–1383 (2002)

    Article  MATH  Google Scholar 

  17. Huang, M.H., Thambiratnam, D.P.: Free vibration analysis of rectangular plates on elastic intermediate supports. J. Sound. Vib. 240(3), 567–580 (2001)

    Article  Google Scholar 

  18. Huang, M.H., Thambiratnam, D.P.: Analysis of plate resting on elastic supports and elastic foundation by finite strip method. Comput. Struct. 79(29), 2547–2557 (2001)

    Article  Google Scholar 

  19. Wang, C.M., Wang, C., Ang, K.K.: Vibration of initially stressed Reddy plates on a Winkler–Pasternak foundation. J. Sound. Vib. 204(2), 203–212 (1997)

    Article  Google Scholar 

  20. Biswas, P.: Vibrations of irregular-shaped orthotropic plates resting on elastic foundation under inplane forces. J. Indian. Inst. Sci. 60(1), 73 (2013)

    MathSciNet  MATH  Google Scholar 

  21. Gürses, M., Civalek, Ö., Korkmaz, A.K., Ersoy, H.: Free vibration analysis of symmetric laminated skew plates by discrete singular convolution technique based on firstorder shear deformation theory. Int. J. Numer. Meth. Eng. 79(3), 290–313 (2009)

    Article  MATH  Google Scholar 

  22. Civalek, Ö.: Analysis of thick rectangular plates with symmetric cross-ply laminates based on first-order shear deformation theory. J. Compos. Mater. 42(26), 2853–2867 (2008)

    Article  Google Scholar 

  23. Civalek, Ö., Korkmaz, A., Demir, Ç.: Discrete singular convolution approach for buckling analysis of rectangular Kirchhoff plates subjected to compressive loads on two-opposite edges. Adv. Eng. Softw. 41(4), 557–560 (2010)

    Article  MATH  Google Scholar 

  24. Jeyaraj, P., Padmanabhan, C., Ganesan, N.: Vibration and acoustic response of an isotropic plate in a thermal environment. J. Vib. Acoust. 130(5), 301–306 (2008)

    Article  Google Scholar 

  25. Shen, H.S., Yang, J., Zhang, L.: Dynamic response of Reissner–Mindlin plates under thermomechanical loading and resting on elastic foundations. J. Sound. Vib. 232(2), 309–329 (2000)

    Article  Google Scholar 

  26. Shen, H.S., Zheng, J.J., Huang, X.L.: Dynamic response of shear deformable laminated plates under thermomechanical loading and resting on elastic foundations. Compos. Struct. 60(1), 57–66 (2003)

    Article  Google Scholar 

  27. Zenkour, A.M., Allam, M.N.M., Radwan, A.F.: Bending of cross-ply laminated plates resting on elastic foundations under thermo-mechanical loading. Int. J. Mech. Mater. Des. 9(3), 239–251 (2013)

    Article  Google Scholar 

  28. Zenkour, A.M., Sobhy, M.: Dynamic bending response of thermoelastic functionally graded plates resting on elastic foundations. Aerosp. Sci. Technol. 29(1), 7–17 (2013)

    Article  Google Scholar 

  29. Jin, G., Ye, T., Su, Z.: Structural Vibration: A Uniform Accurate Solution for Laminated Beams, Plates and Shells with General Boundary Conditions. Science Press, Beijing (2015)

    Book  MATH  Google Scholar 

  30. Liew, K.M., Xiang, Y., Kitipornchai, S., Wang, C.M.: Vibration of Mindlin Plates: Programming the p-Version Ritz Method. Elsevier, Oxford (1998)

    MATH  Google Scholar 

  31. Zamani, H.A., Aghdam, M.M., Salehi, M.: Free damped vibration analysis of Mindlin plates with hybrid material-foundation viscoelasticity. Int. J. Mech. Sci. 121, 33–43 (2017)

    Article  Google Scholar 

  32. Szekrényes, A.: The system of exact kinematic conditions and application to delaminated first-order shear deformable composite plates. Int. J. Mech. Sci. 77(77), 17–29 (2013)

    Article  Google Scholar 

  33. Chakraverty, S., Pradhan, K.K.: Free vibration of exponential functionally graded rectangular plates in thermal environment with general boundary conditions. Aerosp. Sci. Technol. 36, 132–156 (2014)

    Article  Google Scholar 

  34. Ng, C.H.W., Zhao, Y.B., Wei, G.W.: Comparison of discrete singular convolution and generalized differential quadrature for the vibration analysis of rectangular plates. Comput. Method. Appl. Mech. 193(23), 2483–2506 (2004)

    Article  MATH  Google Scholar 

  35. Srikanth, N., Gupta, M.: Damping characterization of Mg–SiC composites using an integrated suspended beam method and new circle-fit approach. Mater. Res. Bull. 37(6), 1149–1162 (2002)

    Article  Google Scholar 

Download references

Acknowledgements

The authors gratefully acknowledge the financial supports from the National Key Basic Research Program of China (No. 2014CB046302).

Author information

Authors and Affiliations

  1. Institute of Vibration, Shock and Noise, State Key Laboratory of Mechanical System and Vibration, Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai Jiao Tong University, Dongchuan Road 800, Shanghai, 200240, China

    Kai Zhou, Jinpeng Su & Hongxing Hua

Authors
  1. Kai Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jinpeng Su
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Hongxing Hua
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Kai Zhou.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Appendices

Appendix A

The displacement components can be written as follows, where H is the vector of modified Fourier series terms and q\(_{i}\) (i=1, 2, 3) denotes the unknown Fourier coefficient eigenvector

$$\begin{aligned} \varphi _x (x,y,t)= & {} \mathbf{Hq}_1 e^{j\omega t} \nonumber \\ \varphi _y (x,y,t)= & {} \mathbf{Hq}_2 e^{j\omega t} \nonumber \\ w(x,y,t)= & {} \mathbf{Hq}_3 e^{j\omega t} \end{aligned}$$
(A1)

The vector of modified Fourier series terms is defined by

$$\begin{aligned} \mathbf{H}= & {} [\mathbf{H}_1 ,\mathbf{H}_2 ,\mathbf{H}_3 ]\nonumber \\ \mathbf{H}_1= & {} [\cos \lambda _0 x\cos \lambda _0 y,\ldots , \cos \lambda _m x\cos \lambda _n y,\ldots , \cos \lambda _M x\cos \lambda _N y]\nonumber \\ \mathbf{H}_2= & {} [\xi _{1b} (y)\cos \lambda _0 x,\ldots ,\xi _{1b} (y)\cos \lambda _M x,\xi _{2b} (y)\cos \lambda _0 x, \ldots ,\xi _{2b} (y)\cos \lambda _M x]\nonumber \\ \mathbf{H}_3= & {} [\xi _{1a} (x)\cos \lambda _0 y,\ldots , \xi _{1a} (x)\cos \lambda _N y,\xi _{2a} (x)\cos \lambda _0 y,\ldots , \xi _{2a} (x)\cos \lambda _N y] \end{aligned}$$
(A2)
$$\begin{aligned} \xi _{1a} (x)= & {} L_1 \left( \frac{x}{L_1 }\right) \left( \frac{x}{L_1 }-1\right) ^{2},\xi _{2a} (x)=L_1 \left( \frac{x}{L_1 }\right) ^{2}\left( \frac{x}{L_1 }-1\right) \nonumber \\ \xi _{1b} (y)= & {} L_2 \left( \frac{y}{L_2 }\right) \left( \frac{y}{L_2 }-1\right) ^{2},\xi _{2b} (y)=L_2 \left( \frac{y}{L_2 }\right) ^{2}\left( \frac{y}{L_2 }-1\right) \end{aligned}$$
(A3)

The unknown Fourier coefficient eigenvector can be written by

$$\begin{aligned} \mathbf{q}_1= & {} [\mathbf{q}_{11} ,\mathbf{q}_{12} ,\mathbf{q}_{13} ]^{T} \,\,\mathbf{q}_2 =[\mathbf{q}_{21} ,\mathbf{q}_{22} ,\mathbf{q}_{23} ]^{T}\quad \mathbf{q}_3 =[\mathbf{q}_{31} ,\mathbf{q}_{32} ,\mathbf{q}_{33} ]^{T}\nonumber \\ \mathbf{q}_{11}= & {} [A_00 ,\ldots , A_mn ,\ldots , A_{MN} ]^{T} \nonumber \\ \mathbf{q}_{12}= & {} [d_{10}^1 ,\ldots , d_{1m}^1 ,\ldots , d_{1M}^1 ,d_{20}^1 ,\ldots , d_{2m}^1 ,\ldots , d_{2M}^1 ]^{T}\nonumber \\ \mathbf{q}_{13}= & {} [f_{10}^1 ,\ldots , f_{1n}^1 ,\ldots , f_{1N}^1 ,f_{20}^1 ,\ldots , f_{2n}^1 ,\ldots , f_{2N}^1 ]^{T}\nonumber \\ \mathbf{q}_{21}= & {} [B_00 ,\ldots , B_mn ,\ldots , B_{MN} ]^{T}\nonumber \\ \mathbf{q}_{22}= & {} [d_{10}^2 ,\ldots , d_{1m}^2 ,\ldots , d_{1M}^2 ,d_{20}^2 ,\ldots , d_{2m}^2 ,\ldots , d_{2M}^2 ]^{T}\nonumber \\ \mathbf{q}_{23}= & {} [f_{10}^2 ,\ldots , f_{1n}^2 ,\ldots , f_{1N}^2 ,f_{20}^2 ,\ldots , f_{2n}^2 ,\ldots , f_{2N}^2 ]^{T}\nonumber \\ \mathbf{q}_{31}= & {} [C_00 ,\ldots , C_mn ,\ldots , C_{MN} ]^{T}\nonumber \\ \mathbf{q}_{32}= & {} [d_{10}^3 ,\ldots , d_{1m}^3 ,\ldots , d_{1M}^3 ,d_{20}^3 ,\ldots , d_{2m}^3 ,\ldots , d_{2M}^3 ]^{T}\nonumber \\ \mathbf{q}_{33}= & {} [f_{10}^3 ,\ldots , f_{1n}^3 ,\ldots , f_{1N}^3 ,f_{20}^3 ,\ldots , f_{2n}^3 ,\ldots , f_{2N}^3 ]^{T} \end{aligned}$$
(A4)

Appendix B

The detail expressions in the stiffness and mass matrices are listed as follows

$$\begin{aligned} \mathbf{K}_{\varphi _x \varphi _x }= & {} \int _V {\left[ {\begin{array}{l} \frac{E_1 (1-(\alpha _{xx} +\nu _{21} \alpha _{yy} )\Delta T)z^{2}}{1-\nu _{12} \nu _{21} }\left( \frac{\partial \mathbf{H}}{\partial x}\right) ^{T}\left( \frac{\partial \mathbf{H}}{\partial x}\right) +kG_{13} \mathbf{H}^{T}{} \mathbf{H} \\ +(G_{12} -\frac{E_2 (\alpha _{yy} +\nu _{12} \alpha _{xx} )\Delta T}{1-\nu _{12} \nu _{21} })z^{2}\left( \frac{\partial \mathbf{H}}{\partial y}\right) ^{T}\left( \frac{\partial \mathbf{H}}{\partial y}\right) \\ \end{array}} \right] } dV \nonumber \\&+\int _0^{L_2 } {\left( \left. {K_{xx0} \mathbf{H}^{T}{} \mathbf{H}} \right| _{x=0} +\left. {K_{xxL_1 } \mathbf{H}^{T}{} \mathbf{H}} \right| _{x=L_1 } \right) } dy+\int _0^{L_1 } {\left( \left. {K_{xy0} \mathbf{H}^{T}{} \mathbf{H}} \right| _{y=0} +\left. {K_{xyL_2 } \mathbf{H}^{T}{} \mathbf{H}} \right| _{y=L_2 } \right) } \hbox {d}x\nonumber \\ \end{aligned}$$
(B1)
$$\begin{aligned} \mathbf{K}_{\varphi _x \varphi _y }= & {} \int _V {[\frac{\nu _{21} E_1 z^{2}}{1-\nu _{12} \nu _{21}} \left( \frac{\partial \mathbf{H}}{\partial x}\right) ^{T}\left( \frac{\partial \mathbf{H}}{\partial y}\right) +G_{12} z^{2}\left( \frac{\partial \mathbf{H}}{\partial y}\right) ^{T}\left( \frac{\partial \mathbf{H}}{\partial x}\right) ]} dV \end{aligned}$$
(B2)
$$\begin{aligned} \mathbf{K}_{\varphi _x w}= & {} \int _V {[kG_{13} \mathbf{H}^{T}\frac{\partial \mathbf{H}}{\partial x}]} dV \end{aligned}$$
(B3)
$$\begin{aligned} \mathbf{K}_{\varphi _y \varphi _y }= & {} \int _V {\left[ {\begin{array}{l} \frac{E_2 (1-(\alpha _{yy} +\nu _{12} \alpha _{xx} )\Delta T)z^{2}}{1-\nu _{12} \nu _{21} }\left( \frac{\partial \mathbf{H}}{\partial y}\right) ^{T}\left( \frac{\partial \mathbf{H}}{\partial y}\right) +kG_{23} \mathbf{H}^{T}{} \mathbf{H} \\ +(G_{12} -\frac{E_1 (\alpha _{xx} +\nu _{21} \alpha _{yy} )\Delta T}{1-\nu _{12} \nu _{21} })z^{2}\left( \frac{\partial \mathbf{H}}{\partial x}\right) ^{T}\left( \frac{\partial \mathbf{H}}{\partial x}\right) \\ \end{array}} \right] } dV \nonumber \\&+\int _0^{L_2 } {\left( \left. {K_{yx0} \mathbf{H}^{T}{} \mathbf{H}} \right| _{x=0} +\left. {K_{yxL_1 } \mathbf{H}^{T}{} \mathbf{H}} \right| _{x=L_1 } \right) } dy+\int _0^{L_1 } {\left( \left. {K_{yy0} \mathbf{H}^{T}{} \mathbf{H}} \right| _{y=0} +\left. {K_{yyL_2 } \mathbf{H}^{T}{} \mathbf{H}} \right| _{y=L_2 } \right) } \hbox {d}x\nonumber \\ \end{aligned}$$
(B4)
$$\begin{aligned} \mathbf{K}_{\varphi _y w}= & {} \int _V {[kG_{23} \mathbf{H}^{T}\frac{\partial \mathbf{H}}{\partial y}]} dV \end{aligned}$$
(B5)

For elastic foundations

$$\begin{aligned} \mathbf{K}_{ww}= & {} \int _V {\left[ {\begin{array}{c} (kG_{13} -\frac{E_1 (\alpha _{xx} +\nu _{21} \alpha _{yy} )\Delta T}{1-\nu _{12} \nu _{21} })(\frac{\partial \mathbf{H}}{\partial x})^{T}(\frac{\partial \mathbf{H}}{\partial x}) \\ +(kG_{23} -\frac{E_2 (\alpha _{yy} +\nu _{12} \alpha _{xx} )\Delta T}{1-\nu _{12} \nu _{21} })(\frac{\partial \mathbf{H}}{\partial y})^{T}(\frac{\partial \mathbf{H}}{\partial y}) \\ \end{array}} \right] } dV \nonumber \\&+\int _0^{L_2 } {\left( \left. {K_{wx0} \mathbf{H}^{T}{} \mathbf{H}} \right| _{x=0} +\left. {K_{wxL_1 } \mathbf{H}^{T}{} \mathbf{H}} \right| _{x=L_1 } \right) } dy+\int _0^{L_1 } {\left( \left. {K_{wy0} \mathbf{H}^{T}{} \mathbf{H}} \right| _{y=0} +\left. {K_{wyL_2 } \mathbf{H}^{T}{} \mathbf{H}} \right| _{y=L_2 } \right) } \hbox {d}x \nonumber \\&+\sum _{i=1}^q {\int _{Ls_{i-1} }^{Ls_i } {\int _0^{L_2 } {(K_{efi} \mathbf{H}^{T}{} \mathbf{H})} } \hbox {d}x\hbox {d}y} \end{aligned}$$
(B6)

For point elastic supports

$$\begin{aligned} \mathbf{K}_{ww}= & {} \int _V {\left[ {\begin{array}{c} (kG_{13} -\frac{E_1 (\alpha _{xx} +\nu _{21} \alpha _{yy} )\Delta T}{1-\nu _{12} \nu _{21} })\left( \frac{\partial \mathbf{H}}{\partial x}\right) ^{T}\left( \frac{\partial \mathbf{H}}{\partial x}\right) \\ +(kG_{23} -\frac{E_2 (\alpha _{yy} +\nu _{12} \alpha _{xx} )\Delta T}{1-\nu _{12} \nu _{21} })\left( \frac{\partial \mathbf{H}}{\partial y}\right) ^{T}\left( \frac{\partial \mathbf{H}}{\partial y}\right) \\ \end{array}} \right] } dV \nonumber \\&+\int _0^{L_2 } {\left( \left. {K_{wx0} \mathbf{H}^{T}{} \mathbf{H}} \right| _{x=0} +\left. {K_{wxL_1 } \mathbf{H}^{T}{} \mathbf{H}} \right| _{x=L_1} \right) } dy+\int _0^{L_1 } {\left( \left. {K_{wy0} \mathbf{H}^{T}{} \mathbf{H}} \right| _{y=0} +\left. {K_{wyL_2 } \mathbf{H}^{T}{} \mathbf{H}} \right| _{y=L_2 } \right) } \hbox {d}x \nonumber \\&+\sum _{i=1}^q {\int _0^{L_2 } {\int _0^{L_1 } {K_{psi} \mathbf{H}^{T}{} \mathbf{H}} } \delta (x-x_i ,y-y_i )\hbox {d}x\hbox {d}y} \end{aligned}$$
(B7)

For line elastic supports

$$\begin{aligned} \mathbf{K}_{ww}= & {} \int _V {\left[ {\begin{array}{c} (kG_{13} -\frac{E_1 (\alpha _{xx} +\nu _{21} \alpha _{yy} )\Delta T}{1-\nu _{12} \nu _{21} })\left( \frac{\partial \mathbf{H}}{\partial x}\right) ^{T}\left( \frac{\partial \mathbf{H}}{\partial x}\right) \\ +(kG_{23} -\frac{E_2 (\alpha _{yy} +\nu _{12} \alpha _{xx} )\Delta T}{1-\nu _{12} \nu _{21} })\left( \frac{\partial \mathbf{H}}{\partial y}\right) ^{T}\left( \frac{\partial \mathbf{H}}{\partial y}\right) \\ \end{array}} \right] } dV \nonumber \\&+\int _0^{L_2 } {(\left. {K_{wx0} \mathbf{H}^{T}{} \mathbf{H}} \right| _{x=0} +\left. {K_{wxL_1 } \mathbf{H}^{T}{} \mathbf{H}} \right| _{x=L_1 } )} dy+\int _0^{L_1 } {(\left. {K_{wy0} \mathbf{H}^{T}{} \mathbf{H}} \right| _{y=0} +\left. {K_{wyL_2 } \mathbf{H}^{T}{} \mathbf{H}} \right| _{y=L_2 } )} \hbox {d}x \nonumber \\&+\sum _{i=1}^{q_1 } {\int _0^{L_2 } {\int _0^{L_1 } {K_{xlsi} } \mathbf{H}^{T}{} \mathbf{H}\delta (y-y_i )\hbox {d}x\hbox {d}y} } +\sum _{i=1}^{q_2 } {\int _0^{L_2 } {\int _0^{L_1 } {K_{ylsi} } } \mathbf{H}^{T}{} \mathbf{H}\delta (x-x_i )\hbox {d}x\hbox {d}y}\nonumber \\ \end{aligned}$$
(B8)
$$\begin{aligned} \mathbf{M}_{\varphi _x \varphi _x }= & {} \int _V {[\rho z^{2}{} \mathbf{H}^{T}{} \mathbf{H}]} dV \end{aligned}$$
(B9)
$$\begin{aligned} \mathbf{M}_{\varphi _y \varphi _y }= & {} \int _V {[\rho z^{2}{} \mathbf{H}^{T}{} \mathbf{H}]} dV \end{aligned}$$
(B10)
$$\begin{aligned} \mathbf{M}_{ww}= & {} \int _V {[\rho \mathbf{H}^{T}{} \mathbf{H}]} dV \end{aligned}$$
(B11)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhou, K., Su, J. & Hua, H. Free and forced vibration analysis of moderately thick orthotropic plates in thermal environment and resting on elastic supports. Arch Appl Mech 88, 855–873 (2018). https://doi.org/10.1007/s00419-018-1346-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-018-1346-1

Keywords

Search

Navigation