Planetary latitudes in medieval Islamic astronomy: an analysis of the non-Ptolemaic latitude parameter values in the Maragha and Samarqand astronomical traditions

Abstract

Some variants in the materials related to the planetary latitudes, including computational procedures, underlying parameters, numerical tables, and so on, may be addressed in the corpus of the astronomical tables preserved from the medieval Islamic period (zīj literature), which have already been classified comprehensively by Van Dalen (Current perspectives in the history of science in East Asia. Seoul National University Press, Seoul, pp 316–329, 1999). Of these, the new values obtained for the planetary inclinations and the longitude of their ascending nodes might have something to do with actual observations in the period in question, which are the main concern of this paper. The paper is in the following sections. In the first section, Ptolemy’s latitude models and their reception in Islamic astronomy are briefly reviewed. In the next section, the medieval non-Ptolemaic values for the inclinations and the longitudes of the nodal lines are introduced. The paper ends with the discussion and some concluding remarks. The derivation of the underlying inclination values from the medieval planetary latitude tables and determining the accuracy of the tables are postponed to “Appendix” in the end of the paper.

Appendix: Planetary inclinations and latitude tables

In order to derive the inclinations from the planetary extremal latitudes and parameter values adopted in the zījes of the Maragha and Samarqand traditions, we make use of both modern and Ptolemy’s methods. The first consists in solving trigonometrical equations resulted from the configuration of the ecliptic, eccentric, and epicycle at the northern or southern limit (in the case of the superior planets) and at the nodes (for the inferior planets). The latter is to extract the inclinations from the maximum and minimum latitudes by interpolation in the epicyclic equation tables, an approximate method explained in Almagest XIII.3.⁵⁹

1.1 Maragha: inferior planets

Figure 3 shows the configuration of the eccentric and epicycle of Venus when the centre of the epicycle is at either of the nodes of the eccentric, i.e., $\pm 90^{\circ }$ from the apsidal line; in this position, the inclination of the epicycle is in the line of sight. The radius of the eccentric $\textit{OC} = R = 60$, the eccentricity $\textit{TO} = e$, the distance from the earth to the centre of the epicycle $\textit{TC} = (R^{2}- e^{2})^{1/2}$, and the radius of the epicycle $\textit{CP} = r$. We let the true epicyclic anomaly $\alpha = \angle \textit{ACP}$, so that $\textit{PP}^{\prime } = \textit{QQ}^{\prime }= r\hbox { sin }\alpha$, $\textit{PQ} = P^{\prime }Q^{\prime } = r\hbox { cos }\alpha \hbox { sin }i_{1\max }$, and $\textit{CQ}^{\prime }= r\hbox { cos }\alpha \hbox { cos }i_{1\max }$. For Mercury, the direction of the inclination of the epicycle is reversed, as the epicyclic apogee A is inclined to the north; also, $\textit{TO} = 2e$. The latitude $\beta = \angle \textit{PTQ}$ is found from the below formula (negative sign for Venus and positive sign for Mercury):

$$\begin{aligned} \sin \beta _{{\mathrm{icl}}} (\alpha )=\pm \frac{\textit{PQ}}{\sqrt{(\textit{TC}+C{Q}^{\prime })^{2}+Q{Q}^{\prime 2}+\textit{PQ}^{2}}}. \end{aligned}$$

(1)

If $\alpha = 180^{\circ }$, for which the latitude of the inferior planets reaches its maximum value, all that is necessary is to solve triangle TBC in which $\angle BTC = \beta _{\max }$:

$$\begin{aligned} \frac{\textit{TC}}{\sin (\angle \textit{TBC})}=\frac{\textit{CB}}{\sin (\angle \textit{CTB})}\hbox { or } \frac{\textit{TC}}{\sin (\beta _{\max } +i_{1\max } )}=\frac{r}{\sin (\beta _{\max })} \end{aligned}$$

(2)

and so, $i_{1\max } = (\beta _{\max }+i_{1\max }) - \beta _{\max }$. Therefore, $i_{1\max }$ can be conveniently found from TC, r, and $\beta _{\max }$.

Fig. 3

Configuration of the epicycle and the eccentric of Venus when the centre of the epicycle is at the ascending node of the eccentric, $\pm 90^{\circ }$ from the apsidal line

The underlying planetary parameters in the zījes of the Maragha tradition are as follows: the eccentricity of Venus in the Īlkhānī Zīj is $e\approx 1{;}2$ where $R = 60$, computed from the maximum tabular value $q_{\max } = 1{;}59^{\circ }$ for the equation of centre of the planet,⁶⁰ in al-Maghribī’s Adwār al-anwār e $\approx$ 1;3, from $q_{\max } = 2{;}0^{\circ }$.⁶¹ The value adopted for the eccentricity of Mercury, $e = 3;0$, and the radii of the epicycles of both the inferior planets in these two zījes are Ptolemaic, Venus: 43; 10, Mercury: 22;30.

Due to Ptolemy’s complicated model for Mercury’s motion in longitude of a movable eccentric, in Fig. 3: $\textit{TC} \ne (R^{2} -e^{2})^{1/2}$, but with Ptolemy’s value $e = 3{;}0, \textit{TC} \approx 56{;}40$.⁶² Then, with al-Maghribī’s value $\beta _{\max } = \beta _{\mathrm{icl}}(180^{\circ }) = 4{;}35^{\circ }$ for the maximum latitude of Mercury, one can compute $i_{1\max } \approx 7{;}2^{\circ }$ from (2).

Our historical method, i.e., Ptolemy’s solution, of which al-Maghribī quite probably made use, is an analogy between the extremal latitudes and inclination and the epicyclic equations and true epicyclic anomalies, respectively, in the sense that the extremal latitudes $\beta _{\mathrm{icl}}$(0) ($=\angle \textit{ATC}$ in Fig. 3; line AT not drawn) and $\beta _{\mathrm{icl}}(180^{\circ })\,(=\angle \textit{BTC})$ can be taken as the epicyclic equations in the correction tables for longitude corresponding, respectively, to the true epicyclic anomalies corresponding to the anomalies $\pm i_{1\max }$ and $180^{\circ }\pm i_{1\max }$ (in Fig. 3, assume that the epicycle is perpendicular to the ecliptic). When the centre of the epicycle of an inferior planet is at either of the nodes, i.e., $\pm 90^{\circ }$ from the apsidal line, its true eccentric anomaly, $\angle \textit{OTC}$ in Fig. 3, is $\kappa = \pm 90^{\circ }$, which corresponds to the mean eccentric anomaly $\bar{{\kappa }}\approx \pm 93^{\circ }$. At this position, from al-Maghribī’s table of the equations of Mercury, the following values for the epicyclic equation p can be derived:⁶³

$$\begin{aligned} 5{;}12^{\circ }\hbox { for } \alpha= & {} 180^{\circ } - i_{1\max }= 172^{\circ }\hbox { and}\\ 4{;}34^{\circ }\hbox { for } \alpha= & {} 180^{\circ }- i_{1\max } = 173^{\circ }. \end{aligned}$$

Al-Maghribī’s $\beta _{\max } = 4{;}35^{\circ }$ falls between these two values. So, with taking it as the epicyclic equation, the linear interpolation between $p = 5{;}12^{\circ }$ and $p = 4{;}34^{\circ }$ results in $\alpha = 180^{\circ }- i_{1\max } \approx 172{;}58^{\circ }$, and thus $i_{1\max }\approx 7{;}2^{\circ }$, which is in best agreement with our earlier derivation.

Table 5 shows that a table computed from this value is in good agreement with al-Maghribī’s tabular entries.⁶⁴

Table 5 Al-Maghribī’s table of the inclination of Mercury $i_{1\max } = 7;2^{\circ }$

In the case of Venus, using formula (2) with al-Maghribī’s value $\beta _{\max } = \beta _{\mathrm{icl}}(180^{\circ }) = 6{;}40^{\circ }$ results in $i_{1\max } = 2{;}37^{\circ }$ (note that because the eccentricity of Venus is small, $\textit{TC} \approx 60$). But this value cannot be derived from al-Maghribī’s table of the epicyclic equation of Venus according to Ptolemy’s procedure. As mentioned earlier, both in the Īlkhānī Zīj and in al-Maghribī’s Adwār, the radius of the epicycle of Venus is Ptolemaic, and as shown in Table 6, the tables of the epicyclic equation of the planet at mean distance in both zījes are equivalent to the corresponding one in the Almagest. Nevertheless, al-Maghribī has different values for the epicyclic equation for arguments $171^{\circ }$–$179^{\circ }$ (enclosed by the dashed lines in Table 6). I cannot explain why these entries are different, larger than the Almagest entries. As mentioned earlier, Ibn Yūnus has a greater value for the radius of the epicycle of Venus than Ptolemy ($r \approx 43{;}28$; see Table 6).⁶⁵ But, al-Maghribī’s equations for arguments $171^{\circ }$–$179^{\circ }$ can in no way be related to Ibn Yūnus’s.

Table 6 Tables of the epicyclic equation of Venus in the Īlkhānī zīj, al-Maghribī’s Adwār, and Ibn Yūnus’ Ḥākimī zīj

With Ptolemy’s procedure, the maximum latitude $\beta _{\max } = \beta _{\mathrm{icl}}(180^{\circ }) = 6{;}40^{\circ }$ taken as the epicyclic equation at mean distance corresponds to an epicyclic anomaly $\alpha = 180^{\circ }- i_{1\max } = 177{;}28{,}38^{\circ }$, and thus $i_{1\max } = 2{;}31{,}22^{\circ }$ which is nearly equal to the Ptolemaic $2{;}30^{\circ }$. It can be assumed that $6{;}40^{\circ }$ is estimated from the observed latitudes of Venus near inferior conjunction with the sun, although estimating latitude in this location is extremely difficult and al-Maghribī’s error, like Ptolemy’s is close to $-2^{\circ }$, but it cannot be determined which of the two values for $i_{1\max }$ al-Maghribī actually derived from it. However, since the tabular entries for the inclination of Venus in his Adwār are in better agreement with computation from $i_{1\max } = 2{;}37^{\circ }$ than from $i_{1\max } = 2{;}30^{\circ }$ (see below), it seems to be safe to conclude that it is the first value that, in reality, underlies al-Maghribī’s table in the Adwār.

In Table 7, Cols. 2 and 3, respectively, indicate the Almagest ⁶⁶ and al-Maghribī’s table of the inclination of Venus in the Adwār. Cols. 4 and 5 give the recomputed values from the two values for $i_{1\max }$. Neither of the two sets of the re-computed latitudes is as consistent with the tabular entries as we have seen earlier in the case of al-Maghribī’s table of the inclination of Mercury (Table 5). The table was probably computed according to the following procedure: the entries for the arguments $0^{\circ }$–$96^{\circ }$) are nearly identical to the corresponding entries in the Almagest, except for the slightly improved increments of $0;1^{\circ }$ for the first five entries; this seems reasonable, since a small change in $i_{1\max }$ from $2{;}30^{\circ }$ to $2{;}37^{\circ }$ causes no critical change in the latitudes in this range (at most, $0{;}3^{\circ }$). But most of the entries in the latter part of the table appear to have been derived from multiplying the corresponding entries in the Almagest table by 6;40/6;22 (see Col. 6). It is noteworthy that applying similar procedures to computing the planetary equation tables can be found in Islamic astronomy, more remarkably, in al-Maghribī’s Tāj al-azyāj ⁶⁷ as well as in the Īlkhānī Zīj.⁶⁸

Table 7 Tables of the inclination $\beta _{\mathrm{icl}}$ of Venus in the Almagest, al-Maghribī’s Tāj, and Adwār the Īlkhānī Zīj

In the Tāj al-azyāj, al-Maghribī has for Venus $\beta _{\max } =\beta _{\mathrm{icl}}(180^{\circ }) = 8{;}30^{\circ }$. The table of the planet’s epicyclic equation in this zīj does not have those strange entries found in the Adwār, but is identical to the Almagest/Handy Tables, and so to the Īlkhānī Zīj (Table 6). Both formula (2) and interpolation in the anomalistic equation table of Venus result in $i_{1\max } \approx 3{;}21^{\circ }$. Al-Maghribī’s values for the inclination and the recomputed values are shown in Table 7 (Cols. 7 and 8).

The entries in the latitude tables of the inferior planets in the Īlkhānī Zīj are given for each integer degree of the argument. Col. 9 in Table 7 shows the entries in the table of the inclination of Venus in the Īlkhānī Zīj. Both solving the trigonometrical equation (2) with $\beta _{\max } = \beta _{\mathrm{icl}}(180^{\circ }) = 8{;}40^{\circ }$ and interpolation in the table of the epicyclic equation of Venus results in $i_{1\max } \approx 3{;}25^{\circ }$. But the first half of the table, in the region of the arguments $0^{\circ }$–$90^{\circ }$, is identical to the corresponding table in the Almagest computed from $i_{1\max } = 2{;}30^{\circ }$. Moreover, re-computation of the table from $i_{1\max } = 3{;}25^{\circ }$ (Col. 10) shows that the results are by no means in agreement with the entries in the latter part of the table. In MS. P (fol. 44r) of the Īlkhānī Zīj, an unknown commentator has restored the latter half of the table to the Ptolemaic numbers and thus reduced the maximum latitude of the planet to $6{;}22^{\circ }$. We are told that this modification was done on the basis of the corresponding table in al-Maghribī’s Zīj, while, as we have seen above, his Tāj and Adwār have, respectively, the values $8{;}30^{\circ }$ and $6{;}40^{\circ }$ for the maximum latitude of Venus. It is worth noting that in his commentary on the Īlkhānī Zīj, al-Nīshābūrī briefly refers to this problem in the table of the latitude of Venus as a subtle point, but he offers no solution.⁶⁹ Since the table is intrinsically contradictory, I cannot speculate about the reasoning behind it. However, it was apparently reasonable enough for Ibn al-Shāṭir and the Samarqand astronomers to quote it in their own zījes.

Table 8 Equations of centre and eccentricities in Ulugh Beg’s Sulṭānī Zīj

1.2 Samarqand: superior planets

The new planetary parameters obtained at the Samarqand observatory, as deduced from Ulugh Beg’s Sulṭānī zīj, are summarized in Tables 8 for the equation of centre and 5 for the equation of anomaly. In both, Cols. 2 and 4 show, respectively, the maximum and minimum equations tabulated in this zīj and Cols. 3 and 5 show the arguments, mean eccentric or true epicyclic anomalies, for which the extremal values are given.

The tables of the equation of centre in the Almagest are symmetrical and additive for half the table and subtractive for the other half, but in the Sulṭānī Zīj, they are displaced and always additive; the values $k_{1} = 1/2(\hbox {Max} + \hbox {Min})$ of the displacements and $q_{\max } = 1/2(\hbox {Max} - \hbox {Min})$ of the maximum equations of centre (note that $k_{1} > q_{\max })$, and the corresponding eccentricities $e=R \cdot \hbox {tan }1/2\,q_{\max }$, where the radius of the eccentric $R = 60$, are given in the last three columns of Table 8.

The tables of the equation of the epicyclic anomaly are also always additive, but they use a different type of the displacement explained as follows: for all the planets, the first half of the table, for arguments $0^{\circ }$–$180^{\circ }$, corresponds to the equation $p_\mathrm{A}$ of the epicyclic anomaly at greatest distance ($R+e$; for Mercury: $R +3e$), when the centre of the epicycle is located at the apogee, but the latter half of the table, for arguments $180^{\circ }$–$360^{\circ }$, to the equation $p_{\Pi }$ of the epicyclic anomaly at the least distance ($R-e$, excepting Mercury), when the centre of the epicycle is located at the perigee. In the case of Saturn and Jupiter, all the entries are increased by an amount $k_{2}$. For Mars and the two inferior planets, the first half of the table gives $p_\mathrm{A}$ while the entries in the latter part of the table were increased by $360^{\circ }$, i.e., $360^{\circ } -p_{\Pi }$.⁷⁰ The values $k_{2}$ are shown in Col. 6. Cols. 7 and 8 display the maximum values of the epicyclic equation, respectively, at apogee and perigee (for Saturn and Jupiter: $p_{\mathrm{A}, \max } = \hbox {Max} - k_{2}$ and $p_{\Pi , \max }=k_{2} - \hbox {Min}$). The last column gives the corresponding epicyclic radii (for all the planets, except Mercury, $r = \hbox {sin}(p_{\mathrm{A}, \max }) \cdot (R+e) = \hbox {sin}(p_{\Pi , \max }) \cdot (R - e))$. In the Sulṭānī zīj, there is a table for the differences $p_{\Pi }- p_{\mathrm{A}}$ and two interpolation tables for each planet, one for the epicyclic anomaly $0^{\circ }$–$180^{\circ }$ and another for the epicyclic anomaly $180^{\circ }$–$360^{\circ }$. The entries of the equation tables are carried to two sexagesimal places, except Mercury to one place, and are given for each integer degree of the argument (for Mars, from $150^{\circ }$ to $210^{\circ }$, the arguments are in steps of $0{;}20^{\circ }$). Their reconstruction on the basis of the values derived above is in good agreement with the tabular entries.

It merits noting that in his Commentary on Zīj of Ulugh Beg, Qūshčī explains the layout of the equation and mean motion tables in this zīj. The values he mentions for the maximum equations agree with what can be extracted from the tables, with the exception of very slight differences in $q_{\max }$ of Saturn ($6{;}37,4{{\mathbf {6}}}^{\circ }$) and Jupiter ($5{;}18, {{\mathbf {42}}}^{\circ }$). The parameters we deduced from the tables are in agreement with those he gives. As Qūshčī remarks, for all the planets, the mean eccentric anomalies are reduced and, inversely, the mean epicyclic anomalies are increased by the above-mentioned values for $k_{1}$ and are then tabulated; and for Saturn and Jupiter, the longitudes of the apogees are decreased by the above-mentioned values for $k_{2}$.⁷¹

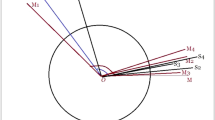
Figure 4 shows the configuration of the epicycle and eccentric, inclined to the ecliptic, of a superior planet when the centre of the epicycle is at the northern limit. In order to derive the inclinations from the extremal latitudes in the Sulṭānī zīj, we should first know the distance ${ TC} = \rho ^{\prime }$ between the earth T and the centre C of the epicycle of a superior planet at the northern limit, which can be computed from the eccentricity (Table 8) and the value adopted for $\omega _{\mathrm{A}}$ as mentioned earlier in Table 3. Where $R = 60$:

Fig. 4

Configuration of the epicycle and the eccentric of the superior planets with respect to the ecliptic when the centre of the epicycle is at the northern limit

In Fig. 4, the distance $\textit{TC} = \rho ^{\prime }$ and the radius of the epicycle $\textit{CP} = r$. We again let the true epicyclic anomaly $\alpha = \angle \textit{ACP}$, and $\angle \textit{CTN}^{\prime } = i_{0}$, so that $\textit{PP}^{\prime } = \textit{QQ}^{\prime } = r\hbox { sin } \alpha , \textit{PQ} = P^{\prime }Q^{\prime } = r\hbox { cos }\alpha \hbox { sin }i_{1 \mathrm{max}}$, and $\textit{CQ}^{\prime } = r\hbox { cos } \alpha \hbox { cos }i_{1 \mathrm{max}}$, and now $QN = Q^{\prime }N^{\prime } = (\textit{TC} + \textit{CQ}^{\prime })$ sin $i_{0}$. The latitude $\beta = \angle PTN$ at either limit can be computed from:

$$\begin{aligned} \sin \left| {\beta (\alpha )} \right|= & {} \frac{(\textit{TC}+C{Q}^{\prime })\sin i_0 -\textit{PQ}\cos i_0 }{\sqrt{(\textit{TC}+C{Q}^{\prime })^{2}+Q{Q}^{\prime 2}+PQ^{2}}}\nonumber \\= & {} \frac{r\cos \alpha \sin (i_0 -i_{1\max } )+{\rho }^{\prime }\sin i_0 }{\sqrt{({\rho }^{\prime }+C{Q})^{\prime 2}+Q{Q}^{\prime 2}+PQ^{2}}}. \end{aligned}$$

(3)

First, in order to derive $i_{0}$, we let $\alpha = 90^{\circ }$ in (3); thus, we have:

$$\begin{aligned} \sin i_0 =\sqrt{1+\frac{r^{2}}{{\rho }^{\prime 2}}}\cdot \sin \left( \left| {\beta _{{\mathrm{icl}}} (90^{\circ })} \right| \right) \end{aligned}$$

(4)

Then, in order to derive $i_{1}$, we can solve a long trigonometric equation resulting from (3) for $\alpha = 180^{\circ }$, after substituting $i_{0}$ computed from (4), a given value for the northern or southern latitude for this epicyclic anomaly ($\beta _{\max }=\angle BTN^{\prime }$), and r and $\rho ^{\prime }$ in (3). Instead, similar to what we have done earlier in the case of the inferior planets, a simpler solution is to solve triangle TCB in which $\angle BTC = \beta _{\max }- i_{0}$:

$$\begin{aligned} \frac{\textit{TC}}{\sin (\angle \textit{TBC})}=\frac{CB}{\sin (\angle \textit{CTB})}\hbox { or} \frac{{\rho }^{\prime }}{\sin (\beta _{\max } -i_0 +i_{1\max } )}=\frac{r}{\sin (\beta _{\max } -i_0 )} \end{aligned}$$

(5)

and thus, $i_{1\max } = (\beta _{\max }- i_{0 }+i_{1\max })- ( \beta _{\max }- i_{0})$.

Our formulae (4) and (5), applying the planetary parameters and the tabular latitudes in Ulugh Beg’s zīj (as mentioned in Tables 2, 8, 9), result in the inclinations in Table 2. Using Ptolemy’s solution, in which the extremal latitudes at the limits are taken as the epicyclic equations and the inclinations as the true epicyclic anomalies, as we have explained for the derivation of $i_{1\max }$ of the inferior planets, results in the same inclinations.

The tables in the Sulṭānī Zīj were generally calculated carefully, showing only minor deviations in the cases that have been examined,⁷² which is also true of the latitude tables at the northern and southern limits. Re-computation of the latitudes from the values derived for the inclinations is in good agreement with the tables in the Sulṭānī Zīj with no difference exceeding $0{;}1^{\circ }$ in the case of Saturn, $0{;}3^{\circ }$ for Jupiter, and $0{;}4^{\circ }$ for Mars. Table 10 is a specimen for Mars at the southern limit, which shows the greatest differences.

Table 9 Equations of the epicyclic anomaly and radii of the epicycles in Ulugh Beg’s Sulṭānī Zīj

Table 10 Ulugh Beg’s table of the latitude of Mars at the southern limit $i_{0} = 1{;}20^{\circ }$, $i_{1\max } = 2{;}7^{\circ }$