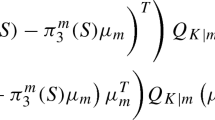On two simple and effective procedures for high dimensional classification of general populations

Abstract

In this paper, we generalize two criteria, the determinant-based and trace-based criteria proposed by Saranadasa (J Multivar Anal 46:154–174, 1993), to general populations for high dimensional classification. These two criteria compare some distances between a new observation and several different known groups. The determinant-based criterion performs well for correlated variables by integrating the covariance structure and is competitive to many other existing rules. The criterion however requires the measurement dimension be smaller than the sample size. The trace-based criterion, in contrast, is an independence rule and effective in the “large dimension-small sample size” scenario. An appealing property of these two criteria is that their implementation is straightforward and there is no need for preliminary variable selection or use of turning parameters. Their asymptotic misclassification probabilities are derived using the theory of large dimensional random matrices. Their competitive performances are illustrated by intensive Monte Carlo experiments and a real data analysis.

Appendix Technical proofs

1.1 Proof of Theorem 1

We first recall two known results on the Marčenko-Pastur distribution, which can be found in Theorem 3.10 in Bai and Silverstein (2010) and Lemma 3.1 in Bai et al. (2009).

Lemma 1

Assume $p/n\rightarrow y\in (0,1)$ as $n\rightarrow \infty$, for the sample covariance matrix $\tilde{\mathbf {S}}= \tilde{\mathbf {A}}/n$, we have the following results

• (1)
  $$\begin{aligned} \frac{1}{p}tr(\tilde{\mathbf {S}}^{-1}) \mathop {\longrightarrow }\limits ^{a.s.} a_1, \quad \frac{1}{p}tr(\tilde{\mathbf {S}}^{-2}) \mathop {\longrightarrow }\limits ^{a.s.} a_2, \end{aligned}$$

  where $a_1=\frac{1}{1-y}$ and $a_2=\frac{1}{(1-y)^3}$;

• (2) Moreover,

  $$\begin{aligned} \bar{\mathbf {x}}^{*\prime }\tilde{\mathbf {S}}^{-i} \bar{\mathbf {x}}^*\mathop {\longrightarrow }\limits ^{a.s.} a_i,\quad \bar{\mathbf {y}}^{*\prime }\tilde{\mathbf {S}}^{-i} \bar{\mathbf {y}}^*\mathop {\longrightarrow }\limits ^{a.s.} a_i, i=1, 2. \end{aligned}$$

Under the data-generation models (a) and (b), let $\Omega =(\tilde{\mathbf {A}}, \bar{\mathbf {x}}^*, \bar{\mathbf {y}}^*)$. Conditioned on $\Omega$, the misclassification probability (7) can be rewritten as

$$\begin{aligned} P_{\Omega }(2|1)&= P \left( K >0 \big | \Omega \right) =P_{\Omega }\left( K >0\right) , \end{aligned}$$

where

$$\begin{aligned} K&= \alpha _1 (\mathbf {z}^*-\bar{\mathbf {x}}^*)^\prime \tilde{\mathbf {A}}^{-1} (\mathbf {z}^*-\bar{\mathbf {x}}^*)\\&-\, \alpha _2 (\mathbf {z}^*-\bar{\mathbf {y}}^*- \tilde{\varvec{\mu }})^\prime \tilde{\mathbf {A}}^{-1} (\mathbf {z}^*-\bar{\mathbf {y}}^*- \tilde{\varvec{\mu }}). \end{aligned}$$

Therefore, $\displaystyle P_\Omega (2|1) =P_\Omega \left( K >0 \right)$ where $\mathbf {z}\in \Pi _1$ is assumed implicitly.

We evaluate the first two conditional moments of $K$.

Lemma 2

Let $\tilde{\mathbf {A}}^{-1}=(b_{ll^\prime })_{l,l^\prime =1, \ldots , p}$. We have

• (1)
  $$\begin{aligned} M_p&= E (K|\Omega )\nonumber \\&= (\alpha _1 -\alpha _2) \text {tr} (\tilde{\mathbf {A}}^{-1}) + \alpha _1 \bar{\mathbf {x}}^{*\prime } \tilde{\mathbf {A}}^{-1}\bar{\mathbf {x}}^*\nonumber \\&-\, \alpha _2 (\bar{\mathbf {y}}^*+ \tilde{\varvec{\mu }})^\prime \tilde{\mathbf {A}}^{-1} (\bar{\mathbf {y}}^*+ \tilde{\varvec{\mu }}); \end{aligned}$$

  (12)
• (2)
  $$\begin{aligned} B_p^2&= Var(K|\Omega ) \nonumber \\&= (\alpha _1 -\alpha _2)^2 (\gamma _x -3) \sum _l b_{ll}^2 + 2(\alpha _1 -\alpha _2)^2 tr(\tilde{\mathbf {A}}^{-2}) + 4\alpha _1^2 \bar{\mathbf {x}}^{*\prime } \tilde{\mathbf {A}}^{-2}\bar{\mathbf {x}}^*\nonumber \\&+ \,4\alpha _2^2 (\bar{\mathbf {y}}^*+ \tilde{\varvec{\mu }})^\prime \tilde{\mathbf {A}}^{-2} (\bar{\mathbf {y}}^*+ \tilde{\varvec{\mu }}) + (4\alpha _1\alpha _2 -4\alpha _2^2)\theta _x \sum _l b_{ll}(\tilde{\mathbf {A}}^{-1} (\bar{\mathbf {y}}^*+ \tilde{\varvec{\mu }}))_l \nonumber \\&-\, 8\,\alpha _1\alpha _2 \sum _{ll^\prime } \bar{x}^*_l b_{ll^\prime }(\tilde{\mathbf {A}}^{-2} (\bar{\mathbf {y}}^*+ \tilde{\varvec{\mu }}))_l + (4\alpha _1\alpha _2 -4\alpha _1^2) \theta _x \sum _l b_{ll}(\tilde{\mathbf {A}}^{-1} \bar{\mathbf {x}}^*)_l.\nonumber \\ \end{aligned}$$

  (13)

Proof of Lemma 2

It is easy to obtain the conditional expectation (12). For the conditional variance of $K$, we first calculate the conditional second moment

$$\begin{aligned} E (K^2|\Omega )&= E _\Omega \Big \{ \alpha _1^2\left[ \mathbf {z}^{*\prime } \tilde{\mathbf {A}}^{-1}\mathbf {z}^{*} - 2 \bar{\mathbf {x}}^{*\prime } \tilde{\mathbf {A}}^{-1}\mathbf {z}^{*} + \bar{\mathbf {x}}^{*\prime } \tilde{\mathbf {A}}^{-1} \bar{\mathbf {x}}^{*}\right] ^2 \\&+\, \alpha _2^2 \left[ \mathbf {z}^{*\prime } \tilde{\mathbf {A}}^{-1}\mathbf {z}^{*} -2 (\bar{\mathbf {y}}^*+ \tilde{\varvec{\mu }})^\prime \tilde{\mathbf {A}}^{-1}\mathbf {z}^{*} +(\bar{\mathbf {y}}^*+ \tilde{\varvec{\mu }})^\prime \tilde{\mathbf {A}}^{-1} (\bar{\mathbf {y}}^*+ \tilde{\varvec{\mu }})\right] ^2 \\&-\,2\alpha _1\alpha _2 \left[ \mathbf {z}^{*\prime } \tilde{\mathbf {A}}^{-1}\mathbf {z}^{*} - 2 \bar{\mathbf {x}}^{*\prime } \tilde{\mathbf {A}}^{-1}\mathbf {z}^{*} + \bar{\mathbf {x}}^{*\prime } \tilde{\mathbf {A}}^{-1} \bar{\mathbf {x}}^{*}\right] \\&\times \,\left[ \mathbf {z}^{*\prime } \tilde{\mathbf {A}}^{-1}\mathbf {z}^{*} -2 (\bar{\mathbf {y}}^*+ \tilde{\varvec{\mu }})^\prime \tilde{\mathbf {A}}^{-1}\mathbf {z}^{*} +(\bar{\mathbf {y}}^*+ \tilde{\varvec{\mu }})^\prime \tilde{\mathbf {A}}^{-1} (\bar{\mathbf {y}}^*+ \tilde{\varvec{\mu }})\right] \Big \}. \end{aligned}$$

Since

$$\begin{aligned}&E _\Omega \left[ \mathbf {z}^{*\prime } \tilde{\mathbf {A}}^{-1}\mathbf {z}^{*}\right] ^2 = (\gamma _x -3) \sum _l b_{ll}^2 + \big (\text {tr} \tilde{\mathbf {A}}^{-1}\big )^2 + 2 \text {tr} \left( \tilde{\mathbf {A}}^{-2}\right) ;\\&E _\Omega \left[ \mathbf {z}^{*\prime } \tilde{\mathbf {A}}^{-1}\mathbf {z}^{*}\cdot \bar{\mathbf {x}}^{*\prime } \tilde{\mathbf {A}}^{-1}\mathbf {z}^{*}\right] = \theta _x \sum _l b_{ll} \big (\tilde{\mathbf {A}}^{-1}\bar{\mathbf {x}}^{*}\big )_l;\\&E _\Omega \left[ \mathbf {z}^{*\prime } \tilde{\mathbf {A}}^{-1}\mathbf {z}^{*}\cdot (\bar{\mathbf {y}}^*+ \tilde{\varvec{\mu }})^\prime \tilde{\mathbf {A}}^{-1}\mathbf {z}^{*} \right] = \theta _x \sum _l b_{ll} \big (\tilde{\mathbf {A}}^{-1}(\bar{\mathbf {y}}^*+ \tilde{\varvec{\mu }})\big )_l; \\&E _\Omega \left[ \bar{\mathbf {x}}^{*\prime } \tilde{\mathbf {A}}^{-1}\mathbf {z}^{*} \cdot \mathbf {z}^{*\prime }\tilde{\mathbf {A}}^{-1} \bar{\mathbf {x}}^{*}\right] = \bar{\mathbf {x}}^{*\prime } \tilde{\mathbf {A}}^{-2}\mathbf {x}^{*};\\&E _\Omega \left[ (\bar{\mathbf {y}}^*+ \tilde{\varvec{\mu }})^\prime \tilde{\mathbf {A}}^{-1}\mathbf {z}^{*} \cdot \mathbf {z}^{*\prime } \tilde{\mathbf {A}}^{-1} (\bar{\mathbf {y}}^*+ \tilde{\varvec{\mu }})\right] = (\bar{\mathbf {y}}^*+ \tilde{\varvec{\mu }})^\prime \tilde{\mathbf {A}}^{-2} (\bar{\mathbf {y}}^*+ \tilde{\varvec{\mu }}), \end{aligned}$$

we obtain

$$\begin{aligned} E (K^2|\Omega )&= (\alpha _1 -\alpha _2)^2 (\gamma _x -3) \sum _l b_{ll}^2 + (\alpha _1 -\alpha _2)^2 \big (\text {tr} (\tilde{\mathbf {A}}^{-1})\big )^2 \\&+\, 2 (\alpha _1 -\alpha _2)^2 tr(\tilde{\mathbf {A}}^{-2})+ \,4\alpha _1^2 \bar{\mathbf {x}}^{*\prime } \tilde{\mathbf {A}}^{-2}\bar{\mathbf {x}}^*+ 4\alpha _2^2 (\bar{\mathbf {y}}^*+\tilde{\varvec{\mu }})^\prime \tilde{\mathbf {A}}^{-2} (\bar{\mathbf {y}}^*+\tilde{\varvec{\mu }}) \\&-\, 8\alpha _1\alpha _2 \bar{\mathbf {x}}^{*\prime } \tilde{\mathbf {A}}^{-2} (\bar{\mathbf {y}}^*+\tilde{\varvec{\mu }})+ \,2\alpha _1(\alpha _1-\alpha _2) tr(\tilde{\mathbf {A}}^{-1}) (\bar{\mathbf {x}}^{*\prime } \tilde{\mathbf {A}}^{-1}\bar{\mathbf {x}}^*) \\&+\, 2\alpha _2(\alpha _2 -\alpha _1) tr(\tilde{\mathbf {A}}^{-1}) (\bar{\mathbf {y}}^*+\tilde{\varvec{\mu }})^\prime \tilde{\mathbf {A}}^{-1} (\bar{\mathbf {y}}^*+\tilde{\varvec{\mu }})\\&+\, \,4\alpha _1(\alpha _2 -\alpha _1) \theta _x \sum _l b_{ll} \big (\tilde{\mathbf {A}}^{-1}\bar{\mathbf {x}}^{*}\big )_l\\&+\, 4\alpha _2(\alpha _1 -\alpha _2) \theta _x \sum _l b_{ll} \big (\tilde{\mathbf {A}}^{-1}(\bar{\mathbf {y}}^*+ \tilde{\varvec{\mu }})\big )_l \\&+\, \big (\alpha _1 \bar{\mathbf {x}}^{*\prime } \tilde{\mathbf {A}}^{-1}\bar{\mathbf {x}}^*- \alpha _2 (\bar{\mathbf {y}}^*+\tilde{\varvec{\mu }})^\prime \tilde{\mathbf {A}}^{-1} (\bar{\mathbf {y}}^*+\tilde{\varvec{\mu }})\big )^2. \end{aligned}$$

Finally, by

$$\begin{aligned} Var(K|\Omega )= E (K^2|\Omega ) - E ^2(K|\Omega ), \end{aligned}$$

Eq. (13) follows. The Lemma 2 is proved. $\square$

The first step of the proof of Theorem 1 is similar to the one of the proof of Theorem 2 where we ensure that $K- E (K)$ satisfies the Lyapounov condition. The details are referred to (13). Therefore, conditioned on $\Omega$, as $n\rightarrow \infty$, the misclassification probability for the D-criterion satisfies

$$\begin{aligned} \lim \left\{ P_\Omega (2|1) - \Phi \left( \frac{M_p}{B_p}\right) \right\} \rightarrow 0. \end{aligned}$$

Next, we look for main terms in $M_p$ and $B^2_p$, respectively, using Lemma 2. For $M_p$, we find the following equivalents for the three terms

• 1.
  $$\begin{aligned} (\alpha _1-\alpha _2) \text {tr}(\tilde{\mathbf {A}}^{-1})&= \frac{p}{n} (\alpha _1 -\alpha _2) \times \frac{1}{p} tr(\tilde{\mathbf {S}}^{-1}) \\&= \frac{a_1}{n} \times \left\{ p\left( \frac{1}{n_2+1} -\frac{1}{n_1+1}\right) \right\} + o\Big (\frac{1}{n}\Big ); \end{aligned}$$
• 2.
  $$\begin{aligned} \alpha _1 \bar{\mathbf {x}}^{*\prime } \tilde{\mathbf {A}}^{-1}\bar{\mathbf {x}}^{*}&= \frac{\alpha _1}{n} \big |\big |\bar{\mathbf {x}}^*\big |\big |^2 \times \left( \frac{\bar{\mathbf {x}}^*}{\big |\big | \bar{\mathbf {x}}^*\big |\big |} \right) ^\prime \tilde{\mathbf {S}}^{-1} \left( \frac{\bar{\mathbf {x}}^*}{\big |\big | \bar{\mathbf {x}}^*\big |\big |} \right) \\&= \frac{a_1}{n} \times \alpha _1 \big |\big |\bar{\mathbf {x}}^*\big |\big |^2+o\Big (\frac{1}{n}\Big ); \end{aligned}$$
• 3.
  $$\begin{aligned} \alpha _2 (\bar{\mathbf {y}}^*+ \tilde{\varvec{\mu }})^\prime \tilde{\mathbf {A}}^{-1}(\bar{\mathbf {y}}^*+ \tilde{\varvec{\mu }})= \frac{a_1}{n} \times \alpha _2 \big |\big |\bar{\mathbf {y}}^*+ \tilde{\varvec{\mu }}\big |\big |^2 + o\Big (\frac{1}{n}\Big ). \end{aligned}$$

Finally,

$$\begin{aligned} M_p = \frac{a_1}{n} \times \left\{ p\left( \frac{1}{n_2+1} -\frac{1}{n_1+1}\right) +\,\alpha _1 \big |\big |\bar{\mathbf {x}}^*\big |\big |^2+ \alpha _2 \big |\big |\bar{\mathbf {y}}^*+ \tilde{\varvec{\mu }}\big |\big |^2\right\} +o\Big (\frac{1}{n}\Big ).\nonumber \\ \end{aligned}$$

(14)

As for $B_p^2$, we find the following equivalents for the seven terms

• 1.
  $$\begin{aligned}&\left| (\alpha _1-\alpha _2)^2 (\gamma _x -3)\sum _l b_{ll}^2\right| \\&\le \frac{1}{n^2}\left( \frac{1}{n_2+1} -\frac{1}{n_1+1}\right) ^2 \big |\gamma _x -3\big | \times \text {tr}(\tilde{\mathbf {S}}^{-2})\\&= \frac{ya_2}{n^3} \big |\gamma _x -3\big | + o\Big (\frac{1}{n^3}\Big ) = O\Big (\frac{1}{n^3}\Big ); \end{aligned}$$
• 2.
  $$\begin{aligned}&2(\alpha _1-\alpha _2)^2 \text {tr}(\tilde{\mathbf {A}}^{-2})\\&= \frac{2}{n^2}\left( \frac{1}{n_2+1} -\frac{1}{n_1+1}\right) ^2 \times \text {tr}(\tilde{\mathbf {S}}^{-2}) \\&= \frac{2ya_2}{n^3} +o\Big (\frac{1}{n^3}\Big )= O\Big (\frac{1}{n^3}\Big ); \end{aligned}$$
• 3.
  $$\begin{aligned} 4\alpha _1^2 \bar{\mathbf {x}}^{*\prime } \tilde{\mathbf {A}}^{-2}\bar{\mathbf {x}}^{*} = 4\alpha _1^2\frac{a_2 ||\bar{\mathbf {x}}^{*}||^2}{n^2} +o\Big (\frac{1}{n^2}\Big ); \end{aligned}$$
• 4.
  $$\begin{aligned} 4\alpha _2^2 (\bar{\mathbf {y}}^*+\tilde{\varvec{\mu }})^\prime \tilde{\mathbf {A}}^{-2} (\bar{\mathbf {y}}^*+\tilde{\varvec{\mu }}) = 4\alpha _2^2 \frac{a_2\big |\big |\bar{\mathbf {y}}^*+\tilde{\varvec{\mu }}\big |\big |^2}{n_2}+o\Big (\frac{1}{n^2}\Big ); \end{aligned}$$
• 5.
  $$\begin{aligned}&4\alpha _2\big |\alpha _1-\alpha _2\big | \theta _x \sum _l b_{ll} (\tilde{\mathbf {A}}^{-1}(\bar{\mathbf {y}}^*+\tilde{\varvec{\mu }}))_l \\&= \frac{4\alpha _2}{n^2}\left| \frac{1}{n_2+1} -\frac{1}{n_1+1}\right| \sum _l c_{ll} (\tilde{\mathbf {S}}^{-1}(\bar{\mathbf {y}}^*+\tilde{\varvec{\mu }}))_l \\&\le \frac{4\alpha _2}{n^2}\left| \frac{1}{n_2+1} -\frac{1}{n_1+1}\right| \left( \sum _l c_{ll}^2\right) ^{\frac{1}{2}} \times \left( \sum _l \left( \tilde{\mathbf {S}}^{-1}(\bar{\mathbf {y}}^*+\tilde{\varvec{\mu }})\right) _l^2\right) ^{\frac{1}{2}}\\&\le \frac{4\alpha _2}{n^3} \sqrt{p} \times \big |\big |\bar{\mathbf {y}}^*+\tilde{\varvec{\mu }}\big |\big |\sqrt{a_2} + o(\frac{1}{n^2\sqrt{n}}); \end{aligned}$$
• 6.
  $$\begin{aligned} 8\alpha _1\alpha _2\sum _{ll^\prime } \bar{x}_l^*b_{ll^\prime } (\tilde{\mathbf {A}}^{-2} (\bar{\mathbf {y}}^*+\tilde{\varvec{\mu }}))_l \le \frac{8\alpha _1\alpha _2}{n^3}\sqrt{p} \times \big |\big |\bar{\mathbf {y}}^*+\tilde{\varvec{\mu }}\big |\big |\sqrt{a_2}+o\Big (\frac{1}{n^2\sqrt{n}}\Big ); \end{aligned}$$
• 7.
  $$\begin{aligned} \Big (4\alpha _1\alpha _2-\alpha _1^2\Big )\theta _x\sum _l b_{ll}(\tilde{\mathbf {A}}^{-1}\bar{\mathbf {x}}^*)_l \le \frac{4\alpha _1}{n^3}\sqrt{p} \times ||\bar{\mathbf {x}}^*||\sqrt{a_2}+o\Big (\frac{1}{n^2\sqrt{n}}\Big ). \end{aligned}$$

It can be proved that almost surely,

$$\begin{aligned}&||\bar{\mathbf {x}}^{*}||^2 -\frac{p}{n_1} \rightarrow 0,\\&\big |\big |\bar{\mathbf {y}}^*+\tilde{\varvec{\mu }}\big |\big |^2 -\left( \frac{p}{n_2} +\Delta ^2\right) \rightarrow 0,\\&\big |\big |\bar{\mathbf {y}}^*+\tilde{\varvec{\mu }}\big |\big | - \sqrt{\frac{p}{n_2} +\Delta ^2} \rightarrow 0. \end{aligned}$$

Then the terms 2 and 3 are of order $O\left( \frac{1}{n^2}\right)$ and 5–7 are of order $o\left( \frac{1}{n^2}\right)$. Finally,

$$\begin{aligned} B_p^2 = 4\alpha _1^2\frac{a_2 ||\bar{\mathbf {x}}^{*}||^2}{n^2} +\,4\alpha _2^2 \frac{a_2\big |\big |\bar{\mathbf {y}}^*+\tilde{\varvec{\mu }}\big |\big |^2}{n^2} +\,o\Big (\frac{1}{n^2}\Big ). \end{aligned}$$

(15)

Since $n_1/n \rightarrow \lambda$, we have

$$\begin{aligned} n_1 \rightarrow n\lambda ,&n_2 \rightarrow n(1-\lambda ). \end{aligned}$$

Finally, it holds almost surely,

$$\begin{aligned} \lim \left\{ \Phi \left( \frac{M_p}{B_p}\right) - \Phi \left( -\frac{\Delta ^2}{\sqrt{\frac{y}{\lambda (1-\lambda )}+\Delta ^2}} \sqrt{1-y}\right) \right\} \rightarrow 0. \end{aligned}$$

This ends the proof of Theorem 1.

1.2 Proof of Theorem 2

By the assumption 2 in Theorem 2, the covariance matrix is $\varvec{\Sigma }=\text {diag}(\sigma _{ll})_{1\le l \le p}$. Under the data-generation models (a) and (b), the misclassification probability (10) can be rewritten as

$$\begin{aligned} P(2|1)&= P\big \{\alpha _1(\mathbf {z}^*-\bar{\mathbf {x}}^*)^\prime \varvec{\Sigma } (\mathbf {z}^*-\bar{\mathbf {x}}^*)\nonumber \\&\quad -\,\alpha _2(\mathbf {z}^*-\bar{\mathbf {y}}^*-\tilde{\varvec{\mu }})^\prime \varvec{\Sigma } (\mathbf {z}^*-\bar{\mathbf {y}}^*-\tilde{\varvec{\mu }}) >0 \big | \mathbf {z}\in \Pi _1\big \}\nonumber \\&= P\left( \sum _{l=1}^p k_l>0 \Big |\mathbf {z}\in \Pi _1\right) , \end{aligned}$$

(16)

where

$$\begin{aligned} k_l=\alpha _1(z^*_l-\bar{x}^*_l)^2 \sigma _{ll}-\alpha _2(z^*_l-\bar{y}^*_l -\tilde{\mu }_l)^2 \sigma _{ll}. \end{aligned}$$

We firstly evaluate the first two moments of $\sum _{l=1}^p k_l$.

Lemma 3

Under the data-generation models (a) and (b), we have

• (1)
  $$\begin{aligned} E (k_l)=-\alpha _2 \sigma _{ll} \tilde{\mu }_l^2, \end{aligned}$$

  and

  $$\begin{aligned} M_p=\sum _{l=1}^p E (k_l)=-\alpha _2||\varvec{\delta }||^2; \end{aligned}$$

  (17)
• (2)
  $$\begin{aligned} Var(k_l)=\sigma _{ll}^2\left\{ \beta _0 +\beta _1(\gamma ) + \beta _2(\theta )\tilde{\mu }_l + 4\alpha _2\tilde{\mu }_l^2\right\} , \end{aligned}$$

  and

  $$\begin{aligned} B_p^2=\sum _{l=1}^p Var(k_l) = \left[ \beta _0 +\beta _1(\gamma )\right] \text {tr}(\varvec{\Sigma }^2) +\beta _2(\theta ) \mathbf {I}^\prime \Gamma ^3\varvec{\delta } +4\alpha _2\varvec{\delta }^\prime \varvec{\Sigma }\varvec{\delta }, \end{aligned}$$

  (18)

  where

  $$\begin{aligned} \beta _0&= \alpha _1^2\frac{6n_1^2+3n_1-3}{n_1^3}+\,\alpha _2^2\frac{6n_2^2+3n_2-3}{n_2^3}+\,2(\alpha _1\alpha _2-1),\\ \beta _1(\gamma )&= \gamma _x\left( \frac{\alpha _1^2}{n_1^3}+(\alpha _1-\alpha _2)^2 \right) +\,\frac{\alpha _2^2}{n_2^3}\gamma _y, \beta _2(\theta ) = 4\alpha _2(\alpha _1 -\alpha _2)\theta _x +\,\frac{4}{n_2^2}\theta _y. \end{aligned}$$

  If removing the small terms with order $O(p/n_*^2)$, then the formula of $B_p^2$ in Theorem 2 is obtained.

Proof of Lemma 3

Since $\mathbf {z}^*, (\mathbf {x}^*_l)$ and $(\mathbf {y}^*_l)$ are independent, the variables $(k_l)_{l=1,\ldots ,p}$ are also independent. For the expectation of $k_l$, we have

$$\begin{aligned} E (k_l)&= \alpha _1 \sigma _{ll} \times E \Big (z^*_l-\bar{x}^*_l\Big )^2 -\alpha _2 \sigma _{ll} \times \, E \Big (z^*_l-\bar{y}^*_l-\tilde{\mu }_l\Big )^2\\&= \alpha _1 \sigma _{ll}\times \alpha _1^{-1}- \alpha _2 \sigma _{ll} \times \,\Big (\alpha _2^{-1}+\tilde{\mu }_l^2\Big ) = -\alpha _2\sigma _{ll}\tilde{\mu }_l^2. \end{aligned}$$

Eq. (17) follows.

For the variance, we have

$$\begin{aligned} Var(k_l)&= E [k_l- E (k_l)]^2\\&= \sigma _{ll}^2 \times E \left\{ \alpha _1 \Big (z^*_l-\bar{x}^*_l\Big )^2-\alpha _2\Big (z^*_l -\bar{y}^*_l-\tilde{\mu }_l\Big )^2 +\alpha _2\tilde{\mu }_l^2\right\} ^2\\&= \sigma _{ll}^2\times \bigg \{\alpha _1^2 E \Big (z^*_l-\bar{x}^*_l\Big )^4 +\alpha _2^2 E \Big (z^*_l-\bar{y}^*_l\Big )^4 + 4 \alpha _2^2\tilde{\mu }_l^2 E \Big (z^*_l-\bar{y}^*_l\Big )^2\\&-\,2\alpha _1\alpha _2 E \left[ \Big (z^*_l-\bar{x}^*_l\Big )^2 \Big (z^*_l-\bar{y}^*_l\Big )^2\right] -4 \alpha _2^2 \tilde{\mu }_l E \Big (z^*_l -\bar{y}^*_l\Big )^3\\&+\, 4\alpha _1 \alpha _2 \tilde{\mu }_l E \Big [\Big (z^*_l-\bar{x}^*_l\Big )^2\Big (z^*_l-\bar{y}^*_l\Big )\Big ]\bigg \}. \end{aligned}$$

Moreover,

$$\begin{aligned} E \Bigg [z^*_l-\bar{x}^*_l\Bigg ]^4&= \gamma _x\left( 1+\frac{1}{n_1^3}\right) +\frac{6n_1^2+3n_1-3}{n_1^3},\\ E \Bigg [z^*_l-\bar{y}^*_l\Bigg ]^4&= \gamma _x+\frac{\gamma _y}{n_2^3}+\frac{6n_2^2+3n_2-3}{n_2^3},\\ E \Bigg [z^*_l-\bar{y}^*_l\Bigg ]^2&= \alpha _2^{-1},\\ E \Bigg [z^*_l -\bar{y}^*_l\Bigg ]^3&= \theta _x -\frac{\theta _y}{n_2^2},\\ E \left\{ \Bigg [z^*_l-\bar{x}^*_l\Bigg ]^2\Bigg [z^*_l-\bar{y}^*_l\Bigg ]^2\right\}&= \gamma _x +\frac{1}{\alpha _1\alpha _2}-1, \end{aligned}$$

and

$$\begin{aligned} E \left\{ \Big (z^*_l-\bar{x}^*_l\Big )^2\Big (z^*_l-\bar{y}^*_l\Big )\right\} =\theta _x. \end{aligned}$$

Finally, we obtain

$$\begin{aligned} Var(k_l)&= \sigma _{ll}^2 \Bigg \{ \alpha _1^2\left[ \gamma _x\left( 1+\frac{1}{n_1^3}\right) +\frac{6n_1^2+3n_1-3}{n_1^3}\right] \\&\quad +\,\alpha _2^2\left[ \gamma _x+\frac{\gamma _y}{n_2^3} +\frac{6n_2^2+3n_2-3}{n_2^3}\right] \\&\quad +\, 4\alpha _2^2\tilde{\mu }_l^2\alpha _2^{-1} -2\alpha _1\alpha _2 \left[ \gamma _x +\frac{1}{\alpha _1\alpha _2}-1\right] \\&\quad + \, 4\alpha _1\alpha _2\tilde{\mu }_l \theta _x -4\alpha _2^2 \tilde{\mu }_l \left[ \theta _x-\frac{\theta _y}{n_2^2}\right] \Bigg \}\\&= \sigma _{ll}^2 \Bigg \{ \gamma _x\left( \alpha _1^2+\frac{\alpha _1^2}{n_1^3}+\alpha _2^2 - 2\alpha _1\alpha _2\right) +\frac{\alpha _2^2\gamma _y}{n_2^3} + \alpha _1^2\frac{6n_1^2+3n_1-3}{n_1^3}\\&\quad +\,\alpha _2^2\frac{6n_2^2+3n_2-3}{n_2^3}-2+ 4\alpha _2\tilde{\mu }_l^2 +2\alpha _1\alpha _2\\&\quad +\, 4\alpha _2(\alpha _1-\alpha _2)\tilde{\mu }_l \theta _x + \frac{4\tilde{\mu }_l}{n_2^2}\theta _y \Bigg \}\\&= \sigma _{ll}^2\Big \{\beta _0 +\beta _1(\gamma ) + \beta _2(\theta )\tilde{\mu }_l + 4\alpha _2\tilde{\mu }_l^2\Big \}. \end{aligned}$$

Eq. (18) follows. Then $B_p^2$ can be rewritten as

$$\begin{aligned} B_p^2&= \Big [ \frac{6n_1+3}{(n_1+1)^2} +\frac{6n_2+3}{(n_2+1)^2} -\frac{2}{n_1+1} -\frac{2}{n_2+1} \\&+\, \frac{2}{(n_1+1)(n_2+1)} -\frac{3}{n_1(n_1+1)^2} -\frac{3}{n_2(n_2+1)^2}\\&+\,\frac{\gamma _x}{(n_1+1)^2} +\frac{\gamma _y}{(n_2+1)^2}-\frac{2\gamma _x}{(n_1+1)(n_2+1)} \\&+\,\frac{\gamma _x}{n_1(n_1+1)^2}+\,\frac{\gamma _x}{n_2(n_2+1)^2}\Big ] \text {tr}(\varvec{\Sigma }^2)\\&+\left[ 4\frac{n_2}{n_2+1}\left( \frac{1}{n_2+1}-\frac{1}{n_1+1}\right) \theta _x +\frac{4}{n_2^2}\theta _y \right] \mathbf {1}_p^\prime \Gamma ^3 \varvec{\delta }\\&+\, 4\frac{n_2}{n_2+1}\varvec{\delta }^\prime \varvec{\Sigma }\varvec{\delta }\\&\approx \left[ \frac{4}{n_1}+\frac{4}{n_2}+\frac{3}{n_1^2} +\frac{3}{n_2^2} +\frac{2}{n_1n_2} -\frac{3}{n_1^3} -\frac{3}{n_2^3} + \frac{\gamma _x}{n_1^2} +\frac{\gamma _y}{n_2^2} -\frac{2\gamma _x}{n_1n_2} +\frac{\gamma _x}{n_1^3}\right. \\&\left. -\,\frac{\gamma _y}{n_2^3}\right] \text {tr}(\varvec{\Sigma }^2)\\&+\, \left[ 4\left( \frac{1}{n_2}-\frac{1}{n_1}\right) \theta _x +\frac{4}{n_2^2}\theta _y\right] \mathbf {1}_p^\prime \Gamma ^3 \varvec{\delta }\\&+ \,4\left( 1-\frac{1}{n_2}\right) \varvec{\delta }^\prime \varvec{\Sigma }\varvec{\delta }. \end{aligned}$$

Only keep the terms with order $O(p)$ and $O(p/n_*)$ we can get the formula of $B_p^2$ in Theorem 2. The Lemma 3 is proved. $\square$

We know that $\left[ k_l- E (k_l)\right] _{1\le l \le p}$ are independent variables with zero mean. We use the Lyapounov criterion to establish a CLT for $\sum _l \left[ k_l- E (k_l)\right]$, that is, there is a constant $b>0$ such that

$$\begin{aligned} \lim _{p\rightarrow \infty } B_p^{-(2+b)}\sum _{l=1}^p E \left[ \big |k_l- E (k_l)\big |^{2+b} \right] \rightarrow 0. \end{aligned}$$

Since

$$\begin{aligned} \big |k_l- E (k_l)\big |&= \sigma _{ll}\big | \alpha _1 \Big (z^*_l -\bar{x}^*_l\Big )^2 -\alpha _2\Big (z^*_l-\bar{y}^*_l\Big )^2 + 2\alpha _2 \tilde{\mu }_l \Big (z^*_l-\bar{y}^*_l\Big ) \big |\\&\le \sigma _{ll}\left\{ \big |z_l^*-\bar{x}_l^*\big |^2 + \big |z_l^*-\bar{y}_l^*\big |^2 +2\big |\tilde{\mu }_l\big | \big |z_l^*-\bar{y}_l^*\big | \right\} \\&\le \sigma _{ll}\left\{ \big |z_l^*-\bar{x}_l^*\big |^2 +2\big |z_l^*-\bar{y}_l^*\big |^2 + \big |\tilde{\mu }_l\big |^2 \right\} \\&\le \sigma _{ll}\left\{ 2\left( \big |z_l^*\big |^2 +\big |\bar{x}_l^*\big |^2 \right) +4 \left( \big |z_l^*\big |^2 +\big |\bar{y}_l^*\big |^2 \right) + \big |\tilde{\mu }_l\big |^2 \right\} \\&\le \sigma _{ll}\left\{ 6\left( \big |z_l^*\big |^2 +\big |\bar{x}_l^*\big |^2 + \big |\bar{y}_l^*\big |^2 \right) + \big |\tilde{\mu }_l\big |^2 \right\} , \end{aligned}$$

the $(2+b)-$norm of $\left[ k_l- E (k_l)\right]$ is

$$\begin{aligned} ||k_l- E (k_l)||_{2+b}&\le \sigma _{ll} \left\{ 6\left[ \Big |\Big | |z_l^*|^2 \Big |\Big |_{2+b} + \Big |\Big | |\bar{x}_l^*|^2\Big |\Big |_{2+b} + \Big |\Big | |\bar{y}_l^*|^2 \Big |\Big |_{2+b} \right] + \big |\tilde{\mu }_l\big |^2\right\} \\&= \sigma _{ll} \left\{ 6\left[ \left( E \big |z_l^*\big |^{4+b^\prime } \right) ^{\frac{1}{4+b^\prime }} +\left( E \big |\bar{x}_l^*\big |^{4+b^\prime } \right) ^{\frac{1}{4+b^\prime }} +\left( E \big |\bar{y}_l^*\big |^{4+b^\prime }\right) ^{\frac{1}{4+b^\prime }} \right] \right. \\&\qquad \left. + \big |\tilde{\mu }_l\big |^2 \right\} \\&\le \sigma _{ll} \left\{ 6\left[ 2\gamma _{4+b^\prime , x}^{1/(4+b^\prime )} +\gamma _{4+b^\prime , y}^{1/(4+b^\prime )}\right] + \big |\tilde{\mu }_l\big |^2 \right\} . \end{aligned}$$

Then

$$\begin{aligned} E \left[ k_l- E (k_l)\right] ^{2+b} \le c_b \sigma _{ll}^{2+b} \cdot \left\{ 1 +\big |\tilde{\mu }_l\big |^{4+b^\prime } \right\} , \end{aligned}$$

where $c_d$ is some constant depending on $b$. Therefore, as $B_p^2 \approx 4\varvec{\delta }^\prime \varvec{\Sigma }\varvec{\delta }=4 \sum _{l=1}^p \tilde{\mu }_l^2 \sigma _{ll}^2$,

$$\begin{aligned} B_p^{-(2+b)} \sum _{l=1}^p E [k_l- E (k_l)]^{2+b}&\le c_b \cdot \frac{\sum _l \sigma _{ll}^{2+b} +\sum _l \sigma _{ll}^{2+b}|\tilde{\mu }_l|^{4+2b}}{\left( \sum _l \sigma _{ll}\delta _l^2 \right) ^{1+b/2}}\\&= c_b\cdot \frac{\sum _l \sigma _{ll}^{2+b} +\sum _l \delta _l^{4+2b}}{(\sum _l \sigma _{ll}\delta _l^2)^{1+b/2}} \quad \rightarrow 0, \end{aligned}$$

by the assumption 4 in Theorem 2. Finally, we have

$$\begin{aligned} B_p^{-1} \sum _{l=1}^p\left[ k_l- E (k_l)\right] \Rightarrow N(0,1), \ as \ p\rightarrow \infty , \ n_*\rightarrow \infty . \end{aligned}$$

This ends of the proof of Theorem 2.