Abstract
Given a large enough population of voters whose utility functions satisfy certain statistical regularities, we show that voting rules such as the Borda rule, approval voting, and evaluative voting have a very high probability of selecting the social alternative which maximizes the utilitarian social welfare function. We also characterize the speed with which this probability approaches one as the population grows.
Similar content being viewed by others
Notes
In fact, Rae and Taylor were interested in maximizing “responsiveness”: the probability that the outcome agrees with the preference of a random individual. But if all voters have equal preference intensities, then maximizing “responsiveness” is equivalent to maximizing the utilitarian SWF. See also Badger (1972), Curtis (1972), Schofield (1972), Straffin (1977), and Dubey and Shapley (1979) for extensions of the Rae–Taylor theorem. Riley (1990) appears to have independently intuited some of the same conclusions. But he did not give any formal proofs. More recently, Fleurbaey (2009) has proved a far-reaching generalization of the Rae–Taylor theorem to a setting where voters may have different preference intensities and arbitrary correlations.
For i.u.d. utilities, this result had been anticipated by Weber (1978, p. 10).
However, approval voting and all rank scoring rules reduce to simple majority vote when there are only two alternatives. Thus, in this setting, our results in Sects. 4 and 5 imply the utilitarian optimality of simple majority voting, and are complementary to the Rae–Taylor theorem and its extensions.
Since they consider a democratic federation of regions, the papers by Barberà and Jackson (2006), Beisbart et al. (2005), Beisbart and Bovens (2007), Beisbart and Hartmann (2010), Laruelle and Valenciano (2008; 2010), etc. presumably posit large populations. However, most of these papers represent each population in reduced form as an averaged utility function, not as a set of individuals, and none of them engage in any sort of asymptotic analysis.
Laslier (2012) discusses several other ways to assign “scores” to alternatives based on the voters’ approval sets, e.g. by computing the stationary probability distribution of an associated Markov process. It might be possible to prove “asymptotic utilitarian” results for these alternative approval scoring systems as well. But for simplicity, we will confine the analysis in this paper to the standard approval scoring system.
Typically, \(\gamma \) and \(\beta \) would have nonoverlapping support; e.g. \(\gamma \) would be a measure on \([0,{\infty })\) while \(\beta \) would be a measure on \((-{\infty },0]\). But we don’t need to assume this. Note that \(\gamma \) and \(\beta \) are not assumed to be Gamma or Beta distributions.
The fourth moment of a probability measure \(\gamma \) is the integral \(\displaystyle \int _{-{\infty }}^{\infty }u^4 \ \mathrm{d}\gamma [u]\). It is finite if d\(\gamma [u]\) decays quickly enough as \(u{\rightarrow }\pm {\infty }\).
The fourth moment of the multivariate probability measure \(\lambda \) is the integral \(\displaystyle \int _{\mathbb {U}}\sum \nolimits _{n=1}^N u_n^4 \ \mathrm{d}\lambda [{\mathbf { u}}]\). It is finite if d\(\lambda [{\mathbf { u}}]\) decays quickly enough as \({\left\| {\mathbf { u}} \right\| _{{}} } {\rightarrow }{\infty }\). For example, the fourth moment of a multivariate normal probability measure is finite.
\(({}^{\scriptscriptstyle \uparrow }\!r^i_1,{}^{\scriptscriptstyle \uparrow }\!r^i_2,\ldots ,{}^{\scriptscriptstyle \uparrow }\!r^i_N)\) are called the order statistics of the sample.
To be more precise, we need an asymptotic condition on the \(L^1\) norm of the covariance matrix of the random variables \(\{c_i\}_{i\in {\mathcal { I}}}\) and \(\{u_i\}_{i\in {\mathcal { I}}}\), as \(I{\rightarrow }{\infty }\).
We do not assume that, for a fixed voter i in \({\mathcal { I}}\), the random errors \(\epsilon _i(a)\) and \(\epsilon _i(b)\) are independent for different alternatives a and b in \({\mathcal { A}}\).
To be precise, we fix an infinite sequence \((\succ _n)_{n=1}^{\infty }\) of ordinal preferences. Then, for any particular value of I, we identify \({\mathcal { I}}\) with \([1\ldots I]\) and let \({\mathcal { P}}_{\mathcal { I}}=\{\succ _n\}_{n=1}^I\). Theorem 5.2 then applies for every possible infinite sequence.
The set of all possible infinite sequences \((\succ _n)_{n=1}^{\infty }\) has a natural sigma-algebra (generated by “cylinder sets”, which are defined by fixing values for any finite number of coordinates). The Endogenous preference model defines a probability measure on this sigma algebra (in fact, it is a Bernoulli stochastic process). In the last step of the proof, we integrate with respect to this probability measure.
References
Abreu D, Sen A (1991) Virtual implementation in Nash equilibrium. Econometrica 59(4):997–1021
Alcantud JCR, Laruelle A (2014) Dis&approval voting: a characterization. Soc Choice Welf 43(1):1–10
Apesteguia J, Ballester MA, Ferrer R (2011) On the justice of decision rules. Rev Econ Stud 78(1):1–16
Azrieli Y, Kim S (2014) Pareto efficiency and weighted majority rules. Int Econ Rev 55(4):1067–1088
Badger WW (1972) Political individualism, positional preferences, and optimal decision-rules. In: Niemi and Weisberg, pp 34–59
Banks J, Duggan J (2004) Probabilistic voting in the spatial model of elections: the theory of office-motivated candidates. In: Austen-Smith D, Duggan J (eds.) Social Choice and Strategic Decisions, Springer, New York, pp 15–56
Barberà S, Jackson MO (2006) On the weights of nations: assigning voting power to heterogeneous voters. J Polit Econ 114(2):317–339
Baujard A, Igersheim H, Lebon I, Gavrel F, Laslier J-F (2014) Who’s favored by evaluative voting? an experiment conducted during the 2012 french presidential election. Elect Stud 34:131–145
Beisbart C, Bovens L (2007) Welfarist evaluations of decision rules for boards of representatives. Soc Choice Welf 29(4):581–608
Beisbart C, Bovens L, Hartmann S (2005) A utilitarian assessment of alternative decision rules in the council of ministers. Eur Union Polit 6(4):395–418
Beisbart C, Hartmann S (2010) Welfarist evaluations of decision rules under interstate utility dependencies. Soc Choice Welf 34(2):315–344
Black DS (1958) Theory of committees and elections. Cambridge University Press, Cambridge
Bordley RF (1983) A pragmatic method for evaluating election schemes through simulation. Am Polit Sci Rev 77:123–141
Bordley RF (1985a) A precise method for evaluating election schemes. Public Choice 46(2):113–123
Bordley RF (1985b) Using factions to estimate preference intensity: improving upon one person/one vote. Public Choice 45(3):257–268
Bordley RF (1986) One person/one vote is not efficient given information on factions. Theory Decis 21(3):231–250
Boutilier C, Caragiannis I, Haber S, Lu T, Procaccia AD, Sheffet O (2012) Optimal social choice functions: a utilitarian view. In: Proceedings of the 13th ACM conference on electronic commerce. EC ’12. ACM, New York, NY, USA, pp 197–214
Bovens L, Hartmann S (2007) Welfare, voting and the constitution of a federal assembly. In: Galavotti MC, Scazzieri R, Suppes P (eds) Reasoning, rationality and probability. CSLI Publications, Stanford
Brams SJ, Fishburn PC (1983) Approval voting. Birkhäuser Boston, Boston
Caragiannis I, Procaccia AD (2011) Voting almost maximizes social welfare despite limited communication. Artif Intell 175(9–10):1655–1671
Coughlin P (1992) Probabilistic voting theory. Cambridge University Press, Cambridge
Curtis RB (1972) Decision-rules and collective values in constitutional choice. In: Niemi and Weisberg, pp 23–33
De Sinopoli F, Dutta B, Laslier J-F (2006) Approval voting: three examples. Int J Game Theory 35(1):27–38
Dhillon A (1998) Extended Pareto rules and relative utilitarianism. Soc Choice Welf 15:521–542
Dhillon A, Mertens J-F (1999) Relative utilitarianism. Econometrica 67:471–498
Dubey P, Shapley LS (1979) Mathematical properties of the Banzhaf power index. Math Oper Res 4(2):99–131
Fleurbaey M (2009) One stake one vote (preprint)
Gelman A, Katz JN, Bafumi J (2004) Standard voting power indexes do not work: an empirical analysis. Br J Polit Sci 34:657–74
Giles A, Postl P (2014) Equilibrium and effectiveness of two-parameter scoring rules. Math Soc Sci 68:31–52
Harter HL, Balakrishnan N (1996) CRC handbook of tables for the use of order statistics in estimation. CRC Press, Boca Raton
Hillinger C (2005) The case for utilitarian voting. Homo Oecon 23:295–321
Kellett J, Mott K, Summer, (1977) Presidential primaries: measuring popular choice. Polity 9(4):528–537
Kim S (2014) Ordinal versus cardinal voting rules: a mechanism design approach (preprint)
Koriyama Y, Laslier J-F, Macé A, Treibich R (2013) Optimal apportionment. J Polit Econ 121(3):584–608
Krishna V, Morgan J (2012) Voluntary voting: costs and benefits. J Econ Theory 147(6):2083–2123
Laruelle A, Valenciano F (2008) Voting and collective decision-making: bargaining and power. Cambridge University Press, Cambridge
Laruelle A, Valenciano F (2010) Egalitarianism and utilitarianism in committees of representatives. Soc Choice Welf 35(2):221–243
Laslier J-F (2012) And the loser is... plurality voting. In: Felsenthal SD, Machover M (eds) Electoral systems: paradoxes, assumptions, and procedures. Studies in choice and welfare. Springer, Berlin, pp 327–351
Laslier J-F, Sanver MR (eds) (2010) Handbook on approval voting. Studies in Choice and Welfare. Springer, Heidelberg
Ledyard JO (1984) The pure theory of large two-candidate elections. Public Choice 44(1):7–41
Lehtinen A (2007) The Borda rule is also intended for dishonest men. Public Choice 133(1–2):73–90
Lehtinen A (2008) The welfare consequences of strategic behaviour under approval and plurality voting. Eur J Polit Econ 24:688–704
Lindbeck A, Weibull JW (1987) Balanced-budget redistribution as the outcome of political competition. Public Choice 52(3):273–297
Lindbeck A, Weibull JW (1993) A model of political equilibrium in a representative democracy. J Public Econ 51(2):195–209
Maaser N, Napel S (2014) The mean voter, the median voter, and welfare-maximizing voting weights. In: Fara R, Leech D, Salles M (eds) Voting power and procedures. Studies in choice and welfare series. Springer, Berlin
Macé A (2013) Voting with evaluations: when should we sum? What should we sum? (preprint)
Macé A, Treibich R (2012) Computing the optimal weights in a utilitarian model of apportionment. Math Soc Sci 63(2):141–51
Matsushima H (1988) A new approach to the implementation problem. J Econ Theory 45(1):128–144
McKelvey RD, Patty JW (2006) A theory of voting in large elections. Games Econ Behav 57(1):155–180
Merrill S (1984) A comparison of efficiency of multicandidate electoral systems. Am J Polit Sci 28:23–48
Myerson RB (2002) Comparison of scoring rules in Poisson voting games. J Econ Theory 103(1):219–251
Niemi RG, Weisberg HF (eds) (1972) Probability models of collective decision making. Charles E Merrill Publishing, Columbus
Nitzan S (2009) Collective preference and choice. Cambridge University Press, Cambridge
Núñez M, Laslier J-F (2014) Preference intensity representation: strategic overstating in large elections. Soc Choice Welf 42(2):313–340
Núñez M, Pivato M (2016) Truth-revealing voting rules for large populations (preprint)
Núñez M (2014) The strategic sincerity of approval voting. Econ Theory 56(1):157–189
Ottewell G (1977) The arithmetic of voting. In: Defense of Variety. http://www.universalworkshop.com/ARVOfull.htm
Pivato M (2013) Voting rules as statistical estimators. Soc Choice Welf 40(2):581–630
Pivato M (2015) Condorcet meets Bentham. J Math Econ 59:58–65
Pivato M (2016a) Dominant strategy utilitarianism in large populations (preprint)
Pivato M (2016b) Epistemic democracy with correlated voters (preprint)
Pivato M (2016c) Statistical utilitarianism. J Theor Polit (to appear)
Rae D (1969) Decision rules and individual values in constitutional choice. Am Polit Sci Rev 63:40–56
Riley J (1990) Utilitarian ethics and democratic government. Ethics 100(2):335–348
Schofield NJ (1972) Is majority rule special? In: Niemi and Weisberg, pp 60–82
Smith WD (2000) Range voting. http://rangevoting.org (unpublished)
Straffin PD Jr (1977) Majority rule and general decision rules. Theory Decis 8(4):351–360
Tangian AS (2000) Unlikelihood of Condorcet’s paradox in a large society. Soc Choice Welf 17(2):337–365
Tanguiane AS (1991) Aggregation and representation of preferences: introduction to mathematical theory of democracy. Springer, Berlin
Taylor M (1969) Proof of a theorem on majority rule. Behav Sci 14:228–231
Weber RJ (1978) Comparison of voting systems. Discussion paper 498, Cowles Foundation for Research in Economics
Acknowledgments
I am grateful to Michel le Breton, Rohan Dutta, Ori Heffetz, Sean Horan, Jérôme Lang, Christophe Muller, Matías Núñez, and Clemens Puppe for helpful comments on earlier versions of this paper. I also thank Gustaf Arrhenius, Miguel Ballester, Marc Fleurbaey, Annick Laruelle, and the other participants of the June 2014 “Workshop on Power” at the Collège d’Études Mondiales in Paris. Finally, I thank two anonymous referees for their careful reading and helpful comments. None of these people are responsible for any errors. Most of this research was done when I was at the Department of Mathematics at Trent Universty, in Canada. This research was supported by NSERC Grant #262620-2008, and by Labex MME-DII (ANR11-LBX-0023-01).
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Background
The proofs in this paper depend on some results from Pivato (2016c). In this appendix, we briefly review these results.
Pivato (2016c) considers the problem of a utilitarian social planner who can only make noisy observations of the utility functions of the individuals in society and the correct system of interpersonal comparisons. For every i in \({\mathcal { I}}\), let \(u_i:{\mathcal { A}}{{\longrightarrow }}{\mathbb {R}}\) be the true cardinal utility function for voter i, and let \(c_i>0\) be a calibration constant, which we will use to make cardinal interpersonal utility comparisons. We suppose that the social planner wants to maximize the utilitarian social welfare function \(U_{\mathcal { I}}:{\mathcal { A}}{{\longrightarrow }}{\mathbb {R}}\) defined by Formula (1); however, she faces the following informational problems.
- (U1) :
-
\(\{c_i\}_{i\in {\mathcal { I}}}\) are unknown. The planner regards \(\{c_i\}_{i\in {\mathcal { I}}}\) as independent (but not necessarily identically distributed) real-valued random variables. There are constants \({\overline{c}}>0\) and \(\sigma _c^2\ge 0\) (independent of I) such that \({\mathbb {E}}[c_i]={\overline{c}}\) and \(\mathrm{var}[c_i]\le \sigma _c^2\), for all \(i\in {\mathcal { I}}\).
- (U2) :
-
The utility functions \(\{u_i\}_{i\in {\mathcal { I}}}\) are not precisely observable. Instead, for each i in \({\mathcal { I}}\), the planner can only observe a function \(v_i:=u_i+\epsilon _i\), where \(\epsilon _i:{\mathcal { A}}{{\longrightarrow }}{\mathbb {R}}\) is a random “error” term. For each alternative a in \({\mathcal { A}}\), the random errors \(\{\epsilon _i(a)\}_{i\in {\mathcal { I}}}\) are independentFootnote 16 (but not necessarily identically distributed), and they all have an expected value of 0 and a variance less than or equal some constant \(\sigma _\epsilon ^2>0\) (which is independent of I). Finally, the random variables \(\{c_i\}_{i\in {\mathcal { I}}}\) are independent of the random functions \(\{\epsilon _i\}_{i\in {\mathcal { I}}}\).
We assume that the utility profile \(\{u_i\}_{i\in {\mathcal { I}}}\) satisfies one or both of the following conditions.
- (U3) :
-
There is a constant \(\Delta >0\) (independent of I) such that \(\max _{{\mathcal { A}}} (U_{\mathcal { I}})-U_{\mathcal { I}}(a)>\Delta \) for every \(a\not \in {{\mathrm{\mathrm{argmax}}}}_{{\mathcal { A}}} (U_{\mathcal { I}})\).
- (U4) :
-
There is a constant \(M>0\) (independent of I) such that
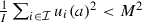 for every a in \({\mathcal { A}}\).
for every a in \({\mathcal { A}}\).
Note that, while we assume that \(\{v_i\}_{i\in {\mathcal { I}}}\) and \(\{c_i\}_{i\in {\mathcal { I}}}\) are random variables, we make no assumptions about the mechanism generating the underlying profile of utility functions \(\{u_i\}_{i\in {\mathcal { I}}}\). These utility functions might be fixed in advance, or they might themselves be generated by some other random process, as long as they satisfy (U4) and (U3). Define the function \(V_{\mathcal { I}}:{\mathcal { A}}{{\longrightarrow }}{\mathbb {R}}\) as in Eq. (2), and define the SWF \(U_{\mathcal { I}}:{\mathcal { A}}\,{{\longrightarrow }}\,{\mathbb {R}}\) as in Eq. (1). Here is Theorem 1 of Pivato (2016c).
Theorem 6.1
For every i in \({\mathcal { I}}\), let \(u_i:{\mathcal { A}}\,{{\longrightarrow }}\, {\mathbb {R}}\) be a utility function. Suppose the profile \(\{u_i\}_{i\in {\mathcal { I}}}\) satisfies (U3) and (U4). If \(\{c_i\}_{i\in {\mathcal { I}}}\), \(\{\epsilon _i\}_{i\in {\mathcal { I}}}\) and \(\{v_i\}_{i\in {\mathcal { I}}}\) are randomly generated according to rules (U1) and (U2), then
For any \(\delta >0\) and \(p\in (0,1)\), we define
Define \(U^*_{\mathcal { I}}:=\max {\left\{ U_{\mathcal { I}}(a) \; ; \; a\in {\mathcal { A}} \right\} }\). Here is Theorem 2 of Pivato (2016c).
Theorem 6.2
Suppose \(\{u_i\}_{i\in {\mathcal { I}}}\), \(\{c_i\}_{i\in {\mathcal { I}}}\), \(\{\epsilon _i\}_{i\in {\mathcal { I}}}\) and \(\{v_i\}_{i\in {\mathcal { I}}}\) satisfy (U1), (U2) and (U4). For any \(\delta >0\) and \(p\in (0,1)\), if \(I\ge {\overline{I}}(\delta ,p)\), then \(\mathrm{Prob}\left[ U_{\mathcal { I}}(a)< U^*_{\mathcal { I}}-\delta \right]\ < \ p\), for all a in \({{\mathrm{\mathrm{argmax}}}}_{{\mathcal { A}}} (V_{\mathcal { I}})\).
Appendix 2: Proofs
Proof of Theorem 3.1
We will derive this from Theorem 6.1. Recall that \(u_i:=w_i/c_i\), so that \(w_i=c_i\,u_i\); with this substitution, formulae (3) and (1) are equivalent. Observe that hypothesis (C) implies (U1) (with \({\overline{c}}:=1\)), hypothesis (E) implies (U2), and hypothesis \((\Delta )\) implies (U3). Meanwhile, hypothesis (U4) is true automatically, with \(M=1\), because the functions \(\{u_i\}_{i\in {\mathcal { I}}}\) range over [0, 1]. The asymptotic probability claim now follows from Theorem 6.1. \(\square \)
Proof of Proposition 3.2
If we set \(M:=1\) in formula (11), we obtain formula (5). The asymptotic probability inequality now follows from Theorem 6.2. \(\square \)
Proof of Theorem 4.1
Let \(g:={\mathbb {E}}[u^i_a\,|\, u^i_a\ge \theta _i]\) and let \(b:={\mathbb {E}}[u^i_a\,|\, u^i_a< \theta _i]\); thus \(g>b\). By \((\Theta 1)\) and \((\Theta 2)\), these values do not depend on i or a. For all \(i\in {\mathcal { I}}\), define \(v_i:{\mathcal { A}}\,{{\longrightarrow }}\,{\mathbb {R}}\) by
[The second equality is by Eq. (6).] Then define \(\epsilon _i(a):=v_i(a)-u_i(a)\) for all \(a\in {\mathcal { A}}\). Thus, \(v_i = u_i+\epsilon _i\). By construction, \({\mathbb {E}}[u_i(a)\,|\,v_i(a)]=v_i(a)\), and thus \({\mathbb {E}}[\epsilon _i(a)]=0\), for all \(i\in {\mathcal { I}}\) and \(a\in {\mathcal { A}}\). Let \({\overline{c}}:=g-b\); then \({\overline{c}}>0\). For all \(i\in {\mathcal { I}}\), let \({\widetilde{u}}_i:=u_i/{\overline{c}}\) and \({\widetilde{c}}_i:={\overline{c}}\cdot c_i\); thus, \(c_i\, u_i = {\widetilde{c}}_i\,{\widetilde{u}}_i\). Thus, \(U_{\mathcal { I}}= \frac{1}{I}\sum _{i\in {\mathcal { I}}} {\widetilde{c}}_i{\widetilde{u}}_i\). For all \(i\in {\mathcal { I}}\), let \({\widetilde{v}}_i:=v_i/{\overline{c}}\) and \({\widetilde{\epsilon }}_i := \epsilon _i/{\overline{c}}\); thus, \({\widetilde{v}}_i = {\widetilde{u}}_i+{\widetilde{\epsilon }}_i\). Let \({\widetilde{V}}_{\mathcal { I}}=\sum _{i\in {\mathcal { I}}} {\widetilde{v}}_i\). Then \({\widetilde{V}}_{\mathcal { I}}=V_{\varvec{{\mathcal { G}}}}+\)(a constant). Thus, \({{\mathrm{\mathrm{argmax}}}}_{\mathcal { A}}({\widetilde{V}}_{\mathcal { I}})={{\mathrm{\mathrm{argmax}}}}_{\mathcal { A}}(V_{\varvec{{\mathcal { G}}}})\). But \({{\mathrm{\mathrm{argmax}}}}_{\mathcal { A}}(V_{\varvec{{\mathcal { G}}}})=\mathrm{Appr}({\varvec{{\mathcal { G}}}})\); thus, it suffices to compute the asymptotic probability that \({{\mathrm{\mathrm{argmax}}}}_{\mathcal { A}}({\widetilde{V}}_{\mathcal { I}})\subseteq {{\mathrm{\mathrm{argmax}}}}_{\mathcal { A}}(U_{\mathcal { I}})\), using Theorem 6.1. To do this, we must verify hypotheses (U1)–(U4). First, let \({\overline{u}}:={\mathbb {E}}[u^i_a]\) and let \(\sigma ^2_u:=\mathrm{var}[u^i_a]\) for any \(i\in {\mathcal { I}}\) and \(a\in {\mathcal { A}}\). By hypothesis \((\Theta 1)\), these values are finite and independent of i and a. Let \(M:={\overline{u}}^2+\sigma _u^2\). \(\square \)
Claim A
\(\displaystyle \lim _{I{\rightarrow }{\infty }} \mathrm{Prob}\quad (M \quad \text {and the profile} \{u_i\}_{i\in {\mathcal { I}}} \ \text {satisfy condition } \; \mathrm{(}U4)) = 1\).
Proof
Fix \(a\in {\mathcal { A}}\). For all \(i\in {\mathcal { I}}\), we have \( {\mathbb {E}}[u_i^2(a)] ={\overline{u}}^2 + \sigma ^2_u = M^2\). Thus, \(\frac{1}{I}\sum _{i\in {\mathcal { I}}} u_i(a)^2\) is an average of I independent random variables (by \((\Theta 1)\)), each with expected value \(M^2\). Thus, the Law of Large Numbers implies that
Thus, since \({\mathcal { A}}\) is finite, the claim follows.\(\diamond \)
Hypotheses \((\Theta 1)\) and \((\Theta 2)\) imply that \(\{{\widetilde{u}}_i\}_{i\in {\mathcal { I}}}\), \(\{{\widetilde{v}}_i\}_{i\in {\mathcal { I}}}\) and \(\{{\widetilde{\epsilon }}_i\}_{i\in {\mathcal { I}}}\) satisfy (U2). Hypothesis (C) implies that \(\{{\widetilde{c}}_i\}_{i\in {\mathcal { I}}}\) satisfies (U1), and hypothesis \((\Delta )\) implies that \(\{{\widetilde{u}}_i\}_{i\in {\mathcal { I}}}\) satisfies (U3) (with \(\widetilde{\Delta }:=\Delta /{\overline{c}}\)). Now apply Claim A and Theorem 6.1 to \(\{{\widetilde{u}}_i\}_{i\in {\mathcal { I}}}\), \(\{{\widetilde{v}}_i\}_{i\in {\mathcal { I}}}\), \(\{{\widetilde{\epsilon }}_i\}_{i\in {\mathcal { I}}}\) and \(\{{\widetilde{c}}_i\}_{i\in {\mathcal { I}}}\) to derive the claimed asymptotic probability. \(\square \)
Proof of Theorem 4.2
The strategy is very similar to the proof of Theorem 4.1. Let g be the mean value of \(\gamma \), and let b be the mean value of \(\beta \); thus \(g>b\). For all \(i\in {\mathcal { I}}\), define \(v_i:{\mathcal { A}}{{\longrightarrow }}{\mathbb {R}}\) by
Then define \(\epsilon _i(a):=v_i(a)-u_i(a)\) for all \(a\in {\mathcal { A}}\). Thus, \(v_i = u_i+\epsilon _i\). By construction, \({\mathbb {E}}[u_i(a)]=v_i(a)\), and thus \({\mathbb {E}}[\epsilon _i(a)]=0\), for all \(i\in {\mathcal { I}}\) and \(a\in {\mathcal { A}}\). Let \({\overline{c}}:=g-b\); then \({\overline{c}}>0\). For all \(i\in {\mathcal { I}}\), let \({\widetilde{u}}_i:=u_i/{\overline{c}}\) and \({\widetilde{c}}_i:={\overline{c}}\cdot c_i\); thus, \(c_i\, u_i = {\widetilde{c}}_i\,{\widetilde{u}}_i\). Thus, \(U_{\mathcal { I}}= \frac{1}{I}\sum _{i\in {\mathcal { I}}} {\widetilde{c}}_i{\widetilde{u}}_i\). For all \(i\in {\mathcal { I}}\), let \({\widetilde{v}}_i:=v_i/{\overline{c}}\) and \({\widetilde{\epsilon }}_i := \epsilon _i/{\overline{c}}\); thus, \({\widetilde{v}}_i = {\widetilde{u}}_i+{\widetilde{\epsilon }}_i\). Let \({\widetilde{V}}_{\mathcal { I}}=\sum _{i\in {\mathcal { I}}} {\widetilde{v}}_i\). Then \({\widetilde{V}}_{\mathcal { I}}=V_{\varvec{{\mathcal { G}}}}+\)(a constant). Thus, \({{\mathrm{\mathrm{argmax}}}}_{\mathcal { A}}({\widetilde{V}}_{\mathcal { I}})={{\mathrm{\mathrm{argmax}}}}_{\mathcal { A}}(V_{\varvec{{\mathcal { G}}}})\). But \({{\mathrm{\mathrm{argmax}}}}_{\mathcal { A}}(V_{\varvec{{\mathcal { G}}}})=\mathrm{Appr}({\varvec{{\mathcal { G}}}})\); thus, it suffices to compute the asymptotic probability that \({{\mathrm{\mathrm{argmax}}}}_{\mathcal { A}}({\widetilde{V}}_{\mathcal { I}})\subseteq {{\mathrm{\mathrm{argmax}}}}_{\mathcal { A}}(U_{\mathcal { I}})\), using Theorem 6.1. \(\square \)
Let \(M_g:=g^2 + \mathrm{var}[\gamma ]\) and \(M_b:=b^2 + \mathrm{var}[\beta ]\). Let \(M:=\sqrt{\max \{M_g,M_b\}}\) and let \({\widetilde{M}}:=M/{\overline{c}}\).
Claim B
\(\displaystyle \lim \limits _{I{\rightarrow }{\infty }} \mathrm{Prob}({\widetilde{M}}\; \text { and the profile } \; \{{\widetilde{u}}_i\}_{i\in {\mathcal { I}}} \; \text { satisfy condition }\; \mathrm{(U4)}) = 1\).
Proof
Fix \(a\in {\mathcal { A}}\). For all \(i\in {\mathcal { I}}\), if \(a\in {\mathcal { G}}_i\), then \({\mathbb {E}}[u_i^2(a)] =M_g\). If \(a\in {\mathcal { B}}_i\), then \({\mathbb {E}}[u_i^2(a)] =M_b\). Either way, \({\mathbb {E}}[u_i^2(a)] \le M^2\). Thus, \(\frac{1}{I}\sum _{i\in {\mathcal { I}}} u_i(a)^2\) is an average of I independent random variables (by (S)), each with expected value \(M^2\). Thus, the Law of Large Numbers implies that
Since \({\widetilde{u}}_i:=u_i/{\overline{c}}\) for all \(i\in {\mathcal { I}}\), it follows that
Thus, since \({\mathcal { A}}\) is finite, the claim follows.\(\diamond \)
Hypothesis (C) implies that \(\{{\widetilde{c}}_i\}_{i\in {\mathcal { I}}}\) satisfies (U1). Define \(\sigma ^2_\epsilon :=\max \{\mathrm{var}(\gamma ),\mathrm{var}(\beta \}/{\overline{c}}^2\). Since \({\widetilde{\epsilon }}_i={\widetilde{u}}_i-{\widetilde{v}}_i\), it follows that \(\mathrm{var}({\widetilde{\epsilon }}_i)\le \sigma ^2_\epsilon \) for all i. Thus, hypothesis (S) implies that \(\{{\widetilde{u}}_i\}_{i\in {\mathcal { I}}}\), \(\{{\widetilde{v}}_i\}_{i\in {\mathcal { I}}}\) and \(\{{\widetilde{\epsilon }}_i\}_{i\in {\mathcal { I}}}\) satisfy (U2). Finally, hypothesis \((\Delta )\) implies that \(\{{\widetilde{u}}_i\}_{i\in {\mathcal { I}}}\) satisfy (U3) (with \(\widetilde{\Delta }:=\Delta /{\overline{c}}\)). Now apply Claim B and Theorem 6.1 to \(\{{\widetilde{u}}_i\}_{i\in {\mathcal { I}}}\), \(\{{\widetilde{v}}_i\}_{i\in {\mathcal { I}}}\), \(\{{\widetilde{\epsilon }}_i\}_{i\in {\mathcal { I}}}\) and \(\{{\widetilde{c}}_i\}_{i\in {\mathcal { I}}}\) to derive the claimed asymptotic probability. \(\square \)
Proof of Proposition 4.3
Define \(\{{\widetilde{u}}_i\}_{i\in {\mathcal { I}}}\), \(\{{\widetilde{v}}_i\}_{i\in {\mathcal { I}}}\), \(\{{\widetilde{\epsilon }}_i\}_{i\in {\mathcal { I}}}\) and \({\widetilde{V}}_{\mathcal { I}}\) as in the proof of Theorem 4.2. From Theorem 6.2, along with Claim B, we immediately obtain the limit Eq. (8). However, to obtain more precise estimates of the convergence speed, we must first estimate the speed of the convergence in Claim B, using the next result. \(\square \)
Claim C
Suppose the fourth moments of \(\gamma \) and \(\beta \) are finite. Then there is some \(C_1>0\) (determined by \(\gamma \) and \(\beta \)) such that, for any \(p\in (0,1)\), if \( I>{C_1}/{p}\), then
The proof is very similar to the proof of Claim E in the proof of Proposition 5.3 (below).
Recall that \(\{{\widetilde{u}}_i\}_{i\in {\mathcal { I}}}\), \(\{{\widetilde{v}}_i\}_{i\in {\mathcal { I}}}\) and \(\{{\widetilde{\epsilon }}_i\}_{i\in {\mathcal { I}}}\) satisfy (U2), with \(\sigma ^2_\epsilon :=\max \{\mathrm{var}(\gamma ),\mathrm{var}(\beta \}/{\overline{c}}^2\). For any \(\delta >0\) and \(p\in (0,1)\), define \({\overline{I}}(\delta ,p)\) as in equation (11). Finally, define \(C_2:=8\,|{\mathcal { A}}|\,({\widetilde{M}}^2\, \sigma _c^2+ \sigma _\epsilon ^2)\). Thus, for any \(p,\delta \in (0,1)\), if \(I>C_2/p\,\delta ^2\), then \(I>{\overline{I}}(\delta ,p/2)\), so that, for any \(a\in \mathrm{Appr}({\varvec{{\mathcal { G}}}})={{\mathrm{\mathrm{argmax}}}}_{\mathcal { A}}({\widetilde{V}}_{\mathcal { I}})\), Theorem 6.2 says
If \(I>C_1/p\) also, then Claim C applies. This, together with inequality (12), implies that \(\mathrm{Prob}\left[ U_{\mathcal { I}}(a)< U^*_{\mathcal { I}}-\delta \right] < \frac{p}{2}+\frac{p}{2} = p\), as desired.
Theorem 5.1 follows from Theorem 5.2, so we will prove that first.
Proof of Theorem 5.2
Since \(\mathrm{Score}_{\mathbf { s}}({\mathcal { P}}_{\mathcal { I}})={{\mathrm{\mathrm{argmax}}}}_{\mathcal { A}}(V^{\mathbf { s}}_{{\mathcal { P}}_{\mathcal { I}}})\), it suffices to compute the asymptotic probability that \({{\mathrm{\mathrm{argmax}}}}_{\mathcal { A}}(V^{\mathbf { s}}_{{\mathcal { P}}_{\mathcal { I}}})\subseteq {{\mathrm{\mathrm{argmax}}}}_{\mathcal { A}}(U_{\mathcal { I}})\), as \(I{\rightarrow }{\infty }\). As usual, we will use Theorem 6.1. Hypothesis (C) implies (U1). For all \(i\in {\mathcal { I}}\) and all \(a\in {\mathcal { A}}\), if we know that i ranks a in kth place (in particular, if we know the preference order \(\succ _i\)), then the expected value of \(u_i(a)\), conditional on this information, is \(s_k\). But, by definition, \(v_i(a)=s_k\). Thus, \({\mathbb {E}}[ u_i(a)|\succ _i]=v_i(a)\). Thus, if we define \(\epsilon _i(a):=u_i(a)-v_i(a)\), then \({\mathbb {E}}[ \epsilon _i(a)|\succ _i]=0\). By hypothesis, the variance of the random variable \(u_i(a)\) is finite; thus, the variance of \(\epsilon _i(a)\) is finite. Finally, by hypothesis (X), the random functions \(\{u_i\}_{i\in {\mathcal { I}}}\) are independent of one another and independent of \(\{c_i\}_{i\in {\mathcal { I}}}\). Thus, the random functions \(\{\epsilon _i\}_{i\in {\mathcal { I}}}\) are independent of one another and independent of \(\{c_i\}_{i\in {\mathcal { I}}}\). This establishes (U2). It remains to verify (U4).
Let \({}^{\scriptscriptstyle \uparrow }\!{\mathbf { u}}=({}^{\scriptscriptstyle \uparrow }\!u_1,\ldots ,{}^{\scriptscriptstyle \uparrow }\!u_N)\in {\mathbb {U}}\) be a \(\lambda \)-random vector. The coordinates \({}^{\scriptscriptstyle \uparrow }\!u_1,\ldots ,{}^{\scriptscriptstyle \uparrow }\!u_N\) are themselves random variables (neither independent, nor identically distributed). Let \(\sigma ^2_1,\ldots ,\sigma ^2_N\) denote their variances. Since \(\lambda \) has finite variance, it is easy to check that \(\sigma ^2_1,\ldots ,\sigma ^2_N\) are all finite. Define \(\sigma ^2_\epsilon :=\max \{\sigma ^2_{1},\sigma ^2_{2},\ldots ,\sigma ^2_{N}\}\). Also, let \(S:=\max \{|s_1|\), \(|s_2|\), \(\ldots ,\) \(|s_N|\}\), and choose any \(M>\sqrt{S^2 + \sigma ^2_\epsilon }\). \(\square \)
Claim D
\(\displaystyle \lim _{I{\rightarrow }{\infty }} \mathrm{Prob}(M \; \text { and the profile }\; \{u_i\}_{i\in {\mathcal { I}}} \; \text { satisfy condition (U4)}) = 1\).
Proof
Fix \(a\in {\mathcal { A}}\). For all \(i\in {\mathcal { I}}\), if a is ranked kth from the bottom by \(\succ _i\), then \(u_i(a)\) is a random variable with mean \(s_k\) and variance \(\sigma ^2_k\). Thus,
Thus, for any \(a\in {\mathcal { A}}\), the sum \(\frac{1}{I}\sum \nolimits _{i\in {\mathcal { I}}} u_i(a)^2\) is an average of I independent random variables, each with expected value smaller than \(M^2\), by inequality (13). Thus, regardless of how the preferences \(\{\succ _i\}_{i\in {\mathcal { I}}}\) are obtained, the Law of Large Numbers implies that
Thus, since \({\mathcal { A}}\) is finite, the claim follows.\(\diamond \)
Finally, hypothesis \((\Delta )\) implies that \(\{u_i\}_{i\in {\mathcal { I}}}\) satisfy (U3). Now apply Claim 1 and Theorem 6.1 to \(\{u_i\}_{i\in {\mathcal { I}}}\), \(\{v_i\}_{i\in {\mathcal { I}}}\), \(\{\epsilon _i\}_{i\in {\mathcal { I}}}\) and \(\{c_i\}_{i\in {\mathcal { I}}}\) to derive the limit (9). \(\square \)
Proof of Theorem 5.1
Define \({\mathbb {U}}\) as in Sect. 5.2, and let \(\lambda \) be the conditionalization of \(\mu \) on \({\mathbb {U}}\). In the Endogenous Preference model of Sect. 5.1, the ordinal preference profile \({\mathcal { P}}_{\mathcal { I}}=\{\succ _i\}_{i\in {\mathcal { I}}}\) is a random variable (determined by the underlying cardinal utility profile \(\{{\mathbf { u}}^i\}_{i\in {\mathcal { I}}}\). (\({\mathcal { P}}_{\mathcal { I}}\) is almost surely a profile of strict preferences, because by hypothesis on \(\mu \), no two alternatives yield the same utility for any voter, almost surely.) However, if we fix a particular realization of \({\mathcal { P}}_{\mathcal { I}}\), then conditional on this realization, the probability distribution of the cardinal profile \(\{{\mathbf { u}}^i\}_{i\in {\mathcal { I}}}\) is described by \(\lambda \) via the Exogenous preference model of Sect. 5.2. Thus, for any particular realization of \({\mathcal { P}}_{\mathcal { I}}\), Theorem 5.2 implies that the limit (9) holds.Footnote 17 Thus, integrating over all possible realizations of \({\mathcal { P}}_{\mathcal { I}}\), and applying Lebesgue’s dominated convergence theorem, we conclude that the limit (9) holds unconditionally.Footnote 18 \(\square \)
Proof of Proposition 5.3
We will apply Theorem 6.2. Define \(\{\epsilon _i\}_{i\in {\mathcal { I}}}\) and M as in the proof of Theorem 5.2. Claim 1 established that \(\lim _{I{\rightarrow }{\infty }} \mathrm{Prob}[M\) and the profile \(\{u_i\}_{i\in {\mathcal { I}}}\) satisfy condition (U4)]\(\,{=}\,\)1. However, to obtain the more precise estimate of convergence speed, we need the next observation.
Claim E
Suppose the fourth moment of \(\lambda \) is finite. Then there is some \(C_1>0\) (determined by \(\lambda \)) such that, for any \(p\in (0,1)\), if \( I>{C_1}/{p}\), then
Proof
If the fourth moment of \(\lambda \) is finite, then there is some \(C'>0\) such that for any \(a\in {\mathcal { A}}\), the fourth moments of each of the random variables \(\{u_i(a)\}_{i\in {\mathcal { I}}}\) is less than \(C'\). In other words, the second moments of each of the random variables \(\{u_i(a)^2\}_{i\in {\mathcal { I}}}\) is less than \(C'\). This implies that there is some \(C''>0\) such that the variance of each of \(\{u_i(a)^2\}_{i\in {\mathcal { I}}}\) is less than \(C''\). Also, these random variables are independent. Thus,
Next, inequality (13) says each of \(\{u_i(a)^2\}_{i\in {\mathcal { I}}}\) has expected value less than \(M^2\). Thus,
Thus, Chebyshev’s inequality and inequalities (14) and (15) imply that there is some \(C_1>0\) (determined by \(C''\)) such that, for any \(p>0\), if \(I>C_1/p\), then
Now, if the profile \(\{u_i\}_{i\in {\mathcal { I}}}\) and M to violate condition (U4), then \(\frac{1}{I}\sum _{i\in {\mathcal { I}}} u_i(a)^2 > M^2\) for some \(a\in {\mathcal { A}}\). Thus, adding together \(|{\mathcal { A}}|\) copies of inequality (16) proves the claim. \(\diamond \)
For any \(\delta >0\) and \(p>0\), let \({\overline{I}}(\delta ,p)\) be as in Eq. (11). Finally, define \(C_2:=8\,|{\mathcal { A}}|\,(M^2\, \sigma _c^2+ \sigma _\epsilon ^2)\). Thus, for any \(p,\delta \in (0,1)\), if \(I>C_2/p\,\delta ^2\), then \(I>{\overline{I}}(\delta ,p/2)\), so that, for all \(a\in {{\mathrm{\mathrm{argmax}}}}_{\mathcal { A}}({\widetilde{V}}_{\mathcal { I}})\), Theorem 6.2 says that
If \(I>C_1/p\) also, then Claim E applies. This, together with inequality (17), implies that \(\mathrm{Prob}\left[ U_{\mathcal { I}}(a)< U^*_{\mathcal { I}}-\delta \right] < \frac{p}{2}+\frac{p}{2} = p\) for any \(a\in {{\mathrm{\mathrm{argmax}}}}_{\mathcal { A}}({\widetilde{V}}_{\mathcal { I}})=\mathrm{Score}_{\mathbf { s}}({\mathcal { P}}_{\mathcal { I}})\), as desired.\(\square \)
Rights and permissions
About this article
Cite this article
Pivato, M. Asymptotic utilitarianism in scoring rules. Soc Choice Welf 47, 431–458 (2016). https://doi.org/10.1007/s00355-016-0971-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00355-016-0971-2




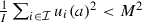 for every a in
for every a in