Optical pressure sensing at MHz rates via collisional line broadening of carbon monoxide: uncertainty quantification in reacting flows

Abstract

An optical method for high-speed line-of-sight pressure measurements using infrared laser absorption spectroscopy is presented with detailed uncertainty analysis related to thermodynamic and compositional variation in combustion environments. The technique exploits simultaneous sub-microsecond sensing of temperature and mole fraction to extract pressure from collisional line broadening at MHz rates. A distributed-feedback quantum-cascade laser near 5 $\upmu$m in a bias-tee circuit is used to spectrally resolve multiple rovibrational transitions in the P-branch of the fundamental band of carbon monoxide, which may be seeded or nascent to reacting flows. A comprehensive approach for estimating collisional line broadening in complex combustion gas mixtures is presented. Uncertainty is quantified for a wide range of conditions, reflecting different fuels, equivalence ratios, reaction progress, and combustion modes (deflagration and detonation), which influence gas composition and temperature. The sensor was evaluated for accuracy and precision in both a high-enthalpy shock-tube facility in hydrocarbon–air ignition experiments and behind ethylene–oxygen detonation waves in a detonation-impulse tube facility at temperatures from 1500 to 3000 K and pressures from 0.5 to 10 bar. Pressure measurements were compared to measurements by piezoelectric pressure transducers and to theoretical estimates from normal-shock and Chapman-Jouguet simulations. The high-speed path-integrated optical pressure measurement offers an alternative to traditional electromechanical transducers that are constrained to values at wall boundaries and have proven unreliable in some harsh reacting flows.

1 Introduction

Pressure measurements are critical to understanding the behavior of thermo-fluid systems. Pressure is indicative of the fluid-mechanical force on solid surfaces in both aerodynamic and propulsive contexts, which is important for understanding thrust/lift/drag generation as well as for structural loading. In many systems, the pressure field is unsteady, with pressure fluctuations traveling at or above the speed of sound. These pressure oscillations may arise from shock/detonation waves, rapid gas compression, turbomachinery [1], or acoustic phenomena, which may be coupled to chemical reactions in the case of combustion instabilities. The timescales associated with these unsteady pressure fluctuations are often in the 100 Hz–100 kHz range. As such, there is a need for high-speed pressure measurements in reacting flows. Conventionally, pressure is measured (electro)mechanically by detecting the force applied by a fluid on a small surface. This force causes the transducer material to strain, which is often linked to a change in an electrical characteristic of the transducer (resistance, capacitance) which then leads to a change in voltage across the sensor. Piezoelectric (PE) or piezoresistive (PR) transducers can perform measurements at up to 100s of kHz through the sensing of charge generation (PE) or mechanical stress (PR) and represent the current state-of-the-art in high-speed pressure measurements for harsh environments.

Despite their broad utility, PE and PR sensors have a few shortcomings in highly dynamic reacting flows. Because of charge migration from the crystal to its surroundings in PE sensors, the pressure measurement changes over long timescales, leading to signal drift [2]. This makes PE sensors unsuitable for measuring static pressure values. Both PE and PR sensors also are susceptible to spurious output signal generation from mechanical vibrations and high temperatures, which are ubiquitous in harsh environments. At combustion-relevant temperatures (>1000 K), the sensor materials begin to degrade, which can lead to total sensor failure after prolonged exposure, on the order of seconds [3, 4]. To combat this, in environments with sustained high heat flux, such as detonation combustors, pressure transducers are often stood off or recessed from the flowfield. This leads to attenuation and distortion of pressure profiles, which can cause errors in peak pressure readings up to 50% [5, 6]. As a result, most approaches to measuring pressure in detonation engines opt to either measure frequency content to infer detonation wave-speed or attenuate high-frequency content altogether to measure time-averaged pressure, also known as capillary-tube attenuated pressure (CTAP) [5].

In addition to the aforementioned practical issues, conventional pressure transducers are constrained to measurements at the boundary of a flowfield. It is often desirable to assess pressure away from solid surfaces, such as for supersonic flows. Boundary-layer effects such as shock bifurcation in dynamic flow fields can induce an offset between pressure in the bulk flow and pressure in the boundary layer [7, 8]. This effect is especially problematic in shock tubes [8], where boundary-layer effects can convolute sidewall pressure measurements made with conventional pressure transducers, increasing the uncertainty in the thermodynamic conditions produced by reflected shocks, particularly for polyatomic driven gases (e.g., CO₂, fuels) [7]. This presents difficulties for shock-tube experiments involving chemical kinetics, as reaction rates are sensitive to combustion pressure. These issues can be mitigated by making pressure measurements at the shock-tube endwall, although this can cause additional experimental complexities. As such, it is desirable to have an alternate method of measuring the pressure in the bulk gas.

Laser-based optical methods can overcome many of the presented challenges, achieving high-speed, non-intrusive, in-situ measurements for which the sensor hardware is not directly exposed to the harsh test gas [9]. Pressure measurements can be made by assessing the collisional line broadening of gaseous spectra, which scales linearly with pressure, as demonstrated previously. Kranendonk et al. [10] measured pressure based on this principle using broadband measurements of the $v_1+v_3$ band of H₂O. Caswell et al. [11] applied this concept to time-resolved measurements of gas pressures in a pulse-detonation combustor, whereas Goldenstein et al. [12] also applied this method to measure pressure in a propane–air flame. Mathews et al. [13] used collisional broadening obtained with wavelength-modulated planar laser-induced fluorescence of CO₂ to make spatially resolved pressure measurements in a room-temperature CO₂–Ar jet. A caveat to collisional-broadening-based pressure measurements is that the scaling factor between pressure and line broadening (known as the collisional-broadening coefficient $\gamma$) is both temperature- and composition-dependent. In the above works, either simple gas mixtures were studied or simplifying assumptions about the gas composition were made. Our group, as well as Mathews et al. [14, 15], recently measured gas pressure at the exhaust of CH₄/O₂ rotating-detonation rocket engine using laser absorption spectroscopy of CO. In these prior works, pressure uncertainty was estimated for the specific applications.

In the present work, the MHz-rate optical pressure-sensing strategy based upon collisional line broadening of CO is presented as a broadly applicable method for interrogating a wide range of dynamic combustion environments, with detailed analysis of a comprehensive range of uncertainty factors. First, in Sect. 2, the high-speed pressure-measurement methodology based on infrared laser absorption spectroscopy is detailed. Then, in Sect. 3, an uncertainty-analysis methodology is introduced to account for the influence of various sources of the uncertainty in the pressure measurement. Uncertainty sources include measurement signal noise, spectroscopic uncertainties, and uncertainty in gas composition. These uncertainties are quantified over a range of conditions, reflecting different fuels, equivalence ratios, reaction progress, and combustion modes (deflagration and detonation), which influence gas composition and temperature. Correlations between uncertainty sources are also assessed. This uniquely comprehensive uncertainty analysis indicates broad utility of the method and enables uncertainty estimation in a variety of applications, representing the primary contribution of the paper. Finally, in Sect. 4, the utility and precision/accuracy of the sensor is demonstrated and compared to conventional techniques in laboratory environments in (1) a high-enthalpy shock tube and (2) a detonation-impulse facility, at temperatures from 1500 to 3000 K and pressures from 0.5 to 10 bar. The Supplemental Document linked at the end of the text provides additional details on the uncertainty analysis and chemical kinetic analysis.

2 Methodology

Fig. 1

Left: Bias-tee laser control schematic used to inject trapezoidal MHz waveform into DFB QCL. Laser light is attenuated by absorbing gas, which is measured by a PV detector and oscilloscope. A germanium etalon may be inserted into the beam path to assess the chirp profile of the laser over a modulation period. Sample raw MHz laser absorption data are shown below. Right: measured sub-microsecond absorbance spectrum of target CO line cluster along with spectral fit. The spectral parameters (areas, linewidth) used to obtain pressure, temperature, and CO partial pressure are indicated on the spectrum. The peak-normalized residual r between the measurement and fit is plotted below

Pressure is inferred in this method from spectrally resolved lineshapes obtained using laser absorption spectroscopy (LAS)¹ [16]. The absorbance $\alpha$ is determined from the attenuation of laser light intensity through an absorbing medium, as pictured in the top left of Fig. 1. A distributed-feedback (DFB) quantum-cascade laser (QCL) is used as a narrowband mid-infrared light source. The transmitted laser intensity is recorded on a photovoltaic (PV) detector. If $I_0$ is the light intensity before attenuation and $I_{\text {tr}}$ is the light intensity after attenuation, absorbance is defined as

$$\begin{aligned} \alpha =-\ln \left( \frac{I_{\text {tr}}}{I_0}\right) \end{aligned}$$

(1)

An absorbance spectrum may be probed during a single measurement by modulating/tuning the laser output wavelength. For DFB lasers, this wavelength tuning is accomplished by changing the temperature of the laser, which changes the resonance of the laser cavity. High-speed tuning is typically achieved using current modulation, which has been traditionally limited in bandwidth to 100s of kHz by the laser controller. A bias-tee tuning configuration (pictured in Fig. 1) can be used to directly inject a current-modulation waveform into the laser, bypassing the controller, enabling wavelength tuning at MHz rates [14]. This has enabled MHz measurements of line clusters with a total output wavenumber amplitude (scan depth) up to 1 cm$^{-1}$ [17, 18]. Assuming a uniform gas medium across the line-of-sight,² the absorbance $\alpha _i$ from single spectral transition i is described by the Beer-Lambert law:

$$\begin{aligned} \alpha _i(\nu ) = S_i(T)p_jL\phi _i(\nu ,P,T,X_1,\ldots ,X_N) \end{aligned}$$

(2)

where $\nu$ is the wavenumber [cm$^{-1}$] of the incident light, $S_i(T)$ [cm$^{-2}$/atm] is the absorption linestrength of transition i at temperature T, $p_j$ [atm] is the partial pressure of gas species Y which is absorbing light, $X_1$–$X_N$ are the set of mole fractions of all N species in the gas, and L [cm] is the optical path length.

The lineshape function $\phi$ is modeled as a Voigt profile [19], which is a convolution of a Lorentzian and a Gaussian profile, resulting from two dominant broadening mechanisms. The Gaussian lineshape is due to the Doppler broadening of the line, whose FWHM termed ‘Doppler width’, $\Delta \nu _{\text {D}}$ [cm$^{-1}$], is given by

$$\begin{aligned} \Delta \nu _{\text {D}}=\nu _0\sqrt{\frac{8k_{\text {B}}T\ln {2}}{mc^2}} \end{aligned}$$

(3)

$\nu _0$ [cm$^{-1}$] is the center wavenumber of the transition, $k_{\text {B}}$ [erg$\cdot$K$^{-1}$] is the Boltzmann constant, m [g] is the mass of the gas species, and c [cm$\cdot$s$^{-1}$] is the speed of light. The Lorentzian lineshape results from collisional broadening (also termed pressure broadening). The Lorentzian FWHM arising from collisional broadening (termed the ‘collision width’), $\Delta \nu _{\text {C}}$ [cm$^{-1}$], is related to the total collision rate $Z_{j-{\text {mix}}}$ [s$^{-1}$] of absorbing species j with the ‘mix’ of gas species in the mixture:

$$\begin{aligned} \Delta \nu _{\text {C}} = \frac{Z_{j-{\text {mix}}}}{\pi {c}} \end{aligned}$$

(4)

For an ideal gas, the total collision rate of Eq. 5 is proportional to the gas pressure P and inversely related to the temperature T:

$$\begin{aligned} Z^{\text {id}}_{j-{\text {mix}}}=P~ [{\text {Ba}}]\cdot \sum _Y{X_Y\pi {\sigma ^2_{j-Y}}\left( \frac{8}{\pi \mu _{j-Y}k_{\text {B}}T}\right) ^{1/2}} \end{aligned}$$

(5)

Here, the subscript Y refers to each species present in the gas mixture that can act as a ‘collision partner’ to the absorbing species. $\sigma _{j-Y}$ [cm] is the ‘optical collision diameter’ of the absorbing species and a collision partner Y, given by

$$\begin{aligned} \sigma _{j-Y} = \frac{1}{2}(\sigma _j+\sigma _Y) \end{aligned}$$

(6)

$\sigma _j$ and $\sigma _Y$ refer to the individual effective diameters of the molecules. $\mu _{j-Y}$ [g] is the ‘reduced mass’ of j and Y and is given by

$$\begin{aligned} \mu _{j-Y} = \frac{m_jm_Y}{m_j+m_Y} \end{aligned}$$

(7)

The temperature and gas mixture dependence of the collisional broadening can be lumped into a single coefficient, termed the ‘collisional broadening coefficient’ $\gamma$ [cm$^{-1}\cdot$atm$^{-1}$], such that Eqs. 4 and 5 can be combined as

$$\begin{aligned} \Delta \nu _{\text {C}}=2\gamma {P} \end{aligned}$$

(8)

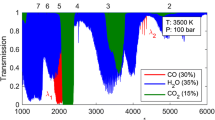
with P in units of atm. $\gamma$ is the half-width at half-maximum (HWHM) per unit pressure for a collisionally broadened lineshape. It is this simple linear dependence of the collision width on pressure in Eq. 8 that is exploited to infer pressure from absorption lineshapes. The pressure dependence of the target CO absorption spectrum for this work, due to the increase in $\Delta \nu _{\text {C}}$, can be seen in Fig. 2.

$\gamma$ can be expressed as the weighted sum over each collision partner with broadening coefficient $\gamma _{j-Y}$:

$$\begin{aligned} \gamma = \sum _Y{X_Y\gamma _{j-Y}} \end{aligned}$$

(9)

Ideally, each $\gamma _{j-Y}$ takes the approximate form:

$$\begin{aligned} \gamma _{j-Y}\approx (9.87\cdot 10^{-7})\frac{\sigma ^2_{j-Y}}{c}\left( \frac{2}{\pi \mu _{j-Y}k_{\text {B}}T}\right) ^{1/2} \end{aligned}$$

(10)

In reality, this temperature scaling of $\gamma _{j-Y}$ is not exact, with the exponent on T deviating from 1/2. To capture this non-ideal effect, $\gamma _{j-Y}$ is often modeled with a power law:

$$\begin{aligned} \gamma _{j-Y}(T)=\gamma _{j-Y,0}\left( \frac{T_0}{T}\right) ^{N_{j-Y}} \end{aligned}$$

(11)

Here, $\gamma _{j-Y,0}$ is a reference value of the collisional broadening coefficient at reference temperature $T_0$, and $N_{j-Y}$ is the ‘temperature exponent’ of the power law. These parameters not only depend on collision partner, but also vary across different spectral transitions for a given molecule. Typically both $\gamma _0$ and N decrease with rotational quantum number and are a weak function of vibrational quantum number [20]. These parameters have been characterized and catalogued for many absorbing species and collision partners in the literature [21]. From Eqs. 9 and 11, knowledge of the collisional-broadening parameters ($\gamma _0$ and N) as well as gas composition and temperature T can enable knowledge of the collisional-broadening coefficient $\gamma$ for a given gas mixture and condition. This knowledge can be used along with measurement of collision line width to measure pressure using Eq. 21.

As a convolution of two simple lineshapes, the Voigt lineshape may be expressed as a function of $\Delta \nu _{\text {D}}$ and $\Delta \nu _{\text {C}}$. In order to isolate changes in linewidth to collisional processes, it is advantageous to fix the value of $\Delta \nu _{\text {D}}$ in spectral fitting routines. As such, knowledge of the gas temperature is required to calculate $\Delta \nu _{\text {D}}$ (and $\gamma$).

Temperature can be obtained using two-line thermometry [16]. In this technique, the spectrally integrated area under an absorption feature, $A_i$, is utilized. This ‘absorbance area’ is related to the gas properties by spectrally integrating the Beer-Lambert law using $\int ^{+\infty }_{-\infty }\phi _i(\nu )d\nu =1$:

$$\begin{aligned} A_i=\int ^{+\infty }_{-\infty }\alpha _i(\nu )d\nu = S_i(T)p_jL \end{aligned}$$

(12)

If the ratio $R_{12}$ of the absorbance areas of two transitions 1 and 2 (as in Fig. 1) are taken, the resulting ratio is purely a function of temperature:

$$\begin{aligned} R_{12}=\frac{A_2}{A_1}=\frac{S_2(T)}{S_1(T)}=\frac{S^0_2}{S^0_1}F_{12}(T) \end{aligned}$$

(13)

Here, $S^0_i$ refers to the room-temperature linestrength of transition i and $F_{12}(T)$ is a temperature-dependent function that depends exponentially on the difference in lower state energies of the two transitions, $\Delta {E}''_{12}=E''_1-E''_2$. Knowledge of the ratio of two absorbance areas of transitions with a large difference in lower state energy enables sensitive temperature measurements, providing knowledge of the Doppler width and collisional-broadening coefficient.

Fig. 2

Simulation of target CO line cluster at fixed temperature, CO mole fraction, and pathlength, with pressure varied. Linestrengths at 2500 K are shown in green

Temperature is also used to evaluate the linestrengths of the spectrally resolved transitions, which enables a quantitative determination of species. Specifically, the linestrength is used with the integrated Beer-Lambert law of Eq. 12 to find the partial pressure of the absorbing gas:

$$\begin{aligned} p_j=\frac{A_2}{S_2(T)L}=\frac{A_1}{S_1(T)L} \end{aligned}$$

(14)

Using the total pressure P determined from collision linewidth, the mole fraction of the absorbing gas $X_j$ can also be determined:

$$\begin{aligned} X_j = \frac{p_j}{P} \end{aligned}$$

(15)

For this work, rovibrational transitions of CO in the mid-infrared are used to simultaneously probe gas pressure, temperature, and CO concentration. Carbon monoxide was selected for several reasons: (i) CO is ubiquitous in hydrocarbon combustion systems as stable intermediate that is a precursor to carbon dioxide CO₂ for fuel-lean systems, or a major product for fuel-rich hydrocarbon combustion systems, (ii) CO can remain in the product gas due to incomplete carbon oxidation or due to the dissociation of CO₂, (iii) CO can be present in reactant gases due to exhaust gas recirculation, and (iv) and CO can be employed as a fuel for some applications [22]. Therefore, the significant concentrations of CO in many modes of combustion make it an attractive target for gas property measurement in combustion systems. In addition, CO concentration is highly sensitive to both equivalence ratio and reaction progress—as such, making CO mole fraction measurements in tandem with collision width measurements can reduce uncertainty in overall mixture composition by providing insight on the combustion state of the test gas.

In addition to these combustion-related arguments, CO is one of the strongest absorbers in the infrared, enabling highly sensitive measurements. Due to its simple diatomic structure and singlet electronic ground state, the CO lines are typically well separated which permits accurate fitting and high confidence to spectral parameters. Recent advances in mid-infrared photonics [23] have enabled access to the CO fundamental band, which has orders of magnitude stronger absorption strength compared to the overtone bands in the near-infrared. In addition, compared to other common species in combustion gas (e.g., H₂O, NH₃), the collisional-broadening coefficients for CO (1) do not vary dramatically with most common collision partners, minimizing the impact of unknown bath gas composition on pressure-measurement accuracy and (2) do not vary significantly with rovibrational quantum number, particularly at high temperatures [14], reducing the uncertainty in the spectroscopic broadening parameters.

In this work, two transitions near 5 $\upmu$m ($\nu _0\sim$ 2008.5 cm$^{-1}$) in the fundamental rovibrational band of CO are targeted: P(2,20) and P(0,31). This line selection has been used in previous works [14, 24,25,26] due to its high absorption strength, relative spectral isolation from other significant combustion species, the close spacing of the two transitions to enable two-line thermometry with a single narrowband laser, and the large difference in lower state energy $\Delta {E}''$ of these transitions. A measurement of the absorbance spectrum of this line cluster is shown on the right side of Fig. 1, and is simulated at various pressures in Fig. 2, highlighting the sensitivity of the spectrum to pressure. The next section of this work details the precision and accuracy of pressure measurement with these specific spectral transitions of CO. Nevertheless, the methods of this work can be applied to any significantly collisionally broadened line selection for any number of gas species of interest.

3 Uncertainty analysis

In this section, we rigorously analyze the uncertainties in the optical pressure measurement arising from several sources. First, Sect. 3.3.1 details the framework used to integrate the influences of various error sources into the overall uncertainty in a measured variable (i.e., pressure). The overall uncertainty in pressure is related to the uncertainty in the measured collision width, $\Delta \nu _{\text {C}}$, and the inferred collisional-broadening coefficient, $\gamma$. As such, Sect. 3.3.2 details the uncertainties influencing $\Delta \nu _{\text {C}}$ and Sect. 3.3.3 examines the uncertainties influencing $\gamma$. Section 3.3.4 combines the potential errors from these two parameters to derive the total uncertainty in pressure. Some extra details of the uncertainty analysis are included in the Supplementary Material, Section S2.

3.1 Uncertainty analysis framework

We use the Taylor Series Method (TSM) [27] to propagate uncertainties between related quantities, as in Refs. [14, 17], with some modifications to account for the directionality and correlation of uncertainties. Uncertainty represents an aggregation of potential errors or deviations between a measurement result and its true value. Since errors are often not known a priori and cannot always be obtained for certain types of measurements, uncertainty is used to reflect the confidence with which a stated measurement result represents the true value of a measured quantity given such unknowns. For a given variable g, the uncertainty in g is written as $\delta {g}^{\{\theta \}}$. $\delta {g}^{\{\theta \}}$ is always a positive number, where the superscript ${\{\theta \}}$ refers to the directionality of the potential error. If $\theta =+1$ (or ‘+’ for short), the potential error is considered positive and if $\theta =-1$ (or ‘−’ for short), the error is considered negative, such that $g^{\text {meas}}-\delta {g^-}{\le }g^{\text {true}}{\le }g^{\text {meas}}+\delta {g^+}$. If g depends on N independent variables $x_1$–$x_N$, the uncertainty in g is assumed to take the following form:

$$\begin{aligned} \delta {g}^{\{\theta \}} =\sum _{k=1}^N \left| \frac{\partial {g}}{\partial {x_k}}\right| \delta {x_k}^{\{d_k\}}=\sum _{k=1}^N(\delta {g})_{x_k}^{\{\theta \}} \end{aligned}$$

(16)

$\delta {x_k}^{\{d_k\}}$ is the uncertainty in the kth input variable $x_k$ and $(\delta {g})_{x_k}^{\{\theta \}}$ is the contribution to the uncertainty in g from the uncertainty in $x_k$, which is the potential error in g from $x_k$. It is assumed that each uncertainty in $x_k$ is small, albeit potentially different in magnitude depending on direction, and that g is locally linear from $x_k-\delta {x_k}^{-}$ to $x_k+\delta {x_k}^{+}$. It should be noted that this summation of potential errors is performed linearly rather than in quadrature in order to more easily account for directionality. A correction factor of $\sqrt{2}$ is later introduced to make overall uncertainty estimates consistent with the more common sum of squared error (SSE) approach. The directionality of the potential error contribution of $x_k$, $\{d_k\}$, depends on the sign of $\partial {g}/\partial {x_k}$:

$$\begin{aligned} d_k=\theta \cdot {\text {sgn}}\left( \frac{\partial {g}}{\partial {x_k}}\right) \end{aligned}$$

(17)

If $\partial {g}/\partial {x_k}$ is positive, then the positive potential error in $x_k$ contributes to the positive uncertainty in g. If $\partial {g}/\partial {x_k}$ is negative, then the negative potential error contribution of $x_k$ contributes to the positive uncertainty in g. This is especially important for errors that are potentially higher in one direction. In this work, if the directionality superscript is dropped from an equation, it is implicit that positive potential error contributions sum to the positive uncertainty in g and negative potential error contributions sum to the negative uncertainty in g.

Often, the relative uncertainty ($\delta {g}/g$) of a parameter is of greater importance than the absolute uncertainty ($\delta {g}$). The individual contributions to $\delta {g}/g$ (potential errors) from each $x_k$ are notated as $E(g,x_k)$, where:

$$\begin{aligned} E(g,x_k) = \left( \frac{\delta {g}}{g}\right) _{x_k} = \frac{(\delta {g})_{x_k}}{g} \end{aligned}$$

(18)

The total relative uncertainty in g is notated as E(g). $E^+(g)$ and $E^-(g)$ refer to the positive and negative relative uncertainties in g. Sometimes, $x_k$ will not refer to a numerical variable, but a general uncertainty source, such as noise in the measured absorbance spectra ($x_k=\alpha$), uncertainty in fundamental spectroscopic parameters ($x_k={\text {spec.}}$), or compositional uncertainty $(x_k={\text {mix}})$.

The sensitivity of g to one of its inputs $x_k$, $s(g,x_k)$, is of importance to quantifying aggregate uncertainty and is defined as

$$\begin{aligned} s(g,x_k)=\frac{x_k}{g}\frac{\partial {g}}{\partial {x_k}} \end{aligned}$$

(19)

For small changes in $x_k$, such that g is linear with $x_k$, $s(g,x_k)$ is the percent change in g per percent change of input $x_k$. A sensitivity s can represent an approximate local relationship between g and $x_k$ of the form $g={x_k}^s$. Using s, Eq. 16 may be rewritten in terms of relative uncertainty as Eq. 20 for uncorrelated potential errors:

$$\begin{aligned} E^{\{\theta \}}(g)= \sum _{k=1}^N\left| s(g,x_k)\right| E^{\{d_k\}}(x_k)=\sum _{k=1}^NE^{\{\theta \}}(g,x_k) \end{aligned}$$

(20)

In the remainder of this work, we also included correlation terms in Eqs. 16 and 20, as per Eqs. S1 and S2 in Section S2.A of the Supplemental Document.

Pressure is the primary measured variable in this work, inferred from the re-arranged form of Eq. 8:

$$\begin{aligned} P=\frac{\Delta \nu _{\text {C}}}{2\gamma } \end{aligned}$$

(21)

The uncertainty in pressure is linked to the uncertainties in the collision width, $\Delta \nu _{\text {C}}$, and the collisional-broadening coefficient, $\gamma$. The collision width is measured directly from a fitted Voigt lineshape to experimental data. As such, the uncertainty in collision width is the potential error due to signal noise in the measurements, $E(\Delta \nu _{\text {C}},\alpha )$. The uncertainty in the collisional broadening coefficient is dominated by the potential errors in the species-specific spectroscopic broadening parameters and the composition of the gas being examined, which largely affect the accuracy of the measurement (rather than precision). In addition, the collisional-broadening coefficient is temperature-dependent, so there is additional uncertainty associated with the temperature measurement. The temperature measurement has potential error contributions from the signal noise and bias from the measurements, $E(T,\alpha )$ and $E(T,{\text {bias}})$, and therefore, is not independent from the collision width potential error contributions. In the following subsections, we investigate the various sources of potential error in the pressure-measurement technique and ultimately discuss the relative impact of each uncertainty source on the overall pressure-measurement uncertainty.

3.2 Collision-width uncertainty

To provide a general description of the factors influencing the measurement of collision width from a measured absorption spectrum, a single Voigt lineshape with measurement noise was simulated and fitted across many pressure/temperature and noise conditions. Several details of this single-line analysis are given in Section S2.B of the supplemental document. Only the most important takeaways are described here.

The potential error in collision width is related to the noise in the absorption measurement, which either presents as high-frequency random ‘white noise’ in the absorbance signal or as low-frequency noise which manifests as a distortion of the non-absorbing baseline of the spectrum. The effect of white noise on precision error is evaluated numerically by fitting Voigt profiles with added white noise. The spread in the fitted collision width is taken as the precision error. It is determined that the precision error in the collision width measurement, notated $E(\Delta \nu _{\text {C}},\alpha )$, scales linearly with the relative noise in the absorbance measurement $E(\alpha _{\text {pk}})=(\delta \alpha /\alpha )_{\text {pk}}$. In addition, the precision error is minimized when collision width is approximately equal to the full Voigt FWHM (termed the Voigtian width $\Delta \nu _{\text {V}}$), as is the case at moderate pressures (here the Voigt lineshape can be closely approximated by a Lorentzian).

Fig. 3

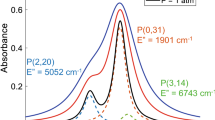
Collision linewidth precision error, normalized by absorbance noise, versus the ratio of scan depth to linewidth for fitted Lorentzian lineshapes. The blue, black, and green curves represent fits of a single line with varied spectral resolution and baseline uncertainty (fitted with a 2nd-order polynomial). The red and purple curves represent fits of blended lineshapes at various line spacings

Spectral sampling parameters, such as scan depth $D_\nu$ [cm$^{-1}$], and spectral wavenumber resolution, $r_\nu$ [cm$^{-1}$], also affect precision error. Figure 3 plots the collision width precision error (normalized by absorbance white noise amplitude $E(\alpha )$) versus the ratio of scan depth to linewidth. When examining the black and blue curves, it can been seen that increasing the scan depth reduces precision error up to approximately five times the transition linewidth, i.e., $D_\nu = 5\Delta \nu _{\text {V}}$. In addition, in comparing the black and blue curves, it can be seen that the precision error scales with the number of data points per linewidth, i.e., $E(\Delta \nu _{\text {C}}, \alpha ) \propto 1/\sqrt{n}$, where $n=r_\nu /\Delta \nu _{\text {V}}$ is the number of data points per FWHM. A convenient summary of the aforementioned trends is encapsulated in the following approximation:

$$\begin{aligned} E(\Delta \nu _{\text {C}},\alpha )\approx \sqrt{\frac{20}{n}} \frac{\Delta \nu _{\text {V}}}{\Delta \nu _{\text {C}}}E(\alpha _{\text {pk}}) \end{aligned}$$

(22)

When time-averaging over $\eta =f_{\text {scan}}/f_{\text {req}}$ measurement samples, precision error is reduced by a factor $\sqrt{\eta }$.

Fig. 4

Plot of precision error in the collision width of the P(0,31) line (left) and in temperature (right) versus pressure and temperature for the multi-line fitting procedure. $X_{\text {CO}}L=0.3$ cm, SNR$_{\text {opt}}=$ 250, $D_\nu =0.7$ cm$^{-1}$, $r_\nu =0.002$ cm$^{-1}$, ${\overline{f}}_{\text {BL}}^{\text {max}}=0.25$ cycles/cm$^{-1}$, and $\Delta \alpha _{\text {BL}}^{\text {max}}=0.5$. Black dashed lines represent level curves of fixed error values

The variation of precision error with changing baseline distortion was also examined. The baseline distortion was modeled as a low-frequency sine wave with random amplitude, frequency, and phase. This distortion increases precision error, as observed by comparing the green and black curves of Fig. 3. A convenient rule of thumb is established: in order to fit the noise with a 1st- or 2nd-order polynomial with minimal precision error, the scanning frequency should be at least ten times or twice the temporal frequency of baseline noise, respectively (see Section S2.B.4 of the Supplemental Document).

Lastly, two overlapping transitions are simulated at variable line spacing $\Delta \nu _{12}$ to investigate the effect of line blending on precision. Blended lines increase the aforementioned scan depth threshold to $D_{\nu } = 5\Delta \nu _{\text {V}}+\Delta \nu _{12}$. Even when the lines are well resolved, there is significant increase in precision error (factor ${\approx }1+2\Delta \nu _{\text {V}}/\Delta \nu _{12}$) when the line spacing is below the linewidth due to the difficulty in separating the contributions of each transition to the spectrum. The red and purple curves of Fig. 3 show the precision versus scan depth for select values of line spacing. While the above analyses of generic Voigt/Lorentzian lineshapes provide valuable insights, a more accurate evaluation accounting for the specific absorption characteristics (temperature dependence, line blending, broadening parameters, etc.) of the multi-line CO spectrum near 2008.5 cm$^{-1}$, used for the particular sensing strategy of this work, was conducted.

For the multi-line analysis, the two primary CO features discussed previously, P(2,20) (line 1) and P(0,31) (line 2), are simulated along with the smaller P(3,14) (line 3) line which contributes significantly to the spectrum at temperatures above 2000 K. Line 3 is not used for thermometry and blends significantly with P(0,31), which adds complications to the spectral fitting procedure. The error analysis was performed over a range of representative conditions: $T =$ 1000–4000 K, $P =$ 0.1–10 atm, with $r_\nu =0.002$ cm$^{-1}$, $D_\nu =0.7$ cm$^{-1}$, $X_{\text {CO}}$ = 3%, and L = 10.32 cm. The lines are simulated using the HITEMP database [21] and the CO–N₂ collisional-broadening model discussed below in Sect. 3.3.1. Low-frequency sinusoidal baseline (BL) noise is added to the simulated spectra (${\overline{f}}_{\text {BL}}>0.25$ cycles/cm$^{-1}$, $\Delta \alpha _{\text {BL}}<0.5$). White noise is added to each simulation using Eq. S3, using the absorbance value at each point in the spectrum to generate a spectrally varying noise profile. The resulting absorbance noise is $<2\%$, with variation across gas conditions (discussed further in Section S2.B of the Supplemental Document). This absorbance noise scales inversely with $X_{\text {CO}}L$. 50 randomly generated baseline and white noise combinations are added to the spectral simulations, resulting in 50 fitted results.

The noisy profiles are fitted using a non-linear least squares fitting routine to the sum of 3 Voigt profiles along with a quadratic polynomial (to fit the baseline noise). This fitting routine is based of that of Ref. [14] with some modifications. In this fitting routine, the relative line positions between the three transitions ($\nu _{0,1}-\nu _{0,2}$ and $\nu _{0,3}-\nu _{0,2}$) are fixed, with the absolute line position $\nu _{0,2}$ floated. The absorbance areas of the two major lines, $A_1$ and $A_2$, are floated, and temperature is obtained using Eq. 13 from the ratio $R_{12}=A_1/A_2$. The absorbance area of the P(3,14) line, $A_3$ is fixed at the value corresponding to the temperature derived from the ratio of the other two-line areas. The Doppler widths for the three lines are also fixed at the value derived from this temperature. The collision width of the dominant P(0,31) line, $\Delta \nu _{{\text {C}},2}$, is floated, with the collision widths of the other two lines fixed at the temperature-dependent ratio predicted by the CO–N₂ broadening model developed in Sect. 3.3.1. The initial guesses for the floated Voigt parameters ($\nu _{0,2}$, $A_1$, $A_2$, $\Delta \nu _{{\text {C}},2}$) are randomized by ±2% of their known values (or of $r_\nu$ for the line position) and the guesses for the baseline polynomial coefficients are set to 0. Each of the 50 noisy profiles for each condition are fitted and the range in the resulting fitted collision width and temperature are assessed. These range values are normalized by the known value of the parameters to obtain $E(\Delta \nu _{{\text {C}},2},\alpha )$ and $E(T,\alpha )$ for each pressure and temperature condition. These measurement errors are plotted in Fig. 4 to show the dependence on temperature and pressure.

For many combustion-relevant conditions, the precision error in $\Delta \nu _{\text {C}}$ and T is 1–5% (SNR$_{\text {meas}}>20$–100). As shown in Fig. 4, precision error is minimized between 1 and 2 atm for temperatures between 2000 and 2500 K, with a minimum error of around 1.5%. At higher temperatures and lower pressures, the reduced spectral resolution and weaker absorption reduces precision. The reduced collision width relative to overall linewidth further increases $E(\Delta \nu _{\text {C}},\alpha )$ at low P / high T conditions, whereas reduced sensitivity of the absorbance area ratio $R_{12}$ with temperature and the increased convoluting effect of the P(3,14) line increase $E(T,\alpha )$ for $T> 2500$ K. At $T \le 1000$ K, the strength of the P(2,20) line decreases, decreasing the precision on its area measurement thus increasing the temperature precision error. At $P \ge 5$ atm, the increased effect of baseline distortion and the blending of the two primary transitions begins to preclude accurate separation of the absorbance features from each other and from low-frequency noise, increasing precision error. The baseline/blending affects temperature much more significantly due to the increased propensity for absorbance area to become convoluted by these factors than linewidth, as discussed in Sections S2.B.4 and S2.B.5 of the Supplemental Document. In addition to the collision width and temperature, the partial pressure of CO may be obtained from the fitting results using Eq. 14. The precision error on $p_{\text {CO}}$ is discussed in Section S2.D of the supplemental document and is in the 1–5% range (SNR$_{\text {meas}}(p_{\text {CO}})\sim$ 20–100) between 1 and 10 atm. It should be noted that above 10 atm, the three-line model is insufficient to characterize real CO spectra, as the wings of neighboring CO transitions begin to overlap with the three lines simulated here.

In addition to the precision error, the potential bias errors associated with assumptions in the fitting procedure were also examined: (1) the linestrength of the perturbing P(3,14) line, whose value from HITEMP 2019 has an uncertainty between 5 and 10%, (2) uncertainty in the collisional-broadening assumptions, namely the relative value of $\gamma _1$ and $\gamma _3$ with respect to the collisional-broadening coefficient of the main line, $\gamma _2$, and (3) potential error associated with the fixed Doppler width. Each of these parameters were evaluated independently, by assuming they were actually 10% higher when generating the simulated spectrum. The spectra were then fitted as normal and the fitting results were compared to the originally generated spectra. This was repeated for all of the temperature/pressure conditions of interest. The effect of an underestimation of $S_3^0$ has the effect of causing an overestimate of $\Delta \nu _{{\rm C},2}$. This potential error is more pronounced at higher temperatures and lower pressures, and is about 1.2% at $P=$ 1 atm and $T=$ 2500 K. If a 10% uncertainty in $\gamma _1/\gamma _2$ is assumed, the potential error associated with an incorrect assumption for $\gamma _1$ relative to $\gamma _2$ contributes about 1% uncertainty at $P=$ 1 atm and $T=$ 2500 K, with a more pronounced effect at higher temperatures and lower pressures. The potential error associated with an incorrect assumption for $\gamma _3$ relative to $\gamma _1$ contributes about 0.8% uncertainty at $P=$ 1 atm and $T=$ 2500 K when a 10% uncertainty on $\gamma _3/\gamma _2$ is assumed. This error is minimized at lower temperatures, and at moderate pressures near 3 atm. In general, error in the Doppler width is less consequential because the broadening is typically collision dominated in conditions of interest to combustion systems, see Section S2.B.1 of the Supplemental Document. Nevertheless, the sensitivity of the collision width measurement to the assumed Doppler width is useful to cases where there is collisional narrowing [16, 28]. At 1 atm and 2500 K, if an uncertainty in the Doppler width of 1% is assumed, the contribution to the uncertainty on $\Delta \nu _{{\rm C}_2}$ is 0.3%.

The aforementioned potential errors in the collision width from measurement noise and biases introduced by the fitting procedure are assumed to be independent, and can be combined using Eq. 20 to obtain the overall uncertainty $E(\Delta \nu _{\rm C})$ in the collision width at a given temperature and pressure condition:

$$\begin{aligned} E(\Delta \nu _{\rm C})=E(\Delta \nu _{\rm C},\alpha )+E(\Delta \nu _{\rm C},{\rm bias}) \end{aligned}$$

(23)

$$\begin{aligned} \begin{aligned} E(\Delta \nu _{\rm C},{\rm bias})&= E(\Delta \nu _{\rm C},S_3^0)+E(\Delta \nu _{\rm C},\gamma _1) \\ {}&+E(\Delta \nu _{\rm C},\gamma _3) +E(\Delta \nu _{\rm C},\Delta \nu _{\rm D}) \end{aligned} \end{aligned}$$

(24)

This uncertainty may be combined with the potential errors in the collisional-broadening coefficient $\gamma$ using Eq. S2 to obtain the overall uncertainty in the pressure measurement. The following subsection will detail the uncertainty in $\gamma$.

3.3 Broadening coefficient uncertainty

In this section, we detail the model used to estimate the collisional-broadening coefficients of CO. Section 3.3.3.1 details the assumptions made for the species-specific collisional-broadening parameters and their associated uncertainty. Section 3.3.3.2 then shows how these parameters are combined including composition uncertainty.

3.3.1 Species-specific broadening coefficient uncertainty

This subsection details the uncertainties in species-specific broadening coefficients which are used to estimate $\gamma$. The effect of errors in $\gamma _{{\rm CO}-Y,0}$ and $N_{{\rm CO}-Y}$ on $\gamma _{{\rm CO}-Y}(T)$ (labeled as $\gamma _{Y0}$, $N_Y$, and $\gamma _Y$ for brevity) is obtained by applying Eqs. 20 to  11:

$$\begin{aligned} \begin{aligned} E(\gamma _Y)=E(\gamma _Y,T)+E(\gamma _Y,\gamma _{Y0}) +E(\gamma _Y,N_Y) \end{aligned} \end{aligned}$$

(25)

The relative potential error due to temperature uncertainty scales with NY:

$$\begin{aligned} E^+(\gamma _Y,T)=|-N_Y|\frac{\delta {T}^-}{T}=N_YE^-(T) \end{aligned}$$

(26)

The potential error contribution to $\gamma _Y$ from $\gamma _0$ is exactly the uncertainty error in $\gamma _{Y0}$:

$$\begin{aligned} E(\gamma _Y,\gamma _{Y0})=\frac{\delta \gamma _{Y0}}{\gamma _{Y0}}=E(\gamma _{Y0}) \end{aligned}$$

(27)

The relative potential error in $\gamma _Y$ scales with the relative uncertainty in N times N and a temperature-dependent scale factor:

$$\begin{aligned} E^+ (\gamma _Y,N_Y) = \left| \ln \left( \frac{T}{T_0}\right) \right| N_Y \times \left\{ \begin{array}{lr} E^+(N_Y), &{} {\rm if } T\le {T_0}\\ E^-(N_Y), &{} {\rm if } T>T_0 \end{array}\right. \end{aligned}$$

(28)

The scale factor increases from 0 to 2.3$N_Y$, as T is increased from $T_0$ to $10 T_0$. For example, at $T = 10T_0$, if $N_Y=0.7$ and the assumed value of $N_Y$ was 10% high, $\gamma _Y$ would be underestimated by $\sim$16%. The above analysis indicates that accurate knowledge of $\gamma _0$ and N are required for accurate determination of $\gamma$ and pressure.

The collisional-broadening parameters $\gamma _{Y0}$ and $N_{Y}$ for CO have been tabulated for a variety of collision partners Y (Y = CO, CO₂, H₂, and He) and rotational quantum numbers [21]. The $N_{Y}$ tabulated in HITRAN are typically valid up to 1000 K and high-temperature coefficients must be used above this limit [29, 30]. At combustion-relevant temperatures, the variation of $\gamma _Y$ with rotational quantum number is significantly reduced [14] and the analysis of 3.2 indicates that the exact knowledge of $J''$-dependence is not crucial to the fitting of the target spectra. As such, the determination of the broadening parameters of the main P(0,31) line, whose collision width is directly used for the pressure measurement, is of the utmost importance. For combustion in air, a majority of the exhaust gas is N₂, with the bulk of the remaining gas composed of CO, CO₂, H₂O, O₂, and H₂. As such CO–N₂ broadening is critical for an accurate assessment of the overall broadening coefficient in air combustion. Hartmann et al. [31] provided CO broadening parameters $\gamma _0$ and N for the collision partners N₂, O₂, CO₂, and H₂O up to $J''=$ 77. These parameters were calculated ab initio, and the resulting mixture-weighted broadening in flames using these parameters were shown to be accurate within 10% via scattering experiments. Since then, various studies have measured select broadening parameters at $T \ge 1000$ K and are employed in this work to refine the values of Hartmann et al.

Table 1 Summary of species-specific collisional broadening coefficients with CO. $\gamma _0$ is at a reference temperature of $T_0=$ 1000 K. For each collision partner: 1st/2nd/3rd line corresponds to P(2,20)/P(0,31)/P(3,14) respectively

Medvecz and Nichols [36] noted that the CO–N₂ coefficients from Hartmann may be overestimated. Chao et al. [33] measured CO broadening by CO, N₂, CO₂, and H₂O for the R(0,11) line in the first overtone band of CO near 2.3 $\upmu$m up to 1100 K. Cai et al. [37] measured CO–N₂ broadening up to 1000 K for the R(0,1) and R(0,2) lines in the same overtone band of CO. Spearrin et al. [29] measured CO–N₂ broadening from 1150–2600 K for the P(0,20) transition near 4.8 $\upmu$m in the CO fundamental band. When the measurements of Chao, Cai, and Spearrin are used to generate $\gamma (T=1000 {\rm K})$, the measurements indicate that Hartmann’s CO–N₂ broadening predictions are about 20% high. Similarly, comparing Spearrin’s measurement of N to Hartmann’s values, we find that Hartmann’s model over-predicts N by about 4%. For this work, Spearrin’s broadening parameters are used to model the P(2,20) line of CO. The broadening parameters of the P(0,31) and P(3,14) line are found by scaling Spearrin’s P(20) values by the ratio of the parameters in Hartmann’s model and averaging these with Hartmann’s values.

Chao’s CO–CO₂ and CO–H₂O broadening measurements indicate that Hartmann’s predictions of $\gamma (T = 1000 {\rm K})$ were overestimated by $\sim$14% and $\sim$24%, respectively [33]. As such, for this work, Hartmann’s predicted values at 1000 K are adjusted to the experimental values of [33]. Hartmann’s N values are retained for these collision pairs. Chao’s CO–CO measurements agree closely with that of Rosasco et al. [32], so Rosasco’s values at $T =$ 1000 K are used for $\gamma _{{\rm CO}-{\rm CO,0}}$ and Rosasco’s measurements from 700 to 1500 K are used to retrieve $N_{{\rm CO}-{\rm CO}}$. Finally, Hartmann’s $\gamma _{{\rm CO}- {{{\rm O}_2},0}}$ at 1000 K is rescaled using Mulvihill et al. [34] measurements at 1100–2100 K, whereas Hartmann’s $N_{{\rm CO}-{{\rm O}_2}}$ value is used un-altered.

There is a lack of data in the literature for high-temperature values of CO–H₂ broadening across the rotational states used in this work. Sur et al. [35] performed measurements of CO–H₂ broadening up to 700 K for the R(0,11) overtone line. In this work, the values of $\gamma _{{\rm CO}-{{{\rm H}_2},0}}$ at the $J''$ of interest are estimated by multiplying the $J''=$ 10 value from Sur et al. by the $J''$-dependent ratio of $\gamma _{{\rm CO}-{{\rm N}_2}}$ from Hartmann. N values for the CO–H₂ broadening are assumed to be equal to that of Hartmann’s CO–N₂.

The aggregated broadening coefficients of CO as aforementioned are summarized in Table 1. For all other species, the broadening is estimated using the scaling argument of Ref. [14], based on Eq. 10. For collision partner Y, the broadening value for CO–N₂ is multiplied by a factor indicating the relative collision rate with CO between Y and N₂. Therefore, lighter molecules, with smaller reduced mass, present higher broadening coefficients:

$$\begin{aligned} \gamma _{{\rm CO}-Y} =\gamma _{\rm CO-{{\rm N}_2}} \left( \frac{\sigma _{{\rm CO}-Y}}{\sigma _{\rm CO-{{\rm N}_2}}}\right) ^2 \sqrt{\frac{\mu _ {{\rm CO}-{{\rm N}_2}}}{\mu _{{\rm CO}-Y}}} \end{aligned}$$

(29)

Implicit in this is the assumption $N_{{\rm CO}-Y}=N_{{\rm CO}-{{\rm N}_2}}$. The scale factors between CO–N₂ broadening and the collision diameters of select broadening partners are summarized in Table 2.

Table 2 Tabulation of assumed broadening scale factors, collision diameters, and references for select species with no tabulated broadening in the literature. The diameters for CO and N₂ are provided, as they are used in Eqs. 6 and 29 to find the scaled broadening values for the other species in the table

In this work, the contribution of each species to the overall collisional broadening (Eq. 9) is defined by $\Gamma$, the ‘partial collisional-broadening coefficient’:

$$\begin{aligned} \Gamma _{{\rm CO}-Y} = X_Y\gamma _{{\rm CO}-Y} \end{aligned}$$

(30)

This term is analogous to partial pressure, and is proportional to CO–Y collision rate. The sum of the partial broadening coefficients is the total mixture-weighted broadening coefficient, combining Eqs. 9 and 30: $\gamma =\sum _Y{\Gamma _{{\rm CO}-Y}}$.

The uncertainties in the broadening model presented here will lead to potential errors in the mixture-weighted broadening coefficient. For each collision partner Y, uncertainty in $\gamma _{{\rm CO}-Y,0}$ and $N_{{\rm CO}-Y}$ will lead to spectroscopic potential error in $\gamma _{{\rm CO}-Y}$ by Eqs. 25–28. The relative spectroscopic potential errors in each collision pair’s broadening coefficient $E(\gamma _{{\rm CO}-Y},{\rm spec})$ are obtained from Eqs. 27 and 28:

$$\begin{aligned} \begin{aligned} E(\gamma _{{\rm CO}-Y},{\rm spec.}) = E(\gamma _{{\rm CO}-Y,0}) +E(\gamma _{{\rm CO}-Y},N_{{\rm CO}-Y}) \end{aligned} \end{aligned}$$

(31)

The total spectroscopic potential error in the mixture-weighted collisional-broadening coefficient, $E(\gamma ,{\rm spec.})$, can be expressed as

$$\begin{aligned} E(\gamma ,{\rm spec.}) = \sum _Y \frac{\Gamma _{{\rm CO}-Y}}{\gamma }E(\gamma _{{\rm CO}-Y},{\rm spec.}) \end{aligned}$$

(32)

In short, the above equation indicates that the error in broadening parameters for collision partners that are present in high quantities and have high broadening coefficients are the most significant.

3.3.2 Compositional uncertainty

As the gas composition changes, the relative contribution of each collision partner’s broadening coefficient with CO changes. In Ref. [14], the error in $\gamma$ associated with this was found by summing $\gamma _{{\rm CO}-Y}\delta {X_Y}$ over the various collision partners Y. The error $\delta {X_Y}$ was found by assessing the change in each $X_Y$ with fuel-to-oxidizer equivalence ratio $\phi$ and with a change between chemically frozen and equilibrium composition. This previous approach overestimates the potential error in $\gamma$ due to composition change, as each $X_Y$ are not independent of one another during a composition change, see Section S2.A of the Supplemental Document. Since all $X_Y$ must sum to one, as one mole fraction increases and the collision rate from that collision partner increases, other mole fractions must necessarily decrease, reducing the collision rates associated with those collision partners. As such, the change in $\gamma$ with compositional change must be assessed by observing how the entire gas composition varies.

To assess the variation of the collisional-broadening coefficient with gas composition, simulations of combustion chemistry were performed in Cantera version 2.7. The primary fuels studied were the hydrocarbons methane (CH₄), ethane (C₂H₆), ethylene (C₂H₄), acetylene (C₂H₂), propane (C₃H₈), and Jet-A (using n-decane, nC₁₀H₂₂, as a surrogate). In addition, non-carbon fuels such as hydrogen (H₂) and ammonia (NH₃) were investigated as extreme cases. Both combustion using air and pure oxygen were studied to extend the range of applications from air-breathing to rocket applications. Various chemical mechanisms were used to simulate the different fuel chemistries³.

Fig. 5

Top: equilibrium composition versus $\phi$ for C₂H₄–air (left) and for C₂H₄–O₂ (right) at 1 atm. Only the species whose concentrations exceed 1% across the equivalence ratio range are plotted. Middle: partial broadening coefficients for the P(0,31) line at $T =$ 2500 K with total mixture-weighted broadening coefficient shown in black. Spectroscopic potential error is indicated by the shaded region around each curve. Bottom: mixture-weighted collisional broadening coefficient, normalized by the CO–N₂ broadening coefficient

The variation in composition is considered for (1) chemical equilibrium versus fuel-to-oxidizer equivalence ratio $\phi$, (2) kinetically in terms of reaction progress as reactants are turned into products, and (3) as the combustion products expand and cool post-combustion. For the equilibrium simulations, each fuel/oxidizer combination was initially set to 1 atm and 1500 K with reactant composition set by the equivalence ratio. Afterwards, the mixture was equilibrated at constant pressure and enthalpy (HP). After equilibration, the ‘major products’ are identified. The major products are defined as those with a mole fraction greater than 1% anywhere across the equivalence ratio range and are shown for C₂H₄–air and C₂H₄–O₂ at the top of Fig. 5. Using broadening coefficients selected in Sect. 3.3.3.1, the partial broadening coefficients (evaluated at a constant $T =$ 2500 K) are plotted versus equivalence ratio of C₂H₄–air and C₂H₄–O₂ in the middle row of Fig. 5. The spectroscopic potential error contribution to $\gamma$ from each partial broadening coefficient (represented by each term in the summation in Eq. 32 times $\gamma$) is represented by the shaded regions. Since only the major products are considered, in order to better estimate the broadening contribution from the minor products, $\gamma$ is multiplied by a correction factor of $(\sum _YX_Y)^{-1}$. This factor typically increases $\gamma$ by less than 1%. $\gamma$ is plotted along with the partial broadening coefficients in the middle row of Fig. 5 in black. For hydrocarbon–air combustion, the total spectroscopic potential error is dominated by the uncertainty in CO–N₂ broadening, as N₂ makes up a majority of the product gas composition. For hydrocarbon–O₂ combustion, the spectroscopic potential error has more diverse contributions, with CO–H broadening uncertainty being most substantial, due to the high broadening of this collision pair (H has the lowest mass of the collision partners) and due to the high uncertainty in the CO–H broadening parameters, which are obtained from scaling relations.

$\gamma / \gamma _{{\rm CO}-{{\rm N}_{2}}}$ is plotted versus equivalence ratio for each studied fuel at the bottom of Fig. 5. For all studied conditions with the hydrocarbons, $\gamma$ was within 40% above $\gamma _{{\rm CO}-{{\rm N}_{2}}}$. $\gamma$ is higher for O₂ combustion compared to air combustion, as there is a larger concentration of lighter molecules. In general, for each studied fuel–oxidizer combination, $\gamma$ increases with increasing equivalence ratio. This is due to the increasing concentration of H₂ and H, which are light molecules that are frequent colliders with CO. At leaner equivalence ratios on the other hand, an excess of O₂ and N₂ is present, which are a relatively heavy molecules with a lower collision rates with CO, leading to reduced broadening. As the equivalence ratio is reduced significantly below 1, the $\gamma$ approaches a weighted sum of $\gamma _{{\text {CO-}} {\text{N}}_2}$ and $\gamma _{{\text {CO-}} {\text{O}}_2}$, which reduces the potential error associated with composition.

The broadening coefficients for the hydrocarbons in air change by about 11% from $\phi =0.5$ to $\phi =2$. For O₂ combustion, the differences between the broadening of the various fuel products is higher. For hydrocarbon–O₂ combustion, $\gamma$ changes by about 25% from $\phi =0.5$ to $\phi =2$. It was found that the sensitivity of $\gamma$ to $\phi$, $s(\gamma ,\phi )$, is typically below 0.1 %/% for the hydrocarbons in air and below 0.2 %/% for the hydrocarbons in O₂, with a peak in sensitivity typically near stoichiometric conditions. Thus, a 5% accuracy in the broadening coefficient is achieved if $\phi$ is known within 20–50%. It is also interesting to note a reduced sensitivity of $\gamma$ to $\phi$ at higher values of $\phi$, particularly for the O₂-combustion cases. This is largely due to the plateauing production of H in the exhaust at very high $\phi$.

When comparing the various fuels, the broadening generally increases as the H/C ratio in the fuel increases, with the C₂H₂ (H/C=1) products having the lowest broadening, and C₂H₆ (H/C=3) products having the highest broadening. This is due to the higher concentration of H₂O, H₂, and H in the exhaust versus CO and CO₂ for the fuels carrying more hydrogen atoms. In general for equilibrium, the exact knowledge of the fuel–oxidizer mixture is not required to obtain gas composition. The equilibrium composition at a given temperature and pressure is dictated by the proportions of the elements C, H, O, and N in the reactant mixture. For many common hydrocarbons (CH₄, C₂H₆, C₂H₄, and Jet-A) the broadening of the product gas in air combustion have almost the same $\phi$ dependence, with the broadening coefficients being within a few percent of each other, due to the fact that their H/C ratios are very similar (2–4). The H₂ product gas has the highest broadening as a majority of the non-N₂ product gas composition is H₂O, H₂ and H. NH₃ represents an intermediate case, with the presence of additional N₂ in the product gas reducing the broadening from that of the case of pure H₂ but higher than that of the hydrocarbons.

Fig. 6

Top: gas composition versus reaction progress, Z, for C₂H₄–air (left) and for C₂H₄–O₂ (right). Middle: partial broadening coefficients for the P(0,31) line for the major collision partners versus Z, evaluated at $T =$ 2500 K, with $\gamma =\sum {\Gamma _{{\rm CO}-Y}}$ shown in black. Spectroscopic potential error is indicated by the shaded region around each curve. Bottom: mixture-weighted collisional-broadening coefficient, normalized by the CO–N₂ broadening coefficient, versus Z for various fuels

Often for in-situ measurements, combustion may be in-progress or incomplete. This means the combustion gas is not well-represented by the equilibrium products discussed in the previous paragraph. To investigate how the collisional-broadening coefficients vary across a combustion reaction, 0-D kinetic simulations were performed using Cantera in a constant pressure and constant enthalpy (HP) reactor ($\phi =1$ and $T_\text {init} = 1500$ K). Simulations were run until the mole fractions of H₂O, CO₂, and NO were within 0.1% of the equilibrium value predicted by the equilibrium simulations. Reaction progress Z was defined in terms of the mass fraction of the products and reactants, as defined in Section S3.A of the Supplemental Document.

For C₂H₄–air and C₂H₄–O₂, the mole fractions of the major species (present in $\ge$1% during the reaction) versus the reaction coordinate Z are shown at the top of Fig. 6. In the middle row of Fig. 6, the partial collisional-broadening coefficient, $\Gamma _{\text {CO}-Y}$, evaluated at $T=$ 2500 K is plotted for each collision partner, with the spectroscopic potential error in each partial broadening coefficient represented by the shaded region around each curve. The sum of the partial broadening coefficients is plotted in black along with its spectroscopic potential error as the black shaded region. As for the equilibrium case, in hydrocarbon–air combustion, this potential error is dominated by the uncertainty in CO–N₂ broadening. For hydrocarbon–O₂ combustion, the potential error is largely dominated by the uncertainty in the CO–fuel broadening coefficient at early points in the reaction and by CO–H broadening towards the end of the reaction.

$\gamma / \gamma _ {{\rm CO}-{{\rm N}_2}}$ at $T=$ 2500 K is plotted versus reaction progress Z for each studied fuel at the bottom of Fig. 6. In general, for each studied fuel–oxidizer combination, $\gamma$ increases with increasing reaction progress, as the composition shifts from fewer/heavier molecules to more/lighter molecules across the reaction, resulting in an increased collision rate per unit pressure. An exception to this trend is H₂, which features a dip in $\gamma$ towards the tailend of the reaction, due to water dissociation. Air mixtures present some stability to $\gamma$ versus Z, due to the large quantity of N₂ in air. Interestingly, at early times, $\gamma$ is very close to the value for CO–N₂ broadening for the hydrocarbon fuels and NH₃, both for air and O₂ combustion. This is due to the very similar collision diameter and molecular weight of many of these fuels to nitrogen, leading to a very similar collision rate with CO. While the presence of fuel tends to increase the broadening coefficient of the reactant mixture, the presence of oxygen has the opposite effect due to its higher molecular weight. These two effects tend to compensate each other, leading to an overall mixture-weighted broadening coefficient similar to that of pure N₂. H₂ is an exception because H₂ is very light and has a high broadening coefficient compared to N₂ as a result. These results imply that for hydrocarbon mixtures at early phases in the combustion process, CO–N₂ broadening provides a very good estimate of the broadening coefficient, with the uncertainty in the fundamental spectroscopic parameters ($\gamma _0$, N) dominating the potential error.

For most of the hydrocarbons studied (CH₄, C₂H₆, C₂H₄, and Jet-A) the broadening of the mixture have nearly the same Z dependence, with the broadening coefficients being within a few percent of each other. These fuel–air combinations see an 8–10% increase in $\gamma$ across the reaction coordinate. For O₂ combustion, the differences between the broadening values for the different fuel mixtures across the reaction space are higher but still on the order of a few percent. These fuel–O₂ combinations see an approximately 30% increase in $\gamma$ across the reaction coordinate. NH₃ has a similar dependence with Z as these hydrocarbons at early points in the reaction, but then diverge to a higher value of $\gamma$ towards the end of the reaction, closer to that of H₂. C₂H₂ diverges from the other hydrocarbons early on in the reaction space due to the high production of CO compared to other exhaust products. It was found that the sensitivity of $\gamma$ to Z is typically $s(\gamma , Z) = \pm$0.1 %/% range for the hydrocarbons in air and in the $s(\gamma , Z) = -0.2$ to $-$0.05 %/% range for the hydrocarbons in O₂. Most of the hydrocarbons present a reduced sensitivity of $\gamma$ to Z towards the last 20% of the reaction. This implies that a single value of $\gamma$ could be used for most mixtures that are in the final oxidation phase of the reaction. It should be noted that at higher equivalence ratios, the change in $\gamma$ across the reaction is magnified, whereas at lower equivalence ratios, the change in $\gamma$ is reduced—the lean mixtures are mainly composed of N₂ (or pure O₂ for oxy-combustion).

In addition to the variation of $\gamma$ with equivalence ratio and reaction progress, the change in $\gamma$ during gas cooling was investigated. This is particularly of interest for O₂ combustion, since the higher temperatures achieved in O₂ combustion lead to higher levels of dissociation of H₂O and CO₂ into light molecules/atoms such as H, O, OH, H₂, O₂, and CO. As the gas temperature drops, recombination reactions occur which convert these dissociation products back into H₂O and CO₂. To investigate this, the gas objects from the end of the kinetic simulations had their temperature reduced isobarically and were allowed to equilibrate at constant pressure and temperature. For each gas, the temperature was reduced from the equilibrium temperature to half the equilibrium temperature. This cooling effect resulted in at most a 2% increase in $\gamma$ in air, and a 6% increase in $\gamma$ for O₂ combustion. To achieve this effect, the gas temperature needs to drop by about 25% ($\sim$750 K), which for isentropic expansion would correlate with a 70–80% drop in pressure. Lower pressures tend to encourage dissociation, so a pressure drop may reduce the composition change.⁴

The uncertainty assigned to $\gamma$ from compositional uncertainty is context-dependent. In certain scenarios, the equivalence mixture ratio, reaction progress, and degree of departure from chemical equilibrium may be more or less certain. In a pure reactant mixture for example, the reaction progress is known to be 0 and for a pre-mixed combustor, $\phi$ can be known precisely. Discretion must be used when choosing the composition at which to evaluate $\gamma$ and when assigning potential error. In general, the compositional potential error may be written as

$$\begin{aligned} E(\gamma ,\text {mix})= E(\gamma ,\phi )+E(\gamma ,Z)+E(\gamma ,\text {eq.}) \end{aligned}$$

(33)

where ‘eq.’ refers to the potential error associated with the thermodynamic state and non-equilibrium of the gas mixture, which may include effects of certainty in combustion mode, such as deflagration versus detonation. The total uncertainty in $\gamma$ may be written as

$$\begin{aligned} E(\gamma )=E(\gamma ,\text {mix})+E(\gamma ,\text {spec.})+E(\gamma ,T) \end{aligned}$$

(34)

In the following subsection, the uncertainty in $\gamma$ is combined with the uncertainty in $\Delta \nu _\text {C}$ to obtain the overall uncertainty in P.

3.4 Total uncertainty in pressure

The three main sources of potential error in the pressure measurement have been identified in the preceding subsections: (1) precision/bias error resulting from the data collection and processing, (2) uncertainties in the spectroscopic constants which characterize CO collisional broadening, and (3) uncertainty in the combustion gas composition. In this subsection, we detail how these potential errors can be combined to assess the overall uncertainty in the pressure measurement.

The uncertainty in the collision width comes entirely from measurement noise and biases from the fitting model. The uncertainty in $\gamma$ also has contributions from these sources via the potential error contribution from the temperature measurement, as indicated in Eq. 34. These potential errors cannot be simply added due to correlations, so Eq. S2 must be used. The other potential error sources stem from the uncertainties in the broadening parameters and composition of the bath gas. The potential error in $\gamma$ from temperature uncertainty can be written as

$$\begin{aligned} E^+(\gamma ,T)=\sum _Y \frac{\Gamma _{\text {CO}-Y}}{\gamma }N_{\text {CO}-Y}E^-(T) \end{aligned}$$

(35)

This may be further broken down into a potential error in $\gamma$ from precision error, $E(\gamma ,\alpha )$, bias error, $E(\gamma ,\text {bias})$, and error from uncertainty in $S_1^0$ and $S_2^0$, $E(\gamma ,S^0)$, stemming from these potential errors in the temperature measurement. The precision and bias errors may be quantified using the methods of Section 3.3.2 through the fitting of noisy absorbance profiles. Of particular note is the potential bias error associated with the uncertainty of the P(3,14) linestrength. This potential error is near-zero at pressures near 2.5 atm, and is generally sub-1% for higher pressures. At $P{\le }1$ atm, this potential error increases beyond 1% when $T{\ge }2500$ K. $E(\gamma ,S^0)$ can be found using the dependence between temperature and the reference linestrengths in Section S2.C of the Supplemental Document:

$$\begin{aligned} \begin{aligned} E^+(\gamma ,S^0)=\frac{kT}{hc\Delta {E}''_{12}}&\frac{\sum _Y{N_Y\Gamma _{\text {CO}-Y}}}{\gamma }\\&\times \left[ E^+(S_1^0)+E^-(S_2^0)\right] \end{aligned} \end{aligned}$$

(36)

Using Eqs. 20 and 21, the uncertainty in P can be expressed as

$$\begin{aligned} \begin{aligned} E^+(P)&=E^+(P,\alpha )+E^+(P,\text {bias}) \\ {}&+E^-(\gamma ,\text {spec.})+E^-(\gamma ,\text {mix})+E^-(\gamma ,S^0) \end{aligned} \end{aligned}$$

(37)

Note that $E(P,\alpha )$ and $E(P,\text {bias})$ are related to the precision error and bias error for $\Delta \nu _\text {C}$ and $\gamma$ (via the temperature measurement), accounting for correlation from measurement noise. These errors may be assessed using the methods of Sect. 3.2 but are closely approximated by the errors in the collision-width measurement due to the weak dependence of $\gamma$ on T. In addition, potential bias error due to line-of-sight non-uniformity is typically below 1% for the conditions of the sensor demonstrations of Sect. 4 and are neglected in this section, see Section S2.E of the supplemental document.

Fig. 7

Contributions of potential error sources to total pressure uncertainty (top 4 bars) for C₂H₄-fueled combustion product gas. Bar color corresponds to temperature condition. Bar hatching pattern indicates if composition-related errors/uncertainties are for air or oxygenated combustion

Fig. 8

Experimental setup used for sensor demonstrations. High-enthalpy shock-tube facility (top) with key dimensions and features labeled. Detonation-impulse tube (bottom left) with deflagration-to-detonation transition length and key components labeled. The optical setup (bottom right) is shown at the cross sections of the measurement planes (Section A–A and Section B–B)

Sample pressure uncertainty values for the combustion products of C₂H₄–air and C₂H₄–O₂ are shown in Fig. 7 for $P=$ 1 atm, $X_\text {CO}L=3\%\cdot$cm, SNR$_\text {opt}=$ 250 at three different temperatures. The figure indicates the potential error contributions from various sources as bars below the top set. Values greater than 0 indicate the upper uncertainty/error bound and values less than zero indicate the lower uncertainty/error bound. Here, the following arbitrary assumptions are made as an example: $E^{\pm }(\phi )=$ 10%, $E^+(Z)=$ 0, $E^-(Z)=$ 10%, $E(\gamma _1/\gamma _2)=E(\gamma _3/\gamma _2)=3\%$. The uncertainties in the reference linestrengths are taken from the HITEMP Database. Here, the final uncertainties/errors are multiplied by a ‘coverage factor’ [27] of $1/\sqrt{2}$ to account the linear addition of errors, as opposed to adding in quadrature. In general, the dominating error contribution comes from uncertainty in the broadening parameters for CO, which increases modestly at higher temperatures. Other spectroscopic errors (linestrenghs) add a few percent uncertainty to the pressure measurement. The potential error from compositional uncertainty is dominated by the uncertainty in the chemical equilibrium state of the gas for oxygenated combustion at lower temperatures, furthest from the adiabatic flame temperature of the gas, where the composition may have changed the most. This can add up to a 5% bias in the pressure measurement. Overall, the uncertainty in pressure is around ±10%.

4 Sensor demonstrations

The pressure-sensing strategy was demonstrated in two laboratory facilities at UCLA: a high-enthalpy shock tube and a pulse-detonation tube. For all experiments, a common optical setup was used. A distributed-feedback quantum-cascade laser (DFB QCL) was maintained a constant temperature using thermoelectric cooling supplied by an Arroyo 6310-QCL laser controller, which also set the DC current input to the laser. The laser output wavelength was modulated at MHz rates using a Rigol DG1032Z function generator multiplexed with the DC current via a bias-tee [14]. The laser modulation waveform is trapezoidal, with the leading-edge ramp rate selected depending on the expected broadening of the target spectral features. Based on the guidelines established in Ref. [18], narrow spectral features at low pressures are scanned using a lower ramp rate to reduce the rate of output wavelength change (chirp rate). This procedure avoided the distortion of narrow spectral features due to detector bandwidth limitations. The waveform duty cycle is typically between 50 and 70%, adjusted to maximize the scan depth for a given ramp rate. This yields an integration time for the measurement on the order of 500–700 ns for each modulation period or laser ‘scan’, see Fig. 9.

Laser light is directed through the flow of interest onto a thermoelectrically cooled, AC-coupled, photovoltaic detector (Vigo PVI-4TE-6-1x1) with a 200-MHz bandwidth coupled with narrow bandpass / neutral density filters, an iris, and a CaF₂ convex lens. The voltage output of the detector is recorded on a Tektronix MSO44 oscilloscope with 200-MHz bandwidth, for measurement periods of 4–10 ms, and sample rates ranging from 1.25–3.125 GS/s. A schematic of the optical setup is shown on the bottom right of Fig 8.

Before each experiment, the light intensity profile is recorded, representing the incident light intensity $I_0$, also referred to as the ‘background’ signal. Another profile is recorded with a 50-mm germanium etalon (mounted on a flip mount) to characterize the laser ouput wavenumber in time, or chirp. During an experiment, the detector measurement is used to obtain the transmitted light intensity through the absorbing gas, $I_\text {t}$. The measurements of $I_\text {t}$, $I_0$, and the chirp profile are used to obtain an absorbance spectrum $\alpha (\nu )$ using Eq. 1 for each laser scan. Sample measurements of $I_0$, $I_\text {tr}$, and $\alpha (\nu )$ are shown in Fig. 9.

The measured absorbance spectrum is fitted to obtain the P(2,20)/P(0,31) absorbance areas and the P(0,31) collision width using the fitting procedure outline in Section 3.3.2. The collisional widths between of the P(2,20) and P(3,14) lines are set by scaling the P(0,31) broadening by the ratio of collisional-broadening coefficients predicted by the assumed gas composition. In addition, a 4th absorbance area is floated in some cases to capture the contribution of the RR(0,57.5) doublet of nitric oxide (NO) at 2008.25 cm$^{-1}$ that can sometimes appear post-ignition with air as the oxidizer. Gas temperature and CO partial pressure are obtained with Eqs. 13 and 14. The gas temperature is used along with an assumption for the gas composition to infer the time-resolved collisional-broadening coefficient, $\gamma$ for P(0,31). The P(0,31) collision width is divided by its collisional-broadening coefficient using Eq. 21 to infer the gas pressure. The CO partial pressure is divided by the total pressure using Eq. 15 to infer the CO mole fraction.

In addition to the LAS pressure measurement, a conventional electromechanical pressure measurement is collected simultaneously using piezoelectric pressure transducers. For the shock-tube experiments, a Kistler 601B1 is used, which has a rise time of 2 $\upmu$s and resonant frequency of 300 kHz. For the detonation tube experiments, a Kistler 603CAA is used, which has a rise time of less than 0.4 $\upmu$s and a resonant frequency greater than 500 kHz. The Kistler output is amplified using a charge amplifier. The amplifier applies a 100-kHz low-pass filter to the raw output signal to suppress excessive high-frequency ringing in the Kistler signal, which are magnified near the natural frequency of the transducer, near 1–5 MHz.

4.1 Shock-tube hydrocarbon–air kinetics

The UCLA high-enthalpy shock-tube (HEST) facility has been extensively described in other works [25, 42]. Various fuel–air mixtures were shock-heated in the 4.9-m driven section using a helium driver gas bursting plastic diaphragms. Optical access is provided by two 3-mm thick wedged sapphire windows located 2 cm from the endwall of the driven section. The optical path length through the inner diameter of the tube is 10.32 cm.

For the experiments, two stoichiometric mixtures of C₂H₄–air and CH₄–air were manometrically prepared in a stirred mixing tank. Both mixtures were seeded with 2% CO to allow for pre-ignition assessment of pressure. The addition of CO was found to have negligible effects on the ignition timescales (1–3% change), see Section S3.B of the Supplemental Document. Before each test, the shock-tube driven section was vacuumed to mTorr pressures and subsequently filled to various initial pressures to target specific post-reflected-shock conditions.

Fig. 9

Top: incident/background intensity profile (black) and transmitted intensity profile (red) plotted for select individual laser scans during shock and detonation tube experiments across various pressure and temperature conditions. Middle: measured absorbance spectra of target CO transitions (black), along with overall spectral fits (red), individual transitions in each fit (dashed lines) and fit of non-absorbing baseline (dashed gray) due to high-temperature / pressure CO₂ absorption. Bottom: the peak-normalized residual r between the fit and measurement

Fig. 10

Time-resolved fitted spectral parameters, including collision-width $\Delta \nu _\text {C}$ [cm$^{-1}$], absorbance areas A [cm$^{-1}$], and collisional-broadening coefficient $\gamma (T)$ [cm$^{-1}\cdot$atm$^{-1}$]. The subscript for $\gamma$ indicates whether the reactant (R) or product (P) gas composition is used to predict the broadening coefficient. The collision width and collisional-broadening coefficient are given for the P(0,31) line

Fig. 11

Top: pressure traces for the two shock-tube experiments. The Kistler-measured pressure is indicated in red. Reference lines indicating predictions from ideal shock relations or chemical equilibrium are indicated in blue. Two LAS measurements of pressure using the reactant collisional-broadening coefficient (black) and product collisional-broadening coefficient (orange) are indicated. The LAS-measured partial pressure of CO is shown in gray. Uncertainty is indicated with the green error bars. Middle: LAS-measured temperature with uncertainties and reference values. Bottom: LAS-measured CO mole fraction with uncertainties and reference values. A $X_\text {CO}$ measurement using the Kistler-measured pressure is shown in red

Two experiments are considered here. In experiment S1, the C₂H₄ mixture is shock-heated to near 2 atm and 1200 K. In experiment S2, the CH₄ mixture is shock-heated to a higher pressure near 4 atm at 1500 K. From the electromechanical Kistler pressure trace (see $P^\text {Kistler}$ later in Fig. 11), distinct time periods in the experiment can be observed. Initially, before time ‘0’ the mixture is at the pre-shock ambient condition at low pressure (not pictured). The pressure increases at time ‘0’ due to the incident shock and at $t \sim$ 100 $\upmu$s due to the reflected shock. Ignition occurs at $t \sim$ 400 $\upmu$s where the pressure signal rises again and begins to oscillate dramatically. Due to the confined volume of the shock tube and the high concentration of reactants, this combustion process is not isobaric. The pressure does decay slightly after its initial peak, corresponding to some gas expansion and cooling.

Post-processing of the spectrally resolved line cluster enables inference of multiple parameters. The top-left pane of Fig. 9 shows sample transmitted laser intensity scan of experiment S1 before and after the ignition event, at $t= 200$ $\upmu$s and $t=585$ $\upmu$s, respectively. Below the raw data, the measured absorption spectra from this test are shown with the spectral fit of the data. The significant baseline absorption in the post-ignition scan is largely due to the broadband absorption of CO₂ [43]. In Fig. 10, the measured absorbance areas and collision widths from experiment S1 are plotted in time from this test. Two values of the broadening coefficient $\gamma$ are plotted: the value predicted using the reactant composition ($\gamma _\text {R}$, in black) and the equilibrium product gas composition ($\gamma _\text {P}$, in orange) calculated from the Cantera model from Section 3.3.3.2. Equations 13–15 and 21 are used to infer gas pressure, temperature, CO partial pressure, and CO mole fraction in time from the areas and collision width measurement. It should be noted that during the incident shock portion of the test, the gas temperature is quite low, so an accurate/precise measurement of the P(2,20) absorbance area is not possible, leading to an inaccurate T and $p_\text {CO}$ measurement. Nevertheless, the pressure measured during this region is included due to the reduced sensitivity of the pressure measurement to errors in temperature. The temperature and pressure measured by the sensor can be readily compared to the temperature and pressure predicted by frozen shock-tube relations, FROSH [44], from the fill pressure, temperature and composition, as well as the incident shock speed. The FROSH predictions for pressure and temperature are plotted as horizontal dashed lines in Fig. 11. The FROSH values predicted behind the incident shock are notated with the subscript ‘2’ and the properties behind the reflected shock are notated with the subscript ‘5’, assuming vibrational equilibrium in both regions (represented by the superscript ‘EE’). The known initial CO mole fraction is plotted as a horizontal dashed line at the bottom of Fig. 11 and this is combined with the $P_5$ prediction to generate a prediction for $p_\text {CO,5}^\text {EE}$, which is plotted in the top panel of the same figure (scaled by a factor of 10).

In Fig. 11, the measured properties from LAS for experiment S1 are shown in black, with each measured property g labeled as $g^\text {LAS}$. The CO partial pressure is plotted in grey to distinguish it from the total pressure measurement. The uncertainty for each measured property is indicated by the green error bars, using the methods of Sect. 3. The contribution of precision error to the uncertainty is not reflected in the error bars due to the self-evident nature of the precision error in the datapoint scatter. The uncertainty is on the order of 3–6% for pressure, 2–5% for temperature, 2–7% for $p_\text {CO}$ and 4–11% for $X_\text {CO}$. The contributions to the uncertainty indicated in Fig. 7 are generally representative of the uncertainty here, with the notable exception that the reduced potential error from $\phi$, due the high certainty in the initial mixture composition. The potential error due to gas cooling is equal to zero, as this is irrelevant for the pre-ignition mixture and the temperature remains close to the equilibrium value after ignition. The potential error due to the uncertainty in reaction coordinate, Z,  is also not included in the error bar. Instead, two pressure calculations are made utilizing the reactants broadening coefficient ($\gamma _\text {R}$, in black) and the broadening coefficient of the products at equilibrium ($\gamma _\text {P}$, in orange). These two points on the reaction coordinate ($Z=0$ and $Z=1$) represent the two extremes in $\gamma$ across the reaction, and as such bound the broadening coefficient across the ignition event. $X_\text {CO}$ is also plotted as two curves corresponding to the same assumptions for $\gamma$. It can be seen that the pressure measured using $\gamma _\text {R}$ closely aligns with $P_2$ and $P_5$ predicted by the frozen shock relations. The LAS pressure behind the reflected shock wave agrees closely with the value measured by the Kistler, with a significant exception. Immediately behind the reflected shock, the LAS pressure rises almost immediately to $P_5$, whereas the Kistler pressure rises to an intermediate value between $P_2$ and $P_5$, after which there is a shallower rise in pressure over 80 $\upmu$s, an overshoot of $P_5$, and a subsequent settling of the pressure near $P_5$. This complex pressure structure observed by the Kistler is caused by the interaction of the reflected shock wave with the boundary-layer formed by the flow behind the incident shock wave, giving rise to a phenomena known as shock bifurcation [45]. Here the reflected shock transitions to an oblique shock near the sidewalls of the tube, leading to a localized boundary region with significantly different gas thermodynamic properties compared to the bulk gas. As a result, the Kistler is unable to probe the thermodynamic state of the bulk gas from its location on the sidewall. The LAS pressure measurement is path-integrated in nature, and as such effectively averages over these disparate regions of pressure. The ability of the LAS sensor to effectively report a path-integrated pressure is discussed in Section S2.E of the Supplemental Document, where knowledge of these two pressure measurements is employed to infer the radial pressure distribution at the measurement location. After the reflected shock passage, both the Kistler and LAS pressure measurements gradually rise in time, corresponding to some nominal dP/dt caused by shock-tube non-idealities [46].

Fig. 12

Measurements of total/CO partial pressure (top), temperature (middle), and CO mole fraction (bottom) for the two detonation experiments. LAS measurements are in black/gray and Kistler-derived measurements are in red. Reference lines indicating predictions from Chapman–Jouguet (CJ) detonation theory are indicated in blue. Uncertainty is indicated with the green error bars

It can also be seen that the temperature, CO partial pressure, and CO mole fraction closely match the region 5 values predicted by the frozen shock relations and the known concentration of seeded CO in the reactant mixture. With the temperature and CO species measurements, the ignition event is much more clear due to the abrupt rise in these two parameters along with pressure rise near 430 $\upmu$s. The values of the measured gas properties after ignition can be compared to the values predicted by thermochemical equilibrium using the Cantera model from before. Here both equilibrium at constant enthalpy/pressure (labeled with ‘HP’) and at constant internal energy/volume (labeled with ‘UV’) are shown as references due to the fact that the combustion process here is bounded by these cases. The initial temperature and pressure conditions for these equilibrium simulations are informed by FROSH. During the lead up to ignition, the LAS pressure measurement begins to rise before the Kistler measurement. This could be due to non-uniform ignition events leading to different pressure values near the wall compared to the bulk flow. After ignition, the LAS pressure measurement tracks with the Kistler pressure, but the LAS pressure oscillates significantly less than the Kistler measurement. The accuracy of the pressure oscillations captured by the two diagnostics can be compared by examining the mole fraction measurement made using either pressure measurement, as the input to Eq. 15 along with the LAS measurement of $p_\text {CO}$. The orange curve indicates the post-combustion LAS prediction of mole fraction whereas the Kistler prediction is shown in red. The LAS measurement of $X_\text {CO}$ is much more stable in time than that predicted by the Kistler pressure. It should be expected that the species concentration over a combustion process do not oscillate as drastically as the Kistler prediction, so it is likely that the extreme oscillations measured by the Kistler are non-physical, or are representative of higher pressure unsteadiness near the tube wall from boundary-layer effects. The peak value of the gas properties measured by LAS are close to that predicted by the UV equilibrium: $P=4.9$ atm, $T=3000$ K, $p_\text {CO}=0.35$ atm, and $X_\text {CO}=7.1$ %. The values these parameters decay to after the initial transient are closer to the values predicted by HP equilibrium.

In Fig. 11, the results of the higher pressure experiment (S2) with CH₄ fuel is pictured on the right. Similar observations as for the previous experiment can be made regarding the comparison of the LAS-measured values to the Kistler pressure, values predicted by frozen shock relations, and values predicted by thermochemical equilibrium. The higher gas temperature behind the incident shock for this experiment allows for a more accurate measurement of T, $p_\text {CO}$, and $X_\text {CO}$, which are now pictured in Fig. 11. This experiment indicates the ability of the compositional model to capture changes in $\gamma$ with variation of hydrocarbon fuel. In addition, the dynamic range of the sensor is on display, with pressure measurements made from pressures of 0.8–8 atm.

4.2 Ethylene–oxygen pulsed detonations

The UCLA Detonation-Impulse Tube(DIT) [47], pictured in Fig. 8, is used to generate near-1D detonation waves via spark ignition and deflagration-to-detonation transition (DDT). Here, the DIT is used to generate detonations using pure O₂ as the oxidizer, yielding gas composition representative of rocket combustion product gas. The tube is 183 cm long and has a 3.81-cm internal diameter. Prior to each test, the tube was vacuumed to sub-Torr pressures after which it was filled with a pure C₂H₄–O₂ mixture to a particular sub-atmospheric pressure, measured by a Baratron pressure transducer. The equivalence ratio $\phi$ for each experiment was set by mixing the fuel and oxidizer in a mixing manifold upstream of the detonation tube, with the flow rates of each reactant being set using MKS GE50A thermal-based mass flow controllers. After filling the tube, a valve was used to shut the tube off from the filling apparatus. The combustible mixture was ignited at one end using a spark ignition system. A Shchelkin spiral was used to accelerate DDT along the length of the tube. The presence of a detonation wave was verified comparing the detonation wave-speed predicted by Chapman–Jouguet (CJ) relations to the experimental speed derived from five piezoelectric time-of-arrival sensors located in the last 36 cm of the tube. The tube is sealed on its downstream end using a thin plastic diaphragm designed to burst upon arrival of a detonation waves. This allows for the combustion products to be evacuated into a surge tank maintained at vacuum, while also allowing for the main tube to be filled to a known pre-detonation pressure. Optical access to the detonation tube is enabled via two wedged sapphire windows located 147 cm downstream of the tube ignition source. The Kistler pressure transducer was placed in the same plane as the optical ports to simultaneously make electromechanical pressure measurements to which the optical pressure measurements can be compared.

These experiments were simulated using a CJ detonation model implemented in Cantera using the Caltech Shock and Detonation Toolbox and USC Mechanism Version II [41, 48, 49], providing the pressure, temperature, and gas composition for an ideal 1-D detonation wave. The predicted gas composition was used to estimate the mixture-weighted broadening coefficient $\gamma$, as done in Section 3.3.3.2 for deflagration combustion. The main difference here is that for detonation combustion, the pressures and temperatures are higher. The higher temperatures lead to increased dissociation of CO₂ and H₂O into smaller molecules/atoms, although some of this effect is reduced by the increased pressure.

Two representative detonation experiments are examined here. In experiment D1, the mixture is stoichiometric ($\phi =$ 1) and pre-detonation fill pressure is 51.7 Torr, whereas experiment D2 is fuel-rich ($\phi =$ 1.5) at higher pre-detonation fill pressure, 207.1 Torr. Figure 12 shows the results of experiments D1 and D2 with the same color scheme as in Fig. 11, with the reference CJ values plotted as blue dashed horizontal lines. After the initial rise in the measured gas properties with the passage of the detonation wave, the pressure drops by about 80% (factor 5) for both experiments over the course of 1 ms, with minor increases due to reflected waves from the diaphragm at the end of the tube. The temperature on the other hand changes by a lesser degree, on the order of 15% for experiment D1 and 25% for experiment D1. The temperature increases less dramatically than pressure across the reflected waves. The CO mole fraction does not change significantly over the test duration.

As can be expected, experiment D2 features a higher peak pressure than experiment D1, due to the higher pre-detonation pressure. The peak temperature for experiment D2 is also higher than for experiment D1 due to the decreased endothermic product dissociation at higher pressures. This effect outweighs the reduction in flame temperature when burning at fuel-rich conditions. The post-detonation CO mole fraction in experiment D2 is roughly double that of the value in experiment D1, due to incomplete oxidation at the fuel-rich condition.

The error contributions to the pressure uncertainty are well represented by the sample C₂H₄–O₂ uncertainty breakdown presented in Fig. 7. Notable exceptions here include: (1) the post-detonation composition used to estimate collisional broadening is estimated from the CJ model, not from a constant-pressure combustion simulation; (2) the uncertainty in the mixture equivalence ratio is greatly reduced due to the accurate measurement of the reactant flow rate; (3) the uncertainty in the reaction progress coordinate is assumed to be negligible, as detonation combustion occurs on extremely fast time scales. As such, the uncertainty is primarily dominated by the uncertainty in the broadening parameters of the individual collision partners of CO.

The LAS measurements can be compared to the values measured by the Kistler and the CJ predictions. For experiment D1 it can be seen that both the Kistler and LAS pressure overshoot the CJ-predicted pressure, whereas for experiment D2, both peak pressure measurements closely match the CJ pressure. This can be attributed to potential pre-pressurization of the reactants before detonation passage, due to propagation of acoustic waves faster than the flame speed during the DDT process. This effect is more pronounced at lower initial pressures, due to the increased time/distance required for DDT. In a similar manner, the CO partial pressure overshoots the CJ prediction in D1 and matches the CJ prediction in D2. In both experiments, the measured post-detonation temperatures and CO mole fractions closely match the CJ predictions.

The Kistler pressure lingers near the peak pressure value for longer than the LAS pressure, due to the LAS measurement’s ability to respond faster to changes in gas condition compared to the 100‘kHz filtered bandwidth of the Kistler. This effect could also be attributed to boundary-layer effects. This is especially pronounced in experiment D1. Evidence that the LAS measurement is more appropriate can be seen by looking at the CO mole fraction measurement. When using the LAS pressure to find $X_\text {CO}$, the CO mole fraction is constant after the detonation. When the Kistler pressure is used, $X_\text {CO}$ starts at the CJ value, dips below the CJ value, and returns to the CJ value afterwards in a non-physical manner.

For both experiments, after the initial pressure spike, the pressure decays substantially. At around 200 $\upmu$s and 600 $\upmu$s, reflected waves from the diaphragm at the end of the tube reach the measurement location and raise the pressure on the order of 10–50%. The ability of the two pressure sensors to capture the pressure changes associated with these reflected waves can be readily observed. The LAS pressure measurement responds quickly to these changes in physical pressure, whereas the Kistler measurement can be seen to lag behind by a few microseconds due to the $\upmu$s-scale response time of the electromechanical sensor. This lag can be seen more clearly when looking at the $X_\text {CO}$ measurements derived from these two pressure measurements. When using the LAS pressure, the $X_\text {CO}$ measurement remains constant, whereas with the lagged Kistler measurement, the $X_\text {CO}$ measurement non-physically spike, as the measured CO partial pressure increases behind the wave while the Kistler pressure remains roughly constant. The ringing in the Kistler measurement also leads to a lower SNR compared to the LAS measurement. The SNR of the Kistler measurement is on the order of 20 whereas the LAS pressure measurement has a higher SNR of 150. The reduced SNR of the Kistler measurement prevents it from registering the reflected wave at 200 $\upmu$s. Overall, this comparison highlight the capability of the optical measurement to perform competitively with the electromechanical transducer in terms of both speed and measurement quality.

5 Conclusions

In this work, a high-speed optical pressure-sensing strategy for dynamic combustion environments was developed based on laser absorption measurements of carbon monoxide linewidths in the mid-infrared. The single-laser, multi-line measurement technique provides for quantification of temperature, pressure, and species density simultaneously, eliminating key unknowns due to interdependency of these thermodynamic parameters. A thorough uncertainty-analysis framework was developed and applied to account for potential measurement error due to noise sources, spectroscopic uncertainty, and gas composition uncertainty, with cross-correlations incorporated in the analysis. The broad applicability and robustness of the pressure measurement was shown via simulated variations in fuel, equivalence ratio, reaction progress, and other parameters. Aggregated uncertainty indicates the MHz-rate optical pressure measurement has a typical total uncertainty of approximately 10%, varying by a few percent over a large range of conditions. The most substantial uncertainty factors in this analysis are the species-specific broadening coefficients. As such, for air combustion with nitrogen as the dominant collision partner and for highly diluted gas mixtures with other inert species, the absolute uncertainty can be lower. Moreover, while absolute pressure uncertainty is limited by the ability to accurately estimate species-specific broadening coefficients, this analysis suggests that changes in pressure (dynamic pressure) will have a lower uncertainty as the directional bias would be unlikely to change for a given dynamic combustion environment. The methods outlined in this paper and associated results allow for more specific estimation of uncertainty for a given application, and offer many useful scaling relations and guiding metrics to design LAS systems with minimized uncertainty.

The measurement technique was demonstrated in dynamic combustion experiments involving shock and detonation waves to highlight capabilities and versatility. Overall, the demonstrations indicate the ability of the pressure sensor to measure dynamically changing pressure in high-temperature air- and oxy-combustion environments with high accuracy and precision at a rate of 1 MHz, over a range of pressures and equivalence ratios. Clear advantages can be observed with the optical pressure sensor over the electromechanical pressure transducer in signal-to-noise ratio and response time. A practical advantage of overcoming boundary-layer effects is shown in a shock tube experiment with shock bifurcation. The analyzed and demonstrated performance of the LAS pressure-sensing strategy indicates strong potential for utilization in both laboratory and field experiments involving shock and detonation waves.