Abstract
We derive a new Hamiltonian formulation of Schlesinger equations in terms of the dynamical r-matrix structure. The corresponding symplectic form is shown to be the pullback, under the monodromy map, of a natural symplectic form on the extended monodromy manifold. We show that Fock–Goncharov coordinates are log-canonical for the symplectic form. Using these coordinates we define the symplectic potential on the monodromy manifold and interpret the Jimbo–Miwa–Ueno tau-function as the generating function of the monodromy map. This, in particular, solves a recent conjecture by A. Its, O. Lisovyy and A. Prokhorov.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Symplectic aspects of the monodromy map for the Fuchsian systems were studied starting from [3, 25, 33]; in these papers it was proved that the monodromy map is a symplectomorphism from a symplectic leaf in the space of coefficients of the system to a symplectic leaf in the monodromy manifold. The non-Fuchsian case was considered in [11, 13, 15, 19, 41]. Remarkably, the simplest non-Fuchsian case of the Painlevé II hierarchy was treated in the paper [19] in 1981, about 15 years before the Fuchsian case was studied in detail in [3, 25, 33]. The key object associated to any Fuchsian or non-Fuchsian system of linear ODE’s is the tau-function introduced by Jimbo, Miwa and Ueno [30]; until now its significance in the framework of the monodromy symplectomorphism remained unclear; the main goal of this paper is to fill this gap and prove a recent conjecture by Its–Lisovyy–Prokhorov [28].
Our interest in this subject stems from the study of monodromy map of a second order equation on a Riemann surface; such a map was also proven to be a symplectomorphism [9, 10, 32, 34]. Remarkably, the generating function of the monodromy symplectomorphism (the “Yang–Yang” function) plays an important role in the theory of supersymmetric Yang–Mills equations [37] ; several steps towards understanding of this generating function were made in [9].
In this paper we address the question about the role of the generating function of the monodromy symplectomorphism in the context of Fuchsian equations on the Riemann sphere. The conclusion we arrive to is somewhat unexpected: such generating function can be naturally identified with the isomonodromic tau-function; moreover, this interpretation allows to define the dependence of the tau-function on monodromy data.
The version of the monodromy map for Fuchsian systems used in the current paper is slightly different from the monodromy map considered in [3, 25, 33]. This version is standard in the theory of isomonodromy deformations [39] and it was also considered in [11, 29] from the symplectic point of view.
To describe the monodromy map we remind the basics of the theory of solutions of Fuchsian systems of differential equations on \({{\mathbb {P}}^1}\), following [39]. Consider the equation
where \(A_i\in sl(n)\) and \(t_j\ne t_k\) such that \(\sum _{i=1}^N A_i=0\). Assume also that eigenvalues of each \(A_j\) are simple and furthermore do not differ by an integer. Choose a system of cuts \(\gamma _1,\dots ,\gamma _N\) connecting \(\infty \) with \(t_1,\dots ,t_N\) respectively, and assume that the ends of these cuts emanating from \(\infty \) are ordered as \((1,\dots ,N)\) counter-clockwise (Fig. 1). The normalization condition \(\Psi (\infty )=\mathbf{1 }\) is then understood in the sense that \(\lim _{z\rightarrow \infty } \Psi (z)=\mathbf{1 }\) where the limit is taken in the sector between \(\gamma _1\) and \(\gamma _N\).
The set of generators \(\sigma _1,\dots ,\sigma _N\) of the fundamental group \(\pi _1({{\mathbb {P}}^1}\setminus \{t_j\}_{j=1}^N,\infty )\) is chosen such that the loop representing \(\sigma _j\) crosses only the cut \(\gamma _j\), and its orientation is chosen so that the relation between \(\sigma _j\) takes the form \( \sigma _N\cdot \dots \cdot \sigma _1=\mathrm{Id}\) (Fig. 1).
The solution \(\Psi \) of (1.1) is single-valued in the simply connected domain \({{\mathbb {P}}^1}\setminus \{\gamma _j\}_{j=1}^N\). Denote the diagonal form of the matrix \(A_j\) by \(L_j\), \(j=1,\dots , N\) (the matrices \(A_j\) are diagonalizable due to our assumption about their eigenvalues). Then the asymptotics of \(\Psi \) near \(t_j\) has the standard form [39]:
The matrix \(G_j\) is a diagonalizing matrix for \(A_j\):
The matrices \(C_j\) are called the connection matrices. Notice that the matrices \(G_j\) and \(C_j\) are not uniquely defined by Eq. (1.1) since a simultaneous transformation \(G_j\rightarrow G_j D_j\) and \(C_j\rightarrow C_j D_j\) with diagonal \(D_j\)’s changes neither the asymptotics (1.2) nor the Eq. (1.1).
Analytic continuation of \(\Psi (z)\) along \(\sigma _j\) yields \(\Psi (z) M_j^{-1}\), where the monodromy matrix \(M_j\in SL(n)\) is related to the connection matrix \(C_j\) and the exponent of monodromy \(L_j\) by:
Alternatively, the matrix \(M_j\) can be viewed as the jump matrix on \(\gamma _j\): orienting \(\gamma _j\) from \(\infty \) towards \(t_j\), the boundary values of \(\Psi \) on the right (“\(+\)”) and left (“−”) sides of \(\gamma _j\) are related by \(\Psi _+=\Psi _i M_j\). Our assumption about the ordering of the branch cuts \(\gamma _j\) and generators \(\sigma _j\) implies the relation
The monodromy map introduced in [39] sends the set of pairs \((G_j,L_j)\) to the set of pairs \((C_j,\Lambda _j)\) for a given set of poles \(t_j\).
The map between the set of coefficients \(A_j\) and the set of monodromy matrices \(M_j\) is a different version of monodromy map associated to Eq. (1.1); the symplectic aspects of this version of the monodromy map were studied in [3, 25, 33].
To describe our framework in more details we introduce the following two spaces. The first space is the quotient
where \({{\mathfrak {h}}}_{ss}^{nr}\) denotes the set of diagonal matrices with simple eigenvalues not differing by integers (non-resonant). The equivalence relation is given by the SL(n) action \(G_j\mapsto S G_j\) with S independent of j.
The second space is the quotient
Similarly to (1.6), the equivalence is given by the SL(n) action \(C_j\mapsto S C_j\) (with the same S for all j’s).
For a fixed set of poles \(\{t_j\}_{j=1}^N\) we denote the “monodromy map” from the (G, L)-space to (C, L)-space by
Poisson and symplectic structures on \({\mathcal {A}}\) and dynamical r-matrix. Let \({\mathcal {H}}:= SL(n,{\mathbb {C}})\times {{\mathfrak {h}}}_{ss} = \{(G,L)\}\). Here \(G\in {SL(N)}\) and \(L=\mathrm{diag}(\lambda _1,\dots ,\lambda _n)\) is a diagonal traceless matrix with \(\lambda _j\ne \lambda _k\) and \(\lambda _1+\dots +\lambda _n=0\). Consider the following 1-form on \({\mathcal {H}}\):
We prove in Proposition 2.1 that the form \(\omega = \,\mathrm{d}\theta \) is non-degenerate, and therefore, is a symplectic form on \({\mathcal {H}}\). For any matrix M we use the following notation for the Kronecker products
Then the Poisson structure on \({\mathcal {H}}\) associated to the symplectic form \(\omega \) is (see Proposition 2.2):
where
and
we use the standard notation \(E_{ij}\) for the matrix with only one non-vanishing element equal to 1 in the (i, j) entry. The matrix r(L) is a simplest example of dynamical r-matrix [17]. Theorem 2.1 shows that the bracket (1.10) induces the Kirillov–Kostant Poisson bracket for \(A=GLG^{-1}\).
The bracket (1.10) can be used to define the Poisson structure on the space \({\mathcal {A}}\) as follows. Denote first by \({\mathcal {A}}_0\) the space of pairs \(\{(G_j,L_j)\}_{j=1}^N\) with the product symplectic structure, or, equivalently, with the following Poisson bracket:
The moment map corresponding to the group action \(G_j\rightarrow SG_j\) (\(S\in SL(n)\)) on \({\mathcal {A}}_0\) is given by \(\sum _{j=1}^N G_j L_j G_j^{-1}\). The space \({\mathcal {A}}\) (1.6) inherits a symplectic form from \({\mathcal {A}}_0\) via the standard symplectic reduction [4]:
Theorem 1
(see Theorem 2.3). The Poisson structure induced on \({\mathcal {A}}\) from the Poisson structure (1.12) on \({\mathcal {A}}_0\) via the reduction on the level set \(\sum _{j=1}^N G_j L_j G_j^{-1}=0\) of the moment map, corresponding to the group action \(G_j\rightarrow SG_j\), is non-degenerate and the corresponding symplectic form is \( \omega _{{\mathcal {A}}}=\,\mathrm{d}\theta _{\mathcal {A}}\), where the symplectic potential \( \theta _{\mathcal {A}}\) for \(\omega _{{\mathcal {A}}}\) is given by
This symplectic structure appeared in [11] but the connection to dynamical r-matrix and associated Poisson structure was not known until now.
Symplectic structure on \({\mathcal {M}}\). Define the following 2-form on the space \({\mathcal {M}}\):
where
with \(K_{\ell }=M_1\cdots M_\ell \) and \(\Lambda _j=e^{2\pi i L_j}\).
The form \(-\omega _1/2\) coincides with the symplectic form on the symplectic leaves \(\Lambda _j=const\) of the SL(n) Goldman bracket (see (3.14) of [2] in the case \(g=0\)). The first result of this paper (see Theorem 3.2 and its proof in Sect. 3) is that given a set of poles \(\{t_j\}_{j=1}^N\) and a point \(p_0\in {\mathcal {M}}\) in a neighbourhood of which the monodromy map is invertible, the pullback of the form \(\omega _{\mathcal {M}}\) under the map \({\mathcal {F}}^t :{\mathcal {A}}\rightarrow {\mathcal {M}}\) coincides with \(\omega _{\mathcal {A}}\):
This statement implies that (see Corollary 3.1 and its proof) the form \(\omega _{\mathcal {M}}\) is closed and non-degenerate, and, therefore, defines a symplectic structure on \({\mathcal {M}}\).
For a given set of monodromy data the monodromy map is invertible outside of a locus of codimension 1 in the space of poles [12]. Since the form \(\omega _{{\mathcal {M}}}\) is independent of \(\{t_j\}\), this form is always non-degenerate on the monodromy manifold.
The equality (1.13) generalizes the results of [3, 25, 33], where it was proved that the monodromy map between the “smaller” spaces—the space of coefficients \(A_j\) with fixed eigenvalues and the symplectic leaf of the GL(n) character variety of N-punctured sphere—is a symplectomorphism; the formula (1.13) was proved in a different way in [11].
Time dependence. To describe the dependence on the \(t_j\)’s (the “times”) we extend the spaces \({\mathcal {A}}\) and \({\mathcal {M}}\) to include also the coordinates \(\{t_j\}\):
The monodromy map \({\mathcal {F}}^t\) then extends to the map \({\mathcal {F}}:\widetilde{{\mathcal {A}}}\rightarrow \widetilde{{\mathcal {M}}}\;\). The locus in \(\widetilde{{\mathcal {M}}}\) where the map is not invertible is usually referred to as the Malgrange divisor. Denote the pullback of the form \(\omega _{\mathcal {A}}\) from \({\mathcal {A}}\) to \(\widetilde{{\mathcal {A}}}\) by \(\widetilde{\omega }_{\mathcal {A}}\) and the pullback of the form \(\omega _{\mathcal {M}}\) from \({\mathcal {M}}\) to \(\widetilde{{\mathcal {M}}}\) by \(\widetilde{\omega }_{\mathcal {M}}\) (notice that the forms \(\widetilde{\omega }_{\mathcal {A}}\) and \(\widetilde{\omega }_{\mathcal {M}}\) are closed but degenerate). Now we are in a position to formulate the next theorem (see Theorem 3.1)
Theorem 2
(see Theorem 3.1 together with Theorem 3.2). The following identity holds between two-forms on \(\widetilde{{\mathcal {A}}}\)
where
are the canonical Hamiltonians of the Schlesinger system.
We remind that the Schlesinger equations [12] consist of the following system of PDEs for the coefficients of A(z)
and they define the deformations of the connection A(z) which preserve the monodromy representation. They are Hamiltonian equations with respect to the standard Kirillov–Kostant Poisson bracket with time–dependent Hamiltonians \(H_k\) as in (1.17).
Tau function and generating function of the monodromy map. The above theorem allows to establish the relationship between the isomonodromic tau-function and the generating function of the monodromy map. Namely, consider some local symplectic potential \(\theta _{\mathcal {M}}\) for the form \(\omega _{\mathcal {M}}\) such that
on the space \({\mathcal {M}}\) (globally \(\theta _{\mathcal {M}}\) can be defined on a covering of \({\mathcal {M}}\)) and denote its pullback to \(\widetilde{{\mathcal {M}}}\) by \(\widetilde{\theta }_{\mathcal {M}}\). Denote by \(\widetilde{\theta }_{\mathcal {A}}\) the pullback of \(\theta _{\mathcal {A}}\) under the natural projection \(\widetilde{{\mathcal {A}}} \rightarrow {\mathcal {A}}\). Then \(\widetilde{\theta }_{\mathcal {A}}\) is the potential of the symplectic form \(\widetilde{\omega }_{\mathcal {A}}\) on \(\widetilde{{\mathcal {A}}}\), and (1.16) implies existence of a locally defined generating function \({\mathcal {G}}\) on \(\widetilde{{\mathcal {A}}}\).
Definition 1.1
The generating function (corresponding to a given choice of the symplectic potential \(\theta _{\mathcal {M}}\)) of the monodromy map between spaces \(\widetilde{{\mathcal {A}}}\) and \(\widetilde{{\mathcal {M}}}\) is defined by
A different choice of \(\theta _{\mathcal {M}}\) (and hence of its pullback \(\widetilde{\theta }_{\mathcal {M}}\)) adds a \(\{t_k\}\)-independent term to \({\mathcal {G}}\) i.e. it corresponds to a transformation \({\mathcal {G}}\rightarrow {\mathcal {G}}+f(\{C,L\})\) for some local function f on \({\mathcal {M}}\).
The dependence of \({\mathcal {G}}\) on \(\{t_j\}\) is, however, completely fixed by (1.19). Namely, locally one can write (1.19) in the coordinate system where \(\{t_j\}_{j=1}^N\) and \(\{C_j,L_j\}_{j=1}^N\) are considered as independent variables. Then derivatives of \(G_j\) on \(\{t_k\}\) for constant \(\{C_j,L_j\}_{j=1}^N\) i.e. for constant monodromy data, are given by Schlesinger equations of isomonodromic deformations in G-variables:
The Eq. (1.20) imply (1.18) but not viceversa. In this paper we obtain the following Hamiltonian formulation of Eq. (1.20):
Theorem 3
(see Theorem 2.2). The Eq. (1.20) are Hamiltonian,
where \(\{.,.\}\) is the quadratic Poisson bracket (1.10) and the Hamiltonians are given by (1.17).
A direct computation shows that in \((t_j,C_j,L_j)\) coordinates the part of \(\widetilde{\theta }_{\mathcal {A}}\) containing \(\,\mathrm{d}t_j\)’s is given by \(2\sum _{j=1}^N H_j \,\mathrm{d}t_j\); together with (1.19) this implies
Therefore, we get the following theorem:
Theorem 4
(see Theorem 3.3). For any choice of symplectic potential \(\theta _{\mathcal {M}}\) on \({\mathcal {M}}\) the dependence of the generating function \({\mathcal {G}}\) (1.19) on \(\{t_j\}_{j=1}^N\) coincides with the \(t_j\)-dependence of the isomonodromic Jimbo–Miwa tau-function. In other words, \(e^{-{\mathcal {G}}}\tau _{JM}\) depends only on monodromy data \(\{C_j,L_j\}_{j=1}^N\).
The above theorem shows that the generating function \({\mathcal {G}}\) can be used to define the tau-function not only as a function of positions of singularities of the Fuchsian differential equation but also as a function of monodromy matrices. The ambiguity built into this definition corresponds to the freedom to choose different symplectic potentials on different open sets of the monodromy manifold.
The symplectic potential we use in this paper was found in [8] using the coordinates introduced by Fock and Goncharov in [21] (for \(SL(2,{\mathbb {R}})\) case these coordinates called shear coordinates are attributed to Thurston, see [16, 20]; see also [14] where the complex analogs of the shear coordinates were used for the explicit parametrization of the open subset of full dimension of the \(SL(2,{\mathbb {C}})\) character variety of four-punctured sphere).
Definition 1.2
The SL(n) tau-function \(\tau \) on \(\widetilde{{\mathcal {M}}}\) is locally defined by the following set of compatible equations. The equations with respect to \(t_j\) are given by the formulas
where
The equations with respect to coordinates on monodromy manifold \({\mathcal {M}}\) are given by
where \(\theta _{\mathcal {M}}[\Sigma _0]\) is a symplectic potential (5.34) for the form \(\omega _{\mathcal {M}}\) defined using the Fock–Goncharov coordinates corresponding to a ciliated triangulation \(\Sigma _0\) (see Sect. 5.4).
Explicit formulas for derivatives of \(\tau \) with respect to Fock–Goncharov coordinates will be given in Sect. 6.
Conjecture by A.Its, O.Lisovyy and A.Prokhorov. Theorem 2 emphasizes a close relationship with the recent work [28] where the issue of dependence of the Jimbo–Miwa tau-function on monodromy matrices was also addressed. In particular, the relevance of the Goldman bracket and the corresponding symplectic form on its symplectic leaves was observed in [28] in the case of \(2\times 2\) system with four simple poles (the associate isomonodromic deformations give Painlevé 6 equation).
Moreover, the authors of [28] introduced a form which we denote by \(\Theta _{ILP}\) (this form is denoted by \(\omega \) in (2.7) of [28]). This form appeared in [28] as a result of computation involving the 1-form introduced by Malgrange in [35], similarly to this work, which in our notations is given by
where \(\,\mathrm{d}_{{\mathcal {M}}}\) denotes the differential with respect to monodromy data. Proposition 2.3 of [28] shows that the external derivative of the form (1.26) is a closed 2-form independent of \(\{t_j\}_{j=1}^N\). Furthermore, in Section 1.6 the authors of [28] formulate the following
Conjecture 1
[Its–Lisovyy–Prokhorov] The form \(\,\mathrm{d}\Theta _{ILP}\) coincides with the natural symplectic form on the monodromy manifold.
There are two natural versions of this conjecture:
-
The “weak” ILP conjecture. In this version \(\,\mathrm{d}_{\mathcal {M}}\) means the differential on a symplectic leaf \(\{\Lambda _j=\mathrm{const}\}_{j=1}^N\) of the SL(n) character variety of \(\pi _1({{\mathbb {P}}^1}\setminus \{t_j\}_{j=1}^N)\) (we denote this symplectic leaf by \({\mathcal {M}}_\Lambda \)). The canonical symplectic form on \({\mathcal {M}}_\Lambda \) is given by the inversion of the SL(n) Goldman’s bracket [23] and can be written explicitly in terms of monodromy data as shown in ([2], formula (3.14) for \(g=0\) and \(k=2\pi \)). By “weak” ILP conjecture we understand the coincidence of \(\,\mathrm{d}\Theta _{ILP}\) (1.26) with the Goldman’s symplectic form on the symplectic leaves.
The problem with this formulation is that the choice of matrices \(G_j\) should be such that they satisfy the Schlesinger equations (1.20); this requirement is not natural from the symplectic point of view.
-
The “strong” ILP conjecture. In this version the differential \(\,\mathrm{d}_{{\mathcal {M}}}\) in (1.26) means the differential on the full space \({\mathcal {M}}\) (1.6) which contains both the eigenvalues of the monodromy matrices and the connection matrices. Then (omitting the pullbacks) the strong ILP conjecture states that
$$\begin{aligned} \,\mathrm{d}\Theta _{ILP}=\omega _{\mathcal {M}}\;. \end{aligned}$$(1.27)
The weak version of the ILP conjecture can be derived from known results of [3, 25] or [33], as shown in Sect. 4.
The strong version of the ILP conjecture is equivalent to our Theorem 2. To see this equivalence it is sufficient to write (1.19) in coordinates which are split into “times” \(\{t_j\}\) and some coordinates on the monodromy manifold \({\mathcal {M}}\). Then the “t-part” of the form \(\widetilde{\theta }_{\mathcal {A}}\) is given by \(2\sum _{k=1}^N H_k d t_k\) (this follows from the isomonodromic Eq. (1.20) for \(\{G_j\}\)) and the monodromy part coincides with the second term of the form (1.26) where the differential \(\,\mathrm{d}_{{\mathcal {M}}}\) is understood as the differential on \({\mathcal {M}}\). Now, taking the external derivative of (1.19) we come to (1.16) where the right-hand side coincides with the form \(\,\mathrm{d}\Theta _{ILP}\) of [28]. Finally, we notice that the formula (1.19) allows to interpret the generating function \({\mathcal {G}}\) as the action of the multi-time hamiltonian system, according to Conjecture 2 of [26] (see also [27]).
Summarizing, the main results of this paper are the following:
-
1.
We give a new hamiltonian formulation of Schlesinger system written in terms of (G, L)-variables; this formulation involves a quadratic Poisson structure defined by the dynamical r-matrix (Sect. 2).
-
2.
We prove that the monodromy map for a Fuchsian system is a symplectomorphism between (G, L) and \((C,\Lambda )\) spaces (Sect. 3).
-
3.
We prove the “weak” (Sect. 4) and “strong” (Theorem 3.2) versions of the Its–Lisovyy–Prokhorov conjecture about coincidence of the external derivative of the Malgrange form with the natural symplectic form on the monodromy manifold
-
4.
We introduce defining equations for the Jimbo–Miwa–Ueno tau-function with respect to Fock–Goncharov coordinates on the monodromy manifold (Definition 6.1 and formula (6.5)).
-
5.
In the SL(2) case we derive equations which define the monodromy dependence of \(\Psi \), \(G_j\) and tau-functions (Theorem 6.1, Corollary 6.1 and Proposition 6.3).
2 Dynamical r-Matrix Formulation of the Schlesinger System
In this section we describe the Hamiltonian formulation of Schlesinger equations. We start from considering the GL(n) case and then indicate the modifications required in the SL(n) case.
2.1 Quadratic Poisson bracket via dynamical r-matrix
Let us introduce the space
where \({{\mathfrak {h}}}_{ss}\) is the space of diagonal matrices with distinct eigenvalues. We denote an element of \({\mathcal {H}}\) by (G, L) where \(G\in GL(n)\) and \(L\in h_{ss}\).
Proposition 2.1
Consider the following one-form on \({\mathcal {H}}\):
Then the 2-form \(\omega =\,\mathrm{d}\theta \) given by
is symplectic on \({\mathcal {H}}\).
Proof
The form \(\omega \) is obviously closed; to verify its non-degeneracy we consider two tangent vectors in \(T_{(G,L)}{\mathcal {H}}\) and represent them as \((X_i,D_i)\in gl(n) \oplus {{\mathfrak {h}}}\) (\(i=1,2\)) where \({{\mathfrak {h}}}\) denotes the Cartan subalgebra of gl(n). Then
Suppose that \(\omega \) is degenerate i.e. the vector \((X_2, D_2)\) can be chosen so that (2.4) vanishes identically for all \((X_1,D_1)\). Then, choosing \(D_1=0\), we have \(\mathrm{tr}(( D_2 + [X_2,L]) X_1)=0\). Then, since \(X_1\) is arbitrary, we have \( D_2 + [X_2,L]=0\); since L is diagonal, the commutator is diagonal-free and hence \(D_2 =0\); since L is semisimple (the eigenvalues are distinct), it follows that \(X_2\) must be diagonal.
Then, choosing \(X_1=0\) and \(D_1\) arbitrary we see that the diagonal part of \(X_2\) must vanish as well. Thus the pairing is nondegenerate and the form \(\omega \) (2.3) is symplectic. \(\square \)
The corresponding Poisson structure is given by the following proposition.
Proposition 2.2
The nonzero Poisson brackets corresponding to the symplectic form \(\omega \) are
Proof
The form (2.4) defines a map \(\Phi _{(G,L)} : T_{(G,L)}{\mathcal {H}}\rightarrow T_{(G,L)}^\star {\mathcal {H}}\) given by
for all \((X_2, D_2)\). Then (2.4) implies
where \(X^{^D}\) and \(X^{^{OD}}\) denote the diagonal and off-diagonal parts of the matrix X, respectively and the identification between a matrix and its dual is defined by the trace pairing. We denote
Given now \((Q,\delta )\in T^\star _{(G,L)}{\mathcal {H}}\) we observe from (2.8) that \(D = -Q^{^D}\) and \(X = \delta + \mathrm{ad}^{-1}_L (Q^{^{OD}})\). The inverse of \(\mathrm{ad}_{L}(\cdot ) = [L,\cdot ]\) is given explicitly by
as a linear invertible map on the space of off–diagonal matrices.
Thus \(\Phi _{(G,L)}^{-1}: T_{(G,L)}^\star {\mathcal {H}}\rightarrow T_{(G,L)} {\mathcal {H}}\) is given by
where \(Q^{^{OD}}\) and \(Q^{^D}\) denote the off-diagonal and diagonal parts, respectively. The Poisson tensor \({\mathbb {P}} \in \bigwedge ^2 T_{(G,L)} {\mathcal {H}}\simeq ( \bigwedge ^2 T^\star _{(G,L)} {\mathcal {H}})^\vee \) is defined by
Using the definition (2.4), (2.6) we get
which is equal to
To obtain the Poisson bracket between the matrix entries of G and L we now write \(Q = G^{-1} \,\mathrm{d}G\) and \(\delta = \,\mathrm{d}L = \mathrm{diag} (\,\mathrm{d}\lambda _1,\dots , \,\mathrm{d}\lambda _n)\).
Choosing \(Q_1 = {\mathbb {E}}_{jk}, \delta _1 =0\) and \(Q_2 = 0, \delta _2 ={\mathbb {E}}_{\ell \ell }\) we have
Choosing \(Q_1 = {\mathbb {E}}_{ij}, Q_2 = {\mathbb {E}}_{k\ell },\ \ \delta _1= \delta _2 = 0\) we have
\(\square \)
Proposition 2.3
Introduce the GL(n) dynamical r-matrix ([17], p.4):
where \(E_{ij}\) is an \(n\times n\) matrix whose (ij) entry equals 1 while all other entries vanish. Introduce also the matrix
Then the bracket (2.5) can be written as follows:
The proof is a straightforward computation. Notice that the formula (2.13) can alternatively be written as follows:
The Jacobi identity involving the brackets \(\{\{\mathop {G}\limits ^1, \mathop {G}\limits ^2\},\mathop {G}\limits ^3\}\) implies (taking into account that \(\displaystyle \mathop {r}\limits ^{ij}=-\mathop {r}\limits ^{ji}\)) the classical dynamical Yang–Baxter equation: (see (3) of [17]).
Remark 2.1
We did not find the construction of this section in the existing literature. In the special case of the SL(2) group, the Poisson algebra (2.12), (2.13) appeared in the work [1] in the context of classical Poisson geometry of \(T^{*}SL(2)\), see formulas (2),(3) in loc.cit.
As it was mentioned to us by L.Feher, the Poisson structure (2.12), (2.13) can be obtained from the canonical Poisson structure on \(T^{*} SL(n)\) as follows. Consider an element \((G,A)\in T^{*} SL(n)\) and denote by L the diagonal form of the matrix \(A\in sl(n)\) (on an open part of the space where the matrix A is diagonalizable). The condition that A is diagonal i.e \(A=L\) is then a constraint of the second kind, according to Dirac’s classification. The computation of the Dirac bracket for the pair (G, L) starting from the canonical Poisson structure on \(T^{*} SL(n)\) leads to the Poisson structure (2.12), (2.13), similarly to a computation given in [18].
2.1.1 Reduction to SL(n)
To reduce to SL(n) we observe that the proof of Proposition 2.1 holds also if we assume \(\mathrm{tr}L=0\) and \(\det G=1\). To compute the corresponding Poisson bracket we recall that inverting the restriction of a symplectic form to a symplectic submanifold is equivalent to the computation of the Dirac bracket.
Let \(h_1 :=\log \det G\) and \(h_2:= \mathrm{tr}L\); the Dirac bracket is then
where \(A_{jk}\) is the inverse matrix to \(\{h_j, h_k\}\): in our case we have
Moreover a simple computation using (2.5) shows that
Then (we denote by \(\{\}_{SL(n)}\) the Dirac bracket restricted to \(\det G =1, \ \mathrm{tr}L =0\))
Equivalently the SL(n) bracket is written as
where now the matrix \(\Omega \) is given by
and \(\alpha _j = \mathrm{diag}(0,\dots , 1,-1,0,\dots )\) are the simple roots of SL(n) and \({\mathbb {A}}\) is the Cartan matrix of SL(n);
2.1.2 Relation to the Kirillov–Kostant bracket
The Kirillov–Kostant bracket on GL(n), in tensor notation, takes the form
Here P is the permutation matrix of size \(n^2\times n^2\) given by
The regular symplectic leaves are the (co)adjoint orbits of diagonal matrices L with distinct eigenvalues, and on the orbit passing through L the symplectic form of the Kirillov–Kostant bracket (2.19) is equal to (see [5], pp. 44, 45):
where G is any matrix diagonalizing A i.e. \(A=GLG^{-1}\). The form \(\omega _{KK}\) is invariant under the transformation \(G\rightarrow GD\) where D is a diagonal matrix which may depend on G; such transformation leaves A invariant.
Theorem 2.1
The map \((G,L)\mapsto A= GLG^{-1}\) is a Poisson morphism between the Poisson structure (2.5) and the Kirillov–Kostant Poisson structure on A;
or, equivalently,
Proof
We have
Then
From the Poisson bracket (2.14) we have
Plugging (2.25) in (2.24) we see that the only terms giving non-trivial contributions are the following:
This expression coincides with the Kirillov–Kostant Poisson bracket (2.22). \(\square \)
A slight modification of this computation shows that the quadratic Poisson bracket (2.5) implies the Kirillov–Kostant bracket in SL(n) case.
2.2 Hamiltonian formulation of the Schlesinger system in G–variables
Consider the Schlesinger system written in terms of the matrices \(G_j\in SL(n)\):
where
Matrices \(L_j\in {{\mathfrak {sl}}}(n)\) are diagonal and the eigenvalues of \(L_j\) are assumed to be distinct.
The Poisson structure of the Schlesinger system (1.18) written in terms of \(A_j\) is known to be linear: it is based on the Kirillov–Kostant bracket. On the other hand, the hamiltonian formulation of the system (2.26) involves the quadratic bracket defined by the dynamical r-matrix.
The following theorem can be checked by direct calculation:
Theorem 2.2
Denote by \({\mathcal {A}}_0 \) the space of matrices \(\{(G_j,L_j)\}_{j=1}^N\) where \(L_j\) are diagonal matrices with distinct eigenvalues. Then the system (2.26) is a multi-time hamiltonian system with respect to the Poisson structure on \({\mathcal {A}}_0 \)
where \(\delta _{jk}\) is the Kronecker delta. The Hamiltonian defining the evolution with respect to “time” \(t_k\) is given by
We notice that for the Schlesinger system for matrices \(A_j\) (1.18) the Hamiltonians \(H_j\) are the same as for the system (2.26).
2.3 Symplectic form and potential
In the sequel we shall use the symplectic form associated to the bracket (2.28). A direct computation using the Poisson bracket (2.16) shows that the matrix \(A= GLG^{-1}\) has the following Poisson brackets with G and L:
Thus \(\{\mathrm{tr}(X A), G\} = X G\) for any fixed matrix \(X\in {{\mathfrak {sl}}}(n)\) and, therefore, the matrix \(A = GLG^{-1}\) is the moment map for the group action \(G\mapsto S G\) on the space \({\mathcal {H}}\). A similar statement, of course, holds for GL(n) using the Poisson bracket (2.5) instead.
Consider now the diagonal group action on \({\mathcal {A}}_0\) given by
where S is an SL(n) matrix. The previous computation shows immediately that the moment map corresponding to the group action \(G_j\rightarrow SG_j\) on \({\mathcal {A}}_0\) is given by
The space \({\mathcal {A}}\) is defined by (1.6) as the space of the orbits of the action (2.30) of in the zero level set of the moment map (2.31). This implies the following theorem proven via the standard symplectic reduction [4]:
Theorem 2.3
The Poisson structure induced on \({\mathcal {A}}\) from the Poisson structure (1.12) on \({\mathcal {A}}_0\) via the reduction on the level set \(\sum _{j=1}^N G_j L_j G_j^{-1}=0\) of the moment map, corresponding to the group action \(G_j\rightarrow SG_j\), is non-degenerate and the corresponding symplectic form is given by
A symplectic potential \( \theta _{\mathcal {A}}\) for \(\omega _{{\mathcal {A}}}\) is given by
3 Monodromy Symplectomorphism via Malgrange’s Form
We start from introducing the Malgrange form associated to a Riemann–Hilbert problem on an oriented graph and discussing some of its properties, following [6, 7, 35]. From now on we work with the SL(n) case.
Let \(\Sigma \) be an embedded graph on \({\mathbb {C}}{\mathbb {P}}^1\) whose edges are smooth oriented arcs meeting transversally at the vertices. We denote by \(\mathbf{V}\) the set of vertices of \(\Sigma \). Consider a “jump matrix” i.e. a function \(J(z):\Sigma \setminus \mathbf{V} \rightarrow SL(n)\) that satisfies the following properties
Assumption 3.1
-
1.
In a small neighbourhood of each point \(z_0\in \Sigma \setminus \mathbf{V} \) the matrix \(J(z)\) is given by a germ of analytic function;
-
2.
for each \(v\in \mathbf{V} \), denote by \(\gamma _1,\dots , \gamma _{n_v}\) the edges incident at v in a small disk centered thereof. Suppose first that all these edges are oriented away from v and enumerated in counter-clockwise order. Denote by \(J^{(v)}_j(z)\) the analytic restrictions of \(J\) to \(\gamma _j\). Assume that each \(J_j^{(v)}(z)\) admits an analytic extension to a full neighbourhood of v and that these extensions satisfy the local no-monodromy condition
$$\begin{aligned} J_1^{(v)}(z)\cdots J^{(v)}_{n_v}(z)=\mathbf{1 }\;. \end{aligned}$$(3.1)If the edge \(\gamma _j\) is oriented towards v then \(J_j^{(v)}(z)\) is taken to be the inverse of \(J(z)\).
Suppose now that the jump matrices form an analytic family depending on some deformation parameters and satisfying Assumption 3.1, and consider a family of Riemann–Hilbert problems on \(\Sigma \).
Malgrange form for an arbitrary Riemann Hilbert Problem. Let \(\Phi (z):{\mathbb {C}}{\mathbb {P}}^1 \setminus \Sigma \rightarrow SL(n)\) be a matrix-valued function, bounded everywhere and analytic on each face of \(\Sigma \). We also assume that the boundary values on the two sides of each edge of \(\Sigma \) are related by
where the \({+/-}\) boundary value is from the left/right, respectively, of the oriented edge.
Definition 3.1
[35]. The Malgrange 1-form on the deformation space of Riemann–Hilbert problems with given graph \(\Sigma \) and jump matrices \(J\) is defined by
where \(\,\mathrm{d}J\) denotes the total differential of \(J\) in the space of deformation parameters for fixed z.
In ([7], Thm. 2.1) it was proved the following formula for the exterior derivative of (3.10):
where
Here the notation \(J^{(v)}_{[a:b]}\) stands for the product \(J^{(v)}_{a} \cdots J^{(v)}_b\) for any two indices \(a<b\).
In [7] the formula for \(\eta _{_{\mathbf{V}}}\) is written in a slightly different form and can be recast as the above expression by using the conditions (3.1).
Malgrange form and Schlesinger systems. Let us now discuss how the form (3.3) can be used in the context of the Fuchsian equation (1.1) and the associated Riemann–Hilbert problem.
Let \({\mathbb {D}}_j\) be small, pairwise non-intersecting disks centered at \(t_j\), \(j=1,\dots , N\).
In order to define the inverse monodromy map unambiguously, we need to fix the determination of the power in (1.2). To this end, fix a point \(\beta _j\) on the boundary of each of the disks \({\mathbb {D}}_j\) and declare that, within the disk \({\mathbb {D}}_j\), the power \((z-t_j)^{L_j}\) stands for \( |z-t_j|^{L_j} \mathrm{e}^{i\arg (z-t_j)L_j}\), where the argument is chosen between \(\arg (\beta _j-t_j)\) and \(\arg (\beta _j-t_j) + 2\pi \). In particular the logarithm \(\ln (z-t_j)\) is assumed to have the branch cut connecting \(t_j\) with \(\beta _j\) and the determination implied by the above.
Choose now a collection of non-intersecting edges \(l_1,\dots , l_N\) connecting \(\infty \) with each of the \(\beta _j\)’s (\(l_j\) is assumed to be transversal to the boundary \(\partial {\mathbb {D}}_j\) at \(\beta _j\)). Denote by \(\Sigma \) the union of all the circles \(\partial {\mathbb {D}}_j\) and the edges \(l_j\). Denote by \({\mathscr {D}}_\infty \) the “exterior” domain which is the complement of the union of the disks \({\mathbb {D}}_j\) and the graph \(\Sigma \).
The solution \(\Psi (z)\) of (1.1) is a single–valued matrix function in \({\mathscr {D}}_\infty \) normalized by \(\lim _{z\rightarrow \infty } \Psi (z) =\mathbf{1 }\) where the direction lies within a sector lying between edges \(l_1\) and \(l_N\). Within each disk, with the above choice of determination of the logarithm, the analytic continuation of \(\Psi \) has the local expression (1.2). The “connection matrices” \(C_j\) are uniquely determined by a choice of \(G_j\) and the determination of the logarithm.
We have therefore defined the (extended) monodromy map
Although this monodromy map depends on \(\Sigma \) and the determinations of the logarithms, we are not going to indicate it explicitly.
An example of the graph \(\Sigma \) is shown in Fig. 2; the graph looks like N “cherries” whose “stems” are attached to the point \(z=\infty \). Introduce the piecewise analytic matrix on its faces as follows
The function \(\Phi \) solves a Riemann–Hilbert Problem on \(\Sigma \) with the jump matrices on its edges indicated in Fig. 2:
where \(l_j\) is the “stem” of the jth cherry.
The matrix function \(\Phi \) given by (3.7) is the unique solution of the Riemann–Hilbert problem with jump matrices (3.8):
The solution of the Riemann–Hilbert problem exists for generic set of data \(\{C_j,L_j,t_j\}\); this solution provides the inverse of the map in (3.6). We emphasize that the inverse monodromy map depends on the isotopy class of \(\Sigma \) and on the fixing of the branches of the logarithms.
In the context of Fuchsian systems the general Malgrange form in Definition 3.1 specializes to the following definition:
Definition 3.2
The Malgrange one form \(\Theta \in T^{*}_p \widetilde{{\mathcal {M}}}\) is the form defined by the expression (3.3), where \(\Phi \) is the solution of the Riemann–Hilbert problem (3.8), (3.9).
It is known [35] that the form \(\Theta \) is a meromorphic form on \(\widetilde{{\mathcal {M}}}\); the set of poles of \(\Theta \) is called the “Malgrange divisor”; on this divisor the Riemann–Hilbert problem fails to have a solution. Moreover, the residue along this divisor is a positive integer [35].
The deformation parameters involved in the expression (3.3) for \(\Theta \) are \(C_j, L_j\) subject to the monodromy relation \(\prod _{j=1}^N C_j \mathrm{e}^{2i\pi L_j} C_j^{-1}=\mathbf{1 }\), and the locations of the poles \(t_1,\dots , t_N\).
Theorem 3.1
The form \(\Theta \in T^{*}\widetilde{{\mathcal {M}}}\) (3.3) and the potential \(\widetilde{\theta }_{{\mathcal {A}}}\in T^{*}\widetilde{{\mathcal {A}}}\) are related by
where \(H_j\) are the Hamiltonians (1.17). Denote now by \(\partial _{t_j} \in T\widetilde{{\mathcal {M}}}\) the vector field of differentiation w.r.t. \(t_j\) keeping the monodromy data constant. Then the contraction of \(\Theta \) with \(\partial _{t_j}\) is given by
Equivalently, the contraction of (the pullback via the inverse monodromy map of) \(\widetilde{\theta }_{\mathcal {A}}\) with \(\partial _{t_j}\) equals \(2H_j\).
Proof
The simplest way to prove (3.10) is via the localization formula [28] using the Riemann–Hilbert problem defined on the graph \(\Sigma \) shown in Fig. 2. To simplify the notation we will not indicate explicitly the pullbacks, but simply consider the matrices \(G_j\) as functions of times and monodromy data via the inverse monodromy map.
In the formula (3.3) the function \(\Phi _-\) coincides with the boundary value of the solution, \(\Psi \), of the ODE (1.1) in the domain \({\mathbb {D}}\). Therefore, denoting \(\,\mathrm{d}\Phi /\,\mathrm{d}z\) by \(\Phi '\) we have:
Here we have used the fact that \(\Phi _-\) coincides with \(\Psi \) and therefore \(\Phi _-'\Phi _-^{-1} = A(z)\). Moreover we have
since \(\Phi _+ = \Phi _- J\). Thus (3.3) can be equivalently written as follows
and further represented as
The first integral in the r.h.s. of (3.14) vanishes since the integrand is holomorphic in \({\mathbb {D}}\). Thus (3.14) reduces to (this is the expression that also appears in [28], formula (1.11)):
The expression (3.15) can be further evaluated in the coordinate system given by \((C_j,L_j,t_j)\). Namely, the contribution of derivatives with respect to monodromy data \((C_j,L_j)\) into (3.15) is obtained by evaluation of \(\,\mathrm{d}\Phi _j(z) \Phi _j^{-1}(z)\) at the poles \(t_j\) which gives the monodromy part of \(\widetilde{\theta }_{{\mathcal {A}}}\) in (3.10).
A straightforward local analysis using (3.7) shows that:
Thus
Finally, due to the Schlesinger equations for \(G_j\) (1.20) we get
Recalling that the Jimbo–Miwa Hamiltonians are given by \(H_j=\sum _{k\ne j}\frac{\mathrm{tr}A_j A_k }{t_j-t_k}\) and that the first term equals the potential \( \widetilde{\theta }_{\mathcal {A}}\) on \(\widetilde{{\mathcal {A}}}\), we arrive at (3.10).
As a corollary of the Schlesinger equations (1.20) the contraction of \(\widetilde{\theta }_{\mathcal {A}}\) with a vector field \(\partial _{t_j}\) (for fixed monodromy data) is
Therefore, the total \(\,\mathrm{d}t_j\)—part of the form \(\Theta \) for fixed monodromies equals to \(\sum _{j=1}^N H_j\,\mathrm{d}t_j\). \(\square \)
Symplectic form on the monodromy manifold. We start from defining the two-form on the monodromy manifold which is one of central objects of this paper.
Definition 3.3
Define the following 2-form on \({\mathcal {M}}\) (1.7):
where
and \(K_{\ell }=M_1\dots M_\ell \).
On the monodromy manifold \(M_1\dots M_N=\mathbf{1 }\) the form \(\omega _{\mathcal {M}}\) is invariant under simultaneous transformation \(C_j\rightarrow S C_j\) with S is an arbitrary SL(n)-valued function on \({\mathcal {M}}\).
Remark 3.1
The restriction of the form \(-2i\pi \omega _{\mathcal {M}}\) on the leaves \(\Lambda _j = \) constant (under such restriction \(\omega _2=0\) and hence \(-2i\pi \omega _{\mathcal {M}}= -\omega _1/2\)) coincides with the symplectic form on the symplectic leaves of the GL(n) Goldman bracket found in [2] (formula (3.14); the case of this formula relevant for us corresponds to \(k=2\pi \) and \(g=0\) in the notation of [2]).
As we prove below in Corollary 3.1, the form \(\omega _{\mathcal {M}}\) is non-degenerate on the space \({\mathcal {M}}\), which is a torus fibration (with fiber the product of N copies of the SL(n) torus of diagonal matrices) over the union of all the symplectic leaves of the Goldman bracket. The fact that \({\mathcal {M}}\) is a torus fibration is simply due to the fact that the fibers of the map \((C_j,\Lambda _j) \rightarrow M_j = C_j \Lambda _j C_j^{-1}\) are obtained by multiplication of the \(C_j\)’s on the right by diagonal matrices.
Let us trivially extend the form \(\omega _{\mathcal {M}}\) to the space \(\widetilde{{\mathcal {M}}}\) (1.15) which includes also the variables \(t_j\). This extension is denoted by \(\widetilde{\omega }_{\mathcal {M}}\).
Relation between forms \(\Theta \) and \(\omega _{{\mathcal {M}}}\). The following theorem was stated in [6] in slightly different notations without direct proof. The proof is given below.
Theorem 3.2
The exterior derivative of the form \(\Theta \) is given by the pullback of the form \(\widetilde{\omega }_{\mathcal {M}}\) (3.16) under the monodromy map:
Proof
Let us apply the formulas (3.4), (3.5) to the graph \(\Sigma \) depicted in Fig. 2 with indicated jump matrices. The integral over \(\Sigma \) in the formula (3.4) then reduces to a sum of integrals over \(\partial {\mathbb {D}}_\ell \)’s because the jump matrix J(z) on the cuts is constant with respect to z. We denote by \(\beta _\ell \) the three-valent vertices where the circles around \(t_\ell \) meet with the edges going towards \(z_0\). Let us consider the contribution of one of the integrals over \(\partial {\mathbb {D}}_\ell \) to (3.4).
We will drop the index \(_\ell \) for brevity in the formulas below. Notice also that \(\,\mathrm{d}L \wedge \,\mathrm{d}L=0\) because the matrix L is diagonal. Letting \(J(z) =C (z-t)^{-L}\) we get
In the course of the computation we have used that
where the integration goes along the circle \(|z-t|=|\beta -t|\) starting at \(z=\beta \). We now turn to the evaluation of the term \(\eta _{_{\mathbf{V}}}\) (3.5). The set of vertices \(\mathbf{V} \) consists of \(\mathbf{V} = \{z_0, \beta _1,\dots , \beta _N\}\). The contribution coming from the vertex \(z_0\) is precisely the first term in \(\omega _1\) (3.17) (in (3.17) this term is simplified using the local no-monodromy condition (3.1)).
To evaluate the contribution of the vertex \(\beta =\beta _\ell \in \mathbf{V} \) we observe that this vertex is tri-valent and the jump matrices on the three incident arcs are
where \(\Lambda := \mathrm{e}^{2i\pi L}\). In the definition it is assumed that \((z-t)^L\) is defined with a branch cut extending from t to \(\beta \). Since \(J_1J_2J_3 =\mathbf{1 }\) the contribution of the vertex to (3.5) reduces to the term
Recall that \(L, \Lambda \) are diagonal; we have then
Then a straightforward computation gives
Summing up (3.20) (the contribution of the integral) with (3.22) (the contribution coming from the vertex \(\beta =\beta _\ell \)) we get
Then summing over all contributions from vertices \(\beta _\ell \) leads to (3.16).
Summarizing, the first term in (3.17) corresponds to the N-valent vertex. The second term in (3.17) together with the term (3.18) arise from the contributions of cherries and the three-valent vertices formed by cherries and their stems. \(\square \)
This theorem immediately implies the following corollary, which can also be deduced from previous results of [11].
Corollary 3.1
The form \(\omega _{\mathcal {M}}\) (3.16) is closed and non-degenerate on the monodromy manifold \({\mathcal {M}}\).
Strong version of Its–Lisovyy–Prokhorov conjecture. The Theorem 3.2 proves the “strong” version of the ILP conjecture (1.26). To state this conjecture in the present setting we consider the form (1.11) or (2.7) of [28] which we denote by \(\Theta _{ILP}\) to avoid confusion with the notations of this paper (see also the identity (4.20) below):
The Conjecture from section 1.6 of [28] refers to the restriction of the form to the symplectic leaves \(L_j=\)constants. We refer to this as the weak Its–Lisovyy–Prokhorov conjecture; in this formulation \(\,\mathrm{d}_{{\mathcal {M}}}\) refers to the differential only with respect to the connection matrices \(C_j\). This “weak” version of the conjecture is proved on the basis of known results [3, 25, 33] in the next section.
The statement of Theorem 3.2 is the strong version of the above conjecture: in this version the differential \(\,\mathrm{d}_{{\mathcal {M}}}\) is with respect to all monodromy data including the \(L_j\)’s.
Generating function of the monodromy map. The closure of \(\omega _{\mathcal {M}}\) guarantees the local existence of a symplectic potential. Denoting any such local potential by \(\theta _{\mathcal {M}}\) (such that \(\,\mathrm{d}\theta _{\mathcal {M}}=\omega _{\mathcal {M}}\)) we define the (local on \(\widetilde{{\mathcal {M}}}\)) generating function \({\mathcal {G}}\) as follows
where \(G_k\) and \(H_k\) are considered as functions on \(\widetilde{{\mathcal {M}}}\) under the inverse monodromy map.
The Eq. (3.24) can be used to extend the definition of Jimbo–Miwa tau-function to include its dependence on monodromies. Irrespectively of the choice of \(\theta _{\mathcal {M}}\), the formula (3.11) implies the following theorem
Theorem 3.3
For any choice of symplectic potential \(\theta _{\mathcal {M}}\) on \({\mathcal {M}}\) the dependence of the generating function \({\mathcal {G}}\) (1.19) on \(\{t_j\}_{j=1}^N\) coincides with \(t_j\)-dependence of the isomonodromic Jimbo–Miwa tau-function. In other words, \(e^{-{\mathcal {G}}}\tau _{JM}\) depends only on monodromy data \(\{C_j,L_j\}_{j=1}^N\).
In Sect. 6 we are going to use this theorem to define the isomonodromic tau function as exponent of the generating function G under a special choice of the symplectic potential \(\theta _{\mathcal {M}}\) based on the use of Fock–Goncharov coordinates.
Remark 3.2
“Extended” character varieties with non-degenerate symplectic form were considered in the ’94 paper [29] and later in the paper [11]. In ([11] Corollary 1) it was proven that the pullback of a symplectic form from the extended monodromy manifold coincides with a symplectic form on \((L_j, G_j)\) side. The description of the corresponding Poisson bracket, construction of symplectic potentials, Malgrange form, the tau-function and coordinatization in term of Fock–Goncharov parameters were not considered before, to the best of our knowledge.
4 Standard Monodromy Map and Weak Version of Its–Lisovyy–Prokhorov Conjecture
Here we show that a weak version of Its–Lisovyy–Prokhorov conjecture can be derived in a simple way from previous results of [3, 25] or [33] where a symplectomorphism between the space of coefficients \(\{A_j\}\) with given set of eigenvalues of the Fuchsian equation (1.1) and a symplectic leaf of Goldman bracket was proved.
First, consider the submanifold \({\mathcal {A}}_L\) of \({\mathcal {A}}\) such that the diagonal form of each of the matrices \(A_j\) is fixed:
where \(\sim \) is the equivalence over simultaneous adjoint transformation \(A_i\rightarrow SA_iS^{-1}\) of all \(A_i\) for \(S\in SL(n)\); \(L=(L_1,\dots ,L_N)\) where \(L_j\) is the diagonal form of \(A_j\) and \({{\mathcal {O}}}(L)\) is the (co)-adjoint orbit of the diagonal matrix L. We assume that diagonal entries of each \(L_j\) do not differ by an integer.
Consider similarly also the space \({\mathcal {M}}_L\) which is the subspace of the SL(n) character variety of \(\pi _1({{\mathbb {P}}^1}\setminus \{t_j\}_{j=1}^N)\) such that the diagonal form of the matrix \(M_j\) equals to \(\Lambda _j=e^{2\pi i L_j}\).
The Kirillov–Kostant brackets (2.19) for each \(A_j\):
can be equivalently rewritten in the r-matrix form
The Schlesinger equations for \(A_j=G_j L_j G_j^{-1}\) which follow from the system (1.20) for \(G_j\) take the form:
These equations are Hamiltonian,
with the Poisson structure given by (4.3) and the (time dependent) Hamiltonians \(H_j\) defined by (1.17). Notice that these Hamiltonians commute \(\{H_k,H_j\}=0\) and satisfy the equations \(\partial _{t_k} H_j = \partial _{t_j} H_k\).
After the symplectic reduction to the space of orbits of the global \(Ad_{GL(N)}\) action and restriction to the level set \(\sum _{j=1}^N A_j=0\) of the corresponding moment map one gets a degenerate Poisson structure; its symplectic leaves coincide with \({\mathcal {A}}_L\) [25]. The symplectic form on \({\mathcal {A}}_L\) can be written as
The form (4.5) is independent of the choice of matrices \(G_j\) which diagonalize \(A_j\); moreover, it is invariant under simultaneous transformation \(A_j\rightarrow S A_j S^{-1}\) and thus it is indeed defined on the space \({\mathcal {A}}_L\).
The SL(n) character variety is equipped with the Poisson structure given by the Goldman bracket defined as follows (see p.266 of [24]): for any two loops \(\sigma ,\widetilde{\sigma }\in \pi _1({{\mathbb {P}}^1}\setminus \{t_i\}_{i=1}^N)\) the Poisson bracket between the traces of the corresponding monodromies is given by
where \(\nu (p)=\pm 1\) is the contribution of point p to the intersection index of \(\sigma \) and \(\widetilde{\sigma }\).
The space \({\mathcal {M}}_L\) is a symplectic leaf of the SL(n) Goldman bracket; the Goldman’s symplectic form on \({\mathcal {M}}_L\) coincides with \(-\frac{1}{2}\omega _1\) [2] where \(\omega _1\) is defined in (3.17). We define
The study of the symplectic properties of the map (1.8) was initiated in [3, 25, 33]. In [3, 25] two different proofs were given of the fact that the monodromy map \({\mathcal {F}}^t\) is a symplectomorphism i.e.
In [33] the brackets between the monodromy matrices themselves were obtained starting from (4.3); the result is given by
where P is the matrix of permutation of two spaces. The brackets (4.9), (4.10) were computed for the basepoint \(z_0=\infty \) on the level set \(\sum _{j=1}^N A_j=0\) of the moment map; thus the algebra (4.9), (4.10) does not satisfy the Jacobi identity. However, the Jacobi identity is restored for the algebra of Ad-invariant objects i.e. for traces of monodromies; moreover, for any two loops \(\sigma \) and \(\widetilde{\sigma }\) we have ([40]; see also Thm. 5.2 of [14] where this statement was proved for \(n=4\), \(N=2\) case):
which gives an alternative proof of (4.8).
Let us now show that (4.8) implies the weak version of the Its–Lisovyy–Prokhorov conjecture. Similarly to (1.14) and (1.15) we introduce the two spaces
Denote the pullback of the form \(\omega _{{\mathcal {A}}}^L\) with respect to the natural projection of \(\widetilde{{\mathcal {A}}}_L\) to \({\mathcal {A}}_L\) by \(\widetilde{\omega }_{{\mathcal {A}}}^L\) and the pullback of the form \(\omega _{{\mathcal {M}}}\) with respect to the natural projection of \(\widetilde{{\mathcal {M}}}_L\) to \({\mathcal {M}}_L\) by \(\widetilde{\omega }_{{\mathcal {M}}}^L\).
Proposition 4.1
The following identity holds between two-forms on \(\widetilde{{\mathcal {A}}}_L\):
where \( H_k\) are the Hamiltonians (1.17).
Proof
Denote by 2d the dimension of the spaces \({{\mathcal {A}}}_L\) and \({{\mathcal {M}}}_L\). Introduce some local Darboux coordinates \((p_i,q_i)\) on \({{\mathcal {A}}}^L\) for the form \(\omega ^L_{\mathcal {A}}\) (4.5) and also some Darboux coordinates \((P_i,Q_i)\) on \({{\mathcal {M}}}^L\) for the form \(\omega ^L_{\mathcal {M}}\) given by (4.7).
We are going to verify (4.14) using coordinates \(\{t_j\}_{j=1}^N\) and \(\{P_j,Q_j\}_{j=1}^d\). Let us split the operator \(\,\mathrm{d}\) into two parts:
where \(\,\mathrm{d}_{\mathcal {M}}\) is the differential with respect to \(\{P_j,Q_j\}_{j=1}^d\). Then relation (4.8) can be written as
The right-hand side can be further rewritten using the Hamilton equations \(\frac{\partial {p_i}}{\partial {t_k}}=-\frac{\partial H_k}{\partial q_i}\); \(\frac{\partial {q_i}}{\partial {t_k}}=\frac{\partial H_k}{\partial p_i}\) (where the Hamiltonians \(H_k\) are given by (1.17)). Using
one gets
To simplify the second sum in (4.16) we recall that
thus the second sum can be written as
Adding all the terms in (4.16) we obtain
The coefficient of \(\,\mathrm{d}t_\ell \wedge \,\mathrm{d}t_k\) vanishes because the Hamiltonians satisfy the zero–curvature equations implied by commutativity of the flows with respect to \(t_j\) and \(t_\ell \); in fact in this particular case they satisfy a stronger compatibility: \(\{H_k ,H_\ell \}=0\) and \(\partial _{t_\ell } H_k = \partial _{t_k}H_\ell \). Therefore we arrive at (4.14). \(\square \)
Let us show that (4.14) implies
Proposition 4.2
(Weak ILP conjecture). The following identity holds on the space \(\widetilde{{\mathcal {M}}}_L\):
where
and matrices \(G_j\) diagonalizing \(A_j\) are chosen to satisfy the Schlesinger equations (1.20); \(\,\mathrm{d}_{\mathcal {M}}\) denotes the differential with respect to monodromy coordinates. The form \( \Theta _{ILP}^L \) is the “weak” version of the form (1.26). The form \(\widetilde{\omega }_{{\mathcal {M}}}^L \) is the pullback of Alekseev–Malkin form (4.7) from \({\mathcal {M}}_L\) to \(\widetilde{{\mathcal {M}}}_L\).
Proof
The symplectic potential for the form \(\tilde{\omega }_{\mathcal {A}}^L\) can be written as
We notice that the potential \(\tilde{\theta }_{\mathcal {A}}^L\), in contrast to the form \(\tilde{\omega }_{\mathcal {A}}^L\) itself, is not well-defined on the space \(\widetilde{{\mathcal {A}}}_L\) due to ambiguity \(G_j\rightarrow G_j D_j\) for diagonal \(D_j\) in the definition of \(G_j\). Under such transformation \(\theta _{\mathcal {A}}^L\) changes by an exact form. Therefore for the purpose of proving (4.17) one can pick any concrete representative for each \(G_j\). The most natural choice is to assume that \(\{G_j\}\) satisfy the system (1.20). Then the “t”-part of potential (4.19) can be computed using (1.20) and the definition of the Hamiltonians (1.17) to give
Therefore, the relation (4.14) can be rewritten as
which coincides with (4.17). \(\square \)
Comparison of weak and strong ILP conjectures. In spite of the formal similarity, there is a significant difference between the statements of the weak and strong ILP conjectures. In the strong version the form \(\sum \mathrm{tr}(L_j \,\mathrm{d}G_j G_j^{-1})\) is a well-defined form on the phase space \({\mathcal {A}}\) as well as on its extension \(\widetilde{{\mathcal {A}}}\).
In the weak version the same form is not defined on the space \({\mathcal {A}}^L\) since to get the equality (4.17) one needs to take the residues \(A_j\) (which are given by a point of \({\mathcal {A}}^L\) up to a conjugation) and then diagonalize each \(A_j\) into \(G_j L_j G_j^{-1}\) in a way which is non-local in times \(t_j\): the matrices \(G_j\)’s themselves must satisfy the Schlesinger system (1.20). This requirement can not be satisfied staying entirely within the space \({\mathcal {A}}^L\) and thus \(G_j\)’s can not be chosen as functionals of \(A_j\)’s only; their choice encodes a highly non-trivial \(t_j\)-dependence which fixes the freedom in the right multiplication of each \(G_j\) by a diagonal matrix which also can be time-dependent.
The strong version of the ILP conjecture (Theorem 3.2) is a stronger statement since the form \(\theta _{\mathcal {A}}\) is a 1-form defined on the underlying phase space.
5 Log–Canonical Coordinates and Symplectic Potential
Here we summarize results of [8] where the form \(\omega _{\mathcal {M}}\) was expressed in \(\log \)-canonical form an open subspace of highest dimension of \({\mathcal {M}}\) using the (extended) system of Fock–Goncharov coordinates [21]. This allows to find the corresponding symplectic potential and use it in the definition of the tau-function.
5.1 Fock–Goncharov coordinates
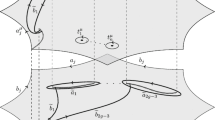
To define the Fock–Goncharov coordinates we introduce the following auxiliary graphs (see Fig. 3):
-
1.
The graph \(\Sigma _0\) with N vertices \(v_{1},\dots , v_{N}\) which defines a triangulation of the N-punctured sphere; we assume that each vertex \(v_j\) lies in a small neighbourhood of the corresponding pole \(t_j\). Since \(\Sigma _0\) is a triangulation there are \(2N-4\) faces \(\{f_k\}_{k=1}^{2N-4}\) and \(3N-6\) edges \(\{e_k\}_{k=1}^{3N-6}\); the edges are assumed to be oriented.
-
2.
Consider a small loop around each \(t_k\) (the cherry) and attach it to the vertex \(v_k\) by an edge (the stem of the cherry). The cherries are assumed to not intersect the edges of \(\Sigma _0\). The union of \(\Sigma _0\), the stems and the cherries is denoted by \(\Sigma _1\).
The graph \(\Sigma _1\) is fixed by \(\Sigma _0\) if one chooses the ciliation at each vertex of the graph \(\Sigma _0\); the ciliation determines the position of the stem of the corresponding cherry.
-
3.
Choose a point \(p_f\) inside each face \(f_k\) of \(\Sigma _0\) and connect it by edges \({\mathcal {E}}_{f}^{(i)}\), \(i=1,2,3\) to the vertices of the face, oriented towards the point \(p_{f}\). We will denote by \(\Sigma \) the graph obtained by the augmentation of \(\Sigma _1\) and these new edges. It is the graph \(\Sigma \) which will be used to compute the form \(\omega _{\mathcal {M}}\).
We will make use of the following notations: by \(\alpha _i\), \(i=1,\dots , n-1\) we denote the simple positive roots of SL(n); by \(\mathrm{h}_i\) the we denote the dual roots:
For any matrix M we define \(M^\star := \mathbf{P}M\mathbf{P}\) where \(\mathbf{P}\) is the “long permutation” in the Weyl group,
In particular \(\alpha _i^\star = -\alpha _{n-i}\), \(\mathrm{h}_i^\star =-{\mathrm h}_{n-i}\;.\) Let
be the signature matrix.
Introduce the \((n-1)\times (n-1)\) matrix \({\mathbb {G}}\) given by
The matrix \({\mathbb {G}}\) coincides with \(n^2 A_{n-1}^{-1}\) with \(A_{n-1}\) being the Cartan matrix of SL(n).
The full set of coordinates on \({\mathcal {M}}\) consists of three groups: the coordinates assigned to vertices of the graph \(\Sigma _0\), to its edges and faces. Below we describe these three groups separately and use them to parametrize the jump matrices of the Riemann–Hilbert problem on the graph \(\Sigma \).
Edge coordinates and jump matrices on \(e_j\). To each edge \(e \in E(\Sigma _0)\) we associate \(n-1\) non-vanishing variables
and introduce their exponential counterparts:
The jump matrix on the oriented edge \(e\in \mathbf{E}(\Sigma _0)\) is given by (see [38])

where \(h_i\) are the dual roots (5.1). For the inverse matrix we have
The notation \(\mathbf{z}^\mathbf{h}\) stands for
The sets of variables (5.3), (5.4) corresponding to an oriented edge e of \(\Sigma _0\) and the opposite edge \(-e\) are related as follows:
Face coordinates and jump matrices on \({\mathcal {E}}_{f}^{(i)}\). To each face \(f\in F(\Sigma _0)\) (i.e. a triangle of the original triangulation) we associate \(\frac{(n-1)(n-2)}{2}\) variables \({\varvec{\xi }}_f = \{\xi _{f;\,abc}:\ \ a, b, c\in {\mathbb {N}},\ \ \ a + b + c= n\}\) and their exponential counterparts \(x_{f;\,abc}:= \mathrm{e}^{\xi _{f;\,abc}}\) as follows.
The variables \(\xi _{f;\,abc}\) define the jump matrices \(A_{i}({\varvec{\xi }}_f)\) on three edges \(\{{\mathcal {E}}_{f}^{(i)}\}_{i=1}^3\), which connect a chosen point \(p_f\) in each face f of the graph \(\Sigma _0\) with its three vertices (these edges are shown in red in Fig. 3). The enumeration of vertices \(v_1\), \(v_2\) and \(v_3\) is chosen arbitrarily for each face f. Namely, for a given vertex v and the face f of \(\Sigma _0\) such that \(v\in \partial f\) we define the index \(f(v) \in \{1,2,3\}\) depending on the enumeration that we have chosen for the three edges \(\{{\mathcal {E}}_{f}^{(i)}\}\) lying in the face f. For example in Fig 3 for the face f containing point \(p_i\) we define \(f(v_\ell )=1\), \(f(v_k)=3\) and \(f(v_s) = 2\).
The matrices \(A_{1,2,3}(\varvec{\xi }_f)\) are defined following [21]. First, the matrix \(A_1\) is defined by the formula
where \(E_{ik}\) are the elementary matrices and
The matrices \(A_2\) and \(A_3\) are obtained from \(A_1\) by cyclically permuting the indices of the variables:
the important property of the matrices \(A_i\) is the equality
which guarantees the triviality of total monodromy around the point \(p_f\) on each face f. In the first two non-trivial cases the matrices \(A_i\) have the following forms:
- SL(2)::
-
there are no face variables and all matrices \(A_i=A\) are given by
$$\begin{aligned} A=\left( \begin{array}{cc} 0&{}1\\ -1&{}-1 \end{array} \right) \;. \end{aligned}$$(5.13) - SL(3)::
-
there is one parameter \(x=x_{111}\) for each face. The matrices \(A_1,A_2\) and \(A_3\) coincide in this case, too; they are given by
$$\begin{aligned} A(x) = \frac{1}{x} \left( \begin{array}{ccc} 0&{}\quad 0&{}\quad 1\\ 0&{}\quad -1&{}\quad -1 \\ {x}^{3}&{}{x}^{3}+1&{}1 \end{array}\right) \; . \end{aligned}$$(5.14)
Jump matrices on stems. The jump matrix on the stem of the cherry connected to a vertex v is defined from the triviality of total monodromy around v.
For each vertex v of \(\Sigma _0\) of valence \(n_v\) the jump matrix on the stem of the cherry attached to v is given by
where \(f_1,\dots , f_{n_v}\) and \(e_1,\dots e_{n_v}\) are the faces/edges ordered counterclockwise starting from the stem of the cherry, with the edges oriented away from the vertex (using if necessary the formula (5.7)). Since each product \(A_{f_i} S_{e_i}\) is a lower triangular matrix, the matrices \(M_v^0\) are also lower–triangular. The diagonal part of \(M^0_v\) will be denoted by \(\Lambda _v\) and parametrized as follows:
Notice that the relation (5.16) can also be written as \(\Lambda _v=\mathbf{m}_v^{\varvec{\alpha }}=\prod _{j=1}^{n-1} m_{v;j}^{\alpha _j}\) where \(\alpha _j\) are the roots (5.1).
In order to express \(\Lambda _v\) in terms of \(\zeta \) and \(\xi \)-coordinates , we enumerate the faces and edges incident at the vertex v by \(f_1,\dots , f_{n_v}\) and \(e_1,\dots , e_{n_v}\), respectively. We assume the edges to be oriented away from v using (5.7). We also assume without loss of generality that the arc \({\mathcal {E}}_{f_j}^{(1)}\) is the one connected to the vertex v for all \(j=1,\dots , n_v\). Then (see (4.20) of [8]) we have
Introduce now the variables \(\mu _{v;\ell }\) via
where the matrix \({\mathbb {G}}\) equals to \(n^2\) times the inverse Cartan matrix [see (5.2)].
The relationship between \(\mu \)’s and variables \(m_v\) is
i.e. \(\mu _{v;\ell }\) defines \(m_{v;\ell }\) up to an nth root of unity. Therefore, the entries \(\lambda _{v;j}\) of the diagonal matrices \(L_v\) are related to \(\mu _{v;j}\) as follows:
Vertex coordinates and jump matrices on cherries To each vertex v of the graph \(\Sigma _0\) we associate a set of \(n-1\) non-vanishing complex numbers \(r_{v;i} \), \(i=1,\dots ,n-1\) in the following way.
Since the matrix \(M^0_v\) is lower-triangular it can be diagonalized by a lower-triangular matrix \(C_v^0\) such that all diagonal entries of \(C_v^0\) equal to 1:
Any other lower-triangular matrix \(C_v\) diagonalizing \(M^0_v\) can be written as
where the matrix \(R_v\) (which equals to the diagonal part of \(C_v\), \(R_v=(C_v)^D\)), is parametrized by \(n-1\) variables \(r_1, \dots , r_{n-1}\) and their logarithmic counterparts
as follows (we omit the index v below):
The jump on the boundary of the cherry is defined to be
The point of discontinuity of the function \(J_v\) on the boundary of the cherry is assumed to coincide with the point where the stem is connected to the cherry (this point is denoted by \(\beta \) in Fig. 4).
5.2 Parametrization of the space \({\mathcal {M}}\)
The set of jump matrices on the graph \(\Sigma \) constructed in the previous section can be used to parametrize the space \({\mathcal {M}}\). Recall that the vertices of the graph \(\Sigma _0\) are in one-to-one correspondence with points \(t_j\); thus the vertex connected to the cherry around \(t_j\) will be denoted by \(v_j\). To construct the monodromy map as SL(n) representation of \(\pi _1( \mathbf{CP}^1\setminus \{t_1,\dots , t_N\}, \infty )\) we topologically identify the punctured sphere with the complement of connected and simply connected neighbourhoods of the \(t_j\)’s that contain also the distal vertex of the stem. The fundamental group of the punctured sphere and of this sphere with deleted neighbourhood is the same. Equivalently, for an element in the fundamental group we choose a representative that does not intersect the cherry and stem.
Then the map is then defined as follows; for \(\sigma \in \pi _1( \mathbf{CP}^1\setminus \{U_1,\dots , U_N\}, \infty )\) the corresponding monodromy is given by
where the product is taken in the same order as the order of the edges being crossed by \(\sigma \) and \(\nu (e,\sigma )\in \{\pm 1\}\) is the orientation of the intersection of the (oriented) edge e and \(\sigma \) at the point of intersection. With this definition the analytic continuation of \(\Psi \) satisfies \(\Psi (z^{\sigma })=\Psi (z) M_\sigma ^{-1}\). This allows us to relate the normalization of the eigenvector matrices \(C_j\) with that of the matrices \(C_j^0\) (5.20). To this end, choose \(z_0^j\) in the connected region of \({\mathbb {P}}^1\setminus \Sigma \) that contains the jth cherry (see Fig. 5).
Then the monodromy matrix \(M_j\) equals to the ordered product of jump matrices at the edges of \(\Sigma \) crossed by \(\sigma _j\) and it has the form
where the matrix \(T_j\) equals to the product of jump matrices on the edges of \(\Sigma \) crossed by \(\sigma _j\) as it is traversed from \(z_0=\infty \) to \(z_0^j\). Therefore, the diagonal form of the monodromy matrix \(M_j\) is:
This determines, unambiguously, the normalization of the matrix \(C_j\) in terms of the Fock–Goncharov coordinates, thus providing a complete parametrization of \(\widehat{{\mathcal {M}}}\).
5.3 Symplectic form
The computation of the symplectic form \(\,\mathrm{d}\Theta = \omega _{{\mathcal {M}}}\) is given in [8].
Theorem 5.1
(Thm. 4.1 of [8]). In the coordinate chart parametrized by coordinates
the symplectic form \(\omega _{\mathcal {M}}\) (3.16) is given by
The variables \(\mu _{v;j}\) are defined by (5.18).
The form \(\omega _v\) in (5.28) is defined as follows: for each vertex \(v\in V(\Sigma _0)\) of valence \(n_v\) let \( \{e_1,\dots e_{n_v}\}\) be the incident edges ordered counterclockwise starting from the one on the left of the stem and oriented away from v. Let \(\{f_1,\dots , f_{n_v}\}\in F(T)\) be the faces incident to v and counted in counterclockwise order from the one containing the cherry. We denote the order relation by \(\prec \). Then
where the subscript f(v) indicates the index a, b or c depending on the value \(f(v) \in \{1,2,3\}\), respectively.
The form \(\omega _f\) for face f is given by
where \(F_{ijk; i'j'k'}\) are the following constants
and
H(x) is the Heaviside function:
We point out that while the coordinates \(\varvec{\xi }, \varvec{\zeta }, \varvec{\rho }\) are defined on a covering space of the character variety (with the deck transformations being shifts by integer multiples of \(2i\pi \)), the symplectic form (5.29) is defined on the character variety itself. Notice also that for SL(2) and SL(3) the form \(\omega _f\) vanishes.
5.4 Symplectic potential
We are going to choose a symplectic potential \(\theta _{\mathcal {M}}\) satisfying the equation \(\,\mathrm{d}\theta _{\mathcal {M}}=\omega _{\mathcal {M}}\) for the symplectic form \(\omega _{\mathcal {M}}\) using the representation (5.28). For convenience we introduce a uniform notation for coordinates \(\zeta _e\) and \(\xi _{f;ijk}\); the number of these coordinates equals \(\mathrm{dim}{\mathcal {M}}-(n-1)N\) (we subtract the number of coordinates \(\rho _j\) from the total dimension of \({\mathcal {M}}\)). These coordinates we denote collectively by
Then the formula (5.28) can be written as
where all \(n_{j\ell }\) are integer numbers and \(\mu _{v;j}\) are linear functions of \(\kappa _j\)’s.
Definition 5.1
The symplectic potential \(\theta _{\mathcal {M}}\) is defined by the following relation:
Obviously, there exist infinitely many choices of the potential for the form \(\omega _{\mathcal {M}}\). Our choice (5.34) is due to Theorem 7.1 of [8] which states that the potential \(\theta _{\mathcal {M}}\) (5.34) remains invariant if any of the cherries is moved to the neighbouring face.
5.5 SL(2) case
For \(n=2\) the general formula in Theorem 5.1 simplifies considerably to the following (for details see [8])
the symplectic potential (5.34) \(\theta _{\mathcal {M}}\) is given by:
Notice that the expression (5.36) “forgets” about the orientation of vertices since the coordinate \(\zeta _e\) remains invariant if the orientation of the edge e is changed i.e. when \(z_e\) transforms to \(-z_e\). Unlike the form \(\omega _{\mathcal {M}}\), the potential \(\theta _{\mathcal {M}}\) depends on the choice of triangulation \(\Sigma _0\); the change of triangulation implies a non-trivial change of \(\theta _{\mathcal {M}}\).
5.5.1 Change of triangulation
One triangulation \(\Sigma _0\) can be transformed to any other by a sequence of “flips” of the diagonal in the quadrilateral formed by two triangles with a common edge, see Fig. 6. Let us assume that the four cherries attached to the vertices are placed as shown in Fig. 6. Then, the assumption that all the monodromies around the four vertices of these triangles are preserved, implies the following equations [8]:
where \( \kappa _j=z_j^2\), \(\tilde{\kappa }_j=\tilde{z}_j^2 \), \(j=1,\dots ,4\); \(\tilde{\kappa }=\tilde{z}^2\) is the variable on the “flipped” edge. The variables \(r_j\) remain invariant under the change of triangulation due to the choice of cherries positions in Fig. 6.
Denote the symplectic potential corresponding to the new triangulation by \(\tilde{\theta }_{\mathcal {M}}\) and introduce the Rogers dilogarithm L which for \(x\ge 0\) is defined by (see (1.9) of [36]):
As it was shown in Prop. 7.1 of [8], the symplectic potentials \(\tilde{\theta }_{\mathcal {M}}\) and \(\theta _{\mathcal {M}}\) are related as follows:
Therefore, the function \(L\left( \frac{\kappa }{1+\kappa } \right) \) is the generating function of the symplectomorphism corresponding to the elementary flip of the edge of \(\Sigma _0\).
6 Tau-Function as Generating Function of Monodromy Symplectomorphism
Here we extend the definition of the Jimbo–Miwa–Ueno tau-function by including an explicit description of its dependence on the monodromy data.
Definition 6.1
The tau function is defined by the following set of compatible equations. The equations with respect to \(t_j\) are given by the Jimbo–Miwa–Ueno formulæ
the equations with respect to coordinates on monodromy manifold \({\mathcal {M}}\) are given by
where \(\theta _{\mathcal {M}}[\Sigma _0]\) is the symplectic potential (5.34) for the form \(\omega _{\mathcal {M}}\); we consider the matrices \(G_j\) as (meromorphic) functions on \(\widetilde{{\mathcal {M}}}\) defined by the formula
with \(\Phi \) the solution of the Riemann–Hilbert problem (3.9).
Using Theorem 3.1 and in particular (3.11), we can rewrite this definition in an alternative form, which encodes the complete system (6.1), (6.2):
Definition 6.1\('\). The tau-function on \(\widetilde{{\mathcal {M}}}\) is locally defined by equations
where \(\Theta \) is the Malgrange form (3.3) corresponding to solution \(\Phi \) (3.9) and \(\widetilde{\theta }_{\mathcal {M}}[\Sigma _0]\) is the pullback to \(\widetilde{{\mathcal {M}}}\) of \(\theta _{\mathcal {M}}[\Sigma _0]\).
The formula (6.2) means that \(\log \tau \) is nothing but the generating function of the monodromy symplectomorphism: \(\,\mathrm{d}\log \tau \) equals to the difference of symplectic potentials defined in terms of the (extended) Kirillov–Kostant symplectic potential \(\theta _{\mathcal {A}}\) and the symplectic potential on the monodromy manifold. It was proven in [35] that the residue of \(\Theta \) along the points of the Malgrange divisor is a positive integer; thus \(\tau \) is actually locally analytic on \(\widetilde{{\mathcal {M}}}\); multiplicity of zero of \(\tau \) equals to the residue of \(\Theta \).
We now analyze in more detail the dependence of \(\tau \) on the Fock–Goncharov coordinates. The tau-function \(\tau \) defined by (6.2) depends on the full set of variables \(({\varvec{z}},\,{\varvec{x}},\, {\varvec{r}})\) on \({\mathcal {M}}\). The right-hand sides of equations (6.2) depend on the choice of the triangulation \(\Sigma _0\) defining the symplectic potential \(\theta _{\mathcal {M}}\). However, according to Thm.6.1 of [8], the potential (5.34) is independent of the choice of ciliation of the graph \(\Sigma _0\).
The next proposition shows how the tau-function defined in Definition 6.1 depends on variables \(\rho _{j,i}\): namely, define the second tau-function \(\tau _1\) by
Proposition 6.1
The tau-function \(\tau _1\) (6.5) is independent of the variables \(\{r_{j;i}\}, \ j=1\dots N\), \( i=1 \dots n-1\) i.e.
Proof
Denote by \(G_j^0\) the set of matrices \(G_j\) which correspond to all variables \(r_{j;i}=1\). Then matrices \(G_j\) can be expressed in terms of \(G_j^0\) and \(r_{j;i}\) as follows:
where the diagonal matrix \(R_j\) is given by (5.22). Then,
Therefore, the first sum in (6.2) gets an additive term equal to
On the other hand, matrices \(C_j\) transform under (6.7) in the same way:
where the matrices \(C_j^0\) are assumed to be triangular with all 1’s on the diagonal.
To get the variation of \(\theta _{\mathcal {M}}\) under the transformation (6.9) we observe that the form \(\omega _{\mathcal {M}}\) (3.16) transforms under (6.9) as follows:
Therefore, according to our definition of \(\theta _{\mathcal {M}}\), the last sum in this expression should be integrated to give
which cancels against (6.8) (alternatively, one can derive (6.10) using the definition of \(\mu _{v;i}\) and \(\rho _{v;i}\) and (5.34)). \(\square \)
The equations for the tau-function with respect to variables \({\varvec{z}}\) and \({\varvec{x}}\) (or, equivalently, \({\varvec{\zeta }}\) and \({\varvec{\xi }}\)) implied by Definition 6.1 can be obtained from expression (5.34) for the potential \(\theta _{\mathcal {M}}\). Below we write these equations explicitly in the SL(2) case.
6.1 SL(2) tau-function
In the SL(2) case the coordinates on \({\mathcal {M}}_N^{SL(2)}\) are given by edge coordinates \(\{\zeta _e\}\) and vertex coordinates \(\{\rho _k\}_{k=1}^N\); the potential \(\theta _{\mathcal {M}}\) is given by (5.36). Then
and the relationship (6.5) becomes:
where \(\mu _j\) is the sum of the \(\zeta _e\) for all edges incident to the j-th vertex. The equations for \(\tau _1\) with respect to the edge coordinates take the following form:
Definition 6.2
For a given triangulation \(\Sigma _0\) the tau-function \(\tau _1\) of an SL(2) Fuchsian system is defined by the system (6.1) with respect to poles \(\{t_j\}_{j=1}^N\) and the following equations with respect to coordinates \(\{\zeta _{e_j}\}_{j=1}^{3N-6}\):
where \(v_1\) and \(v_2\) are vertices of \(\Sigma _0\) connected by the edge e.
This definition depends on the choice of triangulation \(\Sigma _0\). The change of the tau-function \(\tau \) under an elementary flip of an edge of the triangulation \(\Sigma _0\) acting on the underlying triangulation follows from (5.39):
Proposition 6.2
Let \(\tau \) and \(\tilde{\tau }\) be tau-functions corresponding to triangulations related by the flip of the edge e shown in Fig. 6 . Then
under an appropriate choice of branch of the Rogers’ dilogarithm L (5.38).
6.2 Equations with respect to Fock–Goncharov coordinates
Here we derive equations for \(\Psi \), \(G_j\) and \(\tau \) with respect to an edge coordinate \(\zeta \).
First we notice that for any Riemann–Hilbert problem on an oriented contour C with jump matrix J the variation of the solution of the Riemann–Hilbert problem takes the form :
The formula (6.14) can be easily derived by applying the variation \(\delta \) to the equation \(\Psi _+=\Psi _- J\) on C which gives \(\delta \Psi _+=\delta \Psi _- J+\Psi _- \delta J\) and then solving the resulting non-homogeneous Riemann–Hilbert problem via Cauchy kernel.
We apply (6.14) to variations of the solution \(\Psi \) of the Riemann–Hilbert problem on the Fock–Goncharov graph with respect to the variable \(\zeta \) corresponding to the edge e. Without loss of generality we assume that the positions of cherries are chosen as in Fig. 7.
For simplicity we assume that both vertices \(v_1\) and \(v_2\) connected by e are three-valent but it is not a significant restriction.
The jump matrices depending on \(\zeta \) are the following: the jump matrix on the edge e (and the one on the reverse edge) according to the general rules in (5.7) is
Furthermore, using the expression (5.13) for the matrix A and denoting \(S_j= S(\zeta _j)\) the jump matrices \(Q_1\) and \(Q_2\) on the stems \(s_1\) and \(s_2\) depend on \(\zeta \) as follows:
Notice that logarithmic derivatives of the matrices S and \(Q_1^{-1}\) and \(Q_2\) with respect to \(\zeta \) are the same and are given by
Then the exponents of monodromy are
Thus
where
and
where
Introduce the graph \(\Sigma _0'\) by identifying the vertex \(v_j\) with the corresponding pole \(t_j\). The variational formula takes the simplest form if we make an explicit assumption on the growth (1.2) of the solution \(\Psi \) near the poles, that is on the real part of the eigenvalues of \(L_j\); indeed it is known [31] that for a given monodromy representation there is a lattice of solutions to the inverse monodromy representation. The reason is simply that the eigenvalues matrices \(L_j\) are defined up to addition of diagonal matrices in \(sl_n({\mathbb {Z}})\). For \(n=2\) there is therefore a \({\mathbb {Z}}^N\) (N being the number of poles) lattice of inverse solutions. The transformations between different solutions in this lattice are referred to as “discrete Schlesinger transformations”. We use this observation to shift the real part of \(\lambda _j\)’s to a value within the interval \(\mathfrak {R}\lambda _j \in [-\frac{1}{2}, \frac{1}{2})\). Excluding the non-generic cases \(\mathfrak {R}\lambda _j = -\frac{1}{2}\) we have
Theorem 6.1
Denote by \(\zeta _{jk}\) the FG coordinate corresponding to the edge \(e_{jk}\). Suppose all eigenvalues of matrices \(L_j\) satisfy the conditions
Then the function \(\Psi \) satisfies the following system of equations with respect to coordinates \(\zeta _{jk}\):
where the integral along the oriented edge \(e_{jk}\) of \(\Sigma _0'\) in the right hand side is convergent at the endpoints due to condition (6.19). The integral in (6.20) is discontinuous across the edge \(e_{jk}\).
Proof
We denote \(\zeta = \zeta _{jk}\) for simplicity, and \(j=1, k=2\). The expression \(\partial _{\zeta } J J^{-1}\) is nonzero only on the edge, the two stems and the boundaries of the two cherries. A direct computation shows (with the edges oriented as shown in Fig. 7), that the expression of \(\partial _{\zeta } J J^{-1}\) on the edge and on the two stems is equal to \(\sigma _3\). The jump matrix on the cherry 1 equals to \(J_1=C_1 (z-t_1)^{-L_1}\) and on \(c_2\) it equals to \(J_2=C_2 (z-t_2)^{-L_2}\). Then a direct computation gives (since \({L_1}_\zeta =\frac{\sigma _3}{2i\pi }\) and \({L_2}_\zeta =\frac{-\sigma _3}{2i\pi } \)):
Consider the first cherry (the second cherry can be treated in parallel); we shall call \(\beta \) the point of intersection of the stem and the cherry. Within a neighbourhood containing the cherry, we have \(\Psi (z) = \Phi _1(z) (z-t_1)^{L_1} C_1^{-1}\), with \(\Phi _1(t_1) = G_1\). In the integral (6.14) the contribution coming from the first cherry is then the integral
where the contour of integration is the circle \(|w-t_1|= const\) starting at \(\beta _+\) and ending at \(\beta _-\) and the branch-cut of the power is the segment from \(t_1\) to \(\beta \). We also have used that \([C_1,\sigma _+]=0\). Under the condition \(-1< 2\mathfrak {R}\lambda _1\) the contribution of the integration on the cherry tends to zero in the limit of zero radius of the cherry. \(\square \)
Remark 6.1
While the general formula (6.21) is valid without any restriction on the real parts of \(\lambda _j\)’s, the integral on the boundary of the cherries provide some sort of “regularization” to the integral along the edge. However, if the conditions (6.19) in fulfilled, the regularization are not needed and we arrive at the simplified formula (6.20).
Introducing the notation
we can formulate the following
Corollary 6.1
The derivatives of \(G_\ell \) on coordinates \(\zeta _{jk}\) take the form:
where \(f_j = (C_j)_{12}\) and \(f_k = (C_k)_{21}\) as defined in (6.17) and (6.18).
Proof
The first formula follows from the fact that the connection matrices and exponents at the vertices not connected to the edge are constant under the variation. For definiteness assume \(j=1\), \(k=2\). To find \(G_1\) (\(G_2\) can be treated in the same way) we need to evaluate \(\Phi _1(z) =\Psi (z) C_1 (z-t_1)^{L_1}\) at \(z=t_1\). Differentiating the identity \(\Phi _1(z) = \Psi (z) C_1 (z-t_1)^{-L_1}\) with respect to \(\zeta \) and taking the limit \(z\rightarrow t_1\) gives the formula, recalling that \(G_1 = \Phi _1(t_1)\). Indeed
If \(\mathfrak {R}2\lambda _1>-1\) (which is our standing assumption), in the limit as \(z\rightarrow t_1\) we can substitute \(\Phi _1(z)\) by \(G_1\) in the above formula, and we obtain the statement.
On a related note; the same result is obtained by looking at the singular behaviour of the integral (6.20) (using results on Cauchy-type integrals in [22], for example) and simply removing the singular part. \(\square \)
Now we come to the following
Proposition 6.3
The Eq. (6.12) for the tau-function \(\tau _1\) with respect to FG coordinates can be equivalently written as follows:
where F is given by (6.22); the terms of the sum which need the regularization correspond to \(\ell =j\) and \(\ell =k\); they are given by
and
The proof follows from Eqs. (6.23), (6.24) and (6.25). \(\square \)
References
Alekseev, AYu., Faddeev, L.D.: \((T^{*}G)_t\): a toy model for conformal field theory. Commun. Math. Phys. 141(2), 413–422 (1991)
Alekseev, A., Malkin, A.: Symplectic structure of the moduli space of flat connection on a Riemann surface. Commun. Math. Phys. 169, 99–120 (1995)
Alekseev, A., Malkin, A.: The hyperbolic moduli space of flat connections and the isomorphism of symplectic multiplicity spaces. Duke Math. J. 93(3), 575–595 (1998)
Audin, M.: Torus Actions on Symplectic Manifolds, Progress in Mathematics, vol. 93. Birkhäuser, Basel (2004)
Babelon, O., Bernard, D., Talon, M.: Introduction to Classical Integrable Systems. Cambridge University Press, Cambridge (2003)
Bertola, M.: The dependence on the monodromy data of the isomonodromic tau function. Commun. Math. Phys. 294, 539–579 (2010)
Bertola, M.: Correction to: the dependence on the monodromy data of the isomonodromic tau function. Commun. Math. Phys. 381(3), 1445–1461 (2021)
Bertola, M., Korotkin, D.: Extended Goldman symplectic structure in Fock–Goncharov coordinates, arXiv:1910.06744, to appear in J. Diff. Geo. (2021)
Bertola, M., Korotkin, D., Norton, C.: Symplectic geometry of the moduli space of projective structures in homological coordinates. Invent. Math. 210(3), 759–814 (2017)
Bertola, M., Korotkin, D.: WKB expansion for a Yang–Yang generating function and the Berman tau function. Theor. Math. Phys. 206(3), 259–295 (2021)
Boalch, P.: Quasi-Hamiltonian geometry of meromorphic connections. Duke Math. J. 139(2), 369–405 (2007)
Bolibruch, A.A.: Inverse Monodromy Problems of the Analytic Theory of Differential Equations, Mathematical Events of the Twentieth Century, pp. 49–74. Springer, Berlin (2006)
Bondal, A.: A symplectic groupoid of triangular bilinear forms and the braid group. Izv. RAN. Ser. Mat. 68(4), 19–74 (2004)
Chekhov, L., Mazzocco, M.: Shear coordinate description of the quantised versal unfolding of \(D_4\) singularity. J. Phys. A 43(44), 442002 (2010)
Chekhov, L., Mazzocco, M., Roubtsov, V.: Painlevé monodromy manifolds, decorated character varieties, and cluster algebras. IMRN 24, 7639–7691 (2017)
Chekhov, L., Fock, V.: Quantum Teichmüller space. Theor. Math. Phys. 120, 1245–1259 (1999)
Etingof, P.: On the dynamical Yang-Baxter equation, Proceedings of the International Congress of Mathematicians, Vol. II Beijing, (2002), 555–570, Higher Ed. Press, Beijing, 2002. See also Erratum in Proceedings of the International Congress of Mathematicians, Vol. I Beijing, (2002), 649–650, Higher Ed. Press, Beijing (2002)
Fehér, L., Gábor, A., Pusztai, B.G.: On dynamical r-matrices obtained from Dirac reduction and their generalizations to affine Lie algebras. J. Phys. A 34(36), 7335–7348 (2001)
Flaschka, H., Newell, A.C.: The Inverse Monodromy Transform is a Canonical Transformation. Nonlinear Problems: Present and Future (Los Alamos, N. M. , 1981), vol. 61, pp. 65–89 (1982)
Fock, V.V.: Description of moduli space of projective structures via fat graphs, arXiv:hepth/9312193
Fock, V., Goncharov, A.: Moduli spaces of local systems and higher Teichmüller theory. Publ. Math. Inst. Hautes Étud. Sci. 103(1), 1–211 (2006)
Gakhov, F.D.: Boundary Value Problems. Dover Pulications, New York (1990)
Goldman, W.: The symplectic nature of fundamental groups of surfaces. Adv. Math. 54, 200–225 (1984)
Goldman, W.: Invariant functions on Lie groups and Hamiltonian flows of surface group representations. Invent. Math. 85, 263–302 (1986)
Hitchin, N.: Frobenius manifolds, gauge theory and symplectic geometry. In: Hurtubise, J., Lalonde, F. (eds.) NATO ASI Series C, vol. 488. Kluwer, Dordrecht (1997)
Its, A., Prokhorov, A.: On some Hamiltonian properties of the isomonodromic tau functions. Rev. Math. Phys. 30(7), 1840008 (2018)
Its, A., Prokhorov, A.: Connection problem for the tau-function of the sine-Gordon reduction of Painlevé-III equation via the Riemann–Hilbert approach. IMRN 22, 6856–6883 (2016)
Its, A., Lisovyy, O., Prokhorov, A.: Monodromy dependence and connection formulae for isomonodromic tau functions. Duke Math. J. 167(7), 1347–1432 (2018)
Jeffrey, L.: Extended moduli spaces of flat connections on Riemann surfaces. Math. Ann. 298, 667–692 (1994)
Jimbo, M., Miwa, T., Ueno, K.: Monodromy preserving deformation of linear ordinary differential equations with rational coefficients. I. General theory and \(\tau \)-function. Phys. D 2(2), 306–352 (1981)
Jimbo, M., Miwa, T.: Monodromy preserving deformation of linear ordinary differential equations with rational coefficients II. Phys. D 2(3), 407–448 (1981)
Kawai, S.: The symplectic nature of the space of projective connections on Riemann surfaces. Math. Ann. 305, 161–182 (1996)
Korotkin, D., Samtleben, H.: Quantization of Coset space -models coupled to two-dimensional gravity. Commun. Math. Phys. 190(2), 411–457 (1997)
Korotkin, D.: Periods of meromorphic quadratic differentials and Goldman bracket. In: Chiu-Chu, M., Mulase, M. (eds) Proceedings of Symposia in Pure Mathematics, vol. 100 (2018)
Malgrange, B.: Sur les Déformation Isomonodromiques. In: Mathématique et Physique (E.N.S. Séminaire 1979–1982, pp. 401–426. Birkhäuser, Boston (1983)
Nakanishi, T.: Rogers dilogarithms of higher degree and generalized cluster algebras. J. Math. Soc. Jpn. 70(4), 1269–1304 (2018)
Nekrasov, N., Rosly, A., Shatashvili, S.: Darboux coordinates, Yang–Yang functional, and gauge theory. Nuclear Phys. B Proc. Suppl. 216, 69–93 (2011)
Palesi, F.: Introduction to positive representations and Fock–Goncharov coordinates. https://hal.archives-ouvertes.fr/hal-01218570
Sato, M., Miwa, T., Jimbo, M.: Holonomic quantum fields II. The Riemann–Hilbert problem. Publ. RIMS Kyoto Univ. 15, 201–278 (1979)
Schemmel, M.: Stationary Axisymmetric Gravity in the Isomonodromic Canonical Formulation, Diplomarbeit, 86 p., Hamburg preprint: Schemmel, M., (January 1997)
Ugaglia, M.: On a Poisson structure on the space of Stokes matrices. IMRN 9, 473–493 (1999)
Acknowledgements
We thank T.Bridgeland, L.Chekhov, L. Feher, V. Fock, S. Fomin, A. Goncharov, J. Harnad, M. Gekhtman, R. Kashaev, A.Nietzke and M. Shapiro for illuminating discussions. We thank also A. Its, O. Lisovyy and A. Prokhorov for clarifying comments. We thank P.Boalch for bringing the references [11, 29] to our attention and outlining the role of results of these works in the context of this paper. Finally, we thank the anonymous referees for helpful commentary. The work of M.B. was supported in part by the Natural Sciences and Engineering Research Council of Canada (NSERC) Grant RGPIN-2016-06660. The work of D.K. was supported in part by the NSERC grant RGPIN/3827-2015. The completion of this work was supported by the National Science Foundation under Grant No. DMS-1440140 while the authors were in residence at the Mathematical Sciences Research Institute in Berkeley, California, during the Fall 2019 semester Holomorphic Differentials in Mathematics and Physics.
Funding
Open access funding provided by Scuola Internazionale Superiore di Studi Avanzati - SISSA within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by J-d. Gier.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bertola, M., Korotkin, D. Tau-Functions and Monodromy Symplectomorphisms. Commun. Math. Phys. 388, 245–290 (2021). https://doi.org/10.1007/s00220-021-04224-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-021-04224-6