Skip to main content
SpringerLink
Log in

Neural network gradient Hamiltonian Monte Carlo

  • Original paper
  • Published:
Computational Statistics Aims and scope Submit manuscript

Abstract

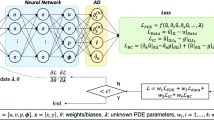
Hamiltonian Monte Carlo is a widely used algorithm for sampling from posterior distributions of complex Bayesian models. It can efficiently explore high-dimensional parameter spaces guided by simulated Hamiltonian flows. However, the algorithm requires repeated gradient calculations, and these computations become increasingly burdensome as data sets scale. We present a method to substantially reduce the computation burden by using a neural network to approximate the gradient. First, we prove that the proposed method still maintains convergence to the true distribution though the approximated gradient no longer comes from a Hamiltonian system. Second, we conduct experiments on synthetic examples and real data to validate the proposed method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  • Baldi P, Sadowski P (2016) A theory of local learning, the learning channel, and the optimality of backpropagation. Neural Netw 83:51–74

    Article  Google Scholar 

  • Betancourt M (2015) The fundamental incompatibility of Hamiltonian Monte Carlo and data subsampling. arXiv preprint arXiv:1502.01510

  • Chen T, Fox E, Guestrin C (2014) Stochastic gradient Hamiltonian Monte Carlo. In: International conference on machine learning, pp 1683–1691

  • Cybenko G (1989) Approximation by superpositions of a sigmoidal function. Math Control Signals Syst (MCSS) 2(4):303–314

    Article  MathSciNet  MATH  Google Scholar 

  • Huang GB, Zhu QY, Siew CK (2004) Extreme learning machine: a new learning scheme of feedforward neural networks. In: Proceedings of IEEE international joint conference on neural networks, IEEE, vol 2, pp 985–990

  • Kingma D, Ba J (2014) Adam: a method for stochastic optimization. arXiv preprint arXiv:1412.6980

  • Lan S, Bui-Thanh T, Christie M, Girolami M (2016) Emulation of higher-order tensors in manifold monte carlo methods for bayesian inverse problems. J Comput Phys 308:81–101

    Article  MathSciNet  MATH  Google Scholar 

  • Leimkuhler B, Reich S (2004) Simulating Hamiltonian dynamics, vol 14. Cambridge University Press, Cambridge

    MATH  Google Scholar 

  • Neal RM (2012) Bayesian learning for neural networks, vol 118. Springer, New York

    MATH  Google Scholar 

  • Neal RM et al (2011) Mcmc using Hamiltonian dynamics. Handbook Markov Chain Monte Carlo 2:113–162

    MathSciNet  MATH  Google Scholar 

  • Rasmussen CE, Bernardo J, Bayarri M, Berger J, Dawid A, Heckerman D, Smith A, West M (2003) Gaussian processes to speed up hybrid monte carlo for expensive bayesian integrals. Bayesian Stat 7:651–659

    MathSciNet  Google Scholar 

  • Welling M, Teh YW (2011) Bayesian learning via stochastic gradient langevin dynamics. In: Proceedings of the 28th international conference on machine learning (ICML-11), pp 681–688

  • Zhang C, Shahbaba B, Zhao H (2017) Hamiltonian monte carlo acceleration using surrogate functions with random bases. Stat Comput 27:1473. https://doi.org/10.1007/s11222-016-9699-1

Download references

Acknowledgements

Babak Shahbaba is supported by NSF Grant DMS1622490 and NIH Grant R01MH115697.

Author information

Authors and Affiliations

  1. Donald Bren School of Information and Computer Sciences, University of California, Irvine, USA

    Lingge Li, Babak Shahbaba & Pierre Baldi

  2. Department of Human Genetics, David Geffen School of Medicine, University of California, Los Angeles, USA

    Andrew Holbrook

Authors
  1. Lingge Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Andrew Holbrook
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Babak Shahbaba
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Pierre Baldi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Lingge Li.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, L., Holbrook, A., Shahbaba, B. et al. Neural network gradient Hamiltonian Monte Carlo. Comput Stat 34, 281–299 (2019). https://doi.org/10.1007/s00180-018-00861-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00180-018-00861-z

Keywords

Search

Navigation