Efficient sample reduction strategy based on adaptive Kriging for estimating failure credibility

Abstract

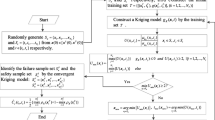
Failure credibility is popular in measuring safety degree of structure under fuzzy uncertainty, but the heavy computational cost is still a challenge in estimating the failure credibility. To alleviate this issue, an iterative method combining adaptive Kriging and fuzzy simulation (AK-FS) has been developed by Ling et al. However, for the problem with complex performance function, a large candidate sampling pool is needed in the AK-FS, which makes the training process of the Kriging model fairly time consuming. In order to improve the estimation efficiency of failure credibility through reducing the size of candidate sampling pool in AK-FS, an efficient sample reduction strategy based on adaptive Kriging (SR-AK) is proposed in this paper. In the SR-AK, the estimation of failure credibility is transformed into searching two active points in candidate sampling pool. After updating the Kriging model in each circle, current active points can be easily identified. Then, according to the properties of the active points and the prediction characteristics of Kriging model, the samples in current candidate sampling pool can be divided into two sets, i.e., the samples affect the estimation of active points and the samples have no effect on it. Obviously, the samples in the latter set can be deleted from current candidate sampling pool to reduce its size. By using this sample reduction strategy, the process for training Kriging model is accelerated circle by circle, which is very helpful to save the analysis time and improve the computational efficiency in estimating failure credibility. Four examples are employed to demonstrate the performance of the proposed SR-AK in fuzzy safety degree analysis.

Appendix: Brief introduction of Kriging and U-learning function

In nature, Kriging starts with the assumption that the actual performance function g(X) is a realization of the stochastic field g_K(X) which is written as:

$$ {g}_K(X)={f}^T(X)\xi +Z(X) $$

(22)

where $f(X)={\left[{f}_1(X),{f}_2(X),\cdots, {f}_{N_f}(X)\right]}^T$ is the N_f-dimensional basis function vector of X, $\xi ={\left[{\xi}_1,{\xi}_2,\cdots, {\xi}_{N_f}\right]}^T$ expresses the N_f-dimensional regression coefficient vector, and Z(X) denotes a stationary Gaussian process with the following statistic characteristics:

$$ {\displaystyle \begin{array}{l} Expectation\kern4.999998em E\left(Z(x)\right)=0\\ {} Var iance\kern6.299996em Var\left(Z(x)\right)={\sigma}_Z^2\\ {} Covariance\kern5.299997em \operatorname{cov}\left[Z\left({x}_{j_1}\right),Z\left({x}_{j_2}\right)\right]={\sigma}_Z^2R\left({x}_{j_1},{x}_{j_2}\right)\end{array}} $$

(23)

where ${x}_{j_1}$ and ${x}_{j_2}$ are the j₁th and j₂th elements among the training sample set, and R(⋅, ⋅) is the kernel function that determines the smoothness of the Kriging model. In this paper, the commonly used Gaussian kernel function (Lophaven et al. 2002) is employed in the Kriging model, and it can be represented as:

$$ R\left({x}_{j_1},{x}_{j_2}\right)=\exp \left[-\sum \limits_{l=1}^n{w}_l{\left({x}_{j_1l}-{x}_{j_2l}\right)}^2\right] $$

(24)

where w_l(l = 1, 2, ⋯, n) is the unknown correlation parameters, and ${x}_{j_1l}$ and ${x}_{j_2l}$ are the lth components of ${x}_{j_1}$ and ${x}_{j_2}$, respectively.

Suppose we already have a q-size training sample set ${x}^t={\left\{{x}_1^t,{x}_2^t,\cdots, {x}_q^t\right\}}^{\mathrm{T}}$ of the inputs and the corresponding model outputs are ${g}^t={\left\{g\left({x}_1^t\right),g\left({x}_2^t\right),\cdots, g\left({x}_q^t\right)\right\}}^{\mathrm{T}}$. By using (x^t, g^t), the estimates of the regression coefficient vector ξ and the process variance ${\sigma}_Z^2$ can be computed as:

$$ \hat{\xi}={\left({F}^{\mathrm{T}}{R}^{-1}F\right)}^{-1}{F}^{\mathrm{T}}{R}^{-1}{g}^t $$

(25)

$$ {\hat{\sigma}}_Z^2={\left({g}^t-F\hat{\xi}\right)}^{\mathrm{T}}{R}^{-1}\left({g}^t-F\hat{\xi}\right)/q $$

(26)

where $F={\left\{f\left({x}_1^t\right),f\left({x}_2^t\right),\cdots, f\left({x}_q^t\right)\right\}}^{\mathrm{T}}$ is a q × M matrix, and R is the correlation function matrix defined by:

$$ R=\left[\begin{array}{cccc}R\left({x}_1^t,{x}_1^t\right)& R\left({x}_1^t,{x}_2^t\right)& \cdots & R\left({x}_1^t,{x}_q^t\right)\\ {}R\left({x}_2^t,{x}_1^t\right)& R\left({x}_2^t,{x}_2^t\right)& \cdots & R\left({x}_2^t,{x}_q^t\right)\\ {}\vdots & \vdots & \ddots & \vdots \\ {}R\left({x}_q^t,{x}_1^t\right)& R\left({x}_q^t,{x}_2^t\right)& \cdots & R\left({x}_q^t,{x}_q^t\right)\end{array}\right] $$

(27)

Note that $\hat{\beta}$ and ${\hat{\sigma}}_Z^2$ in (25) and (26) depend on the correlation parameters w_l(l = 1, 2, ⋯, n) through the correlation function R. Hence, it is necessary to estimate them firstly by the maximum likelihood estimation (MLE) (Jones et al. 1998) as shown in (28):

$$ \hat{w}=\arg \underset{w}{\min}\left\{{\left[\det (R)\right]}^{1/q}{\hat{\sigma}}_Z^2\right\} $$

(28)

where $\hat{w}={\left\{{\hat{w}}_1,{\hat{w}}_2,\cdots, {\hat{w}}_n\right\}}^{\mathrm{T}}$.

After obtaining the model parameters by (25) to (28), the Kriging prediction ${\mu}_{g_K}(x)$ and the corresponding prediction variance ${\sigma}_{g_K}^2(x)$ at arbitrary point x can be computed by (29) and (30), respectively:

$$ {\mu}_{g_K}(x)={f}^{\mathrm{T}}(x)\hat{\xi}+{r}^{\mathrm{T}}(x){R}^{-1}\left({g}^t-F\hat{\xi}\right) $$

(29)

$$ {\sigma}_{g_K}^2(x)={\hat{\sigma}}_Z^2\left[1-{r}^{\mathrm{T}}(x){R}^{-1}r(x)+{\left(F{R}^{-1}r(x)-f(x)\right)}^{\mathrm{T}}{\left({F}^{\mathrm{T}}{R}^{-1}F\right)}^{-1}\left(P{R}^{-1}r(x)-f(x)\right)\right] $$

(30)

where $r(x)={\left\{R\left(x,{x}_1^t\right),R\left(x,{x}_2^t\right),\cdots, R\left(x,{x}_q^t\right)\right\}}^{\mathrm{T}}$ is a q × 1 vector of the correlations between point x and the q training points ${x}_i^t\left(i=1,2,\cdots, q\right)$.

For any untrained sample x, the Kriging model prediction obeys normal distribution, i.e.:

$$ {g}_K(x)\sim N\left({\mu}_{g_K}(x),{\sigma}_{g_K}^2(x)\right) $$

(31)

where N(⋅) denotes the normal distribution.

Based on the sign of ${\mu}_{g_K}(x)$ and the prediction characteristics of the Kriging model g_K(X), the prediction precision of the sign of g(x) by using ${\mu}_{g_K}(x)$ can be discussed by the following two cases:

• Case 1. When ${\mu}_{g_K}(x)\le 0$, the probability of misidentifying the sign of g(x) by ${\mu}_{g_K}(x)$ can be formulated by:

$$ {P}_1=1-\varPhi \left(\frac{0+\mid {\mu}_{g_K}(x)\mid }{\sigma_{g_K}(x)}\right)=\varPhi \left(-\frac{\mid {\mu}_{g_K}(x)\mid }{\sigma_{g_K}(x)}\right) $$

(32)

• Case 2. When ${\mu}_{g_K}(x)>0$, the probability of misidentifying the sign of g(x) by ${\mu}_{g_K}(x)$ can be formulated by:

$$ {P}_2=\varPhi \left(\frac{0-\mid {\mu}_{g_K}(x)\mid }{\sigma_{g_K}(x)}\right)=\varPhi \left(-\frac{\mid {\mu}_{g_K}(x)\mid }{\sigma_{g_K}(x)}\right) $$

(33)

Taking both cases into account, the probability P_mis of misidentifying the sign of g(x) can be expressed as:

$$ {P}_{mis}=\varPhi \left(-U(x)\right) $$

(34)

where U(x) is known as the U-learning function, and it can be expressed as:

$$ U(x)=\frac{\mid {\mu}_{g_K}(x)\mid }{\sigma_{g_K}(x)} $$

(35)

Equations (34) and (35) imply that the smaller the value of U(x) is, the higher the probability of misidentifying the sign of g(x). Thus, for enhancing the ability of the Kriging model in accurately predicting the sign of g(x), the new training sample x^new can be chosen as the sample with the smallest U-learning function in the candidate sampling pool S, i.e.:

$$ {x}^{new}=\underset{x\in S}{\mathrm{argmin}}U\left(\kern0.2em x\right)\kern0.1em $$

(36)

In plenty of existing literature (Ling et al. 2019; Echard et al. 2011; Hu and Mahadevan 2016), it is suggested that the Kriging model is well trained if U(x) ≥ 2 holds for every sample x in S, which illustrates that the probability of misjudging the sign of g(x) is not bigger than Φ(−2) = 0.0228.