Topology optimization of internal partitions in a flow-reversing chamber muffler for noise reduction

Abstract

A topology-optimization-based design method for a flow-reversing chamber muffler is suggested to maximize the transmission loss value at a target frequency considering flow power dissipation. Rigid partitions for high noise reduction should be carefully placed inside the muffler to avoid extreme flow power dissipation due to a 180° change in flow direction from an inlet to an outlet. The optimal flow path for minimum flow power dissipation is well known to change depending on the Reynolds number, which is a function of the inlet flow velocity. To optimize the partition layout with an optimal flow path in an expansion chamber at a given Reynolds number, a flow-reversing chamber muffler design problem is formulated by topology optimization. The formulated topology optimization problem is implemented using the finite element method with a gradient-based optimization algorithm and is solved for various design conditions such as the target frequencies, rigid partition volumes, Reynolds numbers, non-design domain settings, and allowed amounts of flow power dissipation. The effectiveness of our suggested approach is verified by comparing the optimized partition layouts obtained by the suggested method and previous methods.

Appendices

Appendix A

By using integration by parts and applying boundary conditions, the weak form of the governing equation of the acoustic problem in (4) can be derived as

$$ \frac{1}{\rho }{\displaystyle \underset{\varOmega }{\int}\nabla u\cdot \nabla {p}^Hd\mathbf{x}}-\frac{\omega^2}{K}{\displaystyle \underset{\varOmega }{\int }u{p}^Hd\mathbf{x}}+\frac{j\omega }{\rho_{\mathrm{air}}{c}_{\mathrm{air}}}{\displaystyle \underset{\varGamma_o}{\int }u{p}^Hd\mathbf{x}}=j\omega {\displaystyle \underset{\varGamma_i}{\int }ud\mathbf{x}}, $$

(A.1)

where u is a test function, Ω is the analysis domain, and Γ _i and Γ _o denote boundaries of the inlet and the outlet, respectively. The matrix form of the system equation in (A.1) is

$$ {\mathbf{K}}^H{\mathbf{P}}^H={\mathbf{F}}^H, $$

(A.2)

where

$$ {\mathbf{K}}^H={\displaystyle \underset{\varOmega }{\int}\nabla {\mathbf{N}}^T\nabla \mathbf{N}d\mathbf{x}}-\frac{\omega^2}{K}{\displaystyle \underset{\varOmega }{\int }{\mathbf{N}}^T\mathbf{N}d\mathbf{x}}+\frac{j\omega }{\rho_{\mathrm{air}}{c}_{\mathrm{air}}}{\displaystyle \underset{\varGamma_o}{\int }{\mathbf{N}}^T\mathbf{N}d\mathbf{x}}, $$

(A.3a)

$$ {\mathbf{F}}^H=j\omega {\displaystyle \underset{\varGamma_i}{\int }{\mathbf{N}}^T\mathbf{N}d\mathbf{x}}. $$

(A.3b)

In (A.2) and (A.3), P ^H is the nodal vector of the acoustic pressure, and N is the bilinear shape function matrix.

The weak forms for the incompressible steady-state Navier–Stokes equations in (9) are

$$ {\displaystyle \underset{\varOmega }{\int}\left[{w}_i{\rho}_{\mathrm{air}}\frac{\partial {v}_i^N}{\partial {x}_j}{v}_j^N+\frac{1}{2}\left(\frac{\partial {w}_i}{\partial {x}_j}+\frac{\partial {w}_j}{\partial {x}_i}\right){\sigma}_{ij}+{w}_i\alpha {v}_i^N\right]d\mathbf{x}}-{\displaystyle \underset{\varGamma }{\int }{w}_i{n}_j{\sigma}_{ij}d\mathbf{x}=0}, $$

(A.4a)

$$ {\displaystyle \underset{\varOmega }{\int}\tilde{u}}\frac{\partial {v}_i^N}{\partial {x}_i}d\mathbf{x}=0, $$

(A.4b)

where w _i and ũ are test functions for velocity and pressure, respectively. Using the Galerkin method, the weak forms in (A.4) can be discretized as

$$ \mathbf{r}=\left[\begin{array}{cc}\hfill {\mathbf{K}}_c\left({\mathbf{V}}^N\right)+{\mathbf{K}}_d+{\mathbf{K}}_{\alpha}\hfill & \hfill -\mathbf{Q}\hfill \\ {}\hfill -{\mathbf{Q}}^T\hfill & \hfill \mathbf{0}\hfill \end{array}\right]\left\{\begin{array}{c}\hfill {\mathbf{V}}^N\hfill \\ {}\hfill {\mathbf{P}}^N\hfill \end{array}\right\}=\left\{\begin{array}{c}\hfill \mathbf{0}\hfill \\ {}\hfill \mathbf{0}\hfill \end{array}\right\}, $$

(A.5)

where K _c , K _d and K _α are stiffness matrices corresponding to the convective, diffusive and absorption term of (A.4a), respectively, Q is the constraint matrix for incompressibility, and V ^N and P ^N are nodal vectors for the velocity and the pressure, respectively. The nonlinear equation in (A.5) is iteratively solved through linearization.

Using the discretized governing equation in (A.5), the power dissipation in (13) can be rewritten as

$$ E\left({\mathbf{V}}^N,{\mathbf{P}}^N;\boldsymbol{\upchi} \right)=\frac{1}{2}{\left({\mathbf{V}}^N\right)}^T\left({\mathbf{K}}_d+{\mathbf{K}}_{\alpha}\right){\mathbf{V}}^N=\frac{1}{2}{\mathbf{z}}^T\mathbf{C}\mathbf{z}, $$

(A.6)

where

$$ \mathbf{C}=\left[\begin{array}{cc}\hfill {\mathbf{K}}_d+{\mathbf{K}}_{\alpha}\hfill & \hfill \mathbf{0}\hfill \\ {}\hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \end{array}\right]\mathrm{and}\;\mathbf{z}=\left\{\begin{array}{c}\hfill {\mathbf{V}}^N\hfill \\ {}\hfill {\mathbf{P}}^N\hfill \end{array}\right\}. $$

(A.7)

In (A.6), χ is the nodal design variable vector.

Appendix B

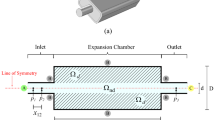
To maximize the transmission loss value at a target frequency, equations in (1), (2), and (5) were solved for Model A in Fig. 1a, where the non-design domain for fluid passage should be defined because the flow power dissipation was not considered. Optimal topologies depending on the partition volume ratio β, target frequency f _t , and width of the non-design domain l ₃ were examined. The acoustic attenuation performance of the optimization results was compared with that of the nominal muffler which does not have any partition inside.

2.1 Effect of partition volume ratio on optimal topologies

Figure 12 illustrates four optimal topologies obtained for different partition volume ratios: (a) β = 0.02, (b) β = 0.06, (c) β = 0.10, and (d) β = 0.14. Since the acoustic space where the acoustic wave does not transmit but stays was decreased relatively if extremely large amount of partitions was used, the formulated problem was solved for small values of β. The target frequency of f _t  = 1000 Hz and the non-design domain width of l ₃ = d ₁ were used to obtain the results. In the optimal topologies, the black area refers to rigid partitions, and the white area denotes the air (fluid) region. To increase the transmission loss value at the target frequency, the rigid partition was built up around the middle of the right end, and the length of the partition increased as more volume was allowed for the rigid partition. When the partition volume ratio increased above a certain value, the left end of the partition was divided into two branches. Figure 13 shows that the transmission loss values of the optimized mufflers at the target frequency were much larger than that of the nominal muffler: 1.68 dB for β = 0.02, 13.30 dB for β = 0.06, 58.83 dB for β = 0.10, and 63.75 dB for β = 0.14 (compared with 0.01 dB for the nominal muffler, β = 0).

2.2 Effect of target frequency on optimal topologies

Figure 14 compares the optimal topologies obtained at four different target frequencies for the same partition volume ratio (β = 0.07) and non-design domain width (l ₃ = d ₁): (a) f _t  = 800 Hz, (b) f _t  = 1000 Hz, (c) f _t  = 1200 Hz, and (d) f _t  = 1400 Hz. The figures show that the optimal topologies were strongly affected by the target frequency. The partitions in Fig. 14a were vertically built up from the top and the bottom, whereas those in the other topologies grew horizontally around the middle of the right wall. In the results of Fig. 14b ~ d, the left ends of the horizontal partitions were stretched straight or divided into two branches depending on the target frequency. The transmission loss value at the target frequencies increased dramatically in the optimal topologies: (a) 29.9 dB from 3.20 dB (nominal muffler) at 800 Hz, (b) 18.1 dB from 0.01 dB (nominal muffler) at 1000 Hz, (c) 29.54 dB from 0.05 dB (nominal muffler) at 1200 Hz, and (d) 22.65 dB from 9.14 dB (nominal muffler) at 1400 Hz.

2.3 Effect of non-design domain on optimal topologies

The rigid partitions of the optimized topologies in Fig. 14a were located on the left edge of the design domain. Thus, the location of the partitions might be affected by the width of the non-design domain l ₃. To investigate this effect, the topology optimization problem was solved for four different values of l ₃ at the same target frequency (f _t  = 800 Hz). Fig. 15 shows the optimized results: (a) l ₃ = d ₁, (b) l ₃ = 0.75d ₁, (c) l ₃ = 0.5d ₁, and (d) l ₃ = 0.25d ₁ For a fair comparison, the same volume of rigid partitions [V _o  ⋅ β in (2)] was allowed in each optimization: β was adjusted considering the volume (V _o ) of the design domain (β = 0.04 for l ₃ = d ₁, β = 0.04 ⋅ 6/7 for l ₃ = 0.75d ₁, β = 0.04 ⋅ 6/8 for l ₃ = 0.5d ₁, and β = 0.04 ⋅ 6/9 for l ₃ = 0.25d ₁). Note that all partitions of the optimal topologies were located at the left edge of the design domain. In Fig. 15a ~ c, the transmission loss value at the target frequency increased as the width of the non-design domain decreased, which was not the case in Fig. 15d; transmission loss values were (a) 9.01 dB, (b) 15.69 dB, (c) 15.90 dB, and (d) 12.69 dB. This result indicates that the non-design domain for fluid passage must be carefully selected before optimization in case that only the transmission loss is considered for optimization formulation and a gradient-based optimizer is used in solving the optimization problem. In the gradient-based optimizations, the optimum result is highly affected by design updates of early iterations, so it is inferred that the sensitivities of design variables around the left end of the design domain are higher than those of other design variables during early iterations. The non-design domain in the expansion chamber is not required if the acoustical and fluidic performances of the muffler are simultaneously considered.

From the viewpoint of the fluid dynamics, the leftward shift of the rigid partition in Fig. 15 certainly results in high flow power dissipation. Figure 16 shows the optimal flow paths with minimum flow power dissipation depending on the inlet flow velocity (or Reynolds number, $\mathrm{R}\mathrm{e}=\frac{\rho_{\mathrm{air}}{v}_{\max }{d}_1}{\eta }$): (a) Re = 1, (b) Re = 300, (c) Re = 600, and (d) Re = 1000. These results were obtained by applying the work of Olesen et al. (2006) to Model B in Fig. 1b with the volume ratio β = 0.78. In the figures, a flow path with higher curvature was obtained for a larger inlet flow velocity. This implies that muffler designers should determine the location of the partitions so as not to intrude on the optimal flow path depending on the inlet flow velocity by considering not only the transmission loss but also the flow power dissipation.

Fig. 12

Optimal topologies of Model A for different partition volume ratios (β) at the target frequency (f _t  = 1000 Hz): (a) β = 0.02, (b) β = 0.06, (c) β = 0.10, and (d) β = 0.14

Fig. 13

Comparison of transmission loss curves of optimal topologies in Fig. 12 and the nominal muffler

Fig. 14

Optimal topologies of Model A for different target frequencies at the partition volume ratio (β = 0.07): (a) f _t  = 800 Hz, (b) f _t  = 1000 Hz, (c) f _t  = 1200 Hz, and (d) f _t  = 1400 Hz

Fig. 15

Optimal topologies of Model A for different widths of the non-design domain (l ₃) at the target frequency (f _t  = 800 Hz): (a) l ₃ = d ₁, (b) l ₃ = 0.75d ₁, (c) l ₃ = 0.5d ₁, and (d) l ₃ = 0.25d ₁

Fig. 16

Optimal topologies of Model B for different Reynolds numbers for the volume ratio β = 0.78: (a) Re = 1, (b) Re = 300, (c) Re = 600, and (d) Re = 1000