Abstract
Continuing (Fuchino et al. in Arch Math Log, 2020. https://doi.org/10.1007/s00153-020-00730-x), we study the Strong Downward Löwenheim–Skolem Theorems (SDLSs) of the stationary logic and their variations. In Fuchino et al. (2020) it has been shown that the SDLS for the ordinary stationary logic with weak second-order parameters \(\textsf {SDLS}({\mathcal {L}}^{\aleph _0}_{stat},{<}\,\aleph _2)\) down to \({<}\,\aleph _2\) is equivalent to the conjunction of CH and Cox’s Diagonal Reflection Principle for internally clubness. We show that the SDLS for the stationary logic without weak second-order parameters \(\textsf {SDLS}^-({\mathcal {L}}^{\aleph _0}_{stat},{<}\,2^{\aleph _0})\) down to \({<}\,2^{\aleph _0}\) implies that the size of the continuum is \(\aleph _2\). In contrast, an internal interpretation of the stationary logic can satisfy the SDLS down to \({<}\,2^{\aleph _0}\) under the continuum being of size \(>\aleph _2\). This SDLS is shown to be equivalent to an internal version of the Diagonal Reflection Principle down to an internally stationary set of size \({<}\,2^{\aleph _0}\). We also consider a  version of the stationary logic and show that the SDLS for this logic in internal interpretation \(\textsf {SDLS}^{int}_+({\mathcal {L}}^{PKL}_{stat},{<}\,2^{\aleph _0})\) for reflection down to \({<}\,2^{\aleph _0}\) is consistent under the assumption of the consistency of ZFC \(+\) “the existence of a supercompact cardinal” and this SDLS implies that the continuum is (at least) weakly Mahlo. These three “axioms” in terms of SDLS are consequences of three instances of a strengthening of generic supercompactness which we call Laver-generic supercompactness. Existence of a Laver-generic supercompact cardinal in each of these three instances also fixes the cardinality of the continuum to be \(\aleph _1\) or \(\aleph _2\) or very large respectively. We also show that the existence of one of these generic large cardinals implies the “\(++\)” version of the corresponding forcing axiom.
version of the stationary logic and show that the SDLS for this logic in internal interpretation \(\textsf {SDLS}^{int}_+({\mathcal {L}}^{PKL}_{stat},{<}\,2^{\aleph _0})\) for reflection down to \({<}\,2^{\aleph _0}\) is consistent under the assumption of the consistency of ZFC \(+\) “the existence of a supercompact cardinal” and this SDLS implies that the continuum is (at least) weakly Mahlo. These three “axioms” in terms of SDLS are consequences of three instances of a strengthening of generic supercompactness which we call Laver-generic supercompactness. Existence of a Laver-generic supercompact cardinal in each of these three instances also fixes the cardinality of the continuum to be \(\aleph _1\) or \(\aleph _2\) or very large respectively. We also show that the existence of one of these generic large cardinals implies the “\(++\)” version of the corresponding forcing axiom.
Similar content being viewed by others
Notes
The adjective “strong” is added to indicate that \(\mathfrak {B}\) in the statement of the property is not merely elementarily equivalent to but also elementary submodel of \(\mathfrak {A}\).
Here, a more straightforward proof is possible e.g. by directly defining \({\mathcal {D}}\). We defined \({\mathcal {D}}\) via definition of \({\mathcal {U}}\) instead since we need \({\mathcal {U}}\) in the proof of (2) in any way.
As before, when we write \(\varphi =\varphi (x_0,\ldots ,\,X_0,\ldots )\), we always assume that the list \(x_0,\ldots \) contains all the free first order variables of \(\varphi \) and \(X_0,\ldots \) all the free weak second order variables of \(\varphi \).
This expansion becomes necessary below when we would like to have
 .
.
References
Baumgartner, J.E., Taylor, A.D.: Saturation properties of ideals in generic extensions I. Trans. Am. Math. Soc. 270(2), 557–574 (1982)
Brickhill, H., Fuchino, S., Sakai, H.: On \(\alpha \)-stationary subsetes of \({\cal{P}_\kappa (\lambda )}\) (in preparation)
Corazza, P.: Laver sequences for extendible and super-almost-huge cardinals. J. Symb. Log. 64(3), 963–983 (1999)
Cox, S.: The diagonal reflection principle. Proc. Am. Math. Soc. 140(8), 2893–2902 (2012)
Fuchino, S., Rodrigues, A.O.M., Sakai, H.: Strong downward Löwenheim–Skolem theorems for stationary logics, I. Arch. Math. Log. (2020). https://doi.org/10.1007/s00153-020-00730-x
Fuchino, S., Rodrigues, A.O.M., Sakai, H.: Strong downward Löwenheim–Skolem theorems for stationary logics, III—mixed support iteration. In: Proceedings of the Asian Logic Conference 2019 (to appear)
Fuchino, S., Sakai, H.: Strong downward Löwenheim–Skolem theorems for stationary logics, IV—more on Laver-generically large cardinals and mixed support iterations (in preparation)
Jech, T.: Set Theory, The Third Millennium Edition. Springer, Berlin (2001/2006)
Kanamori, A.: The Higher Infinite. Springer, Berlin (1994/2003)
Matsubara, Y., Sakai, H., Usuba, T.: On the existence of skinny stationary subsets. Ann. Pure Appl. Log. 170, 539–557 (2019)
Funding
The first author was partially supported by JSPS Kakenhi Grant No. 20K03717. The second author was partially supported by the Monbukagakusho (Ministry of Education, Culture, Sports, Science and Technology) Scholarship, Japan. The third author is supported by JSPS Kakenhi Grant No. 18K03397.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The first author (S. Fuchino) would like to thank Joel Hamkins for several valuable comments and suggestions.
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
An updated and extended version of this paper with more details and proofs is downloadable as: http://fuchino.ddo.jp/papers/SDLS-II-x.pdf
Rights and permissions
About this article
Cite this article
Fuchino, S., Ottenbreit Maschio Rodrigues, A. & Sakai, H. Strong downward Löwenheim–Skolem theorems for stationary logics, II: reflection down to the continuum. Arch. Math. Logic 60, 495–523 (2021). https://doi.org/10.1007/s00153-020-00751-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00153-020-00751-6
Keywords
- Strong downward Löwenheim Skolem theorem
- Stationary logic
- Generically large cardinals
- Mixed support iteration
- Laver function
- Superhuge cardinal
- Continuum problem



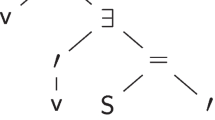
 .
.