A camera model for cameras with hypercentric lenses and some example applications

Abstract

We propose a camera model for cameras with hypercentric lenses. Because of their geometry, hypercentric lenses allow to image the top and the sides of an object simultaneously. This makes them useful for certain inspections tasks, for which otherwise multiple images would have to be acquired and stitched together. After describing the projection geometry of hypercentric lenses, we derive a camera model for hypercentric lenses that is intuitive for the user. Furthermore, we describe how to determine the parameter values of the model by calibrating the camera with a planar calibration object. We also apply our camera model to two example applications: in the first application, we show how two cameras with hypercentric lenses can be used for dense 3D reconstruction. For an efficient reconstruction, the images are rectified such that corresponding points occur in the same image row. Standard rectification methods would result in perspective distortions in the images that would prevent stereo matching algorithms from robustly establishing correspondences. Therefore, we propose a new rectification method for objects that are approximately cylindrical in shape, which enables a robust and efficient reconstruction. In the second application, we show how to unwrap cylindrical objects to simplify further inspection tasks. For the unwrapping, the pose of the cylinder must be known. We show how to determine the pose of the cylinder based on a single camera image and based on two images of a stereo camera setup.

1 Introduction

Hypercentric lenses (sometimes also called pericentric lenses) provide a converging view of an object ([10, Chapter 10.3.9], [1, 17], [2, Chapter 3.4.6], [14, Chapter 4.2.14.1]). This allows imaging the top and the sides of an object with a single view. Therefore, hypercentric lenses are especially useful for certain inspection tasks, for which otherwise multiple cameras would have to be used to cover the object’s surface to be inspected or the object would have to be rotated in front of a single camera to obtain multiple views. The use of a single camera image has additional advantages: no image stitching is necessary and problems caused by the different perspectives obtained from multiple cameras are avoided.

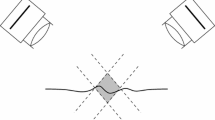
An example is shown in Fig. 1. Here, the print on the label of a bottle shown in Fig. 1a must be inspected. The camera was mounted above the bottle with a perpendicular view down onto the object, as illustrated in Fig. 1b. The entrance pupil of a hypercentric lens lies in front of the lens. The object is placed between the entrance pupil and the front of the lens. In this setup, objects that are closer to the camera appear smaller in the image. Figure 1c shows the image obtained by a camera with a hypercentric lens. The bottle’s cap is imaged in the center and the entire label is visible and imaged as a circular ring. Unfortunately, this is achieved at the expense of severe perspective distortions of the object in the image.

Fig. 1

Using a hypercentric lens to image the top and the side of a bottle. To inspect the label of the bottle (a), a camera with a hypercentric lens is mounted above the bottle (b). The bottle is placed between the entrance pupil and the front of the lens. This results in a converging view of the object. c Image of the bottle taken with a hypercentric lens. d Image of the bottle taken with a conventional perspective lens (for comparison)

Fig. 2

Using a hypercentric lens to image the internal screw thread of a pipe joint. To inspect the screw of the pipe joint (a), a camera with a hypercentric lens is mounted above the pipe joint such that the entrance pupil lies inside the top bottle neck of the pipe joint (b). c Image of the pipe joint acquired with a hypercentric lens. d Image of the pipe joint acquired with a conventional perspective lens (for comparison)

Sometimes, hypercentric lenses are used as long stand-off borescopes [17]. An example is shown in Fig. 2, where the internal screw thread of the pipe joint shown in Fig. 2a must be inspected. The camera is mounted above the pipe joint such that the center of the entrance pupil lies inside the top bottle neck of the pipe joint, as illustrated in Fig. 2b. Therefore, in this setup, the entrance pupil is located between the object to be inspected and the front of the lens. Objects that are closer to the camera appear larger in the image. To obtain a sharp image, usually the focus distance of the lens must be increased beyond the entrance pupil by adding a spacer between the lens and the camera [17]. In contrast to standard borescopes, this setup allows a larger distance between the object and the camera, which makes the placement of a suitable light source easier. Since in this case hypercentric lenses behave like conventional (entocentric) lenses, the conventional camera models for entocentric lenses can be applied. Therefore, we will not handle this case in our paper.

To obtain accurate measurements from images that are acquired by a camera with a hypercentric lens, it is necessary to calibrate the camera, i.e., to determine the parameters of the interior orientation of the camera, including parameters that model lens distortions. Furthermore, camera calibration is necessary whenever metric 2D or 3D measurements are to be derived from images. Finally, because of the severe perspective object distortions that are present in many typical applications of hypercentric lenses, images are typically unwrapped before further inspections are applied. To achieve a highly accurate unwrapping, the camera must be calibrated as well.

In this paper, we describe a camera model for cameras with hypercentric lenses and show some example applications. In Sect. 2, we first describe the geometry of a hypercentric lens, followed by a description of how to model hypercentric lenses in Sect. 3. The calibration process is described in Sect. 4. In Sect. 5, we discuss how to perform 3D stereo reconstruction with hypercentric lenses. Finally, in Sect. 6 we present two methods for unwrapping images of cylindrical objects, one for images that were acquired with a single camera and one that is based on the 3D reconstruction.

Fig. 3

Geometry of an entocentric lens. $O_1$ and $O_2$ are two different object positions; F and $F'$ are the focal points of the lens at a distance of f from the principal planes P and $P'$, respectively; the nodal points N and $N'$ are the intersections of the principal planes with the optical axis; AS is the aperture stop; ENP is the entrance pupil; IP is the image plane. For simplicity, only the chief rays are displayed. In this setup, the image $I_1$ of $O_1$ is in focus, while the image $I_2$ of $O_2$ is blurred. Note that the entrance pupil lies between the objects and the image plane. Therefore, the image of $O_2$ is larger than the image of $O_1$

Our main contribution is a camera model for cameras with hypercentric lenses. A second contribution is an epipolar rectification method for transforming a stereo image pair that was acquired by two opposing cameras with hypercentric lenses into standard epipolar geometry. Rectifying images to standard epipolar geometry is a prerequisite to achieve the most efficient disparity estimation. Our rectification method is optimized for approximately cylindrical objects, since we consider it the main application of hypercentric lenses to inspect approximately cylindrical objects.

2 Geometry of hypercentric lenses

An assembly of lenses can be regarded as a single thick lens [14, Chapter 4.2.11]. In the following, we assume that lenses have the same medium, e.g., air, on both sides of the lens.

Figure 3 shows the thick lens model of an entocentric lens, which is the most common type of lenses. The model is characterized by the principal planes P and $P'$, which are perpendicular to the optical axis, and the focal points F and $F'$, which lie on the optical axis at distances f from P and $P'$, respectively. The intersections of the principal planes with the optical axis are the principal points. For lenses that have the same medium on both sides of the lens, the principal points coincide with the nodal points N and $N'$.

To correctly describe the projection properties of a lens, it is essential to model the aperture stop of the lens [26]. The aperture stop restricts the diameter of the cone of rays that is emitted from the object and imaged sharply in the image plane [14, Chapter 4.2.12.2]. The virtual image of the aperture stop by all optical elements that come before it (i.e., lie left of it in Fig. 3) is called the entrance pupil. Analogously, the virtual image of the aperture stop by all optical elements that come behind it (i.e., lie right of it in Fig. 3) is called the exit pupil [26]. The rays that pass through the center of the aperture stop are called chief rays. They also pass through the center of both pupils [26] (for the entrance pupil, this is indicated by the dashed lines in Fig. 3).

The position of the aperture stop in a lens crucially influences the projection properties of the lens. Essentially, the aperture stop filters out certain rays in object space [26]. For an entocentric lens, the aperture stop is positioned between the two focal points of the lens as shown in Fig. 3 [14, Chapter 4.2.12.4]. This causes the entrance pupil to lie between the object and the image plane. Consequently, objects that are closer to the camera appear larger in the image. Entocentric lenses provide a diverging view of objects because rays in object space that are converging or parallel to the optical axis are filtered out by the aperture stop.

Figure 4 shows the thick lens model of a hypercentric lens. In comparison with the model shown in Fig. 3, the only difference is the position of the aperture stop. For hypercentric lenses, the aperture stop is placed behind the image-side focal point. This causes the entrance pupil to lie in object space [26]. If an object is placed between the entrance pupil and the lens, as in Fig. 1, objects that are closer to the camera appear smaller in the image. Hypercentric lenses provide a converging view of objects because rays in object space that are diverging or parallel to the optical axis are filtered out by the aperture stop. Therefore, the diameter of hypercentric lenses must be significantly larger than the diameter of the imaged objects. If an object is placed before the entrance pupil, as in Fig. 2, a hypercentric lens behaves like an entocentric lens, i.e., objects that are closer to the camera appear larger in the image. However, in contrast to entocentric lenses, the entrance pupil is outside the lens, which makes it useful for applications where the inside of objects must be inspected, as in Fig. 2. As mentioned above, conventional camera models for entocentric lenses can be applied in this case.

Fig. 4

Geometry of a hypercentric lens. $O_1$ and $O_2$ are two different object positions; F and $F'$ are the focal points of the lens at a distance of f from the principal planes P and $P'$, respectively; the nodal points N and $N'$ are the intersections of the principal planes with the optical axis; AS is the aperture stop; ENP is the entrance pupil; IP is the image plane. For simplicity, only the chief rays are displayed. In this setup, the image $I_1$ of $O_1$ is in focus, while the image $I_2$ of $O_2$ is blurred. Note that the objects lie between the entrance pupil and the image plane. Therefore, the image of $O_2$ is smaller than the image of $O_1$. (Note that the lower part of the drawing has been cut off since it contains no additional information)

For the sake of completeness, it should be mentioned that there is a third type of lenses in which the aperture stop is placed exactly at one of the focal points. These lenses are called telecentric lenses. Depending on whether the aperture stop is placed at the object-side or image-side focal point, such a lens is called image-side telecentric or object-side telecentric, respectively [26]. Object-side telecentric lenses provide an orthographic projection because rays in object space that are diverging or converging are filtered out by the aperture stop and only rays that are parallel to the optical axis pass through. Consequently, the entrance pupil moves to infinity. Analogously, for image-side telecentric lenses, the exit pupil moves to infinity. Hence, only rays that are parallel to the optical axis in image space can pass the aperture stop, which is useful for digital sensors to avoid pixel vignetting [26]. In bilateral telecentric lenses, both the entrance and the exit pupil are located at infinity [14, Chapter 4.2.12.4]. They are often preferred over object-side telecentric lenses because of their higher accuracy [26].

In [26], it is shown that modeling lenses with the pinhole model is insufficient because real lenses have two projection centers: the centers of the entrance and exit pupil. Furthermore, the ray angles in image space and object space differ in general. However, it is also shown in [26] that it is valid to apply the pinhole model to cameras in which the image plane is perpendicular to the optical axis (i.e., for cameras with non-tilt lenses). In this case, the projection center of the pinhole model corresponds to the center of the entrance pupil, which is also the relevant projection center for modeling the pose of the camera. For tilt lenses, however, it is essential to model two separate projection centers [26].

Some practical aspect should be considered when setting up an inspection system with hypercentric lenses. As indicated before, one of the most important use cases of hypercentric lenses in machine vision applications is the 360 degree inspection of an object with a single image. By choosing a lens with a diameter that is significantly larger than the diameter of the object to be inspected, we ensure that the lines of sight hit the object’s surface under an angle that is not too small. Smaller angles result in higher perspective distortions, or, when considering stereo applications, in a lower reconstruction accuracy. Whether a lens is suitable for a specific object can be derived from the maximum viewing angle, the working distance, and the position of the entrance pupil (sometimes called the convergence point) [17]. These data are often given by the manufacturer in the specification of the lens.

3 Model for cameras with hypercentric lenses

In this section, we will describe a camera model for hypercentric lenses. We require that the model and its parameterization are intuitive for the user and result in intuitive camera poses.

A comprehensive overview of camera models is given in [28]. To the best of our knowledge, there is no prior art that presents a camera model designed for hypercentric lenses. There exist generalized camera models, like local or discrete ones [28]. They have a higher descriptive power but have more parameters than lens-specific global models. Their advantage is that the exact projection geometry of the lens does not need to be known. Unfortunately, they often require interpolation, which limits the accuracy that can be achieved when applying these models. Furthermore, it is desirable to always use the simplest (i.e., with fewest parameters) model that appropriately and accurately describes reality.

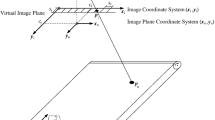
Our camera model is visualized in Fig. 5. Because hypercentric lenses have a projection center, it is obvious to use a central perspective lens model (in contrast to non-central camera models [28]). As discussed in [26], the relevant projection center for modeling the pose of a camera is the entrance pupil. Therefore, we define the center of the entrance pupil as the origin of the coordinate system of a camera. Furthermore, it is desirable that entocentric and hypercentric lenses behave identically with respect to the camera coordinate system. Therefore, we define the z axis of the camera coordinate system to point along the optical axis in the viewing direction. The xy plane of the camera coordinate system is assumed to be parallel to the image plane with the x axis being parallel to the horizontal axis of the sensor. Because the objects lie between the entrance pupil and the front of the lens, points in object space have a negative z coordinate. This ensures that objects with smaller z coordinates are closer to the camera and appear smaller in the image. Furthermore, because the principal point in this model has a negative z coordinate, the principal distance must be negative as well.

Fig. 5

Camera model for a hypercentric lens. ($x_k, y_k, z_k$) denotes the camera coordinate system and ($x_\mathrm {u}, y_\mathrm {u}$) denotes the image plane coordinate system

The derivation of the camera model is based on the description in [27, Chapter 3.9] and [26]. Although we restrict ourselves to cameras with non-tilt lenses, the described model can easily be extended to cameras with tilt lenses, as described in [26]. Because our camera model for hypercentric lenses is based on the model presented in [26], the remainder of this section will include a summary of this model. Modifications or extensions, which are especially necessary for hypercentric lenses, will be explicitly mentioned.

The practical experiments in this paper cover setups of at most two cameras. However, we derive a generic model that can be applied to a multi-view stereo setup case. In [6], the underlying camera model of [27, Chapter 3.9] was successfully applied to a multi-view setup with 40 cameras. Therefore, we do not expect any practical problems in the multi-view case for hypercentric lenses as well.

Suppose we have a multi-view stereo setup with $n_\mathrm {c}$ cameras. For the calibration, we acquire $n_\mathrm {o}$ images of a calibration object in different poses with each camera. Each pose l ($l=1,\ldots ,n_\mathrm {o}$) of the calibration object describes a transformation from the coordinate system of the calibration object to the coordinate system of camera k ($k=1,\ldots ,n_\mathrm {c}$). Because of the requirements stated above, for hypercentric lenses, the origin of the calibration object has a negative z coordinate in the camera coordinate system. Let ${\varvec{p}}_\mathrm {o}=(x_\mathrm {o},y_\mathrm {o},z_\mathrm {o})^\top$ be a point in the coordinate system of the calibration object at pose l. Instead of modeling the transformation of ${\varvec{p}}$ into each camera individually, we define a reference camera (e.g., camera 1) and transform ${\varvec{p}}_\mathrm {o}$ into a point ${\varvec{p}}_l$ in the coordinate system of the reference camera by applying a rigid 3D transformation:

$$\begin{aligned} {\varvec{p}}_l = {{\mathbf {\mathtt{{R}}}}}_l {\varvec{p}}_\mathrm {o} + {\varvec{t}}_l, \end{aligned}$$

(1)

where ${{\mathbf {\mathtt{{R}}}}}_l$ is a rotation matrix and ${\varvec{t}}_l=(t_{l,x},t_{l,y},t_{l,z})^\top$ is a translation vector. The rotation matrix is parameterized by Euler angles ${{\mathbf {\mathtt{{R}}}}}_l={{\mathbf {\mathtt{{R}}}}}_x(\alpha _l) {{\mathbf {\mathtt{{R}}}}}_y(\beta _l) {{\mathbf {\mathtt{{R}}}}}_z(\gamma _l)$. We decided to choose this rotation parameterization because Euler angles are intuitive for the user. They also allow to easily exclude single rotation parameters from the optimization. For example, if the mechanical setup ensures with high accuracy that the calibration target is parallel to the image plane, we should set $\alpha _l=\beta _l=0$ and the camera calibration should keep these parameters fixed [27, Chapter 3.9.4.6].

In the next step, the point ${\varvec{p}}_l$ is transformed into the coordinate system of camera k by applying

$$\begin{aligned} {\varvec{p}}_k = {{\mathbf {\mathtt{{R}}}}}_k {\varvec{p}}_l + {\varvec{t}}_k, \end{aligned}$$

(2)

where the rotation matrix ${{\mathbf {\mathtt{{R}}}}}_k$ and the translation vector ${\varvec{t}}_k$ describe the relative pose of camera k with respect to the reference camera. Note that the transformation in (2) can be omitted if we only calibrate a single camera.

In the next step, the point ${\varvec{p}}_k=(x_k,y_k,z_k)^\top$ is projected into the image plane:

$$\begin{aligned} \left( \begin{array}{@{}c@{}} x_\mathrm {u} \\ y_\mathrm {u} \end{array} \right) = \frac{c}{z_k} \left( \begin{array}{@{}c@{}} x_k \\ y_k \end{array} \right) , \end{aligned}$$

(3)

with the principal distance c. Note that in order to fulfill the above requirements for intuitive model parameters and camera poses, the principal distance must be negative for hypercentric lenses. This is also clear from (3): To ensure that $x_\mathrm {u}$ and $x_k$ as well as $y_\mathrm {u}$ and $y_k$ have identical signs, c and $z_k$ must also have the same sign. Because $z_k$ is negative, c must also be negative.

To model lens distortions, the undistorted point $(x_\mathrm {u},y_\mathrm {u})^\top$ is then distorted to a point $(x_\mathrm {d},y_\mathrm {d})^\top$. By analogy with [26], we support two distortion models: the division model [3, 8, 13, 15, 16] and the polynomial model [4, 5].

In the division model, the undistorted point is computed from the distorted point by using

$$\begin{aligned} \left( \begin{array}{@{}c@{}} x_\mathrm {u} \\ y_\mathrm {u} \end{array} \right) = \frac{1}{1+\kappa r_\mathrm {d}^2} \left( \begin{array}{@{}c@{}} x_\mathrm {d} \\ y_\mathrm {d} \end{array} \right) , \end{aligned}$$

(4)

with $r_\mathrm {d}^2=x_\mathrm {d}^2 + y_\mathrm {d}^2$. One advantage of the division model is that it can be inverted analytically:

$$\begin{aligned} \left( \begin{array}{@{}c@{}} x_\mathrm {d} \\ y_\mathrm {d} \end{array} \right) = \frac{2}{1+\sqrt{1-4\kappa r_\mathrm {u}^2}} \left( \begin{array}{@{}c@{}} x_\mathrm {u} \\ y_\mathrm {u} \end{array} \right) , \end{aligned}$$

(5)

with $r_\mathrm {u}^2=x_\mathrm {u}^2 + y_\mathrm {u}^2$ and the lens distortion parameter $\kappa$.

In the polynomial model, the undistorted point is computed by

$$\begin{aligned} \left( \begin{array}{@{}c@{}} x_\mathrm {u} \\ y_\mathrm {u} \end{array} \right) = \left( \begin{array}{@{}c@{}} x_\mathrm {d}(1 + K_1 r_\mathrm {d}^2 + K_2 r_\mathrm {d}^4 + K_3 r_\mathrm {d}^6) \\ + \,(P_1(r_\mathrm {d}^2+2x_\mathrm {d}^2)+2 P_2 x_\mathrm {d} y_\mathrm {d}) \\ y_\mathrm {d}(1 + K_1 r_\mathrm {d}^2 + K_2 r_\mathrm {d}^4 + K_3 r_\mathrm {d}^6) \\ + (2P_1 x_\mathrm {d} y_\mathrm {d}+P_2(r_\mathrm {d}^2 + 2 y_\mathrm {d}^2)) \end{array} \right) , \end{aligned}$$

(6)

with the lens distortion parameters $K_1$, $K_2$, $K_3$, $P_1$, and $P_2$. Note that the division model only supports radial lens distortions while the polynomial model additionally supports decentering lens distortions. One drawback of the polynomial model is, however, that it cannot be inverted analytically. This results in higher computation times when computing the distorted point because a numerical algorithm must be used.

In the final step, the distorted point $(x_\mathrm {d},y_\mathrm {d})^\top$ is transformed into the image coordinate system:

$$\begin{aligned} \left( \begin{array}{@{}c@{}} x_\mathrm {i} \\ y_\mathrm {i} \end{array} \right) = \left( \begin{array}{@{}c@{}} x_\mathrm {d}/s_x+c_x \\ y_\mathrm {d}/s_y+c_y \end{array} \right) , \end{aligned}$$

(7)

where $s_x$ and $s_y$ are the pixel pitch on the sensor and $(c_x,c_y)^\top$ denotes the principal point.

Summing up, our camera model consists of:

• The exterior orientation, which models the pose of the calibration object with respect to the reference camera in the $n_\mathrm {o}$ images, represented by the vector ${\varvec{e}}_l$ that contains the six parameters $\alpha _l$, $\beta _l$, $\gamma _l$, $t_{l,x}$, $t_{l,y}$, and $t_{l,z}$. In contrast to conventional perspective cameras [26], $t_{l,z}$ is negative for hypercentric lenses (the origin of the coordinate system of the calibration object is in the center of the calibration object).

• The relative orientation, which models the pose of the $n_\mathrm {c}$ cameras with respect to the reference camera, each represented by the vector ${\varvec{r}}_k$ that contains the six parameters $\alpha _k$, $\beta _k$, $\gamma _k$, $t_{k,x}$, $t_{k,y}$, and $t_{k,z}$.

• The interior orientation of the $n_\mathrm {c}$ cameras, each represented by the vector ${\varvec{i}}_k$ that contains the parameters c; $\kappa$ or $K_1$, $K_2$, $K_3$, $P_1$, $P_2$; $s_x$, $s_y$, $c_x$, and $c_y$ (omitting the subscripts k for readability reasons). In contrast to conventional perspective cameras [26], c is negative for hypercentric lenses.

4 Calibration of cameras with hypercentric lenses

4.1 Calibration method

The camera calibration is performed by using the planar calibration object (see Fig. 6) introduced in [26] with a hexagonal layout of control points. See [26] for a discussion of the advantages of this calibration object.

Fig. 6

Planar calibration object with a hexagonal layout of control points

Let $p_j$ ($j=1,\ldots ,n_\mathrm {m}$) denote the known 3D coordinates of the centers of the control points of the calibration object. As described in [26], the calibration object does not need to be visible in all images simultaneously. However, it is essential that there is a chain of observations of the calibration object in multiple cameras that connects all the cameras. The calibration is performed by minimizing the following function [26]:

$$\begin{aligned} \varepsilon ^2 = \sum _{l=1}^{n_\mathrm {o}} \sum _{k=1}^{n_\mathrm {c}} \sum _{j=1}^{n_\mathrm {m}} v_{jkl} \Vert \varvec{\pi }^{-1}_\mathrm {i}({\varvec{p}}_{jkl},{\varvec{i}}_k) - \varvec{\pi }_\mathrm {u}({\varvec{p}}_j, {\varvec{e}}_l, {\varvec{r}}_k,{\varvec{i}}_k)\Vert ^2_2. \end{aligned}$$

(8)

Here, the variable $v_{jkl}$ is 1 if the control point j of the observation l of the calibration object is visible in the image of camera k, and 0 otherwise. $\varvec{\pi }_\mathrm {u}$ denotes the projection of a point ${\varvec{p}}_j$ from world coordinates to the undistorted image plane, and hence represents Eqs. (1), (2), and (3). $\varvec{\pi }_\mathrm {i}^{-1}$ denotes the projection of a point ${\varvec{p}}_{jkl}$ from the image coordinate system back to the undistorted image plane, and hence represents the inverse of Eqs. (7), and (4) or (6), respectively. Minimizing the error in the undistorted image plane has the advantage that an arbitrary mixture of distortion models can be calibrated efficiently.

The optimization of (8) is performed by using a sparse implementation of the Levenberg–Marquardt algorithm [11, Appendix A6]. To obtain the points ${\varvec{p}}_{jkl}$, subpixel-accurate edges are extracted [24, Chapter 3.3], [25] at the border of each imaged control point. Then, ellipses are fitted to the extracted edges [7] and the ${\varvec{p}}_{jkl}$ are set to the centers of the ellipses. Note that this introduces a small bias because the projection of the center of a circle in 3D in general is not the center of the ellipse in the image. Furthermore, in the case of lens distortions the projection of a circle in the image is no longer an ellipse. Both bias effects can be removed as described in [26].

The optimization of (8) requires initial values for the unknown parameters. Initial values for the interior orientation parameters can be obtained or derived from the specification of the camera and the lens (see [26] for details). Note that according to Sect. 3, the negative focal length of the lens must be passed as the initial value for the principal distance.

Initial values for the parameters of the exterior orientations of the calibration object in each camera can be derived from the ellipse parameters of the imaged control points [12, Chapter 3.2.1.2], [13]. Note that according to Sect. 3, the z value of the translation component must be negative. Because we are using a planar calibration object, we obtain two possible poses of the calibration object for each calibration image. The two poses (${{\mathbf {\mathtt{{R}}}}}_1$, ${\varvec{t}}_1$) and (${{\mathbf {\mathtt{{R}}}}}_2$, ${\varvec{t}}_2$) are related by

$$\begin{aligned} {{\mathbf {\mathtt{{R}}}}}_2= & {} {{\mathbf {\mathtt{{R}}}}}_1 {{\mathbf {\mathtt{{R}}}}}_z(\pi ) \end{aligned}$$

(9)

$$\begin{aligned} {\varvec{t}}_2= & {} -{\varvec{t}}_1 \end{aligned}$$

(10)

From the two poses, the one with a negative translation in z must be selected.

Finally, initial values for the parameters of the relative orientations of the cameras can be computed from the initial values of the exterior orientations.

The calibration algorithm allows to exclude any combination of parameters from the optimization. Note that the principal distance c functionally depends on $s_x$ and $s_y$. Consequently, these three parameters cannot be determined uniquely. Therefore, in practical applications, $s_y$ is typically left at its initial value [26].

4.2 Experiments

We tested our calibration method with an Opto Engineering hypercentric lens PC 23030XS with a diameter of 116 mm and a working distance of 20–80 mm. We attached the lens to an SVS-Vistek exo834MTLGEC camera with a resolution of $4224 \times 2838\,\hbox {pixels}$, a pixel pitch of $3.1\,\upmu \hbox {m}$, and a sensor size of 1 in. Because the lens was designed for a 2/3 in. sensor, we limit all image processing applications to a circular region of radius 900 pixels in the center of the image.

Fig. 7

One example of the 25 calibration images. The control points that could be extracted in the image are visualized by white contours. For this image, the planar calibration object was rotated such that the part that appears in the upper image half appears smaller in the image, i.e., is closer to the camera, than the part that appears in the lower image half

Table 1 Result of the calibration of a single camera with a hypercentric lens

We acquired 25 images¹ of the calibration object of Fig. 6 (width: 40 mm) under different poses. Figure 7 shows one example of the 25 images. The calibration converged with an RMS error of 0.54 pixel for the polynomial lens distortion model and with an RMS error of 0.68 pixel for the division lens distortion model. The results of the calibration are shown in Table 1 for both lens distortion models. Furthermore, we calculated the standard deviations of the estimated camera parameters by inverting the normal equations and applying error propagation [9, Chapter 4]. The standard deviations are also shown in Table 1. Note that because we excluded $s_y$ from the calibration, its standard deviation is zero. Because of the higher number of degrees of freedom of the polynomial lens distortion model, the RMS error is slightly lower compared to that of the division lens distortion model. Note that according to our camera model, c is negative.

The estimated pose of the calibration object of Fig. 7 in the camera coordinate system is $t_x=-3.0\,{\hbox {mm}}$, $t_y=1.0\,{\hbox {mm}}$, $t_z=-50.6\,{\hbox {mm}}$, $\alpha =29.7\,{^{\circ }}$, $\beta =0.3\,{^{\circ }}$, and $\gamma =2.0\,{^{\circ }}$. Note that according to our camera model, $t_z$ is negative. Furthermore, the value of $\alpha$ indicates that the calibration object was rotated by approximately $30\,{^{\circ }}$ around its x axis. Because in this example the x axis points to the right hand side in the image, the calibration object was rotated such that the part that appears in the upper image half appears smaller in the image, i.e., is closer to the camera, than the part that appears in the lower image half. This is consistent with the real pose of the calibration object that we used to acquire this image.

From the experiments, we can draw two important conclusions: First, the small RMS errors indicate that our model is able to represent the geometry of a real hypercentric lens correctly. Second, the resulting pose parameters are intuitive for the user and consistent with the real setup.

In another experiment, we evaluated the repeatability of the results and the influence of the number of calibration images. For this, we randomly selected from the 25 calibration images a subset of N images and performed the calibration. We repeated this experiment 500 times and calculated the mean RMS error and the standard deviation of each resulting camera parameter. Figure 8 shows the results for $N=5\ldots 20$. The RMS error, which is approximately 0.5 pixels, slightly increases when increasing the number of calibration images and converges to approximately 0.54. The reason for the slight increase is the ability of the optimization to better equalize measurement errors when only few observations are available. The standard deviations of all parameters decrease for increasing number of calibration images. While this is not surprising, it is interesting to note that the standard deviation of all parameters decreases faster with the number of images than we could expect from a purely statistical point of view. We could expect the standard deviation to decrease proportionally to $N^{-0.5}$ for independent measurements [27]. In this example, the standard deviation of $s_x$ decreases roughly proportionally to $N^{-1.3}$, that of c decreases roughly proportionally to $N^{-1.2}$, that of $c_x$ and $c_y$ roughly proportionally to $N^{-1.1}$, and that of $K_1$, $K_2$, $K_3$, $P_1$, and $P_2$ roughly proportionally to $N^{-1.0}$. It is also interesting to note that for $N \rightarrow 25$, the standard deviations consistently converge to the values that were obtained by error propagation (see Table 1).

Fig. 8

Mean RMS error and standard deviations (Std.) for the estimated camera parameters (polynomial lens distortion model) when repeating the camera calibration 500 times with random subsets drawn from the set of 25 calibration images. The number of images N in the subsets were varied from 5 to 20

5 Stereo reconstruction with hypercentric lenses

To exploit the benefits of hypercentric lenses for stereo reconstruction, one obvious stereo setup is to place the object to be reconstructed between two opposing cameras that look at each other. The setup is illustrated in Fig. 9a. A real setup is shown in Fig. 9b. With this setup, the complete lateral surface of the object can be reconstructed with a single pair of images.

Fig. 9

a Illustration and b realization of a stereo setup with two opposing cameras with hypercentric lenses. The object to be reconstructed is placed on a transparent plate between the two cameras and illuminated by a ring light

5.1 Stereo calibration

To perform the stereo reconstruction, the relative pose of both cameras must be known. To determine the relative pose of the cameras, the calibration object must be visible in both cameras simultaneously. Because of the geometry of the stereo setup (see Fig. 9), we place the planar calibration object between both cameras in such a way that it is approximately parallel to the optical axes and close to the image borders. Figure 10 shows one example stereo image pair. The centers of the control points are extracted in each calibration image by using the method described in Sect. 4.1. The fitted ellipses of the control points that could be extracted in both images are also visualized in Fig. 10.

Fig. 10

One example stereo image pair of the calibration object. The control points that could be extracted in both images are visualized by white ellipses. Additionally, a small square part is enlarged for better visibility

We calibrated the parameters of the interior and relative orientation of the cameras simultaneously. As the lens distortion model, we selected the polynomial model. First, we acquired 25 images of the calibration object in different poses with each camera separately. Then, we additionally acquired twelve image pairs of the calibration object in different poses such that it was visible from both cameras simultaneously. For the stereo calibration, we minimized (8) over all 74 images. The calibration converged with an RMS error of 0.92 pixel. The resulting relative pose of the two cameras is $t_x=2.7\,{\hbox {mm}}$, $t_y=0.4\,{\hbox {mm}}$, $t_z=-106.2\,{\hbox {mm}}$, $\alpha =179.8\,{^{\circ }}$, $\beta =0.8\,{^{\circ }}$, and $\gamma =1.3\,{^{\circ }}$.

5.2 Epipolar rectification

To efficiently reconstruct 3D points from two images that were acquired from two different perspectives, the images must be rectified by exploiting the epipolar geometry [27, Chapter 3.10.1.1]. This is typically done by perspectively transforming the images such that corresponding points occur in the same row of the rectified images. With this, the search space of the stereo matching can be reduced to a 1D search along an image row.

For the stereo setup of Fig. 9 with two opposing cameras, this rectification method would fail because the epipoles, which are the images of the entrance pupils, lie within the images. During the rectification, they would be transformed to infinity. Consequently, the rectified images would become infinitely large. Note that this problem is not a peculiarity of using hypercentric lenses. A similar problem arises, for example, when rectifying images that were obtained at two different points in time by a forward-moving camera (with a conventional lens). In this case, the epipoles also lie within the images. To handle this case, in [23] a method is proposed that rectifies the images onto a cylinder instead of a plane. In [22], a simpler method is proposed, which rectifies the images by using polar coordinates around the epipoles. The method is further improved in [20], where the images are first transformed by a homography before applying the polar transformation to reduce image distortions due to perspective effects. While these methods also would work for cameras with hypercentric lenses, the resulting perspective image distortions often prevent stereo matching algorithms from robustly establishing correspondences. Figure 11a, b shows two stereo images of the bottle of Fig. 1a acquired with the setup illustrated in Fig. 9. Figure 11c, d shows the rectified images when applying a rectification that uses polar coordinates around the epipoles similar to [22]. Note the different perspective distortions of several corresponding parts of both images. This causes problems during stereo matching. Further note that the homography approach of [20] tries to minimize perspective effects for a certain plane in 3D space. Therefore, applications in which cylindrical objects like the bottle in Fig. 1 must be inspected would only marginally benefit from this approach.

Fig. 11

a, b Stereo image pair. c, d Stereo image pair rectified with polar coordinates similar to [22]. According to the epipolar geometry, corresponding points are mapped to the same image row in both rectified images. However, many corresponding image parts show different perspective distortions in both rectified images, which causes problems during stereo matching. In d, the image was mirrored horizontally to obtain the same point order along corresponding image rows

Therefore, we propose a new approach to rectify stereo images of opposing cameras with hypercentric lenses. The approach is illustrated in Fig. 12. The basic idea is to minimize the perspective distortion differences of both rectified images for objects that are approximately cylindrical in shape. This is justified by the fact that with stereo setups similar to the one shown in Fig. 9, predominantly cylinder-like objects can be reconstructed.

Fig. 12

Stereo rectification for cameras with hypercentric lenses. a Points on the surface of a cylinder are sampled in an equidistant manner by sampling z with an equidistant step width and calculating the sampled points r along the ray within the center plane, i.e., within the xy plane of the center plane coordinate system (CPCS). The point ${\varvec{c}}$ denotes the origin of the CPCS in the coordinate system of camera 1. b Generation of half planes that are bounded by the base line. The orientation of a half plane is defined by the angle $\phi$ of its intersection with the xy plane and the x axis of the CPCS

In the first step, we define a new coordinate system, the center plane coordinate system (CPCS). The origin of the CPCS is the center point between the centers of the entrance pupils of both cameras. The z axis is collinear with the base line and oriented in the viewing direction of camera 1. Let ${{\mathbf {\mathtt{{R}}}}}$ and ${\varvec{t}}$ be the relative orientation between the two cameras that transform a point ${\varvec{p}}_2$ in camera 2 to a point ${\varvec{p}}_1$ in camera 1 by ${\varvec{p}}_1 = {{\mathbf {\mathtt{{R}}}}} {\varvec{p}}_2 + {\varvec{t}}$. Then, the center ${\varvec{c}}$ of the CPCS in the coordinate system of camera 1 is ${\varvec{c}}=\frac{1}{2}{\varvec{t}}$. The z axis of the CPCS in camera 1 is given by ${\varvec{z}}_\mathrm {c}={\varvec{c}}/\Vert {\varvec{c}}\Vert$. The rotation of the CPCS around its z axis can be chosen arbitrarily. We set the x axis of the CPCS to the projection of the x axis of camera 1 into the plane ${\varvec{z}}_\mathrm {c}=0$, i.e., $\tilde{{\varvec{x}}}_\mathrm {c}=(1-z_{\mathrm {c},x}^2,-z_{\mathrm {c},x} z_{\mathrm {c},y}, -z_{\mathrm {c},x} z_{\mathrm {c},z})^\top$. Thus, the x axis of the CPCS in the coordinate system of camera 1 is ${\varvec{x}}_\mathrm {c}=\tilde{{\varvec{x}}}_\mathrm {c}/\Vert \tilde{{\varvec{x}}}_\mathrm {c}\Vert$. Finally, the y axis of the CPCS in the coordinate system of camera 1 is obtained by the vector product ${\varvec{y}}_\mathrm {c} = {\varvec{z}}_\mathrm {c} \times {\varvec{x}}_\mathrm {c}$.

In the next step, we generate half planes that are bounded by the base line. The orientation of a half plane is defined by the angle $\phi$ of its intersection with the xy plane and the x axis of the CPCS (see Fig. 12b). By intersecting the half plane with the image planes, an oriented epipolar line is obtained in each image. Different epipolar lines are generated by sampling $\phi$ within the interval $[0,2\pi )$. To avoid border effects in window-based stereo matching approaches, the interval should be enlarged by half the window height in both directions and reduced to the interval $[0,2\pi )$ after the matching. To maintain the information content of the image, the step width $\varDelta \varphi$ of the sampling should be chosen such that $\varDelta \varphi$ approximately results in a 1 pixel displacement in the image corners.

In the final step, each epipolar line is sampled in the radial direction. The sampling is performed in the center plane along the ray that is obtained by intersecting the current half plane with the center plane. The resulting sampled 3D points are then projected into the images. To obtain similar perspective distortions in both rectified images, the sampling cannot be performed in an equidistant manner along the ray. Instead, we propose to sample the points such that the surface of a cylinder is sampled in an equidistant manner. The approach is illustrated in Fig. 12a. Let z be the distance of a point on the unit cylinder from the xy plane of the CPCS. When projecting the point into the xy plane, the distance r of the projected point from the origin of the CPCS is obtained by

$$\begin{aligned} r=\frac{\Vert {\varvec{c}}\Vert }{\Vert {\varvec{c}}\Vert -z}. \end{aligned}$$

(11)

Thus, an equidistant sampling on the cylinder surface is obtained by sampling z with an equidistant step width and calculating the sampled points along the ray according to (11). Minimum and maximum values for z can be obtained, for example, by restricting the image part that should be rectified to a circular ring around the principal point by specifying the minimum and maximum radius of that ring. Furthermore, the step width of the sampled z values should be chosen such that the information content in the rectified images is maintained. Note that the computation of r needs to be done only once because the sampling is the identical for all epipolar lines.

The resulting sampled points in the xy plane of the CPCS are projected into the images and the images are rectified accordingly. Figure 13 shows the result of the rectification. Note that the perspective distortions in corresponding image parts are more homogeneous compared to the result obtained with the approach of [22], which is shown in Fig. 11c, d.

Fig. 13

a, b Stereo image pair of Fig. 11a, b rectified with the proposed approach. According to the epipolar geometry, corresponding points are mapped to the same image row in both rectified images. Corresponding image parts show more homogeneous perspective distortion compared to the result obtained with an approach that uses polar coordinates shown in Fig. 11c, d. In d, the image was mirrored horizontally to obtain the same point order along corresponding image rows

Finally, the rectification mapping can be stored in a look-up table to efficiently rectify images that were taken with the same stereo setup.

Note that the proposed epipolar rectification is optimized for a stereo setup with two opposing cameras as shown in Fig. 9. It assumes that a standard disparity estimation method is used to establish correspondences between the two rectified stereo images. In this case, the proposed rectification provides more homogeneous perspective distortions for objects that are approximately oriented along the stereo base line. The rectification causes points to appear approximately independent of their distance from the camera in the rectified image. This results in a more robust disparity estimation compared to state-of-the art rectification that uses a simple polar transformation. It should be noted, however, that the proposed rectification is not restricted to cylindrical objects. Even for non-cylindrical surfaces, the proposed rectification will improve the disparity estimation compared to a polar transformation. Finally, we would like to point out that for stereo setups with hypercentric lenses and non-opposing cameras (i.e., cameras for which the angle between the viewing directions is typically smaller than 90 degrees), standard rectification methods can be applied, for example, [27, Chapter 3.10.1.4].

5.3 Stereo matching

The rectified images are used for efficient stereo matching. We compute the disparity image for the rectified image of Fig. 13a by applying the HALCON operator binocular_disparity_ms [19] and filling up holes in the disparity image by applying a harmonic interpolation with the HALCON operator harmonic_interpolation [19]. The resulting subpixel-precise disparity image is shown in Fig. 14a.

Fig. 14

a Subpixel-precise disparity image of the rectified image of Fig. 13a. b 3D stereo reconstruction with texture mapping

To evaluate the benefit of our proposed epipolar rectification of Sect. 5.2, we also applied the stereo matching to the images of Fig. 11c, d that were rectified by applying a polar transformation around the epipoles, similar to [22]. Furthermore, we applied a consistency check [27, Chapter 3.10.1.8] as follows: We computed the disparity not only from the first to the second rectified image but also from the second to the first image. The disparity value for a pixel was accepted as correct only if both directions resulted in the same value. For the images that were rectified by using the polar transformation, 25.1 % of the pixels passed the consistency check. For the images that were rectified by using our proposed method, 57.5 % of the pixels passed the consistency check. This clearly demonstrates the benefit of our proposed method, which results in a higher stereo matching robustness.

5.4 Stereo reconstruction

Based on the disparity image, we reconstruct the 3D geometry of the object. For each pixel in the first rectified image, the image coordinates in the original image are computed. Furthermore, for each pixel in the first rectified image, the corresponding point in the second rectified image is computed by adding the calculated disparity value of that pixel. For the corresponding point in the second rectified image, the image coordinates in the original image are computed. The computation of the original image coordinates can be done either analytically or by storing the original image coordinates for each pixel in the rectified images. In the latter case, the original image coordinates for the second image must be interpolated if the disparity values were computed with subpixel precision.

Two corresponding points in the original image planes with the two optical centers of the cameras define two optical rays. The reconstruction of the 3D position is obtained by intersecting the two optical rays in 3D space.

Figure 14b shows the result of the 3D stereo reconstruction. For visualization purposes, we mapped the gray values of the original images to the reconstructed 3D points. For each reconstructed 3D point, the gray value was selected from the image with higher local contrast.

6 Unwrapping of objects

Many machine vision inspection tasks can be simplified by unwrapping the images of cameras with hypercentric lenses. For example, if the text on the label of the bottle in Fig. 1 should be read by using OCR, the cylindrical surface of the text label should be unwrapped into a plane. To unwrap the cylindrical surface, it is necessary to know the pose of the cylinder with respect to the camera(s). In the following, we will describe two methods that can be used to determine the pose of the cylinder.

6.1 Unwrapping with a single camera

The first method uses the image of a single camera to estimate the pose of the cylinder and unwrap the image. The pose of a circle with respect to a calibrated camera can be determined from its perspective projection if the radius of the circle is known [21]. Therefore, to determine the pose of the cylinder, it is sufficient to determine the pose of one of its circular cross sections.

In the example of Fig. 1, we can easily determine the contour of the circular ground plane of the bottle in the image. For this, we extract the subpixel-accurate edge at the border of the imaged bottle [24, Chapter 3.3],  [25] and fit an ellipse to the extracted edges [7]. The fitted ellipse is shown in Fig. 15. Because we know the diameter of the bottle, we can use the approach of [21] to determine the pose of the circle with respect to the camera. From the perspective projection of a circle, the pose of the circle cannot be determined uniquely. Therefore, we obtain two possible circle poses. In our setup, the z axis of the camera was approximately parallel to the symmetry axis of the bottle. Therefore, we compute the angle of the normal vector of both circles with the z axis of the camera and select the circle pose with the smaller angle.

To improve the accuracy, we determine the pose of a second circle. For the second circle, we use the top planar part of the circular screw cap of the bottle, of which we also know the diameter. The fitted ellipse is also shown in Fig. 15. From the two possible circle poses, we again select the correct one as described above. Finally, the axis of the cylinder of the text label is obtained as the line defined by both 3D circle centers.

An alternative and more general way to resolve the ambiguity of the circle poses is to pair each of the two possible solutions of the first circle with each of the two possible solutions of the second circle. The two correct ones are characterized by being parallel.

Fig. 15

Two extracted ellipses (white) of the circular ground plane (large ellipse) and the circular screw cap (small ellipse) of the bottle that are used to determine the pose of the cylindrical surface of the text label

With the pose of the cylinder, the image of Fig. 15 can be unwrapped. The result is shown in Fig. 16.

Fig. 16

Result of the cylinder unwrapping of the image of Fig. 15 with a single camera

The proposed unwrapping of objects with a single camera assumes that the shape of the object is known precisely. Even though the object in the presented example was a cylinder, the unwrapping can be done with other developable surfaces as well (a cone, for example), as long as the pose of the object can be determined.

6.2 Unwrapping with a stereo camera setup

The second unwrapping method uses the two images of a stereo camera setup to estimate the pose of the cylinder and unwrap the image. In this case, we robustly fit a cylinder to the reconstructed 3D points that were obtained as described in Sect. 5.4: we minimize the sum of square distances of the points from the cylinder surface by using the Levenberg–Marquardt algorithm [11, Appendix A6]. Outliers in the reconstructed 3D points are suppressed by using the Tukey weight function [18]. Figure 17 shows the reconstructed 3D points with the fitted cylinder.

Fig. 17

Cylinder (dark gray) robustly fitted to the reconstructed 3D points

With the pose of the cylinder, the images of Fig. 11a, b can be unwrapped. The results are shown in Fig. 18.

Fig. 18

Result of the cylinder unwrapping of the images of Fig. 11a, b with a stereo camera setup

Fig. 19

a, b Stereo image pair of an AA alkaline battery. c, d Rectified stereo images. d, f Result of the unwrapping

For a second example, we applied our method to the stereo images of an AA alkaline battery with a height of about 50 mm and a diameter of about 14 mm (see Fig. 19). Again, we rectified the acquired stereo images, performed the 3D reconstruction, fitted a cylinder to the reconstructed points, and finally unwrapped the stereo images by using the cylinder pose.

Similar to the unwrapping with a single camera, also the proposed unwrapping with a stereo camera setup can be extended to other developable surfaces: If the true object shape is known (as in the example), the object pose might be obtained by fitting the shape to the reconstructed 3D points. In case of an unknown object shape, the surface of the object might be determined by triangulating the reconstructed 3D surface points, for example.

7 Conclusion

We have proposed a camera model for cameras with hypercentric lenses that is intuitive for the user. We showed that it is useful to assume a camera model that behaves identically to the model of an entocentric lens with respect to the camera coordinate system. In contrast to cameras with entocentric lenses, however, for hypercentric lenses the objects lie between the projection center and the image plane. Therefore, the z coordinates of objects in the camera coordinate system are negative. Furthermore, the principal distance c must be negative as well. We also showed how to calibrate cameras with hypercentric lenses by using a planar calibration object.

From the experiments, we can draw two important conclusions: First, the small RMS errors of the calibration indicate that our model is able to represent the geometry of a real hypercentric lens correctly.

Second, the resulting pose parameters are intuitive for the user and consistent with the real setup.

We also applied our camera model to two example applications: in the first application, we showed how two cameras with hypercentric lenses can be used for dense 3D reconstruction. For an efficient and robust reconstruction, we proposed a novel rectification method for objects that are approximately cylindrical in shape. In the second application, we showed how to unwrap cylindrical objects to simplify further inspection tasks. For this, we described two methods to determine the pose of the cylinder: based on a single camera image and based on two images of a stereo camera setup.

It is important to note that the camera model for hypercentric lenses that we proposed in Sect. 3 is general. The same holds for the calibration procedure that we proposed in Sect. 4, which is additionally general with regard to the number of cameras. Furthermore, it allows the calibration of a system of cameras with mixed lens types (hypercentric and entocentric, for example). In contrast, the epipolar rectification that we proposed in Sect. 5.2 is optimized for a stereo setup with two opposing hypercentric cameras as shown in Fig. 9.

The proposed camera model is available in the machine vision software HALCON, version 18.05 and higher [19].