1 Introduction

Depth cameras have multiple advantages compared to conventional 2D cameras in people detection and tracking applications. As stated in [12], depth is a powerful cue for foreground segmentation, 3D shape and metric observations simplify foreground object classification, occlusions can be detected and handled more explicitly, and the third dimension can be used for the prediction step in tracking. Shape matching-based detection may take the advantage of 3D information when evaluating the fitness of the model (e.g. [30]), and gradient-based methods become more robust as the depth image gradients depend only on scene geometry and not on texture properties (e.g. [23, 29]). Typically, depth cameras are based on active illumination, and thus, they are not as sensitive to changes in lighting conditions such as 2D cameras, and they can also operate in completely dark environments. An important advantage of using depth in people tracking is that depth-based systems are privacy preserving which can be a precondition for public installations.

Early depth-based people tracking systems used stereo [5] or time-of-flight (ToF) cameras [4] to generate disparity or depth maps from the scene. However, stereo imaging suffers partly from the same problems as 2D cameras, and the first ToF cameras were expensive and rather inaccurate for practical use in the people tracking context. Microsoft Kinect was the first commodity device with an accurate depth camera and an operation range suitable for people tracking applications. Since the Kinect device was released, several studies on depth-based and RGB-D (RGB and depth)-based people detection and tracking have been carried out (see [8] for a survey). Many works focus particularly on detection from the side view using template matching-based approaches (e.g. [15, 23, 29]). Such methods are beneficial for moving camera platforms such as mobile robots, but the drawback is that they are computationally intensive and cannot be efficiently used in embedded platforms. Additionally, they suffer from occlusions, and the camera position and orientation are restricted to certain views. Another common technique, especially for static camera installations, is the plan-view approach [12]. In the approach, the depth map is first transformed to a 3D point cloud in the camera coordinate system, which is rotated and rendered to generate a top-view height map or occupancy map of the scene [5, 12]. Assuming a static scene, people can be detected from the height or occupancy map, e.g. with local maxima search [31] or template matching techniques [26].

As depth cameras have limited range and field of view, multi-camera systems are used to enlarge the tracking volume. They also reduce occlusion-related problems in configurations where the cameras are installed at low angles and people occlude each other. In the first scenario, the cameras are typically installed so that their overlap is minimal or non-existent; and in the second scenario, the system takes the advantage of capturing the same scene from multiple views. Whether the goal is to fuse the original point clouds or pre-processed information such as people locations, the data must be aligned to a common coordinate system. Thus, the relative pose of the cameras and possibly the intrinsics (sensor and lens characteristics) has to be determined.

With 2D cameras, a common technique for multi-camera calibration is to use a known calibration target, such as a checkerboard plane, and capture multiple images of the target in different poses. The calibration routine estimates the parameters of the cameras by minimizing the total reprojection error of the detected checkerboard corners [32]. In [25], a laser pointer was used as a calibration target. Using 3D reconstruction techniques, the approach estimated the scene structure (laser pointer positions) and the camera parameters simultaneously. Similar techniques have also been proposed for RGB-D camera systems. For example, in [2, 19], a number of RGB and depth frames from a checkerboard plane were collected to solve the topology of the camera network and the initial poses of the cameras. Then, a global bundle adjustment routine minimizing the total reprojection error of the checkerboard corners and the corresponding errors in depth was used to refine the parameters. In [21], spherical calibration targets were used to calibrate the extrinsics (position and orientation) of multiple depth cameras. A globally optimal solution for both the centres of the spheres as well as for the camera parameters was found by minimizing the reprojection error of the spheres in depth images.

Manual calibration of a camera network is a tedious task, and in practical applications, auto-calibration methods are preferred. The goal of camera network auto-calibration is to automatically solve the network topology, the extrinsics and possibly the intrinsics of the cameras so that they can operate in a common coordinate system. It is a widely studied problem with 2D cameras (e.g. [28] reviews such methods), but only a few works address the problem with depth camera networks. The method presented in [27] employs the plan-view approach for depth-based people tracking. In the approach, the cameras are aligned to a common top-view coordinate system using pairwise affine transformations, and one large height map of the scene is constructed. The transformations are defined by matching the simultaneous observations of people, but it remains unclear how they are estimated in a multi-camera scenario. In [18], a method for registering two depth cameras without user input is presented. In the approach, the moving objects (people) are extracted from each camera with a depth histogram-based background subtraction, and the corresponding point cloud centroids are used with RANSAC (random sample consensus) to search for a rough estimate of the rigid transformation between the cameras. The result is refined with a grid-search-based optimization routine that optimizes transformation parameters as well as temporal differences (time synchronization) between the cameras. In the previous approaches, the cameras’ intrinsics are calibrated beforehand.

In this paper, we address the problem of calibrating depth camera networks such that the observations of different sensors are accurately aligned for data fusion and tracking. Our main contribution is an auto-calibration method for people tracking systems that utilize the plan-view approach. With the proposed method, the sensor network topology and the 2D transformations that map the sensor observations to the common coordinate system are solved automatically using observations from people as the only input. We also propose using thin-plate-spline (TPS) mappings to compensate for linear and nonlinear measurement errors directly in plan-view domain. We evaluate how different mappings perform, and experiment with rigid, similarity, affine, homography and TPS mappings. For the evaluation, we recorded several real-life data sets from four different depth camera configurations consisting of three to six cameras. We conducted multiple experiments to analyse the robustness, accuracy and precision of the method and compared the results to a checkerboard-based calibration method and to the ground truth data collected with a mobile robot.

Our approach has many benefits. It enables fast deployment of depth camera-based people tracking systems without the need of accurate pre-calibration of the intrinsics or manual calibration of the extrinsics. As the system is calibrated from the observations made of real people, neither special calibration targets nor manoeuvres are needed. The only requirements are that sensors have at least partial pairwise overlap, and form a connected graph. The method does not make any assumptions about the systematic measurement errors of the sensors, and it can be used with any kind of depth imaging device.

Fig. 1
figure 1

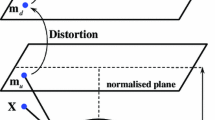
Overview of our people tracking system, relevant modules and coordinate transformations. Multiple nodes generate measurements in a 2D plan-view coordinate system that are sent to the centralized server for data fusion and tracking. The system calibration module takes a set of observations from different nodes as input, and outputs the transformations that align the observations to the common coordinate frame. Dashed arrows refer to inputs from another node. Symbols are as in the text

Full size image

2 Methods

2.1 System overview

Our people tracking system consists of multiple distributed depth camera nodes and a centralized server. The nodes are responsible for detecting people in their own plan-view coordinate system, whereas the server maps the observations to a global coordinate frame, performs data fusion and constructs the spatio-temporal tracks for each person visible in one or more cameras. We assume that the camera views are partly overlapping, and that they form a connected graph. The cameras can be installed at any angle or height.

We use low-cost ARM-based single-board PCs as embedded computing platforms, therefore lightweight depth processing methods are desirable. We employ the plan-view approach with background subtraction to detect people from the depth frames. In the approach, captured depth frames are first converted to 3D point clouds which are then rotated to top-view perspective. A height map image is created from the rotated point cloud, and the people are detected with local maxima search. The observations are transformed back to the plan-view domain (the 2D metric coordinate system of the floor plane), and sent to the server. We call the pose parameters (orientation, height) of the cameras the local extrinsics, and the mappings that transform the observations to a global frame as the global extrinsics of the sensors. The camera focal length, principal point, lens model parameters and depth distortion parameters are called the intrinsic parameters or the intrinsics. Figure 1 shows the different modules, transformations and relations of the system.

Accurate mapping of sensor observations to global coordinate system is crucial for successful data association, data fusion as well as for track management. Inaccurate extrinsics and intrinsics, and depth measurement distortions cause systematic errors in the observations, and they must be taken into account when transforming them to the global frame. We use the factory calibration for the intrinsics and do not model the depth distortions explicitly. Instead, we use mappings that have more degrees of freedom than the rigid transformation to translate and rotate the points, and to compensate the linear and nonlinear measurement errors as well. Thus, we avoid calibrating the cameras beforehand but still obtain accurate alignment of the observations from different nodes.

The local extrinsics are defined in the nodes, either automatically or using external information about the camera’s orientation and height. The (distorted) observations are transformed to the global frame on the server side, which holds the mappings (global extrinsics) for each node. The mapping calibration routine is performed offline using recorded observations. The method first uses a RANSAC-based method for finding the connected sensor pairs and their relative 2D rigid transformations in the plan-view domain. We construct a graph from the pairwise mappings where the nodes represent the global extrinsics of the sensors and the edges represent their connectivity. We transform the observations to the global coordinate frame, and similarly to 3D bundle adjustment methods [11]; we refine the mapping parameters and the positions of the observations using a global optimization routine. Finally, we re-estimate the local extrinsics with mappings that have more degrees of freedom compared to the rigid transformations and use the optimized observation positions as calibration target.

2.2 Plan-view transformation of depth maps

We make the conversion from the depth images to 3D point clouds using the standard pinhole camera model. Given a (non-homogeneous) 3D point \({\mathbf {X}}=(X,Y,Z)^\top \) in the camera coordinate frame, its projection to the image plane is defined by the camera intrinsics and the perspective projection: \({\mathbf {u}}=(f_u\frac{X}{Z}+c_u, f_v\frac{Y}{Z}+c_v)^\top \), where \(f_u\) and \(f_v\) are the camera focal lengths in horizontal and vertical dimensions, and \((c_u,c_v)^\top \) is the principal point. Accordingly, given a depth image pixel \({\mathbf {u}}=(u,v)^\top \), the corresponding 3D point at depth d is \((d(u-c_u)/f_u, d(v-c_v)/f_v, d)^\top \). A \(3\times 3\) matrix containing the camera intrinsics is denoted with \(\mathbf {K}\). We ignore the lens and depth distortion from the camera model and use the default factory calibration for the rest of the intrinsics.

The plan-view coordinate transformation is done by rotating the original point cloud with the camera orientation matrix \(\mathbf {R}\) so that the floor plane becomes parallel to the depth image plane, and its distance from the camera origin equals the camera height. The resulting point cloud is rendered to a height map image using an orthographic projection, which transforms the points to height map image pixels coordinates. The point depths are subtracted from the camera height h, such that the floor level equals zero and the targets’ heights appear as positive pixel values in the resulting height map image. A height map pixel is represented as a homogeneous 2.5D point \({}^{\mathcal {H}}{}{\mathbf {U}}\). The transformation of a homogeneous 2.5D point \({}^{\mathcal {D}}{}{\mathbf {U}} = ({d}u, {d}v, d, 1)^\top \) that corresponds to a depth image pixel at position \(\mathbf {u}=(u,v)^\top \) and to a depth value d can be expressed as

(1)

where \(\mathbf {P}\) combines the orthogonal projection and the transformation to the height map image domain, s is the side length of the height map image (in pixels), \(x_0\) and \(y_0\) are the minimum x and y values of the top-view point cloud, and \(\Delta x\) and \(\Delta y\) are the ranges of the point cloud in x and y dimensions. In the above-mentioned, the height map image is assumed to be square, and the x and y dimensions are scaled with similar scale factor.

Fig. 2
figure 2

Illustration of the measurement errors of a depth sensor from the top-view perspective. Black circles refer to paper cones with a radius of 10 cm and a height of 50 cm from the floor. Red dots refer to measurements of the cones in two experiments: a the sensor set to a height of 25 cm and directed towards the cones, b the sensor set to a height of 2 m with an approximate pitch angle of 30 degrees downwards. The cameras are located at the origin. The units of the plots are in metres

Full size image

2.3 Mapping observations to global frame

With ideal depth camera intrinsics and local extrinsics, the transformation of the depth image pixels to the plan-view domain is distortion free, and the observations from different sensors are accurately aligned with rigid 2D transformations. Denoting a sensor measurement in the plan-view domain with a homogeneous 2D point \({}^{\mathcal {C}}{}{{\mathbf {x}}}=({}^{\mathcal {C}}{}{x}, {}^{\mathcal {C}}{}{y}, 1)^{\top }\), the transformation to the global frame is defined by a \(3\times 3\) matrix \(\mathbf {M}_{\text {R}}\):

$$\begin{aligned} {}^{\mathcal {G}}{}{{\mathbf {x}}}= \mathbf {M}_{\text {R}} {}^{\mathcal {C}}{}{{\mathbf {x}}}, \end{aligned}$$
(2)

where prescripts \(\mathcal {G}\) and \(\mathcal {C}\) refer to the global and the local (plan-view) coordinate systems, respectively.

However, inaccurate intrinsics and local extrinsics, lens distortions and depth measurement errors introduce both linear and nonlinear errors, and a rigid mapping does not transform the points correctly. Figure 2 illustrates the problem. It shows two top-view images rendered from the depth maps that were captured from multiple paper cones placed on the floor. In the first image, the camera was parallel to the floor and directed perpendicularly to the cones. In the second image, the camera was raised and angled downwards. Both images show errors in scale, shear, projective errors as well as complex nonlinear errors.

Several depth camera models and calibration methods have been proposed that take into account the depth distortions (e.g. [3, 13]). However, as our goal is to avoid explicit camera modelling and a manual pre-calibration step, we compensate for the errors directly in the plan-view domain by including an error model to the global extrinsics. For linear errors, we use rigid, similarity, affine and homography transformations, and replace \(\mathbf {M}_{\text {R}}\) in Eq. 2 with a corresponding \(3\times 3\) transformation matrix. Although the previous mappings can be solved with linear methods [11], we estimate them using a nonlinear optimization routine and minimize the point transfer error:

$$\begin{aligned} \mathop {{{\,\mathrm{arg\,min}\,}}}\limits _{ \mathbf {M} } \left\{ \sum _{i=1}^{n} \rho d\left( {}^{\mathcal {G}}{}{\hat{\mathbf {x}}}_{i}, \mathbf {M} {}^{\mathcal {C}}{}{{\mathbf {x}}_{i}} \right) ^2 \right\} , \end{aligned}$$
(3)

where \(\mathbf {M}\) is any of the previous mappings, \({}^{\mathcal {G}}{}{\hat{\mathbf {x}}}_{i}\) are the known reference points, \({}^{\mathcal {C}}{}{{\mathbf {x}}_{i}}\) are the corresponding sensor measurements and \(d(\cdot ,\cdot )\) is the Euclidean distance between the points. As an initial guess for \(\mathbf {M}\), we use the rigid transformation \(\mathbf {M}_\text {R}\). The optimization problem is made more robust by using by a loss function \(\rho \), for which we use Huber loss. To compensate linear and nonlinear errors, we use thin-plate spline (TPS) mappings [6], which we briefly review here. The TPS mappings have been widely used in image warping, and also to model the distortions of depth cameras [3]. They produce smooth spatial mappings by minimizing the approximate curvature

$$\begin{aligned} I= \int \int \left[ \left( \frac{\partial ^2f}{\partial x^2}\right) ^2 + 2\left( \frac{\partial ^2f}{\partial x \partial y}\right) ^2 + \left( \frac{\partial ^2f}{\partial y^2}\right) ^2 \right] \hbox {d}x \hbox {d}y. \end{aligned}$$
(4)

The TPS is an \(\mathbb {R}^2 \rightarrow \mathbb {R}\) mapping that consists of an affine part and a nonlinear part defined by the TPS kernel \(\phi \). For a set of p control points \((c_{xi}, c_{yi})\), \(i=1, \ldots , p\) and associated weights \((w_1, w_2, \ldots , w_p)\), the TPS maps a point (x, y) as

$$\begin{aligned} f (x,y) = a_x x + a_y y + a_0 + \sum _{i=1}^{p} w_i \phi (r_i), \end{aligned}$$
(5)

where \(r_i=\Vert (c_{xi}, c_{yi}) - (x,y) \Vert \) and \(\phi (r)=r^2 \, \text {log} \, r\), and where the affine part is defined by \(a_x\), \(a_y\) and \(a_0\). To construct an \(\mathbb {R}^2 \rightarrow \mathbb {R}^2\) TPS warp, two TPS mappings sharing the common control points \(\mathbf {c}_i = (c_{xi},c_{yi},1)^{\top }\) sampled from \({}^{\mathcal {G}}{}{\hat{\mathbf {x}}}_{i}\) are used, and the transformation of Eq. 2 can be written as

$$\begin{aligned} {}^{\mathcal {G}}{}{{\mathbf {x}}}= \mathbf {M}_{\mathtt {A}} {}^{\mathcal {C}}{}{{\mathbf {x}}} + \mathbf {W} \varPhi \left( {}^{\mathcal {C}}{}{{\mathbf {x}}}\right) , \end{aligned}$$
(6)

where \(\mathbf {W}\) is a \(3 \times p\) matrix of column vectors \(\mathbf {w}_i=(w_{xi}, w_{yi}, 0)^\top \) (\(w_{xi}\) and \(w_{yi}\) being the weights in x and y dimensions), and

$$\begin{aligned} \varPhi ({\mathbf {x}})=(\phi _1({\mathbf {x}}),\phi _2({\mathbf {x}}),\ldots ,\phi _p({\mathbf {x}}))^{\top } \end{aligned}$$

with

$$\begin{aligned} \phi _i({\mathbf {x}})=d({\mathbf {x}}, {\mathbf {c}}_i)^2\log (d({\mathbf {x}},{\mathbf {c}}_i)). \end{aligned}$$

Thus, the complete TPS has \(2\times (3+p)\) parameters.

For Eq. 4 to have a square integrable second derivatives, the TPS has the following constraints

$$\begin{aligned} \sum _{i=1}^{p} w_i = 0,\quad \sum _{i=1}^{p} w_i c_{xi} = 0 \quad \text {and}\quad \sum _{i=1}^{p} w_i c_{yi} = 0, \end{aligned}$$
(7)

and a linear system for solving the coefficients of the TPS can be constructed:

(8)

where \(\mathbf {K}_{ij}=\phi (\Vert (c_{xi},c_{yi}) - (c_{xj},c_{yj}) \Vert )\), the ith row of \(\mathbf {P}\) is \((c_{xi}, c_{yi}, 1)\), \(\mathbf {w}=(w_1, w_2, \ldots , w_p )^\top \) and \(\mathbf {a}=(a_x, a_y, a_0)^\top \). A regularization parameter \(\lambda \) is added to the system to smooth the mapping in noisy circumstances. With \(\lambda = 0\), the interpolation is exact, and the larger the value, the smoother the mapping. In practice, \(\lambda \) is incorporated into the system by replacing the matrix \(\mathbf {K}\) with \(\mathbf {K} + \lambda \mathbf {I}\), where \(\mathbf {I}\) is a \(p\times p\) identity matrix. We used a normalized value for \(\lambda \) and a scale factor of 1 as described in [10]. To reduce the computational burden, we avoid using all of the target points as control points for the TPS. Instead, we sample the control points from \({}^{\mathcal {G}}{}{\hat{\mathbf {x}}}_{i}\) using a 50 mm Euclidean distance threshold.

2.4 Initial calibration of the sensor network

The sensor network topology and the initial pairwise mappings between the sensors are solved using a RANSAC-based method. The first step is to find a set of point correspondences \(S= \{ \mathbf {x}_i \leftrightarrow \{ \mathbf {x}'_j \} \} \) between the measurements of the first sensor and the second sensor. For each measurement \(\mathbf {x}_i\), we search for a set of putative point correspondences L using the temporal proximity of the measurements as matching criteria. A point \(\mathbf {x}'_j\) is added to L if the absolute difference between the timestamps of \(\mathbf {x}_i\) and \(\mathbf {x}'_j\) is less than a predefined limit (0.1 s in our experiments). From L, we search for clusters of spatially close observations, and from each cluster we save only the element with the smallest absolute time difference. With this approach, we avoid associating \(\mathbf {x}_i\) to multiple measurements of the same person within the current time interval. On the other hand, the sensors do not necessarily observe the same persons, and thus, there may be multiple actual correspondences for each \(\mathbf {x}_i\). We use a distance of 500 mm to cluster the observations belonging to L.

The initial pairwise mappings are estimated using RANSAC. For each iteration, we sample three point pairs from S, and estimate the rigid 2D transformation \( \hat{\mathbf {M}}_{\text {R}} \) between the point sets. Using \( \hat{\mathbf {M}}_{\text {R}} \), we transform the points \(\{ \mathbf {x}'_j \}\) to the first sensor’s coordinate frame, and count the number of inliers, i.e. the points with a transfer error less than a predefined limit (300 mm in experiment 1 and 500 mm in experiments 2 and 3, see Sect. 3.2). If the inlier count is larger than a predefined threshold, we re-estimate \( \hat{\mathbf {M}}_{\text {R}} \) using all the inliers and re-calculate the number of inliers as to evaluate the fitness of the model. A larger number of inliers do not necessarily correlate with a better model, since it does not take into account the possibility of invalid matches that may occur if the sensors have seen different targets simultaneously. Therefore, each time the second inlier count increases, we calculate an additional score and accept the improvement in the model only if the additional score has increased as well.

The additional score is based on the assumption that the people which move in the overlapping area of a sensor pair are visible to both sensors. For the score, we calculate the convex hull of all measurements for each sensor, and find the intersection. Then, the score is computed by calculating the ratio of inliers that belong to the intersection versus the number of all point pairs that belong to the intersection. The score could be evaluated in each RANSAC iteration, but we found it too slow for practical applications. Thus, we calculate the number of inliers first, and whenever it has increased, we calculate the additional score. In our experiments, it was approximately 100 times slower to evaluate the additional score compared to the plain inlier test. Figure 3 illustrates the approach. Given a confidence level, the number of iterations needed to obtain the correct model can be estimated using the standard method. For example, assuming that 5% of the point correspondences are inliers, approximately \( n=\frac{\log (1-0.99)}{\log (1-0.05^3)} \approx 37{,}000 \) iterations are required to find the correct mapping with a confidence level of 99%.

Fig. 3
figure 3

Finding the initial pairwise mappings with a RANSAC-based procedure: a an initial set of point correspondences between the measurements of the first sensor (solid dots) and the measurements of the second sensor (open dots) are searched based on their temporal proximity (dashed lines). The candidates are spatially clustered (ellipses), and from each cluster, the measurement with the smallest time difference is saved (solid lines). b At each RANSAC iteration, the measurements and the view (dashed rectangle) of the second sensor are transformed to the first sensor’s coordinate system using the current transformation hypothesis. The intersection of the sensor views is calculated (grey area), and the fitness of the model is evaluated by calculating the ratio of the inliers to the number of all point pairs that belong to the intersection. c The result from another iteration round. In contrast to b, there is only one outlier that belongs to the intersection, and the transformation hypothesis is given a higher score

Full size image

The number of inliers and the additional score can be used to determine which sensor pairs observe a common area, and thus are connected. In our experiments, we construct a two-element vector for each sensor pair consisting of the normalized number of inliers and the additional score. We use the k-means algorithm to classify the sensor pairs into groups of connected and disconnected pairs. To normalize the number of inliers, we divide the value with the area of the intersection.

From the connectivity information and the estimated pairwise mappings, we construct a graph where the vertices represent the sensors (the rigid transformations from the sensors’ coordinate system to the global coordinate system), and the edges represent their connectivity. As we construct the graph, we select one of the sensors as the base sensor, and find the shortest paths from that one to each of the other sensors. For each sensor, we find the transformation that maps the sensor measurements to the base sensor’s coordinate system by traversing the graph and combining the transformations at each node. The transformation of the base sensor is set to identity.

Our initial calibration method has some similarities with [24], which focused on estimating pairwise homographies and connectivity information in 2D camera networks. To constrain the homography estimation, the method used a guided sampling of temporally matched trajectories. The candidate homographies were given a score based on the number of inliers, and the homography with the highest score was used to validate the connectivity. A score similar to ours and a fixed threshold were used in the validation step. In contrast to the method, we do not make any assumptions about the observations in sampling and treat them equally. We include the validation step to the RANSAC loop which increases the likelihood for obtaining the correct mapping. Finally, we employ both the number of inliers and the additional score for determining the connectivity which yields more robust results.

2.5 Global optimization of the parameters

Lastly, we refine the initial global extrinsics with a global optimization routine. Similar to 3D bundle adjustment approaches [11], we not only optimize the mapping parameters (cameras in bundle adjustment) but the structure (i.e. the target positions in the global frame) as well. Thus, the goal is to find the estimates for the target positions and for the global extrinsics that minimize the global transfer error. Denoting the (homogeneous) 2D target points in the global frame with \( {}^{\mathcal {G}}{}{\hat{\mathbf {x}}_i}\), and the corresponding observations made by sensor j with \({}^{\mathcal {C}}{}{\mathbf {x}}^j_i\), the solution is obtained by solving the following minimization problem

(9)

where \(\mathbf {M}^j_{\text {R}}\) is the rigid transformation of the jth sensor and v(i, j) is an indicator function that has value 1 if the point i has been measured by the jth sensor, and 0 otherwise. The measurements \({}^{\mathcal {C}}{}{\mathbf {x}}^j_i \) are the inliers resulting from the RANSAC method. Additionally, we complement the original inlier set with the points that have a larger transfer error (500 mm in experiment 1 and 2000 mm in experiments 2 and 3, see Sect. 3.2), and thus obtain more points for the optimization. We initialize the points \({}^{\mathcal {G}}{}{\hat{\mathbf {x}}_i}\) by transforming the measurements \({}^{\mathcal {C}}{}{\mathbf {x}}^j_i\) to the base sensor’s coordinate system using the initial global extrinsics and calculating the average position of the transformed points. The influence of outliers is reduced by using a loss function \(\rho \), for which we use Huber loss. We solve the system using the Levenberg–Marquardt algorithm.

3 Experiments

3.1 System implementation

3.1.1 System set-up

In our people tracking system, the depth processing nodes are built upon Utilite PCs with ARM Cortex-A9 processors running at 1 GHz with 2 GB of RAM. We use Asus Xtion structured light depth cameras to obtain depth frames from the scene. The software is implemented in C++, and we use integer arithmetic and pre-calculated lookup tables whenever possible to speed up the processing time. The nodes are synchronized with the network time protocol (NTP), and the data is sent via the user datagram protocol (UDP) to the server. The data processing in nodes is single threaded so that one processing step from capturing a depth frame to sending the observations to the server takes less than 40 ms, and a frame rate of 25–30 FPS is achieved.

For the experiments, we recorded depth video sequences at a frame rate of 30 Hz and with a resolution of \(320\times 240\) pixels. We processed the depth frames offline using a standard laptop PC and the same depth processing pipeline implementation we used in the nodes. The calibration method was implemented in C++ with OpenCV [7] and Boost [22] libraries, and the nonlinear optimization problems were modelled and solved with the Ceres solver [1].

3.1.2 Detecting people from height maps

To detect people from depth frames, we use background subtraction which we apply in the height map domain. Depth cameras do not produce a uniform response from different types of surfaces and materials, and objects may appear noisy, contain holes and parts of them may flicker between consecutive frames. Thus, the distribution of height map pixel values in the background is bimodal, consisting of zero values (no depth observed) and values from the actual background. Although memory efficient and fast to compute, simple recursive filters are not optimal with bimodal distributions.

In our model, we maintain two buffers for each height map pixel: a short-term buffer and a long-term buffer. Both buffers have a length of five samples. We store the latest five pixel values in the short-term buffer. Once a predefined time interval \(\Delta t\) has elapsed, we update the oldest value of the long-term buffer with the maximum value of the short-term buffer. The background model is also updated by taking the median value of the long-term buffer. Thus, the update rate of the background model is determined by \(\Delta t\). In our experiments, we used a short 10 s value for \(\Delta t\).

Fig. 4
figure 4

The camera configurations 1–3 and their view frustums illustrated from the top-view perspective. a The configuration 1 included six cameras attached to the ceiling in a grid, and directed downwards. b The configuration 2 included four cameras aligned pairwise in parallel. The camera pairs were directed to the opposite sides of the space with a downward pitch angle of approximately 30 degrees. c The configuration 3 was similar to the configuration 2, but the cameras were placed in the corners of the area and directed to the centre. In each plot, the solid black line refers to the ground truth trajectory visible to any of the cameras. In b, c, the dashed triangles refer to the cameras’ position and field of view. In a, there are a total of 15 possible sensor pair combinations in which 3 are horizontally connected (aligned in x-axis), 4 vertically connected, 4 diagonally connected and 4 disconnected. The tick marks are in 2 m intervals

Full size image

The foreground image is extracted from the background model in a pixel-wise manner. Given a height map pixel value h and a corresponding background pixel value b, the resulting foreground height map is determined as follows:

$$\begin{aligned} h = {\left\{ \begin{array}{ll} h &{} \quad \text {if} \quad h \ge b+t \\ 0 &{} \quad \text {otherwise} \end{array}\right. }, \end{aligned}$$
(10)

where t is a threshold margin (300 mm in our experiments). To remove speckle noise from the foreground, we apply a 2D median filter with a kernel size of \(5 \times 5\) pixels.

We detect people from the foreground height map image by searching for local maxima with a search radius of approximately 40 cm. In our implementation, we divide the height map image into square windows of equal size, find local maxima from each window and store them in a list of candidates. For non-maxima suppression, we first sort the candidate list in ascending order by height. Then, we iterate through the list and compare each candidate with the remaining candidates. If the Euclidean distance between the candidate pair is less than the search radius, we remove the current candidate. The remaining list contains the observations of people. Finally, the observations are converted from the height map domain back to the plan-view domain.

For the experiments, we prune spatially redundant observations by binning them into equally spaced \(100\times 100\) mm bins, and keeping only the first values of each bin. This introduces a quantization error; however, it is relatively small compared to the noise level and depth quantization errors of the cameras that are used in our implementation.

3.1.3 Determining the plan-view transformation parameters

When floor pixels are visible, the cameras’ local extrinsics can be obtained from the depth images. We assume that the cameras are installed such that their roll angles are zero, and that they are rotated around their lateral (pitch) axes only. Thus, the raw disparity map pixels that correspond to the floor plane can be detected using the v-disparity image technique [17]. From the depth image pixels that correspond to the floor, we determine the normal vector of the floor plane in the camera’s coordinate system. The normal vector is used to construct the local extrinsic’s rotation matrix \(\mathbf {R}\), as well as the camera height h from the floor. As there may be several planes parallel to the ground plane in the scene (e.g. tables), we select the plane that is lowest. To populate the entries of matrix \(\mathbf {P}\) in Eq. 1, we first create a point cloud that we transform with \(\mathbf {R}\), and then search for the values \(x_0\), \(y_0\), \(\Delta x\) and \(\Delta y\). We use a size of \(200\times 200\) pixels for the height map image.

3.2 Data sets

To evaluate the proposed method, we collected multiple data sets from three different sites and four camera configurations: Metro station entrance, Cafeteria 1 and 2, and Room. For Metro station entrance and Cafeteria configurations, we recorded two data sets: one using a mobile robot as the only visible target, and one from daily use with multiple people moving in the environment. For room configuration, we recorded a mobile robot run, and a set of RGB images to be used for the checkerboard-based calibration. For the robot data sets, we also recorded the ground truth trajectories. The data were collected as raw depth frames at a frame rate of 30 Hz and with a frame resolution of \(320\times 240\) pixels. Although we processed the frames offline using a standard laptop PC, we used the exact same implementation that is used for real-time operation on the depth camera nodes. Figure 4 illustrates the camera configurations 1–3 and the corresponding ground truth trajectories. The details of each configuration are presented below.

3.2.1 Ground truth from robot measurements

To collect ground truth observations, we attached a Styrofoam ball of 40 cm diameter to a mobile robot. The ball was installed at a height of 150 cm using a white plastic pipe. To obtain ideal data, we manually cleaned the robot observations of false positives and turned off the spatial pruning of observations. The robot was remotely controlled, and it was driven at a constant speed of 0.5 m/s. To determine the ground truth position, the robot was equipped with wheel odometry and a Hokyo UTM-30LX scanning range finder providing data with a 40 Hz scan rate. First, an occupancy grid map was created with [16]. After that, the robot pose was estimated using the adaptive Monte Carlo localization (AMCL) [14] with initial position set manually. Both algorithms are available in [20].

3.2.2 Configuration 1: Metro station entrance

The first configuration consisted of six cameras that were attached to the ceiling of a metro station entrance and directed downwards. The installation height of the cameras was 6.5 m, and the floor area covered by the cameras was approximately 140 \(\text {m}^2\). The cameras were organized in a grid of 3 rows and 2 columns, and the overlap of the camera frustums was from 0.5 to 1 m at the floor level. The spacing between the cameras varied from 4 to 6 m. The real-life data set was acquired over 30 min. After spatial pruning and temporal matching the observations between the camera pairs, the remaining number of observations varied from 184 to 709 (mean 464) per sensor, and the total number of individual observations (i.e. the points \( {}^{\mathcal {G}}{}{\hat{\mathbf {x}}_i}\) in Eq. 9) was 1334. The robot data had 501–1028 observations per sensor (mean 706) and 1971 individual targets. The real-life data had 172 TPS control points, the robot data 146 and the ground truth data 530. Figure 4 also illustrates the vertically, horizontally and diagonally connected sensor pairs that we refer to in the later sections of this paper. The main direction of the traffic was along the vertically connected sensors (along the y-axis in Fig. 4).

3.2.3 Configuration 2: Cafeteria 1

The second camera configuration consisted of four cameras which were attached to the walls of a cafeteria of approximately \(10\times 12\) m. The cameras were aligned pairwise on opposite sides of the area such that the distance between the camera pair was 1.5 m, and their optical axes were parallel. The cameras were installed at a height of 2.3 m, and aimed downwards at approximately 30 degrees. The site had multiple tables limiting the free movement of people, and the tables were moved to collect the robot data. The real-life data set was acquired over 60 min. After spatial pruning and temporal matching the observations between the camera pairs, the remaining number of observations varied from 1329 to 1578 (mean 1406) per sensor, and the total number of individual observations was 2315. The robot data had 3006–3874 observations per sensor (mean 3438), and 5718 individual targets. The real-life data had 1242 TPS control points, the robot data 1057 and the ground truth data 1356.

3.2.4 Configuration 3: Cafeteria 2

The third configuration was similar to the second, but we moved the cameras to the corners of the cafeteria and directed them towards the centre. The real-life data set was acquired over 60 min. After spatial pruning and temporal matching the observations between the camera pairs, the remaining number of observations varied from 1578 to 1831 (mean 1689) per sensor, and the total number of individual observations was 2761. The robot data had from 3922 to 5325 observations per sensor (mean 4259), and 6975 individual targets. The real-life data had 1247 TPS control points, the robot data 1155 and the ground truth data 1262.

3.2.5 Configuration 4: Room

In the fourth configuration, three cameras were installed to the ceiling of an empty room of size \(7.5 \times 4.0\) m. The installation height of the cameras was 2.6 m, and the angle approximately 25 degrees downwards. The cameras were set to three corners of the room, and aimed so that the longer sides of the room were completely covered by the cameras. For the data set, the robot was driven along a \(4 \times 7\) grid path spanning the room completely. After the pruning, the data from different sensors contained from 832 to 1057 observations. In contrast to the other data sets, the outliers (mainly false positives due to noise) were not removed from the data. In the experiments, we used a threshold of 2000 mm for the outliers.

3.3 Evaluation procedures

3.3.1 Initial calibration

In the first set of experiments, the goal was to evaluate the robustness of the RANSAC-based method to find the initial pairwise mappings, and thus the ability of the method to find the network topology. We used configuration 1 for the experiments, as it had both connected and disconnected sensor pairs. We randomly selected 5, 10 and 30 min sequences from the data set and ran the method for 5000, 20,000 and 50,000 iterations. Each experiment was repeated 20 times. For each experiment, we stored the global extrinsic matrix, the number of inliers, the area of the overlap between the sensor views and the quality score defined in Sect. 2.4. For each pairwise mapping, we defined a two-element feature vector consisting of the number of inliers relative to the overlap area, and the mapping quality score. Then, we applied the k-means algorithm on the feature vectors to classify the mappings in two groups: connected and disconnected sensor pairs. Finally, we compared the classification results to the ground truth.

There are two types of errors that can occur during the classification procedure: a disconnected sensor pair may be classified as connected (we call this error type A) and a connected pair may be classified as disconnected (error type B). Error type A is critical since it can lead to a wrong network topology, and the people tracking becomes unpredictable. Error type B is less severe. In the case of such error, an edge is absent from the graph, and depending on the network topology, it may be compensated by traversing the graph along another path. A typical example of such a scenario is when two sensors have a large overlap and a third sensor has a small overlap with the first sensor and a large overlap with the second sensor. The first and third sensors may be classified as disconnected, but a path can still be constructed via the second sensor. From the classification results, we calculated the number of times error types A and B occurred.

To evaluate the precision of the initial pairwise mappings, we calculated the standard deviations of rotation angles between the mappings and the absolute differences between the smallest and largest angles. Additionally, we created histograms of the angle deviations. We analysed the horizontally, vertically and diagonally connected sensor pairs separately.

3.3.2 Experiments with different mappings

The goal of the second set of experiments was to compare and analyse how different mappings perform with the proposed auto-calibration method, and to compare our approach to typical checkerboard-based calibration method. In experiments 1–4, we first evaluated how the mappings compensate for systematic errors in the ideal case and calibrated the system using the ground truth as reference data. Then, we applied the auto-calibration method and calibrated the system using first robot data and second real-life data, and compared the results to both the ground truth and the estimated robot trajectory. In experiment 5, we calibrated the camera system using a planar checkerboard-based method and used the results in our system for the evaluation. The details of the experiments are presented below.

  • Experiment 1 The sensors were calibrated using the ground truth data points as calibration targets and sensor observations as input. Similarity, affine and homography transformations were obtained by solving Eq. 3, using the rigid transformations \(\mathbf {M}_{\text {R}}\) as initial estimates. The TPS mapping was solved using Eq. 8. The goal of the experiment was to analyse how different mappings compensate for systematic errors. The sensor observations were transformed using the estimated mappings, and the accuracy and precision of the transformed points relative to the ground truth were computed.

  • Experiment 2 The sensors were calibrated using the auto-calibration method and the robot data as input. The results were evaluated by transforming the sensor observations to the common coordinate frame using the estimated mappings, and comparing the transformed observations to the ground truth. A similarity transformation between the common coordinate frame of the sensors and the coordinate frame of the ground truth was applied before comparison. The goal of the experiment was to analyse the absolute performance of the auto-calibration method compared to the ground truth.

  • Experiment 3 The sensors were calibrated as in experiment 2. The results were evaluated by transforming the sensor observations to the common coordinate frame using the estimated mappings, and comparing the transformed observations to the estimated robot trajectory (\({}^{\mathcal {G}}{}{\hat{\mathbf {x}}_i}\) in Eq. 9). To make the results comparable with experiments 1 and 2, the errors were scaled with the scale factor of the similarity transformation solved in experiment 2. The goal of the experiment was to evaluate how precisely the observations from different nodes can be aligned in a common coordinate system, which is crucial in data association and tracking tasks.

  • Experiment 4 The sensors were calibrated using the auto-calibration method and the real data as input. The results were evaluated as in experiment 3. The goal of the experiment was to evaluate how precisely the observations from different nodes can be aligned in a common coordinate system using real-life data as input.

  • Experiment 5 The goal of the experiment was to compare our method to conventional planar checkerboard-based calibration approach. One of the sensors was selected as a base sensor, and the transformations between the base sensor and the other sensors were estimated using OpenCV’s stereo calibration routine [7]. The coordinate transformation between the floor plane and the base sensor was estimated by placing the checkerboard calibration target to several positions on the floor, and computing the average camera height and pitch and roll angles from corresponding images. The calibration was conducted from the RGB images of the sensors using the resolution of \(1280 \times 960\) pixels. The intrinsics and lens distortions of the RGB cameras were calibrated beforehand. The factory settings for both depth sensor intrinsics and the coordinate transformations between the depth cameras and the RGB cameras were used. For the calibration, a \(4 \times 5\) checkerboard target with the square size of 14 cm was used. The resulting camera poses were decomposed to local and global extrinsics to be used in our system. For the evaluation, the observations were first transformed to common coordinate frame by using the checkerboard-based calibration, and then, the results were transformed to robot coordinate frame by using the rigid and the similarity mappings.

For each experiment, we calculated the mean absolute errors and the standard deviations relative to the reference data (ground truth in experiments 1, 2 and 5, and reconstructed robot trajectory in experiments 3 and 4). As the errors are not Gaussian, we also estimated their distributions using the kernel density estimation (KDE) method, and calculated the 75% and 90% confidence regions of the error distributions (experiments 1–4). Finally, we calculated the ratio of observations with transfer error less than 40 cm of the reference data (experiments 1–4).

Table 1 The number of horizontally and vertically connected camera pairs classified as disconnected (error type B), and their relative ratio to ground truth in parentheses (\({n}=140\) for each experiment)
Full size table
Fig. 5
figure 5

An example of clustering the initial pairwise mappings. (a) The ground truth clusters. Red crosses are the disconnected sensors, blue crosses are the horizontally or vertically connected sensors, and black circles are the diagonally connected sensors. The x-axis is the normalized inlier count, and the y-axis is the score defined in Sect. 2.4. (b) The result of clustering with the k-means algorithm. Red crosses are the sensor pairs classified as disconnected, and blue crosses are the sensor pairs classified as connected. The coordinate axes are the same as in plot (a)

Full size image

4 Results

4.1 Initial calibration

Table 1 shows the number of horizontally and vertically connected sensor pairs that were erroneously classified as disconnected (error type B). Due to very small overlap between the sensor views, the diagonally connected pairs were typically classified as disconnected. To emphasize the results for adequate sensor overlaps, we omit the diagonally connected pairs from the table. The ratio of erroneously classified results to the ground truth varies from 2.9 to 13.6% in different experiments. Typically, best results were obtained with 50,000 iterations, but the results were very similar to those with 20,000 iterations. The sequence length did not notably affect the results.

Table 2 Robustness and accuracy of the initial calibration
Full size table
Fig. 6
figure 6

Deviations of the rotation angles of the initial pairwise rigid transformations. a Horizontally connected sensor pairs, b vertically connected sensor pairs, c diagonally connected sensor pairs. In a, b the histogram bin size is 2 degrees and in c the histogram bin size is 5 degrees. In b, the smallest values are found in the \({-}\) 10 degrees bin. See Table 2 for the actual range

Full size image
Table 3 Mean absolute errors and standard deviations (in parentheses) for the experiments evaluating different mappings
Full size table
Fig. 7
figure 7

The error distributions of the sensor observations transformed to the global frame and compared to the ground truth for experiment 1. The error distributions were estimated using the KDE method. The outer contours refer to the 90% confidence region and the inner to the 75% confidence region. The units are in metres

Full size image

Whenever the sensor pairs were correctly classified as connected, the estimated mappings were typically correct as well. The success ratio was 100% for the horizontally and vertically connected pairs, and it failed 2 times out of 145 with the diagonally connected pairs. The method is also robust to error type A. In the experiments, the disconnected sensor pairs were only classified as connected 4 times out of 360 (2 disconnected pairs, 9 experiments and 20 runs each). All errors occurred with the 5 min sequence: once with 5000 iterations, once with 20,000 iterations, and twice with 50,000 iterations.

Figure 5 shows an example of the classification results for an experiment with a 30 min data set and 50,000 iterations. The disconnected sensor pairs form a relatively tight cluster in the scatter plot, whereas the connected pairs are more widely spread. However, the two clusters are easy to separate with the k-means clustering algorithm. As stated above, the diagonally connected pairs are typically classified as non-overlapping pairs (error type B).

To evaluate the precision of the initial calibration routine, we calculated the standard deviations of the rotation angles of the pairwise rigid transformations. Table 2 shows that for the horizontally connected pairs, the standard deviation was smallest at 1.2 degrees. For the vertically connected pairs, the standard deviation was 2.7 degrees and for the diagonally connected pairs, it was 13.4 degrees. Table 2 also shows the number of correctly classified sensor pairs and the maximum absolute differences between the rotation angles. Figure 6 shows the distributions of the angle deviations as histograms. The horizontally connected sensor pairs had most of their values within \({\pm }\,2\) degrees, and the distribution is quite symmetric. The vertically connected pairs had most of their values within 2–4 degrees, and the distribution is skewed to the left. The diagonally connected pairs had no clear peak, and the distribution had no clear shape.

Table 4 The share of transformed observations with an absolute error less than 40 cm compared to the reference data
Full size table
Fig. 8
figure 8

The error distributions of the sensor observations transformed to the common coordinate frame and compared to the estimated robot trajectory for experiment 3. The error distributions were estimated using the KDE method. The outer contours refer to the 90% confidence region and the inner to the 75% confidence region. The units are in metres

Full size image
Fig. 9
figure 9

Plan-view plots of the transformed points in experiment 1 (left column), in experiment 2 (middle column) and in experiment 3 (right column). The top row plots were generated using configuration 1, the middle row using configuration 2, and the bottom row using configuration 3. Yellow dots are reference points: ground truth in experiments 1 and 2, and the estimated robot trajectory in experiment 3. Dark blue dots are observations mapped using the rigid transformation, light blue using the affine transformation and orange using the TPS. The tick marks represent 2-metre intervals (color figure online)

Full size image

4.2 Experiments with different mappings

The results of experiments 1–5 are shown in Table 3. The table contains the mean absolute errors and the standard deviations of the sensor measurements transformed to the global frame using the estimated mappings and compared to the reference data (the ground truth in experiments 1, 2 and 5, and the estimated robot trajectories in experiments 3 and 4).

In experiment 1, using configuration 1, the TPS had a mean error of 0.113 m and a standard deviation of 0.064 m. The homography, affine and similarity transformations had slightly larger errors: 0.156, 0.160 and 0.167 m, respectively, and a standard deviation of 0.080 m. The rigid transformation had an average error of 0.405 m and a standard deviation of 0.245 m. Using configurations 2 and 3, the errors for the TPS were similar, but for the homography, affine and similarity transformations the errors increased from approximately 50–80 mm. For the rigid transformation, the errors increased more: 0.169 m using configuration 2, and 0.232 m using configuration 3. Using configuration 4, the errors for the TPS slightly increased, probably due to the outliers that were not removed from the data.

In experiment 2, the results for all the mappings were quite similar using configuration 1, but different using configurations 2 and 3. Using configuration 2, the errors were in the range of 0.248 m (the TPS) to 0.344 m (the rigid transformation), and the standard deviations were approximately 0.2 m. Using configuration 3, the errors were in the range of 0.186 (TPS) to 0.339 m (rigid transformation). The results for the configuration 4 were near similar.

In experiment 3, the TPS had the smallest errors: 0.062 m using configuration 1, 0.092 m using configuration 2 and 0.102 m using configuration 3. As in experiments 1 and 2, the rigid mapping had the largest errors, which varied from 0.114 m using configuration 1 to 0.282 m using configuration 3. The standard deviations varied similarly. For the TPS, the standard deviations ranged from 0.046 m using configuration 1 to 0.076 using configuration 3, and for the rigid transformation from 0.087 m using configuration 1 to 0.170 using configuration 3. As in experiments 1 and 2, the results for the other mappings were between the results of the TPS and the rigid transformation. The results for experiment 4 behaved similarly to experiment 3, but were slightly larger in general.

In experiment 5, the observations were first transformed to common coordinate frame using the results from the checkerboard-based calibration, and then to the robot coordinate system using rigid and similarity mappings. Table 3 shows that with the rigid mapping, the results are in line with experiment 1. Due to depth measurement errors, inaccurate (factory) intrinsics and depth-RGB calibration, the checkerboard-based calibration does dot properly align the observations from different sensors. The final mean absolute differences to ground truth were 0.638 m for the rigid mapping and 0.533 m for the similarity mapping.

Figures 7 and 8 visualize the error distributions of experiments 1 and 3 using the KDE method. The plots show that using the TPS, approximately 90% of the transformed measurements were within \({\pm }\, 0.25 \) m of the reference points (ground truth in experiment 1 and reconstructed trajectories in experiment 3). Using the other mappings, the errors were similar or slightly more spread using configuration 1 and larger using configuration 2 and 3. Also, using configurations 2 and 3, the shapes of the distributions were less symmetric in both the x and y dimensions for mappings other than TPS.

Table 4 shows the ratio of transformed observations with an absolute error less than 40 cm. Although the quantity does not separate the noise from the systematic errors, the table shows that errors decreased with mappings that have more degrees of freedom, and that TPS outperformed other mappings in 11 out of 12 cases. For experiment 1, the results of the TPS varied from 99.5 to 99.9%, the homography transformation from 85.8 to 99.8%, the affine transformation from 85.3 to 99.7%, the similarity transformation from 84.3 to 99.6% and the rigid transformation from 38.7 to 54.4%. The values for experiment 2 were lower, and, e.g. using the TPS, they varied from 85.1 to 95.6%. However, the exception is the rigid transformation as it had better results for experiment 2. In experiment 3, TPS had similar results compared to experiment 1. The results were better with the other mappings. In general, the results of experiment 4 were a few percentage points lower compared to the results of experiment 3.

Figure 9 illustrates the results from the top-view perspective. In the plots, the sensors’ observations are mapped to the global coordinate system using the rigid, affine and TPS transformations. The reference points are included as well. Plots (a), (d) and (g) show the results of experiment 1. Due to measurement errors, the rigid transformations could not accurately align the observations with the ground truth. The affine transformation performed well using configuration 1, but using configurations 2 and 3, it suffered from nonlinear measurements errors. The TPS compensated for the errors in all cases, and the observations were accurately aligned with the ground truth. Plots (b), (e) and (h) show the results of experiment 2. All the mappings performed relatively well using configuration 1. The distortions of configurations 2 and 3 were worse, and none of the mappings could accurately align the observations with the ground truth. Plots (c), (f) and (i) show the results of experiment 3. The experiment shows that although the resulting mappings do not accurately align the measurements with the ground truth, the results are precise, and the observations from different nodes are aligned with each other.

5 Discussion and conclusion

We proposed an auto-calibration method for embedded depth camera networks using the plan-view approach for people tracking applications. The method enables fast installation of such systems as it automatically solves both the network topology and the transformations that map the sensor measurements to a common coordinate system. The approach is able to compensate for not only linear errors that originate from inaccurate intrinsics and local extrinsics, but nonlinear errors caused by lens distortions and depth measurement errors as well. The method is suitable for sensor networks which have both small and large pairwise camera overlaps.

We evaluated the method using Asus Xtion depth cameras. Since the method does not make any assumptions about how the depth data are generated, it can be used with other kinds of depth imaging devices. We used a simple and fast people detection algorithm based on background subtraction and local maxima search, but naturally the proposed approach can be used with any other people detection method as long as the observations are made in or converted to the plan-view domain.

To our knowledge, there are no prior studies that report solving the depth camera network topology and estimating the sensors’ extrinsics simultaneously. Previous approaches apply affine transformations to align the observations from different sensors, which are not able to compensate for nonlinear errors. Our experiments show that homography and TPS mappings, especially, outperform the affine transformations in terms of accuracy and precision when aligning observations from multiple nodes. Other prior auto-calibration methods for depth camera networks aim to find full rigid 6-DoF transformations between the cameras, and assume that the cameras’ intrinsics, lenses and depth distortions are modelled and calibrated beforehand.

Compared to conventional planar checkerboard-based calibration routine, our method has several advantages. The checkerboard calibration target has to be visible to two or more sensors simultaneously which limits how the cameras can be configured to the scene, especially when the angle between the optical axes of the cameras is large. Without careful pre-calibration of the depth sensors’ intrinsics and depth distortions, the checkerboard-based methods are likely to suffer from misalignment errors. In our experiments, we used factory settings for the depth camera intrinsics and depth-RGB calibration, and the checkerboard-based calibration method was not able to deliver satisfactory results. In [19], a post-processing method for refining the checkerboard-based calibration was proposed. In the approach, it was assumed that one person only is moving in front of the cameras, and its average trajectory was used as a reference target in the refinement process. In contrast to our method, the procedure does not compensate for nonlinear depth measurement distortions.

Depending on the input data and the size of the camera overlap, RANSAC-based matching may lead to missed or false initial pairwise sensor mappings. We search for point correspondences between sensor pairs based only on their temporal proximity, and in some configurations the solution may not be unique. Thus, the robustness of finding initial pairwise mappings could be improved by using other metrics for the observations as well. Examples are geometric features such as size or shape of the target, dynamic features such as speed, or image-based properties such as texture or intensity histogram of the infra-red image typically available from depth sensors. Including additional features would enable using variants of RANSAC such as PROSAC (progressive sample consensus) [9] for faster and more reliable convergence.

Since we do not make any assumptions about the targets’ movement or depth camera characteristics, the measurement errors are accumulated in the reconstructed trajectories. Thus, although the alignment of measurements from different sensors is precise, they may not accurately align with the ground truth. We suspect that results with less distortion could be obtained by assuming, e.g. straight trajectories for moving people and including the trajectory parameters and the TPS mapping parameters into the global optimization routine.