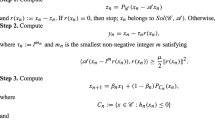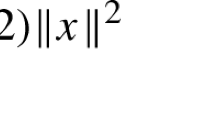Skip to main content
SpringerLink
Log in

Analysis of the generalized total least squares problemAX≈B when some columns ofA are free of error

  • Published:
Numerische Mathematik Aims and scope Submit manuscript

Summary

This paper studies the algebraic properties and perturbation theory of the generalized total least squares problem (GTLS)AX≈B in whichA =(A 1,A 2),A 1 is free of error, and the error contained in (A 2,B) is of the formEC withC a given nonsingular matrix. The problem was proposed by Van Huffel and Vandewalle in [15]. The solvability conditions, formulas for the GTLS solutions, their residuals, and the minimum norm correction matrices are obtained, and a perturbation theory for the GTLS problem is given.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Demmel, J.W. (1987): The smallest perturbation of a submatrix which lowers the rank and a constrained total least squares problem. SIAM J. Numer. Anal.24, 199–206

    Google Scholar 

  2. De Moor, B., Golub, G.H. (1991): The restricted singular value decomposition: properties and applications. SIAM J. Matrix Anal. Appl.12, 401–425

    Google Scholar 

  3. Gallo, P.P. (1982): Consistency of regression estimates when some variables are subject to error. Commun. Stat. Theory Methods11, 973–983

    Google Scholar 

  4. Golub, G.H., Van Loan, C.F. (1980): An analysis of the total least squares problem. SIAM J. Numer. Anal.17, 883–893

    Google Scholar 

  5. Golub, G.H., Van Loan, C.F. (1989): Matrix computations 2nd Edn., The Johns Hopkins University Press, Baltimore

    Google Scholar 

  6. Golub, G.H., Hoffman, A., Stewart, G.W. (1987): A generalization of the Eckart-Young-Mirsky matrix approximation theory. Linear Algebra Appl.88–89, 317–327

    Google Scholar 

  7. Horn, R.A., Johnson, C.A. (1985): Matrix analysis. Cambridge University Press, Cambridge

    Google Scholar 

  8. Lawson, C.L., Hanson, R.J. (1974): Sovling least squares problems. Prentice-Hall, Englewood, Cliffs, NJ

    Google Scholar 

  9. Paige, C.C. (1986): Computing the generalized singular value decomposition. SIAM J. Sci. Stat. Comput.7, 1126–1146

    Google Scholar 

  10. Paige, C.C., Saunders, M.A. (1981): Towards a generalized singular value decomposition. SIAM J. Numer. Anal.18, 398–405

    Google Scholar 

  11. Paige, C.C., Wei, M.: Ranks of submatrices of a matrix and its inverse (submitted for publication)

  12. Pearson, K. (1901): On lines and planes of closest fit to points in space. Philos. Mag.2, 559–572

    Google Scholar 

  13. Sprent, P. (1969): Models in regression and related topics. Methuen, London

    Google Scholar 

  14. Van Huffel, S. (1987): Analysis of the total least squares problem and its use in parameter estimation. Ph.D. Thesis, Department Elect. Eng., Katholieke University Leuven, Belgium

    Google Scholar 

  15. Van Huffel, S., Vandewalle, J. (1989): Analysis and properties of the generalized total least squares problemAX≈B when some or all columns inA are subject to error. SIAM J. Matrix Anal. Appl.10, 294–315

    Google Scholar 

  16. Van Huffel, S., Vandewalle, J. (1991): The total least squares problem: computational aspects and analysis. SIAM, Philadelphia

    Google Scholar 

  17. Van Huffel, S., Zha, H. (1991): Restricted total least squares problem: formulation, algorithm, and properties. SIAM J. Matrix Anal. Appl.12, 292–309

    Google Scholar 

  18. Van Loan, C.F. (1976): Generalizing the singular value decomposition. SIAM J. Numer. Anal.13, 76–83

    Google Scholar 

  19. Watson, G.A. (1988): The smallest perturbation of a submatrix which lowers the rank of the matrix. IMA J. Numer. Anal.8, 295–303

    Google Scholar 

  20. Wei, M. (1992): The analysis for the total least squares problem, with more than one solution. SIAM J. Matrix. Anal. Appl.13, 746–763

    Google Scholar 

  21. Wei, M. (1992): Algebraic relations between the total least squares and least squares problems with more than one solution. Numer. Math.62, 123–148

    Google Scholar 

  22. Wei, M., Majda, G.: On the accuracy of the least squares and the total least squares methods. Math. Comput. (to appear)

  23. Zha, H. (1991): Restricted singular value decomposition of matrix triples. SIAM J. Matrix Anal. Appl.12, 172–194

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Computer Science, McGill University, H3A 2A7, Montreal, Quebec, Canada

    Christopher C. Paige

  2. Department of Mathematics, East China Normal University, 200062, Shanghai, China

    Musheng Wei

Authors
  1. Christopher C. Paige
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Musheng Wei
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

This author was supported by NSERC of Canada Grant No. A9236

This author was supported by the National Natural Sciences Foundation, P.R. China. This work was carried out when this author was visiting the School of Computer Science. McGill University, Montreal, Quebec, Canada

Rights and permissions

Reprints and permissions

About this article

Cite this article

Paige, C.C., Wei, M. Analysis of the generalized total least squares problemAX≈B when some columns ofA are free of error. Numer. Math. 65, 177–202 (1993). https://doi.org/10.1007/BF01385747

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF01385747

Mathematics Subject Classification (1991)

Search

Navigation