Pulse-Detonation Hydrojet

Abstract

Geometrical configuration and operational parameters of a valveless pulse-detonation hydrojet have been determined based on extensive numerical simulations using 2D two-phase flow equations. The theoretical propulsive performance of such a hydrojet in terms of the specific impulse was shown to be on the level of modern liquid propellant rocket engines and amount 350–400 s. Based on the results of numerical simulation a valveless pulse-detonation hydrojet operating on liquid hydrocarbon fuel (regular gasoline) and gaseous oxygen has been designed and fabricated. For firing the hydrojet, a special test rig with flowing water was designed and assembled. Experiments showed that the measured values of the specific impulse varied within the range from 255 to 370 s which overlaps the theoretical range, thus demonstrating the predictive capabilities of the numerical approach.

Introduction

In our patent [4] and articles [1,2,3] we suggested to replace conventional screw propellers used in boats and ships by a pulse-detonation hydrojet. Such a propulsion device is composed of a pulse-detonation tube inserted in a properly shaped water guide submerged in water. The detonation tube is cyclically filled with a fuel mixture which is cyclically ignited to generate a detonation wave. High-momentum detonation (shock) wave enters cyclically a water guide and involves bubbly water therein in accelerated motion toward the exit nozzle due to increased compressibility of water saturated with gas bubbles of a previous operation cycle. The objective of this communication is to investigate possible geometrical configurations and operational parameters of such a hydrojet and to assess its propulsive performance using both numerical simulation and experiments.

Numerical Simulation

Below we consider bubbly liquid that consists of two phases, namely, dispersed gas phase (subscript 1) whose volume fraction is α₁ and carrier liquid phase (subscript 2) with volume fraction α₂. The following simplifying assumptions are adopted: (1) gas compressed in a bubbly liquid is not dissolved in the liquid while the liquid is not evaporated inside bubbles; (2) the liquid phase density depends solely on the liquid temperature T₂; (3) flow of the bubbly liquid is laminar; (4) effects of gravity, lifting and friction forces at bounding surfaces on the relative phase motion in a bubbly liquid are ignored.

The mathematical model of the two-phase flow is based on partial differential equations of mass, momentum, and energy conservation derived within the framework of mutually penetrating continua [5, 6]:

$$\frac{{\partial \alpha_{i} \rho_{i} }}{\partial t} + \nabla \cdot \alpha_{i} \rho_{i} {\mathbf{v}}_{i} = 0$$

$$\frac{{\partial \alpha_{i} \rho_{i} {\mathbf{v}}_{i} }}{\partial t} + \nabla \cdot \alpha_{i} \rho_{i} {\mathbf{v}}_{i} {\mathbf{v}}_{i} = - \alpha_{i} \nabla p_{i} + \nabla \cdot \alpha_{i} \tau_{i} + {\mathbf{M}}_{ij}$$

(1)

$$\frac{{\partial \alpha_{i} \rho_{i} h_{i} }}{\partial t} + \nabla \cdot \alpha_{i} \rho_{i} \text{v}_{i} h_{i} = \nabla \cdot \alpha_{i} \text{q}_{i} + \nabla \cdot \alpha_{i} \tau_{i} \cdot \text{v}_{i} + \alpha_{i} \frac{{\partial p_{i} }}{\partial t} + \text{H}_{ij} ,$$

where $t$ is the time, i and j are the indices of phases, $\nabla$ is the differential operator with respect to radius vector ${\mathbf{r}}$, $\rho_{{}}$ is the phase density, ${\mathbf{v}}$ is the phase velocity vector, $p_{{}}$ is the phase pressure, ${\varvec{\uptau}}$ is the phase tensor of viscous stress, ${\mathbf{q}}$ is the phase heat flux, terms ${\mathbf{M}}_{ij}$ and $\text{H}_{ij}$ describe the interphase momentum and energy exchange, respectively, $h_{{}}$ is the phase total enthalpy given by

$$h_{i} = h_{i,0} + \int\limits_{{T_{i,0} }}^{{T_{i} }} {c_{p,i} \;dT} + \frac{1}{2}{\mathbf{v}}_{i} {\mathbf{v}}_{i} .$$

(2)

here, $c_{p,i}$ is the phase specific heat at constant pressure, $T$ is the phase temperature, and index 0 denotes the initial values of variables.

The set of Eqs. (1), (2) is supplemented with the relationships for fluxes ${\varvec{\uptau}}_{i}$, ${\mathbf{q}}_{i}$, ${\mathbf{M}}_{ij}$, and $\text{H}_{ij}$:

$${\varvec{\uptau}}_{i} = \mu_{i} \left[ {\left( {\nabla {\mathbf{v}}_{i} + \nabla {\mathbf{v}}_{i}^{T} } \right) - \frac{2}{3}\nabla \cdot {\mathbf{v}}_{i} } \right]$$

$${\mathbf{q}}_{i} = \frac{{\kappa_{i} }}{{c_{p,i} }}\nabla h_{i}$$

$${\mathbf{M}}_{12} = C_{D} \frac{{A\rho_{2} \;\left| {{\mathbf{v}}_{12} } \right|{\mathbf{v}}_{12} }}{8};\;{\mathbf{M}}_{21} = - {\mathbf{M}}_{12}$$

$$\text{H}_{12} = Nu\frac{{\kappa_{2} A(T_{1} - T_{2} )}}{{d_{1} }};\;\text{H}_{21} = - \text{H}_{12}$$

where $\mu_{{}}$ is the phase dynamic viscosity, $\kappa_{{}}$ is the phase thermal conductivity, ${\mathbf{v}}_{12} = {\mathbf{v}}_{1} - {\mathbf{v}}_{2}$ is the relative velocity of phases, $d_{1}$ is the bubble diameter, $A = \frac{{6\alpha_{1} }}{{d_{1} }}$ is the total interphase surface area in a unit volume of bubbly liquid, $C_{D}$ and $Nu$ are the hydrodynamic drag coefficient and Nusselt number, which in general depend on Reynolds number of relative motion of phases $\text{Re}_{12} = \frac{{\rho_{2} \text{v}_{12} d_{1} }}{{\mu_{2} }}$ and liquid Prandtl number $\Pr_{2} = \frac{{c_{p,2} \mu_{2} }}{{\kappa_{2} }}$[6]:

$$C_{D} = \hbox{min} \left[ {\frac{24}{{\text{Re}_{12} }}(1 + 0.15\text{Re}_{12}^{0.687} ),\frac{72}{{\text{Re}_{12} }}} \right]$$

$$Nu = 2 + 0.6\text{Re}_{12}^{0.5} \Pr\nolimits_{2}^{0.33} .$$

The set of Eqs. (1) and (2) and supplementary relationships for fluxes contain 12 dependent variables $\alpha_{1}$, $\alpha_{2}$, $\rho_{1}$, $\rho_{2}$, ${\mathbf{v}}_{1}$, ${\mathbf{v}}_{2}$, $p_{1}$, $p_{2}$, $h_{1}$, $h_{2}$, $T_{1}$, and $T_{2}$. To close the statement of the problem we add four more relationships:

$$\rho_{2} = \rho_{2} (T_{2} );\,\alpha_{2} = 1 - \alpha_{1} ;\,p_{1} = \rho_{1} RT_{1} ;\,p_{2} = p_{1} .$$

(3)

The resultant equations are also supplemented by initial and boundary conditions for the listed variables and their derivatives.

In [3], we carried out an a priori analysis of stability of Eqs. (1) for isothermal case with nonzero fluxes. It has been proven that allowance for momentum fluxes (${\varvec{\uptau}}_{1}$, ${\varvec{\uptau}}_{2}$) within phases at $p_{2} = p_{1}$ makes the evolution problem well-posed.

The multi-phase balance Eqs. (1) can be expressed for every phase k = 1, 2 in the form of a general differential equation for the mean flow variable $\phi_{k}$(x, t) which reads

$$\underbrace {{\frac{{\partial \alpha_{k} \rho_{k} \phi_{k} }}{\partial t}}}_{R} + \underbrace {{\nabla \cdot \alpha_{k} \rho_{k} {\mathbf{v}}_{k} \phi_{k} }}_{C} - \underbrace {{\nabla \cdot \alpha_{k} \Gamma_{\phi \,k} \nabla \phi_{k} }}_{D} = \underbrace {{\nabla \cdot \alpha_{k} {\mathbf{S}}_{\phi \,k}^{A} + S_{\phi \,k}^{V} }}_{S} \, .$$

(4)

The term R on the left-hand side denotes the rate of change of the transported quantity $\phi_{k}$. The term C stands for the convective transport rate, D represents the diffusive transport, where $\Gamma_{\phi \,k}$ stands for the diffusion coefficient, and S on the right-hand side denotes the specific sources or sinks of $\phi_{k}$. The latter term consists of the volumetric term $S_{\phi k}^{V}$ and the surface term $\nabla \cdot \alpha_{k} S_{\phi \,k}^{A}$ accounting for the diffusion flux, which is not included in the diffusion flux in D. The interphase exchange terms, M ₁₂ and H ₁₂ in Eq. (1), are part of the volumetric source $S_{\phi \,k}^{V}$.

After applying the Gauss theorem for a grid cell P surrounded by its neighbors P _j , and with the outward surface (cell–face) vectors A, the discretized control volume equation can be written as

$$\begin{aligned} \underbrace {{\frac{\text{d}}{{\text{d}t}}\left( {\alpha_{k} \rho_{k} \phi_{k} \, V_{{\text{cel}}} } \right)_{P} }}_{R} + \sum\limits_{f = 1}^{{n_{f} }} {\underbrace {{\left( {\alpha_{k} \rho_{k} {\mathbf{v}}_{k} {\mathbf{A}}\phi_{k} } \right)_{f} }}_{{C_{f} }}} - \sum\limits_{f = 1}^{{n_{f} }} {\underbrace {{\left( {\alpha_{k} \Gamma_{\phi \,k} \nabla \phi_{k} {\mathbf{A}}} \right)_{f} }}_{{D_{f} }}} & = \\ & \sum\limits_{f = 1}^{{n_{f} }} {\underbrace {{\left( {\alpha_{k} {\mathbf{S}}_{\phi \,k}^{A} {\mathbf{A}}} \right)_{f} }}_{{S_{\phi }^{A} }}} + \underbrace {{\left( {S_{\phi \,k}^{V} V_{{\text{cel}}} } \right)_{P} }}_{{S_{\phi }^{V} }}, \\ \end{aligned}$$

(5)

where subscript P denotes the cell-center and f face-center values; C _f and D _f are the convective and diffusion transport through face f, respectively; n _f is the number of cell faces surrounding grid cell P, and V _cel is the cell volume. It is assumed that P is bounded by piecewise smooth surfaces. All dependent variables, such as volume fraction, density, velocity, pressure, and enthalpy, are evaluated at the cell center. The cell–face-based connectivity and interpolation practices for gradients and cell–face values are introduced to accommodate an arbitrary number of cell faces. A second-order midpoint rule is used for integral approximation and a second-order linear approximation for any value at the cell face. The cell gradients can be calculated by using either the Gauss theorem or a linear least-square approach. The convection is solved by an upwind scheme. The time derivative R is discretized by the implicit first-order accurate Euler (two levels) scheme.

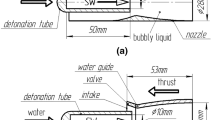
Figure 1 shows the schematic of the valveless pulse-detonation hydrojet comprising a detonation channel 1 of 20 mm high and 400 mm long and a shaped water guide 2 of length 600 mm and width 80 mm with intake 3 and nozzle 4. This hydrojet configuration was obtained as a result of extensive parametric study.

Fig. 1

Schematic of a pulse-detonation hydrojet: 1—detonation tube, 2—water guide, 3—intake, 4—nozzle

Figure 2 shows a two-dimensional (2D) computational domain (CD) of dimensions 430 x 1950 x 1 mm with adopted boundary conditions. Initially, the flow everywhere in the CD except for the interior of the detonation tube is the homogeneous flow of bubbly water with low gas volume fraction ($\alpha_{1} = 10^{ - 2}$). The detonation tube with one closed (left) and one open (right) ends is initially filled with a quiescent fuel—air mixture at pressure 0.1 MPa and temperature 293 K. At the inlet (left boundary of CD), the mass flow rate of water equal to 2.33 kg/s is set to simulate the homogeneous approach stream velocity of 5 m/s. At the upper boundary of CD, a constant pressure of 0.1 MPa is fixed. At the outlet (right boundary of CD), the Dirichlet boundary conditions with constant pressure (0.1 MPa) are adopted. At the symmetry plane (lower boundary of CD), zero gradients normal to the boundary are set. At the rigid walls of the hydrojet the velocity nonslip conditions are adopted.

Fig. 2

Computational domain: 1—water inlet, 2—symmetry plane, 3, 4—constant pressure boundaries

Once started, the calculation is continued until a steady-state flow is established in the entire CD including the inner flow in the water guide. Thereafter, the first detonation pulse is triggered in the detonation tube by temporarily applying a proper value of the mass flow rate (0.03 kg/s) of detonation products with the Chapman–Jouguet temperature of 2500 K at its left end to obtain a detonation wave propagating at a constant velocity of about 1700 m/s along the tube. After the detonation wave travels along the detonation tube for 0.3 ms approaching the right (open) end of the tube, the left inlet boundary is instantaneously replaced by a rigid wall, thus generating a rarefaction wave running toward the open end. When the detonation wave reaches gas–water interface it is partly reflected from it and partly transmitted through it into the compressible bubbly water as a shock wave. Further flow dynamics includes the propagation of the transmitted shock wave through the nozzle accompanied by shock-induced acceleration of water towards the nozzle exit, followed by the expansion of a cloud of hot gaseous detonation products in the water guide. After complex wave—water flow interactions inside the water guide—the cloud of gas detonation products is separated from the detonation tube exit and is convected downstream in the nozzle and outside. At this instant, the left boundary of the detonation tube is instantaneously replaced by the inlet boundary to fill the tube with fresh fuel mixture at a proper mass flow rate and to start the next operation cycle. Contrary to the first cycle, in all subsequent cycles a detonation wave, when reaching the gas–water interface, is transmitted into the bubbly water with bubbles of gaseous detonation products of the previous operation cycle.

Figure 3 shows the snapshots of one operation cycle of the pulse-detonation hydrojet, where white color corresponds to “pure” water ($\alpha_{1} = 10^{ - 2}$) and black color corresponds to “pure” detonation products ($\alpha_{2} = 10^{ - 6}$). Clearly, the first and the last snapshots are quite similar to each other thus representing the repetitive initial conditions for subsequent cycles at overall operating frequency of 9–10 Hz.

Fig. 3

Spatial and temporal evolution of gas volume fraction in one operation cycle of the pulse-detonation hydrojet

Figure 4 shows the calculated time history of the instantaneous force F (N/m in 2D geometry) acting on all internal rigid walls of the hydrojet in seven successive operation cycles. Clearly, after three initial transient cycles the operation process becomes nearly periodic: the last four cycles are well reproducible and show a positive mean force acting on the hydrojet (the force is directed against the approaching water stream). The peak positive force attains 20 kN/m. One can distinguish three main stages of force development in each cycle: the first stage with a peak positive force caused by pressure rise in the detonation tube followed by a peak negative force caused by reflection of the shock wave from the contracting portion of the water guide nozzle; the second relatively long stage of shock wave propagation in the diverging part of the nozzle followed by extension of the gas cloud therein with positive force; and the third stage with negative force during which a new portion of water fills the water guide. The theoretical specific impulse $I_{\text{sp,calc}}$ (dimension in s) defined as the integral-mean force $\overline{F}_{\text{calc}}$ (N/m) in Fig. 4 divided by the mass flow rate of fuel mixture $\dot{m}$ (kg/(m·s) in 2D geometry) and acceleration of gravity, g (m/s²),

$$I_{\text{sp,calc}} = \overline{F}_{\text{calc}} /\dot{m}g$$

Fig. 4

Time history of instantaneous force acting on the pulse-detonation hydrojet in seven successive cycles

is equal to 350–400s. This means that the valveless pulse-detonation hydrojet of the considered design is capable of producing a positive thrust with a specific impulse on the level of modern liquid propellant rocket engines.

Experimental Studies

Based on the results of numerical simulation we have designed and fabricated a valveless pulse-detonation hydrojet operating on liquid hydrocarbon fuel (regular gasoline) and gaseous oxygen. For firing the hydrojet, a special test rig was designed and assembled. Figures 5 and 6 show the schematic and photographs of the test rig with flowing water. The test rig includes (see Fig. 5) water pool 1, pump 2 with suction and pressure tubing, support beam 3, thrust-measuring frame 4 with a load cell, and with suspended hydrojet 5.

Fig. 5

Schematic of the test rig

Fig. 6

Photographs of the test rig (a) and thrust-measuring system with a suspended pulse-detonation hydrojet

Figure 7 shows the example of load cell record in one of the experimental runs. It shows the time history of instantaneous force acting on the hydrojet operating in the pulse-detonation mode at a frequency of 3 Hz in a water stream of 5 m/s entering the pool from the pump. The mass flow rate of near-stoichiometric gasoline–oxygen mixture is $\dot{m} \approx$ 8 g/s in this run. The mixture was cyclically ignited in the detonation tube by a standard automotive spark plug and the arising deflagration was transitioned to a detonation at a short distance. Based on the record of Fig. 7 one can estimate the experimental specific impulse $I_{\text{sp,exp}} \approx$ 300 s, which is close to the theoretical value of $I_{\text{sp,calc}}$ of 350–400 s. Note that the registered force of hydrodynamic drag acting on the hydrojet during a water purging stage (prior to triggering the pulse-detonation operation process) was negligible as compared to the forces arising during hydrojet firing.

Fig. 7

Load cell record in one of the experimental runs with the pulse-detonation hydrojet operating at a frequency of 3 Hz in a water stream of 5 m/s

Table 1 summarizes the results of seven experimental runs with different operation frequencies (cycle timing) in the pulse-detonation mode, ranging from 6 to 1 Hz. In all runs, the approach velocity of the water stream was 5 m/s, water in the water guide was artificially aerated with air bubbles to have $\alpha_{1} \approx 0.04$ and the mass flow rate of fuel mixture was $\dot{m} \approx$ 8 g/s. The last column in Table 1 shows the estimated values of the experimental specific impulse $I_{\text{sp,exp}}$. Clearly, the measured values of $I_{\text{sp,exp}}$ vary within the range from 255 to 370 s which overlaps the theoretical range of 350–400 s.

Table 1 Results of seven experimental runs

Conclusions

Geometrical configuration and operational parameters of a valveless pulse-detonation hydrojet have been determined based on extensive numerical simulations using 2D two-phase flow equations. The theoretical propulsive performance of such a hydrojet in terms of the specific impulse was shown to be on the level of modern liquid propellant rocket engines and amount 350–400 s. Based on the results of numerical simulation a valveless pulse-detonation hydrojet operating on liquid hydrocarbon fuel (regular gasoline) and gaseous oxygen has been designed and fabricated. For firing the hydrojet, a special test rig with flowing water was designed and assembled. Experiments showed that the measured values of the specific impulse varied within the range from 255 to 370 s which overlaps the theoretical range, thus demonstrating the predictive capabilities of the numerical approach. Further efforts will be focused on improving the propulsive performance of the valveless hydrojet and on computer-aided design of an efficient valved hydrojet.

This work was supported by the Ministry of Education and Science of Russian Federation (contract ID RFMEFI60914X0001).