An Improved Mechanical Material Model for Ballistic Soda-Lime Glass

Abstract

In our recent work (Grujicic et al., Int. J. Impact Eng., 2008), various open-literature experimental findings pertaining to the ballistic behavior of soda-lime glass were used to construct a simple, physically based, high strain rate, high-pressure, large-strain mechanical model for this material. The model was structured in such a way that it is suitable for direct incorporation into standard commercial transient non-linear dynamics finite element-based software packages like ANSYS/Autodyn (Century Dynamics Inc., 2007) or ABAQUS/Explicit (Dessault Systems, 2007). To validate the material model, a set of finite element analyses of the edge-on-impact tests was conducted and the results compared with their experimental counterparts obtained in the recent work of Strassburger et al. (Proceedings of the 23rd International Symposium on Ballistics, Spain, April 2007; Proceedings of the 22nd International Symposium on Ballistics, November 2005, Vancouver, Canada). In general, a good agreement was found between the computational and the experimental results relative to: (a) the front shapes and the propagation velocities of the longitudinal and transverse waves generated in the target during impact and (b) the front shapes and propagation velocities of a coherent-damage zone (a zone surrounding the projectile/target contact surface which contains numerous micron and submicron-size cracks). However, substantial computational analysis/experiment disagreements were found relative to the formation of crack centers, i.e. relative to the presence and distribution of isolated millimeter-size cracks nucleated ahead of the advancing coherent-damage zone front. In the present work, it was shown that these disagreements can be substantially reduced if the glass model (Grujicic et al., Int. J. Impact Eng., 2008) is advanced to include a simple macrocracking algorithm based on the linear elastic fracture mechanics.

Introduction

Ballistic glass is a material (or more often a system of materials) designed to be optically transparent while providing the necessary level of protection against blast and ballistic/fragmentation impacts. This class of materials is used in such diverse applications as protective visors for non-combat usage (e.g. riot control or explosive ordinance disposal) or as transparent-armor systems (to protect on-board instruments/sensors from fragments and debris, and to protect vehicle occupants from terrorist actions or other hostile conflicts). The critical importance of transparent armor has become evident by recent experiences of the U.S. military forces in the Operation Iraqi Freedom. With continuing escalations in the number and variety of threats, the needs for rapidly deployable threat-specific weight/cost-performance-optimized transparent armor and armor systems have greatly increased. There are numerous efforts by the researchers in the United States and elsewhere around the world to help accelerate the development of transparent-armor systems. Traditionally, transparent armor is made of monolithic glass or transparent-elastomer inter-layered glass laminates. Among the new transparent-armor materials and technologies available today, the following have received most attention: crystalline ceramics (e.g. aluminum-oxinitride spinel, AlON (Ref 1)), new transparent polymer materials (e.g. transparent nylon (Ref 2)), new interlayer technologies (e.g. polyurethane bonding layers (Ref 1)), and new laminate designs (e.g. Ref 1). Due to their large size and curved shape, the majority of armor windows are still being constructed using glass. While ever increasing demands for reductions in weight and for improvements in ballistic protection performance of transparent armor are calling for the use of new transparent materials (e.g. transparent crystalline ceramics, advanced transparent polymeric materials) and advanced technologies (e.g. multi-material functionally graded laminated transparent armor), glass (as well as glass ceramics) continues to remain an important material choice in ground-vehicle transparent-armor applications. Compositional modifications, chemical strengthening, and controlled crystallization have demonstrated to be capable of significantly improving the ballistic properties of glass (Ref 3). Glass windshields and windows can also be produced in large sizes with curved geometries, and can be produced to provide incremental ballistic performance at incremental cost.

The development of new glass-based transparent-armor systems aimed at reducing the vulnerability of the military vehicle occupants and on-board instrumentation to various threats typically includes extensive experimental test programs. Such experimental test programs are critical for ensuring the utility and effectiveness of the transparent-armor systems. However, the use of experimental test programs is generally expensive, time-consuming, and involves destructive testing. While the role of experimental test programs remains critical, they are increasingly being complemented by the corresponding computation-based engineering analyses and simulations. The knowledge of the armor-material response under high-deformation rate/high-pressure loading conditions, as described by the corresponding material model, is one of the key components in such analyses greatly affecting their utility and fidelity. The main objective of the present article is to help advance the use of these computational engineering analyses and simulations in transparent-armor design applications by further developing and improving the simple, computationally efficient, physically based material model for soda-lime ballistic glass proposed in Ref 4.

It is well established that glass exhibits quite different behavior under quasi-static (i.e. low deformation rate) and dynamic (i.e. high-deformation rate) loading conditions. Under quasi-static loading conditions, pre-existing flaws/defects situated primarily in the surface regions of glass play a dominant role in the fracture process and fracture results in the formation of few large fragments (Ref 5-7). In sharp contrast, under dynamic loading conditions, high-intensity stresses may cause the nucleation of bulk/volume defects so that the fracture process becomes less surface-flaw controlled and results in the comminution (i.e. the formation of numerous fine fragments) (Ref 8, 9). Bulk cracks are seldom observed under quasi-static loading conditions except under very specific loading conditions (e.g. such as those encountered during high-temperature testing of glass fibers (Ref 10), compression testing of glass spheres (Ref 11), etc.).

As mentioned above, brittle failure in ceramics and glasses is the result of nucleation (on pre-existing flaws) and propagation of the cracks, and it is accompanied by stress attenuation and fragments formation. Finite element analyses have been extensively used over the last dozen of years to elucidate the underlying mechanisms and quantify the ballistic performance of ceramic targets under high-velocity impact and penetration conditions. In these analyses, most of the effort was typically devoted to modeling the complicated post-failure initiation response of ceramic materials (i.e. the mechanical/structural response of these materials to impact loads in the presence of cracks). In general, all the existing brittle-fracture models reported in the literature can be categorized as being either (a) continuum-based or (b) being of a discrete nature.

The continuum approaches (e.g. Ref 7, 12) generally involve homogenization of a crack-laden (damaged) material into an equivalent crack-free continuum material with degraded stiffness and strength. The fundamental assumption in these models is that the elastic stiffness degradation is the result of inelastic deformation caused by micron and submicron-size cracks and that this degradation can be quantified using a so-called damage tensor whose evolution during loading can be formulated using a generalized Griffith-type crack initiation and propagation criteria for brittle materials. In addition, some of the continuum models account for the interactions between the cracks, their coalescence, friction between fragments, etc. However, most of these phenomenological models have shortcomings in that they cannot describe damage-induced anisotropy and also that their parameters are difficult to determine experimentally.

To overcome the aforementioned limitations of the continuum models, Espinosa and co-workers (Ref 13, 14) proposed a multiple crack-plane (continuum) micromechanics constitutive model for brittle materials which can be parameterized by measuring experimentally the fundamental material properties (e.g. fracture toughness). Within the model, the dynamic growth of microcracks with different orientations is considered leading to damage-induced anisotropy while the rate effects are naturally incorporated in the model. In spite of these improvements, the continuum models continue to be criticized because they require assumptions regarding the size and distribution of pre-existing crack-nucleating defects, and because they cannot be used to describe the growth of dominant cracks (the cracks which lead to failure), which, due to their size, cannot be smeared out/homogenized. On the computational side, the continuum models suffer from the problem that at very large deformations and under high-strain rates, finite element distortions may reduce the integration time steps below an acceptable level. One of the possible means to circumvent this problem is the application of adaptive meshing (e.g. Ref 15), a procedure in which a region containing highly distorted elements is re-meshed, in the course of an analysis, using regularly shaped elements. However, repeated application of adaptive meshing during the analysis is also computationally quite costly.

The discrete models for brittle fracture (e.g. Ref 16) deal with the nucleation, propagation, and coalescence of discrete (rather then smeared out/homogenized) cracks during deformation. Among these models, the one proposed by Camacho and Ortiz (Ref 16) appears to be the most comprehensive. Within this model, conical and longitudinal cracks are allowed to nucleate at any node in a finite element mesh when the resolved normal or shear stress at that node reaches an effective fracture stress. Cracks are nucleated by duplicating nodes and propagated, along the element boundary, by continuing to duplicate nodes. Adaptive re-meshing is used to provide a rich enough set of possible fracture paths around the crack tip. The forces at the cracked surfaces are brought to zero in accordance with the Griffith criterion accounting for unloading, before reaching the critical fracture opening. This enables the formation of fragments as cracks coalesce in a closed path. Thereafter, contact and friction between the fragments is accounted for. The major disadvantages of the discrete models, such as the one described above, are that they are extremely computationally intensive and become intractable as the number of cracks increases. In order to capture all possible crack-nucleating sites, meshes with micron-size element are ultimately required.

The detailed review of the continuum and discrete material models (like the ones mentioned above) carried out in the present work clearly established that these models are capable of revealing complex intrinsic mechanisms and phenomena associated with fracture in brittle materials and are, hence, very important for gaining a better understanding of the behavior of these classes of materials. However, as argued in Ref 4, it is the effect of these mechanisms/phenomena on the material response rather than their explicit analysis that is sufficient/needed when one is attempting to develop a computationally efficient material model suitable for use in large-scale computational analyses of the multi-hit ballistic performance of geometrically complex, multi-layered, functionally optimized transparent-armor systems. In the present work, an effort is made to further advance the simple high-strain rate, high-pressure, large-strain material model for soda-lime ballistic glass proposed in Ref 4 in order to improve the aspects of the model dealing with formation and growth of isolated millimeter-size cracks ahead of the advancing coherent-damage zone front. This was done by introducing in the model (Ref 4) a linear elastic fracture mechanics based algorithm for macrocracking.

The organization of the article is as follows: In Sect 2.1, a brief overview is provided of the quasi-static and dynamic failure regimes observed in amorphous brittle materials like glass. A brief summary of the material model for ballistic soda-lime glass including its physical foundation and the governing equations is presented in Sect 2.2 and 2.3. A newly proposed model for macrocracking is presented in Sect 2.4. Model parameterization and its implementation into a subroutine suitable for use with commercial finite element programs are presented in Sect 2.5 and 2.6, respectively. Details of a transient non-linear dynamics computational analysis of an edge-on-impact (EOI) test used to validate the material model for soda-lime ballistic glass are discussed in Sect 3. The main results obtained in the present work are presented and discussed in Sect 4. The key conclusions resulted from the present work are summarized in Sect 5.

Derivation of the Material Model

As discussed earlier, the main purpose of the present work is to improve the simple large-strain, high-deformation rate, high-pressure material model for soda-lime ballistic glass developed in our recent work (Ref 4) so that better agreement can be obtained between the model predictions and their experimental counterparts regarding the nucleation and growth of isolated millimeter-size cracks. The model in question was found to be computationally quite efficient while physical soundness of the model was retained by addressing within it the key underlying physical phenomena/processes controlling the mechanical response of soda-lime glass under ballistic loading conditions. In the remainder of this section, a brief account is first given of the essential features of the material model for soda-lime ballistic glass, the derivation procedure used to construct various components of the model and the approach used for parameterization of the model. Then, a brief discussion is presented of the modifications of the model introduced in the present work in order to better account for nucleation and growth of the isolated millimeter-size cracks.

Physical Foundation of the Model

Many experimental studies (e.g. Ref 1, 2) have clearly established that the mechanical response of soda-lime glass is drastically different under low deformation rate (i.e. quasi-static) and high-deformation rate (i.e. impact) loading conditions. Under quasi-static loading conditions, glass typically fails by the propagation of a single or a couple of discrete cracks and only a few fragments are created after complete fracture. In sharp contrast, under dynamic loading conditions, glass tends to undergo substantial damage (resulting from the formation of a large number of micron and submicron-size cracks) and tends to undergo comminution (i.e. forms a large number of sub-millimeter size fragments). In both cases, however, the failure is believed to be controlled by pre-existing flaws which, when subjected to sufficiently large stresses, can become cracks. A brief overview of the two failure regimes (i.e. the quasi-static coarse fragmentation regime and the dynamic comminution regime) is presented later while more quantitative discussion of the same can be found in Ref 4.

The occurrence of the two fracture regimes is believed to be the result of the two internal processes accompanying loading of glass: (a) crack formation at the pre-existing flaws and crack growth. The nucleation of cracks is accompanied by the formation of so-called shielding zones, i.e. the zones surrounding the cracks within which the stresses are highly relaxed and the probability for nucleation of additional cracks is very small; and (b) the increase in stress level which promotes the formation of additional cracks (at less potent pre-existing flaws). Since the crack formation process is typically associated with mechanical instability (i.e. once a crack is nucleated, it grows at a terminal velocity, until it reaches the free surface or another crack), low loading rates tend to promote the coarse fragmentation fracture regime. In other words, once a crack or a couple of cracks are formed, they can extend over the entire structure before the stress at other flaws has reached a high enough level to form additional cracks. Conversely, high loading rates promote the formation of large number of cracks, i.e. the critical stress level for crack nucleation is reached at many pre-existing flaws before the previously nucleated cracks have a chance to extend far enough and shield these flaws from the externally applied stress.

In the EOI tests, reviewed in more detail in Sect 3.1, it is also observed that both regimes of fragmentation take place, i.e. in the region of the glass-plate target surrounding the projectile-impacted surface, in which the loading rates are very high, fracture is dominated by the fine-scale (coherent) damage and the comminution (with occasional appearance of few coarse fragments). On the other hand, in target regions further away from the impact surface in which the loading rate is relatively low, isolated cracks (crack centers) are formed and grow until they are swept by the advancing coherent damage (i.e. the comminution) front.

Simplifying Assumptions and Basic Components of the Model

In this section, more details are provided regarding the physical foundation of the ballistic material model for glass developed in Ref 4. The following are the key simplifying assumptions and basic components of the model:

• (a) The distribution of pre-existing flaws throughout the material was assumed to follow the Weibull-type distribution (discussed in next section). In order to account for the differences in the flaw distributions between the target surface and the bulk, different (typical) Weibull distribution parameters for soda-lime glass were used when dealing with surface and near-surface regions versus the bulk region of the material (Table 1).

• (b) Both the nucleation of microcracks (which leads to comminution) and macrocracks (which leads to coarse fragmentation) were postulated to be governed by the same stress level-based damage-initiation criterion. Crack initiation was assumed to be controlled by the largest principal normal stress and only the normal mode (mode I) of cracking was considered.

• (c) It was further assumed that it is the loading/stress rate at the moment of crack nucleation which determines if a crack will remain a single macrocrack within the given finite element resulting in the coarse fragmentation failure mode of the element or the crack will be accompanied by the formation of many additional microcracks leading to progressive damage and ultimate multiple fragmentation failure of the element. A single critical stress rate value ($\dot{\upsigma }_{\text{crit}}, = {\text{ca}}.\,1000\,{\text{MPa}}/\upmu\text{s}$, estimated using a simple constant stress rate analysis) was introduced to separate these two regimes of fracture. At stress rates below this critical value, a single crack fracture regime was assumed while at stress rates above it a multiple crack regime was assumed.

• (d) When an element begins to fail via the single crack mode, the (single) crack nucleated within that element was assumed to extend at the terminal velocity (defined in the next section) and the total time for element failure was obtained by dividing the characteristic element dimension by the terminal crack velocity. Once an element is fractured in a single crack mode, it is removed from the model. In other words, multi-axial macrocracking was not handled explicitly. When an element is undergoing fracture via the growth of the single crack, stiffness and strength properties of this element were assumed to degrade linearly with the corresponding crack strain from the point of crack initiation to the point of complete traversal of the element by the crack.

• (e) Once an element has started undergoing (coherent) damage due to the formation of multiple cracks, stress-shielding and path-crossing effects prevent, initially, the nucleation of macrocracks. However, when the extent of coherent damage within a single element reaches a critical value, this element was assume to fracture by microcrack coalescence and to loose most of its ability to support load. To account for the experimental observations that the resulting microfragments are typically confined by the surrounding non-fractured material and can support compressive and shear loads, the elements that failed in the multi-fragmentation regime were not removed from the model. Instead, they were retained and assigned small residual normal and shear stiffness values. As shown in the next section, the critical level of coherent damage at which element failure takes place was found to be stress rate invariant.

• (f) When an element is subjected to coherent damage, the extent of damage was taken to be governed by a damage evolution equation and the extents of degradation of the corresponding stiffness and stress properties of the material were assumed to be governed by the appropriate damage-dependent stiffness and strength material constitutive relations (presented in the next section).

Table 1 Mechanical property parameters for soda-lime glass used in the present work

Mathematical Formulation of the Model

Coarse-Fragmentation Quasi-Static Failure Regime

As mentioned earlier, under low-rate (i.e. quasi-static) loading conditions, glass is typically observed to fracture in the coarse fragmentation failure regime in which the failure of the complete structure is caused by the nucleation and propagation of a single crack or a few cracks. This observation has been rationalized as follows: under low deformation rates, stresses are increasing slowly within the material. When the stresses become high enough, the first crack nucleates and begins to propagate at a terminal crack velocity. As the crack grows, so does its shielding zone within which stresses are relaxed and all flaws located within the shielding zone become impotent. Due to a low rate of stress increase in the remainder of the material, the stresses typically never reach a critical level needed to nucleate a large number of additional cracks and, consequently, the coarse fragmentation regime ensues. Under such conditions, the fracture strength of the brittle material behaves as a stochastic quantity, i.e. the fracture resistance of a brittle material is not defined using a single (mean value) fracture strength, but rather by a failure probability function. To derive an expression for the failure probability, the coarse fragmentation fracture regime is analyzed using a Poisson point-process framework and the resulting failure probability function, commonly referred to as the Weibull distribution function, was derived as:

$$ P_{\text{F}} = 1 - \exp \left[ {\uplambda_{t} Z} \right] $$

(1)

The failure probability P_F in Eq 1 defines the probability of finding at least one crack-nucleating flaw in the domain Z while the stress-dependence flaw density λ_t is defined as:

$$ \uplambda_{t} = \uplambda_{0} \left({\frac{\upsigma }{{S_{0} }}} \right)^{m} $$

(2)

where λ₀ and S₀ are the reference density and a stress normalizing parameter, while the exponent m is generally referred to as the Weibull modulus.

Using the standard expressions for the mean value for a single-variate distribution function and Eq 1 and 2, the mean quasi-static fracture strength and its standard deviation can were derived as (Ref 17):

$$ \upsigma_{\text{f,static}} = \frac{{S{}_{0}}}{{\left( {Z_{\text{eff}} \uplambda_{0} } \right)^{1/m} }}\Upgamma \left( {1 + \frac{1}{m}} \right) $$

(3)

and

$$ \upsigma_{\text{sd}} = \sqrt {\frac{{S_{0}^{2} }}{{\left( {Z_{\text{eff}} \uplambda_{0} } \right)^{2/m} }}\Upgamma \left( {1 + \frac{2}{m}} \right) - \upsigma_{\text{f,static}}^{ 2} } $$

(4)

where Γ denotes the gamma function which is defined as:

$$ \Upgamma (x) = (x - 1)! $$

(5)

where the probability distribution function for the fracture strength is obtained by combining Eq 1 and 2 and differentiating the resulting equation with respect to σ.

Multiple Fine Fragmentation/Comminution Dynamic Failure Regime

As stated earlier, under high-rate (i.e. dynamic) loading conditions, it is generally observed that damage and the final failure occurs by nucleation, growth, and interconnection of multiple micron- and millimeter-size cracks. The reason for the nucleation of multiple cracks is that, due to a high rate of stress increase within the material, stress levels at many defects become high enough to nucleate cracks before shielding zones of the previously nucleated nearby cracks can extend over these defects. Under such conditions, material damage is distributed and when the extent of damage becomes extensive, fine-scale fragmentation (often referred to as comminution) takes place.

To obtain more insight into the size and topology of the damage/fracture zone and the morphology and distribution of the cracks within such a zone, EOI tests are typically carried out. The following key aspects of the damage zone are generally observed: (a) in a region surrounding the place of impact, a coherent-damage zone is typically observed within which the damage is caused by micron and submicron-size cracks. In addition, ahead of the coherent-damage zone front, multiple millimeter-size cracks are observed; (b) these cracks are typically aligned in radial directions with respect to the place of impact; (c) the cracks appear to be mainly of the mode I opening and, hence, are caused by high tensile hoop stresses. The latter are most likely the result of target-material motion in the radial directions accompanying the projectile penetration into the target; (d) a crack is believed to form in a dynamic fashion as a result of high tensile stresses propagated by the stress wave (generated at the place of impact) and its growth ceases when the surrounding cracks cause significant stress reductions in the shielding zone of the crack in question; and (e) crack distribution is highly non-uniform and anisotropic.

Following the original work of Denoual and Hild (Ref 17, 18), Grujicic et al. (Ref 4) recently proposed a physically based computationally efficient material dynamic multiple-fragmentation fracture model for soda-lime glass. The key components of this model are as follows:

• (a) When a defect is activated and the associated crack is nucleated, a shielding zone is created around the crack within which stress component responsible for crack nucleation is relaxed to zero. Consequently, any defect residing in such a zone will become impotent (i.e. will no longer represent the potential nucleus for a crack). As a crack grows, its shielding zone also grows but in a self-similar fashion. Consequently, the size of the shielding zone at a time t associated with a crack which was nucleated at the time τ was defined by the following relation:

  $$ Z_{\text{sh}} (t,\uptau ) = S\left[ {kC(t - \uptau )} \right]^{n} $$

  (6)

  where $C = \left[ {E/\uprho } \right]^{0.5}$ is the speed of sound (i.e. the speed of the impact-generated stress wave), E the Young’s modulus, ρ the mass density, k = 0.2–0.4, a ratio of the crack speed and the sound speed, n a defect-distribution dimensionality factor (=2, for surface-flaw dominated failure and =3, for bulk flaw dominated failure), and S is a shielding zone shape factor (=4π/3, for a spherically shaped bulk shielding zone).

• (b) Under quasi-static loading conditions, as discussed above, once a crack is nucleated, it can traverse the entire structure (while its shielding zone spreads over the entire surface/volume of the structure) before the stress on other defects can become sufficiently high to cause the nucleation of additional cracks. Under dynamic loading, on the other hand, the condition for crack nucleation will be met at many flaws leading to a multiple-cracking fracture mode. However, the neighboring cracks with compatible opening modes and orientations, via their shielding zone, will mutually terminate each other’s growth, giving rise to relatively short cracks.

• (c) Due to the shielding effects discussed above, one can distinguish between the non-shielded and shielded defects and the total defect density can be decomposed as:

  $$ \uplambda_{t} = \uplambda_{\text{non}{\text{-sh}}} + \uplambda_{\text{sh}} $$

  (7)

  where both λ_non-sh and λ_sh are defined by dividing the corresponding number of defects by the total domain size.

• (d) The extent of defect shielding is controlled by the competition between the expansion of the shielding zone(s) (which promote defect shielding) and higher rates of loading (which promote activation of new defects in the regions outside the shielding zones). As the rate of loading is decreased, a larger number of defects will become shielded and, in the limit of quasi-static loading, all defects (except for the one which nucleated the first crack) will be shielded, leading to the coarse fragmentation failure mode.

• (e) As the loading rate increases, the density of shielded defects will decrease (at a given level of stress, i.e. at a given level of total defect density). This, in turn, will give rise to higher fracture-strength levels, as a larger portion of the domain will remain unshielded (i.e. undamaged) and could support the applied load.

The (mean) fracture strength for a brittle material in the single-fragmentation failure mode is defined by Eq 3 and is rate-independent. The failure strength for the multiple-fragmentation failure mode is derived in the remainder of this section and, as argued in point (e) above, is expected to be an increasing function of the loading rate.

During derivation of the multiple-fragmentation brittle-fracture model (Ref 4), the case of uniform loading at a constant stress rate $(\dot{\upsigma })$ was considered first and a distinction was made between the externally applied macroscopic stress, Σ, and an internal stress $\upsigma = \dot{\upsigma }t$, where t is the time of loading. Due to the formation of cracks and their shielding zone (within which the internal stress is relaxed), only non-shielded portions of the brittle-material structure was assumed to support σ. Next, a damage variable, D, was defined as a ratio of the union of all shielding-zone volumes and the structure volume, yielding the following relations existing between Σ and σ:

$$ \Upsigma = \upsigma (t)(1 - D(\upsigma )) = \dot{\upsigma }t(1 - D(\dot{\upsigma },t)) $$

(8)

where D is implied to depend on $\dot{\upsigma }$ and t, since these quantities affect the density/number of cracks via $\upsigma = \dot{\upsigma }t$ and Eq 2 while t affects the size of the shielding zones via Eq 6.

According to Eq 8, as the loading time increases, the σ(t) increases while the $(1 - D(\upsigma ))$ term decreases. The macroscopic multiple-fragmentation fracture strength is then defined as the peak value of Σ, i.e. σ_f,dynamic = Σ_max, and is obtained from the relation:

$$ \frac{{{\text{d}}\Upsigma }}{{{\rm{d}}\upsigma }} = 0 $$

(9)

Following Denoual and Hild (Ref 17, 18), D was next set equal to the probability of defect shielding, P_sh, which is then defined using Eq 1 as:

$$ D = P_{\text{sh}} = 1 - \exp ( - \uplambda_{t} Z_{\text{sh}} ) $$

(10)

where $Z_{\text{sh}}$ is the average size of the shielding zone defined as:

$$ \uplambda_{t} (t)Z_{\text{sh}} (t) = \int\limits_{0}^{t} {\left. {\frac{{{\text{d}}\uplambda_{t} }}{{{\rm{d}}t}}} \right|}_{\uptau } \left[ {kC(t - \uptau )} \right]^{n}\, {\text{d}}\uptau $$

(11)

Equation 11 states that, in order to compute $Z_{\text{sh}}$ at time t, when the total defect density is λ_t(t), one must take into account that cracks may have nucleated at a time, 0 ≤ τ ≤ t, and that their shielding-zone size is, hence, $\left[ {kC(t - \uptau )} \right]^{n}$. Furthermore, the probability that a crack present at time t was nucleated at time τ is expected to be proportional to the rate of activation of the flaws at time τ, i.e. to scale with $\frac{1}{{\uplambda_{t} (t)}}\left. {\frac{{{\text{d}}\uplambda_{t} }}{{{\rm{d}}t}}} \right|_{\uptau }$ while $\int_{0}^{t} {\left. {\uplambda_{t} (t)\frac{{{\text{d}}\uplambda_{t} }}{{{\rm{d}}t}}} \right|}_{\uptau } {\text{d}}\uptau = 1.$

In the case of uniform loading under constant stress rate conditions and via Eq 2, the term $\left. {\frac{{{\text{d}}\uplambda_{t} }}{{{\rm{d}}t}}} \right|_{\uptau }$ becomes:

$$ \left. {\frac{{{\text{d}}\uplambda_{t} }}{{{\rm{d}}t}}} \right| = \frac{{\uplambda_{0} m\dot{\upsigma }^{m} t^{m - 1} }}{{S_{0}^{m} }} $$

(12)

When Eq 12 is substituted into Eq 11 and, in turn, in Eq 10, and integrated, the following expression for the damage extent is obtained:

$$ D = 1 - \exp \left( { - \frac{{m!n!\left( {\frac{\upsigma }{{\upsigma_{\text{c}} }}} \right)^{m + n} }}{(m + n)!}} \right) $$

(13)

where $\upsigma_{\text{c}}$ is a characteristic stress defined as:

$$ \upsigma_{\text{c}} = \dot{\upsigma }t_{\text{c}} = \left[ {\frac{{S_{0}^{m} \dot{\upsigma }^{n} }}{{\uplambda_{0} S(kC)^{n} }}} \right]^{{\frac{1}{m + n}}} $$

(14)

After substituting Eq 13 into Eq 8 and after differentiating the resulting equation in accordance with Eq 9, one obtains:

$$ \left. \upsigma \right|_{{\Upsigma_{\max } }} = \left( {\frac{{S_{0}^{m} \dot{\upsigma }^{n} }}{{\uplambda_{0} S\left( {kC} \right)^{n} }}} \right)^{{\frac{1}{m + n}}} \left( {\frac{(m + n - 1)!}{m!n!}} \right)^{{\frac{1}{m + n}}} $$

(15)

and

$$ \upsigma_{\text{f,dynamic}} = \Upsigma_{\max } = \upsigma_{\text{c}} \left[ {\frac{1}{e}\frac{{\left( {m + n - 1} \right)!}}{m!n!}} \right]^{{\frac{1}{m + n}}} $$

(16)

Then Eq 15 and 13 are combined to get:

$$ \left. D \right|_{{\Upsigma_{\max } }} = 1 - \left( {\frac{1}{e}} \right)^{{\frac{1}{m + n}}} $$

(17)

Likewise, $\upsigma = \dot{\upsigma }{t}$ and Eq 15 are combined to get:

$$ \left. t \right|_{{\Upsigma_{\max } }} = \left( {\frac{{S_{0}^{m} }}{{\uplambda_{0} S\left( {kC} \right)^{n} \dot{\upsigma }^{m} }}} \right)^{{\frac{1}{m + n}}} \left( {\frac{(m + n - 1)!}{m!n!}} \right)^{{\frac{1}{m + n}}} $$

(18)

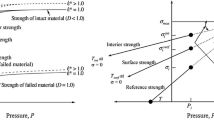
An example of the relationship between the expressions for the quasi-static and dynamic fracture strengths (Eq 3 and 16, respectively) for soda-lime glass in the case when brittle fracture is controlled by bulk flaws is displayed in Fig. 1. To help interpret fracture strength versus stress rate plot displayed in Fig. 1, a second horizontal axis, Z_eff/Z_c, is introduced. The relevant mechanical property parameters used in the construction of Fig. 1 are listed in Table 1 while Z_eff was set to a representative fixed value of 10⁻⁴ m³. It should be noted that in Fig. 1, the two expressions for the (mean) fracture strength, Eq 3 and 16, are valid only over a limited range of stress rates and that the ranges are different for the two relations. That is, at high stress rates, defect shielding is limited and, hence, the static coarse fragmentation fracture strength relation, Eq 3, which assumes complete shielding of all flaws by the first nucleated crack is not valid. Likewise, Eq 16 is not valid in the low stress rate range (i.e. at lower values of Z_eff/Z_c), since in this case, a shielding zone must grow beyond the total structure volume before a single defect is shielded. Thus the multiple cracking fracture mode is not feasible. The results displayed in Fig. 1 further show that, as expected, the fracture strength increases with an increase in stress rate in the multiple-fragmentation regime at high stress rates, while it is essentially stress-rate independent in the single-fragmentation fracture mode at low stress rates.

Fig. 1

The transition between the static coarse fragmentation and the dynamic fine fragmentation brittle-fracture modes as a function of an increase in stress rate

As mentioned earlier, coherent damage causes degradation of the material strength and stiffness and, in order to assess the temporal evolution of this degradation, a damage evolution equation is needed. This was obtained in Ref 4, by differentiating Eq 13 for the extent of damage, D, with respect to stress, σ, to get:

$$ \frac{{{\text{d}}D}}{{{\rm{d}}\upsigma }} = \frac{{m!n!(m + n)\upsigma^{m + n - 1} }}{{(m + n)!\upsigma_{\text{c}}^{m + n} }}(1 - D) $$

(19)

It should be noted that, as implied by Eq 13 and 19, damage is assumed to be isotropic and, hence, degraded glass, like the virgin glass, is considered as an isotropic material. Degradation of the Young’s modulus of the glass is then defined by the following relation:

$$ E = E_{0} (1 - D) $$

(20)

where subscript 0 is used to denote a quantity pertaining to glass in its initial condition.

One of the key features of the soda-lime glass multiple-fragmentation model (Ref 4) is that, in accordance with Eq 19, the evolution of coherent damage is controlled by the internal stress, $\upsigma$ (i.e. the stress residing in the non-shielded portion of the finite element in question, while the overall stress state of that element is defined by a macroscopic stress, $\Upsigma = \upsigma (1 - D(\upsigma ))$. Thus, the internal stress level is controlled by the initial stiffness of soda-lime glass while the macroscopic stress level is controlled by the degraded material stiffness.

Macrocracking Fracture Model

As discussed earlier, the ballistic glass model developed in Ref 4 handled the phenomenon of macrocracking using a very simple approach. That is, only a stress-based crack nucleation criterion was considered which typically resulted in the formation of single element long isolated cracks (crack centers). Since the EOI results of Strassburger et al. (Ref 1, 2) revealed the presence of significantly longer cracks, a good computation/experiment agreement could not be attained. To overcome this shortcoming of the ballistic glass model (Ref 4), the stress-based crack nucleation criterion is complemented with a fracture toughness-based crack growth criterion in the present work. This is accomplished as follows:

• (a) Adjacent failed elements aligned in a particular direction are used to define the associated crack length in that direction.

• (b) For an element located at a crack tip, the stress intensity factor K_I is calculated by multiplying its maximum principal stress with a factor $\sqrt {\uppi a}$, where a is the crack half-length.

• (c) Then, crack extension occurs by failure of an element described in (b) when the following condition is satisfied: K_I > K_IC, where K_IC is the stress intensity factor of the ballistic glass.

• (d) For simplicity, only five crack propagation directions were considered. Three of these were aligned with the edges of the cube-shaped finite element, while the remaining two are aligned at a ±45° angle in the 2-3 plane.

Parameterization of the Model

As discussed earlier, brittle failure of glass in either of the coarse fragmentation or fine fragmentation mode is assumed to be controlled by pre-existing flaws and to comply with the Weibull distribution. However, to account for the fact that surface regions can contain higher density of flaws, different Weibull distribution parameters were used for the finite elements residing on the target faces, Table 1. Table 1 also contains the values for the linear elastic properties for soda-lime glass. As stated earlier, transition between the coarse fragmentation and fine fragmentation brittle-fracture modes is assumed to take place at a constant stress rate, which, based on Fig. 1, was set to 1000 MPa/μs. A typical value of 0.3 was assigned to the ratio between the crack terminal velocity and the sound speed, k. The crack shielding zones are assumed to be circular or spherical depending on whether the failure is controlled by surface or volume flaws.

The macrocracking growth model proposed in Sect 2.4 is associated with a single material parameter, i.e. the critical mode I stress intensity factor, K_IC. In accordance with the macrocracking initiation criterion, the critical mode I stress intensity factor was taken to be a stochastic quantity given by the same Weibull distribution parameters as the corresponding fracture strength. Also, the same mean value of 0.75 MPa m^1/2 (Ref 19) was used for the critical mode I stress intensity factor in both the surface and bulk regions of the material.

Implementation of the Material Model in a User Material Subroutine

The brittle-fracture material model for soda-lime glass developed and parameterized in the previous sections is next implemented in a VUMAT Material User Subroutine of the commercial finite element program ABAQUS/Explicit (Ref 15). This subroutine is compiled and linked with the finite element solver and enables ABAQUS/Explicit to obtain the needed information regarding the state of the material and the material mechanical response during each time step, for each integration point of each element.

The essential features of the coupling between the ABAQUS/Explicit finite element solver and the VUMAT Material User Subroutine at each time increment at each integration point of each element can be summarized as follows:

• (a) The corresponding previous time increment stresses and material state variables as well as the current time-step strain increments are provided by the ABAQUS/Explicit finite element solver to the material subroutine. In the present work, the strain components, the extent of coherent damage, and a variable defining the deletion status of the element in question are used as state variables.

• (b) Using the information provided in (a), and the soda-lime glass material model presented in Sect 2.4, the material stress state as well as values of the material state variables at the end of the time increment are determined within the VUMAT and returned to the ABAQUS/Explicit finite element solver. It should be also noted that in order to implement the new algorithm for macrocracking, global three-dimensional matrices containing the location, the failure status and the direction of cracking (where appropriate) had to be assembled and used during each call of the VUMAT subroutine.

Validation of the Material Model

The material model for soda-lime glass developed and parameterized in the previous section is validated in this section by carrying out a series of transient non-linear dynamics analyses of the EOI tests of a glass target and by comparing the computational results with the experimental results obtained recently by Strassburger et al. (Ref 1, 2). In the remainder of this section, a brief description of the EOI test and the nature of the results obtained in this test are presented. This is followed by the description of the computational procedure used to simulate the test.

Edge-on-Impact Test

Test Set-up and Procedure

EOI tests are frequently used to study the deformation and damage of (non-transparent) conventional structural ceramic armor systems and involves real-time, reflection-mode, optical monitoring of the armor deformation and damage during impact. In the recent work of Strassburger et al. (Ref 1, 2), the EOI set-up is coupled with a high-speed 0.10 μs resolution Cranz-Schardin camera and utilized in a number of studies to visualize damage propagation and dynamic fracture in structural ceramics. Strassburger et al. (Ref 1, 2) also reconfigured the EOI test set-up in order to record photographically the evolution of damage in transparent-armor systems using the plane-light shadowgraphs transmission mode (the shadowgraphs mode). In addition, the test set-up was modified by adding crossed polarizers to visualize the propagation of stress waves using a dynamic photo-elasticity technique (the photo-elasticity mode). A schematic of the EOI test set-up with the added crossed polarizers is displayed in Fig. 2. A close-up view of the projectile/target interaction and a schematic of the resulting damage and wave-swept zones are provided in Fig. 3.

Fig. 2

A schematic of the edge-on-impact (EOI) experimental set-up with two cross polarizers and a single Cranz-Schardin camera

Fig. 3

A close-up view of the projectile/target interaction in an EOI set-up

In the work of Strassburger et al. (Ref 1, 2), a projectile is used to strike one side face (generally referred to as an edge) of a plate-like specimen/target and damage formation and fracture propagation is recorded by photographing (in transparent mode) the broad faces of the target during the first 20 μs following the impact. Plate-shape 100 × 100 × 10 mm test specimens/targets are typically impacted using either solid right circular cylinder-shape steel projectiles (30 mm diameter, 23 mm length) or using 16-mm-diameter solid sphere-shaped projectiles. The impact velocities used are normally in a range between 270 and 925 m/s. In the shadowgraph mode of the optical set-up, the target is placed between the condensing lens and the camera. In the photo-elasticity mode of the optical set-up, two sheet polarizers (one on each side of the target) are attached to the transparent sides of the target chamber so that broad polarizers’ faces are parallel with the broad target faces, Fig. 2.

To help clarify the nature of the shadowgraph-type and the photo-elasticity-type EOI results, simple schematics of these results are provided in Fig. 4(a) and (b), respectively. Schematics shown in Fig. 4(a) and (b) both pertain to the corresponding photographic positives, i.e. due to the damage induced, the coherent-damage zone as well as the isolated crack centers appear as dark regions in the shadowgraphs. Differences in the light intensity associated with the longitudinal wave and transverse wave swept regions in the case of shadowgraph mode are dominated by stress-induced birefringence effects (in the case of the longitudinal wave) and by surface reflection phenomena (in the case of the transverse wave). In the case of the photo-elastic imaging mode, stress-induced birefringence in the target material gives rise to a 90° switching in the beam polarization vector producing bright regions in the stressed areas.

Fig. 4

Schematic of the typical (a) shadowgraph and (b) birefringence results obtained in the work by Strassburger et al. (Ref 1, 2)

Typical EOI Test Results for Soda-Lime Glass

As discussed in the previous section, two different optical configurations were employed in the work of Strassburger et al. (Ref 1, 2): a regular transmitted plane-light shadowgraph set-up was used to observe wave and damage propagation, while a modified configuration, in which the specimens were placed between crossed polarizers to create a photo-elastic effect, was used to visualize the stress-wave propagation. Pairs of impact tests at approximately identical velocities were conducted in transmitted plane (shadowgraphs) and crossed polarized light. The two sets of results were next compared to establish the extent of wave and damage propagation and to establish correlation between damage initiation and the stress components most likely responsible for the observed damage.

The main observations made by Strassburger et al. (Ref 1, 2) during the EOI testing of soda-lime glass can be summarized as follows:

• (a) Damage appears to be in two distinct forms: (i) as a coherent, continuous (damage) zone emanating from the impacted target edge and (ii) as discrete crack centers located at some distance from the advancing coherent-damage zone front. To overcome the limitations of the side-view shadowgraph optical set-up that always provides photographic images with superimposed bulk damage and surface damage contributions, Strassburger et al. (Ref 1, 2) also carried out a simultaneous top-view shadowgraph imaging of the target-damage process. The results obtained revealed that the material damage initiates both in the bulk of the target and on the side faces. The advancement of damage from the impacted edge of the specimen was found to be greater in the case of bulk damage. This finding was somewhat surprising since, in the case of glass, it is generally postulated that damage-inducing flaws are primarily concentrated in the surface regions of the sample.

• (b) While both the shadowgraph optical mode and the photo-elastic mode revealed the positions of the advancing longitudinal and shear waves, the positions of the wave front revealed by the two optical set-ups were somewhat different. This discrepancy was explained to be the result of differences in the physical phenomena responsible for the light-intensity differences (contrast) in the two cases. That is, in the case of plain-light shadowgraph optical set-up, the transmitted light intensity is controlled by the second derivative of the refractive index while in the case of cross-polarizers set-up, the transmitted-light intensity is controlled by the underlying photo-elastic effect.

• (c) The longitudinal wave velocity was found to be around 5760 m/s while the propagation velocity of the transverse waves was found to be ca. 3520 m/s. Both of these velocities are consistent with their counterparts (5708 and 3224 m/s) computed using the Young’s modulus of 73 GPa, a shear modulus of 29 GPa and a density of 2240 kg/m³ for glass (Ref 4, 20).

• (d) The damage propagation velocity (defined as the velocity at which new crack centers are nucleated ahead of the advancing coherent-damage zone front) was found to be ca. 3270 m/s and thus quite close to the transverse wave velocity. This finding suggests that the most likely mechanism for damage initiation is mode I cracking induced by the tensile hoop stresses at pre-existing material flaws.

Transient Non-Linear Dynamics Analysis of the EOI Test

In this section, a brief description is provided regarding the construction of the geometrical model and the computational procedure used to simulate the EOI tests on soda-lime glass as carried out by Strassburger et al. (Ref 1, 2).

Plate-like soda-lime glass targets with L × W × H = 100 mm × 100 mm × 10 mm dimensions are used and one of their edges is impacted with either a 4340 steel spherical projectile (diameter = 16 mm) or a 4340 steel cylindrical projectile (diameter = 30 mm, height = 23 mm). For brevity and due to the fact that experiment/computation agreement was similar for two types of projectiles, only the results pertaining to the case of the spherical projectile will be presented in this article. The projectile was meshed using four-node reduced integration tetrahedron solid elements. Since initial work showed that no plastic deformation takes place in the projectile during impact, 4340 steel was modeled as a linear elastic material with a Young’s modulus E = 210 GPa and a Poisson’s ratio ν = 0.3. To enable easy determination of the relative location of the elements (needed in the present formulation of the macrocracking model), the target was meshed using equal size cube-shaped eight-node reduced integration brick elements. The soda-lime glass target was modeled using the high-deformation rate, high-pressure, large strain model presented in the previous section. Also, since only the normal impact of the projectile on the target is analyzed, advantage is taken of the inherent symmetry of the model, i.e. only one quarter of the model is analyzed. Typically, the spherical projectile was divided into ~8000 elements, while the target contained 200,000 elements. An example of the typical meshed model used in the present work is displayed in Fig. 5. The mesh size was varied initially in order to validate that the results are not significantly mesh size-dependent.

Fig. 5

A typical (quarter) meshed model used for the projectile and the target

All the calculations were carried out using ABAQUS/Explicit computer program (Ref 15). The material model for the soda-lime glass was implemented into a VUMAT User Material Subroutine and linked with ABAQUS/Explicit before the model could be used.

Interactions between the projectile and the target as well as between different fragments of the target are modeled using the Hard Contact Pair type of contact algorithm. Within this algorithm, contact pressures between two bodies are not transmitted unless the nodes on the slave surface contact the master surface. No penetration/over closure is allowed and there is no limit to the magnitude of the contact pressure that could be transmitted when the surfaces are in contact. Transmission of shear stresses across the contact interfaces is defined in terms of a static, μ_st, and a kinematic μ_kin, friction coefficient and an upper-bound shear stress limit, τ_slip (a maximum value of shear stress which can be transmitted before the contacting surfaces begin to slide).

The impact of the projectile with the target is modeled by assigning an initial (translational) velocity to the projectile (the initial condition). The initial velocity of the target was set to zero and, during the impact simulation, the narrow side face of the target normal to the impacted face was kept at a fixed position (the boundary conditions).

To prevent hour-glassing effects which may arise due to the use of reduced-integration elements, a default value of hour-glass stiffness was used. No mass-scaling algorithm was used to increase the maximum stable time increment. Computational analyses were run on a machine with a single 2.79 GHz dual-core Intel Pentium D processor with 3 GB of RAM. A typical 20 μs impactor/target computational analysis would require 5 min of (wall-clock) time.

Results and Discussion

Edge-on-Impact Analysis

In Sect 3.2, a detailed description was provided regarding the transient non-linear dynamics finite element analysis of the EOI tests of plate-like soda-lime glass targets with a spherical projectile as reported in Ref 1, 2. In the present section, the main results of the EOI computational analysis are presented and discussed.

Propagation of Longitudinal and Transverse Stress Waves

To verify that the pre-damage initiation elastic portion of the material model for soda-lime glass was implemented correctly into the VUMAT User Material Subroutine and correctly linked with the ABAQUS/Explicit finite element solver, the propagation of the (elastic) longitudinal stress waves and transverse (more specifically, the maximum principal) stress waves were investigated first. The contour plots displayed in Fig. 6(a) and 7(a) show, respectively, the positions of the longitudinal and transverse stress wave fronts 7.7 μs after the impact with the spherical projectile (propelled with an initial velocity of 440 m/s). For comparison, the corresponding results obtained experimentally in Ref 1 (using a cross-polarization photo-elastic experimental technique) are shown in Fig. 6(b) and 7(b), respectively. It is evident that both the computed shape of the stress-wave fronts and their locations are in fairly good agreement with their experimental counterparts. The same conclusion is reached after analyzing the results displayed in Fig. 8(a, b) and 9(a, b). In these figures, a comparison is made between the computed and experimental results pertaining to the position of the longitudinal and transverse stress wave fronts 15.7 μs after the impact with the same spherical projectile propelled with the same initial velocity.

Fig. 6

A comparison of the longitudinal stress wave fronts obtained (a) computationally and (b) experimentally (in Ref 1, 2) for the case of a spherical impactor with an initial velocity of 440 m/s and a post-impact time of 7.7 µs. The inset in (a) shows a typical longitudinal wave trace

Fig. 7

A comparison of the transverse stress wave fronts obtained (a) computationally and (b) experimentally (in Ref 1, 2) for the case of a spherical impactor with an initial velocity of 440 m/s and a post-impact time of 7.7 µs. The inset in (a) shows a typical transverse wave trace

Fig. 8

A comparison of the longitudinal stress wave fronts obtained (a) computationally and (b) experimentally (in Ref 1, 2) for the case of a spherical impactor with an initial velocity of 440 m/s and a post-impact time of 15.7 µs

Fig. 9

A comparison of the transverse stress wave fronts obtained (a) computationally and (b) experimentally (in Ref 1, 2) for the case of a spherical impactor with an initial velocity of 440 m/s and a post-impact time of 15.7 µs

As mentioned earlier, a similar agreement between the computed and the experimental results pertaining to the positions of the longitudinal and transverse stress wave fronts was obtained in the case of the cylindrical projectile (the results are not shown for brevity).

To further validate the implementation of the elastic part of the material model, a number of gage points were placed along the centerline of the target (in the direction of propagation of projectile motion) and the moment of arrival of the longitudinal and transverse stress wave fronts recorded. Typical stress versus time traces obtained are shown (as insets) in Fig. 6(a) and 7(a). From the distances between the gage points and the time-of-arrival of the stress waves to the gage points, the average longitudinal and transverse stress wave velocities were obtained as v_long = 5890 ± 100 m/s and v_trans = 3410 ± 70 m/s. These results are in quite good agreement with their experimental counterparts (5763 and 3518 m/s) and the ones obtained by using the Young’s and shear moduli and the material density (5407 and 3413 m/s), respectively. This finding suggests that the transverse normal stress wave (i.e. the wave associated with the maximum principal stress) travels at a speed which is comparable to that of the corresponding shear wave. This could be justified by the fact that due to mutual normality of the wave vector and the polarization vector in the case of transverse normal stress wave, the propagation of this wave relies on shear-like coupling between the material particles just ahead and just behind the wave front.

Based on the results obtained and discussed in this section, it can be concluded that the elastic portion of the soda-lime glass material model is appropriate, correctly implemented in the VUMAT user material subroutine and properly linked with the ABAQUS/Explicit solver.

Temporal Evolution of the Coherent-Damage/Comminution Zone

As discussed in Sect 3.1, the region surrounding the target face impacted by the projectile suffers damage (and ultimately fine fragmentation fracture) due to formation of the micron and submicron-size cracks. The extent of this coherent damage at a given material point is represented in the present work by a scalar material state variable, D. While in many brittle-fracture material models existing in the literature damage is represented using a tensorial quantity (in order to account for the anisotropic nature of the damage), the extent of such anisotropy within the coherent-damage zone is generally quite small. Since very small differences in the computational results were obtained in the present work when the anisotropic nature of the coherent damage was taken into account while the computational cost was more than doubled, the use of a damage tensor was deemed unwarranted.

To test the ability of the present material model for soda-lime glass to account for the temporal evolution of size and shape of the coherent-damage zone, a comparison is made in Fig. 10 and 11 between the computational results pertaining to the size and shape of the coherent-damage zone (obtained in the present work) and their experimental counterparts (obtained in the shadowgraph technique in Ref 1, 2). In Fig. 10 and 11, part (a) contains the computational results while part (b) contains the corresponding experimental results.

Fig. 10

A comparison of the coherent-damage zone fronts obtained (a) computationally and (b) experimentally (in Ref 1, 2) for the case of a spherical impactor with an initial velocity of 440 m/s and a post-impact time of 7.7 µs

Fig. 11

A comparison of the coherent-damage zone fronts obtained (a) computationally and (b) experimentally (in Ref 1, 2) for the case of a spherical impactor with an initial velocity of 440 m/s and a post-impact time of 15.7 µs

The results displayed in Fig. 10 and 11 pertain to the case of a spherical projectile (the initial velocity = 440 m/s and the post-impact times of 7.7 and 15.7 μs, respectively). It should be noted that while the computational results can reveal detailed spatial distribution of damage within the coherent-damage zone, similar details cannot be obtained using the shadowgraph technique. Consequently, only the size and the shape of the coherent-damage zone are used for comparison of the computational and the experimental results.

A careful examination of the results displayed in Fig. 10(a) and (b) shows that at a post-impact time of 7.7 μs, (a) there is a reasonably good agreement between the computational and the experimental results pertaining to the shape of the coherent-damage zone and its depth along the impact direction; (b) there is also a reasonably good agreement between the computational and the experimental results pertaining to the extent of the coherent-damage zone along the target face impacted by the projectile. It should be recalled that the extent of the coherent-damage zone along the target face impacted by the projectile is controlled by surface flaws while the evolution of damage in the remainder of the target is controlled by bulk flaws; and (c) both the computation and the experiment provide no evidence of coherent damage along the clamped top and bottom edges of the target.

A careful examination of the results displayed in Fig. 11(a) and (b) reveals that at a post-impact time of 15.7 μs, (a) there is a reasonably good agreement between the computational and the experimental results pertaining to the extent of coherent damage along the target strike face; (b) on the other hand, the overall size and depth of the computed coherent-damage zone is significantly smaller than the experimental damage zone counterparts from the work of Strassburger et al. (Ref 1, 2). However, if the size and depth of the entire (coherent damage and macrocracking) computed damage zone (Fig. 11a) is compared with the corresponding experimental results in Fig. 11(b), a reasonably good agreement is obtained. It should be noted that the shadowgraph technique used by Strassburger et al. (Ref 1, 2) has limitations in fully distinguishing between the coherent-damage and macrocracking failure modes. Thus, the overall computation/experiment agreement pertaining to the size and shape of the coherent-damage zone obtained in the present work may be better than the one suggested by comparing the coherent-damage zone displayed in Fig. 11(a) with the overall experimentally observed damage zone displayed in Fig. 11(b); and (c) the onset of damage along the (top and bottom) clamped faces of the target observed experimentally is not predicted computationally (e.g. Fig. 11b versus 11a). There are several potential reasons for this discrepancy. Two most likely reasons are: (i) the fixtures used to hold the target during impact introduce stresses into the target which, when superimposed with the impact-induced stresses, can cause an early damage initiation in the regions near the target top and bottom surfaces; and (ii) cutting and grinding of the side faces of the target used during the target manufacturing process may have changed the distribution and potency of surface flaws relative to those corresponding to the surface-flaw Weibull distribution parameters listed in Table 1. Both of the aforementioned hypotheses were tested in the present work. The first hypothesis was tested by adding compressive-normal and shear tractions to the top and bottom target faces, while the second hypothesis was investigated by reducing the mean fracture strength for the finite elements which reside on the impacted as well as the top and bottom clamped faces of the target. The results obtained (not shown for brevity) suggest that both of the hypothesized reasons may account for the observed discrepancy between the computed and experimental shapes of the coherent-damage zones. Thus, additional experimental investigation is needed to help resolve this uncertainty. Such experimental investigation may involve the use of chemical polishing which can reduce considerably the amount of damage induced by cutting/grinding.

To summarize, based on the results presented in this section, it appears that the proposed material model for soda-lime glass can capture the essential features of the spatial distribution and temporal evolution of the coherent-damage zone at shorter post-impact times. On the other hand, a good agreement between the computational and the experimental results at longer post-impact times pertaining to the damage zone size and shape can be obtained only if the computed total (coherent damage and macrocracking) damage zone is compared with the experimentally observed overall damage zone. It is also found that more experimental work is needed to establish if target fixturing or cutting/grinding-induced surface flaws alter the stress/microstructural state of the surface regions. Either of these effects can be readily included as fixturing-induced loads (i.e. through the changes in boundary conditions) or through changes in the values of the surface-flaw Weibull distribution parameters used in the present material model for soda-lime glass.

Temporal Evolution of the Discrete Damage

As discussed earlier, the experimental investigations carried out by Strassburger et al. (Ref 1, 2) revealed the formation of millimeter-size discrete cracks (i.e. crack centers) at a small distance ahead of the advancing coherent-damage zone front. To allow for the formation of discrete cracks, as discussed in Sect 2.3 and 2.4, a stress rate and a linear fracture mechanics based criteria were proposed to control the mode of damage initiation and ultimate failure of the ballistic soda-lime glass under impact loading conditions. That is, material points residing within the finite elements which reach the stress-based damage-initiation condition at a stress rate higher than a critical stress rate are assumed to undergo coherent damage and to fail in a dynamic-type multiple-fragmentation mode. This was justified by the fact that at high-stress rates and the associated high-stress levels, the criterion for crack nucleation is met at many points within the element. Conversely, material points residing within the finite elements which reach the stress-based damage-initiation condition at a stress rate lower than the critical stress rate are assumed to fail in a static-type coarse fragmentation failure mode, to reflect the fact that the first crack to form in these elements would traverse the entire element before additional cracks can nucleate. As discussed in Sect 2.4, when an element is located at a tip of a crack, its stress level is enhanced so that it is more likely to fail by the extension (growth) of the crack. Thus, in this case, despite the fact that the stress level (and perhaps the stress rate) may be high throughout the entire element in question, the static single-fragmentation fracture mode is assumed to take place.

The results obtained in the present work, Fig. 10(a, b) and 11(a, b), can be used to carry out a comparison between the computational results obtained in the present work and their experimental counterparts in Ref 1, 2 with respect to temporal evolution and spatial distribution of macrocracking. A comparison of the results displayed in Fig. 10(a) and (b) reveals a good computation/experiment agreement, i.e. no clear evidence of macrocracking is seen at the post-impact time of 7.7 μs. On the other hand, at a post-impact time of 15.7 μs, the computed results (Fig. 11a) reveal that a substantial portion of the overall damage zone is associated with macrocracking and that macrocracking primarily takes place in the regions ahead of the advancing coherent-damage zone front. These observations are fully consistent with the ones made by Strassburger et al. (Ref 1, 2) and, as pointed out earlier, one must recall that the experimental technique employed in their work had serious limitations concerning the discrimination between the two modes of damage. Consequently, the predictions made by the current material model for soda-lime glass regarding the spatial distribution and temporal evolution of macrocracking can be considered as encouraging.

In passing, it should be noted that the computational results obtained in the present work reveal that formation of macrocracks does not significantly affect the ability of the glass to absorb the kinetic energy of the projectile. In other words, macrocracking does not seriously compromise the ballistic protection performance of soda-lime glass. However, the formation of a large macrocracking zone surrounding the central coherent-damage zone during the frontal impact of a soda-lime glass based transparent armor can seriously degrade the functional performance of the armor by reducing its transparency/clarity.

Crack Morphology in Frontal Impact of a Laminated Transparent-Armor System

In an attempt to further validate the present material model for ballistic glass, a comparison was made between the computational results obtained in the present work and the corresponding experimental findings pertaining to the spatial distribution of damage and cracking during frontal impact of the glass panel by a hard projectile.

A review of the public-domain literature carried out in the present work was unsuccessful in identifying the appropriate experimental investigation involving frontal impact of monolithic glass panels. Instead, a comprehensive investigation carried out by Bless and Chen (Ref 21) pertaining to the frontal impact of glass-polyurethane-polycarbonate laminated transparent-armor system was located. Despite the fact that the transparent-armor system studied in the work of Bless and Chen (Ref 21) included other materials (polyurethane and polycarbonate), it was selected for the validation of the present material model for ballistic glass due to its completeness and relevant range of projectile velocity (ca. 1000 m/s). A brief summary of the relevant experimental findings reported by Bless and Chen (Ref 21) of the computational procedure used in the present work to study the frontal impact of the transparent-armor system and of the material models used in the present computational analysis for polyurethane and polycarbonate is provided below. A more detailed account of the above will be reported in our future communication (Ref 22).

In the work of Bless and Chen (Ref 21), the glass strike face of a nine-layer (seven 300 × 300 mm glass layers backed by two 360 × 360 mm polycarbonate layers) laminate with a total thickness of 88.7 mm was impacted with a 0.5 caliber chisel-nosed circular cylindrical projectile at a nominal velocity of 1000 m/s. Adjacent glass layers were separated by 0.6 mm polyurethane adhesive films. The armor laminate was placed in a vertical position and fixed along its two vertical sides using straps and a wooden block during impact. A post-mortem visual micrographic analysis was conducted on the partially penetrated armor plates and on the glass fragments. The main findings obtained in the work of Bless and Chen (Ref 21) which are relevant to the present investigation can be summarized as follows:

• (a) The projectile managed to fully penetrate only the front-most 6.4-mm-thick glass lamina and to partially penetrate the second 12.7-mm-thick glass lamina. The resulting crater radius was found to be ca. 31 mm. In the process of penetration, the projectile was compressed from its initial 18 mm length to a length of 8 mm.

• (b) While the remaining glass laminae were not penetrated by the projectile, they all experienced substantial damage. The damaged region surrounding the tip of the projectile was composed of very fine (sub-millimeter size) cracks (coherent damage) while in the region farther away from the projectile tip millimeter-size, isolated radial cracks, and fan-shaped and bow-tie-shaped crack bundles were observed. The extent of damage region in the radial direction at the bottom of the crater was ca. 70 mm, while at the back face of the last glass lamina was ca. 150 mm.

• (c) At the strike face of the armor, coherent damage was observed in a 20-mm-thick circular band region around the crater. At larger radial distances up to ca. 100 mm from the crater, isolated radial cracks and crack bundles were observed.

• (d) No evidence of deformation/damage in the two back-most polycarbonate layers was observed.

To test the ability of the present material model for ballistic glass to correctly account for the aforementioned experimental findings of Bless and Chen (Ref 21), a transient nonlinear dynamic analysis of the frontal impact of the laminated transparent-armor system was carried out in the present work. An example of the finite element mesh used in this portion of the work is shown in Fig. 12. To take advantage of the inherent symmetry of the problem, only a quarter of the model is analyzed, while the appropriate symmetry-plane boundary conditions are applied. Due to a very low thickness of the polyurethane films, the films were not modeled explicitly. Rather, their contribution was included through the use of the appropriate cohesive-zone interfaces. A derivation for the cohesive-zone material model for polyurethane was previously reported in Ref 23. The polycarbonate laminae were represented using an elastic/strain rate-dependent plastic material model (Ref 24) with a plastic strain-based damage initiation and a total plastic displacement-based failure criterion. Typically, the projectile was meshed using 500 tetrahedron elements, while the laminated transparent armor was meshed using 250,000 cubic/near-cubic eight-node reduced-integration solid elements. The projectile was initially assigned a velocity of 1118 m/s, while the top and bottom nodes of two opposing lateral faces of the armor were kept fixed during the analysis. As mentioned earlier, a more detailed account of the geometrical model of the laminated transparent armor, of the material models for polyurethane and polycarbonate and of the computational analysis will be presented in our future communication (Ref 22).

Fig. 12

A typical (quarter) meshed model used for the projectile and the laminated transparent-armor system used in the work by Bless and Chen (Ref 21)

A comparison between the computational results obtained in the present work and the corresponding experimental results obtained in the work of Bless and Chen (Ref 21) is shown in Fig. 13(a, b) and 14(a, b). The results displayed in Fig. 13(a) and (b) pertain to the post-mortem spatial distribution of damage over the vertical center cut-plane passing through the glass portion of the transparent-armor system. The results displayed in Fig. 14(a) and (b), on the other hand, show the spatial distribution of damage over the armor strike face. For both Fig. 13 and 14, the part (a) shows the computed results, while the part (b) displays the corresponding experimental results. Due to copyright restrictions, only schematics of the experimental results from Ref 21 could be displayed in Fig. 13(b) and 14(b).

Fig. 13

Distribution of coherent damage and macrocracking over the vertical center cut-plane of a frontally impacted transparent-armor system: (a) computational results obtained in the present work and (b) experimental results obtained in the work by Bless and Chen (Ref 21)

Fig. 14

Distribution of coherent damage and macrocracking over the strike face of a frontally impacted transparent-armor system: (a) computational results obtained in the present work and (b) experimental results obtained in the work by Bless and Chen (Ref 21)

A careful comparison of the computational results displayed in Fig. 13(a) and the corresponding experimental results displayed in Fig. 13(b) pertaining to the post-mortem spatial distribution of damage along a vertical center cut-plane reveals that:

• (a) The computed depth of armor penetration by the projectile closely matches its experimental counterpart (to within 5%).

• (b) The extent and shape of the total damage region (coherent damage and macrocracking) in the transparent armor found in the experimental work is reproduced with reasonable accuracy by the computation. However, the extent of coherent damage is somewhat over-estimated while the macrocracking is under-predicted.

• (c) In good agreement with the experiment, the computational results predict the formation of more extensive coherent damage at the back face of the last glass lamina. This damage was found to be caused by the release tensile stress waves generated by reflection of the incident compressive stress waves at the glass/polycarbonate interface.

• (d) The experimental results displayed in Fig. 13(b) show the presence of a coherent-damage free region (denoted as the compacted disk region) ahead of the projectile extending over four glass laminae. The computed results also reveal the presence of a coherent-damage free region, but this region is confined to within only two glass laminae.

A careful comparison between the computational results displayed in Fig. 14(a) and the corresponding experimental results in Fig. 14(b) pertaining to the post-mortem spatial distribution of damage over the transparent armor strike face yielded the following findings: While the experimental results indicate five distinct zones (central circular impact crater, the innermost circular ring region containing very fine bundled radial cracks, the intermediate circular ring region containing fan-shaped crack bundles, the outer circular ring region containing well-spaced coarse radial cracks and outermost crack-free region listed from the center of impact outward), four of these regions except for the intermediate region with fan-shaped cracks are reproduced well computationally. In addition, the size of the central circular impact crater, the innermost circular ring region containing very fine bundled radial cracks and the outer circular ring region containing well-spaced coarse radial cracks are matched within 10-30%. The intermediate central circular ring region containing fan-shaped crack bundles (not observed computationally) was postulated in Ref 21 to form by the release stress waves reflected from the target’s free lateral surfaces. Although stress wave reflection was observed in the present work, the stress magnitudes were not sufficiently high to nucleate cracks. Another possible reason for the lack of the formation of fan-shaped crack bundles is that the number of possible macrocrack growth directions (five on the strike face surface) was highly limited.

In summary, the overall computation/experiment agreement regarding the spatial distribution of coherent damage and macrocracking both over the transparent armor vertical center cut-plane and the strike face can be deemed as reasonable.

Summary and Conclusions

Based on the material model development procedure utilized and the results of the subsequent computational analyses, the following main summary remarks and conclusions can be drawn:

• 1. The simple, physically based, high-strain rate, high-pressure, large-strain mechanical model for ballistic soda-lime glass originally proposed in Ref 4 has been extended to include a linear fracture mechanics-based model for macrocracking. This extension enables modeling of the formation and growth of millimeter-size isolated cracks and crack bundles.

• 2. To test the model, a series of transient non-linear dynamics analyses pertaining to the EOI of plate-like monolithic soda-lime glass targets with a spherical projectile and frontal impact of laminated glass/polycarbonate transparent-armor system with a chisel-nosed cylindrical projectile was conducted and the results obtained compared with their experimental counterparts as reported by Strassburger et al. (Ref 1, 15) and Bless and Chen (Ref 21), respectively.

• 3. A comparison between the computed and experimental EOI results revealed that the proposed model fairly well accounts for the propagation of the elastic (longitudinal and transverse) waves in the target following impact and that the predicted speeds of these waves are quite comparable with their experimental counterparts. Likewise, a good agreement between the computed and experimental results is obtained relative to the temporal evolution of size and the shape of the coherent damage and macrocracking zones. The observed computation/experiment disagreements were attributed to the effect of clamping-induced contact stresses and/or cutting/grinding-induced flaw-population changes along the lateral faces of the target.

• 4. A comparison between the computed and the experimental frontal impact results revealed a reasonably good agreement with respect to spatial distribution and the extent of coherent damage and macrocracking both along the transparent-armor strike face and along a vertical center cut-plane. Minor computation/experiment discrepancies were observed relative to the absence of fan-shaped crack bundles over the transparent-armor strike-face in the computational results and these were attributed to the low intensity of the release tensile stress waves and a limited number of possible crack-growth directions.