Abstract
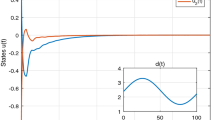
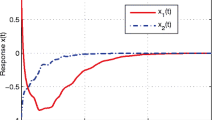
This paper investigates global convergence for a novel class of delayed neural networks with non-Lipschitz neuron activations and impulses based on the topological degree theory and Lyapunov functional method. Some suffcient conditions are derived to ensure the existence, and global exponential stability of the equilibrium point of neural networks. Finally, a numerical example is given to demonstrate the effectiveness of the obtained result.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Zhou, L., Hu, G.: Global Exponential Periodicity and Stability of Cellular Neural Networks with Variable and Distributed Delays. Applied Mathematics and Computation 195, 402–411 (2008)
Li, T., Fei, S.: Stability Analysis of Cohen-Grossberg Neural Networks with Time-Varying and Distributed Delays. Neurocomputing 71, 1069–1081 (2008)
Zhang, Q., Wei, X., Xu, J.: Delay-Dependent Exponential Stability Criteria for Non-Autonomous Cellular Neural Networks with Time-Varying Delays. Chaos, Solitons and Fractals 36, 985–990 (2008)
Zhao, W.: Dynamics of Cohen-Grossberg Neural Network with Variable Coefficients and Time-Varying Delays. Nonlinear Analysis: Real World Applications 9, 1024–1037 (2008)
Xiong, W., Zhou, Q., Xiao, B., Yu, Y.: Global Exponential Stability of Cellular Neural Networks with Mixed Delays and Impulses. Chaos, Solitons and Fractals 34, 896–902 (2007)
Huang, Z., Yang, Q., Luo, X.: Exponential Stability of Impulsive Neural Networks with Time-Varying Delays. Chaos, Solitons and Fractals 35, 770–780 (2008)
Long, S., Xu, D.: Delay-Dependent Stability Analysis for Impulsive Neural Networks with Time-Varying Delays. Neurocomputing 71, 1705–1713 (2008)
Wu, H., Xue, X.: Stability Analysis for Neural Networks with Inverse Lipschitzian Neuron Activations and Impulses. Applied Mathematical Modelling 32, 2347–2359 (2008)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2009 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Fu, C., Wu, A. (2009). Global Exponential Stability of Delayed Neural Networks with Non-lipschitz Neuron Activations and Impulses. In: Cai, Z., Li, Z., Kang, Z., Liu, Y. (eds) Advances in Computation and Intelligence. ISICA 2009. Lecture Notes in Computer Science, vol 5821. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-04843-2_11
Download citation
DOI: https://doi.org/10.1007/978-3-642-04843-2_11
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-04842-5
Online ISBN: 978-3-642-04843-2
eBook Packages: Computer ScienceComputer Science (R0)