Abstract
The multispecies coalescent (MSC) model provides a compelling framework for building phylogenetic trees from multilocus DNA sequence data. The pure MSC is best thought of as a special case of so-called “multispecies network coalescent” models, in which gene flow is allowed among branches of the tree, whereas MSC methods assume there is no gene flow between diverging species. Early implementations of the MSC, such as “parsimony” or “democratic vote” approaches to combining information from multiple gene trees, as well as concatenation, in which DNA sequences from multiple gene trees are combined into a single “supergene,” were quickly shown to be inconsistent in some regions of tree space, in so far as they converged on the incorrect species tree as more gene trees and sequence data were accumulated. The anomaly zone, a region of tree space in which the most frequent gene tree is different from the species tree, is one such region where many so-called “coalescent” methods are inconsistent. Second-generation implementations of the MSC employed Bayesian or likelihood models; these are consistent in all regions of gene tree space, but Bayesian methods in particular are incapable of handling the large phylogenomic data sets currently available. Two-step methods, such as MP-EST and ASTRAL, in which gene trees are first estimated and then combined to estimate an overarching species tree, are currently popular in part because they can handle large phylogenomic data sets. These methods are consistent in the anomaly zone but can sometimes provide inappropriate measures of tree support or apportion error and signal in the data inappropriately. MP-EST in particular employs a likelihood model which can be conveniently manipulated to perform statistical tests of competing species trees, incorporating the likelihood of the collected gene trees on each species tree in a likelihood ratio test. Such tests provide a useful alternative to the multilocus bootstrap, which only indirectly tests the appropriateness of competing species trees. We illustrate these tests and implementations of the MSC with examples and suggest that MSC methods are a useful class of models effectively using information from multiple loci to build phylogenetic trees.
You have full access to this open access chapter, Download protocol PDF
Similar content being viewed by others
Key words
1 Introduction
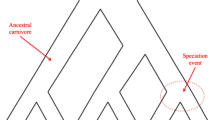
The concept of a phylogeny or “species tree,” a bifurcating dendrogram graphically depicting the relationships among a group species, is one of the oldest and most powerful icons in all of biology. After Charles Darwin sketched the first species tree (in Transmutation of Species, Notebook B, 1837), he remained fascinated by the image for 22 years, eventually including a species tree as the only figure in On the Origin of Species [1]. Though species trees reached their aesthetic apogee with Ernst Haeckel’s Tree of Life in 1886, the pursuit of ever-more scientifically accurate trees has kept phylogenetics a vibrant discipline for the 150 years since.
Because the direct evolution of species in the past is not observable (not even in the fossil record), relationships among species are often inferred by shared characteristics among extant taxa. Until the 1970s, this effort took place almost exclusively by using morphological characters. Although this approach had many successes, the paucity of characters and the challenges of comparing species with no obvious morphological homologies were persistent problems [2, 3]. When molecular techniques were developed in the late 1960s, it soon became clear that the sheer volume of molecular data that could be collected would represent a vast improvement. When DNA sequences became widely available for a range of species [4], molecular comparisons quickly became de rigueur [5,6,7,8]. Nonetheless, it was recognized early on that molecular phylogenies had their own suite of problems; the concept that not all gene tree topologies would match the true species tree topology (i.e., would not be speciodendric sensu Rosenberg [9]) was implicit in early empirical allozyme and mitochondrial DNA studies [10, 11]. However, it was generally assumed that the idiosyncratic genealogical history of any one gene, as reconstructed from extant mutations, was an acceptable approximation for the true history of the species given the potentially overwhelming quantity and seductive utility of molecular data [12,13,14,15]. Indeed, this assumption is still prevalent in the thinking of those who favor concatenation or supermatrix approaches as a means of combining information from multiple genes that may still differ in their genealogy from each other and from the species tree [16, 17]. In the meantime, the term “phylogeny” frequently became conflated with “gene tree,” the entity produced by many of the leading phylogenetic packages of the day. The term “species tree,” in use since the late 1970s to emphasize the distinction between lineage histories and gene histories (reviewed in [11, 18]), was only gradually acknowledged, despite the fact that species trees are the rightful heirs to the term “phylogeny” and better encapsulate the true goals of molecular and morphological systematics [19].
1.1 Stopgap Approaches to Gene Tree Heterogeneity
By and large, the ensuing decades of molecular phylogenetics has fulfilled much of its potential, revolutionizing taxonomies and resolving conundrums previously considered intractable. However, as the amount of genetic data per species becomes ever-more voluminous, it has become clear that the conflicts between individual genes with each other and with the overarching species tree, both in topology and branch lengths, can have practical consequences for phylogenetic analysis if not dealt with properly [18,19,20,21,22,23]. At first, some researchers treated this phenomenon as though it were an information problem: when working with only a few mutations, you were bound to occasionally get unlucky and sequence a gene whose random signal of evolution did not match that of the taxa being studied. The reasoning was surely more and/or longer sequences would fix that problem and cause gene trees to converge [16]. However, as more genes were sequenced, and as the properties of gene lineages within populations were studied in detail [24, 25], the twin realities of gene tree heterogeneity and “incomplete lineage sorting” [11] (ILS) became clear (Figs. 1 and 2). The probability of an event such as incomplete lineage sorting, which if considered alone would lead to inferring the wrong species tree, was worked out theoretically for the four allele/two species case first [26], followed by the three allele/three species case [7, 13] and more general cases [12, 27]. Pamilo and Nei [12] were among those that proposed that the solution was to simply acquire more gene sequences, after which the central tendency of this gene set would point to the correct relationships, a “democratic vote” method, where each gene was allowed to propose its own tree, and the topology with the most “votes” was declared the winner and therefore the true phylogeny. Though generally true for three-species case, it can sometimes produce the wrong topology with four or more species [28]. In fact, we now know that with four or more species, there is an “anomaly zone” for species trees with short branch lengths as measured in coalescence units, in which the addition of more genes for sampled taxa is guaranteed to lead to the wrong species tree topology for the democratic vote method [29, 30]. (Coalescent time units, equivalent to t/Ne where t is the number of generations since divergence and Ne is the effective population size of the lineage, are a convenient unit for discussions of gene tree/species tree heterogeneity. For a clear explanation, see Box 2 of Degnan and Rosenberg [28].) Such anomaly zones may be rare empirically [31], but empirical examples are emerging [32, 33], and even the theoretical possibility remains disconcerting. In addition, because the number of possible tree topologies increases as the double factorial of the number of tips, for species trees with more than four tips, a very large number of genes are required to determine which gene tree is in fact the most frequent. Advanced consensus methods [34] can circumvent some of the problems of the democratic vote by using novel assembly methods, such as rooted triple consensus [35], greedy consensus [36], or supertree methods [37]. However, although such methods suffer from lack of a biological model motivating the method of consensus, approaches such as that proposed by Steel and Rodrigo [38] might help approximate the dynamics of biological models while allowing for faster and more flexible extensions and should be further developed.
An example showing the utility of multiple gene trees in producing species tree topologies. (a) Nine unlinked loci are simulated (or inferred without error) from a species group with substantial amounts of incomplete lineage sorting. Note that no single gene recovers the correct relationship between clades. Furthermore, despite identical conditions for all nine simulations, no two genes agree on the correct topology, let alone the correct divergence times. (b) Superimposing the nine gene trees on top of each other clarifies the relationships. It can be (correctly) inferred that the true tree is perfectly ordered, with (ABC) diverging from D about 1500 generations ago, the (AB)-C split occurring at 800, and A diverging from B about 600 generations ago. Also, the amount of crossbreeding within the recently diverged taxa implies (correctly) that C has the effective smallest population size
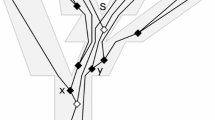
The relationship between gene trees and species trees. Lines within the species trees indicate gene lineages. Simplified gene trees are shown below each species tree. Whereas gene trees on the left vary due to deep coalescence, gene trees on the right are topologically concordant but vary slightly in branch lengths due to the coalescent. Modified with permission from [19]
The second empirical approach to the problem of conflicting gene trees was to bypass it altogether. Concatenation methods appended the sequence of one gene to that of the next, to create long alignments or supermatrices [39], a technique that in some situations was superior to standard consensus methods in resolving discordance or achieving statistical consistency [40]. But some researchers, including those who questioned the “total-evidence” approach to systematics (e.g., [41]), advocated against concatenation when, for whatever reason, gene trees appeared to conflict with one another. One problem with the concatenation approach was that it assumed full linkage across the supermatrix, a situation that would obviously not be the case if genes were on different chromosomes. Even when the lineage lengths in a species tree are long in coalescent units, such that gene tree topologies are congruent, the branch lengths of trees of genes on different chromosomes will differ subtly from one another due to the stochasticity of the coalescent process. The early implementations of this method also assumed the same distribution of mutation rates across the sequence, which was clearly not the case if the matrix included coding and noncoding regions. Like democratic vote methods, concatenation of many genes was sometimes defended as sufficient to override the conflicting signal across genes [42, 43], despite widespread acknowledgment that gene tree heterogeneity is ubiquitous and that concatenation can sometimes give the wrong answer, especially although not exclusively in the anomaly zone [44, 45].
Concatenation as a method of combining phylogenomic data still remains popular by default [16, 46], particularly among phylogenetic studies of higher taxa where incomplete lineage sorting is assumed to be rare. However, this logic suffers from two flaws frequently seen in the literature. First, “deep” phylogenetic studies among higher taxa are no more immune to the problems of ILS than are studies among closely related species, because it is the length of a given branch, not its depth in the tree, that is relevant to probability of gene tree discordance [28]. Detecting such ILS and ruling out gene tree congruence will indeed be more challenging in deep phylogenomic studies, but it should not be assumed that ILS will be less prevalent at deep scales than at shallow scales. Second, current implementations of concatenation represent only one way of species tree construction in which each gene is forced to have the same topology. The real distinction between concatenation and coalescent models is not the presence or absence of ILS but rather the possibility of conditional independence of gene trees as mediated by recombination between genes [47]. Even if all gene trees in an analysis are topologically identical, physically connecting different genes in a single supermatrix does not capture variation in branch lengths that recombination will allow in nature. More effort should be devoted to “supermatrix-like” methods that constrain gene trees to the same topology but allow recombination between genes and conditional independence of branch lengths, since these qualities will influence how signal is accumulated as more genes are added [47]. A final problem with concatenation is that, in a strict sense, concatenation also does not generate species trees, in so far as the method treats all nucleotides as if they were part of a single non-recombining gene, and thus does not distinguish between gene and species trees [19]. In the end, concatenation is best thought of as a special case of more general models of phylogenetic inference that acknowledge gene tree heterogeneity and conditional independence of genes. One such model is the multispecies coalescent model [23, 28, 48]. It is this model that provides the basis for a recent flurry of promising methods that permit efficient and consistent estimation of species trees under a variety of conditions.
2 The Multispecies Coalescent Model
A plausible probabilistic model for analyzing multilocus sequences should involve not only the phylogenetic relationship of species (species tree) but also the genealogical history of each gene (gene tree) and allow different genes to have different histories. Unlike concatenation, such a multispecies coalescent model (MSC) explains the evolutionary history of multilocus sequences through two levels of biological hierarchy, the gene tree and the species tree, rather than just one [23, 49]. Models acknowledging these two levels require an explicit description of how sequences evolve on gene trees, the traditional likelihood equation of Felsenstein [50] and others, as well as how gene trees evolve in the species tree, the likelihood for which was first described by Rannala and Yang [48]. With a few exceptions (described below), the genealogical relationship (gene tree) of neutral alleles can be simply depicted by a coalescence process in which lineages randomly coalesce with each other backward in time. The MSC is a simple application of the single population coalescent model to each branch in a species tree [28]. It holds the standard assumptions found in many neutral coalescent models: no natural selection or gene flow among populations, no recombination within loci but free recombination between loci, random mating and a Wright-Fisher model of inheritance down each branch of the species tree. Despite these seemingly oversimplified assumptions, the pure coalescent model is fundamental in explaining the gene tree-species tree relationship because it forms a baseline for incorporating additional evolutionary forces on top of random drift [28, 49]. More importantly, the pure coalescent model provides an analytic tool to detect the evolutionary forces responsible for the deviation of the observed data (molecular sequences) from those expected from the model.
The coalescent process works, in effect, by randomly choosing ancestors with replacement from the population backward through time for each sequence in the original sample. Eventually, two of these lineages will share a common ancestor, and the lineages are said to “coalesce.” The process continues until all lineages coalesce at the most recent common ancestor (MRCA). Multispecies coalescence works the same way but places constraints on how recently the coalescences occur, corresponding to the species’ divergence times. Translating this model into computer algorithms for inferring species trees has led to a plethora of models [51,52,53,54,55], some of which first build gene trees by traditional methods and then combine them into a species tree with the highest likelihood or other criteria (“two-step” methods, e.g., [56] or [57]), others of which, particularly Bayesian methods [58,59,60], simultaneously estimate gene trees and species tree. In general for likelihood or Bayesian approaches, a species tree has been proposed, and the likelihood of each gene tree is evaluated using the MSC, with or without various priors, to evaluate the likelihood of the data (DNA sequences in the case of Bayesian methods or gene trees in the case of likelihood methods like MP-EST [56]) given the species tree or the posterior probability of the species tree. In this way, traditional multispecies coalescent methods are the converse of consensus methods; rather than each locus proposing a potentially divergent species tree, a common species tree is assumed and evaluated, given the sometimes divergent patterns observed among multiple loci.
A number of implementations of this idea have been developed (reviewed by Edwards [19, 54]). Several “two-step” packages are available for moving from independently built gene trees to species trees, including minimization of deep coalescence [61], STEM [62], JIST [63], GLASS [64], STAR, STEAC [65], NJst [66], and ASTRAL [57, 67]. Three methods to date utilize “one-step” Bayesian methods to infer gene trees and the species tree, with the input data being DNA sequences: BEST [58, 68, 69], *BEAST2 [59], and a new model (A00) in the Bayesian Phylogenetics and Phylogeography (bpp) package [70,71,72]. An additional “one-step” method, SVD Quartets [73], derives species trees directly from aligned, unlinked single-nucleotide polymorphisms using the method of invariants in a coalescent framework. Species tree methods exhibit a number of attractive advantages over concatenation methods in terms of performance. These advantages are not restricted to the anomaly zone, occur across broad regions of tree space, and include less susceptibility to long-branch attraction [74] and missing data [75]. Another attractive aspect of species tree methods and multispecies coalescent models is that they deliver more appropriate estimated levels of confidence that are more evenly spread across genes and appear to be less susceptible to the inflation of posterior probabilities that was early on attributed to Bayesian analyses (e.g., [76, 77]) but may also be due to model misspecification due to concatenation [53]. Bayesian methods are generally agreed to be the most efficient and accurate, capturing all details of the MSC model seamlessly [52]. However, one drawback is that the estimation of larger numbers of parameters (population sizes and divergence times in addition to topologies) can slow computation, may not be relevant in some situations [78], and is generally not possible with the large data sets that are routinely seen today in phylogenomics [59]. Thus far, two-step methods such as ASTRAL, STAR, NJst, and MP-EST have proven the most widely used for large-scale phylogenomic studies, such as the Avian Phylogenomics Project [79] and large-scale phylogenomics of fish [80] and plants [81].
2.1 Sources of Gene Tree/Species Tree Discordance and Violations of the Multispecies Coalescent Model
2.1.1 Population Processes
The “standard” and most common reason why gene trees are not speciodendritic is incomplete lineage sorting, i.e., lineages have not yet been reproductively isolated for long enough for drift to cause complete genetic divergence in the form of reciprocal monophyly of gene trees ([82]; Figs. 1 and 2). This source of gene tree heterogeneity is guaranteed to be ubiquitous, if only because it arises from the finite size populations of all species that have ever come into existence. Almost all the techniques and software packages discussed above are designed to approximate uncertainties in species tree topology arising from this phenomenon.
2.1.1.1 Delimitation of Species and Diverging Lineages
For recent divergences, the definition of “species” can become problematic for species tree methods [63], and the challenge of delimiting species has, if anything, increased now that the overly conservative strictures of gene tree monophyly as a delimiter of species have been mostly abandoned [82]. This fundamental issue in a phylogenetic study—whether the extent of divergence among lineages warrants species status—has not gone away in the genomic era. However, traditional species tree methods using the MSC need not use “good” species as OTUs; they will work perfectly well on lineages that have recently diverged, so long as they have ceased exchanging genes. The key issue is not whether the OTUs in species tree analyses are in fact species but rather whether they have ceased exchanging genes, which has been shown to compromise traditional MSC methods [83, 84] (see below).
The problem of species delimitation may ultimately be solved by data other than genetics, and today few species concepts use strictly genetic criteria [85]. Some have suggested that the line between a population-level difference and a species-level difference can be drawn empirically and with consistency in well-studied taxa such as birds, using morphological, environmental, and behavioral data simultaneously [86]. Thus, there is some hope that species delimitation can be performed rigorously a priori in many cases. Researchers who opt for delimiting species primarily with molecular data have a wide array of techniques and prior examples available to them, although not all without controversy [71, 87,88,89,90,91,92,93]. Recent progress in species delimitation is motivated by the conceptual transition from “biological/reproductive isolation species” to the “lineage species concept,” which defines species not in terms of monophyly of gene lineages but as population lineage segments in the species tree [93]. Under that expanded concept, boundaries of species (i.e., lineages in the species tree) can be facilitated by collection and analysis of gene trees in the framework of the multispecies coalescent model [72]. The recent suggestion that coalescent species delimitation methods define only structure but not species [90] was, in our view, already well-established, with confusion stemming largely from the term “species delimitation,” as opposed to “delimitation of populations between which gene flow has ceased.”
2.1.1.2 Gene Flow
There are a number of other situations in which the assumptions of the coalescent are violated. MSC models involve a series of isolation events unaccompanied by gene flow. In this regard, they are like the isolation-migration models of phylogeography [94, 95] but without the migration. The assumption of no gene flow naturally restricts their utility, but gene flow of course compromises other methods of phylogenetic inference, including concatenation methods, as well. Additionally, situations in which gene flow yields a prominent molecular signal often are detectable primarily among very closely related species in the realm of phylogeography [96]. If some substantial gene flow continues between species after divergence, then the multispecies coalescent can quickly destabilize, especially for a small number of loci and as the rate of genetic introgression increases (Fig. 6 in [87, 97,98,99]). We recommend model comparison algorithms like PHRAPL [87] for determining whether a given data set conforms to the assumptions of the MSC.
2.1.2 Molecular Processes
In addition to species delimitation and gene flow, there are at least three mechanisms that generate discordance on the molecular level (Fig. 3). These include horizontal gene transfer (HGT), which can pose a serious risk to phylogenetic analysis; gene duplication, whose risks can be avoided by certain models; and natural selection, which generally poses no direct threat but, depending on its mode of action and consequences for DNA and protein sequences, can be the most challenging of all.
Three examples of gene histories that depart from the standard multispecies coalescent model. (a) A duplication event that precedes a speciation event can lead to incorrect inference of divergence times in the species tree if copy 1 is compared to copy 2. This can be particularly difficult if one of the gene copies has been lost or not sequenced by the researcher. (b) Convergent evolution can occur at the molecular level, for example, in certain genes under strong natural selection or highly biased mutational processes. These processes will tend to bring together distantly related taxa in the phylogenetic tree and are likely to be given additional false support by morphological data. (c) Horizontal gene transfer causes difficulties in some current species tree methods, because it establishes a spurious lower bound to divergence times. Though rare in eukaryotes, it is by no means unknown and is likely to become a more difficult problem in the future when species trees are based on tens of thousands of loci
2.1.2.1 Horizontal Gene Transfer
HGT is now known to be so widespread across the Tree of Life, especially in prokaryotes, that some have suggested a web of life may be a more appropriate paradigm for phylogenetic change [100,101,102]. Growing evidence shows that even eukaryotic genomes contain substantial amounts of “uploaded” genetic material from bacteria, archaea, viruses, and even fellow eukaryotes [103,104,105]. Even though effective techniques are not yet widely available for detecting HGT in eukaryotes, enough individual cases have been “accidentally” discovered that researchers have given up trying to list them all [103].
The implications of HGT for species tree construction vary depending on the method used. For example, following the standard assumption in coalescent theory that allelic divergences must occur earlier in time than the divergences of species harboring those alleles, some species tree techniques [48, 58], as well as classical approaches (e.g., [13]), assume that the gene tree exhibiting the most recent divergence between taxon A and taxon B establishes a hard upper limit on the divergence time of those species in the species tree. For small sets of genes in taxa where HGT is rare, a researcher would need to be quite unlucky to choose a horizontally transferred gene for analysis. However, as the genomic era advances, it becomes more likely that at least one of the thousands of genes studied will have been transferred horizontally and thus establish a spurious upper bound for clade divergence at the species level. When selective introgression of genes from one species to another is considered, this number of genes coalescing recently between species will increase [106]. Although HGT is clearly a problem for some current methodologies, if transferred genes can first be identified, then they could be extremely useful as genomic markers for monophyletic groups that have inherited such genes and would otherwise be difficult to resolve [107]. However, for other species tree methods that calculate averages of coalescence times, such as STAR [65], HGT events will have less of an impact. Liu et al. [56] examined the effect of HGT on the pseudo-likelihood method MP-EST and predicted that, mathematically, species tree branch lengths may be biased by HGT but that topologies were fairly robust. Davidson et al. [108] found that quartet-based methods, such as ASTRAL-II, were fairly robust to HGT in the presence of ILS. Removal of genes suspected to be transferred via HGT prior to species tree analysis would be warranted; however, some methods to detect such events rely both on having the true species tree already in hand and also on the absence of other mechanisms causing gene tree discordance [109,110,111,112]. Recent work aims to incorporate HGT into other mechanisms of gene tree incongruence (reviewed in [113]); how much we need to invest in such synthetic methods will likely depend on the prevalence of HGT in particular taxonomic groups.
2.1.2.2 Gene Duplication
Gene duplication presents another violation of the basic MSC model (Fig. 3); like HGT, its potential problems are worst when they go unrecognized [49]. Imagine a taxon where a gene of interest duplicated 10 Mya into copy α and copy β; the taxon then split 5 Mya into species 1 and 2. A researcher investigating the daughter species would therefore sequence four orthologous genes, with the potential to compare α1 to β2 and β1 to α2 and thus generate two gene trees where the estimated split time was 10 Mya, rather than 5 Mya. Such a situation will be easily recognized if copy α and β have diverged sufficiently by the time of their duplication, and a number of methods of coalescent analysis have incorporated gene duplication (e.g., [114, 115]; reviewed in [116]). Additionally, failure to recognize the situation may not have drastic consequences for phylogenetic analysis if the paralogs have coalesced very recently or are species-specific, in which case the estimated gene coalescence would be approximately correct no matter which comparison was made. However, if one of the copies has been lost and only one of the remaining copies is sequenced, then the chances of inferring an inappropriately long period of genetic isolation are larger and will increase as the size of the family of paralogs increases. Assessing paralogs in phylogenomic data is a major challenge, particularly in groups like plants and fish, and a growing number of dedicated methods ([117]; assessed in [118]) or filtering protocols [119] for doing so exist. This problem will tend to overestimate gene coalescence times, and some species tree methods depend on minimum isolation times among a large set of genes. These deep coalescences might spuriously increase inferred ancestral population sizes. A systematic search for biases incurred by species tree methods due to gene duplication is needed.
2.1.2.3 Natural Selection
Natural selection causes yet another violation of the multispecies coalescent model. Selection can cause serious problems in some cases, although in other circumstances it is predicted not to cause problems of phylogenetic analysis [47, 120]. The usual stabilizing selection can be helpful to taxonomists working at high levels because it slows the substitution rate; likewise selective sweeps, directional selection, and genetic surfing [121] tend to clarify phylogenetic relationships by accelerating reciprocal monophyly for genes in rapidly diverging clades. However, challenges to phylogenetic inference are posed by any evolutionary force that may bias the reconstruction of gene trees, including convergent neutral mutations (homoplasy), balancing selection, and selection-driven convergent evolution (e.g., [122]). Balancing selection tends to preserve beneficial alleles at a gene for long periods of time and is probably the most insidious form of selection with respect to accurately reconstructing gene trees and species trees.
2.2 More About Violations and Model Fit of the Multispecies Coalescent Model
Many of the instances of violations of the coalescent model will occur at individual genes and usually will not dominate the signal of the entire suite of genes sampled for phylogenetic analysis. Reid et al. [123] conducted one of the few tests of the fit of the MSC to multilocus phylogenetic data. Although the title of their article suggests that the MSC overall provides a “poor fit” to empirical data, we suggest that their results provide a more hopeful picture. The most important thing is that they investigated the fit of the MSC to individual loci in phylogenetic data sets and were able to identify loci that failed to fit the MSC. They were less successful at identifying the causes of departure from the MSC for individual loci.
More common but still rare are efforts to determine which models of phylogenetic inference, the MSC or concatenation, provide a better fit to empirical phylogenomic data. Edwards et al. [124] and Liu and Pearl [58] both used the Bayesian species tree method BEST [68] to ask using Bayes factors whether the MSC or concatenation fits empirical data sets better. Uniformly, they found that the MSC fit empirical data sets better than concatenation, often by a large margin. However, further work in this area is still needed. Most discussions in the literature have focused on the perceived failings or violations of the MSC by empirical data sets—such as evidence for recombination within loci—even when such failings or assumptions also apply to concatenation [47]. Given that all models are approximations of reality, a better focus would be to ask which model better fits empirical data sets better. The limited research that has been done suggests overwhelmingly that the MSC provides a better fit to empirical data sets than concatenation.
Are there better models for phylogenomics than the MSC? Depending on the data set, almost surely there are (Fig. 4). Several authors working with phylogenomic data sets have suggested that gene flow is detectable, even among lineages that diverged a long time ago (e.g., [129, 130]). The increasing number of reports of hybridization and introgression among phenotypically distinct species suggests that hybridization may be a typical component of speciation and that even phylogenetic models can be improved by incorporating such reticulation (e.g., [47, 106, 131]). The pure MSC is best thought of as a special case of so-called “multispecies network coalescent” models, or MSNC [127, 132,133,134] (Fig. 4), in which gene flow connects some branches of the species tree. In the end, empiricists will need to decide what level of model fit they are willing to tolerate and which software packages can accommodate the large data sets that are now routine in phylogenomics.
Diversity of phylogeographic models. Species trees estimated by the multispecies coalescent are naturally related to previous phylogeographic models by their shared demographic parameters, usually measured in units of mutation rate or substitutions per site (μ), including genetic diversity or effective population size (4Nμ, where N = effective population size; gene flow M/μ, where M = the scaled migration rate; 4Nm, where m is the number of migrants per generation; and divergence time τ = μt, where t is the divergence time in generations). (a) Equilibrium migration models as envisioned by early versions of the software MIGRATE [125]. (b) Isolation-migration models envisioned by Hey and coworkers [48, 95, 126]. Subscript A indicates ancestral population size. (c) Species tree models estimated by the multispecies coalescent [28]. (d) Multispecies network coalescent models or phylogenetic network models including divergence and gene flow [127, 128]
2.2.1 Phylogenetic Outlier Loci
Genes whose phylogenetic signal differs significantly from that of the remainder of data set can be thought of as phylogenetic outliers. These loci are conceptually similar to outliers in population genetics, which have been the focus of many studies (reviewed in [135,136,137]). However, there has been little work in detecting phylogenomic outliers. Much attention has been paid to particular sites in a data set that differ from the majority and therefore exhibit homoplasy or incongruence with the rest of the data set [76, 138]. The sources of such incongruence are many and can include mutational processes (e.g., gene duplication), HGT, as well homoplasy (e.g., [139, 140]). Incongruence of particular sites, or entire loci, may also be due to technical issues such as contamination, misassembly, mistaken paralogy, annotation mistakes, and alignment errors (e.g., [119]). Here, in an analogy with work in population genetics, we will focus primarily on entire loci that deviate from the expected distribution governed by neutral processes due to natural selection. Understanding the distribution of gene tree topologies expected under the neutral multispecies coalescent [25] is a good starting point for identifying loci that may be targets of natural selection.
2.2.2 Genomic Signals of Phylogenetic Outliers
When faced with a surprising or nonconvergent species tree, one possibility is that an unusual gene tree is to blame. Though techniques for dealing with violations of the coalescent model are in their infancy, researchers do have a few options. Below we list several ideas, some borrowed from classical phylogenetics or from methods used in bioinformatics. It is likely that the several tests constructed to detect phylogenetic outliers in classical phylogenetics can be extended slightly to incorporate the additional variation among genes expected due to the coalescent process. Of course, with larger data sets, at least with some coalescent methods, single anomalous genes may have little effect on the resulting species tree, particularly in species tree methods utilizing summary statistics [65]. However, as pointed out above, species tree methods such as BEST that relies on “hard” boundaries for the species tree by individual genes could be derailed due to the anomalous behavior of even a single gene.
Jackknifing: A straightforward approach to detecting phylogenetic outliers under the multispecies coalescent model is to rerun the analysis n times, where n is the number of loci in the study, leaving one locus out each time. An outlier can then be identified if the analysis that does not include that gene differs from the remaining analyses in which that gene is included. This approach has been applied successfully in fruit flies by Wong et al. [21], who considered their problem resolved when the elimination of one of the ten genes unambiguously resolved a polytomy. There may be other metrics of success that are more robust or sensitive or do not depend as strongly on a priori beliefs about the relationships among taxa. Because some duplications or horizontal transfers may affect only one taxon, whole-tree topology summary statistics are unlikely to be sensitive enough to detect recent events. However, the cophenetic distance of each taxon to its nearest neighbor in the complete species tree could be compared across jackknife results. This procedure will produce a distribution of “typical” distances, and significance can therefore be assigned to highly divergent results. The drawback to such an approach is the computational demand. Species tree analyses on their own can be extremely time consuming to run even once, so jackknifing may prove intractable for studies involving many species and loci (see ref. 141).
2.2.3 Simulation Approaches to Detecting Phylogenetic Outliers
Simulating gene trees from a species tree is another method for identifying gene trees that differ from the majority of loci in the data set. Several species tree methods yield estimate of the phylogeny that include branch lengths in coalescent units [56, 57, 70], which are required to simulate gene trees from a species tree. Branch lengths in the estimated species tree can be decomposed into a number of substitutions per site and an estimate of θ = 4Nμ that are compatible with the original branch length in coalescent units. For example, using any number of algorithms, including maximum likelihood or Bayesian methods, the length of species tree branch lengths in substitutions per site can be approximated by fitting the concatenated alignment of genes to the estimated species tree topology, yielding a tree with the same topology but branch lengths in substitutions per site (μt, where t is the time span of the branch in either generations or years). With these branch lengths in hand, estimates of θ can then be applied to each branch so that the original coalescent units t/2N ≈ μt/θ from the species tree are retained. Care needs to be taken to preserve the appropriate ploidy units when simulating gene trees from an estimated species tree. Packages such as MP-EST yield estimates of species tree branch lengths in coalescent units of 4N generations, appropriate for diploids, whereas packages such as Phybase [142] simulate gene trees from a species tree in estimates of 2N units, appropriate for haploids. Another issue that is important to be aware of is the distinction between gene coalescence times and species tree branch lengths [143, 144]. Whereas species tree branch lengths are estimates of lineage or population branch lengths in the species tree, the DNA sequence alignment that is fitted to the species tree will yield branch lengths reflecting the coalescence time of genes in ancestral species. This discrepancy occurs because gene coalescence times by necessity predate and record a more ancient event than do species divergence times. The discrepancy may represent a small fraction of the branch length if species divergence times are large, but Angelis and dos Reis [143] have suggested that the discrepancy can be quite large even in comparisons of distantly related species, such as exemplars of mammalian orders. There is a great need for methods of molecular dating and combining fossils and DNA data that distinguish between gene coalescence times and speciation times, the latter of which is usually of primary interest.
Once the branch lengths of the species tree are prepared for simulation, gene trees can be simulated using a number of packages (Phybase, [142]; TreeSim, [145]; CoMus, [146]). Even packages traditionally used in phylogeography can be used to simulated gene trees on species trees, given the close relationship between species trees and phylogeographic models like isolation migration [147, 148]. One can then compare the distribution of gene tree topologies and branch lengths observed in one’s data set with those simulated under the neutral coalescent model. A common approach is to calculate the distribution of Robinson-Foulds [149] distances among simulated gene trees and compare these to those observed in the original data set. Such approaches have been used to determine if a data set is consistent with the MSC or the percent of the observed gene tree variation that is explained by the MSC. Other statistics, such as the similarity in number of minority gene tree triplets produced by a given species tree at each node, can also be compared to the observed distribution. Song et al. [150] used coalescent simulations using Phybase to propose that the MSC could explain a large (>75%) fraction of the observed gene tree variation in a mammalian data set. Such simulations assume that the gene tree variation observed is biological in origin and not due to errors in reconstruction. They also noted that the near equivalence in frequency of minority triplets in gene trees at various nodes in the mammal tree suggested broad applicability of the neutral coalescent without gene flow or other complicating factors. Still, many papers observe some level of departure of the patterns in the observed data set from those expected under simulation. Usually the source of this departure is unknown. Natural selection or any other force such as HGT or anomalous mutation might be culprits in these cases. Heled et al. [151] proposed a simulation regime that incorporates gene flow between species and thus can be used to test for the effects of migration on gene trees and species tree estimation.
To detect possible phylogenetic outliers, Edwards et al. [152] applied a recently proposed method of detecting gene tree outliers, KDEtrees [153], to a series of phylogenomic data sets. KDEtrees uses the kernel density distribution of gene tree distances to estimate the 95% confidence limits on gene tree topologies in a given data set. Surprisingly, using default parameters, Edwards et al. [152] could not detect a higher-than-expected number of gene tree outliers in any data set, despite the fact that the data sets in several cases contained hundreds of loci. No data set possessed more than the expected 5% of outliers given the test implemented in KDEtrees. Clearly further work is needed to understand the pros and cons of various tests of phylogenetic outliers. For the time being, we can note the robustness of various species tree methods to phylogenetic outliers. One attractive prospect of algorithms for species tree construction that use summary statistics, such as STAR and STEAC, is that these methods are powerful and fast, yet they appear less susceptible to error due to deviations of single genes from neutral expectations. These methods do not utilize all the information in the data and hence can be less efficient than Bayesian or likelihood methods [52], yet they perform well with moderate amounts of gene tree outliers due to processes like HGT.
3 Hypothesis Testing Using the Multispecies Coalescent Model
Hypothesis testing is a cornerstone of phylogenetic analysis but has received little attention in the context of the MSC (see ref. 154). Bayesian species tree inference [58, 59, 68,69,70] provides perhaps the most seamless approach to hypothesis testing. One can relatively easily assess the fit of the collected data to alternative tree topologies and compare the fit using Bayes factors or other approaches. One can also assess the fit of various models of analysis to the collected data [155]. Liu and Pearl [58] and Edwards et al. [124] used Bayes factors to determine whether concatenation or the MSC was a more appropriate model for several data sets; in all cases tested thus far, the MSC provides a far better fit to multilocus data (BF > 10) than does concatenation, in which all gene trees among loci are identical. Further work is needed to apply Bayes factors and likelihood ratio tests to multilocus data.
The bootstrap, introduced to phylogenetics by Felsenstein [156], is the most common statistic applied to phylogenetic trees [157]. In the era of multilocus phylogenetics, the “multilocus bootstrap” of Seo [158] has been recommended as a more suitable approach to assessing confidence limits than the traditional bootstrap. In the traditional bootstrap, sites within a locus, or a series of concatenated loci, are resampled with replacement to create pseudomatrices, which are then subjected to phylogenetic analysis, after which a majority rule consensus tree is usually made. By contrast, in the multilocus bootstrap, sites within loci and the loci themselves are resampled with replacement. In the context of the MSC, resampled pseudomatrices of the same number of loci as the original data set, which may contain duplicates of specific loci due to the random nature of the bootstrap, are then made into gene trees, from which a species tree can be made. The bootstrap and various other measures of branch-specific support [159] have been proposed as a means of assessing confidence in species trees made using the multilocus coalescent. Care should be taken in the comparison of different studies using different measures of support, since not all measures can be directly compared to one another. For example, as pointed out by Liu et al. [160], the measure of posterior support for ASTRAL trees proposed by Sayyari and Mirarab [159] is not the same as traditional bootstrap supports, and we do not yet know how they will scale under different conditions compared to the bootstrap. Edwards [161] summarized knowledge about the use of phylogenomic subsampling, in which data sets of increasing size or signal are analyzed so as to understand the stability and speed of approach to certainty of phylogenetic estimates under the MSC and under concatenation. He found that MSC methods tended to approach phylogenomic certainty more smoothly and monotonically than do concatenation methods, which jump around erratically in their certainty for sometimes conflicting topologies, especially when sampling smaller numbers of genes. Although we cannot simply translate many conclusions from the gene tree era of phylogenetics to the MSC era—for example, contrary to gene tree conclusions, it is not clear for MSC models that more taxa are always better than more loci [74]—many of these discussions about hypothesis testing echo early comparisons of posterior probabilities and bootstrap proportions used in the gene tree era of phylogenetics.
The bootstrap has always provided a means of hypothesis testing that is very indirect with respect to comparing alternative phylogenetic hypotheses. Aside from the tests allowed by Bayesian approaches, there have been few discussions of testing of alternative phylogenetic trees in the era of the multispecies coalescent. In this regard, the pseudo-likelihood model provided by MP-EST [56] provides a convenient framework for hypothesis testing using species trees. This framework is not available in most other species tree methods, including ASTRAL, STAR, and STEAC, since these methods do not employ a likelihood model. MP-EST takes advantage of the likelihood model of Rannala and Yang [48] to assess the fit of a species tree to a collection of gene trees and can thus be used to compare alternative species tree topologies and branch lengths directly.
To conduct a direct comparison of species trees using the likelihood ratio test, we first compare the likelihoods of two trees to find the most probable species tree that can explain the empirical set of gene trees. The likelihood of a set of gene trees given a species tree with branch lengths can be ascertained using functions in Phybase [142]. Let Tree 1 be the null tree and Tree 2 be the alternative tree. The likelihood ratio test statistic is t = 2(L Tree2 − L Tree1), in which L Tree1 and L Tree2 are the log-likelihoods of the null and alternative hypotheses. The log-likelihood of the null hypothesis can be obtained from the output of the program MP-EST by fitting the branch lengths and topology of Tree 1 to the set of empirical gene trees. Similarly, we can find the log-likelihood of the alternative tree Tree 2 using MP-EST. The null distribution of the test statistic t is approximated by a parametric bootstrap. Specifically, we generate 100 or more bootstrap samples of gene trees under the null tree Tree 1. For each sample of these bootstrapped trees, we calculate the log-likelihoods of the null and alternative trees using the procedure described above. The null distribution of the test statistic t is approximated by the test statistics of the bootstrap samples. If t for the null and alternative species trees is outside the expected distribution of the bootstrap sample statistics, then the result can be considered significant.
We applied this approach to assessing alternative phylogenetic hypotheses to an example from birds (fairy wrens; [162]; Fig. 5). This data set consists of 18 genes and 26 taxa, with loci coming from a variety of marker types (exons, introns, anonymous loci). Lee et al. [162] applied a number of MSC approaches to this data set but did not compare alternative trees directly, having only used bootstrap approaches. Here, we consider three-species trees generated from the rearrangement of the three major clades of wrens: the core fairy wrens (Malurus), emu-wrens (Stipitirus), and grasswrens (Amytornis; Fig. 5). Rearranging these major clades results in three alternative rooted species trees. Based on traditional taxonomy and because the gene trees in this data set were highly variable, even among the three major clades, we consider these three alternative hypotheses true alternatives and not “straw men.” Rooted maximum likelihood gene trees were built from the alignments of each locus using RaxML [163] and then used as input data for the likelihood ratio test described above. The LRT was applied first to Tree 1 (null) versus Tree 2 and was also applied to Tree 1 versus Tree 3 and Tree 2 versus Tree 3. The results indicate that Tree 1 fits to the empirical gene trees significantly better than does Tree 2 or Tree 3 does (p < 0.01), and there is no significant difference between Trees 2 and 3 in their fit to the empirical gene trees (p = 0.52). Thus, the LRTs strongly favor Tree 1 over both Tree 2 and Tree 3.
Example of hypothesis testing of alternative phylogenetic trees under the multispecies coalescent model. Top: alternative phylogenetic hypotheses involving the rearrangement of major groups of Australo-Papuan fairy wrens based on Lee et al. [162]. The three alternative phylogenetic trees are colored to indicate the three major groups whose relationships are being tested. Bottom: results of the likelihood ratio test (LRT) and estimates of confidence limits on the test statistic t using parametric bootstrapping. The plots show the distributions of the test statistic t resulting from gene trees built from resampled, bootstrapped sequence data. Despite the use of sequence data to generate the bootstrap gene tree distributions, the LRT is only an indirect test of the signal in the sequence data and instead is best thought of as a test of the fit of the estimated gene tree distribution on alternative phylogenies. See main text for further details
It is important to note that the LRT described above is not a direct test of the phylogenetic signal in the DNA sequence data. Rather, it is a test of the distribution of gene trees inferred from the sequence data and assumes that the gene trees provided as data are without error. It does indirectly test the signal in the sequence data, because if the DNA sequences provide strong and consistent support of the gene trees, then the bootstrapped set of gene trees will be highly similar to one another, and the confidence limits on t will be very tight. By contrast, if the DNA sequence data does not have a strong signal, then the confidence limits on t will be very wide, and it will be difficult to reject alternative species trees. The LRT described here does not involve nested models. If the gene trees are known without error, then the value of t itself can be used to assess significance, assuming a chi-square distribution with 2 degrees of freedom. Further research is needed on methods for comparing and testing alternative species trees in the context of the MSC.
4 Future Directions
Species tree methods are likely to continue to gain ascendancy as the strongest evidence of taxonomic relationship in phylogenetic research. As with any form of evidence, the conclusions of a species tree analysis are fallible, with each method susceptible to biases in the input data. For example, Xi et al. [164] showed that Phyml [165] yields biased gene trees when there is little information in the DNA sequences and can therefore result in biased species trees. This issue is particularly problematic when using MP-EST v. 1.5, which, unlike ASTRAL or MP-EST v. 2.0, does not randomly resolve or appropriately accommodate gene trees with polytomies or 0 or near 0-length branches. This bias may have affected the performance of MP-EST in previous side-by-side comparisons with ASTRAL. In the future, further work should be devoted to discovering and quantifying additional biases in inference of species trees. With the size of phylogenomic data sets increasing, even small biases can be amplified and result in poorly estimated species trees.
Many in the field agree that the most appealing statistical models for species tree inference using the MSC include Bayesian and full-likelihood models [52]. But it is still clear, at least to empiricists, not only that “two-step” methods of species tree inference work quite well in general but also that the large phylogenomic data sets available today prohibit the use of full-likelihood methods. Regardless, we now know that both types of models clearly outperform concatenation across wide swaths of parameter space, especially if one also evaluates the reliability of the confidence limits on the estimate of phylogeny and not only the point estimate of the topology. The major directions for future research in the field of species tree inference therefore include increasing the scalability of computational inference of species trees, further development of frameworks for hypothesis testing using the MSC, developing additional models of divergence with gene flow and network coalescent models (Fig. 4), and improvement in the estimation of gene trees and species trees from SNP data [166]. Linking mutations in species trees and heterogeneous gene trees to diverse phenotypic and ecological data will be another important avenue for the future [167, 168]. We view the MSC, with its application of population genetic models to higher-level systematics, as a key component of the long-term goal of uniting microevolution and macroevolution. Even if it proves incomplete in the long term, the neutral MSC provides a powerful null model for the understanding of genetic diversity across time and space.
5 Practice Problems
-
1.
Consider the following discordant set of gene trees. {Gene 1 = (A:10,(B:8,C:8):2); Gene 2 = (B:9,(A:6,C:6):3); Gene 3 = ((A:4,B:4):4,C:8)}. Assuming that these genes perfectly reflect the time of genetic divergence, and the only cause of discordance is incomplete lineage sorting or deep coalescence, what is the most likely species tree? Answer: ((A:4,B:4):2,C:6)
-
2.
Find the data set for 30 noncoding loci from 4 species of Australian grass finches (3 Poephila, plus out-group Taeniopygia) from Jennings and Edwards [169]. It can be found in the web page for Liang Liu’s BEST program: http://faculty.franklin.uga.edu/lliu/content/BEST. Use the Bayesian program BEST [68] or BPP [70] and the nonparametric method in STAR [65] to estimate the species tree for the four species, using Taeniopygia as the out-group. Do you estimate the same topology with both methods? What about the support for the single internal branch? If the support is not the same, what could be causing the difference? Answer: The BEST or BPP tree should have higher support than the STAR tree, but they both should have the same topology. The STAR tree might have lower support because in the data set about half of the gene trees have a topology differing from the species tree; whereas the full Bayesian model accommodates this variation accurately, nonparametric “two-step” methods interpret this type of gene tree variation as discordance, in conflict with the majority of the gene trees and with the species tree.
-
3.
For the above data set, make individual gene trees using RaXml [170], and use the likelihood functions and bootstrap capabilities of Phybase [142] to conduct a likelihood ratio test of the two alternative species tree topologies for the four grass finches. Alternatively, you could use the posterior distribution of gene trees generated in BEST to estimate the confidence limits on the test statistic t. Is the tree estimated in question 2 significantly better than alternative trees? Answer: The LRT indicates that the tree estimated in question 2 is significantly better than alternative trees.
References
Darwin C (1859) On the origin of species, vol Facsimile of 1st Edition. Harvard University Press, Cambridge, p 513
Hillis DM (1987) Molecular versus morphological approaches to systematics. Annu Rev Ecol Syst 18:23–42
Scotland RW, Olmstead RG, Bennett JR (2003) Phylogeny reconstruction: the role of morphology. Syst Biol 52:539–548
Kocher TD, Thomas WK, Meyer A, Edwards SV, Pääbo S, Villablanca FX, Wilson AC (1989) Dynamics of mitochondrial DNA evolution in animals: amplification and sequencing with conserved primers. Proc Natl Acad Sci U S A 86:6196–6200
Miyamoto MM, Cracraft J (1991) Phylogeny inference, DNA sequence analysis, and the future of molecular systematics. In: Miyamoto MM, Cracraft J (eds) Phylogenetic analysis of DNA sequences. Oxford University Press, New York, NY, pp 3–17
Swofford DL, Olsen GJ, Waddell PJ, Hillis DM (1996) Phylogenetic inference. In: Hillis DM, Moritz C, Mable BK (eds) Molecular systematics. Sinauer, Sunderland, MA
Nei M (1987) Molecular evolutionary genetics, vol 512. Columbia University Press, New York
Nei M, Kumar S (2000) Molecular evolution and phylogenetics. Oxford University Press, New York
Rosenberg NA (2002) The probability of topological concordance of gene trees and species trees. Theor Popul Biol 61:225–247
Cavalli-Sforza LL (1964) Population structure and human evolution. Proc R Soc Lond Series B 164:362–379
Avise JC, Arnold J, Ball RM, Bermingham E, Lamb T, Neigel JE, Reeb CA, Saunders NC (1987) Intraspecific phylogeography: the mitochondrial DNA bridge between population genetics and systematics. Annu Rev Ecol Syst 18:489–522
Pamilo P, Nei M (1988) Relationships between gene trees and species trees. Mol Biol Evol 5:568–583
Takahata N (1989) Gene genealogy in three related populations: consistency probability between gene and population trees. Genetics 122:957–966
Avise JC (1994) Molecular markers, natural history and evolution. Chapman and Hall, New York
Wollenberg K, Avise JC (1998) Sampling properties of genealogical pathways underlying population pedigrees. Evolution 52:957–966
Gatesy J, Springer MS (2014) Phylogenetic analysis at deep timescales: unreliable gene trees, bypassed hidden support, and the coalescence/concatalescence conundrum. Mol Phylogenet Evol 80:231–266
de Queiroz A, Gatesy J (2007) The supermatrix approach to systematics. Trends Ecol Evol 22:34–41
Maddison WP (1997) Gene trees in species trees. Syst Biol 46:523–536
Edwards SV (2009) Is a new and general theory of molecular systematics emerging? Evolution 63:1–19
Carstens BC, Knowles LL (2007) Estimating species phylogeny from gene-tree probabilities despite incomplete lineage sorting: an example from melanoplus grasshoppers. Syst Biol 56:400–411
Wong A, Jensen JD, Pool JE, Aquadro CF (2007) Phylogenetic incongruence in the Drosophila melanogaster species group. Mol Phylogenet Evol 43:1138–1150
Knowles LL, Kubatko LS (2010) Estimating species trees: an introduction to concepts and models. In: Knowles LL, Kubatko LS (eds) Estimating species trees: practical and theoretical aspects. Wiley-Blackwell, New York, pp 1–14
Liu L, Yu L, Kubatko L, Pearl DK, Edwards SV (2009) Coalescent methods for estimating phylogenetic trees. Mol Phylogenet Evol 53:320–328
Neigel JE, Avise JC (1986) Phylogenetic relationships of mitochondrial DNA under various demographic models of speciation. In: Karlin S, Nevo E (eds) Evolutionary processes and theory. Academic, New York, pp 515–534
Degnan JH, Salter L (2005) Gene tree distributions under the coalescent process. Evolution 59:24–37
Tajima F (1983) Evolutionary relationships of DNA sequences in finite populations. Genetics 105:437–460
Mehta RS, Bryant D, Rosenberg NA (2016) The probability of monophyly of a sample of gene lineages on a species tree. Proc Natl Acad Sci U S A 113:8002–8009
Degnan JH, Rosenberg NA (2009) Gene tree discordance, phylogenetic inference, and the multispecies coalescent. Trends Ecol Evol 24:332–340
Degnan JH, Rosenberg NA (2006) Discordance of species trees with their most likely gene trees. Public Lib Sci Genet 2:762–768
Rosenberg NA, Tao R (2008) Discordance of species trees with their most likely gene trees: the case of five taxa. Syst Biol 57:131–140
Huang HT, Knowles LL (2009) What is the danger of the anomaly zone for empirical phylogenetics? Syst Biol 58:527–536
Sackton TB et al (2018) Convergent regulatory evolution and the origin of flightlessness in palaeognathous birds. bioRxiv. https://doi.org/10.1101/262584
Linkem CW, Minin VN, Leaché AD (2016) Detecting the anomaly zone in species trees and evidence for a misleading signal in higher-level skink phylogeny (Squamata: Scincidae). Syst Biol 65:465–477
Bryant D (2003) A classification of consensus methods for phylogenetics. In: Janowitz M et al (eds) BioConsensus. American Mathematical Society, Providence, RI, pp 163–183
Ewing GB, Ebersberger I, Schmidt HA, von Haeseler A (2008) Rooted triple consensus and anomalous gene trees. BMC Evol Biol 8:118
Degnan JH, DeGiorgio M, Bryant D, Rosenberg NA (2009) Properties of consensus methods for inferring species trees from gene trees. Syst Biol 58:35–54
Ranwez V, Criscuolo A, Douzery EJ (2010) SuperTriplets: a triplet-based supertree approach to phylogenomics. Bioinformatics 26:i115–i123
Steel M, Rodrigo A (2008) Maximum likelihood supertrees. Syst Biol 57:243–250
Wiens JJ (2003) Missing data, incomplete taxa, and phylogenetic accuracy. Syst Biol 52:528–538
Gadagkar SR, Rosenberg MS, Kumar S (2005) Inferring species phylogenies from multiple genes: concatenated sequence tree versus consensus gene tree. J Exp Zool B Mol Dev Evol 304:64–74
Bull JJ, Huelsenbeck JP, Cunningham CW, Swofford DL, Waddell PJ (1993) Partitioning and combining data in phylogenetic analysis. Syst Biol 42:384–397
Rokas A, Williams B, King N, Carroll S (2003) Genome-scale approaches to resolving incongruence in molecular phylogenies. Nature 425:798–804
Driskell AC, Ane C, Burleigh JG, McMahon MM, O’Meara BC, Sanderson MJ (2004) Prospects for building the tree of life from large sequence databases. Science 306:1172–1174
Rokas A (2006) Genomics. Genomics and the tree of life. Science 313:1897–1899
Kubatko LS, Degnan JH (2007) Inconsistency of phylogenetic estimates from concatenated data under coalescence. Syst Biol 56:17–24
Wu M, Eisen JA (2008) A simple, fast, and accurate method of phylogenomic inference. Genome Biol 9:R151
Edwards SV et al (2016) Implementing and testing the multispecies coalescent model: a valuable paradigm for phylogenomics. Mol Phylogenet Evol 94:447–462
Rannala B, Yang Z (2003) Bayes estimation of species divergence times and ancestral population sizes using DNA sequences from multiple loci. Genetics 164:1645–1656
Bravo GA et al (2019) Embracing heterogeneity: coalescing the Tree of Life and the future of phylogenomics. PeerJ 7:e6399. https://doi.org/10.7717/peerj.6399
Felsenstein J (1981) Evolutionary trees from DNA sequences: a maximum likelihood approach. J Mol Evol 17:368–376
Rannala B, Yang ZH (2008) Phylogenetic inference using whole genomes. Annu Rev Genomics Hum Genet 9:217–231
Xu B, Yang Z (2016) Challenges in species tree estimation under the multispecies coalescent model. Genetics 204:1353–1368
Liu L, Xi Z, Wu S, Davis CC, Edwards SV (2015) Estimating phylogenetic trees from genome-scale data. Ann N Y Acad Sci 1360:36–53
Edwards SV (2016) Inferring species trees. In: Kliman R (ed) Encyclopedia of evolutionary biology. Elsevier Inc., New York, pp 236–244
Castillo-Ramírez S, Liu L, Pearl D, Edwardsm SV (2010) Bayesian estimation of species trees: a practical guide to optimal sampling and analysis. In: Knowles LL, Kubatko LS (eds) Estimating species trees: practical and theoretical aspects. Wiley-Blackwell, New Jersey, pp 15–33
Liu L, Yu L, Edwards S (2010) A maximum pseudo-likelihood approach for estimating species trees under the coalescent model. BMC Evol Biol 10:302
Mirarab S, Warnow T (2015) ASTRAL-II: coalescent-based species tree estimation with many hundreds of taxa and thousands of genes. Bioinformatics 31:i44–i52
Liu L, Pearl DK (2007) Species trees from gene trees: reconstructing Bayesian posterior distributions of a species phylogeny using estimated gene tree distributions. Syst Biol 56:504–514
Ogilvie HA, Bouckaert RR, Drummond AJ (2017) StarBEAST2 brings faster species tree inference and accurate estimates of substitution rates. Mol Biol Evol 34(8):2101–2114
Heled J, Drummond AJ (2010) Bayesian inference of species trees from multilocus data. Mol Biol Evol 27:570–580
Maddison WP, Knowles LL (2006) Inferring phylogeny despite incomplete lineage sorting. Syst Biol 55:21–30
Kubatko LS, Carstens BC, Knowles LL (2009) STEM: species tree estimation using maximum likelihood for gene trees under coalescence. Bioinformatics 25:971–973
O’Meara BC (2010) New heuristic methods for joint species delimitation and species tree inference. Syst Biol 59:59–73
Mossel E, Roch S (2010) Incomplete lineage sorting: consistent phylogeny estimation from multiple loci. IEEE/ACM Trans Comput Biol Bioinform 7:166–171
Liu L, Yu L, Pearl DK, Edwards SV (2009) Estimating species phylogenies using coalescence times among sequences. Syst Biol 58:468–477
Liu L, Yu L (2011) Estimating species trees from unrooted gene trees. Syst Biol 60:661–667
Mirarab S, Reaz R, Bayzid MS, Zimmermann T, Swenson MS, Warnow T (2014) ASTRAL: genome-scale coalescent-based species tree estimation. Bioinformatics 30:i541–i548
Liu L (2008) BEST: Bayesian estimation of species trees under the coalescent model. Bioinformatics 24:2542–2543
Liu L, Pearl DK, Brumfield RT, Edwards SV (2008) Estimating species trees using multiple-allele DNA sequence data. Evolution 62:2080–2091
Rannala B, Yang Z (2017) Efficient Bayesian species tree inference under the multispecies coalescent. Syst Biol 66:823–842
Yang Z (2015) The BPP program for species tree estimation and species delimitation. Curr Zool 61:854–865
Yang Z, Rannala B (2010) Bayesian species delimitation using multilocus sequence data. Proc Natl Acad Sci U S A 107:9264–9269
Chifman, J Kubatko L (2014) Quartet inference from SNP data under the coalescent model. Bioinformatics 30:3317–3324
Liu L, Xi ZX, Davis CC (2015) Coalescent methods are robust to the simultaneous effects of long branches and incomplete lineage sorting. Mol Biol Evol 32:791–805
Xi ZX, Liu L, Davis CC (2016) The impact of missing data on species tree estimation. Mol Biol Evol 33:838–860
Shen X-X, Hittinger CT, Rokas A (2017) Contentious relationships in phylogenomic studies can be driven by a handful of genes. Nat Ecol Evol 1:0126
Suzuki Y, Glazko GV, Nei M (2002) Overcredibility of molecular phylogenies obtained by Bayesian phylogenetics. Proc Natl Acad Sci U S A 99:16138–16143
Huang HT, He QI, Kubatko LS, Knowles LL (2010) Sources of error inherent in species-tree estimation: impact of mutational and coalescent effects on accuracy and implications for choosing among different methods. Syst Biol 59:573–583
Jarvis ED et al (2014) Whole-genome analyses resolve early branches in the tree of life of modern birds. Science 346:1320–1331
Hughes LC et al (2018) Comprehensive phylogeny of ray-finned fishes (Actinopterygii) based on transcriptomic and genomic data. Proc Natl Acad Sci U S A 115:6249–6254
Wickett NJ et al (2014) Phylotranscriptomic analysis of the origin and early diversification of land plants. Proc Natl Acad Sci U S A 111:E4859–E4868
Avise JC, Ball RMJ (1990) Principles of genealogical concordance in species concepts and biological taxonomy. Oxf Surv Evol Biol 7:45–67
Solis-Lemus C, Yang M, Ane C (2016) Inconsistency of species tree methods under gene flow. Syst Biol 65:843–851
Stenz NW, Larget B, Baum DA, Ane C (2015) Exploring tree-like and non-tree-like patterns using genome sequences: an example using the inbreeding plant species Arabidopsis thaliana (L.) Heynh. Syst Biol 64:809–823
Hudson RR, Coyne JA (2002) Mathematical consequences of the genealogical species concept. Evolution 56:1557–1565
Tobias JA, Seddon N, Spottiswoode CN, Pilgrim JD, Fishpool LDC, Collar NJ (2010) Quantitative criteria for species delimitation. Ibis 152:724–746
Jackson ND, Carstens BC, Morales AE, O’Meara BC (2017) Species delimitation with gene flow. Syst Biol 66:799–812
Leache AD, Zhu T, Rannala B, Yang Z (2018) The spectre of too many species. Syst Biol 66:379
Solis-Lemus C, Knowles LL, Ane C (2015) Bayesian species delimitation combining multiple genes and traits in a unified framework. Evolution 69:492–507
Sukumaran J, Knowles LL (2017) Multispecies coalescent delimits structure, not species. Proc Natl Acad Sci U S A 114:1607–1612
Carstens BC, Pelletier TA, Reid NM, Satler JD (2013) How to fail at species delimitation. Mol Ecol 22:4369–4383
Carstens BC, Dewey TA (2010) Species delimitation using a combined coalescent and information-theoretic approach: an example from North American Myotis bats. Syst Biol 59:400–414
De Queiroz K (2007) Species concepts and species delimitation. Syst Biol 56:879–886
Pinho C, Hey J (2010) Divergence with gene flow: models and data. Annu Rev Ecol Evol Syst 41:215–230
Hey J, Nielsen R (2007) Integration within the Felsenstein equation for improved Markov chain Monte Carlo methods in population genetics. Proc Natl Acad Sci U S A 104:2785–2790
Carstens BC, Morales AE, Jackson ND, O’Meara BC (2017) Objective choice of phylogeographic models. Mol Phylogenet Evol 116:136–140
Wakeley J (2001) The effects of subdivision on the genetic divergence of populations and species. Evolution 54:1092–1101
Solís-Lemus C, Yang M, Ané C (2016) Inconsistency of species tree methods under gene flow. Syst Biol 65:843–851
Eckert AJ, Carstens BC (2008) Does gene flow destroy phylogenetic signal? The performance of three methods for estimating species phylogenies in the presence of gene flow. Mol Phylogenet Evol 49(3):832–842
Doolittle WF, Bapteste E (2007) Pattern pluralism and the Tree of Life hypothesis. Proc Natl Acad Sci U S A 104:2043–2049
Boto L (2010) Horizontal gene transfer in evolution: facts and challenges. Proc Biol Sci 277:819–827
Soucy SM, Huang J, Gogarten JP (2015) Horizontal gene transfer: building the web of life. Nat Rev Genet 16:472–482
Keeling PJ, Palmer JD (2008) Horizontal gene transfer in eukaryotic evolution. Nat Rev Genet 9:605–618
Soanes D, Richards TA (2014) Horizontal gene transfer in eukaryotic plant pathogens. Annu Rev Phytopathol 52:583–614
Thomas J, Schaack S, Pritham EJ (2010) Pervasive horizontal transfer of rolling-circle transposons among animals. Genome Biol Evol 2:656–664
Mallet J, Besansky N, Hahn MW (2015) How reticulated are species? BioEssays 38:140–149
Huang J, Gogarten JP (2006) Ancient horizontal gene transfer can benefit phylogenetic reconstruction. Trends Genet 22:361–366
Davidson R, Vachaspati P, Mirarab S, Warnow T (2015) Phylogenomic species tree estimation in the presence of incomplete lineage sorting and horizontal gene transfer. BMC Genomics 16(Suppl 10):S1
Linz S, Semple C, Stadler T (2010) Analyzing and reconstructing reticulation networks under timing constraints. J Math Biol 61:715–737
Linz S, Radtke A, von Haeseler A (2007) A likelihood framework to measure horizontal gene transfer. Mol Biol Evol 24:1312–1319
Rasmussen MD, Kellis M (2011) A Bayesian approach for fast and accurate gene tree reconstruction. Mol Biol Evol 28:273–290
Rasmussen MD, Kellis M (2007) Accurate gene-tree reconstruction by learning gene- and species-specific substitution rates across multiple complete genomes. Genome Res 17:1932–1942
Szöllosi GJ, Tannier E, Daubin V, Boussau B (2015) The inference of gene trees with species trees. Syst Biol 64:e42–e62
Sanderson MJ, McMahon MM (2007) Inferring angiosperm phylogeny from EST data with widespread gene duplication. BMC Evol Biol 7(Suppl 1):S3
Thomas PD (2010) GIGA: a simple, efficient algorithm for gene tree inference in the genomic age. BMC Bioinform 11:312
Boussau B, Szollosi GJ, Duret L, Gouy M, Tannier E, Daubin V (2013) Genome-scale coestimation of species and gene trees. Genome Res 23:323–330
Conte MG, Gaillard S, Droc G, Perin C (2008) Phylogenomics of plant genomes: a methodology for genome-wide searches for orthologs in plants. BMC Genomics 9:183
Altenhoff AM, Gil M, Gonnet GH, Dessimoz C (2013) Inferring hierarchical orthologous groups from orthologous gene pairs. PLoS One 8:e53786
Irisarri I et al (2017) Phylotranscriptomic consolidation of the jawed vertebrate timetree. Nat Ecol Evol 1:1370–1378
Edwards SV (2009) Natural selection and phylogenetic analysis. Proc Natl Acad Sci U S A 106:8799–8800
Ray N, Excoffier L (2009) Inferring past demography using spatially explicit population genetic models. Hum Biol 81:141–157
Castoe TA, de Koning APJ, Kim H-M, Gu W, Noonan BP, Naylor G, Jiang ZJ, Parkinson CL, Pollock DD (2009) Evidence for an ancient adaptive episode of convergent molecular evolution. Proc Natl Acad Sci U S A 106:8986–8991
Reid NH, Hird SM, Brown JM, Pelletier TA, McVay JD, Satler JD, Carstens BC (2014) Poor fit to the multispecies coalescent is widely detectable in empirical data. Syst Biol 63:322–333
Edwards SV, Liu L, Pearl DK (2007) High-resolution species trees without concatenation. Proc Natl Acad Sci U S A 104:5936–5941
Beerli P, Felsenstein J (2001) Maximum likelihood estimation of a migration matrix and effective population sizes in n subpopulations by using a coalescent approach. Proc Natl Acad Sci U S A 98:4563–4568
Hey J, Wakeley J (1997) A coalescent estimator of the population recombination rate. Genetics 145:833–846
Solis-Lemus C, Bastide P, Ane C (2017) PhyloNetworks: a package for phylogenetic networks. Mol Biol Evol 34:3292–3298
Than C, Ruths D, Nakhleh L (2008) PhyloNet: a software package for analyzing and reconstructing reticulate evolutionary relationships. BMC Bioinform 9:322
Hallström BM, Janke A (2010) Mammalian evolution may not be strictly bifurcating. Mol Biol Evol 27:2804–2816
Kutschera VE, Bidon T, Hailer F, Rodi JL, Fain SR, Janke A (2014) Bears in a forest of gene trees: phylogenetic inference is complicated by incomplete lineage sorting and gene flow. Mol Biol Evol 31:2004–2017
Mavárez J, Salazar CA, Bermingham E, Salcedo C, Jiggins CD, Linares M (2006) Speciation by hybridization in Heliconius butterflies. Nature 441:868–871
Wen D, Nakhleh L (2017) Coestimating reticulate phylogenies and gene trees from multilocus sequence data. Syst Biol 67(3):439–457
Yu Y, Nakhleh L (2015) A maximum pseudo-likelihood approach for phylogenetic networks. BMC Genomics 16(Suppl 10):S10
Stenz NW, Larget B, Baum DA, Ané C (2015) Exploring tree-like and non-tree-like patterns using genome sequences: an example using the inbreeding plant species Arabidopsis thaliana (L.) Heynh. Syst Biol 64(5):809–823
Beaumont MA, Balding DJ (2004) Identifying adaptive genetic divergence among populations from genome scans. Mol Ecol 13:969–980
Storz JF (2005) Using genome scans of DNA polymorphism to infer adaptive population divergence. Mol Ecol 14:671–688
Barrett RDH, Hoekstra HE (2011) Molecular spandrels: tests of adaptation at the genetic level. Nat Rev Genet 12:767–780
Swofford DL (1991) When are phylogeny estimates from molecular and morphological data incongruent? In: Miyamoto MM, Cracraft J (eds) Phylogenetic analysis of DNA sequences. Oxford University Press, Oxford, pp 295–333
Dufraigne C, Fertil B, Lespinats S, Giron A, Deschavanne P (2005) Detection and characterization of horizontal transfers in prokaryotes using genomic signature. Nucleic Acids Res 33:e6
Roettger M, Martin W, Dagan T (2009) A machine-learning approach reveals that alignment properties alone can accurately predict inference of lateral gene transfer from discordant phylogenies. Mol Biol Evol 26:1931–1939
Zimmermann T, Mirarab S, Warnow T (2014) BBCA: improving the scalability of *BEAST using random binning. BMC Genomics 15(Suppl 6):S11
Liu L, Yu L (2010) Phybase: an R package for species tree analysis. Bioinformatics 26:962–963
Angelis K, dos Reis M (2015) The impact of ancestral population size and incomplete lineage sorting on Bayesian estimation of species divergence times. Curr Zool 61:874–885
Edwards SV, Beerli P (2000) Perspective: gene divergence, population divergence, and the variance in coalescence time in phylogeographic studies. Evolution 54:1839–1854
Stadler T (2011) Simulating trees with a fixed number of extant species. Syst Biol 60:676–684
Papadantonakis S, Poirazi P, Pavlidis P (2016) CoMuS: simulating coalescent histories and polymorphic data from multiple species. Mol Ecol Resour 16:1435–1448
Anderson CNK, Ramakrishnan U, Chan YL, Hadly EA (2005) Serial SimCoal: a population genetics model for data from multiple populations and points in time. Bioinformatics 21:1733–1734
Excoffier L, Foll M (2011) fastsimcoal: a continuous-time coalescent simulator of genomic diversity under arbitrarily complex evolutionary scenarios. Bioinformatics 27:1332–1334
Robinson DF, Foulds LR (1981) Comparison of phylogenetic trees. Math Biosci 53:131–147
Song S, Liu L, Edwards SV, Wu SY (2012) Resolving conflict in eutherian mammal phylogeny using phylogenomics and the multispecies coalescent model. Proc Natl Acad Sci U S A 109:14942–14947
Heled J, Bryant D, Drummond AJ (2013) Simulating gene trees under the multispecies coalescent and time-dependent migration. BMC Evol Biol 13:44
Edwards SV, Potter S, Schmitt CJ, Bragg JG, Moritz C (2016) Reticulation, divergence, and the phylogeography–phylogenetics continuum. Proc Natl Acad Sci U S A 113:8025–8032
Weyenberg G, Huggins PM, Schardl CL, Howe DK, Yoshida R (2014) KDETREES: non-parametric estimation of phylogenetic tree distributions. Bioinformatics 30:2280–2287
Gaither, J Kubatko L (2016) Hypothesis tests for phylogenetic quartets, with applications to coalescent-based species tree inference. J Theor Biol 408:179–186
McVay JD, Carstens BC (2013) Phylogenetic model choice: justifying a species tree or concatenation analysis. J Phylogenet Evol Biol 1:114
Felsenstein J (1985) Confidence limits on phylogenies: an approach using the bootstrap. Evolution 39:783–791
Lemoine F, Domelevo Entfellner JB, Wilkinson E, Correia D, Davila Felipe M, De Oliveira T, Gascuel O (2018) Renewing Felsenstein’s phylogenetic bootstrap in the era of big data. Nature 556:452–456
Seo TK (2008) Calculating bootstrap probabilities of phylogeny using multilocus sequence data. Mol Biol Evol 25:960–971
Sayyari E, Mirarab S (2016) Fast coalescent-based computation of local branch support from quartet frequencies. Mol Biol Evol 33:1654–1668
Liu L et al (2017) Reply to Gatesy and Springer: Claims of homology errors and zombie lineages do not compromise the dating of placental diversification. Proc Natl Acad Sci U S A 114:E9433–E9434
Edwards SV (2016) Phylogenomic subsampling: a brief review. Zool Scr 45:63–74
Lee JY, Joseph L, Edwards SV (2012) A species tree for the Australo-Papuan Fairy-wrens and Allies (Aves: Maluridae). Syst Biol 61:253–271
Stamatakis A (2014) RAxML version 8: a tool for phylogenetic analysis and post-analysis of large phylogenies. Bioinformatics 30:1312–1313
Xi Z, Liu L, Davis CC (2015) Genes with minimal phylogenetic information are problematic for coalescent analyses when gene tree estimation is biased. Mol Phylogenet Evol 92:63–71
Guindon S, Dufayard JF, Hordijk W, Lefort V, Gascuel O (2009) PhyML: fast and accurate phylogeny reconstruction by maximum likelihood. Infect Genet Evol 9:384–385
Leaché AD, Oaks JR (2017) The utility of single nucleotide polymorphism (SNP) data in phylogenetics. Annu Rev Ecol Evol Syst 48:69–84
Pease JB, Haak DC, Hahn MW, Moyle LC (2016) Phylogenomics reveals three sources of adaptive variation during a rapid radiation. PLoS Biol 14:e1002379
Hahn MW, Nakhleh L (2016) Irrational exuberance for resolved species trees. Evolution 70:7–17
Jennings WB, Edwards SV (2005) Speciational history of Australian grass finches (Poephila) inferred from 30 gene trees. Evolution 59:2033–2047
Stamatakis A (2006) RAxML-VI-HPC: maximum likelihood-based phylogenetic analyses with thousands of taxa and mixed models. Bioinformatics 22:2688–2690
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this protocol
Cite this protocol
Liu, L., Anderson, C., Pearl, D., Edwards, S.V. (2019). Modern Phylogenomics: Building Phylogenetic Trees Using the Multispecies Coalescent Model. In: Anisimova, M. (eds) Evolutionary Genomics. Methods in Molecular Biology, vol 1910. Humana, New York, NY. https://doi.org/10.1007/978-1-4939-9074-0_7
Download citation
DOI: https://doi.org/10.1007/978-1-4939-9074-0_7
Published:
Publisher Name: Humana, New York, NY
Print ISBN: 978-1-4939-9073-3
Online ISBN: 978-1-4939-9074-0
eBook Packages: Springer Protocols