Abstract
Polaritons are quasi-particles that combine light with matter, enabling precise control of light at deep subwavelength scales. The excitation and propagation of polaritons are closely linked to the structural symmetries of the host materials, resulting in symmetrical polariton propagation in high-symmetry materials. However, in low-symmetry crystals, symmetry-broken polaritons exist, exhibiting enhanced directionality of polariton propagation for nanoscale light manipulation and steering. Here, we theoretically propose and experimentally demonstrate the existence of symmetry-broken polaritons, with hyperbolic dispersion, in a high-symmetry crystal. We show that an optical disk-antenna positioned on the crystal surface can act as an in-plane polarized excitation source, enabling dynamic tailoring of the asymmetry of hyperbolic polariton propagation in the high-symmetry crystal over a broad frequency range. Additionally, we provide an intuitive analysis model that predicts the condition under which the asymmetric polaritonic behavior is maximized, which is corroborated by our simulations and experiments. Our results demonstrate that the directionality of polariton propagation can be conveniently configured, independent of the structure symmetry of crystals, providing a tuning knob for the polaritonic response and in-plane anisotropy in nanophotonic applications.
Similar content being viewed by others
1 Introduction
Exploiting ultra-confined and highly directional polaritons [1,2,3,4,5,6,7,8,9,10] at the nanoscale is essential for developing integrated nanophotonic devices, circuits and chips [11,12,13,14,15]. High-symmetry crystals have been extensively studied for this purpose, with particular focus on hyperbolic polaritons (HPs), including out-of-plane hyperbolicity [16,17,18] in hexagonal crystals (e.g., boron nitride) [5, 6], and in-plane low-loss HPs in trigonal (e.g., calcite) [7] and orthorhombic (e.g., α-MoO3) [8,9,10] crystals. However, the in-plane HP propagation in high-symmetry optical crystals usually exhibits four mirror-symmetric beams, which reduces the directionality and energy transporting efficiency. Recently, hyperbolic shear polaritons [19,20,21,22], characterized with mirror-symmetry-broken hyperbolic wavefronts, have been discovered in low-symmetry monoclinic crystals, which exhibit enhanced directional propagation despite suffering from large losses. The nontrivial asymmetries of these shear polaritons arise from the intrinsic non-Hermitian permittivity tensor of the low-symmetry crystals [19,20,21,22], which thus are not available in high-symmetry crystals.
Here, we investigate the impact of in-plane linearly polarized sources [23,24,25,26,27,28,29] on generating symmetry-broken HPs with enhanced directional propagation in high-symmetry, low-loss systems. We theoretically and experimentally demonstrate that controlling the near-field excitation source can configure the excitation and propagation of in-plane HPs. This leads to the breaking of polariton mirror symmetry without the need of low crystalline symmetry. Our source-configured approach enables the tuning of the polariton asymmetry propagation over a broad frequency range, thereby establishing in a new degree of freedom [27,28,29] for the dynamic and robust control of light guiding [30,31,32] and propagation on the nanoscale. Our results expand the possibilities for manipulating asymmetric polaritons and can be applied to reconfigurable polaritonic devices [33,34,35,36,37,38] for polarization-dependent nanophotonic circuits [37] or optical isolation [38].
2 Results and discussion
To distinguish mirror-asymmetric HP behaviors in low- and high-symmetry crystals, we conducted numerical simulations of dipole-launched polaritons as shown in Fig. 1. First, we compared the HPs launched by a vertical dipole (px = py = 0, pz ≠ 0) on monoclinic (Fig. 1a) and orthorhombic (Fig. 1b) crystals, where off-diagonal terms εxy associated with shear phenomena were present and absent in their permittivity tensors, respectively.
Dipole-launching of hyperbolic polaritons. a Schematic of z-oriented dipole-launching of hyperbolic shear polaritons in a monoclinic crystal with off-diagonal permittivity (\({\varepsilon }_{xx}=-3.73+0.55\mathrm{i }, {\varepsilon }_{yy}=2.34, {\varepsilon }_{zz}=-3.73+0.55\mathrm{i },{\varepsilon }_{xy}=-1+0.3\mathrm{i}\)). b Schematic of z-oriented dipole-launching of symmetric hyperbolic polaritons in an orthorhombic crystal with a diagonal permittivity (\({\varepsilon }_{xx}=-3.73+0.55\mathrm{i }, {\varepsilon }_{yy}=2.34, {\varepsilon }_{zz}=-3.73+0.55\mathrm{i}\)). c Schematic of in-plane oriented dipole-launching of symmetry-broken hyperbolic polaritons in the same orthorhombic crystal as in (b). d–f Simulated real part of the near-field distribution Ez above the surface of the monoclinic or orthorhombic crystal, respectively. Perpendicular black lines represent the direction of crystal axis. g–i Corresponding absolute value of the two-dimensional FFT, with perpendicular white lines denoted as O1 and O2, the direction of the two effective optic axes. In (a–c) a1, a2 and a3 denote vectors of the unit cell
Our results showed highly asymmetric hyperbolic shear polaritons in the low-symmetry monoclinic crystal, as evidenced by the atypical tilted hyperbolic wavefronts with the mirror symmetry being broken along the real-space crystal axis (perpendicular black lines) (Fig. 1d). The corresponding Fourier transform also indicated a mirror-asymmetric wavevector distribution with respect to axes O1 and O2 (Fig. 1g). In contrast, when the permittivity tensor was diagonalized in the orthorhombic crystal, the wavefronts in real space became mirror-symmetric with respect to the crystal axis (Fig. 1e), and the k-space dispersion also exhibited symmetric hyperbola with respect to both the O1 and O2 axes (Fig. 1h). Note that, the tilted crystal axis (or effective optic axes) were corrected for the orthorhombic crystal and were found to be along the principal orthogonal x and y (or kx and ky) directions.
We further considered a dipole exciting HPs on the orthorhombic crystal, with the dipole orientation changed to the in-plane direction (px ≠ 0, py ≠ 0, pz = 0) as shown in Fig. 1c. Compared with the results shown in Fig. 1e, the HPs now mostly spread in the first or third quadrant with respect to the coordinate system of the orthorhombic plane, resulting in a clear broken mirror symmetry of wavefronts in the high-symmetry crystal (Fig. 1f). However, in this case the wavefronts were not rotated, which is different from hyperbolic shear polaritons. Anomalously, the propagation of HPs was weakly emitted and even forbidden along the dipolar orientation (brown double arrow). This behavior contrasted with the excitation of polaritons on the in-plane isotropic polar crystals such as SiC (Additional file 1: Fig. S5). These observations inspired a new proposal of realizing symmetry-broken HP propagation. Instead of reducing the lattice symmetry or engineering the energy band of materials, symmetry-broken HPs can also be realized by configuring the polarization of the excitation source, as confirmed via the Fourier transform of the real-space electric field Ez in Fig. 1i.
To shed light on the mechanism of asymmetric hyperbolic polaritons caused by an excitation source, we used the theory of near-field interference [28], which describes the angular spectrum of dipole sources while considering momentum conservation. Because we experimentally excited HPs with a transverse magnetic (TM) wave, we only considered a TM-polarized component wherein the dipole moment was defined per unit length as p = [px, py, pz]. Furthermore, the dipole’s electric field was divided into spatial-frequency components kx and ky in an isotropic medium with permittivity ε1 and permeability μ1 via a dyadic Green function (cf. Additional file 1: Note S1):
where \({k}_{t}=\sqrt{{k}_{x}^{2}+{k}_{y}^{2}}\) and \({k}_{z}=\sqrt{{\varepsilon }_{1}{\mu}_{1}{k}_{0}^{2}-{k}_{t}^{2}}\) are the in-plane and out-of-plane wavevectors, respectively, and \({k}_{0}=\omega \sqrt{{\mu }_{0}{\varepsilon }_{0}}\) is the wavevector in free space.
The electric field intensity distribution, denoted as \({|E}_{z}^{p}|\), can be mapped onto the kx-ky momentum space using Eq. (1), given the polarization of the dipole p in free space. Panel 1 in Fig. 2a shows the contour distribution of a linearly-polarized electric dipole with p = [cosφ, sinφ, 0], where φ represents the polarization angle of dipole polarization p relative to the y-axis in a Cartesian coordinate system. Note that the direction of minimum contour \({{|E}_{z}^{p}|}_{\mathrm{min}}\) (indicated by the yellow dashed line) is perpendicular to both real-space dipolar orientation (red arrow) and the direction of \({{|E}_{z}^{p}|}_{\mathrm{max}}\) (red solid line), leading to several intriguing consequences, as described below. Subsequently, we investigate the unique dispersion of anisotropic hyperbolic systems in Panel 2. In this scenario, the source-free Maxwell equations in the anisotropic system with an arbitrary dielectric tensor \(\widetilde{\varepsilon }\) must be solved, considering the polariton wave carrying a fixed frequency of wavevector (kx, ky, kz). The hyperbolic dispersion can be derived from the determinant of secular equation as shown in Additional file 1: Note S2:
Symmetry-broken hyperbolic polaritons configured by an in-plane dipole source. a Theoretical schematics. Panel 1: Calculated angular spectrum \(|{E}_{z}^{p}|\) in momentum space induced by an in-plane dipole p with polarization angle φ. Red line and yellow dashed line represent maximum and minimum contours of \({|E}_{z}^{p}|\), respectively. Panel 2: Calculated \(|{E}_{z}^{p}|\) overlapped with the dispersion of a hyperbolic system. Thick red curves denote the iso-frequency contours. 2θ is the angle between the asymptotes. Gray regions represent the absence of the effect of \({|E}_{z}^{p}|\). Panel 3: Projected hyperbolic dispersion onto \(|{E}_{z}^{p}|\). b Calculated φ- and θ-dependence of \(|{\Delta E}_{z}|\). Black or green dashed lines represent the occurrence conditions of symmetry-broken or symmetric states, respectively. White circles denote where the highest degree of symmetry-breaking is achieved. c–e Simulations of absolute value, real part and Fourier transform of Ez marked by yellow triangle patch. The yellow dashed line represents the \({{|E}_{z}^{p}|}_{\mathrm{min}}\) of the Panel 1 in a. f Simulated electric field intensity |Ez| as a function of φ in calcite (θ = 45° at 1470 cm−1). g Amplitude profiles extracted along the dashed lines in f. h Calculated electric field intensities \(|{E}_{z}^{\mathrm{I}}|\), \(|{E}_{z}^{\mathrm{II}}|\) for peaks I, II and their difference as a function of φ
It should be note that the hyperbolic isofrequency contour (IFC) in Eq. (2) is solely determined by the dielectric constant \(\widetilde{\varepsilon }\), which reflects the crystal properties. Additionally, the dipolar orientation has no effect on the open angle θ of the IFC (θ denotes the angle between the asymptote of the hyperbolic IFC and ky -axis in momentum space). Finally, we explore the influence of the \({|E}_{z}^{p}|\) distribution on the hyperbolic IFC, as demonstrated in Panel 3. Coupling with the asymmetric \({|E}_{z}^{p}|\) induced by the horizontal dipole, certain propagation modes in the hyperbolic dispersion can be selectively excited (indicated by the red solid line in Panel 3) or not excited (indicated by the red dotted line in Panel 3). Consequently, our source-configured method can support symmetry-broken HP propagation at any anisotropic material systems in theory (Additional file 1: Fig. S6).
To demonstrate the propagation of polariton with broken mirror symmetry, we intentionally selected two points, A and B (shown in Panel 3 of Fig. 2a), which were located close to the direction of open angles, to calculate the variation of \(|{\Delta E}_{z}|\) (i.e. \(\left|{|E}_{z}^{\mathrm{A}}|-|{E}_{z}^{\mathrm{B}}|\right|\)) based on polarization angle φ and open angle θ. As shown in Fig. 2b, for any θ, the difference \(|{\Delta E}_{z}|\) only became zero when the in-plane dipolar orientation was aligned with the crystal axis of high-symmetry crystals, satisfying the conditions φ = 0° or ± 90° in our sample (indicated by green dashed lines). This led to symmetrically hyperbolic polariton behaviors. Otherwise, different degrees of mirror symmetry breaking occurred (i.e. \(|{\Delta E}_{z}|\ne 0\)), where mirror symmetry breaking refered to the absence of any mirror symmetry axis in either the real-space wavefronts or the k-space wavevector. Specifically, when the minimum contour \({{|E}_{z}^{p}|}_{\mathrm{min}}\) coincides with the direction of open angle, that is φ = θ ± 90°, the difference \(|{\Delta E}_{z}|\) reached its maximum. We defined this maximum difference \({|{\Delta E}_{z}|}_{\mathrm{max}}\) for the “symmetry-broken” state, as illustrated by black dashed lines in Fig. 2b (More details in Additional file 1: Fig. S2).
Using our definition, we simulated the distributions of |Ez|, Re(Ez) and fast Fourier transform FFT[Re(Ez)] in one of the symmetry-broken cases at φ = 90° − θ = 55° (where θ is 35° at 1450 cm−1 marked by the yellow triangle patch) in calcite [7]. As expected, both field distributions of |Ez| and Re(Ez) exhibited symmetry-broken propagation in Fig. 2c, d. The Fourier analysis in Fig. 2e coincided with our previous theoretical IFC in Panel 3, where the contour of \({{|E}_{z}^{p}|}_{\mathrm{min}}\) (yellow dashed line) overlapped with the direction of open angle θ. Interestingly, the polariton propagation along the direction of dipolar polarization p was lost in Fig. 2c, d, which cannot emerge in an in-plane isotropic system. This unusual feature can be attributed to the hyperbolic anomalous dispersion (Additional file 1: Fig. S5), causing a mismatch between the directions of energy flow and wavevector [16, 17]. The demonstrated asymmetry contrast of polariton in Fig. 2c could be further enhanced theoretically. The maximum symmetry-broken behavior occurred at θ = 45° (i.e. \({{|E}_{z}^{p}|}_{\mathrm{min}}\) and \({{|E}_{z}^{p}|}_{\mathrm{max}}\) overlap with the directions of both θ and –θ, respectively) when φ was ± 45°, as marked by the white circle in Fig. 2b.
We initiated the study by simulating the most asymmetric HPs in calcite at 1470 cm−1, with an open angle 45° denoted by θ. Considering the even symmetry of \(\left|{\Delta E}_{z}\left(\varphi ,\theta \right)\right|\) in Fig. 2b, we analyzed the change in the symmetry of HPs with varying polarization angle φ in the range of 0°–90°. Figure 2f provides a visual representation of the impact of dipolar orientation on the symmetry of polaritonic rays. As previously analyzed, the mirror asymmetry of polaritonic rays appears when the the dipolar orientation is not aligned with the directions of crystal axis in calcite. To determine the defined symmetry-broken state, the degree of polariton asymmetry must be quantified with respect to polarization angle φ. The amplitude profiles |Ez| along the horizontal dashed white lines in Fig. 2f were analyzed, and the distinct growth and extinction trends of electric field intensities in Peak I and Peak II were observed by analyzing the peak intensity of the symmetric conditions (φ = 0° or 90°) as shown in Fig. 2g. These asymmetric behaviors are derived from a near-field interference effect of the dipole source. Furthermore, their difference (ΔS) in Fig. 2h shows a trend of first rising and then falling, reaching its maximum at φ = 45°, corresponding to the peak of \(|{E}_{z}^{\mathrm{I}}|\) and the dip of \(|{E}_{z}^{\mathrm{II}}|\), confirming the validity of our theoretical analysis related to the cause of mirror asymmetry. Hitherto, we demonstrated a feasible method for source-configurable symmetry-broken polaritons from the perspective of theoretical calculation and simulation.
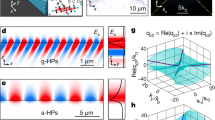
To visualize the effect of source polarization on the symmetric-broken HPs in the near-field imaging experiments, we fabricated a gold disk with a diameter of 1.6 μm and a thickness of approximately 50 nm as an optical nanoantenna on the surface of a bulk crystal calcite (see Methods). The nanoimaging concept is illustrated in Fig. 3a. Upon illumination with a TM-polarized infrared beam of electric field Ein, the gold disk focused the incident field into a nanoscale spot at its extremities. This nanoscale hotspot served as a local point source with an in-plane dipolar moment for inducing highly confined HPs on the calcite surface. The induced polaritonic field Ep was coherently superimposed with the illumination field Ein during propagation. Eventually, the resultant field |Ein + Ep| and its phase spectrum were collected by the tip of scattering-type scanning near-field optical microscopy (s-SNOM). Further discussion can be found in Additional file 1: Fig. S7. Figure 3b clearly shows typical dipolar distributions at the disk extremities and a nearly 180° phase jump at the disk center. Moreover, the orientation of the antenna was parallel to the direction of phase jump, as illustrated by polarization angle φ (black double arrow) with respect to y-axis. This orientation can be dynamically tailored by rotating the polarization direction of illumination field with a simple far-field control, which involves rotating the sample. The near-field signal were demodulated at the second harmonic without specification.
Experimental observation of the tunable symmetry of antenna-launched HPs in calcite. a Schematic of the near-field polariton-launching experiment. (b) Near-field image displaying the dipolar electric field distributions on gold disk antenna. The center of positive and negative phases is denoted by + and − , respectively. The polarization direction of the gold disk antenna is indicated by a double-headed arrow. c,d Experimental near-field amplitude |Ein + Ep|. c and near-field distribution with background subtracted |Ep|. d of the antenna-launched HPs at various values of φ. The illuminating frequency was 1470 cm−1. The extremity of the gold disk is highlighted by yellow circles. e Experimental (solid curves) and simulated (dashed curves) amplitude profiles |Ep| extracted along dashed line in d (cf. Additional file 1: Fig. S10b). ΔS represents the difference in electric field peak intensities for two rays of different direction. f Normalized ΔS as a function of φ
The near-field amplitude images of HPs were measured with illuminating frequency 1470 cm−1 where θ = 45° for calcite, at four different polarization angles φ (see also experimental data in Additional file 1: Fig. S8), as shown in Fig. 3c. These experimental images were corroborated with the numerical simulations in Additional file 1: Fig. S9, showing an excellent agreement in the amplitude images. Figure 3c exhibits two types of asymmetric HP behaviors: the universal asymmetric HP patterns on both sides of the antenna under the oblique incidence (with an angle 30° to the calcite surface) and their fringe spacing constantly changes with the variation of polarization angle φ, which is a typical characteristic of interference with the incidence field. The offset of intrinsic hyperbolic dispersion induced by the oblique incidence is responsible for the change of interference fringes |Ein + Ep|, as demonstrated in the Fourier analysis of Additional file 1: Fig. S9c. However, HP propagations still maintain a certain degree of mirror symmetry with respect to x-axis at φ = 90° (or y-axis at φ = 0°).
Figure 3c also shows another non-symmetric behavior witnessed at φ = 70° or 45° when the antenna polarization was no aligned with the direction of real-space crystal axis. To avoid any illumination-caused effects, the background signals were filtered out (see Methods), and the near-field signals of polaritons |Ep| were extracted, as shown in Fig. 3d. All of these signals exhibit ray-like polariton propagation along the normal direction of open angle θ without interference fringes. Additionally, numerical simulations under the normal incidence were performed in Additional file 1: Fig. S10b to remove the factor of oblique incidence completely. We highlight that background-free polariton signals in Fig. 3d exhibited remarkable consistency with the simulations of normal incidence. This indicates that mirror symmetry breaking is not related to the interference with far-field illumination but rather to the dipolar moment induced by the polarization of the gold disk antenna, as discussed previously.
Figure 3e illustrated the electric field intensity line profiles extracted from both the experiment (Fig. 3d) and simulation (Additional file 1: Fig. S11b). They exhibited excellent consistency in terms of amplitude trends, displaying constructive or destructive interference behaviors similar to those observed in Fig. 2g. Hence, the theoretical trend of asymmetry degree in HPs can be obtained via fitting simulation results of ΔS at different φ. As shown in Fig. 3f, the theoretical trend of ΔS was consistent with experimental points (marked by star symbols) and shares very similar features with the trend of \(|{E}_{z}^{\mathrm{I}}-{E}_{z}^{\mathrm{II}}|\) in Fig. 2h. However, it exhibited an asymmetrical distribution on both sides of the maximum at φ = 45° owing to the existence of off-diagonal elements εyz in the trigonal calcite crystal (Additional file 1: Fig. S10). Notably, when the symmetry-broken state occurred at φ = 45° as θ equals 45° (see peak in Fig. 3f), the dipolar orientation of the gold disk antenna, where the scattering field intensity is strongest (i.e. the direction of \({{|E}_{z}^{p}|}_{\mathrm{max}}\) in Fig. 2a), coincided exactly with the direction of the open angle of hyperbolic IFCs. At this point, the ray propagated along the antenna polarization, and by our definition, was almost erased. On the other hand, the peak intensity of the other one reaches its maximum for all φ and is almost twice as much as the symmetric case in Fig. 3e (but it is not applicable to all θ, Additional file 1: Fig. S11c). This feature confirms that our source-configured method not only breaks the mirror symmetry of HPs but also results in the hyperbolic energy flow being efficiently coupled into rays in one direction rather than being divided into four equal branches, provided that the antenna orientation was appropriately tuned with respect to the direction of open angle θ.
Finally, we investigated the difference in symmetry-broken HP excitation and propagation at different open angles θ by adjusting the illumination frequency. Our previous analysis (Fig. 2) enabled us to determine the response (φ = 90° − θ) to ideal symmetry breaking for an arbitrary given θ. Conversely, we could also determine θ when φ was known. Note that φ was derived from the theoretical IFC of calcite (Additional file 1: Fig. S4) in advance, whereas θ was measured after the experiment. Experimental visualization of the symmetry-broken HPs were shown in Fig. 4a, b, where three different polarization angles φ were calculated as followed: 50° at 1460 cm−1, 55° at 1450 cm−1, and 60° at 1440 cm−1. Remarkably, the degree of mirror-symmetry breaking of HPs in these three cases is largely maintained while ramping the illumination frequency ω over a large range. Furthermore, the energy flow of HPs did not travel in the direction of antenna polarization but was blocked under the symmetry-broken conditions (Fig. 4b). Relevant principles have been covered in Fig. 2c–e. The corresponding Fourier spectra (Fig. 4c) also confirm the mirror symmetry breaking in the wavevector distribution, providing an advantage in the dynamical broadband regulation with our source configuration methods. This advantage arises from the fact that the open angle θ can be finely tuned almost throughout the Reststrahlen band in calcite. We intentionally combined three FFT images into a colormap in Fig. 4d to visibly demonstrate the evolving symmetry-broken behaviors with the change in θ. Apart from the decisive effect of \({{|E}_{z}^{p}|}_{\mathrm{min}}\) on the mirror symmetry breaking, we also highlight the dominant role of \({{|E}_{z}^{p}|}_{\mathrm{max}}\) in the excitation efficiency of HPs (details in Additional file 1: Fig. S11). Note that the intensity of asymmetric polaritonic rays in Fig. 4b gradually weakenes as the open angle θ increases from 1460 cm−1 to 1440 cm−1, in accordance with the decline of \({|{\Delta E}_{z}|}_{\mathrm{max}}\) when θ varies from 39° to 27° in Fig. 2b. This weakening occurred due to the different degrees of deviation between the dipolar orientation of the antenna (i.e., \({{|E}_{z}^{p}|}_{\mathrm{max}}\)) and the direction of the open angle under the symmetry-broken state. The relationship between θ and φ under symmetry-broken conditions is shown in Fig. 4e, which exhibits a good linear correlation within reasonable experimental error when the infrared frequency ω ranges within 1420–1480 cm−1, satisfying the theoretical relation θ = 90° − φ as shown in Fig. 2b. These observations support the suitability of our theoretical study for the antenna-excited HPs in practice.
Broadband tunable symmetry-broken HPs in calcite. a, b Experimental near-field images of symmetry-broken HPs with and without background, respectively, at three different frequencies. c Absolute value of the Fourier transforms of the images shown in a; d The filtered experimental data extracted from (b). White dashed lines denote asymptotes of the experimental IFC. d Experimental open angle θ (orange rhombus) and theoretical polarization angle φ (green circle and line) of HPs plotted against frequency. Note that we used different disk antennas but with the same size at ω = 1460 cm−1 compared to the case at ω = 1450 cm−1 or 1440 cm−1, all of them exhibited obvious symmetry-broken HP phenomena, which proved the robustness of the experimental results
In summary, we have introduced and experimentally demonstrated a source-configured method to break the mirror symmetry of HP propagation in high-symmetry crystals, which enables the manipulation of polariton asymmetry in a simple and robust manner. By controlling the near-field excitation source, we can achieve a broad range of symmetry-broken behaviors in almost all HP responses across a wide frequency spectrum. Our simulated and experimental results provide a comprehensive understanding of asymmetrically polaritonic phenomena and contribute to the development of fully controllable engineering of light steering at the nanoscale. Furthermore, this approach can be extended to other polaritonic and nanophotonic systems, creating exciting opportunities for robust, dynamical, and ultrafast nano-light routing based on polarization. Our study shows that symmetry-broken polaritons in a high-symmetry crystal offer higher directionality of symmetry-broken polaritons, enabling energy coupling in specific directions, as well as the advantages of high-symmetry crystal polaritons with low loss and easy device processing. Additionally, symmetry-broken polaritons in a high-symmetry crystal can be combined with methods such as graphene heterojunction, twist engineering, and chemical doping, which offer potential applications in areas such as nanoimaging, near-field radiation management, photonic circuits for nanoscale light propagation, and quantum physics.
Availability of data and materials
The data that support the findings of this study are available from the corresponding authors upon reasonable request.
Abbreviations
- AFM:
-
Atomic force microscope
- FFT:
-
Fast Fourier transform
- HP:
-
Hyperbolic polariton
- IFC:
-
Isofrequency contour
- s-SNOM:
-
Scattering-type scanning near-field optical microscopy
- TM:
-
Transverse magnetic
References
Basov, D. et al. Polaritons in van der Waals materials. Science 354, aag1992 (2016).
S. Dai et al., Efficiency of launching highly confined polaritons by infrared light incident on a hyperbolic material. Nano Lett. 17, 5285–5290 (2017)
G. Hu et al., Phonon polaritons and hyperbolic response in van der Waals materials. Adv. Opt. Mater. 8, 1901393 (2020)
T. Low et al., Polaritons in layered two-dimensional materials. Nat. Mater. 16, 182–194 (2017)
S. Dai et al., Tunable phonon polaritons in atomically thin van der Waals crystals of boron nitride. Science 343, 1125–1129 (2014)
G. Hu et al., Topological polaritons and photonic magic angles in twisted α-MoO3 bilayers. Nature 582, 209–213 (2020)
W. Ma et al., Ghost hyperbolic surface polaritons in bulk anisotropic crystals. Nature 596, 362–366 (2021)
W. Ma et al., In-plane anisotropic and ultra-low-loss polaritons in a natural van der Waals crystal. Nature 562, 557–562 (2018)
Q. Zhang et al., Hybridized hyperbolic surface phonon polaritons at α-MoO3 and polar dielectric interfaces. Nano Lett. 21, 3112–3119 (2021)
Z. Dai et al., Edge-oriented and steerable hyperbolic polaritons in anisotropic van der Waals nanocavities. Nat. Commun. 11, 6086 (2020)
J.D. Caldwell et al., Low-loss, infrared and terahertz nanophotonics using surface phonon polaritons. Nanophotonics 4, 44–68 (2015)
Z. Dai et al., Artificial Metaphotonics Born Naturally in Two Dimensions. Chem. Rev. 120, 6197 (2020)
D.Y. Fedyanin et al., Surface plasmon polariton amplification upon electrical injection in highly integrated plasmonic circuits. Nano Lett. 12, 2459–2463 (2012)
S.S. Kou et al., On-chip photonic Fourier transform with surface plasmon polaritons. Light Sci. Appl. 5, e16034 (2016)
F.P. Mezzapesa et al., Chip-Scale Terahertz Frequency Combs through Integrated Intersubband Polariton Bleaching. Laser Photonics Rev. 15, 2000575 (2021)
Z. Guo et al., Hyperbolic metamaterials: From dispersion manipulation to applications. J. Appl. Phys. 127, 071101 (2020)
L. Ferrari et al., Hyperbolic metamaterials and their applications. Prog. Quantum Electron. 40, 1–40 (2015)
Lee, D. et al. Hyperbolic metamaterials: fusing artificial structures to natural 2D materials. eLight 2, 1–23 (2022).
N.C. Passler et al., Hyperbolic shear polaritons in low-symmetry crystals. Nature 602, 595–600 (2022)
Hu, G. et al. Real-space nanoimaging of hyperbolic shear polaritons in a monoclinic crystal. Nat. Nanotechnol., 18, 64–70 (2023)
S. Xue et al., Vortex-induced quasi-shear polaritons. Advanced Photonics Nexus 2, 015001 (2023)
Matson, J. et al. Controlling the Propagation Asymmetry of Hyperbolic Shear Polaritons in Beta-Gallium Oxide. Research Square (2023). https://doi.org/10.21203/rs.3.rs-2365178/v1
M.F. Picardi et al., Janus and Huygens dipoles: near-field directionality beyond spin-momentum locking. Phys. Rev. Lett. 120, 117402 (2018)
K.Y. Bliokh et al., Extraordinary momentum and spin in evanescent waves. Nat. Commun. 5, 3300 (2014)
Neugebauer, M. et al. Emission of circularly polarized light by a linear dipole. Sci. Adv. 5, eaav7588 (2019).
Wang, M. et al. Spin-orbit-locked hyperbolic polariton vortices carrying reconfigurable topological charges. eLight 2, 12 (2022).
P.V. Kapitanova et al., Photonic spin Hall effect in hyperbolic metamaterials for polarization-controlled routing of subwavelength modes. Nat. Commun. 5, 3226 (2014)
F.J. Rodríguez-Fortuño et al., Near-field interference for the unidirectional excitation of electromagnetic guided modes. Science 340, 328–330 (2013)
M.F. Picardi et al., Unidirectional evanescent-wave coupling from circularly polarized electric and magnetic dipoles: An angular spectrum approach. Phys. Rev. B 95, 245416 (2017)
D.M. Di Paola et al., Ultrafast-nonlinear ultraviolet pulse modulation in an AlInGaN polariton waveguide operating up to room temperature. Nat. Commun. 12, 3504 (2021)
J. Gosciniak et al., Theoretical analysis of long-range dielectric-loaded surface plasmon polariton waveguides. J. Lightwave Technol. 29, 1473–1481 (2011)
O. Jamadi et al., Edge-emitting polariton laser and amplifier based on a ZnO waveguide. Light Sci. Appl. 7, 82 (2018)
Y. Zeng et al., Tailoring Topological Transitions of Anisotropic Polaritons by Interface Engineering in Biaxial Crystals. Nano. Lett. 22, 4260 (2022)
I. Söllner et al., Deterministic photon–emitter coupling in chiral photonic circuits. Nat. Nanotechnol. 10, 775–778 (2015)
P. Li et al., Reversible optical switching of highly confined phonon–polaritons with an ultrathin phase-change material. Nat. Mater. 15, 870–875 (2016)
M. Wang et al., Programmable controls of multiple modes of spoof surface plasmon polaritons to reach reconfigurable plasmonic devices. Adv. Mater. Technol. 4, 1800603 (2019)
Z. Guo, Y. Long, H. Jiang, J. Ren, H.J.A.P. Chen, Anomalous unidirectional excitation of high-k hyperbolic modes using all-electric metasources. Adv. Photonics 3, 036001 (2021)
C. Sayrin et al., Nanophotonic optical isolator controlled by the internal state of cold atoms. Phys. Rev. X 5, 041036 (2015)
Acknowledgements
We also thank the Analytical and Testing Center of HUST for help with the measurements.
Funding
We acknowledge the support from the National Natural Science Foundation of China (Grant No. 62075070 and 52172162), National Key Research and Development Program of China (Grant No. 2021YFA1201500), Hubei Provincial Natural Science Foundation of China (Grant No. 2022CFA053) and the Innovation Fund of WNLO. Z.D. acknowledges support from the Natural Science Foundation of Guangdong Province (2022A1515012145), Shenzhen Science and Technology Program (JCYJ20220530162403007), and Key Research and Development Plan of Hubei Province. W.M. acknowledges the support from the Fundamental Research Funds for the Central Universities, HUST (Grant No. 2022JYCXJJ009).
Author information
Authors and Affiliations
Contributions
ZD, XY, XZ, and PL conceived the study. CH, TS fabricated the samples. CH, ZY performed the theory analysis coordinated by WM and PL, CH, ZY, and TS performed the s-SNOM measurements with the help of WM, CH, TS, and WM performed the simulations. ZD, XY, XZ, and PL coordinated and supervised the work. CH, ZD, XY, and PL wrote the manuscript with input from all co-authors. All authors read and approved the final manuscript.
Corresponding authors
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Competing interests
The authors declare no competing interests.
Supplementary Information
Additional file 1: Note S1.
Field calculation from an electric dipole. Note S2. Dispersions in high- and low-symmetry crystals. Note S3. More details of numerical simulations. Additional figures.
Methods
Methods
1.1 Permittivity of the calcite crystal
We employed calcite, a common trigonal crystal, with a diagonalizable permittivity tensor that is represented by \(\widetilde{\varepsilon }\) = diag [ε⊥, ε||, ε⊥], where ε|| and ε⊥ correspond to the principal components parallel and perpendicular to the optical axis, respectively. These components exhibit opposite signs in the mid-infrared Reststrahlen band, spanning from 1410 to 1550 cm−1, ε||> 0 and ε⊥ < 0. To fit its permittivity, we used Lorentz oscillator models with two Lorentz oscillators for ε⊥ and one oscillator for ε||, according to the equation:
where \({\omega }_{\mathrm{TO},i}\) and \({\omega }_{\mathrm{LO},i}\) are the i-th TO and LO phonon frequencies for different Lorentz oscillators, respectively. The parameters Гi and ε∞,i represent the damping constant and the high-frequency permittivity. Detailed information regarding all of the parameters is available in reference [7].
1.2 Numerical simulations
To simulate the near-field distributions of hyperbolic polariton along the surface of calcite, we employed COMSOL, a finite-element simulation software. We used the scattered field in the electromagnetic wave frequency domain module to directly launch the surface-confined HPs without any background. For further details regarding each simulation figure, please refer to Additional file 1: Note S3.
1.3 Experimental background subtraction
In order to remove the effect of background, we first selected a clean background area away from the interference fringes (a circular area with a radius of 1 μm in our paper). We then calculated the mean of the real part and imaginary part of total field signals within the truncated region, respectively. By performing a complex-valued subtraction, the background-free near-field amplitude |Ep| can be obtained using the equation:
where A2(x, y) and Ψ2(x, y) are the amplitude and phase in the demodulated experimental signals measured at the arbitrary position, respectively. And A2,bg(x, y) and Ψ2,bg(x, y) are the mean value of the amplitude and phase in the selected background areas.
1.4 s-SNOM measurements
For our near-field imaging experiments, we employed a commercial s-SNOM system from Neaspec GmbH that consists of an atomic force microscope (AFM). The Pt-coated AFM tip was operated in tapping mode with an oscillation amplitude of ~ 50 nm at a cantilever resonance frequency Ω ≈ 270 kHz. The system was continuously tuned using a continuous-wave quantum cascade laser ranging from 1310 to 1470 cm−1.
The backscattered field signal was collected with a pseudo-heterodyne interferometer, and the interferometric detector signal was demodulated at a higher harmonic nΩ (n ≥ 2) to suppress far-field background contribution in the tip-scattered field, thereby yielding near-field images of amplitude sn and phase φn with a high spatial resolution of ~ 20 nm.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hu, C., Sun, T., Zeng, Y. et al. Source-configured symmetry-broken hyperbolic polaritons. eLight 3, 14 (2023). https://doi.org/10.1186/s43593-023-00047-1
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1186/s43593-023-00047-1