Introduction

Digital computation has played a central role in modern technologies as a robust way to process data. It can be realized with standard digital computers composed of a series of vacuum tubes, discrete transistors, integrated circuits, pneumatic valves or optical logic gates [1]. However, intrinsic challenges of this technology consist in high power consumption, long processing time due to the serial data processing, and large footprints. Optical analog computation is being explored as a promising candidate to replace digital signal processing, as it can deal with highly parallel data processing, ultrafast processing times, and high efficiency. In this paradigm, the complex wavefront of electromagnetic waves, as the information carrier, can be tailored by analog computing devices for designated field distributions.

Fourier transform is a powerful mathematical operation that manipulates signals for data analysis and processing due to its alternate representation of universal signal and corresponding mathematical properties [2]. This operation can be implemented in the temporal and the spatial domains, both amenable to analog computation [3]. Fourier transformation in the temporal domain requires processing of pulse signals with relatively large size and limited input ports [4, 5], which leads to difficult parallel processing. In contrast, spatial analog computing can significantly increase the throughput of designated mathematical operations, such as differential equation solvers [6], edge detection of pattern imaging [7], optical memory or temporal integrators [8], photonic neural networks [9, 10] and multi-operator by susceptibility tensors [11].

In terms of physical architectures and hardware, traditional analog computers mainly focus on mechanical, electronic, and hybrid devices [12, 13], which, however, suffer from relatively large size and slow response. To enhance the figure of merit of analog computational devices and to reduce electric dimensions and energy losses, the concept of computational metamaterials was recently introduced to perform mathematical operations, through engineering of the propagation of electromagnetic waves in artificial materials with tailored refractive index [14]. Metasurfaces, two-dimensional arrays of subwavelength meta-atoms [15], have been extensively studied in recent years, and have been shown to relax the demanding fabrication requirements and reduce the profile of volumetric metamaterials, while maintaining the powerful capability of manipulating electromagnetic waves at will. With the development of computational science and advanced fabrication technologies, studies in the field of metasurfaces have experienced rapid growth over the past decade [16,17,18,19]. However, conventional designs of metasurfaces based on symmetric and asymmetric resonances [15] or Pancharatnam-Berry (P-B) phase elements [20, 21], are generally accompanied by poor efficiency, which makes it difficult to envision their usefulness in various technological platforms. Huygens’ metasurfaces have the potential to improve the processing efficiency, reduce the geometrical footprint and simplify the fabrication process. By controlling electric and magnetic responses in meta-atoms, Huygens’ metasurfaces have been demonstrated to realize arbitrary amplitude and phase control of both transmission and reflection coefficients [22], which have been further exploited for various functionalities, such as beam-steering [23, 24], focusing [25], beam-shaping [26] and 3D imaging with depth retrieval [27].

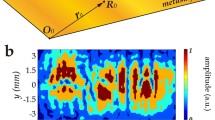
In this paper, a Huygens’ metasurface based on the Fourier transform is experimentally demonstrated, showing that it can process holographic images and apply a wide set of desired linear operations. The structure is designed to modulate scattered electromagnetic waves based on the fundamental mathematical properties of Fourier transform, with additional benefits of low transmission losses, subwavelength thickness and easy fabrication. Specifically, our proposed metasurface design resorts to the properties of the Fourier transform to rotate and spatially project a holographic image towards desired elevation and azimuth angles, as shown in Fig. 1. For the physical implementation, a set of 15 Huygens’ meta-atoms, discretizing the full transmission phase coverage with transmission amplitude above 0.9, are tailored as building blocks. The proposed transmission-type Huygens’ metasurfaces allow to achieve the high-throughput, low-loss and high-speed holographic image operations by direct modulation in frequency-domain, facilitating other ultrafast analog computing devices, such as differentiators and integrators.

Fig. 1
figure 1

a Schematic diagram of frequency-domain modulating metasurface performing the Fourier transform properties. b The implementations of rotational invariance, spatial shifting and scaling properties utilizing Huygens’ metasurface

Full size image

Methods

According to surface equivalence principle, metasurface can be described as an ensemble of elaborately designed field source elements. Therefore, by analogy with analysis of aperture antenna, the transmitted pattern Ef(θ, φ) can be written as the superposition of the electric field Ein(m, n) associated to each meta-atom. Under the paraxial approximation and ignoring higher order small terms, the projected electric field intensity at distance r, elevation angle θ and azimuth angle φ can then be written as (see section 1 of Supplementary Information for more details) [28, 29].

$$ {\displaystyle \begin{array}{l}\left|{E}_f\left(\theta, \varphi \right)\right|=\frac{1+\cos \theta }{2\lambda r}{D}_x{D}_y{E}_a\left({s}_x,{s}_y\right)\\ {}{E}_a\left({s}_x,{s}_y\right)=\left|\sum \limits_{m=0}^{M-1}\sum \limits_{n=0}^{N-1}{E}_{in}\left(m,n\right){\mathrm{e}}^{j\left({ms}_x+{ns}_y\right)}\right|\end{array}} $$
(1)

where sx = kDx sin θ cos φ, sy = kDy sin θ sin φ, Dx and Dy represent the pixel periods, M, N are the total number of meta-atoms along x- and y-axis, respectively, and \( k\frac{2\pi }{\lambda } \)is the wave number in free space. The projected electric field distribution can be divided into two parts, the directivity-related amplitude function of single meta-atom \( \frac{1+\cos \theta }{2\lambda r} \), and the distribution coefficient Ea, which deals with the major information, i.e. the amplitude of the wave, and indicates the two-dimensional inverse Fourier transform. Hence, Eq. 1 demonstrates the Fourier relationship between the projected electromagnetic wave described by space angles (θ and φ ) in spherical coordinates and the electric field distribution on the metasurface in Cartesian coordinates. Particularly, the above derivation process is based on the far-field approximation to focus on the analysis of space-angle transformation. In the context of microwave holography, such operation can be utilized for multiple image processing techniques. To design a phase-only hologram, the transmission amplitude of each meta-atom should be unity, i.e. Ein(m, n) = ejϕ(m, n), where ϕ(m, n) ϕmn denotes the abrupt transmission phase discontinuity of the wave through the (mth, nth) meta-atom. A direct relationship between the electric field distribution and the arrangement of Huygens’ meta-atoms can then be derived for designated image-processing techniques [30].

In order to demonstrate this concept, we assume that the initial holographic image consists of six foci at hexagon vertices, as shown in Fig. 1b. Huygens’ meta-atoms as shown in Fig. 2a are utilized to effectively modulate the transmitted wave by tailoring the electromagnetic responses of electric and magnetic dipoles [31]. As illustrated by the main surface currents in Fig. 2b, the split-ring resonator on one side of the dielectric substrate acts as a magnetic dipole [32] and the electric-LC resonator on the other side serves as an electric dipole [33]. The equivalent circuit model shows that the manipulation of the meta-atom’s geometrical parameters induces a variation of the inductance and capacitance values and further influences the resonance characteristics for desired transmission coefficient. Figure 2c provides the simulation results of 15 meta-atoms varying the geometrical parameters le and lm, as described in Supplementary Information (section 2). The optimized Huygens’ meta-atoms achieve 24° transmission phase step along with transmission amplitude above 0.9 at 10 GHz, revealing efficient manipulation of the electromagnetic field. The next step is the construction of a metasurface hologram. We note that the required interfacial field discontinuity contains a variation of both amplitude and phase response. We implement the weighted Gerchberg-Saxton (GSW) algorithm to obtain the required phase hologram (details in section 3 of Supplementary Information for more details) [34]. For the original six-focus imaging at 10 GHz, the metasurface is composed of 40 × 53 meta-atoms, covering an area of 200 × 187 mm2. As shown in Figs. 3a, b and c, after encoding the phase profiles into the proposed meta-atoms, the Huygens’ hologram demonstrates excellent imaging performance at microwave frequencies in both simulated and experimental results. It is important to note that for superior image quality, the resolution of the reconstructed image can be further improved by increasing the number of meta-atoms [35]. For experimental verification, the holographic Huygens’ metasurface sample is tested in a microwave anechoic chamber, with a feeding horn antenna to provide quasi-planar wave illumination and a near-field probe to measure the transmitted electric field point by point, as shown in Fig. 2d.

Fig. 2
figure 2

Design of transmission-type Huygens’ metasurface and experimental setup. a Geometric structure of the proposed Huygens’ meta-atom patterned on both sides of the dielectric substrate (εr = 2.2, tan δ = 0.002). b Surface currents and equivalent electric circuits of the proposed meta-atom. c Simulated transmission amplitude and phase of 15 extracted meta-atoms with different geometrical parameters, lm and le at 10 GHz. d Experimental setup utilized for characterizing the metasurface hologram. The right side is a zoomed-in view of the fabricated Huygens’ metasurface

Full size image
Fig. 3
figure 3

Design of the original Huygens’ metasurface hologram and the rotational invariance property based on it. a Phase map of the original holographic image based on the modified GSW algorithm. b Numerical simulations and c experimental results of holographic electric field intensity distribution at a focal length of 100 mm for 10 GHz working frequency. d Phase map of the rotational invariance property utilizing Huygens’ metasurface. e Numerical simulations (at 100 mm) and f. experimental results of holographic electric field intensity distribution at 10 GHz working frequency

Full size image

Results and discussion

According to our above theoretical derivation, the ensemble of meta-atoms arranged on a two-dimensional surface provide holographic images following Eq. 1, which can be used here to physically modulate the electromagnetic field distribution for specific image processing through the designated mathematical operation of Fourier transform. Our particular interest in this work is to exploit rotational invariance, spatial shifting and scaling, which are of extreme importance in image matching, retrieval and processing [36]. Without loss of generality, we assume the initial field generated by the Huygens’ metasurface (Ein(m, n)) to be the six-foci image (E0(sx, sy)) which may be written in the spatial domain using the inverse Fourier transform as ℱ−1{Ein(m, n)} = E0(sx, sy). Besides, based on the Fourier transform properties, the modulated image pattern \( {E}_1\left({\tilde{s}}_x,{\tilde{s}}_y\right) \) is generated as \( {E}_1\left({\tilde{s}}_x,{\tilde{s}}_y\right)={E}_0\left(L\left({s}_x,{s}_y\right)\right) \), where L(sx, sy) defines the linear transformation relationship, which corresponds to rotation, shifting and scaling operations respectively.

Rotational invariance property

Mathematically, rotational invariance maps the relationship between the rotation of the input frequency-domain information on the Huygens’ metasurface and the rotation of the output image, denoted as ℱ−1{Ein(ρ, β + β0)} = E0(s, α + β0). Here the dummy variables are the polar coordinates (ρ, β)and (s, α) in the frequency and spatial domains, respectively. For this operation, an encoded phase distribution of Huygens’ metasurface (200 mm × 187 mm with 40 × 53 meta-atoms) is designed to be self-rotated at the desired angle β0, which can be described as \( \tilde{\phi}\left(\tilde{m},\tilde{n}\right)=R\left({\beta}_0\right)\phi \left(m,n\right) \). Specifically, the corresponding coordinate rotation, denoted as the numbering of the unit cells, is depicted as

$$ \left(\begin{array}{c}\tilde{m}\\ {}\tilde{n}\end{array}\right)=R\left({\beta}_0\right)\left(\begin{array}{c}m\\ {}n\end{array}\right)=\left(\begin{array}{cc}\cos {\beta}_0& -\sin {\beta}_0\\ {}\sin {\beta}_0& \cos {\beta}_0\end{array}\right)\left(\begin{array}{c}m\\ {}n\end{array}\right) $$
(2)

where the tilde (˜) denotes the transformed variables after specific Fourier computing operations. Hence, in time domain the scattered-field distribution \( {E}_1\left({\tilde{s}}_x,{\tilde{s}}_y\right) \) is changed as.

$$ {\displaystyle \begin{array}{c}{E}_1\left({\tilde{s}}_x,{\tilde{s}}_y\right)=\left|\sum \limits_{m=0}^{M-1}\sum \limits_{n=0}^{N-1}{e}^{j\tilde{\phi}\left(\tilde{m},\tilde{n}\right)}{e}^{j\left({ms}_x+{ns}_y\right)}\right|=\left|\sum \limits_{\tilde{m}}\sum \limits_{\tilde{n}}{e}^{j\tilde{\phi}\left(\tilde{m},\tilde{n}\right)}{e}^{j\left[{s}_x\left(\tilde{m}\cos {\beta}_0+\tilde{n}\sin {\beta}_0\right)+{s}_y\left(-\tilde{m}\sin {\beta}_0+\tilde{n}\cos {\beta}_0\right)\right]}\right|\\ {}=\left|\sum \limits_{\tilde{m}}\sum \limits_{\tilde{n}}{e}^{j\tilde{\phi}\left(\tilde{m},\tilde{n}\right)}{e}^{j\left[\tilde{m}\left({s}_x\cos {\beta}_0-{s}_y\sin {\beta}_0\right)+\tilde{n}\left({s}_x\sin {\beta}_0+{s}_y\cos {\beta}_0\right)\right]}\right|\\ {}={E}_0\left({s}_x\cos {\beta}_0-{s}_y\sin {\beta}_0,{s}_x\sin {\beta}_0+{s}_y\cos {\beta}_0\right)\end{array}} $$
(3)

which indicates that the rotation of phase distribution on the metasurface leads to the same self-rotation angle β0 of the original scattered field, described as \( L\left({s}_x,{s}_y\right)=R\left({\beta}_0\right)\left(\begin{array}{c}{s}_x\\ {}{s}_y\end{array}\right) \). As illustrated in Fig. 3d-f where the rotation angle β0 is set as 30°, the simulated and measured results both exhibit the same 30° rotation transformation of the original electric field distribution. Besides, the experiment results show the excellent performance with 78.6% transmittance efficiency [37], 61.7% imaging pattern efficiency [38] and 86.6 signal-to-noise ratio (SNR) [39], suggesting the superior manipulation capacity. To evaluate the consistency between the electromagnetic wave distribution before and after the corresponding operations, the normalized dot product ratio (NDPR) is utilized here to calculate the similarity between two equal-length sequences of numbers. The detailed definition and measurements of those figures of merits are provided in Supplementary information (section 4). The NDPR of the rotational operation is calculated as 0.84, which demonstrates the excellent functionality of Huygens’ metasurface, and further validates the computational mechanism that self-rotation in frequency domain generates the same self-rotation angle in real space domain with no other variation in functional characteristics.

Spatial shifting property

In general, the spatial shifting properties of Fourier transform state that the real-space scattered signals (which corresponds to time-domain variables in Eq. 1) being shifted by a fixed angle corresponds to the multiplication of the eigenmode signals with the original ones in the spatial frequency domain. In mathematical terms, this can be written as \( {\mathcal{F}}^{-1}\left\{{e}^{-j\left({ms}_{x_0}+{ns}_{y_0}\right)}{E}_{in}\left(m,n\right)\right\}={E}_0\left({s}_x-{s}_{x_0},{s}_y-{s}_{y_0}\right) \). Relying on this property of Fourier transform, a Huygens’ metasurface can be designed as a superposition of the original phase distribution of the Huygens’ metasurface and designated phase sequences ϕx and ϕy along x- and y-axis respectively, which can be written as \( \tilde{\phi}\left(\tilde{m},\tilde{n}\right)=\phi \left(m,n\right)+{\phi}_x(m)+{\phi}_y(n)=\phi \left(m,n\right)-{ms}_{x_0}-{ns}_{y_0} \). More explicitly, the distribution coefficient will be modified as

$$ {\displaystyle \begin{array}{c}{E}_1\left({\tilde{s}}_x,{\tilde{s}}_y\right)=\left|\sum \limits_{m=0}^{M-1}\sum \limits_{n=0}^{N-1}{e}^{j\tilde{\phi}\left(\tilde{m},\tilde{n}\right)}{e}^{j\left({ms}_x+{ns}_y\right)}\right|=\left|\sum \limits_{m=0}^{M-1}\sum \limits_{n=0}^{N-1}{e}^{j\phi \left(m,n\right)}{e}^{-j\left({ms}_{x_0}+{ns}_{y_0}\right)}{e}^{j\left({ms}_x+{ns}_y\right)}\right|\\ {}=\left|\sum \limits_{m=0}^{M-1}\sum \limits_{n=0}^{N-1}{e}^{j\phi \left(m,n\right)}{e}^{j\left[m\left({s}_x-{s}_{x_0}\right)+n\left({s}_y-{s}_{y_0}\right)\right]}\right|={E}_0\left({s}_x-{s}_{x_0},{s}_y-{s}_{y_0}\right)\end{array}} $$
(4)

where \( {\tilde{s}}_x={kD}_x\sin \tilde{\theta}\cos \tilde{\varphi} \), \( {\tilde{s}}_y={kD}_y\sin \tilde{\theta}\sin \tilde{\varphi} \) and \( {s}_{x_0}={kD}_x\sin {\theta}_0\cos {\varphi}_0 \), \( {s}_{y_0}={kD}_y\sin {\theta}_0\sin {\varphi}_0 \) denote real space domain variables after the Fourier spatial shifting operation and the corresponding spatial frequency shift values respectively. According to Eq. 4, the linear phase superposition of the original Fourier transformer induces a modulation of the output electromagnetic wave function, described as \( L\left({s}_x,{s}_y\right)=\left(\begin{array}{c}{s}_x-{s}_{x_0}\\ {}{s}_y-{s}_{y_0}\end{array}\right) \). Hence, the transformation on image pattern satisfies.

$$ \sin \tilde{\theta}\cos \tilde{\varphi}=\sin \theta \cos \varphi -\sin {\theta}_0\cos {\varphi}_0 $$
(5a)
$$ \sin \tilde{\theta}\cos \tilde{\varphi}=\sin \theta \cos \varphi -\sin {\theta}_0\cos {\varphi}_0 $$
(5b)

Particularly, if the original output function fits the vertical holographic imaging with no refraction, both the initial elevation angle θ and azimuth angle φ are 0. Therefore, the transformed projection angles (\( \tilde{\theta} \) and \( \tilde{\varphi} \)) exactly equal the offset components (θ0 and φ0), which means that the spatial shifting operations can induce the angle projection of the original scattered field distribution.

For verification, two Huygens’ metasurfaces have been designed with specific two-dimensional phase superpositions. Figures 4a-f depict the simulation and experimentally observed results of the projected holographic patterns at θ = 30 ° , φ = 0° and θ = 30 ° , φ = 30°. The transmission efficiency keeps above 71.2% in both cases and the imaging efficiency is respectively measured to be 56.9% and 51.2% with negligible disturbance on the original electromagnetic field distribution. Moreover, SNR of the steered pattern is calculated as 78.4 and 92.0, and NDPR is 0.88 and 0.88 respectively. The above quantitative evaluation parameters indicate the feasibility and high efficiency of the proposed Huygens’ metasurface with spatial shifting of image, which indicate the great potential of image projection and processing technologies.

Fig. 4
figure 4

Spatial shifting and scaling properties of Fourier transform for space projection on the original holographic pattern. a-c The projection angle is set as θ = 30 ° , φ = 0°. a Phase map for the first spatial-shifting sample. b Numerical simulations and c. experimental results of electric field intensity distribution at 100 mm focal length and 10 GHz working frequency. d-f The projection angle is set as θ = 30 ° , φ = 30°. d Phase map of the second spatial-shifting sample. e Numerical simulations and f experimental results of electric field intensity distribution at 100 mm focal length and 10 GHz working frequency. g-i The magnification value along x-axis is set as 2 for the scaling operational Huygens’ metasurface. g Phase map of the scaling sample. h Numerical simulations and i. experimental results of electric field intensity distribution at 100 mm focal length and 10.3 GHz working frequency

Full size image

Scaling invariance property

To perform the operation defined as \( {\mathcal{F}}^{-1}\left\{{E}_{in}\left( am, bn\right)\right\}={E}_0\left(\frac{s_x}{a},\frac{s_y}{b}\right) \), the dimension of each Huygens’ meta-atom is amplified in frequency domain, which is implemented by increasing the number of meta-atom with the same design to form a super meta-atom. For our phase-only hologram metasurface, the transformed phase distribution can be expressed as \( \tilde{\phi}\left(\tilde{m},\tilde{n}\right)=\phi \left( am, bn\right) \).Therefore, the function description of scattered field can be written as

$$ {\displaystyle \begin{array}{c}{E}_1\left({\tilde{s}}_x,{\tilde{s}}_y\right)=\left|\sum \limits_{m=0}^{M-1}\sum \limits_{n=0}^{N-1}{e}^{j\tilde{\phi}\left(\tilde{m},\tilde{n}\right)}{e}^{j\left({ms}_x+{ns}_y\right)}\right|=\left|\sum \limits_{m=0}^{M-1}\sum \limits_{n=0}^{N-1}{e}^{j\phi \left( am, bn\right)}{e}^{j\left({ms}_x+{ns}_y\right)}\right|=\left|\sum \limits_{\tilde{m}}\sum \limits_{\tilde{n}}{e}^{j\tilde{\phi}\left(\tilde{m},\tilde{n}\right)}{e}^{j\left[\tilde{m}\frac{s_x}{a}+\tilde{n}\frac{s_y}{b}\right]}\right|\\ {}={E}_0\left(\frac{s_x}{a},\frac{s_y}{b}\right)\end{array}} $$
(6)

where \( {\tilde{s}}_x={kD}_x\sin \tilde{\theta}\cos \tilde{\varphi} \), \( {\tilde{s}}_y={kD}_y\sin \tilde{\theta}\sin \tilde{\varphi} \) and sx = kDx sin θ cos φ, sy = kDy sin θ0 sin φ0. Besides, a and b are defined as the magnification factor along x- and y-axis, respectively. Hence, the scaling operation induces the transformation \( L\left({s}_x,{s}_y\right)=\left(\begin{array}{c}\raisebox{1ex}{${s}_x$}\!\left/ \!\raisebox{-1ex}{$a$}\right.\\ {}\raisebox{1ex}{${s}_y$}\!\left/ \!\raisebox{-1ex}{$b$}\right.\end{array}\right) \), which means that the azimuth angle \( \tilde{\theta} \) and pitching angle \( \tilde{\varphi} \) of scattered electric field will be transformed as

$$ \sin \tilde{\theta}\cos \tilde{\varphi}=\frac{\sin \theta \cos \varphi }{a} $$
(7a)
$$ \sin \tilde{\theta}\sin \tilde{\varphi}=\frac{\sin \theta \sin \varphi }{b} $$
(7b)

Let us suppose that a = 2 and b = 1, which can be physically implemented by combining two identical meta-atoms into one super meta-atom along x-direction. The above designed projection image at θ = 30 ° , φ = 30° is utilized here as the original condition. Therefore, the steering angles (\( \tilde{\theta} \), \( \tilde{\varphi} \)θ1, φ1) after scaling operations are calculated as \( \tilde{\theta}=6{}^{\circ},\tilde{\varphi}=49{}^{\circ} \). Figures 4h-g show the simulated and measured images at the derived angle, with 85.5% transmission efficiency, 52.4% imaging efficiency, 99.0 SNR, and 0.82 NDPR. The output result keeps the same as the original model without sacrificing the image quality, proving that the holographic image spatial projection angle can be further controlled accurately and effectively with Huygens’ metasurface.

The mechanism of scaling operation, which demonstrates that the expansion (compression) in Fourier domain can induce the compression (expansion) in spatial domain, opens the door to a wide variety of applications. For the examples of microwave holography, phase step is always discretized as several fractions of the full phase shift 2π in consideration of machining accuracy, so the steering angles are limited to discrete values. The scaling transformation in Fourier spectral view can establish the capacity of continuous projection-angle control utilizing specific physical means, such as the stretchable materials as mechanically tunable polydimethylsiloxane substrates [40, 41], which can engineer different electromagnetic responses with variation of meta-atom dimensions. Moreover, various other tunable and switchable methods exist, such as varactor diodes, microelectromechanical switches, liquid metal resonators that could manipulate the electric and magnetic responses in each meta-atom. By combining the stretchable substrates and dynamic meta-atoms into designs, the variation in both the material electromagnetic properties and geometrical dimensions can significantly extend the dynamic range. Therefore, utilization of scaling property can offer technological prospects in continuous and wide range microwave control.

Conclusions

Our proposed technique to realize holographic image projection may significantly contribute to microwave holography based on analog Fourier transform. According to correlative research studies, the modular scheme to perform analog computations mainly focuses on the three sub-blocks: a Fourier transform module [1, 6, 14, 42], typically in the form of a lens, a spatial filter in the Fourier plane of the lens to impart the desired operation, and an inverse Fourier transform module. In these designs, to guarantee the correspondence between the spatial frequency of impinging electromagnetic wave and azimuth angle of diffraction spots on the interface, the distance between the Fourier transform module and the spatial filter should meet the designated focal length, which means that the system will extend over a large region of space, especially at microwave frequencies. To decrease layer numbers, the reflective analog-computing metasurfaces have been proposed with only two layers since the incident and reflective waves propagate through the same gradient index (GRIN) lens [16], but spatial angle of signals is required to keep the non-interference of the input and output waves. Solving differential equations for edge detection of input signal with just one single layer could also be done with the metasurface based on specific electromagnetic response under limited range of incidence angle [7, 18, 43], which means that a set of meta-atom designs only applies to single computation. In our proposed scheme, the analog mathematical operations can be applied to image transformation and processing technique by only modulating the phase information on the interface without the utilization of a GRIN metalens, taking advantage of the particular Fourier relationship between the imaging field and hologram metasurface, which can significantly improve the manipulation efficiency and decrease the total geometrical dimensions. More sophisticated computing can also be adopted for more elaborately designed meta-atoms to manipulate both the transmitted wave amplitude and phase. Since each meta-atom in subwavelength scale can be regarded as an input port, various analog parallel computations can be implemented directly and efficiently. Besides, by adding tunable factors into the design of Huygens’ meta-atom, the high through-output mathematical operations can be achieved dynamically [44,45,46]. Lastly, the concept of metasurface Fourier transformation is not only limited to microwave regime, but also can be extended to higher frequencies, such as terahertz and optical regimes.

In summary, we proposed a robust and straightforward technique to perform holographic image operations with a physical real-time operator: Huygens’ metasurface. Utilizing the surface equivalence principle, the transmitted field distribution is demonstrated to be the two-dimensional inverse Fourier transform of the phase distribution on the metasurface. By introducing a solely simple modulation of the original phase distribution at the interface resorting to the properties of Fourier transform, corresponding spatial operations can be realized when the impinging wave propagates through the specifically designed metasurfaces, resulting in the original holographic image self-rotation and projection at desired elevation and azimuth angles. Instead of multiple recalculations and reconstructions, the Fourier transform properties can significantly simplify the transformation operations on scattered field with the modulation of original Huygens meta-atom sequences. The manipulation mechanism of Huygens’ meta-atoms promises low transmission losses and excellent imaging performance, and the experimental results show good agreement with theoretical predictions. Besides, the spatial modulation enhances the speed and capacity of data processing, making our proposed scheme a valuable candidate for potential applications in analog computing, image processing and wavefront shaping.