Abstract
The unified stochastic particle method based on the Bhatnagar-Gross-Krook model (USP-BGK) has been proposed recently to overcome the low accuracy and efficiency of the traditional stochastic particle methods, such as the direct simulation Monte Carlo (DSMC) method, for the simulation of multi-scale gas flows. However, running with extra virtual particles and space interpolation, the previous USP-BGK method cannot be directly transplanted into the existing DSMC codes. In this work, the implementation of USP-BGK is simplified using new temporal evolution and spatial reconstruction schemes. As a result, the present algorithm of the USP-BGK method is similar to the DSMC method and can be implemented efficiently based on any existing DSMC codes just by modifying the collision module.
Similar content being viewed by others
1 Introduction
Multi-scale gas flows widely exist in aerospace engineering [1] and micro-electro-mechanical systems (MEMS) [2]. Due to the invalidity of the continuous methods in the rarefied regime and the inefficiency of the kinetic methods in the continuum regime, it is challenging for the traditional numerical methods to simulate multi-scale gas flows accurately and efficiently. One of the strategies to overcome this difficulty is combining the continuous and kinetic methods. For example, the CFD-DSMC hybrid method [3,4,5] implements the CFD solver and direct simulation Monte Carlo (DSMC) method in different regions. Another example is the general synthetic iterative scheme (GSIS) [6] developed recently, which is solved by the CFD and discrete velocity method (DVM) together in the whole region but at different levels. The hybrid methods need to exchange the information between different solvers, which will bring extra complexity even stability problem [7]. Therefore, besides the hybrid methods, a straightforward approach is to extend the application of the kinetic methods to the continuum regime. Following this direction, many multi-scale schemes based on kinetic models, such as Bhatnagar–Gross–Krook (BGK) [8,9,10] and Fokker-Planck (FP) [11,12,13], have been proposed in recent decades. One of the categories is the deterministic DVM methods with asymptotic preserving (AP) property, such as the BGK-type penalization method [14], the implicit-explicit (IMEX) method [15, 16], the unified gas-kinetic scheme (UGKS) [17] and the discrete unified gas kinetic scheme [18]. However, representing the probability density function (PDF) with discrete velocities requests a large memory consumption, especially for hypersonic gas flows. An alternative category is the stochastic particle methods, such as the BGK particle method [19] and the Fokker-Planck particle method [20]. Unlike DVM, stochastic particle methods describe the PDF using simulation particles, of which each represents a large number of real gas molecules of a certain velocity. Since the distribution of computational particles can adaptively be refined in the velocity space, the curse of dimensionality is circumvented compared to the DVM method.
As decoupling the particle motion and collision in most stochastic particle methods, they only asymptotically preserve the Euler limit. For example, considering the traditional stochastic particle BGK (SP-BGK) method [8, 19], when the time step is much larger than the mean collision time, its numerical viscosity is of the first order of the time step, i.e. \( {\mu}_{BGK}^{num}\sim \Delta t \). An important exception is the Fokker-Planck particle method, for which particle motion and collisions can be solved simultaneously [11]. When the time step is much larger than the mean collision time, its numerical viscosity \( {\mu}_{FP}^{num} \) converges to 2μ, where μ is the gas viscosity, that is, independent of the time step [13]. Therefore, the Fokker-Planck particle method could asymptotically preserve the Navier-Stokes limit.
Recently, a unified stochastic particle method preserving the Navier-Stokes limit based on the BGK model, which is referred to as the USP-BGK method, has also been developed [21] by combining a modified continuous collision term with particle motions. It has been demonstrated by a variety of gas flows [21, 22] that with the Crank–Nicolson scheme in the particle motion step, the USP-BGK method has second-order accuracy in the continuum regime. In the aspect of implementation, the USP-BGK method is quite similar to the other particle methods such as DSMC. However, to involve the collision effect in the process of particle motions, virtual particles need to be introduced. In addition, to make the spatial accuracy consist with the temporal accuracy, a second-order interpolation in space is employed to obtain the mean quantities related to the individual particle. Since these two aforementioned procedures are not contained in the original DSMC method, transplanting the USP-BGK method into the existing DSMC program code is not straightforward. To make the principle of USP-BGK easier to be understood and minimize the difference of implementation between USP-BGK and DSMC, an efficient algorithm of USP-BGK is developed in the present work.
The remainder of this paper is organized as follows. In section 2, we first review the principle and the solution algorithm of the unified stochastic particle BGK method. Then, the temporal evolution and spatial reconstruction of the efficient algorithm is introduced in section 3. Note that the simplified time scheme without virtual particles was already developed in the hybrid USPBGK-DSMC method [23]. Here we present a sole USP-BGK version for the sake of clarity. In section 4, we provide numerical results for several typical gas flows, and the accuracy of the proposed method is also validated.
2 Review of the USP-BGK method
The BGK model simplifies the Boltzmann collision term using a relaxation process. In general, its dimensionless kinetic equation can be written as
where f(c; x, t) is the weighted probability density function, which is defined as n = ∫ f(c; x, t)dc. n is the number density, and c is the molecule velocity at position x and time t. The subscript i indicates the i-th component in three-dimensional space. ft is a target distribution function for the relaxation process [19]. In the original BGK model, ft is assumed to be the Maxwellian distribution function, i.e.
where C = c − U is the peculiar molecular velocity, U is the mean velocity, and T is temperature. The Prandtl number (Pr) of the original BGK model is always unity for any gas flows. To correct the Prandtl number, the Shakhov [24] (SBGK) and ellipsoidal statistical [25] (ESBGK) BGK models are usually applied. Non-dimensional variables used in the present paper are defined as,
where x∗ and n∗ are the reference length and number density, respectively, \( \overline{C}=\sqrt{8{RT}_{\ast }/\pi } \) is the mean thermal reference velocity and T∗ is the reference temperature. R = kB/m is the gas constant, m is the molecular mass, and kB is the Boltzmann constant. Therefore, the Knudsen number ε is defined as \( \varepsilon =\overline{C}/\left({\upsilon}_{BGK}{x}_{\ast}\right) \), where υBGK = p/μ is the collision frequency of the BGK model, μ is the gas viscosity and p is the pressure. For the sake of simplicity, all the equations, unless specified differently, will be presented in the dimensionless form without hats on top of the variables.
The BGK equation can be either solved using the DVM [26] or stochastic particle [8] methods. Similar to DSMC, the traditional SP-BGK method [19] decouples the particle motion and collision, i.e., the BGK equation is numerically solved in sequence,
and
Decoupling the particle motion and collision is easily and naturally implemented in the stochastic particle methods. Note that the particle motion step as shown in Eq. (4a) is represented by a collisionless kinetic equation, so if the time step is larger than the mean collision time, its numerical dissipation is of the first order of the time step size. To extend the applicability of the SP-BGK method, a unified stochastic particle method based on the BGK model (USP-BGK) has been proposed recently [21]. Similarly, the USP-BGK method also consists of particle motion and collision steps, i.e.
and
The key difference is that the collision term in the USP-BGK method is divided into two parts, and the continuous part is calculated with particle motion simultaneously. For monoatomic gas, the continuous part J(USPBGK) is closed by the 13 moments Grad’s distribution function f|Grad, i.e.
where ρ is the density, σij is the shear stress, qi is the heat flux, and C<iCj> denotes the symmetric and trace-free part of the tensor CiCj. The multi-scale parameter Pc, which denotes the degree of the continuum, tends to 1 in the continuum regime and 0 in the rarefied regime. It is employed to avoid the negativity of the first-order Chapman-Enskog expansion assumed in the modified collision term. In the present paper, we choose Pc = e−αε/Δt and set α = 0.1. Note that ε/Δt is also a good estimator for the rarefication as presented in ref. [23], and importantly it can be calculated from the PDF of local computational particles. Therefore, with small Knudsen numbers, the particle motion step as shown in Eq. (5a) is represented by a first-order Chapman-Enskog expansion of the BGK equation and converges to the NS limit. Otherwise, with large Knudsen numbers, the USP-BGK method reduces to the traditional SP-BGK method as shown in Eqs. (4a, 4b).
For the particle motion step as shown in Eq. (5a), to obtain a second order of accuracy in time, it is numerically solved with the Crank–Nicolson scheme, i.e.
with the initial condition f∗(c; x, 0) = f(c; x, 0). By introducing two auxiliary PDFs [18],
and
Eq. (7) can be rewritten as
Therefore, \( {\tilde{f}}^{\ast}\left(\mathbf{c};\mathbf{x},\Delta t\right) \) can be obtained after tracking the computational particles along the characteristic line dx/dt = c as same as the traditional SP-BGK method. Additionally, the PDF f∗(c; x, Δt) after the particle motion step needs to be reconstructed from Eq. (8a).
For the collision step as shown in Eq. (5b), using the initial PDF generated by the particle motion step f∗(c; x, Δt), the integration solution is applied as same as the traditional SP-BGK method, that is,
It should be noted that if the time step is larger than the mean collision time, the target distribution function ft(c; x, t) is no longer reasonable to be assumed constant as in the SP-BGK method, so a particle velocity resampling should be exactly implemented based on Eq. (10). Finally, we can construct \( \overset{\frown }{f}\left(\mathbf{c};\mathbf{x},\Delta t\right) \) using Eq. (8b) and consider it as the initial PDF for the next time step. The procedure described above starting from Eq. (7) is repeated until the simulation is finished, and the detailed algorithm can be found in reference [21].
3 An efficient algorithm of the USP-BGK method
Compared to the traditional SP-BGK method, three more operations need to be implemented in the USP-BGK method. First, according to Eqs. (8a, 8b), the auxiliary PDFs \( \tilde{f} \) and \( \overset{\frown }{f} \) should be constructed before and after particle motion; second, according to Eq. (10), an exact integral term of PDF needs to be sampled; third, to be consistent with the second order of accuracy in time, the spatial reconstruction based on the particle location should also be implemented. In the previous paper [21], the auxiliary PDFs are constructed by adding virtual particles and a new time sampling method is applied to deal with the integral term. Besides, linear interpolation is used to reconstruct the macroscopic quantities of calculated particles with second-order accuracy in space. The aforementioned operations would inevitably increase the complexity of computation. To make the USP-BGK method as simple as the other particle methods such as DSMC, an efficient algorithm improving temporal evolution and spatial reconstruction is proposed in the present paper.
3.1 Temporal evolution
To avoid employing virtual particles, one can directly update the simulation based on the auxiliary PDFs themselves as shown in the particle motion step Eq. (9). Therefore, only the collision step (Eq. (10)) needs to be modified. For this purpose, the governing equation of the collision step, i.e. Eq. (5b), is modified as
where the proposed target distribution fU is assumed as
where ψ1 and ψ2 are two undetermined coefficients. Using the initial PDF \( {\tilde{f}}^{\ast}\left(\mathbf{c};\mathbf{x},\Delta t\right) \) obtained from Eq. (9), the numerical solution of Eq. (11) can be written as,
Letting the right-hand side of Eq. (13) equal to \( \overset{\frown }{f}\left(\mathbf{c};\mathbf{x},\Delta t\right) \) that obtained from Eq. (10), then ψ1 and ψ2 can be determined. Note that Eqs. (9) and (13) have the same form as the solutions of the particle motion and collision steps of the traditional SP-BGK method [23] except for the different target distribution. In this way, virtual particles are not needed for simulation.
Next, we exactly derive Eq. (10) in the USP-BGK method. In the present algorithm, the Shakhov BGK model is employed to correct the Pr number, i.e. the target distribution reads
Substituting it into Eq. (10), we have
Multiplying mCiC2/2 on both sides of Eq. (5b) and taking ensemble average, the moment equation of the heat flux is obtained as
Hence, the solution of the heat flux at time t is
Substituting it into the right-hand side of Eq. (15), then \( \overset{\frown }{f}\left(\mathbf{c};\mathbf{x},\Delta t\right) \) is obtained
Compared Eq. (13) with Eq. (18), the undetermined coefficients are calculated as
and
From Eq. (13), we can obtain \( \overset{\frown }{f}\left(\mathbf{c};\mathbf{x},\Delta t\right) \) after the collision step, and then it is directly applied to particle motions in the next time step. Note that this technique has been first introduced in the USPBGK-DSMC hybrid method [23]. In the hybrid method, the USP-BGK method is only applied to the continuum regime, and the rarefied regime is solved by DSMC. In this work, with the multi-scale parameter Pc, the present algorithm is used in the whole flow regimes.
3.2 Spatial reconstruction
To reach a second-order accuracy, besides the temporal evolution, it also requires the same order of accuracy in space. In the particle motion step, the particle tracking is exactly solved; however, in the collision step, to reconstruct the target distribution at the location of the simulated particle, the mean velocity and temperature with second-order accuracy need to be interpolated based on the flow field. In CFD, there are a lot of methods to obtain second-order interpolation, such as the linear interpolation used in the previous paper [21]. However, calculating interpolation would bring extra complexity to the program code. Moreover, its statistical noise would introduce additional numerical dissipation and instability. On the other hand, in most stochastic particle methods such as DSMC, they only need to deal with the local macro variables. Therefore, the interpolation module is usually not required in DSMC codes. In order to transplant the USP-BGK method to the existing DSMC software easily, an interpolation technique based on particle tracking is proposed as follows.
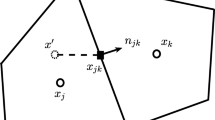
Mean quantities of the computational particle, such as the mean velocity uk(xp, t) and temperature Tk(xp, t), equal to the macro velocity U(xp, t) and temperature T(xp, t) of the flow field at the particle location xp and time t, i.e. uk(xp, t) = U(xp, t) and Tk(xp, t) = T(xp, t). We assume that the macro variables of the flow field at the same location are averaged from surrounding particles, taking macro velocity as an example, it is approximated as
where U(xj, t; xp + Δx ∈ j) represents the macro velocity of the cell j, which contains the sampling particle located at xp + Δx, and xj is the cell center. K(Δx) is a symmetric kernel, which represents the spatial distribution of sampling particles. The number of sampling particles is
Note that the auxiliary PDFs do not change the averaging results. In Eq. (20), we approximate the mean velocity of the sampling particle at xp + Δx with the macro velocity of the cell. As shown in proposition 3.1, the estimator of U(xp, t) with such simplification can also obtain second-order accuracy.
Proposition 3.1 With a symmetric kernel K(Δx), the macro velocity and its derivation obtained from Eq. (20) have second-order accuracy.
Proof If replaced U(xj, t; xp + Δx ∈ j) by the exact mean velocity of sampling particle at xp + Δx, then Eq. (20) is rewritten as
Using Tayler expansion, Eq. (22) is expanded as
If choosing K(Δx) as a symmetric function, it is easily found that the first-order term vanishes and the macro velocity and its derivation based on Eq. (22) have second-order accuracy.
Next, combining Eqs. (20) and (22), the error between U(xp, t) and U ' (xp, t) is calculated as
Taking Tayler expansion around xp again, we obtain
Since xj is determined by Δx and xp, it can be expanded as xj = xp + a1Δx + a2Δx2 + O(Δx3). Substituting it into Eq. (25), it is obtained
where the first-order term of Δx vanishes due to the symmetric kernel. Therefore, according to Eqs. (23) and (26), the estimator U(xp, t) introduced in Eq. (20) also satisfies the second-order accuracy in space, if a symmetric kernel is employed.
In simulations, it is not necessary to take the average for Np particles as Eq. (20) at every time step. Instead, only one sampling particle is required, i.e. a random distance Δx can be first sampled based on the kernel function, then the mean velocity of the computational particle is taken as the macro velocity of the cell where the sampling particle is located. Therefore, we can simply assume the mean velocity of the simulated particle as
Similarly, the temperature of the computational particle is taken as
Applying Eqs. (27) and (28), only the macro variables of the cell are required when calculating the collision step.
Two symmetric kernels are employed and tested in the present paper, one is the uniform kernel, i.e.
where Δh is the cell size. Another one is the Gaussian kernel, i.e.
where σx = (Δh/2)2. Note that it is free to use any other symmetric kernels.
3.3 Implementations of the efficient algorithm of the USP-BGK method
According to the algorithm introduced in sections 3.1 and 3.2, its implementations are outlined in Table 1.
In addition, after resampling particle velocity in the collision step, the momentum and energy conservation should be ensured in every cell. Therefore, the particle velocities need to be modified as,
where c' and c represent the velocities before and after modification, respectively. Nc is the number of particles in the cell.
4 Numerical simulations
4.1 Homogeneous relaxation
The relaxation process in the homogeneous flow is first investigated to validate the time scheme in the collision step, i.e. Eq. (13). The initial velocity PDF is described by the 13 moments Grad’s distribution function, i.e.
where the number density is set to be n0 = 1.885 × 1020 m−3, the initial velocity is zero and temperature is T0 = 273K. The initial shear stress and heat flux are 0.1p0 and \( 0.1{p}_0\sqrt{k_B{T}_0/2m} \), respectively, and p0 = n0kBT0. Argon gas is considered and Pc is set to be zero for the homogeneous case. Four different time-step sizes are calculated and compared, i.e. Δt ∈ {0.1τc, 0.25τc, 2.0τc, 4.0τc}, and τc is the mean collision time. Figure 1(a) shows the relaxation of shear stress and heat flux. All of the results are consistent with each other and independent of the time step. Figure 1(b) gives the evolution of the temperature. We note that energy conservation is also well ensured for a wide range of time step size.
4.2 Sod tube
The Sod’s 1D shock tube problem is a typical multiscale gas flow, and here a case selected from ref. [27] is simulated. The length of the tube is 1 m, and initially there exists a discontinuity in the density at x = 0.5 m. The initial density on the left and right-hand sides of the discontinuities are 10−4kg/m3 and 0.125 × 10−4kg/m3, respectively. The macro velocity of the gas flow is zero and the temperature is 273 K at the beginning. Argon gas is considered, and the viscosity exponent ω is 0.81, i.e. μ = μ0(T/Tref)ω, μ0 = 2.117 × 10−5Pa ⋅ s and Tref = 273K. In this simulation, 60 uniform cells were employed, and the time step size was four times larger than the mean collision time of the left-hand side tube. The efficient USP-BGK method computes up to the final time tfinal = 6.8 × 10−4s, and two kernel functions, i.e. uniform and Gaussian, are tested. Figure 2 shows the temperature and density distribution at the final time. The results of the two kernel functions agree with each other and both are in good agreement with DSMC. Due to the varied density, the ratio between the time step and the local mean collision time changes from 4.0 to 0.5 through the tube, i.e. Δt ∈ [0.5τc, 4.0τc]. Therefore, the results of Fig. 2 also indicate that the efficient USP-BGK method with both uniform and Gaussian kernels can well capture the multi-scale gas flow.
(Color online) Sod tube case. a temperature and b density at the final time tfinal = 6.8 × 10−4s. The solid lines are results of DSMC obtained by S. Tiwari [27] and the symbols refer to the efficient USP-BGK results
4.3 Poiseuille flow
The Poiseuille flow is confined between two infinite and parallel plates and is driven by a pressure gradient dp/dx along the plates. The temperature of the upper and lower plates is fixed at 273 K, and the fully diffusive boundary condition is employed for these two plates. The Argon gas is initially set up at the standard condition (p =1 atm and T = 273K). Two different Knudsen numbers (Kn = λ/L) are calculated, i.e., Kn = 0.1 and Kn = 0.001. L is the distance of the two plates and λ is the mean free path. The pressure gradients are 4.0 × 106 Pa m−1 for Kn = 0.001 and 4.0 × 1010 Pa m−1 for Kn = 0.1, respectively. Uniform computational cells are employed and the CFL number is 1.0 for Kn = 0.1 and 0.5 for Kn = 0.001. We compared the L2-norm of error for velocities of the traditional SP-BGK and USP-BGK methods, i.e.,
where \( {u}_x^s \) is the reference velocity and the symbol 〈⋯〉 denotes an ensemble average over all meshes. \( {u}_x^s \) is determined by the NS solution for Kn = 0.001 and obtained from the finest simulation data for Kn = 0.1. Both the SP-BGK and USP-BGK methods employ the same spatial reconstruction proposed in section 3.2 and the uniform kernel is applied. However, their temporal evolution is different, where the SP-BGK method decouples the particle motion and collision and performs as ref. [8]. Figure 3 shows that in the continuum regime (Kn = 0.001) the USP-BGK method has smaller numerical dissipation and second-order accuracy; in the rarefied regime (Kn = 0.1), when the time step is much smaller than the mean collision time, the USP-BGK method reduces to the SP-BGK method and both methods have similar performance.
4.4 Taylor-Green vortex flow
The Taylor-Green vortex flow [28] is widely used to investigate the order of accuracy. For a 2D and low Mach number flow, the analytic solutions of the Taylor-Green vortex flow can be obtained from the Navier–Stokes equation, i.e.
and
where U0 and p0 are the reference velocity and pressure, respectively. kx = 2π/Lx and ky = 2π/Ly represent the wavenumbers in x and y directions, and \( k=\sqrt{k_x^2+{k}_y^2} \). Lx and Ly are the length of the two-dimensional computational domain, Lx = Ly = 1.0 m. In the current simulation, we set the Mach number \( Ma={U}_0/\sqrt{\gamma {RT}_0}=0.1 \), and the reference temperature T0 = 273K. The Reynolds number Re = ρ0U0Lx/μ0 = 100, and the reference viscosity is set as same as that in the Sod tube case. The initial velocity of the particles is sampled from the PDF of first-order Chapman-Enskog expansion, in which the macro quantities and their derivatives are computed by the analytical solutions in Eqs. (34) and (35) at t = 0. Besides, the initial density is assumed to be uniform in the computational domain and equals to ρ0. Then the initial temperature is calculated from Eq. (36).
The Taylor-Green vortex flow is simulated up to the final time t = ln(2)/(k2μ/ρ). Uniform meshes in two dimensions are employed, and the number of computational cells changes from 20 × 20 to 50 × 50. The time step is determined by the CFL number, which is 0.4 in all cases. Figure 4 presents the L2-norm of errors of Ux depended on the cell size Δh, and \( {U}_x^s \) is the accurate solution obtained in Eq. (34). We note that both the uniform and Gaussian kernels can obtain second-order accuracy, and the numerical dissipation of the uniform kernel is smaller than the Gaussian one.
4.5 Two-dimensional Riemann problem
For the compressive gas flow, one of the two-dimensional Riemann problems is studied [29]. The computational domain is set as [0, 1] × [0, 1] (m2). Constant initial data is taken in each quadrant, i.e.
where U and V normalized by \( \sqrt{RT_0} \) are the macro velocity in x and y direction, and T0 = 273K. The density and pressure are normalized by ρ0 = 1.78kg/m3 and p0 = ρ0RT0, respectively, and Argon gas is applied. A 200 × 200 uniform mesh is employed, and the CFL number is set to be 0.4. The viscosity is also set as same as that in the Sod tube case. Figure 5 shows the density contours at \( t=0.2/\sqrt{RT_0} \). It is noted that the uniform and Gaussian kernels obtain a consistent result and both can capture the shock wave properly.
5 Conclusion
The USP-BGK method can calculate the multi-scale gas flow much more efficient than the traditional stochastic particle methods. To simplify the implementation of the USP-BGK method, a new temporal evolution and spatial reconstruction scheme was presented in the present work. Four typical numerical cases, such as the homogeneous and multi-scale sod tube flows, the weak and strong compressive flows, have been used to validate this efficient algorithm. Without additional virtual particles and spatial interpolation, the efficient algorithm of USP-BGK implements as same as DSMC except for the collision term, which resampling a target distribution like the traditional BGK particle method [19]. Therefore, a USP-BGK programme can be easily accomplished based on any DSMC codes by replacing the collision module only. This algorithm can also be implemented in the hybrid USPBGK-DSMC method and would reduce the complexity of the computing programme significantly.
Availability of data and materials
All data and materials are available from the authors of this paper.
References
Ivanov MS, Gimelshein SF (1998) Computational hypersonic rarefied flows. Ann Rev Fluid Mech 30(1):469–505. https://doi.org/10.1146/annurev.fluid.30.1.469
Titov E, Gallagher-Rogers A, Levin D, Reed B (2008) Examination of a collision-limiter direct simulation Monte Carlo method for micropropulsion applications. J Propuls Power 24(2):311–321. https://doi.org/10.2514/1.28793
Hash DB, Hassan HA (1996) Assessment of schemes for coupling Monte Carlo and Navier-Stokes solution methods. J Thermophys Heat Transf 10(2):242–249. https://doi.org/10.2514/3.781
Sun Q, Boyd ID, Candler GV (2004) A hybrid continuum/particle approach for modeling rarefied gas flows. J Comput Phys 194(1):256–277. https://doi.org/10.1016/j.jcp.2003.09.005
Zhang J, John B, Pfeiffer M, Fei F, Wen D (2019) Particle-based hybrid and multiscale methods for nonequilibrium gas flows. Adv Aerodyn 1(1):12. https://doi.org/10.1186/s42774-019-0014-7
Su W, Zhu L, Wang P, Zhang Y, Wu L (2020) Can we find steady-state solutions to multiscale rarefied gas flows within dozens of iterations? J Comput Phys 407:109245. https://doi.org/10.1016/j.jcp.2020.109245
Wijesinghe H, Hadjiconstantinou N (2004) Discussion of hybrid atomistic-continuum methods for multiscale hydrodynamics. Int J Multiscale Comput Eng 2(2):189–202. https://doi.org/10.1615/IntJMultCompEng.v2.i2.20
Gallis MA, Torczynski JR (2000) The application of the BGK model in particle simulations. In: 34th AIAA Thermophysics conference, Denver, CO, June 2000, AIAA paper no. 2000-2360
Burt JM, Boyd ID (2006) Evaluation of a particle method for the ellipsoidal statistical Bhatnagar–Gross–Krook equation. In: 44th AIAA aerospace science meeting and exhibit, Reno, NV, Jan. 2006, AIAA Paper, pp 2006–2989
Tumuklu O, Li Z, Levin DA (2016) Particle ellipsoidal statistical Bhatnagar–Gross–Krook approach for simulation of hypersonic shocks. AIAA J 54(12):3701–3716. https://doi.org/10.2514/1.J054837
Jenny P, Torrilhon M, Heinz S (2010) A solution algorithm for the fluid dynamic equations based on a stochastic model for molecular motion. J Comput Phys 229(4):1077–1098. https://doi.org/10.1016/j.jcp.2009.10.008
Gorji MH, Torrilhon M, Jenny P (2011) Fokker–Planck model for computational studies of monatomic rarefied gas flows. J Fluid Mech 680:574–601. https://doi.org/10.1017/jfm.2011.188
Fei F, Liu Z, Zhang J, Zheng CG (2017) A particle Fokker-Planck algorithm with multiscale temporal discretization for rarefied and continuum gas flows. Commun Comput Phys 22(2):338–374. https://doi.org/10.4208/cicp.OA-2016-0134
Filbet F, Jin S (2010) A class of asymptotic-preserving schemes for kinetic equations and related problems with stiff sources. J Comput Phys 229(20):7625–7649. https://doi.org/10.1016/j.jcp.2010.06.017
Dimarco G, Pareschi L (2017) Implicit-explicit linear multistep methods for stiff kinetic equations. SIAM J Numer Anal 55(2):664–690. https://doi.org/10.1137/16M1063824
Hu JW, Zhang XX (2017) On a class of implicit-explicit Runge-Kutta schemes for stiff kinetic equations preserving the Navier-Stokes limit. J Sci Comput 73(2-3):797–818. https://doi.org/10.1007/s10915-017-0499-3
Xu K, Huang JC (2010) A unified gas-kinetic scheme for continuum and rarefied flows. J Comput Phys 229(20):7747–7764. https://doi.org/10.1016/j.jcp.2010.06.032
Guo Z, Xu K, Wang R (2013) Discrete unified gas kinetic scheme for all Knudsen number flows: low-speed isothermal case. Phys Rev E 88(3):033305. https://doi.org/10.1103/PhysRevE.88.033305
Pfeiffer M (2018) Particle-based fluid dynamics: comparison of different Bhatnagar-Gross-Krook models and the direct simulation Monte Carlo method for hypersonic flows. Phys Fluids 30(10):106106. https://doi.org/10.1063/1.5042016
Gorji MH, Torrilhon M (2021) Entropic Fokker-Planck kinetic model. J Comput Phys 430:110034. https://doi.org/10.1016/j.jcp.2020.110034
Fei F, Zhang J, Li J, Liu ZH (2020) A unified stochastic particle Bhatnagar-Gross-Krook method for multiscale gas flows. J Comput Phys 400:108972. https://doi.org/10.1016/j.jcp.2019.108972
Zhang J, Yao S, Fei F, Ghalambaz M, Wen D (2020) Competition of natural convection and thermal creep in a square enclosure. Phys Fluids 32(10):102001. https://doi.org/10.1063/5.0022260
Fei F, Jenny P (2021) A hybrid particle approach based on the unified stochastic particle Bhatnagar-Gross-Krook and DSMC methods. J Comput Phys 424:109858. https://doi.org/10.1016/j.jcp.2020.109858
Shakhov EM (1968) Generalization of the Krook kinetic relaxation equation. Fluid Dyn 3:95–96. https://doi.org/10.1007/BF01029546
Holway L (1965) Kinetic theory of shock structure using an ellipsoidal distribution function. In: Rarefied gas dynamics: proceedings of the 4th International Symposium, vol 1. Academic Press, New York, pp 193–215
Dimarco G, Pareschi L (2014) Numerical methods for kinetic equations. Acta Numerica 23:369–520. https://doi.org/10.1017/S0962492914000063
Tiwari S, Klar A, Hardt S (2009) A particle-particle hybrid method for kinetic and continuum equations. J Comput Phys 228(18):7109–7124. https://doi.org/10.1016/j.jcp.2009.06.019
Taylor GI, Green AE (1937) Mechanism of the production of small eddies from large ones. Proc R Soc A 158:499–521. https://doi.org/10.1098/rspa.1937.0036
Lax PD, Liu XD (1998) Solution of two-dimensional Riemann problems of gas dynamics by positive schemes. SIAM J Sci Comput 19(2):319–340. https://doi.org/10.1137/S1064827595291819
Acknowledgements
Not applicable.
Funding
This work was supported by the National Numerical Wind-Tunnel Project (No. NNW2018-ZT3B07) and the National Natural Science Foundation of China (No. 51506063). Jun Zhang would like to thank the support of the National Natural Science Foundation of China (No. 92052104).
Author information
Authors and Affiliations
Contributions
Fei Fei: Conceptualization, Formal analysis, Methodology, Software, Writing - original draft. Yang Ma: Validation. Jie Wu: Resources, Writing - review & editing. Jun Zhang: Resources, Writing - review & editing. All authors read and approved the final manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 Calculation of macroscopic quantities from the auxiliary PDFs
Since the collision operator conserves mass, momentum, and energy, the conserved variables can be calculated from the auxiliary PDFs directly, they are
and
Multiplying Eq. (8) with mC<iCj> and mC2Ci/2 and taking integral over the velocity space, the shear stress and heat flux can be obtained as
and
In a computational cell with volume Vc and Nc particles, the above macro quantities are averaged over particles using Eqs. (A1)–(A5), i.e. in detail
The factor 1/(Nc − 1) in the temperature and shear stress occurs to produce unbiasedness of T and σij, respectively. Similarly, the unbiased factor in the heat flux is Nc/(Nc − 1)(Nc − 2) [19].
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fei, F., Ma, Y., Wu, J. et al. An efficient algorithm of the unified stochastic particle Bhatnagar-Gross-Krook method for the simulation of multi-scale gas flows. Adv. Aerodyn. 3, 18 (2021). https://doi.org/10.1186/s42774-021-00069-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s42774-021-00069-8