Introduction

Climate change in the current decades is one of the major threats of human food security all over the world; where its consequences affect millions of people every year (Tirado et al. 2010; Mohammed and Fallah 2019; Mohammed et al. 2019a). Generally, climate change events can be divided into two major groups: the first one needs a long period to be noticed, where it developed in silence as drought (Mukherjee et al. 2018). While the second group developed suddenly and created a big mass in the ecosystem such as flash flood (Lehner et al. 2006). Among climate change indicators, drought is considered to be one of the most current phenomena which started to hit new places (countries and regions), that used to be rarely subjected to droughts such as Europe and many other parts of the world (Sepulcre-Canto et al. 2012). So far, many drought indices had been developed such as the Palmer Drought Severity Index (PDSI) (Palmer 1965); Standardized Precipitation Index (SPI) (McKee et al. (1993, 1995), Crop Moisture Index (CMI) (Palmer 1968); Standardized Runoff Index (SRI) (Shukla and Wood 2008), Drought Severity Index (DSI) and many others for different reasons. Within this context, PDSI and SPI used for meteorological drought monitoring, CMI for agricultural drought, SRI for hydrological drought, and DSI for regional drought (Narasimhan and Srinivasan 2005; Dai 2011; Mukherjee et al. 2018). However, SPI is one of the common indices for detecting drought on a different scale (i.e., 1, 3, 6, 9, 12 months); which is widely used in many countries such as Romania (Ionita et al. 2016); Ethiopia (El Kenawy et al. 2016); Italy (Bonaccorso et al. 2015); Syria (Mohammed et al. 2019b), India (Dutta et al. 2015), Poland (Łabędzki 2007); China (Zhang et al. 2009), Hungary (Mohammed and Harsányi 2019); Greece (Livada and Assimakopoulos 2007); USA (Hayes et al. 1999), and many other parts of the world.

For Hungary, some research can be found in sub-regional levels for detecting drought trends and analysis. Makra et al. (2002) analyzed climatic data for the eastern part of Hungary and concluded that the period between 1901 and 1940 was wet, while the rest of the years until the 1990s were found to be significantly drier. Similarly, Szép et al. (2005) reported that soil conditions became drier during the twentieth century. On the national scale, Szinell et al. (1998) detected an existing general drying tendency in Hungary. Alsafadi et al. (2020) reported a significant increase (P < 0.05) of the area affected by very extreme drought in Hungary between 1960-2010. Bartholy et al. (2013) predicted significant drought in Hungary for the period 2071–2100, due to the significant decrease of rainfall in the summer compared to 1961–1990 as a reference period

Even though many studies had been conducted lately to analyze drought in Hungary, few studies deal with drought on the sub-regional scale. Thus, the main aim of this study is to analyze hydrological and agricultural drought episodes in the Debrecen Region in Hungary from 1950 to 2010.

Material and methods

Study area

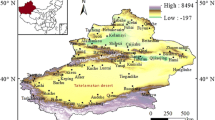
Our study area—Debrecen Region—is located in the eastern part of Hungary (47.5N, 21.5E), 100–150 m above sea level (Fig. 1). This region has a continental climate where the winter is cold (mean temperature in January is − 2°) and the summer is warm (21 °C in July). The mean annual temperature is 10.5 °C, while the yearly average rainfall is 560 mm. The Western part (from N to SE) of the surroundings of the town Debrecen is dominated by chernozem soil with excellent water management characteristics and fertility. East to Debrecen (from N to SE), sandy soils are typical with large drought sensitivity and reduced fertility.

Fig. 1
figure 1

Location of Debrecen Region in Hungary

Full size image

Meteorological database and drought analysis

Our research was based on the 60-year-long (1951–2010) monthly precipitation dataset of Debrecen Meteorological Station (Hungarian Meteorological Service). As a first step, primary statistical analysis for each year was conducted which include mean, standard deviation, skewness, and many other tests.

To track drought episodes within the study area, three indices were used: the Standardized Precipitation Index (SPI) (McKee et al. 1993), Precipitation Concentration Index (PCI), and the dry Precipitation Concentration Index (dPCI) (supra-seasonal scale) (Oliver 1980).

The PCI and dPCI are typically used as an indicator of rainfall pattern and erosivity. Values of PCI were calculated for each year, and the dPCI was calculated from April to September for monitoring changes in the rainfall pattern, which highly affected agricultural production.

The PCI can be calculated using the following equation:

$$ \mathrm{PCI}=\frac{\sum_{i=1}^{12}{p}_i^2}{{\left({\sum}_{i=1}^{12}{p}_i\right)}^2}\ast 100 $$
(1)

where pi is monthly precipitation of any month i.

Also, the dPCI can be calculated for 6 months from April until August as follows:

$$ \mathrm{dPCI}=\frac{\sum_{i=1}^6{p}_i^2}{{\left({\sum}_{i=1}^6{p}_i\right)}^2}\ast 50 $$
(2)

Classification of PCI and dPCI can be seen in Table 1.

Table 1 The PCI and dPCI range and classification
Full size table

In the next step, trend of rainfall (R), PCI, and dPCI were analyzed by applying the Cramer-von Mises test (CM). In our study, we adapted the CM for trend analysis; where the determination of trend depends on the p value. If P value > α (i.e., 0.05) → Ha is rejected. However, if P value < α → Ha is accepted, and if P value = 0 → test was failed. However, the CM can be calculated for variables x1,…xN, for a specific continuous distribution f(x) as follows:

$$ {\omega}^2={\int}_{-\infty}^{\infty }{\left[{f}_N(x)-f(x)\right]}^2 df(x) $$
(3)

For discrete data we use

$$ {\omega}^2=\frac{1}{12n}+{\sum}_{i=1}^n{\left(\frac{2i-1}{2n}-F\left({x}_i\right)\right)}^2 $$
(4)

where fN(x) was defined as empirical distribution function.

Also, we applied the SPI as a worldwide index used for drought monitoring (Park et al. 2019), which can be calculated by using the SPI software recommended by the WMO https://drought.unl.edu/droughtmonitoring/SPI/SPIProgram.aspx as follows:

$$ \mathrm{SPI}=\frac{X_{ij}-{X}_{im}}{\sigma } $$
(5)

where Xij is the seasonal precipitation; Xim is the mean of long-term period; and σ is the standard deviation. For drought study, SPI values can be categorized into moderate drought (− 1.49 to − 1), severe drought (− 1.99 to − 1.5), and extreme drought (SPI < − 2). Usually, SPI is calculated for different scales (i.e., 1, 3, 6, 9, 12, 24, 36 months).

In a final step, the smoothing technique was used for detecting the trend of SPIs by using polynomial regression and weights, computed from Gaussian density function adopted from the SigmaPlot program.

Drought impact on vegetation greening

For tracking the impact of drought variability on vegetation greening, we analyzed the correlation between SPI (drought) and NDVI (land cover sensitivity to SPI variation). The SPI data for 3 and 6 months were collected from the Climate of the Carpathian region project-CARPATCLIM, where data of 72 gridded points over the county was employed, this dataset at spatial resolution 10 km × 10 km (CARPATCLIM 2019; Szalai et al. 2013). All records of semi-monthly NDVI dataset from the NOAA-AVHRR satellite (i.e., recognized NDVI datasets) were collected from the Global Inventory Modelling and Mapping Studies GIMMS3g. (https://ecocast.arc.nasa.gov/data/pub/gimms/3g.v1/). The GIMMS3g is one of the globally NDVI datasets which widely used (Vicente-Serrano et al. 2019). The quality of this data assured carefully through consideration of the effects of atmospheric, cloud cover and other quality control linked by sensor and satellite, e.g., solar and viewing angle due to satellite drift (Tucker et al. 2005; Pinzon and Tucker 2014). Ultimately, results were converted by using Geographic Information System (GIS) while maintaining the same original spatial resolution.

Results

Trends of R, PCI, and dPCI in the study area from 1951 until 2010

Tracking rainfall changes in the study area showed that the maximum rainfall reached 953 mm while the minimum was 321 mm (Fig. 2), and the average rainfall for the whole time series was 561 mm.

Fig. 2
figure 2

Yearly rainfall changes in the studied area from 1950 to 2010

Full size image

On a monthly scale, the average rainfall ranged from 30 mm (March) to 64mm (June); the minimum rainfall ranged between 0 mm (September) and 19 mm (June); however, the maximum rainfall was recorded in August with 232 mm (Table 2). The statistical analysis also showed also that the variation coefficient ranges from 49 to 88%, while Skewness ranges from 0.35 to 1.73 and Kurtosis reaches 6.2 as can be seen in Table 2 and Fig. 3. These results indicate the presence of extreme events in the study area as proposed by (Aladaileh et al. 2019).

Table 2 The statistical analysis for monthly rainfall from 1951 to 2010
Full size table
Fig. 3
figure 3

Boxplot analysis of monthly rainfall from 1950 to 2010

Full size image

The PCI values ranged between 9.4 and 15.8 with an average of 11.8, while the dPCI values range between 8.6 and 20.7 with an average 10.9 (Fig. 4). These results indicate a seasonality in rainfall distribution with changes from year to year. Table 3 showed a positive but not significant trend for R, PCI and a positive significant trend for dPCI, which emphasizes the fact that most of the rainfall had irregular distribution within a year.

Fig. 4
figure 4

Trends of PCI and dPCI in the study area

Full size image
Table 3 The CM Trend for R, PCI and dPCI in the study area from 1951 till 2010
Full size table

SPI variability from 1951 to 2010

Drought analysis showed that more than 103 events of severe agricultural drought (SPI-1, SPI-3, SPI-6) were detected for the whole studied period (Table 4).

Table 4 Distribution of Agricultural drought events from 1951 till 2010
Full size table

In connection with this, severe hydrological drought (SPI-9, SPI-12, SPI-24, SPI-36) was recorded in 16% of the total rainfall events from 1950 to 2010 as can be seen in Table 5.

Table 5 Distribution of Hydrological drought events from 1951 till 2010
Full size table

For the SPI-6, as a representative of agricultural drought, we can highlight the years of 1962, 1974, 1976, 1990; 1992, 2000, and 2007 as the most affected years by drought, where the agricultural production was badly affected. In a similar vein, hydrological drought for SPI-36 was distinguished in 1961–1965, 1973–1974, and 1992–1995, where recharge of natural bodies was affected by severe drought. However, regardless the drought time scale, the periods of 1962–1964, 1968, 1971–1974, 1986–1987, 1990, 1992–1995, and 2006–2007 can be selected as the most affected years by different types of drought as can be seen in Figs. 5 and 6.

Fig. 5
figure 5

SPI variability from 1951 to 2010

Full size image
Fig. 6
figure 6

SPI trends of the study area in different time scale by using smoothing technique

Full size image

Correlation matrix between SPI (-3, -6) and NDVI

The NDVI was used as an indicator of vegetation cover. The NDVI ranges between − 1 and 1 where − 1 indicate poor vegetation cover while + 1 indicate good vegetation cover. In return, we choose SPI-3 and SPI-6 as an indicator of agricultural drought. In other words, high correlation between SPI and NDVI revel to drought conditions in the study area. Figures 7 and 8 depict the correlation matrix between both choose SPI (-3, -6) and NDVI. Results showed a significant correlation between studied indices in summer and early fall, which could be explained by decreasing of vegetation cover as well as increasing drought level in the study area. The highest correlation was recorded on August, September, and October.

Fig. 7
figure 7

Spatial-temporal correlation between monthly SPI-3-time scale and NDVI during the period of 1981 to 2010, the dots indicate a statistically significant correlation at 95% confidence level (P < 0.05)

Full size image
Fig. 8
figure 8

Spatial-temporal correlation between monthly SPI-6-time scale and NDVI during the period of 1981 to 2010, the dots indicate to a statistically significant correlation at 95% confidence level (P < 0.05)

Full size image

Discussion

The smoothing technique analysis emphasised the previous results where the Debrecen Region was subjected to drought in two distinguished periods, the first of which was between 1960 and 1970, while the second one between 1990 and 2000. However, the trend of SPI-1, SPI-3, and SPI-6 showed a positive trend for the whole time series, while a negative trend was detected for SPI-9, SPI-12, SPI-24, and SPI-36 which indicate the tendency to drought in a large time scale (Fig. 6).

Generally, SPI and dPCI use only monthly rainfall data. Thus, any changes in rainfall potentially affect the results of both indices. In the dPCI cases, our results showed a moderate precipitation distribution (Fig. 4), while the SPI results indicate two periods from 1960 to 1970, and from 1990 to 2000 as most affected years by drought. Many researchers argued that rainfall data cannot be sufficient to track drought where more climate elements such as temperature and evapotranspiration should be taken into consideration. However, rainfall in Hungary was affected by different types of circulation (Cwsw, Cse, Cwnw), which have a negative trend as well as rainfall amount (Maheras et al. 2018). In connection with this, our results support this idea where an increased frequency of hydrological drought was detected (Fig. 5) with a remarkable decrease of rainfall between 1985 and 2000 (Fig. 2). Interestingly, Maheras et al. (2018) concluded that Debrecen (part of the Debrecen Region) was more subjected to extreme events (rainfall) which is consistent with our results in Table 2.

Generally, the highest portion of agricultural land is cultivated by maize followed by wheat and other crops (Széles et al. 2012), where the common agricultural system is rainfed system. Thus, any changes of rainfall patterns could have a bad impact on crop productivity. Interestingly, Adrienn and Janos (2012) reported that drought (i.e., agricultural drought) was the main reason of yield reduction in Hungary.

Yet, to our knowledge, few studies were conducted to measure the effect of drought on ecosystems, Móricz et al. (2018) indicate that the severe drought in last decades (1992–1993, 2000–2003, and 2011–2012) badly affected the Black pine growing in southwest Hungary. Similarly, Gulácsi and Kovács (2018) highlighted those years (2000, 2001, 2002, and 2003) as dry years in Danube-Tisza intersection (central of Hungary). These results are in conformity with our research as can be seen in Figs. 5 and 6.

Conclusion

This present study helps to track drought episodes in an important agricultural region in Hungary where the economic damages of severe drought in the Hungarian agricultural sector reach 145 million USD annually. The key funding of this research can be summarized as follows:

  1. 1.

    The PCI values ranged between 9.4 and 15.8 with an average of 11.8, while the dPCI values range between 8.6 and 20.7 with an average 10.9.

  2. 2.

    The most affected years by agricultural drought (i.e., SPI 6) were 1962, 1974, 1976, 1990; 1992, 2000, and 2007.

  3. 3.

    The most affected years by Hydrological drought (i.e., SPI-36) were 1961–1965, 1973–1974, and 1992–1995.

  4. 4.

    A notable significant correlation between SPI (-3, -6) and NDVI in summer and early fall was detected.

To sum up, the SPI index could provide an easy tool for drought monitoring in the study area. Successive steps should be taken on a national scale for drought monitoring and detecting by integrating different data sources such as remote sensing and other climatic data.