Fault ride-through capability improvement in a DFIG-based wind turbine using modified ADRC

Abstract

In this paper, an overview of several strategies for fault ride-through (FRT) capability improvement of a doubly-fed induction generator (DFIG)-based wind turbine is presented. Uncertainties and parameter variations have adverse effects on the performance of these strategies. It is desirable to use a control method that is robust to such disturbances. Auto disturbance rejection control (ADRC) is one of the most common methods for eliminating the effects of disturbances. To improve the performance of the conventional ADRC, a modified ADRC is introduced that is more robust to disturbances and offers better responses. The non-derivability of the fal function used in the conventional ADRC degrades its efficiency, so the modified ADRC uses alternative functions that are derivable at all points, i.e., the odd trigonometric and hyperbolic functions (arcsinh, arctan, and tanh). To improve the efficiency of the proposed ADRC, fuzzy logic and fractional-order functions are used simultaneously. In fuzzy fractional-order ADRC (FFOADRC), all disturbances are evaluated using a nonlinear fractional-order extended state observer (NFESO). The performance of the suggested structure is investigated in MATLAB/Simulink. The simulation results show that during disturbances such as network voltage sag/swell, using the modified ADRCs leads to smaller fluctuations in stator flux amplitude and DC-link voltage, lower variations in DFIG velocity, and lower total harmonic distortion (THD) of the stator current. This demonstrates the superiority over conventional ADRC and a proportional-integral (PI) controller. Also, by changing the crowbar resistance and using the modified ADRCs, the peak values of the waveforms (torque and currents) can be controlled at the moment of fault occurrence with no significant distortion.

1 Introduction

Because of the decrease in non-renewable fuel sources, the need for renewable energy sources, e.g., wind energy, has increased [1]. The addition of 93.6 GW of wind energy in 2021 increased its global cumulative capacity to 837 GW, representing a growth of 12% over the previous year. The global wind energy market is expected to grow by an average of 6.6% per year over the next five years [2]. Currently, wind projects are large enough to affect transmission network security, performance, and planning.

Despite the existence of other topologies such as synchronous and induction machines, the DFIG has become popular in the energy market because of its many benefits such as low converter rating, high power efficiency, good power quality, low losses, and small size of power electronics devices. These advantages lead to reduced investment costs, improved power factor, and separate adjustments of active and reactive power [3,4,5,6,7,8,9]. Therefore, the DFIG is a good choice for connecting wind turbines to the grid.

Over the years, wind power technology has been advancing by increasing the diameter of the rotor and using power electronic devices to operate at variable velocity, while seeking to absorb the maximum possible energy from the wind [10]. Variable speed wind turbines (VSWTs) have many benefits over fixed speed, e.g., the elimination of network disturbances is improved, and the problem of flickering is reduced [11,12,13]. VSWTs can be based on a direct drive synchronous generator or a DFIG. In the direct drive type, no gearbox is required, so its operating speed is equal to the rotational speed of the blades, while the power of the converters is equal to the rated generator power. On the other hand, there is a need for a gearbox if using a DFIG, but the power of the converters is about 20–30% of the rated generator power (if the turbine speed is in the range of ± 20–30% of its rated value) [14, 15]. The converters and controllers are selected according to which of these structures is used.

In a DFIG, the stator is connected directly to the network while the rotor is connected to the network via a back-to-back converter, i.e., a rotor side converter (RSC) and a grid side converter (GSC). In this case, the main goal of the converter connected to the rotor terminal, i.e., the RSC, is to maximize the energy absorbed from the wind by controlling the power at the stator terminal [3, 16,17,18,19].

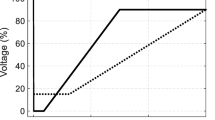
Because of the increase in electricity generation from wind energy and its injection into the power network, the transient stability of the network becomes very important. Therefore, different countries have updated their network codes to require wind turbines to stay connected to the network and provide reactive power depending on the severity and duration of the fault. In the literature, this mechanism is called fault ride-through (FRT) [20]. Any faults in the power system can lead to voltage disturbances such as voltage sag and swell. The FRT requirements of the network codes for several countries are shown in Fig. 1 [21]. The area above/below the low/high voltage ride-through line is marked such that the DFIG should remain connected to the grid, otherwise it can be disconnected from the grid. The FRT requirements for network codes are given as follows:

• During a predetermined time for a certain level of voltage sag/swell, wind turbines must remain connected to the network.

• During voltage sag/swell, wind turbines must generate reactive power to improve voltage stability.

• After the fault is cleared, wind turbines must generate active power immediately to stabilize the network frequency.

Fig. 1

FRT requirements of the network codes in several countries [21]

Considering that in a DFIG, the stator is directly connected to the network, its sensitivity to network disturbances such as voltage sag/swell is high. If for any reason, the network voltage suddenly decreases or increases, then because of the coupling between the rotor and the stator, large current can enter the rotor and induce significant overvoltage. Therefore, the RSC could be damaged by excessive voltage or current. This also negatively impacts the lifespan of the entire wind turbine system.

As shown in Fig. 2, there are two ways to enhance the FRT capability in a DFIG: (1) hardware techniques; and (2) control (software) techniques. The hardware techniques are also divided into two subgroups: (1) protection circuits and storage-based approaches; and (2) device-based reactive power injection procedures. Software techniques include traditional and advanced control methods. The advantages and disadvantages of using these methods in a DFIG are presented in Table 1.

Fig. 2

Methods used to improve the FRT capability in the DFIG system

Table 1 Control methods used for the FRT capability improvement

The protection circuits and storage-based approaches are summarized as follows:

• Crowbar circuit [22] Crowbar is the most common technique to increase protection on the rotor side of the DFIG. Under normal operating conditions, the crowbar is not in the circuit but enters the circuit during faults to protect the RSC. This technique is simple and easy to implement. However, when the crowbar is activated, the control of active and reactive power is lost because the RSC exits the circuit. In this case, the DFIG is in an uncontrolled situation, acting as a squirrel cage induction generator and absorbing reactive power from the grid, which may lead to further voltage sag and delay in grid voltage recovery after the fault. To solve this problem, the combination of crowbar with series R-L [23], series braking resistor (SBR) [24], and DC-link chopper [24] have been suggested to keep the RSC connected during the fault so the control of active and reactive power is retained.

• DC-link chopper The chopper acts to reduce the DC-link overvoltage. Here a resistor is installed in parallel with the DC-link to keep the DC-link voltage within an acceptable range by dissipating excessive energy. If only the chopper is used to protect the DFIG during the faults, then the rotor overcurrent will still flow through the RSC diodes and cause damage. Also, the time required for disengagement and restoration of the RSC is longer than with the crowbar circuit, since the chopper does not help to demagnetize the DFIG after the fault [25].

• Energy-storage based technique An energy storage system (ESS) stores excess energy during the fault and sends it back to the network after fault clearance to reduce DC-link voltage fluctuations [26]. The advantage of this technique is that it works without switching in different operating conditions, so there is no transient process related to switching. In addition, the control of the system is continuous. The disadvantage of using an ESS is that to effectively control the rotor current during the fault, the RSC capacity must be increased to prevent its damage, leading to cost increase.

• Series dynamic braking resistor (SDBR) SDBR is installed in series at the rotor/stator terminal and is equipped with a bypass power electronic switch. During the fault, SDBR attenuates the stator flux thus further attenuating the rotor voltage and current to protect the DFIG. However, using SDBR increases losses [24].

• Series grid side converter (SGSC) SGSC is an extra converter that connects in series with the stator on the AC side, while its DC side is connected to the DC-link in the DFIG system. The SGSC output voltage is adjusted to control the voltage of the stator, so as to assist the DFIG in overcoming voltage sag and decrease/remove the transient DC and negative sequence of flux [27].

• Fault current limiter (FCL) FCLs have been used in the connection of networks to each other to limit fault currents [28], while such devices are now being used to limit overcurrent in DFIG converters. Superconducting fault current limiters (SFCLs) can limit fault currents based on their quenching mode. These devices do not add any impedance to the network in normal operation. During a fault, they switch from superconducting to quenching mode and limit overcurrent in a unique way [29].

The reactive power injection equipment to improve FRT capability in the DFIG system is divided into three groups: (1) shunt compensators; (2) series compensators; and (3) hybrid compensators. The first category is summarized as follows:

• Static VAR compensator (SVC) An SVC consists of an inductor and a capacitor, and its reactive power exchanged with the grid is smoothly controlled by thyristors. Therefore, the bus voltage connected to the SVC can be adjusted. Since SVCs can compensate for the reactive power, they are used to stabilize the grid voltage [30].

• Static synchronous compensator (STATCOM) In large wind farms, a STATCOM is used with induction generators for fault recovery. In the steady state, maintaining the bus voltage and preventing fluctuations are important issues, so a STATCOM helps to achieve this goal by injecting/absorbing reactive power. In transient modes, the STATCOM injects maximum reactive current into the grid to help recover voltage. Compared to an SVC, a STATCOM has better transient response and the ability to run overload capability. However, the cost of a STATCOM is high [30, 31].

The second category (series compensators) is summarized as follows:

• Dynamic voltage restorer (DVR) A DVR includes a voltage source converter that is used to regulate the AC voltage. This device is connected in series between the wind turbine and the network through a coupling transformer that has an energy source and contains filters for harmonic suppression. There is no need to use complicated methods to control the DFIG converters. The structure of a DVR is similar to a static synchronous series compensator that performs direct voltage control and includes a capacitive bank and an energy storage device. This equipment is used to improve FRT capability. Although it is expensive to use a DVR for FRT, it can effectively eliminate transient generator current and power during network faults [32].

• Magnetic energy recovery switch (MERS) A series compensation using MERS is composed of four electronic switches and a DC-link capacitor. This structure has two series converter terminals. The MERS is used to improve FRT capability in squirrel cage induction generator-based wind turbines. This equipment injects harmonics into the line current, whose effects do not cause an acute problem but do interfere with the grid resonance frequency. More study is needed to prevent this disturbance [33]. The use of this device to improve FRT capability in a DFIG has not been widely studied and further investigation is necessary.

The third category, a hybrid compensator, performs better than the previous two categories. Since it conducts both series and parallel compensation, it can reduce various power quality problems. The back-to-back structure of converters is known as a unified power quality conditioner (UPQC) [34]. The unified power flow conditioner (UPFC) has a similar structure to a UPQC, except that the UPFC and UPQC are used in transmission and distribution systems, respectively. Limiting the fault current is an important issue in a network, as a large fault current causes voltage sag at the point of common coupling, and this affects the load in other feeders. Simultaneous use of a UPQC and an FCL leads to good clearance of voltage drop with small spikes in load voltage [35].

The traditional control methods are given below.

• Blade pitch orientation control By wind velocity variations, the blade pitch orientation is changed by the controller to regulate the rotor velocity, limit the power extracted from the wind and prevent damage to the wind turbine and DFIG system. The wind turbine output torque is used to control angular velocity and, consequently, mechanical power. Wind turbines with large-scale generators are used with a pitch orientation controller to support the generators against abrupt wind variations. This controller can also reduce frequency deviations to help power stabilization. The traditional pitch orientation controller used during normal operation compares the generator output power with the nominal value and regulates the pitch orientation when the wind velocity exceeds the nominal. In addition, some controllers determine the desired pitch orientation reference by comparing the velocities [36].

• Modified vector control The most common method used to control DFIG power converters is vector control based on stator flux orientation [37]. The role of the RSC is to control the reactor power of the stator and the electromagnetic torque. To simplify the design of the current controller, the flux of the stator is usually assumed to be constant and is considered to be aligned along the d-axis of the d-q coordinate. Another feature of vector control is the separate control of active and reactive power between the GSC and the network. The role of the GSC is to maintain the voltage of the DC-link. During voltage sag, the stator flux decreases because of direct connection to the network, and its q-axis component fluctuates instead of being zero. Consequently, it is necessary to study the stator flux dynamics during the implementation of the current controller. Current-based techniques such as feed-forward and transient current control, hysteresis control, and model predictive control are considered. These are used in modified vector control.

• Hysteresis control This control block includes a feedback loop and multi-level comparators. If the error exceeds the tolerance band, switching pulses are generated. The hysteresis current controller provides an optimal function for switching. As a result, it significantly reduces the average RSC switching frequency and output current fluctuations. Since this controller uses the instantaneous values of rotor current, it is robust to disturbances such as voltage fluctuations and variations of parameters [38, 39].

• Transient current controller by feed-forward compensator (TCCFFC) Adding the feed-forward part to a traditional current controller creates such a controller for an RSC. During the fault, this controller aligns the AC side voltage of the RSC with the transient voltage, thus reducing rotor current in transient conditions and minimizing interruptions of the crowbar. At the same time, by injecting transient compensation parts into the power and current control loops, torque fluctuations are reduced during network faults. This method also decreases the torque pulsations created by the negative sequence current [40].

The advanced control methods are as follows:

• Sliding mode control (SMC) SMC is a nonlinear procedure based on the discontinuous control signal, which changes the system dynamics. This method controls the system for sliding at a cross-section of the normal behavior. Because of the need for a robust controller, SMC is proposed as a suitable choice for solving the FRT problem of a DFIG. The high order SMC improves the FRT capability in the DFIG because of its robustness against disturbances. The suggested SMC can command the RSC in the event of network faults to suppress fluctuations of stator reactive power and electromagnetic torque. It can also stabilize the DC-link voltage and the active output power of the entire system by controlling the GSC [41].

• Fuzzy logic control (FLC) This controller can control the power flow of the DFIG system. It includes linguistic rules designed without any information on the precise parameters of the system as is needed in the setting of a traditional PI controller. By applying a fuzzy controller to the DFIG stator, the active and reactive powers are controlled separately. Comparing FLC with SMC demonstrates good efficiency in regulating active and reactive power and suppression of DC-link overvoltage during network faults. Thus, fuzzy control creates a new arena for improving the FRT capability in a DFIG [41, 42].

• Model predictive control (MPC) The exponential expansion of processors for network analysis leads to the use of predictive control. An objective function is specified, and MPC is the vector of voltage that minimizes this function. MPC, based on a limited control situation, uses confined switching modes of the converter to solve the system optimization problem. The switching operation minimizes a specific objective function and is used for the power converter, so there is no need for a modulator. This method also takes into account nonlinear factors and system constraints. Therefore, MPC-based methods can significantly handle abnormal conditions during network faults [43, 44].

• Auto disturbance rejection control (ADRC) In wind turbine systems, PI controllers don't operate satisfactorily during sudden wind changes. Also, the machine parameters vary due to operating conditions (such as temperature and saturation). This leads to incorrect operation of these controllers. In addition, these changes degrade the efficiency of most control methods. To reduce the effects of this problem, various optimization algorithms have been suggested in the literature. These algorithms lead to an increase in computational volume and complexity of the control methods. To solve these control problems, ADRC was introduced as an alternative. It includes three essential parts: a tracking differentiator (TD), nonlinear state error feedback (NLSEF) and an extended state observer (ESO). Because of the robustness of ADRC to changes in process parameters, it can be a valuable tool to the control engineering community. Using a feed-forward compensator and adding disturbances to the system, an integration system is created [45]. Numerous studies have suggested using different types of ADRC to improve the FRT capability in a DFIG [46,47,48], but these methods have advantages and disadvantages, as listed in Table 1.

Given that the fractional-order controller has a more robust operation than the integer-order controller [49], various fractional-order controllers have been proposed, e.g., fractional-order SMC [50, 51], fractional-order intelligent PID controller [52], fractional-order PID controller [53], etc. The main goal of ADRC is to enhance the system's robustness by using the ESO. As one of the important parts of ADRC, the ESO can estimate and eliminate the total disturbances. In [54], an ADRC including fractional-order TD (FTD), fractional-order PID controller, and fractional-order ESO (FESO) is suggested for nonlinear fractional-order projects. The stability region of a fractional-order project is flexible and can be larger or smaller than the integer-order project [55]. In [56], FESO is used to convert a generic second-order system into a cascaded fractional-order integrator so that the stability of the closed-loop system can be achieved using a proportional controller. In a fractional-order system, it is common to use a fractional-order controller for closed-loop stabilization [57]. In [58], a fractional-order ADRC based on FESO is proposed to convert the fractional-order system to a cascaded fractional-order integrator. In [59], an ADRC and fractional-order PID hybrid control for a hydro turbine speed governor system is proposed, while a new ADRC based on an improved FESO is delivered for a class of fractional-order systems [60]. To improve ADRC performance, various optimization algorithms, such as fuzzy logic, have been proposed [61, 62].

In all the above cases, if linear ADRC is used, the control circuit has a weaker performance than nonlinear ADRC. But if nonlinear ADRC is used, the non-derivability of the fal function in some points has adverse effects on control circuit performance. Some efforts have been made to solve the non-derivability problem, e.g., using alternative functions but the number of calculations is increased [62,63,64].

• Other advanced techniques Several new control methods have been proposed to analyze and improve the FRT capability of a DFIG. In [65], an inductance-emulating control technique for a DFIG-based wind turbine is suggested to suppress the post-fault rotor current and enhance its FRT capability. A feed-forward current references control strategy for the RSC of a DFIG-based wind turbine is introduced to enhance transient control performance during grid faults [66], whereas a scaled current tracking control for an RSC is proposed to improve the behavior of the DFIG under severe grid faults without flux observation [67]. In this technique, the rotor current is controlled to track the stator current on a particular scale, and with proper tracking the overcurrent and overvoltage of the rotor are controlled during severe faults. DVR with fault current limiting function [68] and control methods based on a genetic algorithm [69] have been suggested to improve the FRT capability. The flux tracking-based control technique, presented in [70], suppresses the rotor current during the fault. A coordinated control method of the RSC and GSC using auxiliary hardware during the fault is suggested in [71], where the two controllers use a fuzzy controller tuned by genetic algorithms.

A new approach to enhance FRT capability by including a flexible FRT method is investigated through simulation in [72], in which power systems with high penetration of wind power are considered. The temporary overloading ability of the DFIG is intended to increase the protection against minor faults and prevent tripping when the crowbar is disconnected after clearing moderate faults.

Some other suggested methods to improve FRT capability in a DFIG include: storing a part of the energy captured from wind in the rotor kinetic energy [73], conversion of unbalanced energy to kinetic energy [37], a two-degree-of-freedom internal model control [74], linear quadratic output-feedback decentralized controllers for the RSC and GSC [75], coordinated control of RSC and GSC to achieve smooth torque and constant active power [76], etc.

In this work, the FRT capability in DFIG-based wind turbines is improved by modifying the structure of conventional ADRC. The main contributions of this paper include:

• As the fal function used in conventional ADRC is not derivable at all points, it degrades its efficiency. Therefore, alternative functions to the fal function are used to improve the ADRC performance. Since the fal function is odd, odd trigonometric and hyperbolic functions (arcsinh, arctan, and tanh) are used instead. The three functions have an initial similarity with the fal function and are derivable at all points.

• Since fractional-order functions are more controllable than integer-order functions and provide better results, these functions are used in ADRC subblocks. In addition, the coefficients of state error feedback and observer are adjusted using fuzzy logic and the Fibonacci sequence, respectively. As a result, an FFOADRC is created for the first time.

• In the mentioned fuzzy system, instead of the error derivative, its linear combination is used to increase the performance and controllability of the FFOADRC. In this regard, stability analysis is presented.

• The RSC and GSC vector control is conducted separately using a PI controller, conventional ADRC, and proposed FFOADRCs with different fal functions. The comparative study of these controllers is carried out and simulations are undertaken to demonstrate the robustness of FFOADRCs during network voltage sag/swell.

The rest of the paper is organized as follows: Sect. 2 describes the configuration and equations of wind turbines based on a DFIG, and the improvement of ADRC performance is expressed in Sect. 3. DFIG vector control using a PI controller, conventional ADRC, and modified ADRC is conducted in Sect. 4, whereas the simulation results are presented and analyzed in Sect. 5. In Sect. 6, stability analysis is explained, and finally, conclusions are stated in Sect. 7.

2 Configuration and equations of wind turbine system using a DFIG

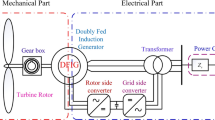
The structural diagram of a DFIG-based wind generation system is presented in Fig. 3. Depending on the operating conditions, both the rotor and stator windings in a DFIG exchange power between the machine and the network. As said before, the rotor of the DFIG is fed by a back-to-back converter to work at variable velocity, i.e., the RSC and GSC. Between these two converters, there is a DC-link capacitor. RSC is used to control torque, velocity, and power factor, while the role of the GSC is to maintain the DC-link voltage under a variety of circumstances. The rating of these converters depends on the speed range of operation, while they regulate the velocity of DFIG according to the wind velocity to absorb maximum power generated.

Fig. 3

Block diagram of the wind generation system using a DFIG [77]

The operation of DFIGs has been known for many years. They have had a significant impact on the development of wind energy projects. When using DFIG, then compared to other fixed speed wind turbines, power generation is increased by up to 30%. This decreases investment costs [77].

In this part, the VSWT model with DFIG is described, including turbine model with a focus on wind velocity and energy absorbed by the turbine, and the model of the overall system.

2.1 Wind turbine model

The turbine rotates the shaft by converting the kinetic energy of wind into mechanical torque [78]. The aerodynamic power captured by the wind turbine is given as:

$$P_{t} = \frac{1}{2}\rho \pi R_{t}^{2} V_{w}^{3} C_{p} \left( {\lambda ,\beta } \right)$$

(1)

where ρ is the density of air, R_t is the rotor blades radius, V_w is the wind speed, λ is the tip speed ratio, β is the pitch angle of the blades, and C_p(λ,β) is the power coefficient, which represents the maximum energy captured at each wind speed and depends on λ and β, as described by [78]:

$$C_{p} (\lambda ,\beta ) = 0.5176\left( {\frac{116}{{\lambda_{i} }} - 0.4\beta - 5} \right)e^{{\left( { - \frac{21}{{\lambda_{i} }}} \right)}} + 0.0068\lambda$$

(2)

where

$$\frac{1}{{\lambda_{i} }} = \frac{1}{\lambda + 0.08\beta } - \frac{0.035}{{\beta^{3} + 1}}$$

(3)

The tip speed ratio is defined as:

$$\lambda = \frac{{R_{t} \Omega_{t} }}{{V_{w} }}$$

(4)

where Ω_t is the angular speed of the turbine shaft. At wind speeds less than its rated value, β is usually maintained at zero, and the peak C_p (C_p−peak) is achieved by maximizing (2) to λ. So from (2) to (3), there is:

$$C_{p,peak} (\lambda ,0) = 0.48\;for\;\lambda_{opt} = 8.1$$

(5)

2.2 Dynamical modeling of a DFIG

Usually, the DFIG dynamic model is presented in the d−q reference frame, which is based on either stator voltage orientation or stator flux orientation [78]. So the supply voltages, v_ds and v_qs, and the rotor voltages, v_dr and v_qr, are given as:

$$\left\{ \begin{gathered} v_{qs} = \dot{\lambda }_{qs} + \omega_{s} \lambda_{ds} + R_{s} i_{qs} \hfill \\ v_{ds} = \dot{\lambda }_{ds} - \omega_{s} \lambda_{qs} + R_{s} i_{ds} \hfill \\ v_{qr} = \dot{\lambda }_{qr} + \omega_{r} \lambda_{dr} + R_{r} i_{qr} \hfill \\ v_{dr} = \dot{\lambda }_{dr} - \omega_{r} \lambda_{qr} + R_{r} i_{dr} \hfill \\ \end{gathered} \right.$$

(6)

where Rs and Rr are the stator and rotor resistances, i_ds and i_qs are the d−q components of the stator current, i_dr and i_qr are the d−q components of the rotor current, and ω_s and ω_r are the stator and rotor electrical speed, respectively. The equations of stator and rotor fluxes are given as:

$$\left\{ \begin{gathered} \lambda_{qs} = L_{s} i_{qs} + L_{m} i_{qr} \hfill \\ \lambda_{ds} = L_{s} i_{ds} + L_{m} i_{dr} \hfill \\ \lambda_{qr} = L_{r} i_{qr} + L_{m} i_{qs} \hfill \\ \lambda_{dr} = L_{r} i_{dr} + L_{m} i_{ds} \hfill \\ \end{gathered} \right.$$

(7)

where L_m is the mutual inductance, and L_r and L_s are the inductances of the rotor and stator, respectively.

According to (6), the flux equations of the DFIG in the d-q frame are given as:

$$\left\{ \begin{gathered} \dot{\lambda }_{qs} = v_{qs} - R_{s} i_{qs} - \omega_{s} \lambda_{ds} \hfill \\ \dot{\lambda }_{ds} = v_{ds} - R_{s} i_{ds} + \omega_{s} \lambda_{qs} \hfill \\ \dot{\lambda }_{qr} = v_{qr} - R_{r} i_{qr} - \omega_{r} \lambda_{dr} \hfill \\ \dot{\lambda }_{qr} = v_{dr} - R_{r} i_{dr} + \omega_{r} \lambda_{qr} \hfill \\ \end{gathered} \right.$$

(8)

The active and reactive powers of the stator are:

$$\left\{ \begin{gathered} P_{s} = \frac{3}{2}\left( {v_{ds} i_{ds} + v_{qs} i_{qs} } \right) \hfill \\ Q_{s} = \frac{3}{2}\left( {v_{qs} i_{ds} - v_{ds} i_{qs} } \right) \hfill \\ \end{gathered} \right.$$

(9)

2.3 Drive train equations

The mechanical part of the wind generation system consists of the gearbox, high-speed shaft, and low-speed shaft. In this regard, a comprehensive study has been conducted in [79]. To implement this part, a two-mass model is used, and the related equations in per unit (pu) are [80]:

$$\left\{ {\begin{array}{*{20}c} {\dot{\omega }_{r,pu} = \frac{{T_{sh,pu} - T_{em,pu} }}{{2H_{g} }},} & {\dot{\omega }_{t,pu} = \frac{{T_{t,pu} - T_{sh,pu} }}{{2H_{t} }}} \\ {T_{sh,pu} = k_{sh} \theta + D_{sh} \dot{\theta },} & {\dot{\theta } = \frac{{\omega_{t,pu} - \omega_{r,pu} }}{{\omega_{b} }}} \\ \end{array} } \right.$$

(10)

where ω_t,pu and ω_r,pu are the velocities of the turbine and machine in (pu), respectively. T_t,pu and T_sh,pu are the torques of the turbine and shaft in (pu), respectively. T_em,pu is the electromagnetic torque in (pu). H_t and H_g are the inertia constants of the turbine and machine in seconds. K_sh is the factor of shaft stiffness in (pu/rad), and D_sh is the damping factor in (pu). θ is the angle of shaft twist in rad., and ω_b is the base angular velocity.

2.4 Modeling of back-to-back PWM converters

This converter allows bidirectional power exchange between the rotor and the network. Figure 4 presents the back−to−back PWM converters. S_mn demonstrates the switching functions with m specifying the converter arms and n the rectifier/inverter. Ig, i_rec, and i_inv are the filter current, rectifier current, and inverter current, respectively. The relations are given as [81]:

$$\left\{ \begin{gathered} C\dot{u}_{dc} = i_{rec} - i_{inv} \hfill \\ i_{rec} = \frac{3}{2}(s_{qr} I_{qg} + s_{dr} I_{dg} ) \hfill \\ V_{df} = R_{f} I_{dg} + L_{f} \dot{I}_{dg} + V_{dg} - \omega_{s} L_{f} I_{qg} \hfill \\ V_{qf} = R_{f} I_{qg} + L_{f} \dot{I}_{qg} + V_{qg} + \omega_{s} L_{f} I_{dg} \hfill \\ V_{df} = S_{dr} u_{dc} \hfill \\ V_{qf} = S_{qr} u_{dc} \hfill \\ \end{gathered} \right.$$

(11)

where u_dc is the voltage of the DC−link, C is DC−link capacitance value, I_dg and I_qg are the d−q components of the filter current, V_dg and V_qg are the d−q components of the network voltage, V_df and V_qf are the d−q components of V_f, which is the AC voltage of the rectifier output on the filter side. R_f is the filter resistance, and L_f is the filter inductance. S_dr and S_qr are the modulating signals to regulate the rectifier voltage and adjust the currents i_r and i_g.

Fig. 4

Topology of the back-to-back converter [81]

3 Improvement of ADRC performance

This section first introduces the conventional ADRC. Then, with the simultaneous use of the new fal functions, fuzzy logic, and fractional-order functions, the modified ADRC is presented to enhance the performance of the DFIG control circuit during network faults.

3.1 ADRC

DFIG control with a PI controller is widely used. However, when the internal parameters of the DFIG change because of the effects of temperature and saturation, it is a major problem that affects the performance of the regulators. The proposed ADRC theory, which operates according to the ESO [82], does not require a precise model of the plant. The advantage of ADRC is to observe all internal and external disturbances of the system (such as cross-coupling terms, parameter uncertainties due to the temperature, and load variation), while it calculates and eliminates their adverse effects in real-time. Consider a second-order single-input single-output (SISO) plant as [83]:

$$y^{\prime\prime}(t) = f(y(t),y^{\prime}(t),d(t),u(t)) + b_{0} u(t)$$

(12)

The state equations of the plant are:

$$\left\{ \begin{gathered} \dot{x}_{1} (t) = x_{2} (t) \hfill \\ \dot{x}_{2} (t) = f(x_{1} (t),x_{2} (t),d(t)) + b_{0} u(t) \hfill \\ y(t) = x_{1} (t) \hfill \\ \end{gathered} \right.$$

(13)

where u(t) and y(t) are the respective input and output of the plant, d(t) and f(.) are the respective external and total disturbances, and b₀ is the known part of the plant.

The structure of the ADRC is shown in Fig. 5. As mentioned, the ADRC includes three main components: TD, NLSEF, and ESO.

• (a) second-order TD

Fig. 5

ADRC schematic diagram for a second order SISO system [82, 83]

The relations of this part are given by:

$$\left\{ \begin{gathered} \dot{v}_{1} (t) = v_{2} (t) \hfill \\ \dot{v}_{2} (t) = R^{2} .\psi \left( {v_{1} (t) - v(t),\frac{{v_{2} (t)}}{R}} \right),\,\,\;\psi (0, \, 0) = 0 \hfill \\ \end{gathered} \right. \,$$

(14)

where v(t) is the reference input, v₁(t) is the tracking amount of v(t), and v₂(t) is the derivative of v₁(t). R is a positive factor that needs to be tuned, and ψ(.) is a nonlinear function.

• (b) third-order ESO

The relations of the observer mentioned above are given as:

$$\left\{ \begin{gathered} \dot{z}_{1} (t) = z_{2} (t) + \beta_{1} g_{1} (y(t) - z_{1} (t)) \hfill \\ \dot{z}_{2} (t) = z_{3} (t) + \beta_{2} g_{2} (y(t) - z_{1} (t)) + b_{0} u(t) \hfill \\ \dot{z}_{3} (t) = \beta_{3} g_{3} (y(t) - z_{1} (t)) \hfill \\ \end{gathered} \right. \,$$

(15)

where u(t) is the plant input, β_i (i = 1, 2, 3) are the observer gains, g_i (i = 1, 2, 3) are the appropriate nonlinear functions, while z₁(t) is the tracking amount of y(t). z₂(t) is the derivative of z₁(t) and z₃(t) is the total disturbance estimation, while b₀ has been previously defined. By appropriately selecting g_i (i = 1, 2, 3) and regulating β_i (i = 1, 2, 3), the states z_i (i = 1, 2) and z₃ estimate the states x_i (i = 1, 2) and total disturbances, respectively.

• (iii) NLSEF

This block generates the control law of ADRC as:

$$u(t) = \frac{1}{{b_{0} }}\left( {\psi \left( {z(t) - v(t)} \right) - z_{3} (t)} \right)$$

(16)

where z(t) = (z₁(t), z₂(t)) and v(t) = (v₁(t), v₂(t)).

For fast and optimal control of a second-order SISO plant, the ADRC equations are given as:

$$\left\{ \begin{gathered} TD: \, \left\{ \begin{gathered} \dot{v}_{1} = v_{2} \hfill \\ \dot{v}_{2} = - r.{\text{sgn}} \left( {v_{1} (t) - v(t) + \frac{{v_{2} (t)\left| {v_{2} (t)} \right|}}{2r}} \right) \hfill \\ \end{gathered} \right. \, \hfill \\ NLSEF:\left\{ \begin{gathered} e_{1} = v_{1} - z_{1} , \, e_{2} = v_{2} - z_{2} = \dot{e}_{1} \, \hfill \\ {\text{u}}_{{0}} = k_{p} fal(e_{1} , \, \alpha_{1} , \, \delta_{1} ) + k_{d} fal(e_{2} , \, \alpha_{2} , \, \delta_{2} ) \hfill \\ \end{gathered} \right. \, \hfill \\ ESO:\left\{ \begin{gathered} \dot{z}_{1} (t) = z_{2} (t) - \beta_{1} (z_{1} (t) - y(t)) \hfill \\ \dot{z}_{2} (t) = z_{3} (t) - \beta_{2} fal\left( {z_{1} (t) - y(t), \, 0.5, \, \delta } \right) + b_{0} u(t) \hfill \\ \dot{z}_{3} (t) = - \beta_{3} fal\left( {z_{1} (t) - y(t), \, 0.25, \, \delta } \right) \hfill \\ \end{gathered} \right. \hfill \\ control \, law: \, u(t) = \frac{1}{b}\left( {u_{0} (t) - z_{3} (t)} \right) \hfill \\ \end{gathered} \right.$$

(17)

where r determines the tracking speed (r > 0), sgn is the sign function, and k_d and k_p are the derivative and proportional factors, respectively. α₁, δ₁, α₂, δ₂, and δ are the parameters of ADRC that need to be determined. The expression of the fal(.) function is:

$$fal(e, \, \alpha , \, \delta ) = \left\{ \begin{gathered} \left| e \right|^{\alpha } {\text{sgn}} (e) \, \left| {\text{e}} \right| > \delta \hfill \\ \frac{e}{{\delta^{1 - \alpha } }} \, \left| {\text{e}} \right| \le \delta \hfill \\ \end{gathered} \right.$$

(18)

If α < 1, fal(.) delivers a large/small error with a small/large gain.

3.2 Modified ADRC

In this section, using the new fal functions, fractional-order functions, and fuzzy logic, a modified ADRC is introduced to improve the performance of the control circuit.

3.2.1 New fal functions

It is seen from (18) that the fal function has one input (e) and two parameters (α and δ), and has two different rules depending on the input value of e. The parameter δ is usually less than one. For the values of α = 0.5 and δ = 0.05, this function is plotted in Fig. 6. Since fal is an odd function, its continuity and derivability are examined only at the point e = δ and the result will be similar at the point e = −δ.

$$\left\{ \begin{gathered} \left\{ \begin{gathered} \left. {fal^{\prime}} \right|_{{e = \delta^{ + } }} = \left. {\alpha e^{\alpha - 1} } \right|_{{e = \delta^{ + } }} = \alpha \delta^{\alpha - 1} \hfill \\ \left. {fal^{\prime}} \right|_{{e = \delta^{ - } }} = \frac{1}{{\delta^{1 - \alpha } }} \hfill \\ \end{gathered} \right. \Rightarrow \alpha \delta^{\alpha - 1} \ne \frac{1}{{\delta^{1 - \alpha } }} \hfill \\ \left\{ \begin{gathered} \left. {fal} \right|_{{e = \delta^{ + } }} = \left. {e^{\alpha } } \right|_{{e = \delta^{ + } }} = \delta^{\alpha } \hfill \\ \left. {fal} \right|_{{e = \delta^{ - } }} = \left. {\frac{e}{{\delta^{1 - \alpha } }}} \right|_{{e = \delta^{ - } }} = \delta^{\alpha } \hfill \\ \end{gathered} \right. \, \Rightarrow \delta^{\alpha } = \delta^{\alpha } \hfill \\ \end{gathered} \right.$$

(19)

Fig. 6

The fal function for α = 0.5 and δ = 0.05

It can be seen that the fal function is continuous at the point e = δ but is not derivable, which can lead to non-smooth output of the blocks in which this function is used. The continuity and non-derivability of the fal function at e = δ and e = −δ are shown in Fig. 6. The problem expressed in the fal function is to be solved by defining new forms of the fal function with fewer criteria to reduce the amount of computation. It is seen from (18) and Fig. 6 that the fal function is odd, so the new functions that will be defined must be odd too. Among the trigonometric and hyperbolic functions, the arcsinh, arctan, and tanh functions are similar to the diagram in Fig. 6 but do not have the problem of derivation. So they are selected as the candidates. The relation of fal function with arcsinh (fal_arcsinh) is:

$$fal_{\arcsin h} (e,\alpha ,\delta ) = k_{1} .\arcsin h(e) + k_{2}$$

(20)

From the value of the function at the origin and e = δ, there are:

$$\left\{ \begin{gathered} k_{1} .\arcsin h(0) + k_{2} = 0 \, \hfill \\ k_{1} .\arcsin h(\delta ) + k_{2} = \delta^{\alpha } \, \hfill \\ \end{gathered} \right.$$

(21)

From the above equations, there is:

$$fal_{\arcsin h} (e,\alpha ,\delta ) = \left( {\frac{{\delta^{\alpha } }}{\arcsin h(\delta )}} \right)\arcsin h(e)$$

(22)

Similarly, for fal functions with arctan (fal_arctan) and tanh (fal_tanh), there are:

$$fal_{\arctan } (e,\alpha ,\delta ) = \left( {\frac{{\delta^{\alpha } }}{\arctan (\delta )}} \right)\arctan (e)$$

(23)

$$fal_{\tanh } (e,\alpha ,\delta ) = \left( {\frac{{\delta^{\alpha } }}{\tanh (\delta )}} \right)\tanh (e)$$

(24)

In (17), the fal functions used in NLSEF and ESO can be any of the functions of the default fal, fal_arcsinh, fal_arctan or fal_tanh.

3.2.2 Fuzzy fractional-order ADRC (FFOADRC)

The structure of FFOADRC is presented in Fig. 7. As shown, a linear combination of v₂ and z₂ (E₂ = k₁v₂−k₂z₂) has been used instead of the error derivative (e₂ = v₂−z₂) to enhance the performance of ADRC, improve its controllability and increase its degree of freedom. Since fractional-order functions are more controllable than integer-order ones, NFESO and FTD are used. The fractional calculation is a generalization of integration and differentiation to non-integer order. The non-integer order fundamental operator is introduced as follows [84]:

$${}_{a}D_{t}^{\alpha } = \left\{ \begin{gathered} \frac{{d^{\alpha } }}{{dt^{\alpha } }}{\text{ Re }}\left[ \alpha \right] > {0} \hfill \\ 1{\text{ Re }}\left[ \alpha \right] = {0} \hfill \\ \int\limits_{a}^{t} {(d\tau )^{ - \alpha } } {\text{ Re }}\left[ \alpha \right] < {0} \hfill \\ \end{gathered} \right.$$

(25)

where α is the order of the operation. In Fig. 7, if the commensurate order of the plant is equal to α, then the differential equation will be as follows:

$$y^{(2\alpha )} = f(u,d,y,y^{(\alpha )} ) + b_{0} u$$

(26)

Fig. 7

Block diagram of the FFOADRC

Considering $x_{1} = y$, $x_{2} = y^{(\alpha )}$ and $x_{3} = f(u,d,y,y^{(\alpha )} )$ so that $x_{1}$ and $x_{2}$ are the states of the system and $x_{3}$ is the extended state, the state equations are obtained as:

$$\left\{ \begin{gathered} x^{(\alpha )} = Ax + Bu + Eh \hfill \\ y = Cx \hfill \\ \end{gathered} \right.$$

(27)

where $x = \left[ {\begin{array}{*{20}c} {x_{1} } \\ {x_{2} } \\ {x_{3} } \\ \end{array} } \right]$, $x^{(\alpha )} = \left[ {\begin{array}{*{20}c} {x_{1}^{(\alpha )} } \\ {x_{2}^{(\alpha )} } \\ {x_{3}^{(\alpha )} } \\ \end{array} } \right]$, $A = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{array} } \right]$, $B = \left[ {\begin{array}{*{20}c} 0 \\ {b_{0} } \\ 0 \\ \end{array} } \right]$, $C = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ \end{array} } \right]$, $E = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ 1 \\ \end{array} } \right]$, and $h = f^{(\alpha )} ( \cdot )$.

To estimate $x_{1}$, $x_{2}$, and $x_{3}$, a NFESO is considered as follows:

$$\left\{ \begin{gathered} z_{1}^{(\alpha )} (t) = z_{2} (t) - \beta_{1} (z_{1} (t) - y(t)) \hfill \\ z_{2}^{(\alpha )} (t) = z_{3} (t) - \beta_{2} fal\left( {z_{1} (t) - y(t), \, 0.5, \, \delta } \right) + b_{0} u(t) \hfill \\ z_{3}^{(\alpha )} (t) = - \beta_{3} fal\left( {z_{1} (t) - y(t), \, 0.25, \, \delta } \right) \hfill \\ \end{gathered} \right.$$

(28)

As previously expressed, β₁, β₂, and β₃ are the observer gains. In (28), z₁, z₂, and z₃ are the estimations of x₁, x₂, and x₃, respectively. Meanwhile, the fal function can be any of the functions default fal, fal_arcsinh, fal_arctan or fal_tanh. Using numerical calculations and based on the Fibonacci sequence, the coefficients β₁, β₂, and β₃ are obtained as [83]:

$$\beta_{1} = \frac{1}{h}, \, \beta_{{2}} = \frac{1}{{3h^{2} }}, \, \beta_{{3}} = \frac{1}{{32h^{3} }}$$

(29)

where h is the sampling period. By selecting the coefficients according to (29), the system states and total disturbances are estimated satisfactorily. If the NFESO coefficients are tuned correctly, then the extended state can be accurately tracked. By considering the control law of ADRC as $u = \frac{{u_{0} - z_{3} }}{{b_{0} }}$, an integration system is available in the form of $y^{(2\alpha )} \approx u_{0}$. In Fig. 7, the FTD relations are [54]:

$$\left\{ \begin{gathered} v_{1}^{(\alpha )} = v_{2} \, \hfill \\ v_{2}^{(\alpha )} = - r.{\text{sgn}} \left( {v_{1} - v + \frac{{\Gamma^{2} (\alpha + 1)}}{r.\Gamma (2\alpha + 1)}v_{2} \left| {v_{2} } \right|} \right) \hfill \\ \end{gathered} \right.$$

(30)

where Г(.) is the Gamma function.

3.2.2.1 Adjustment of NLSEF block coefficients (kp and kd) in FFOADRC

In NLSEF, the proper selection of coefficients k_p and k_d is essential [85]. Increasing k_p leads to a shorter transient time of responses and improves tracking accuracy, but higher overshoot which has adverse effects on dynamic performance. Increasing k_d leads to faster process response, but high−frequency noise appears. So fuzzy logic is used to specify the suitable coefficients for NLSEF. The rules of the fuzzy system are presented in Table 2. The rules are defined to zero e₁ and E₂ such that "NB ≡ Negative Big", "NM ≡ Negative Medium", "NS ≡ Negative Small", "ZO ≡ Zero", "PS ≡ Positive Small", "PM ≡ Positive Medium", and "PB ≡ Positive Big". As mentioned, e₁ is the error (e₁ = v₁ − z₁) and E₂ is the linear combination of the derivative of errors (E₂ = k₁v₂ − k₂z₂).

Table 2 Fuzzy rules used for k_p and k_d

4 DFIG vector control using modified ADRC

In this part, vector control of the RSC and GSC is conducted separately using PI controller and FFOADRC.

4.1 Control of the RSC and GSC using FFOADRC

Because of the importance of selecting NLSEF coefficients and appropriate control of NFESO and FTD, in this part, the RSC and GSC vector control is performed using FFOADRC. The default fal, fal_arcsinh, fal_arctan and fal_tanh functions are used separately.

4.1.1 Speed sensorless vector control of RSC

The RSC control block diagram is presented in Fig. 8 where the current and velocity control loops are implemented using FFOADRC.

Fig. 8

Speed sensorless vector control of the RSC using the FFOADRC

4.1.1.1 Current control loops of RSC

From (6) to (7), the stator flux derivatives are:

$$\left\{ \begin{gathered} \frac{{d\lambda_{qs} }}{dt} = v_{qs} - \frac{{R_{s} }}{{L_{s} }}\lambda_{qs} - \omega_{s} \lambda_{ds} + \frac{{R_{s} L_{m} }}{{L_{s} }}i_{qr} \hfill \\ \frac{{d\lambda_{ds} }}{dt} = v_{ds} - \frac{{R_{s} }}{{L_{s} }}\lambda_{ds} + \omega_{s} \lambda_{qs} + \frac{{R_{s} L_{m} }}{{L_{s} }}i_{dr} \hfill \\ \end{gathered} \right.$$

(31)

where $\sigma = 1 - \frac{{L_{m}^{2} }}{{L_{s} L_{r} }}$ is the leakage coefficient. Using (7), the rotor fluxes are:

$$\left\{ \begin{gathered} \lambda_{qr} = \frac{{L{}_{m}}}{{L_{s} }}\lambda_{qs} + \sigma L_{r} i_{qr} \hfill \\ \lambda_{dr} = \frac{{L{}_{m}}}{{L_{s} }}\lambda_{ds} + \sigma L_{r} i_{dr} \hfill \\ \end{gathered} \right.$$

(32)

From (31) and (32), the rotor flux derivatives are given as:

$$\left\{ \begin{gathered} \frac{{d\lambda_{qr} }}{dt} = \frac{{L_{m} }}{{L_{s} }}v_{qs} - \frac{{R_{s} L_{m} }}{{L_{s}^{2} }}\lambda_{qs} - \frac{{L_{m} }}{{L_{s} }}\omega_{s} \lambda_{ds} \, + \frac{{R_{s} L_{m}^{2} }}{{L_{s}^{2} }}i_{qr} + \sigma L_{r} \frac{{di_{qr} }}{dt} \hfill \\ \frac{{d\lambda_{dr} }}{dt} = \frac{{L_{m} }}{{L_{s} }}v_{ds} - \frac{{R_{s} L_{m} }}{{L_{s}^{2} }}\lambda_{ds} + \frac{{L_{m} }}{{L_{s} }}\omega_{s} \lambda_{qs} + \frac{{R_{s} L_{m}^{2} }}{{L_{s}^{2} }}i_{dr} + \sigma L_{r} \frac{{di_{dr} }}{dt} \hfill \\ \end{gathered} \right.$$

(33)

Substituting (33) in (7), the rotor current derivatives are obtained as:

$$\left\{ \begin{gathered} \frac{{di_{qr} }}{dt} = \frac{{v_{qr} }}{{\sigma L_{r} }} - \frac{1}{{\sigma L_{r} }}\left( {R_{r} + R_{s} \frac{{L_{m}^{2} }}{{L_{s}^{2} }}} \right)i_{qr} - \frac{{\omega_{r} \lambda_{dr} }}{{\sigma L_{r} }} \hfill \\ \, - \frac{{L_{m} }}{{\sigma L_{s} L_{r} }}v_{qs} + \frac{{R_{s} L_{m} }}{{\sigma L_{s}^{2} L_{r} }}\lambda_{qs} + \frac{{L_{m} \omega_{s} }}{{\sigma L_{s} L_{r} }}\lambda_{ds} \hfill \\ \frac{{di_{dr} }}{dt} = \frac{{v_{dr} }}{{\sigma L_{r} }} - \frac{1}{{\sigma L_{r} }}\left( {R_{r} + R_{s} \frac{{L_{m}^{2} }}{{L_{s}^{2} }}} \right)i_{dr} + \frac{{\omega_{r} \lambda_{qr} }}{{\sigma L_{r} }} \hfill \\ \, - \frac{{L_{m} }}{{\sigma L_{s} L_{r} }}v_{ds} + \frac{{R_{s} L_{m} }}{{\sigma L_{s}^{2} L_{r} }}\lambda_{ds} - \frac{{L_{m} \omega_{s} }}{{\sigma L_{s} L_{r} }}\lambda_{qs} \hfill \\ \end{gathered} \right.$$

(34)

From (7) and the definition of stator flux oriented (SFO) control, in which the d-axis of the reference frame is aligned to the stator flux vector, there are:

$$\left\{ \begin{gathered} i_{ds} = \frac{{\lambda_{ds} - L_{m} i_{dr} }}{{L_{s} }}, \, i_{qs} = - \frac{{L_{m} }}{{L_{s} }}i_{qr} \hfill \\ \lambda_{dr} = \frac{{L_{m} }}{{L_{s} }}\lambda_{ds} + \sigma L_{r} i_{dr} , \, \lambda_{qr} = \sigma L_{r} i_{qr} \hfill \\ \end{gathered} \right.$$

(35)

Given the SFO and neglecting the impact of stator resistance, stator voltages in the d−q coordinate are v_ds=0 and v_qs=ω_sλ_ds. So (34) can be simplified as:

$$\left\{ \begin{gathered} \frac{{di_{qr} }}{dt} = \frac{{v_{qr} }}{{\sigma L_{r} }} - \frac{{R_{r} }}{{\sigma L_{r} }}i_{qr} - \omega_{r} \left( {\frac{{L_{m} }}{{\sigma L_{s} L_{r} }}\lambda_{s} + i_{dr} } \right) \hfill \\ \frac{{di_{dr} }}{dt} = \frac{{v_{dr} }}{{\sigma L_{r} }} - \frac{{R_{r} }}{{\sigma L_{r} }}i_{dr} + \omega_{r} i_{qr} \hfill \\ \end{gathered} \right.$$

(36)

The derivatives of (36) are given as:

$$\left\{ \begin{gathered} \frac{{d^{2} y_{qr} (t)}}{{dt^{2} }} = b_{or} u_{qr} (t) + f_{3qr} \hfill \\ \frac{{d^{2} y_{dr} (t)}}{{dt^{2} }} = b_{or} u_{dr} (t) + f_{3dr} \hfill \\ b_{0r} = - \frac{{R_{r} }}{{\sigma^{2} L_{r}^{2} }} \hfill \\ \end{gathered} \right.$$

(37)

where y_dr(t)=i_dr(t) and y_qr(t)=i_qr(t) are the observer inputs, and u_dr(t)=v_dr(t) and u_qr(t)=v_qr(t) are the output signals used for controlling the RSC. f_3dr and f_3qr are the total disturbances with the following relations:

$$\left\{ \begin{gathered} f_{3qr} = - \frac{{\omega_{r} }}{{\sigma L_{r} }}v_{dr} + \frac{1}{{\sigma L_{r} }}\frac{{dv_{qr} }}{dt} + \left( {\frac{{R_{r}^{2} }}{{\sigma^{2} L_{r}^{2} }} - \omega_{r}^{2} } \right)i_{qr} \hfill \\ \, + \frac{{{\text{2R}}_{{\text{r}}} \omega_{r} {\text{i}}_{{{\text{dr}}}} }}{{\sigma L_{r} }} + \frac{{{\text{R}}_{{\text{r}}} {\text{L}}_{{\text{m}}} \omega_{r} \lambda_{{\text{s}}} }}{{\sigma^{2} {\text{L}}_{{\text{s}}} L_{r}^{2} }} \, \hfill \\ f_{3dr} = + \frac{{\omega_{r} }}{{\sigma L_{r} }}v_{qr} + \frac{1}{{\sigma L_{r} }}\frac{{dv_{dr} }}{dt} + \left( {\frac{{R_{r}^{2} }}{{\sigma^{2} L_{r}^{2} }} - \omega_{r}^{2} } \right)i_{dr} \hfill \\ { - }\frac{{{\text{2R}}_{{\text{r}}} \omega_{r} {\text{i}}_{{{\text{qr}}}} }}{{\sigma L_{r} }}{ - }\frac{{{\text{L}}_{{\text{m}}} \omega_{r}^{2} \lambda_{{\text{s}}} }}{{\sigma {\text{L}}_{{\text{s}}} L_{r} }} \, \hfill \\ \end{gathered} \right.$$

(38)

The overall structural diagram is presented in Fig. 8. Using third−order observers, there are z_3dr=f_3dr and z_3qr=f_3qr. From (38), there is:

$$\begin{gathered} - L_{m} \lambda_{s} i_{qr} \omega_{r}^{2} + \left( {L_{s} \left( {v_{qr} i_{qr} + v_{dr} i_{dr} - 2R_{r} \left( {i_{dr}^{2} + i_{qr}^{2} } \right)} \right) - \frac{{R_{r} L_{m} i_{dr} \lambda_{s} }}{{\sigma L_{r} }}} \right)\omega_{r} \hfill \\ + L_{s} \left( {i_{qr} \frac{{dv_{dr} }}{dt} - i_{dr} \frac{{dv_{qr} }}{dt}} \right) + \sigma L_{s} L_{r} \left( {z_{3qr} i_{dr} - z_{3dr} i_{qr} } \right) = 0 \hfill \\ \end{gathered}$$

(39)

As ω_s−ω_m=ω_r, the estimated electrical speed of the rotor $(\hat{\omega }_{m} )$ is given in (40), where the rotor speed is estimated from the machine parameters. If for any reason (internal or external) the equilibrium point of the DFIG changes, FFOADRC considers these changes in real−time in the estimation of the disturbances (z_3dr and z_3qr). Then the speed estimator estimates the new speed of the rotor so that the DFIG control can be performed at the new equilibrium point by calculating the rotor angle. From Fig. 8, two FFOADRCs are used in the d−q coordinate. The FFOADRC outputs (v_dr, v_qr) should be converted into the d−q frame to be used in the PWM modulator to generate switching pulses. The angle required for this conversion ($\hat{\theta }_{m}$) is obtained from the output of the speed estimator, while the rotor currents are converted into the d-q frame to enter the FFOADRCs. Since the RSC control circuit operates with currents of the rotor transmitted to the stator side, conversion of currents/voltages to the rotor side should be conducted before producing the signals for the modulator. Therefore, the u factor is used and

$$\begin{gathered} \hat{\omega }_{m} = \omega_{s} - \hfill \\ \, \left( {\frac{{ - L_{s} \left( {v_{qr} i_{qr} + v_{dr} i_{dr} - 2R_{r} \left( {i_{dr}^{2} + i_{qr}^{2} } \right)} \right) + \frac{{R_{r} L_{m} i_{dr} \lambda_{s} }}{{\sigma L_{r} }} \pm \sqrt {\left( {L_{s} \left( {v_{qr} i_{qr} + v_{dr} i_{dr} - 2R_{r} \left( {i_{dr}^{2} + i_{qr}^{2} } \right)} \right) - \frac{{R_{r} L_{m} i_{dr} \lambda_{s} }}{{\sigma L_{r} }}} \right)^{2} + 4L_{m} \lambda_{s} i_{qr} \left( {L_{s} \left( {i_{qr} \frac{{dv_{dr} }}{dt} - i_{dr} \frac{{dv_{qr} }}{dt}} \right) + \sigma L_{s} L_{r} \left( {z_{3qr} i_{dr} - z_{3dr} i_{qr} } \right)} \right)} }}{{ - 2L_{m} \lambda_{s} i_{qr} }}} \right) \hfill \\ \end{gathered}$$

(40)

specified as u = N_s/N_r, where N_r and N_s are the number of turns of the rotor and stator windings, respectively. Given that the controller design is similar for the d-axis and q-axis, this design is only expressed for the d-axis. Equations (28) and (29) are used to design the observer, and the control law of FFOADRC is given as:

$$\left\{ \begin{gathered} e_{1dr} = v_{1dr} - z_{1dr} \, \hfill \\ E_{2dr} = k_{1d} .v_{2dr} - k_{2d} .z_{2dr} = k_{1d} .v_{1dr}^{(\alpha )} - k_{2d} .z_{1dr}^{(\alpha )} \hfill \\ v_{dr - 0} = k_{p} fal(e_{1dr} ,\alpha_{1} ,\delta_{1} ) + k_{d} fal(E_{2dr} ,\alpha_{2} ,\delta_{2} ) \hfill \\ \end{gathered} \right.$$

(41)

where α is the fractional-order, $v_{2dr} = v_{1dr}^{(\alpha )}$, and $z_{2dr} = z_{1dr}^{(\alpha )}$. As stated in Sect. 3.2.2.1, k_d and k_p are specified using fuzzy logic. With a feed-forward compensator, the FFOADRC output is:

$$v_{dr} = v_{dr - 0} - \frac{{z_{3dr} }}{{b_{0r} }} = v_{dr - 0} + \left( {\frac{{\sigma^{2} L_{r}^{2} }}{{R_{r} }}} \right)z_{3dr}$$

(42)

The extended state of the system (z_3dr) is estimated by the observer. In the α-β coordinate, the stator fluxes are [86]:

$$\left\{ \begin{gathered} \lambda_{\alpha s} = \int {\left( {v_{\alpha s} - R_{s} i_{\alpha s} } \right)dt} \hfill \\ \lambda_{\beta s} = \int {\left( {v_{\beta s} - R_{s} i_{\beta s} } \right)dt} \hfill \\ \end{gathered} \right.$$

(43)

where v_αs, v_βs, i_αs, and i_βs are the stator voltage/current components in the α-β coordinate. So the flux observer calculates the stator flux amplitude and stator voltage vector angle using:

$$\left\{ \begin{gathered} \lambda_{s} = \sqrt {\lambda_{\alpha s}^{2} + \lambda_{\beta s}^{2} } \hfill \\ \theta_{s} = \tan^{ - 1} \left( {\frac{{\lambda_{\beta s} }}{{\lambda_{\alpha s} }}} \right) \hfill \\ \end{gathered} \right.$$

(44)

According to the SFO and using (9) and (35), the stator reactive power is:

$$Q_{s} = \frac{3}{2}\left( {v_{qs} .\underbrace {{\frac{1}{{L_{s} }}\left( {\lambda_{ds} - L_{m} i_{dr} } \right)}}_{{i_{ds} }} - \underbrace {{v_{ds} }}_{ \cong 0}i_{qs} } \right) = \frac{{3\omega_{s} \lambda_{s} }}{{2L_{s} }}\left( {\lambda_{s} - L_{m} i_{dr} } \right)$$

(45)

Therefore, the d component related to the reference current of the rotor is:

$$i_{dr}^{ref} = \frac{1}{{L_{m} }}\left( {\lambda_{s} - \frac{2}{3}\frac{{L_{s} }}{{\omega_{s} \lambda_{s} }}Q_{s}^{ref} } \right)$$

(46)

From [86] and using SFO, the electromagnetic torque is:

$$T_{em} = \frac{3}{2}p\frac{{L_{m} }}{{L_{s} }}\left( {\underbrace {{\lambda_{qs} }}_{ \cong 0}i_{dr} - \lambda_{ds} i_{qr} } \right) = - \frac{3}{2}p\frac{{L_{m} }}{{L_{s} }}\lambda_{s} i_{qr}$$

(47)

Therefore, the q component related to the reference current of the rotor is:

$$i_{qr}^{ref} = - \frac{2}{3}\frac{{L_{s} }}{{pL_{m} \lambda_{s} }}T_{em}^{ref}$$

(48)

where p is the number of pole pairs.

4.1.1.2 Speed control loop of RSC

The mechanical equation of the DFIG is [81]:

$$J\frac{{d\Omega_{m} }}{dt} = T_{em} - T_{r} - f\Omega_{m}$$

(49)

where J is the inertia of the DFIG, Ω_m is the mechanical speed of the shaft, T_r is the load torque, and f is the friction coefficient. From (49) there is:

$$\frac{{d\Omega_{m} }}{dt} = \frac{1}{J}T_{em} - \left( {\frac{{T_{r} + f\Omega_{m} }}{J}} \right)$$

(50)

The derivative of (50) is:

$$\left\{ \begin{gathered} \frac{{d^{2} \Omega_{m} (t)}}{{dt^{2} }} = b_{ors} u_{rs} (t) + f_{3r} \hfill \\ b_{0rs} = - \frac{f}{{J^{2} }} \hfill \\ \end{gathered} \right.$$

(51)

where u_rs(t) = T_em. f_3r is the total disturbances estimated by the observer and its relation is:

$$f_{3r} = \frac{1}{J}\left( {\frac{{dT_{em} }}{dt} - \frac{{dT_{r} }}{dt}} \right) + \frac{f}{{J^{2} }}\left( {f\Omega_{m} + T_{r} } \right)$$

(52)

4.1.2 GSC vector control

The schematic of the GSC vector control is presented in Fig. 9. From the actual and reference of the DC-link voltage $(V_{bus} , \, V_{bus}^{ref} ),$ the reference active power exchanged with the network $(P_{g}^{ref} )$ is specified using the PI controller. The current control loops are also implemented using FFOADRC.

Fig. 9

Vector control of the GSC using the FFOADRC

4.1.2.1 Current control loops of GSC

The power (active and reactive) exchanged with the network are [86]:

$$\left\{ \begin{gathered} P_{g} = \frac{3}{2}\left( {v_{dg} i_{dg} + v_{qg} i_{qg} } \right) \hfill \\ Q_{g} = \frac{3}{2}\left( {v_{qg} i_{dg} - v_{dg} i_{qg} } \right) \hfill \\ \end{gathered} \right. \,$$

(53)

Given an assumption of network voltage orientation and that this voltage is aligned along the d−axis, there are:

$$\left\{ \begin{gathered} P_{g} = \frac{3}{2}v_{dg} i_{dg} \, \Rightarrow \, i_{dg} = \frac{2}{{3v_{dg} }}P_{g} \hfill \\ Q_{g} = \frac{ - 3}{2}v_{dg} i_{qg} \, \Rightarrow \, i_{qg} = \frac{{ - 2}}{{3v_{dg} }}Q_{g} \, \hfill \\ \end{gathered} \right. \,$$

(54)

In Fig. 9, the filter currents (i_ag, i_bg, i_cg) are converted into the α−β coordinate and are then converted into the d−q frame to be used in FFOADRCs. The network voltage angle (θ_g) is required for conversion between the d−q and α−β frames. This is obtained using a phase−locked loop (PLL). The network voltages in the d−q frame (v_dg, v_qg) were expressed in (11), so the derivatives of the filter currents are obtained as:

$$\left\{ \begin{gathered} \frac{{di_{dg} }}{dt} = - \frac{{R_{f} }}{{L_{f} }}i_{dg} { - }\frac{{1}}{{L_{f} }}v_{dg} + \omega_{{\text{s}}} i_{qg} + \frac{{1}}{{L_{f} }}v_{df} \hfill \\ \frac{{di_{qg} }}{dt} = - \frac{{R_{f} }}{{L_{f} }}i_{qg} - \omega_{{\text{s}}} i_{dg} + \frac{{1}}{{L_{f} }}v_{qf} \hfill \\ \end{gathered} \right. \,$$

(55)

The derivatives of (55) are:

$$\left\{ \begin{gathered} \frac{{d^{2} i_{dg} (t)}}{{dt^{2} }} = b_{og} u_{dg} (t) + f_{3dg} \hfill \\ \frac{{d^{2} i_{qg} (t)}}{{dt^{2} }} = b_{og} u_{qg} (t) + f_{3qg} \hfill \\ b_{0g} = - \frac{{R_{f} }}{{L_{f}^{2} }} \hfill \\ \end{gathered} \right.$$

(56)

where u_dg(t)=v_df(t) and u_qg(t)=v_qf(t) are the control signals of FFOADRCs for controlling the GSC. f_3dg and f_3qg are the total disturbances estimated using NFESOs and their equations are given as:

$$\left\{ \begin{gathered} f_{3dg} = \left( {\frac{{R_{f}^{2} }}{{L_{f}^{2} }} - \omega_{s}^{2} } \right)i_{dg} - \frac{{2R_{f} \omega_{s} }}{{L_{f} }}i_{qg} \hfill \\ \, + \frac{{R_{f} }}{{L_{f}^{2} }}v_{dg} + \frac{{\omega_{s} v_{qf} }}{{L_{f} }} + \frac{1}{{L_{f} }}\left( {\frac{{dv_{df} }}{dt} - \frac{{dv_{dg} }}{dt}} \right) \, \hfill \\ f_{3qg} = \left( {\frac{{R_{f}^{2} }}{{L_{f}^{2} }} - \omega_{s}^{2} } \right)i_{qg} + \frac{{2R_{f} \omega_{s} }}{{L_{f} }}i_{dg} \hfill \\ \, - \frac{{\omega_{s} }}{{L_{f} }}\left( {v_{df} - v_{dg} } \right) + \frac{1}{{L_{f} }}\frac{{dv_{qf} }}{dt} \, \hfill \\ \end{gathered} \right.$$

(57)

Using the third order NFESOs, we have z_3dg=f_3dg and z_3qg=f_3qg.

4.2 RSC and GSC control using the PI controller

In this part, comparison of the PI controller and FFOADRCs, vector control of RSC and GSC is conducted using the PI controller.

4.2.1 Vector control of RSC with speed sensor

The RSC control circuit is presented in Fig. 10 where the current control loops are implemented using the PI controller. From (36), the rotor voltages in the d-q coordinate are:

$$\left\{ \begin{gathered} v_{dr} = R_{r} i_{dr} + \sigma L_{r} \frac{{di_{dr} }}{dt}\underbrace {{ - \omega_{r} \sigma L_{r} i_{qr} }}_{{coupling{\text{ term}}}} \hfill \\ v_{qr} = R_{r} i_{qr} + \sigma L_{r} \frac{{di_{qr} }}{dt}\underbrace {{ + \omega_{r} \sigma L_{r} i_{dr} + \omega_{r} \frac{{L_{m} }}{{L_{s} }}\lambda_{s} }}_{{coupling{\text{ term}}}} \hfill \\ \end{gathered} \right.$$

(58)

Fig. 10

Vector control of the RSC with speed sensor using the PI controller [87]

Figure 10 shows that the mentioned coupling terms are combined with the PI controller outputs to generate reference rotor voltages. The rotor electrical speed (ω_m) is measured using an encoder. In Fig. 10, the transfer function related to the current control loops is [87]:

$$\frac{{i_{dr} (s)}}{{i_{dr}^{ref} (s)}} = \frac{{i_{qr} (s)}}{{i_{qr}^{ref} (s)}} = \frac{{\frac{{k_{pr} s + k_{ir} }}{{\sigma L_{r} }}}}{{s^{2} + (\frac{{k_{pr} + R_{r} }}{{\sigma L_{r} }})s + \frac{{k_{ir} }}{{\sigma L_{r} }}}}$$

(59)

If (59) is written in the form of $\frac{{\frac{{k_{pr} s + k_{ir} }}{{\sigma L_{r} }}}}{{s^{2} + 2\xi_{r} \omega_{nr} s + \omega_{nr}^{2} }}$ while considering $\xi_{r} = 1$, then $k_{pr} = 2\sigma L_{r} \omega_{nr} - R_{r}$ and $k_{ir} = \sigma L_{r} \omega_{nr}^{2}$, where $\xi_{r}$ is the damping coefficient and $\omega_{nr}$ is the natural frequency of the mentioned loops. In this condition, both poles are placed at $- \omega_{nr}$ and the control system is stable.

4.2.2 GSC control

The GSC control circuit is presented in Fig. 11. From (11) and under the condition of network voltage orientation, the output voltages of GSC are:

$$\left\{ \begin{gathered} v_{df} = R_{f} i_{dg} + L_{f} \frac{{di_{dg} }}{dt} + \underbrace {{v_{dg} { - }\omega_{{\text{s}}} L_{f} i_{qg} }}_{{coupling{\text{ term}}}} \hfill \\ v_{qf} = R_{f} i_{qg} + L_{f} \frac{{di_{qg} }}{dt} + \underbrace {{\omega_{{\text{s}}} L_{f} i_{dg} }}_{{coupling{\text{ term}}}} \hfill \\ \end{gathered} \right. \,$$

(60)

Fig. 11

Vector control of the GSC using the PI controller [88]

As shown in Fig. 11, the mentioned coupling terms are combined with the PI controller outputs to generate reference voltages of the GSC output. Next, the voltages associated with the output of GSC are generated using sequential conversions, which are used in the PWM modulator to generate switching signals. In Fig. 11, the transfer function related to the current control loops is [88]:

$$\frac{{i_{dg} (s)}}{{i_{dg}^{ref} (s)}} = \frac{{i_{qg} (s)}}{{i_{qg}^{ref} (s)}} = \frac{{\frac{{k_{pg} s + k_{ig} }}{{L_{f} }}}}{{s^{2} + (\frac{{k_{pg} + R_{f} }}{{L_{f} }})s + \frac{{k_{ig} }}{{L_{f} }}}}$$

(61)

By equating (61) in the form of $\frac{{\frac{{k_{pg} s + k_{ig} }}{{L_{f} }}}}{{s^{2} + 2\xi_{g} \omega_{ng} s + \omega_{ng}^{2} }}$ and considering $\xi_{g} = 1$, $k_{pg} = 2L_{f} \omega_{ng} - R_{f}$ and $k_{ig} = L_{f} \omega_{ng}^{2}$, where $\xi_{g}$ is the damping coefficient and $\omega_{ng}$ is the natural frequency of the mentioned loops. In this condition, both poles are placed at $- \omega_{ng}$ and the control system is stable.

5 Simulation analysis

In this section, the effect of using different fal functions in conventional ADRC is examined first. Then the DFIG-based wind turbine is simulated in MATLAB/Simulink, in which the RSC and GSC are controlled separately using a PI controller, conventional ADRC, and FFOADRCs with different fal functions (default fal, fal_arcsinh, fal_arctan, and fal_tanh). The performance of these controllers during disturbances such as voltage sag and voltage swell is examined and compared. The parameters of the simulated system are presented in Table 3.

Table 3 Parameters of the simulated system

5.1 The effect of different fal functions

For α = 0.5 and δ = 0.05, the mentioned fal functions are plotted in Fig. 12. It can be seen that the functions fal_arcsinh, fal_arctan, and fal_tanh are very close to each other at the origin. Therefore, in the steady state where the error (e) tends to zero, the three functions will have the same results, while the differences in their performance are in transient states and under disturbance conditions. Since the values of the functions fal_arcsinh, fal_arctan, and fal_tanh increase (or decrease) with a larger slope than the default fal function near the origin, it is expected that these three functions perform better than the default fal function.

Fig. 12

Curves of the default fal (red), fal_arcsinh (black), fal_arctan (blue), and fal_tanh (pink)

To compare the behavior of a conventional ADRC using different fal functions, a 2nd order system is considered, whose transfer function is $\frac{10}{{s^{2} + 3s + 1}}$. The ADRC is implemented according to (17). The input applied to the system is a square wave, with amplitude of one and frequency of 1 Hz. A strong positive disturbance, a strong negative disturbance, and a weak positive disturbance are applied to the system at 0.75 s, 1.25 s, and 1.55 s, respectively. These disturbances are in the form of step functions, and the simulation results are presented in Fig. 13.

Fig. 13

Input square wave (black) and the outputs of the system based on the different fal functions (default fal: blue, fal_arcsinh: red, fal_arctan: green, and fal_tanh: purple)

It can be seen from Fig. 13 that at 0.75 s and 1.25 s, the overshoot and undershoot values are around 72% when using the default fal, but with fal_arcsinh, fal_arctan, and fal_tanh, they are almost 0%, indicating that the system is very robust to step disturbance. Similarly, at 1.55 s when a weak step disturbance is applied to the system, the overshoot rate is about 0.5% for the default fal, while the rate is 0% using fal_arcsinh, fal_arctan, and fal_tanh. At 0.5 s, if the default fal and fal_arcsinh are used, the system reaches the steady-state as critical damping, with the overshoot rates of 5% and 0.5%, respectively. This value becomes almost zero when fal_arctan and fal_tanh are used (critical damping), so the settling time in these two cases is less than the others. The simulation results are similar at 1 s and 1.5 s. The summary of the results with different fal functions in conventional ADRC is presented in Table 4.

Table 4 Comparison of the different fal functions used in the conventional ADRC

5.2 Voltage sag/swell

During an abrupt voltage sag, the stator flux reaches its final steady state more slowly than the stator voltage. Since the phases of rotor current and stator flux are opposite to each other, this leads to a faster reduction of flux. During an abrupt decrease of stator voltage, this variation should be accompanied by an abrupt change in rotor voltage to prevent a sharp increment in rotor current. Because of the slow decrease of stator flux, the rotor voltage becomes greater than its value in the steady-state. Thus, the range of rotor voltage should be higher, especially at the start of the voltage sag, so that rotor current control is not lost and this current is kept within an allowable range. Because the back-to-back converters are not able to handle the high rotor voltage, the circuit thus becomes uncontrollable. To solve this problem, the crowbar is used here. The behavior of the DFIG during voltage sag is investigated using a crowbar in [89]. Here a circuit breaker involving a diode, a resistance, and a switch is used. When this protection is activated, the resistance is located in the terminals of the rotor.

Voltage swell is an anomaly in the grid and usually occurs when the reactive power exceeds the requirements of a power system. Overvoltage due to the sudden removal of large loads, asymmetric faults in the network, and the entry of a capacitive bank into the grid can damage the power electronic converters used in a DFIG. At the moment of overvoltage, a large electromagnetic force due to the transient leakage flux of the stator is induced in the DFIG rotor. As a result, it will create an overcurrent in the rotor. It is noted that after increasing the network voltage, the voltages of the stator and rotor increase, and their currents decrease. Also, the electromagnetic torque increases with decreasing rotor velocity. As expected, stator and rotor fluxes increase when the overvoltage occurs. According to the Australian network codes [21], a DFIG should withstand up to 1.3 times the nominal voltage without losing synchronism.

In this paper, using the mentioned controllers, the effects of symmetrical and asymmetrical voltage sag/swell on the DFIG are investigated separately.

5.2.1 Implementation of symmetrical voltage sag

In this section, symmetrical voltage sag is implemented according to the Spanish network code [21]. The voltage sag happens at 7 s, and the voltage reaches 20% of its initial amount. Within 7.5 to 8 s, the network voltage ramps up and reaches 80% of its initial value (Fig. 14). During the simulation, the wind speed is assumed to be constant at 8.5 m/s. The protection is enabled in the time range of 7 s to 7.1 s, and during this time, the RSC is out of the circuit so as not to be damaged. As soon as the protection is enabled, the flux of the stator is reduced by the resistance. To investigate the effect of the crowbar resistance on system performance, a detailed study has been performed [89], which shows that the resistance value affects the peak of the electromagnetic torque and the fault current passing through it.

Fig. 14

Network voltage during symmetrical voltage sag (Spanish network code)

In the RSC controller circuit, $i_{dr}^{ref}$ goes from zero to its nominal value at 7.15 s. Thus according to (45), Q_s is the negative and reactive power injected into the network through the stator. Since the total network requirements are met by $i_{dr}^{ref}$ in the period between 7.15 and 8 s, $i_{qr}^{ref}$ must be zero during this period. Therefore, according to (47), T_em will also be zero during this period, while at other times, torque is controlled by the MPPT algorithm. When the crowbar is activated (7 s to 7.1 s), all the machine's energy is lost in the crowbar resistance and the GSC, and remains in the circuit to keep the DC-link voltage constant. So in the time interval between 7.15 s and 8 s, $i_{qr}^{ref}$ is zero but at other times this current is controlled by the MPPT algorithm. Meanwhile, $i_{dr}^{ref}$ changes from the nominal value to zero at 8 s.

After the network voltage returns to the steady-state (t > 8 s), the stator flux also retrieves the nominal value so that magnetization is carried out correctly once more and the DFIG operates normally. The stator fluxes during symmetrical voltage sag for R_crowbar = 0.01 Ω using different controllers are shown in Fig. 15. It can be seen that during voltage sag and using the PI controller (Fig. 15a), the fluctuation amplitude of stator flux is significant, and even after the voltage returns to the new value (t > 8 s), the amplitude is still high so that the flux reaches the steady-state value over a long period. The comparison of Fig. 15b and c shows the superiority of FFOADRC over conventional ADRC. Also, the use of FFOADRCs with trigonometric and hyperbolic functions (Fig. 15d–f) leads to the lowest fluctuation of stator flux during voltage sag (7 s < t < 8 s) and after return to steady-state (t > 8 s). The d and q components of the stator flux are presented in Fig. 16. It is seen that during the voltage sag and its recovery time (7 s < t < 8 s), using the PI controller (Fig. 16a), the flux has the highest fluctuations. The use of conventional ADRC reduces the fluctuations slightly (Fig. 16b), while Fig. 16c clearly shows the superiority of FFOADRC over conventional ADRC in reducing the fluctuations. In addition, using trigonometric and hyperbolic functions in FFOADRC results in the smallest fluctuations (Fig. 16d–f).

Fig. 15

Stator flux during symmetrical voltage sag for R_crowbar = 0.01 Ω: (a) PI controller [89, 90], (b) Conventional ADRC with default-fal [45, 79], (c) FFOADRC with default-fal, (d) FFOADRC with fal-arcsinh, (e) FFOADRC with fal-arctan, and (f) FFOADRC with fal-tanh

Fig. 16

The d and q components of the stator flux during symmetrical voltage sag for R_crowbar = 0.01 Ω: (a) PI controller [89, 90], (b) Conventional ADRC with default-fal [45, 79], (c) FFOADRC with default-fal, (d) FFOADRC with fal-arcsinh, (e) FFOADRC with fal-arctan, and (f) FFOADRC with fal-tanh

The stator fluxes during the symmetrical voltage sag for R_crowbar = 0.8 Ω are presented in Figs. 17 and 18. It is seen that with the increase of the crowbar resistance, the performance of the PI controller, conventional ADRC, and FFOADRC with default fal function (Figs. 17a–c, 18a–c) become worse. In this situation, the performances of FFOADRC with trigonometric and hyperbolic functions (Figs. 17d–f, 18d–f) do not change much, which also indicates their superiority. From Figs. 15, 16, 17 and 18, it can be seen that by choosing the appropriate resistance of the crowbar circuit [89] and using the FFOADRC with trigonometric and hyperbolic functions, it is possible to reduce the fluctuations and peak values of the DFIG parameters such as flux, torque, current, etc.

Fig. 17

Stator flux during symmetrical voltage sag for R_crowbar = 0.8 Ω: (a) PI controller [89, 90], (b) Conventional ADRC with default-fal [45, 79], (c) FFOADRC with default-fal, (d) FFOADRC with fal-arcsinh, (e) FFOADRC with fal-arctan, and (f) FFOADRC with fal-tanh

Fig. 18

The d and q components of the stator flux during symmetrical voltage sag for R_crowbar = 0.8 Ω: (a) PI controller [89, 90], (b) Conventional ADRC with default-fal [45, 79], (c) FFOADRC with default-fal, (d) FFOADRC with fal-arcsinh, (e) FFOADRC with fal-arctan, and (f) FFOADRC with fal-tanh

The DFIG speeds using different controllers are shown in Fig. 19a. It is seen that the decrease in network voltage leads to an almost linear increase in speed. This is because, during the voltage sag, the energy transmitted to the grid is reduced, while the energy captured by the turbine remains constant, leading to an increase in turbine speed. After fault clearance and voltage recovery, the rotor speed returns to the new value and all the parameters, such as speed, are controlled by the MPPT algorithm.

Fig. 19

a DFIG speed during symmetrical voltage sag; b zoom of a

It is seen from Fig. 19b that at full voltage recovery (t = 8 s), using the PI controller and conventional ADRC with default fal, the DFIG velocity starts to decrease abruptly. This sudden change in the velocity, accompanied by a sudden change in DFIG acceleration, can cause damage to the shaft and other related equipment (acceleration is positive and negative at t < 8 s and t > 8 s, respectively). In contrast, using FFOADRCs with different fal functions, the velocity changes smoothly and there is no problem with the stress on the DFIG. Also, after full voltage recovery, using different kinds of ADRC compared to the PI controller, the DFIG speed reaches a stable value faster. Figure 19b shows that during the voltage sag, with the simultaneous use of FFOADRC and trigonometric and hyperbolic functions, the velocity variations are lower.

The voltages of the DC-link at the time of the voltage sag using different controllers are represented in Fig. 20. It can be seen that when the voltage sag appears and disappears (t = 7 s and t = 8 s), the DC-link voltages change suddenly, and during the fault (7 s to 8 s), the DC voltages fluctuate around the reference value. The range of these variations is within a narrow band, and is due to extra energy fed into the converters (energy imbalance between inputs and outputs of the converters) and the rapid response of the regulators that control the GSC. In the period of voltage sag (7 s < t < 8 s) and using the PI controller (Fig. 20a), the DC voltage has high-frequency oscillations. However, using conventional ADRC and different FFOADRCs (Figs. 20b–f), there are no high-frequency oscillations which show their superiority over the PI controller. Also, before and after the voltage sag (t < 7 s and t > 8 s), using fal_arctan (Fig. 20e) results in the lowest range of voltage fluctuations.

Fig. 20

DC bus voltage of the DFIG during symmetrical voltage sag: (a) PI controller [89, 90], (b) Conventional ADRC with default-fal [45, 79], (c) FFOADRC with default-fal, (d) FFOADRC with fal-arcsinh, (e) FFOADRC with fal-arctan, and (f) FFOADRC with fal-tanh

The rotor and stator currents are shown in Figs. 21 and 22, respectively. As shown, the fal_arcsinh function is selected as the candidate to check the effect of the crowbar resistance variations, with the values of 0.01 Ω, 0.2 Ω, 0.4 Ω, and 0.6 Ω being considered. As expected, at the moment of fault occurrence (t = 7 s), the peak values of the rotor and stator currents decrease with the increase of crowbar resistance. In addition, it is seen that after the removal of the crowbar resistance from the circuit and during the times of voltage sag and its recovery (7.1 s < t < 8 s), FFOADRC with the fal_arcsinh function properly controls the rotor and stator currents with no significant distortion. Using the fal_arctan and fal_tanh functions in the FFOADRC also provide similar results. Therefore, using trigonometric and hyperbolic functions in FFOADRC and changing the value of the crowbar resistance [89], the peak values of the rotor and stator currents are controllable at the moment of fault occurrence.

Fig. 21

Rotor current of the DFIG during symmetrical voltage sag for different values of R_crowbar. (a) R_crowbar = 0.01 ohm, (b) R_crowbar = 0.2 ohm, (c) R_crowbar = 0.4 ohm, and (d) R_crowbar = 0.6 ohm

Fig. 22

Stator current of the DFIG during symmetrical voltage sag for different values of R_crowbar. (a) R_crowbar = 0.01 ohm, (b) R_crowbar = 0.2 ohm, (c) R_crowbar = 0.4 ohm, and (d) R_crowbar = 0.6 ohm

The rotor voltage during voltage sag and its recovery is presented in Fig. 23. As previously stated in Sect. 5.2, during a sudden decrease in the stator voltage, the rotor voltage must also change quickly to avoid a sharp increase in the rotor current. In this condition, because of the slow reduction of the stator flux, the rotor voltage becomes larger than its steady-state value. The electromagnetic torque during the fault is shown in Fig. 24. According to (47), and because iqr is zero, the torque is zero, while at other times, it is controlled by the MPPT algorithm.

Fig. 23

Rotor voltage of the DFIG during symmetrical voltage sag

Fig. 24

Electromagnetic torque of the DFIG during symmetrical voltage sag

5.2.2 Implementation of the symmetrical voltage swell

In this section, the symmetrical voltage swell is implemented according to the Australian network code [21]. The voltage swell happens at 7 s, and the voltage reaches 130% of its initial value. In the period from 7.5 to 8.44 s, the network voltage ramps down (Fig. 25). During the simulation, the wind speed is assumed to be constant at 8.5 m/s. After the network voltage returns to 110% of its initial value (t > 8.44 s), the stator flux also retrieves the new value so that the DFIG operates normally.

Fig. 25

Network voltage during symmetrical voltage swell (Australian network code)

The stator fluxes during voltage swell using the PI controller and different ADRCs are shown in Fig. 26. It can be seen that by using the PI controller (Fig. 26a), the amplitude of fluctuations is more significant. After the voltage returns to the new value, large fluctuations still exist and the flux takes a long time to reach the steady-state. Comparing Fig. 26a and b, it shows that the use of conventional ADRC reduces the amplitude of fluctuations during the voltage swell (7 s < t < 7.5 s) and recovery time (7.5 s < t < 8.44 s). According to Fig. 26b and c, using fractional-order functions and fuzzy logic, reduces the amplitude of fluctuations at recovery time. Using trigonometric and hyperbolic functions in FFOADRC (Fig. 26d–f) improves the controller performance so that the amplitude of fluctuations is significantly reduced throughout the simulation time. The d and q components of the stator flux are presented in Fig. 27. It is seen that during the voltage swell and its recovery time (7 s < t < 8.44 s), with the PI controller (Fig. 27a), the flux has the highest fluctuations. Using conventional ADRC reduces these fluctuations slightly (Fig. 27b), while the superiority of FFOADRC over conventional ADRC in reducing the range of fluctuations is evident from Fig. 27b, c. In addition, using trigonometric and hyperbolic functions in FFOADRC results in the smallest fluctuations (Fig. 27d–f).

Fig. 26

Stator flux of the DFIG during symmetrical voltage swell: (a) PI controller [89, 90], (b) Conventional ADRC with default-fal [45, 79], (c) FFOADRC with default-fal, (d) FFOADRC with fal-arcsinh, (e) FFOADRC with fal-arctan, and (f) FFOADRC with fal-tanh

Fig. 27

The d and q components of the stator flux during symmetrical voltage swell: (a) PI controller [89, 90], (b) Conventional ADRC with default-fal [45, 79], (c) FFOADRC with default-fal, (d) FFOADRC with fal-arcsinh, (e) FFOADRC with fal-arctan, and (f) FFOADRC with fal-tanh

The rotor and stator currents, and electromagnetic torque are shown in Figs. 28, 29, and 30, respectively. The fal_arcsinh function is selected as the candidate to check the effect of the crowbar resistance variations on system performance, with the values of 0.01 Ω, 0.2 Ω, 0.4 Ω, and 0.6 Ω being considered. From Figs. 28, 29, and 30, it is seen that when crowbar protection is activated (t = 7 s), the peak values of the waveforms decrease with the increase of the crowbar resistance. After deactivating crowbar protection and during the fault (7.1 s < t < 8.44 s), using FFOADRC with the fal_arcsinh function properly controls the electromagnetic torque and the currents with no significant distortion. Using the fal_arctan and fal_tanh functions in FFOADRC provides similar results. Therefore, using trigonometric and hyperbolic functions in FFOADRC, and changing the value of the crowbar resistance [89], the peak values of the waveforms are controllable at the moment of fault occurrence.

Fig. 28

Rotor current of the DFIG during symmetrical voltage swell for different values of R_crowbar . (a) R_crowbar = 0.01 ohm, (b) R_crowbar = 0.2 ohm, (c) R_crowbar = 0.4 ohm, and (d) R_crowbar = 0.6 ohm

Fig. 29

Stator current of the DFIG during symmetrical voltage swell for different values of R_crowbar. (a) R_crowbar = 0.01 ohm, (b) R_crowbar = 0.2 ohm, (c) R_crowbar = 0.4 ohm, and (d) R_crowbar = 0.6 ohm

Fig. 30

Electromagnetic torque of the DFIG during symmetrical voltage swell for different values of R_crowbar. (a) R_crowbar = 0.01 ohm, (b) R_crowbar = 0.2 ohm, (c) R_crowbar = 0.4 ohm, and (d) R_crowbar = 0.6 ohm

The harmonic spectra of the stator current using the PI controller and different kinds of ADRC are presented in Fig. 31. The harmonic contents are considered for ten cycles with a starting time of 11 s. The THDs of the stator currents are shown in Table 5. It is seen that the PI controller leads to the highest THD (Fig. 31a), conventional ADRC (Fig. 31b) reduces the THD, while simultaneous use of fractional-order functions and fuzzy logic (Fig. 31c) also reduces the THD, which demonstrates the superiority of FFOADRC over conventional ADRC. In addition, the trigonometric and hyperbolic functions in FFOADRC (Fig. 31d–f) result in the lowest THD.

Fig. 31

Harmonic spectrum of the stator current using different controllers: (a) PI controller [89, 90], (b) Conventional ADRC with default-fal [45, 79], (c) FFOADRC with default-fal, (d) FFOADRC with fal-arcsinh, (e) FFOADRC with fal-arctan, and (f) FFOADRC with fal-tanh

Table 5 THD% of the stator current using different controllers

5.2.3 Implementation of the asymmetrical voltage sag

Asymmetrical voltage sag can be caused by single-phase-to-ground fault, phase-to-phase-to-ground fault, and phase-to-phase fault. In this section, it is assumed that a phase-to-phase fault occurs. The voltage applied to the DFIG through the stator and GSC is in accordance with Fig. 32, where the voltage of phase a is normal while in phases b and c, both amplitudes are reduced and there are phase shifts compared to the normal state. The asymmetrical voltage sag starts at 7 s and ends at 7.5 s. In this situation, to work with positive and negative sequences of voltage and current, current control loops related to the mentioned sequences are used. The simulation results are shown in Figs. 33, 34 and 35. In these conditions, because of voltage asymmetry and stator flux fluctuation, the torque, rotor current, and stator current fluctuate. To investigate the effect of using trigonometric and hyperbolic functions in FFOADRC, the fal_arcsinh function is selected to check the impact of crowbar resistance variations on the waveforms throughout the fault time, with the values of 0.01 Ω, 0.2 Ω, 0.4 Ω, and 0.6 Ω being considered. The crowbar resistance enters the circuit at 7 s to protect the RSC, and is removed from the circuit at 7.1 s. From Figs. 33, 34 and 35, it is seen that at the moment of fault occurrence (t = 7 s), the peak values of the electromagnetic torque, rotor current, and stator current decrease with the increase of crowbar resistance. After removing the crowbar resistance from the circuit and during the voltage sag (7.1 s < t < 7.5 s), FFOADRC with the fal_arsinh function properly controls the torque and currents with no significant distortion. Therefore, the performance of the control circuit is improved throughout the fault time. Using the fal_arctan and fal_tanh functions in the FFOADRC provides similar results.

Fig. 32

Unbalance caused by phase-to-phase fault; a three-phase voltages and b phasor diagram

Fig. 33

Rotor current of the DFIG during asymmetrical voltage sag for different values of R_crowbar. (a) R_crowbar = 0.01 ohm, (b) R_crowbar = 0.2 ohm, (c) R_crowbar = 0.4 ohm, and (d) R_crowbar = 0.6 ohm

Fig. 34

Stator current of the DFIG during asymmetrical voltage sag for different values of R_crowbar. (a) R_crowbar = 0.01 ohm, (b) R_crowbar = 0.2 ohm, (c) R_crowbar = 0.4 ohm, and (d) R_crowbar = 0.6 ohm

Fig. 35

Electromagnetic torque of the DFIG during asymmetrical voltage sag for different values of R_crowbar. (a) R_crowbar = 0.01 ohm, (b) R_crowbar = 0.2 ohm, (c) R_crowbar = 0.4 ohm, and (d) R_crowbar = 0.6 ohm

6 Stability analysis

As shown in Fig. 8, the structures of the d-axis and q-axis current controllers are the same. Hence only the stability of the d-axis controller is expressed. There are many parameters of ADRC that need to be regulated. Therefore linear ADRC is suggested since it offers better performance than nonlinear ADRC [90]. As previously mentioned, if FFOADRC is used to control a 2nd order linear fractional plant, $y^{(2\alpha )} \approx u_{0}$. So from (41), there is:

$$\begin{aligned} i_{dr}^{(2\alpha )} & \approx v_{dr - 0} = k_{p} e_{1dr} + k_{d} E_{2dr} \\ & = k_{p} (v_{1dr} - z_{1dr} ) + k_{d} (k_{1d} .v_{1dr}^{(\alpha )} - k_{2d} .z_{1dr}^{(\alpha )} ) \\ & \approx k_{p} (i_{dr}^{ref} - i_{dr} ) + k_{d} (k_{1d} .i_{dr}^{ref(\alpha )} - k_{2d} .i_{dr}^{(\alpha )} ) \\ \end{aligned}$$

(62)

Using the Laplace transform, the transfer function for the RSC control circuit while using FFOADRC is as follows, and the corresponding equivalent circuit is presented in Fig. 36.

$$\frac{{i_{dr} (s)}}{{i_{dr}^{ref} (s)}} = \frac{{k_{d} k_{1d} s^{(\alpha )} + k_{p} }}{{s^{(2\alpha )} + k_{d} k_{2d} s^{(\alpha )} + k_{p} }}$$

(63)

Fig. 36

Equivalent circuit of the RSC control circuit using FFOADRC

In (63), if k_p and k_d are respectively selected as $\omega_{c}^{2}$ and 2ω_c (ω_c is the controller bandwidth), then the denominator roots of the transfer function for all positive k_2d are placed in the left half plane. So the plant will be stable. In order to analyze the stability, the effect of coefficients ω_c, α, k_1d and k_2d are considered separately. For this, step response and the concepts of phase margin (PM) and gain margin (GM) are used. For the system shown in Fig. 36, PM and GM are given in (64) and (65), respectively.

$${\text{PM}} = \left( {{\text{tan}}^{{ - 1}} \left( {\frac{{k_{d} k_{1d} \omega^{\alpha } .\sin \frac{\alpha \pi }{2}}}{{k_{p} + k_{d} k_{1d} \omega^{\alpha } .\cos \frac{\alpha \pi }{2}}}} \right) - {\text{tan}}^{{ - 1}} \left( {\frac{{\omega^{\alpha } .\sin \frac{\alpha \pi }{2}}}{{k_{d} (k_{2d} - k_{1d} ) + \omega^{\alpha } .\cos \frac{\alpha \pi }{2}}}} \right) + \left( {1 - \frac{\alpha }{2}} \right)\pi } \right)_{{\frac{{\sqrt {\left( {k_{p} + k_{d} k_{1d} \omega^{\alpha } .\cos \frac{\alpha \pi }{2}} \right)^{2} + \left( {k_{d} k_{1d} \omega^{\alpha } .\sin \frac{\alpha \pi }{2}} \right)^{2} } }}{{\omega^{\alpha } .\sqrt {\left( {k_{d} (k_{2d} - k_{1d} ) + \omega^{\alpha } .\cos \frac{\alpha \pi }{2}} \right)^{2} + \left( {\omega^{\alpha } .\sin \frac{\alpha \pi }{2}} \right)^{2} } }} = 1}}$$

(64)

$${\text{GM(dB)}} = \left( {{ - 20} \times {\text{log }}\left( {\frac{{\sqrt {\left( {k_{p} + k_{d} k_{1d} \omega^{\alpha } .\cos \frac{\alpha \pi }{2}} \right)^{2} + \left( {k_{d} k_{1d} \omega^{\alpha } .\sin \frac{\alpha \pi }{2}} \right)^{2} } }}{{\omega^{\alpha } .\sqrt {\left( {k_{d} (k_{2d} - k_{1d} ) + \omega^{\alpha } .\cos \frac{\alpha \pi }{2}} \right)^{2} + \left( {\omega^{\alpha } .\sin \frac{\alpha \pi }{2}} \right)^{2} } }}} \right)} \right)_{{{\text{tan}}^{{ - 1}} \left( {\frac{{k_{d} k_{1d} \omega^{\alpha } .\sin \frac{\alpha \pi }{2}}}{{k_{p} + k_{d} k_{1d} \omega^{\alpha } .\cos \frac{\alpha \pi }{2}}}} \right) - \frac{\alpha \pi }{2} - {\text{tan}}^{{ - 1}} \left( {\frac{{\omega^{\alpha } .\sin \frac{\alpha \pi }{2}}}{{k_{d} (k_{2d} - k_{1d} ) + \omega^{\alpha } .\cos \frac{\alpha \pi }{2}}}} \right) = - \pi }}$$

(65)

6.1 The role of the k _1d and k _2d in sustainability

In conventional ADRC, k_1d = k_2d = 1. In this part, by choosing k_2d = 1, α = 0.7, ω_c = 10, and for different k_1d, the system's step response and its evaluation parameters are presented in Fig. 37 and Table 6, respectively. It can be seen that for k_1d > 1, the overshoot and settling time increase, which is not desirable, though the rise time is reduced, which is favorable. In addition, the GM is negative which indicates an instability in the system, while the PM is reduced.

Fig. 37

Step response of the RSC control circuit using FFOADRC (for k_2d = 1, α = 0.7, ω_c = 10, and different k_1d)

Table 6 GM and PM of the RSC control circuit using FFOADRC (for k_2d = 1, α = 0.7, ω_c = 10, and different k_1d)

As k_1d < 1, the settling and rise times increasing indicates that the system is being slowed down, which is undesirable. In this case, increasing the PM indicates that the system becomes more stable.

Similarly, by choosing k_1d = 1, α = 0.7, ω_c = 10, and for different k_2d, the step responses are drawn in Fig. 38, and the results are shown in Table 7. It is seen that if k_2d < 1, the negative GM will lead to system instability. In addition, increasing k_2d to a value of more than one (k_2d > 1) leads to an increase in the PM, making the system more stable. This increase slows down the system and the system does not enter the unstable zone (If PM is greater than 180 degrees, then the system will be unstable).

Fig. 38

Step response of the RSC control circuit using FFOADRC (for k_1d = 1, α = 0.7, ω_c = 10, and different k_2d)

Table 7 GM and PM of the RSC control circuit using FFOADRC (for k_1d = 1, α = 0.7, ω_c = 10, and different k_2d)

With the given explanations, it is seen that if k_2d > k_1d, then the closed-loop system of the DFIG rotor with FFOADRC is always stable. Otherwise, the mentioned system becomes unstable and needs another controller to return to stable conditions.

6.2 The role of the α in sustainability

In this part, by choosing k_2d = 1.1, ω_c = 10, k_1d = 1, and for different α, the step responses are drawn in Fig. 39, and the results are presented in Table 8.

Fig. 39

Step response of the RSC control circuit using FFOADRC (for k_2d = 1.1, ω_c = 10, k_1d = 1, and different α)

Table 8 GM and PM of the RSC control circuit using FFOADRC (for k_2d = 1.1, ω_c = 10, k_1d = 1, and different α)

As α > 1, the transient time of the process ends later. Therefore, the tracking accuracy is reduced, and at the same time, the overshoot is increased. This has an adverse effect on dynamic performance. In this case, the PM is reduced which also has an adverse impact on system stability. For α = 1.8, the system becomes one of sinusoidal damping, and PM is less than 30 degrees which is not desirable (the suitable PM for stability is over 30 degrees).

As α < 1, the system becomes over damped, and the response speed increases. This improves the dynamic performance, but high-frequency noise may be amplified. In addition, the PM is increased. Therefore, the system becomes more stable. The reduction of α should be such that the PM does not enter the unstable zone (PM > 180 degrees).

6.3 The role of the ω _c in sustainability

In this part, by choosing k_2d=1.1, k_1d=1, α=0.9, and for different ω_c, the step responses are presented in Fig. 40. It can be seen that increasing ω_c reduces the settling and rise times. This improves the dynamic performance but high−frequency noise may be problematic. Therefore, the proper selection of k_p and k_d is an essential factor in maintaining system stability. These coefficients were determined by fuzzy logic.

Fig. 40

Step response of the RSC control circuit using FFOADRC (for k_2d = 1.1, k_1d = 1, α = 0.9, and different ω_c)

7 Conclusions

A DFIG is sensitive to disturbances such as network voltage sag/swell. To overcome this and improve FRT capability, various control techniques are presented, and their advantages and disadvantages are reviewed in this paper. The results show that conventional ADRC is robust against disturbances in operational conditions and improves the efficiency of WECS.

A modified ADRC is introduced in this paper to enhance the FRT capability of a DFIG-based wind turbine. With this new ADRC, to achieve continuity and the derivability of the new fal function at all points, arcsinh, arctan, and tanh functions are considered as candidates. These functions are similar to the default fal function and all are odd functions (odd trigonometric and hyperbolic functions). Fractional-order functions and fuzzy logic are used to achieve better results and increase controllability. DFIG vector control is performed separately using a PI controller, conventional ADRC, and modified ADRC. From the simulations in the case of simultaneous use of fractional-order functions, fuzzy logic, trigonometric and hyperbolic functions in ADRC, the following results are obtained in comparison with the PI controller and conventional ADRC: (1) smaller fluctuations in stator flux amplitude during voltage sag/swell and recovery time; (2) reduced variations in velocity and DC-link voltage during voltage sag; and (3) lower THD of stator current during voltage swell. Therefore, the superiority of the modified ADRC over PI controller and conventional ADRC is confirmed.

For the future, we intend to examine: (1) Other protection circuits such as ESS, SDBR, SGSC, crowbar with series R-L, crowbar with SBR. Also a crowbar with DC-link chopper will be used with the modified ADRC to investigate the improvement of FRT capability. (2) The modified ADRC will be used to control a DFIG during other disturbances such as frequency deviations and different types of phase voltage imbalances. Simulation and laboratory results will be analyzed and compared with other controllers such as predictive control, sliding mode control, and backstepping control.