1 Introduction

The microgrid is considered a promising self-sufficient energy system to incorporate renewable energy sources (RES) into the main grid. It is defined as a small cluster of distributed generators (DGs) and energy storage systems (ESS). These can operate in grid-connected or isolated modes [1]. Energy management is usually designed for microgrid operation to improve energy efficiency and minimize the operational cost [2]. From the view of microgrid control and operation, energy management can be considered as the high-level (tertiary) control in the hierarchical microgrid control architecture [3]. The objectives of energy management are to decide the amount of electricity buying (selling) from (to) the main grid and dispatch the available energy resources in a microgrid (e.g., ESS, DGs). In an energy management strategy, the energy storage system plays a key role in compensating for power mismatch. Many kinds of storage devices can be used as an ESS in a microgrid, such as supercapacitors, batteries, and fuel cells. Power density and energy density are the two main metrics for selecting the proper devices. With the increase of RES penetration level in the microgrid, intermittency, uncertainty, and non-dispatchability of RES make it challenging to maintain the supply–demand balance. To address the instantaneous fluctuations of RES and meet different operational requirements, hybrid ESS (HESS), consisting of various types of storage devices (typically battery and supercapacitor), inherits advantages of each type, and therefore can be deployed as an effective infrastructure to support microgrid operation. Different types of energy storage devices have different characteristics. For instance, a battery usually has a high energy density but low power density, while, in contrast, a supercapacitor has a low energy density but high power density. To fully exploit the HESS, the different types of devices should be optimally coordinated so that the operational cost is reduced.

In previous studies, many algorithms have been proposed for HESS-based microgrid operation. These can be generally categorized into rule-based and optimization-based approaches [4]. Rule-based methods [5,6,7] are based on experience and empirical evidence, and are widely used for real-time operation because of their simplicity. However, rule-based methods are limited by the short-vision and may not accurately reflect the actual conditions of ESS in the long run. Optimization-based approaches employ advanced optimization theory and can be classified into global (off-line) optimization [8,9,10,11,12] and real-time (on-line) optimization [13,14,15]. Nevertheless, optimization-based algorithms are complex and usually cause heavy computational burden in online applications [4]. In addition, the uncertainties from RES affect the effectiveness of optimization methods. For example, stochastic optimization suffers from heavy computational burden, and usually requires the probability distributions of RES that are difficult to obtain, while robust optimization has to make the trade-off between economy and conservatism.

Recently, there has been increased interest in using deep reinforcement learning (DRL) to make real-time, sequential, and reliable decisions with the existence of uncertainty. Reference [16] proposes an energy management approach for real-time scheduling of microgrids considering the uncertainty of demand, RES, and electricity price, while [17] establishes a DRL-based energy management strategy in the energy internet. An intelligent multi-microgrid energy management method based on deep learning and model-free reinforcement learning (RL) is introduced in [18]. However, existing works on DRL-based energy management only focus on long or short-term economic dispatch of ESS operation under different conditions without considering the coordination of different types of storage devices. In addition, previous studies mostly adopt the single-stage dispatch model. However, simply implementing a DRL agent in the system may lead to unexpected decisions. In addition, entirely depending on a DRL agent to make decisions lacks reliability in practical operation, and interpretability is usually unsatisfactory.

To address the highlighted problems, this paper proposes the use of a two-stage coordinated approach to guide a DRL agent so that it can select actions within a proper range to improve the reliability of decisions. A DRL-based multi-timescale coordinated operation method for microgrids with HESS is developed. The microgrid has two types of ESS, i.e., battery with high energy density and supercapacitor with high power density. This method realizes multi-timescale coordination by introducing a hierarchical two-stage dispatch model. The first stage makes an initial decision without considering the RES uncertainties to minimize the operational cost, including the degradation cost and regulation cost from the utility grid. Power references of the battery and electricity from the utility grid are also calculated, and these will be further used in the second stage. The second stage generates corrective actions to compensate for the first-stage decision after the uncertainty is realized. The first stage is a nonlinear programming problem and is solved by an off-the-shelf solver over a longer timescale (1 h), while the second stage is modeled as a Markov decision process addressed by DRL in real-time.

The Soft Actor-Critic (SAC), as an efficient DRL algorithm for a continuous control problem [19], is adopted in the approach. The SAC is a stochastic off-policy actor-critic algorithm based on the concept of entropy, and it returns a probability distribution over the action space. The entropy term is used to evaluate the randomness of the policy, while the SAC introduces an entropy term in the reward function so that the return and exploration can be maximized at the same time during the training process. This improves exploration and robustness. Compared with the deep deterministic policy gradient (DDPG), another effective DRL method [20], the policy learned by the SAC is a stochastic policy that returns a probability distribution over the action space, while DDPG often has larger variations and can easily converge to a local optimum [21]. Thus, the SAC can better address the uncertainty existing in the decision due to its stochastic policy.

The contributions of this paper can be summarized as follows:

  1. (1)

    A DRL-based two-stage energy management framework is established for microgrids with HESS. The first stage schedules the output of battery and regulation from the utility grid (buying/selling electricity from/to grid), while the second stage adjusts the scheduling from the first stage and determines the power of the supercapacitor to deal with the instantaneous fluctuations of RES.

  2. (2)

    The degradation models of battery and supercapacitor are derived and considered during operation so that the long-term capital cost and short-term operational cost can be coordinated.

  3. (3)

    An advanced DRL algorithm, namely the SAC, is derived to improve training efficiency and performance in the second stage. The results show that the SAC agent has low variation and stable performance.

2 Microgrid operation modelling

2.1 Microgrid

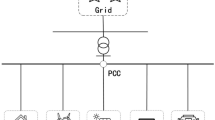
Here the microgrid consists of HESS and RES, including photovoltaic (PV) and wind turbine (WT), and aggregated load. The microgrid can interact with the utility grid through the point of common coupling (PCC). Figure 1 shows the schematic of the microgrid for energy management. When the microgrid operates in the grid-connected mode, it can benefit from selling electricity to the utility grid or buying electricity from the grid to maintain the power balance. The power balance to be maintained can be expressed as:

$$P_{L} = P_{PV} + P_{WT} + P_{Grid} + \underbrace {{P_{B} + P_{SC} }}_{{P_{ESS} }}$$
(1)
Fig. 1
figure 1

Microgrid model for energy management

Full size image

Among these variables, \(P_{L}\), \(P_{PV}\) and \(P_{WT}\) are considered to be uncontrollable, and the objective of energy management is to determine optimal values for \(P_{Grid}\), \(P_{B}\) and \(P_{SC}\) so that the microgrid operation cost can be minimized. We also assume that the utility grid adopts a dynamic real-time pricing scheme in which the price is determined based on the bidding of the electricity market participants and is usually available for the public several hours ahead, allowing customers to make a schedule in advance [22]. The price data from the Energy Market Authority (EMA) in Singapore [23] over a year is used in this work.

2.2 Renewable energy sources

PV panels and WTs are deployed as generation units. PV generation varies dramatically with weather conditions, especially for passing clouds. Similar, wind power depends on wind speed that varies from day to day, and from season to season. The power generation uncertainty makes it difficult to deal with the instantaneous supply–demand balance. The objective of the proposed multi-timescale coordinated method is to dispatch different storage devices based on their characteristics to deal with the instantaneous fluctuations of RES. The PV and WT hourly predicted power generation data are from [9], which are used in the first stage. In order to simulate the uncertain fluctuations of RES, a 10% forecast error is added on the predicted data in the second stage.

2.3 Hybrid energy storage systems (HESSs)

The microgrid has two kinds of ESS: battery and supercapacitor. The battery has high energy density to store energy, while the supercapacitor has high power density and can rapidly respond to charging/discharging events. Because of their different characteristics, the battery and supercapacitor should be scheduled for different objectives, i.e., the battery is scheduled for economic dispatch over a longer timescale while the supercapacitor maintains instantaneous power balance. Particularly, the degradation cost during operation is considered in this paper, where the models are presented in the following sections.

2.3.1 Battery degradation model

Degradation of life is important for battery operation, and is visible in two main aspects, i.e., the aging of cycle life and the reduction of capacity. The primary determinant of lifecycle and capacity is the depth of discharge (DOD), which is defined as the energy that is discharged from a fully charged battery, divided by the battery capacity. The curve of battery lifecycles under different DODs, \(L_{B}\), can be fitted by the formula in [9]:

$$L_{B} (DOD) = a \times DOD^{ - b} \times e^{ - c \cdot DOD}$$
(2)

where a, b, c are curve-fitting coefficients.

Then the degradation cost \(C_{BDC} (t)\) related to the discharging/charging events can be expressed as:

$$C_{BDC} (t) = \frac{{C_{B}^{R} \cdot |P_{B} (t)|\Delta t}}{{2L_{B} \cdot E_{cap}^{B} (t) \cdot DOD \cdot \eta_{c}^{B} \cdot \eta_{d}^{B} }}$$
(3)

where \(C_{B}^{R}\) is the battery replacement cost, and \(\eta_{c}^{B}\) and \(\eta_{d}^{B}\) are the charging and discharging efficiencies, respectively. It is worth mentioning that the degradation cost of charging events equals that of discharging events. The battery capacity will depreciate after this cycling event as:

$$E_{cap}^{B} (t + \Delta t) = E_{cap}^{B} (t) - \frac{{E_{rated}^{B} }}{{L_{B} }}$$
(4)

where \(E_{rated}^{B}\) is the rated capacity of the battery.

2.3.2 Supercapacitor degradation model

The predominant advantage of a supercapacitor over a battery is that the supercapacitor can weather several tens of thousands of discharge/charge cycles under very high current. Degradation of its lifetime centres on the increase of equivalent series resistance and the reduction of capacity. Reference [24] indicates that the aging of a supercapacitor is closely related to the evaporation rate of electrolytes, while the temperature and voltage are two principal factors influencing the aging rate.

A supercapacitor can work for its estimated lifetime under normal operating conditions (i.e., within the proper temperature and voltage ranges). Therefore, the supercapacitor degradation cost can be treated as a linear function of DOD per charging/discharging event [10]. Considering a time interval \([t,t + \Delta t]\) and given the estimated supercapacitor lifetime \(L_{SC}\) and the replacement cost \(C_{SC}^{R}\), the degradation cost can be expressed as:

$$C_{SCDC} (t) = \frac{{C_{SC}^{R} \cdot \Delta t}}{{L_{SC} }}$$
(5)

As (5) shows, the cost is linear over time if used properly in a microgrid. Therefore, a supercapacitor is suitable for dealing with instantaneous power imbalance.

3 Multi-timescale coordinated two-stage operation of microgrid with HESS

In this section, a two-stage multi-timescale coordinated method considering the complementary characteristics of battery and supercapacitor is developed. The first stage addresses a deterministic optimization problem using the hourly predicted data, and then corrective action is taken in the second stage to compensate for the first-stage decision after the uncertainty is realized.

Figure 2 illustrates the framework of the proposed DRL-based multi-timescale coordinated microgrid operation, where \(T_{f}\) and \(T_{s}\) are the lengths of the prediction horizons for the first stage and second stage, respectively. The first stage consists of a nonlinear model predictive control framework with a time horizon \(t_{f} \in \{ 1,2,...,T_{f} \}\), while the second stage is a Markov decision process solved by a DRL algorithm (Soft Actor-Critic) with a time horizon \(t_{s} \in \{ 1,2,...,T_{s} \}\), using the reference values provided by the first stage. For both stages, the power balance constraint shown in (1) needs to be met at all times. In addition, the following constraints also need to be satisfied:

$$P_{Grid}^{\min } \le P_{Grid} (t) \le P_{Grid}^{\max } ,t \in \{ t_{f} ,t_{s} \}$$
(6)
$$P_{B}^{\min } \le P_{B} (t) \le P_{B}^{\max } ,t \in \{ t_{f} ,t_{s} \}$$
(7)
$$P_{SC}^{\min } \le P_{SC} (t_{s} ) \le P_{SC}^{\max }$$
(8)
$$SOC_{B}^{\min } \le SOC_{B} (t) \le SOC_{B}^{\max } ,t \in \{ t_{f} ,t_{s} \}$$
(9)
$$SOC_{SC}^{\min } \le SOC_{SC} (t) \le SOC_{SC}^{\max } ,t \in \{ t_{f} ,t_{s} \}$$
(10)
Fig. 2
figure 2

Framework of the proposed DRL based multi-timescale coordinated microgrid operation

Full size image

Equation (6) is the power limit constraint of buying/selling electricity from/to utility grid, while (7), (8) are the charging or discharging power limits of the battery and supercapacitor, respectively. Equations (9), (10) are the state of charge (SOC) limits required to avoid the battery and supercapacitor over-charging or over-discharging, respectively.

State dynamics of the battery and supercapacitor are depicted as (11) in terms of charging/discharging power [9]:

$$E^{B} (t + \Delta t) = \left\{ {\begin{array}{*{20}c} {E^{B} (t) - P_{B} (t)\Delta t \cdot \eta_{c}^{B} , \, P_{B} (t) \le 0} \\ {E^{B} (t) - P_{B} (t)\Delta t/\eta_{d}^{B} , \, P_{B} (t) > 0} \\ \end{array} } \right.$$
(11)
$$E^{SC} (t_{s} + \Delta t_{s} ) = \left\{ {\begin{array}{*{20}c} {E^{SC} (t_{s} ) - P_{SC} (t_{s} )\Delta t_{s} \cdot \eta_{c}^{SC} , \, P_{SC} (t_{s} ) \le 0} \\ {E^{SC} (t_{s} ) - P_{SC} (t_{s} )\Delta t_{s} /\eta_{d}^{SC} , \, P_{SC} (t_{s} ) > 0} \\ \end{array} } \right.$$
(12)

where \(t \in \{ t_{f} ,t_{s} \}\) and \(\Delta t \in \{ \Delta t_{f} ,\Delta t_{s} \}\), \(E^{B} (t)\) and \(E^{SC} (t)\) are the remaining energy in the battery and supercapacitor at time t respectively, and \(SOC_{B/SC} = E^{B/SC} /E_{cap}^{B/SC}\). Since the supercapacitor is scheduled only at the second stage, the state dynamics in (12) and constraint in (8) are only considered in the second stage with a short timescale.

3.1 Mathematical model for first stage

The objective of the first stage is to optimize the decision variables \(\{ P_{Grid}^{f} (t_{f} ),P_{B}^{f} (t_{f} )\}\) with hourly predicted data, including load, PV, and WT power generation, to minimize the operational cost. The objective function is expressed as:

$$\sum\limits_{{t_{f} = 1}}^{{T_{f} }} {C_{Grid}^{f} (t_{f} ) + C_{B} (t_{f} )}$$
(13)

where \(C_{Grid}^{f}\) is the cost of buying electricity from the utility grid, which can be expressed as:

$$C_{Grid}^{f} (t_{f} ) = \left\{ {\begin{array}{*{20}c} {c_{g}^{buy} (t_{f} ) \cdot P_{Grid}^{f} (t_{f} )\Delta t_{f} , \, P_{Grid}^{f} (t_{f} ) > 0} \\ {c_{g}^{sell} (t_{f} ) \cdot P_{Grid}^{f} (t_{f} )\Delta t_{f} , \, P_{Grid}^{f} (t_{f} ) \le 0} \\ \end{array} } \right.$$
(14)

where \(c_{g}^{buy} (t_{f} )\) is the buying price in the market at time \(t_{f}\) and \(c_{g}^{sell} (t_{f} )\) is the selling price. When \(P_{Grid}^{f} > 0\), it means the microgrid buys electricity from the utility grid, and when \(P_{Grid}^{f} < 0\) the microgrid sells electricity to the grid. \(t_{f}\) is the battery operation cost, given as:

$$\begin{gathered} C_{B} (t_{f} ) = C_{BDC} (t_{f} ,DOD(t_{f} )) \\ - [1 - \delta (t_{f} )] \cdot C_{BDC} (t_{f} ,DOD(t_{f} - 1)) \\ \end{gathered}$$
(15)

where \(\delta (t)\) is an auxiliary function to indicate the state transition on the charging and discharging events in two consecutive time intervals, as:

$$\delta (t_{f} ) = \left\{ {\begin{array}{*{20}c} {0, \, P_{B}^{f} (t_{f} ) \cdot P_{B}^{f} (t_{f} - 1) > 0} \\ {1, \, P_{B}^{f} (t_{f} ) \cdot P_{B}^{f} (t_{f} - 1) \le 0} \\ \end{array} } \right.$$
(16)

The depth of discharge, \(DOD(t_{f} )\), is calculated based on the accumulated energy before the cycling event changes as:

$$DOD(t_{f} ) = \frac{{E_{a}^{B} (t_{f} )}}{{E_{cap}^{B} (t_{f} )}}$$
(17)

where \(E_{a}^{B} (t_{f} )\) is the accumulated energy before the cycling event changes, formulated as:

$$E_{a}^{B} (t_{f} ) = [1 - \delta (t_{f} )] \cdot E_{a}^{B} (t_{f} - 1) + P_{B}^{f} (t_{f} )\Delta t_{f}$$
(18)

Based on the above equations, the optimization problem in the first stage is summarized as:

$$\min \sum\limits_{{t_{f} = 1}}^{{T_{f} }} {C_{Grid}^{f} (t_{f} ) + C_{B} (t_{f} )}$$
$$s.t.\;(1) - (4),(6),(7),(9),(11),(14) - (18)$$
(19)

3.2 Mathematical model for second stage

The second stage aims to modify the decisions (i.e., battery output power and utility regulation) from the first stage and make a schedule for the supercapacitor so that variations caused by RES uncertainties can be minimized. The decision variables are \(\{ P_{Grid}^{{s,t_{t} }} (t_{s} ),P_{B}^{{s,t_{t} }} (t_{s} ),P_{SC}^{{s,t_{t} }} (t_{s} )\}\) for each first-stage time slot \([t_{f} ,t_{f} + \Delta t_{f} ]\), and they should satisfy (6)-(8). This stage is modeled as a Markov decision process. To apply the DRL algorithm and achieve the real-time decision-making, several necessary components (i.e., observations, actions, reward function) should first be defined.

3.2.1 Observations

For the second stage, the environment is the microgrid, and therefore the state of the environment (usually termed as observations) at \(t_{s}\) in the time slot \([t_{f} ,t_{f} + \Delta t_{f} ]\) can be expressed as:

$$s(t_{s} ) = \{ P_{L}^{net} (t_{s} ),SOC_{B} (t_{s} ),SOC_{SC} (t_{s} )\}$$
(20)

where \(SOC_{B} (t_{s} ),SOC_{SC} (t_{s} )\) are the current states of charge of the battery and supercapacitor, respectively, and satisfy (9) and (10). \(P_{L}^{net} (t_{s} )\) is the net load at current time step, given by:

$$P_{L}^{net} (t_{s} ) = P_{L} (t_{s} ) - P_{PV} (t_{s} ) - P_{WT} (t_{s} )$$
(21)

3.2.2 Actions

The actions performed by the DRL agent are corrective items for the first stage decisions and the output power of the supercapacitor, shown as:

$$a(t_{s} ) = \{ \Delta P_{Grid} (t_{s} ),\Delta P_{B} (t_{s} ),P_{SC} (t_{s} )\}$$
(22)

The relations between the decision variables \(\{ P_{Grid}^{{s,t_{f} }} (t_{s} ),P_{B}^{{s,t_{f} }} (t_{s} ),P_{SC}^{{s,t_{f} }} (t_{s} )\}\) and actions are summarized as:

$$P_{Grid}^{{s,t_{f} }} (t_{s} ) = P_{Grid}^{f} (t_{f} ) + \Delta P_{Grid} (t_{s} )$$
(23)
$$P_{B}^{{s,t_{f} }} (t_{s} ) = P_{B}^{f} (t_{f} ) + \Delta P_{B} (t_{s} )$$
(24)
$$P_{SC}^{{s,t_{f} }} (t_{s} ) = P_{SC} (t_{s} )$$
(25)

From (23)–(25), it can be seen that the actions generated by the second stage are corrective terms for the decisions made in the first stage. The first stage is a deterministic optimization process without considering the uncertainties of RES, and therefore an additional second stage is introduced so that the trained DRL agent can make real-time decisions after the uncertainties are realized.

3.2.3 Reward function

The state transition follows the rule stated in (11) and (12). As mentioned, the first stage provides reference values for the second stage and the realized uncertainties are dealt with by the supercapacitor. Therefore, penalties for deviations from the reference values can be defined as:

$$c_{g}^{p} (t_{s} ) = [\Delta P_{Grid} (t_{s} )]^{2}$$
(26)
$$c_{B}^{p} (t_{s} ) = [\Delta P_{B} (t_{s} )]^{2}$$
(27)

where \(c_{g}^{p} (t_{s} )\) is the penalty cost of deviation of the power from/to utility grid, and \(c_{B}^{p} (t_{s} )\) is the penalty cost of deviation of the battery power. Apart from these two penalties, the SOC of the supercapacitor at the end of each time interval \([t_{s} - \Delta t_{s} ,t_{s} ]\) should be maintained at a nominal value so that it has enough energy for the next time interval. Therefore, the penalty term that accounts for the SOC of the supercapacitor can be expressed as:

$$c_{sc}^{p} (t_{s} ) = (SOC_{SC} (t_{s} )/100 - 1)^{2}$$
(28)

Based on (27)–(29), the reward function is defined as:

$$r(t_{s} ) = - c_{g}^{p} (t_{s} ) - c_{B}^{p} (t_{s} ) - c_{sc}^{p} (t_{s} ) - C_{SCDC}$$
(29)

where the first three items are penalty costs, and the last is the supercapacitor degradation cost.

With the above definitions, the optimization problem in the second stage when considering the future rewards is formulated as:

$$\max \sum\limits_{{t_{s} = 1}}^{{T_{s} }} {\gamma^{{t_{s} }} \cdot r(t_{s} )}$$
$$s.t.\;(1),(5) - (12),(20) - (29)$$
(30)

where \(\gamma\) is the discount factor. This problem will be solved by the DRL algorithm, SAC. Since the policy is composed of deep neural networks, a completely trained agent can compute the dispatch actions within a few seconds for real-time decision-making.

3.3 SAC training process

The SAC is one of the actor-critic approaches similar to DDPG and Twin delayed DDPG (TD3) but has better performance for continuous control problems. In the actor-critic architecture, the actor uses the policy gradient to find the optimal policy while the critic evaluates the policy produced by the actor. Instead of using only the Q function, the critic in the SAC takes both the Q function and the value function to evaluate the policy. This can stabilize the training and provide convenience to train simultaneously with the other networks. There are three networks in the SAC, one actor network (policy network) to find the optimal policy, and two critic networks (a value network and a Q network) to evaluate the policy. They will be explained in detail in the following sections.

3.3.1 Critic network

The critic in the SAC uses both the value function and the Q function to evaluate the learned policy, and the two functions are approximated by two separate deep neural networks. The value network is denoted by \(V\), the parameter of the network is \(\psi\) and the parameter of the target value network is \(\psi^{\prime }\). Therefore,\(V_{\psi } (s)\) is the value function (state value) approximated by a neural network parameterized by \(\psi\). In the entropy-based reinforcement learning framework, the theoretical state value \(V\) is calculated as:

$$V(s) = {\rm E}_{\pi } [Q(s,a) - \alpha \log \pi (a|s)]$$
(31)

where \(Q(s,a)\) is the state-action value function (Q-value), \(\pi\) is the stochastic policy that maps the state to a probability distribution over the action space, \(\alpha \log \pi (a|s)\) is the entropy term, and \(a_{i}\) is the entropy weight, which is adjusted dynamically during the training process. Two neural networks \(Q_{\theta 1}\) and \(Q_{\theta 2}\) are used to compute the \(Q\) value, and this can avoid overestimation during the training process [25]. The policy is expressed by the actor network (policy network) \(\pi_{\phi }\) parameterized by \(\phi\). Therefore, the loss function of the value network can be defined as:

$$L_{V} (\psi ) = \frac{1}{N}\sum\limits_{i} {[\mathop {\min }\limits_{j = 1,2} Q_{{\theta_{j} }} (s_{i} ,a_{i} ) - \alpha \log \pi_{\phi } (a_{i} |s_{i} ) - V_{\psi } (s_{i} )]^{2} }$$
(32)

where N is the number of state transitions sampled from replay buffer D, i is the index of sample, \(s_{i}\) and \(a_{i}\) are state observation and action defined in (20) and (22), respectively. The value network parameter \(\psi\) is updated by gradient descent, as:

$$\psi = \psi - \lambda \nabla_{\psi } L_{V} (\psi )$$
(33)

where \(\lambda\) is the learning rate. Then the target value network is updated by soft replacement, as:

$$\psi^{\prime } = \tau \psi + (1 - \tau )\psi^{\prime }$$
(34)

where \(\tau\) is the soft replacement coefficient that is set to 0.001.

For the two \(Q\) networks, \(Q_{\theta 1}\) and \(Q_{\theta 2}\), the loss functions are defined as:

$$L_{Q} (\theta_{1} ) = \frac{1}{N}\sum\limits_{i} {[r_{i} + \gamma V_{\psi } (s_{i}^{\prime } ) - Q_{{\theta_{1} }} (s_{i} ,a_{i} )]^{2} }$$
(35)
$$L_{Q} (\theta_{2} ) = \frac{1}{N}\sum\limits_{i} {[r_{i} + \gamma V_{\psi } (s_{i}^{\prime } ) - Q_{{\theta_{2} }} (s_{i} ,a_{i} )]^{2} }$$
(36)

where \(r_{i}\) is the immediate reward defined in (29), \(\gamma\) is the discount factor that gives importance to the immediate reward or future rewards. \(s_{i}^{\prime }\) is the new state after the action \(a_{i}\) is performed. Then \(\theta_{1}\) and \(\theta_{2}\) are updated by the following rules:

$$\theta_{1} = \theta_{1} - \lambda \nabla_{{\theta_{1} }} L_{Q} (\theta_{1} )$$
(37)
$$\theta_{2} = \theta_{2} - \lambda \nabla_{{\theta_{2} }} L_{Q} (\theta_{2} )$$
(38)

3.3.2 Critic network

The actor network, also named policy network, is parameterized by \(\phi\). The loss function is defined as:

$$L_{\pi } (\phi ) = \frac{1}{N}\sum\limits_{i} {[\mathop {\min }\limits_{j = 1,2} Q_{{\theta_{j} }} (s_{i} ,a_{i} ) - \alpha \log \pi_{\phi } (a_{i} |s_{i} )]^{2} }$$
(39)

Then the actor network parameter can be updated by:

$$\phi = \phi + \lambda \nabla_{\phi } L_{\pi } (\phi )$$
(40)

3.4 Algorithm

The proposed DRL based method for multi-timescale coordinated operation of microgrid is summarized in Algorithm 1.

figure a

4 Case studies

4.1 Simulation settings

In this section, the DRL based method for multi-timescale coordinated operation of microgrids is demonstrated. The model shown in Sect. 3 and the SAC algorithm are implemented in MATLAB. The optimization problem in the first stage is solved by Gurobi [26], and the DRL training process is conducted by the MATLAB Reinforcement Learning Toolbox [27].

The simulation parameters are listed in Table 1. The scheduling horizon is set as 48 h, the length of the time interval in the first stage is 1 h and the time interval in the second stage is set to 5 min. It is worth mentioning that although in this paper the time interval is set as 5 min for simplicity, the proposed method can adapt to a shorter one. The data about the power of load, PV and WT can be found in [9], while the uncertainties of the PV and WT power generation in the second stage are expressed by a 10% forecast error. The real-time electricity price data are obtained from [23], and the charging/discharging efficiencies of the battery and supercapacitor are set as 0.95 and 0.92, respectively. For the DRL training process, the DRL parameters, including the iteration number, learning rate \(\lambda\), discount factor \(\gamma\), size of replay buffer and soft replacement coefficient \(\tau\), are set as 600, \(3 \times 10^{ - 4}\), 0.99, 1000, and 0.001, respectively. Figure 3 shows the reward value of each training episode of the SAC agent. As shown, episode reward is the total reward in the scheduling horizon 48 h, and average reward is the average of rewards of all finished episodes. After several hundreds of training episodes, episode and average rewards converge to a maximum value, and it can be seen that the SAC algorithm converges very quickly. After the training process, entropy weight \(\alpha\) is set to 0.2296 and the DRL agent with the optimal policy is implemented for real-time decision-making.

Table 1 Energy storage device parameters
Full size table
Fig. 3
figure 3

Episode and average rewards during the training process

Full size image

4.2 Numerical results

The results of optimal dispatch based on the real-time pricing scheme computed by the proposed two-stage framework are shown in Figs. 4 and 5. Figure 4 is the results of the first stage without considering the uncertainties of PV and WT power generation, whereas Fig. 5 is the results of the second stage considering the uncertainties. As shown, the battery is rapidly discharged at hours 16, 20 and 37 when the electricity price is high, while when the electricity price is lower from hours 0–8 and 21–35 the microgrid buys a large amount of electricity from the main grid to satisfy demand and charge the battery. The average computation time of the first stage is 18.85 s. From Fig. 5, it can be seen that the supercapacitor is scheduled to rapidly respond to the instantaneous fluctuations of PV and WT power generation. The computation time of a step in the second stage is 0.86 s. Figures 6 and 7 show the SOCs of the battery and supercapacitor during the scheduling horizon respectively. These present the periodic features as expected. As seen, the SOC curve of the battery is much smoother than that of the supercapacitor since the output power of the supercapacitor is closely related to the variations of RES.

Fig. 4
figure 4

First-stage economic dispatch without considering the uncertainty

Full size image
Fig. 5
figure 5

Second-stage economic dispatch considering the PV and WT uncertainties (10% forecast error)

Full size image
Fig. 6
figure 6

SOC of battery during dispatch horizon

Full size image
Fig. 7
figure 7

SOC of supercapacitor during dispatch horizon

Full size image

Figures 8 and 9 provide the overview of battery degradation cost and utility grid regulation cost over the scheduling horizon, respectively. Comparing Figs. 8 and 5, it can be seen that the degradation cost is high when the battery is quickly charged or discharged. It can also be seen from Figs. 9 and 5 that the profile of the utility grid regulation cost is closely related to the electricity price. Table 2 gives the detailed dispatch results. As seen, the total operation cost is $264.2974 and the battery degradation cost is $0.9222. After the DRL agent is completely trained, it takes 0.1563 s to make the decisions for each step. This is sufficiently quick for real-time operation.

Fig. 8
figure 8

Battery degradation cost during dispatch horizon

Full size image
Fig. 9
figure 9

Utility grid regulation cost during dispatch horizon

Full size image
Table 2 Numerical results
Full size table

5 Conclusions

In this study, a DRL based method for multi-timescale coordinated microgrid operation is developed. The first stage makes an initial decision irrespective of the uncertainties to minimize the operation and degradation costs, while the second stage aims to generate corrective actions to compensate for the first-stage decision after the uncertainty is realized. The first stage is a non-linear model predictive control problem while the second stage is modeled as a Markov decision process solved by an SAC. Since the battery has high energy intensity while the supercapacitor has high power intensity, the battery is scheduled to store a large amount of energy over a long timescale while the supercapacitor works for instantaneous power balancing. The training results of the SAC agent show that this method can stabilize the performance well and converges to the optimal policy quickly. For online application, the agent can adjust the power bought from the main grid, battery power, and supercapacitor power in real-time to maintain the power balance under the fluctuations of RES.

In summary, this paper establishes a feasible data-driven multi-timescale coordinated microgrid operation method. In future work, the problem in the first stage will be further analyzed and solved by the DRL algorithm to form a multi-agent DRL-based coordinated framework. In addition, more types of energy storage device will be considered.