Introduction

Financial markets are becoming increasingly complex. Investors must therefore consider many factors and various aspects of markets to increase their profits. With progress in financial engineering, many methods have been developed to explore the behavior of financial markets (Chao et al. 2019; Kou et al. 2019a). Most investors attach their wealth to stock exchange markets, and most prefer combinations of different stocks since single stocks carry inherent risks. Portfolio selection is therefore an important topic of investigation (Li et al. 2017; Wu et al. 2019).

The problem of portfolio selection has been widely explored across several fields, ranging from traditional and quantitative finance to machine learning and artificial intelligence (Li and Hoi 2014). Generally, portfolio selection aims to achieve certain long-term targets by allocating wealth to a set of assets (Li et al. 2015a, b). While previous studies have extensively investigated portfolio selection based on financial considerations, it is also worthwhile to consider nonfinancial issues. As with any decision-making problem, many factors are directly and indirectly involved in portfolio selection. In this regard, investigating, recognizing, ranking, and applying criteria to assess and select portfolios has posed a challenge for researchers, managers, investors, and practitioners. The present study, therefore, aimed to develop a fuzzy analytic network process (FANP) to rank portfolios on the Tehran Stock Exchange (TSE). The research questions are as follows:

  1. 1.

    What are the main criteria for assessing and selecting portfolios?

  2. 2.

    What are the factor determinants of stock selection for a portfolio on the TSE?

  3. 3.

    How can FANP be used to improve stock selection in a TSE portfolio?

When a decision-maker has to consider different criteria to choose from different alternatives, the problem becomes one of multiple-criteria decision-making (MCDM) to be solved by related tools (Kou et al. 2012; Kou et al. 2016). In this regard, FANP can be considered a proper tool since

  1. 1.

    It can consider numerous criteria to assess portfolios;

  2. 2.

    Internal relationships among decision-making criteria can be considered; and

  3. 3.

    It can express the judgments of decision-makers using linguistic expression; moreover, previous studies have frequently combined MCDM tools with fuzzy logic.

This study focused on the TSE, which was established in 1967 and is Iran’s largest stock exchange. As of 2012, there were 339 companies on the TSE with an aggregate market capitalization of 104.21 billion dollars. Using the TSE, this research developed a method for applying the proper criteria to evaluate and select portfolios. Specifically, the FANP approach was used to rank portfolios in consideration of uncertain environments and decision-makers’ judgments. This study’s approach is novel in that it integrates important financial and nonfinancial criteria using FANP to assess and select portfolios. To the best of the authors’ knowledge, this study is the first to adopt such an approach.

The rest of this paper is organized as follows. Section 2 discusses the related literature and identifies gaps in the existing research. Next, section 3 outlines the developed research method. After that, section 4 presents and discusses the results. Finally, section 5 provides the conclusions, implications, and directions for future research.

Literature review

This section examines prior research on portfolio selection. For the sake of organization, this part is divided into four subsections: portfolio selection, portfolio selection criteria, related work, and research gap identification.

Portfolio selection

Portfolio selection aims to assess a combination of securities from a large quantity of available alternatives. It aims to maximize the investment returns of investors. According to Markowitz (1952), investors must make a trade-off between return maximization and risk minimization. Investors can maximize the return for a considered risk level, or they can focus on risk minimization for a predetermined level of return. Markowitz also calculated investment return as the expected value of securities’ earnings. According to Markowitz, risk is defined as the variance from the expected value (Huang 2006).

The Markowitz mean-variance (MV) model took variance in the expected returns and estimated income from securities as its main inputs. Since then, many researchers have attempted to simplify the input data in the portfolio selection problem. While some approaches, such as index models, have been successfully applied, most still have some limitations. The Markowitz model is considered too basic since it neglects real-world issues related to investors, trading limitations, portfolio size, and so on. Besides, considering all these constraints in mathematical formulation produces nonlinear mixed-integer models that are very complex compared to basic models. Although researchers have tried to tackle this issue through various approaches, such as cutting planes, interior point models, and decomposition, there is still room for improvement (Crama and Schyns 2003). Several studies have focused on MV models with risk and return considerations. Moreover, MV models have been improved to address real-world problems. However, most studies have neglected other important issues in portfolio selection. There is, for example, controversy regarding the adequacy of solely considering risk and return in portfolio selection, and more recent studies have suggested considering additional criteria (Steuer et al. 2008). The present study, therefore, regarded portfolio selection as an MCDM problem.

Portfolio selection criteria

There are numerous criteria to consider in portfolio selection. These criteria vary according to the different concerns of managers, practitioners, researchers, and investors. Although portfolio selection criteria affect the final decisions of investors, they underexamined in the literature. This is mainly because the diversity and potential overlap of criteria make it difficult to distinguish differences between them.

Expected value (EV) is commonly applied in portfolio selection. Specifically, the methods of Tobin (1958), Markowitz (1952), and Sharpe (1963) are often used; however, there are many criticisms of these approaches. According to Feldstein (1969) and Hakansson (1972), EV is only applicable when the decision-maker’s expected utility is maximized, the utility function is quadratic, or the distribution probability of the return is normal (Mcnamara 1998). Ogryczak (2000), meanwhile, established an MCDM model with risk consideration. Hurson and Ricci-Xella (2002) applied return, common risk, and residual risk to portfolio selection. Conflicting criteria such as liquidity, risk, and rate of return are often simultaneously considered in portfolio selection. Abdelaziz et al. (2007), for example, developed a multiobjective stochastic programming model with conflicting objective functions for portfolio selection.

After filtering inefficient portfolios using historical data, Ballestero et al. (2007) provided a decision table to consider multiple scenarios and select portfolios. Xidonas et al. (2009) proposed an MCDM framework to select common stock portfolios while Liu et al. (2012) showed the suitability of MCDM approaches by applying transaction cost, return, skewness, and risk. Meanwhile, Mihail et al. (2013) developed potential criteria and subcriteria for selecting financial plans.

Table 1 summarizes portfolio selection criteria, showing sample references and the application of factor analysis and principal component analysis (PCA) to criteria development. The table shows that while most studies developed portfolio selection criteria based on literature reviews, a few have employed PCA or factor analysis to develop criteria.

Table 1 Portfolio selection criteria
Full size table

Related work

In the past couple decades, studies of portfolio selection have developed complex mathematical models to consider additional real-world factors. Chunhachinda et al. (1997) found that the returns of 14 major stock markets were not normally distributed; they suggested that skewness should be integrated into investors’ decisions to improve optimal decision-making. Later, Tanaka et al. (2000) proposed two types of portfolio selection models considering possibility and fuzzy distributions and applied a numerical example to illustrate the model. Inuiguchi and Ramık (2000), meanwhile, showed the applicability of fuzzy approaches for optimal portfolio selection.

Similar to fuzzy approaches, metaheuristic algorithms have been applied to portfolio selection. Xia et al. (2000) developed a genetic algorithm (GA) for portfolio selection and illustrated it with a numerical example, comparing the outputs with Markowitz’s model. Lim and Zhou (2002), meanwhile, focused on MV and continuous-time portfolio selection, considering random interest rates, volatility coefficients, and appreciation rates to develop a portfolio selection model. Similarly, Crama and Schyns (2003) applied simulated annealing (SA) to a compound portfolio selection problem.

Most studies have considered more than one objective in portfolio selection. Huang (2006), for example, developed a bi-objective portfolio selection model to maximize investors’ returns and the likelihood of achieving a specified return level. Abdelaziz et al. (2007), meanwhile, developed a multiobjective deterministic portfolio-selection model for the Tunisian stock market. Mathematical models have been integrated with other techniques, such as fuzzy logic. Carlsson et al. (2007), for example, proposed a fuzzy mixed-integer programming approach to select R&D portfolios. Li et al. (2010), meanwhile, developed a skewness concept for fuzzy variables in portfolio selection. MCDM techniques have also been investigated in recent portfolio selection research. Jeng and Huang (2015), for example, developed a systematic MCDM approach and applied decision-making trial and evaluation laboratory (DEMATEL), analytic network process (ANP), and the modified Delphi method (MDM) to portfolio selection. Adopting additional criteria, Mehlawat (2016) applied risk, wealth, liquidity, number of assets, and transaction cost to portfolio assessment. Meanwhile, according to Huang and Di (2016), uncertain portfolio selection can be conducted in the presence of background risk, background assets, and security returns based on expert assessment rather than historical data. Mashayekhi and Omrani (2016) developed a multiobjective mathematical model that integrated the Markowitz MV model with data envelopment analysis (DEA) cross-efficiency considering risk, efficiency, and returns. Recently, Nystrup et al. (2018) developed multiperiod forecasting for the mean and covariance of financial returns from a time-varying portfolio selection model.

Though some studies have investigated FANP (Hemmati et al. 2018), it is generally underexamined in portfolio selection. Mohanty et al. (2005) used FANP to select R&D projects, applying fuzzy logic to address the vagueness of preferences. In summary, while real-world economic and financial problems have been widely investigated using MCDM tools (Kou et al. 2014; Zhang et al. 2019), there are many other approaches for predicting the behavior of stock markets (Zhong and Enke 2019; Nayak and Misra 2018; Kaucic et al. 2019). Table 2 shows a summary of prior research on portfolio selection.

Table 2 Related work
Full size table

Gaps in the research

As shown in Tables 1 and 2, there are numerous criteria for assessing and selecting portfolios. While most studies have focused on financial criteria, other important criteria should be considered. Managers, decision-makers, and investors face different factors in portfolio assessment. According to the performance measurement concept, using fewer but more efficient metrics is strongly preferred. In this regard, portfolio selection criteria should be specifically applicable for use by investors. Therefore, to address the first gap in prior research, this study aimed to develop and prioritize specific criteria for portfolio selection. According to decision-making theory, there is no single-criterion decision in real-world problems. Thus, most problems are considered MCDMs where different criteria should be concurrently considered. However, existing MCDM approaches have some limitations. First, some approaches (e.g., the analytic hierarchy process (AHP)) do not consider the internal relations between criteria; these are addressed by other approaches, such as the analytic network process (ANP). In addition, most decision-makers prefer to make comparisons/judgments in fuzzy environments. Thus, MCDM approaches should be integrated with fuzzy logic. To fill this gap in the literature, the present study developed specific criteria for portfolio selection to be used by those who are involved in important financial decision-making. In addition, FANP was further applied to address uncertainty concerns in financial decision-makers. To the best of the authors’ knowledge, no prior study has applied FANP to portfolio selection in this way.

Method

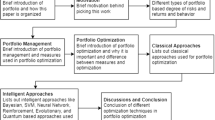
Figure 1 shows the steps required to achieve the aims of this study. The figure shows that the research involves three main steps: determining portfolio selection criteria, prioritizing the criteria, and selecting a portfolio using FANP. As such, this work has implications for both researchers and investors who are interested in the portfolio selection problem.

Fig. 1
figure 1

Research Steps

Full size image

First phase: develop the Main portfolio selection criteria

As discussed earlier, numerous factors should be considered in portfolio selection. As such, different keywords (e.g., portfolio selection criteria, portfolio selection measures, portfolio selection metrics, effective factors of portfolio selection, portfolio assessment criteria) were used to enhance the quality of the findings. These keywords were searched on sites such as Springer, Science Direct, Emerald Insight, IEEE, Inderscience, and Taylor & Francis. In this way, most portfolio selection criteria were investigated and discussed in this phase (Table 1 shows the output).

Second phase: prioritize the portfolio selection criteria

As established earlier, it is necessary to apply the most important criteria when assessing portfolios. In addition, there are some measures that have similar functions. Consequently, applying redundant criteria decreases the quality of the results. Therefore, the second phase involved identifying the most important criteria for portfolio selection. To this end, a questionnaire including the major criteria for portfolio selection (as shown in Table 1) was designed and distributed to experts. The questionnaire included 23 questions regarding representative portfolio selection criteria. A pilot test was conducted to verify the questions and check for mistakes. The questionnaire was validated accordingly.

Third phase: portfolio selection with FANP

There are many MCDM techniques for ranking alternatives (Li et al. 2016; Kou et al. 2019b), and they all have various advantages and disadvantages. It is necessary, therefore, to apply an efficient approach in consideration of the specific characteristics of the problem. This study aimed to rank different portfolios on the TSE, and there are various factors for investors to consider when selecting portfolios. Therefore, those factors were applied as decision-making criteria. In addition, since there are different portfolios to be selected by decision-makers, those alternatives should be considered in the third level of the decision-making hierarchy. Though many studies have used AHP, it does not consider some important factors in decision-making. First, AHP is not an appropriate approach when there is an internal relation between criteria; therefore, previous studies have suggested applying ANP. Second, ANP cannot reflect the ambiguities and uncertainties that exist in decision-making environments. Moreover, decision-makers often prefer to express their judgments using linguistic expression to address real-world problems. In this regard, previous studies suggest integrating fuzzy logic with MCDM techniques. Therefore, FANP is an appropriate approach since it considers the internal relations among decision-making criteria and allows decision-makers to express their judgments using linguistic expression. Generally speaking, an advantage of MCDM is that investor(s) can assign large weights to risks and returns and consider small weights for other criteria. In addition, FANP can be applied by both single and multiple decision-makers. In summary, FANP can flexibly assign more weight to risks and returns, and it can be applied by one, two, or multiple decision-makers.

Compared to other MCDM techniques, ANP considers internal relations between criteria, which is very important in the decision-making process. Similar to AHP, the relative importance of a given criterion or alternative is displayed based on a ratio scale. For simplification, Saaty and Takizawa’s (1986) approach was applied rather than Saaty’s original super matrix. As mentioned, an advantage of ANP is that it considers explicit relations in the calculation; thus, the accuracy of portfolio selection results increases. However, classic AHP and ANP models cannot reflect human thinking since decision-makers prefer to state their judgments using linguistic expression. Therefore, to address the ambiguities of humans and their linguistic expression, fuzzy logic is integrated with classic MCDM techniques. Furthermore, in most decision-making studies, numerous people are involved, which makes the problem into one of group decision-making. Thus, geometric mean is applied for expert consensus. However, the FANP approach can be applied to both single and group decision-making problems. As such, this study’s method can be used by single or multiple investors. Below are the related equations applied in FANP (Chang 1996):

$$ {M}_{ij}=\left({l}_{ij},{m}_{ij},{u}_{ij}\right), $$
(1)
$$ {l}_{ij}=\min \left({B}_{ij k}\right), $$
(2)
$$ {m}_{ij}=\sqrt[n]{\prod \limits_{k=1}^n{B}_{ij k}}, $$
(3)
$$ {u}_{ij}=\mathit{\max}\ \left({B}_{ij k}\right). $$
(4)

According to fuzzy set theory, l, m, and u are triangular fuzzy numbers (TFNs), as shown in eq. (1). Bijk signifies the score of kth experts for comparing the significance of Ci – Cj criteria. Similarly, algebraic operations are applied for the TFNs of M1 and M2, as shown in the following equations:

$$ {M}_1+{M}_2=\left({l}_1+{l}_2,{m}_1+{m}_2,{u}_1+{u}_2\right), $$
(5)
$$ {M}_1\ast {M}_2=\left({l}_1\ast {l}_2,{m}_1\ast {m}_2,{u}_1\ast {u}_2\right), $$
(6)
$$ {M}_1^{-1}=\left(\frac{1}{u_1},\frac{1}{m_1},\frac{1}{l_1}\right),{M}_2^{-1}=\left(\frac{1}{u_2},\frac{1}{m_2},\frac{1}{l_2}\right). $$
(7)

It is worth noting that the output of multiplying two TFNs or convex TFNs is no longer a TFN. In other words, these equations provide an approximation for the output of this multiplication. Eq. (8) is applied to identify the TFN Sk in addition to the fuzzy combined value of ith entity:

$$ {S}_k=\sum \limits_{j=1}^n{M}_{kj}\ast {\left[\sum \limits_{i=1}^m\sum \limits_{j=1}^n{M}_{ij}\right]}^{-1}. $$
(8)

The possibility degree for each two Sk should be calculated after the computation process of eq. (8). So, assuming M1 and M2 as two TFNs, the possibility degree of M1 over M2 can be calculated as in eq. (9):

$$ {\displaystyle \begin{array}{l}\left\{\begin{array}{l}\mathrm{V}\left({\mathrm{M}}_1\ge {\mathrm{M}}_2\right)=1\kern11em \mathrm{if}\ {\mathrm{M}}_1\ge {\mathrm{M}}_2\ \\ {}\mathrm{V}\left({\mathrm{M}}_1\ge {\mathrm{M}}_2\right)=0\kern11em \mathrm{if}\ {\mathrm{L}}_1\ge {\mathrm{U}}_2\ \\ {}\mathrm{V}\left({\mathrm{M}}_1\ge {\mathrm{M}}_2\right)=\mathrm{hgt}\ \left({\mathrm{M}}_1\cap {\mathrm{M}}_2\right)\kern5.5em \mathrm{otherwise}\kern0.75em \end{array}\right\}\\ {}\end{array}} $$
(9)
$$ hgt\left(M1\cap M2\right)=\frac{u_{1-}{l}_2}{\left({u}_1-{l}_2\right)+\left({m}_2-{m}_1\right)}. $$
(10)

FANP faces a large scale of TFNs from residual k numbers of triangular values achieved from eq. (9):

$$ V\left({M}_1\ge {M}_2\dots {M}_k\right)=V\left({M}_1\ge {M}_2\right),\dots, V\left({M}_1\ge {M}_k\right). $$
(11)

Equation (12) is applied to calculate the weight of indices in pairwise comparison matrices. Therefore, W(xi) can be calculated as follows:

$$ W\left({x}_i\right)=\mathit{\operatorname{Min}}\ \left\{V\ \left({S}_i\ge {S}_k\right)\right\}\kern0.50em \ \kern0.50em \ k=1,2,3,\dots, n\ \kern0.50em k\ne i. $$
(12)

Consequently, eq. (13) defines the weight vectors as follows:

$$ w\hbox{'}\left({X}_i\right)={\left[W\hbox{'}\left({C}_1\right),W\hbox{'}\left({C}_2\right),W\hbox{'}\left({C}_n\right)\right]}^T. $$
(13)

These values are the same as fuzzy AHP nonnormal coefficients. Therefore, eq. (14) provides the normal values of eq. (11). These normal values are called W as follows:

$$ {W}_i=\frac{{w_i}^{\hbox{'}}}{\sum {w_i}^{\hbox{'}}}. $$
(14)

Then, the correlation effect of the criteria is calculated. To do this, it is necessary to conduct pairwise comparison matrices. Eq. (15) is applied to calculate the relative correlation of criteria:

$$ {W}_c=B.W. $$
(15)

Results and discussion

Determining the criteria and subcriteria for portfolio selection

There are different criteria to be applied in portfolio selection. According to the performance measurement concept, diversity among different criteria in assessing the performance of a system or selecting an alternative is a challenge for decision-makers. In addition, most decision-making criteria are similar to each other whereby their concurrent consideration imposes extra costs on companies. As shown in section 2, there are 23 portfolio selection criteria that are more frequently applied in the previous literature. A Likert-type questionnaire was designed based on these 23 criteria. Then, experts were asked to complete it and specify their importance; that is, the experts determined the importance of each criterion to be applied in portfolio selection. Once the questionnaires were completed, the obtained data were analyzed, and the mean value of each criterion was determined. Table 3 shows the results obtained from the questionnaires. Figure 2 displays the FANP decision-making hierarchy applied in portfolio selection.

Table 3 Ranking of criteria
Full size table
Fig. 2
figure 2

FANP Decision Hierarchy

Full size image

Once the decision-making criteria and subcriteria are determined, it is critical to initiate the different steps of FANP. The first step is to compare the main criteria of portfolio selection. In the case of group decision-making, it is critical to aggregate experts’ comments into a single score. In other words, as discussed in section 3, FANP can be applied to both single and group decision-making problems. Table 4 shows the pairwise comparison matrix of the criteria.

Table 4 Pairwise comparison matrix of the criteria
Full size table

Decision-makers provide different judgments when comparing diverse alternatives. Therefore, it is difficult to track their previous judgments. Assume a decision-maker decides that A is more important than B. When B is also more important than C, it is logical to assume that A is more important than C. So, it is compulsory for judgments to be consistent and valid. According to Gogus and Boucher (1998), the inconsistency ratio should be less than 0.1 for all tables. Table 5 shows the calculated inconsistency. CRm and CRg represent the consistency ratio of the middle number of the triangular fuzzy matrix and the geometric mean of the first and last numbers of the triangular fuzzy matrix, respectively. Following the consistency approval of the calculations, the final weights of the criteria are normalized and tabulated (Table 6).

Table 5 Inconsistency test for criteria
Full size table
Table 6 Normalized weights of the criteria
Full size table

Weighting the subcriteria

Here, the weighting process of the subcriteria are discussed according to profitability, growth, market, and risk. Since the structure of the tables is similar, the required tables for profitability’s subcriteria are provided. The remaining tables can be found in the Appendix. The profitability subcriteria include earnings per share, net profit margin, and return on assets. Table 7 shows the pairwise comparison matrix of the profitability subcriteria. Similar to what was discussed in the previous section, the consistency condition of the calculations is checked and displayed in Table 8. Finally, all subcriteria are normalized, as shown in Table 9.

Table 7 Pairwise comparison matrix of profitability subcriteria
Full size table
Table 8 Inconsistency test for profitability subcriteria
Full size table
Table 9 Normalized weights of profitability subcriteria
Full size table

Similarly, three subcriteria were considered for growth: earnings per share growth rate, net profit growth rate, and revenue growth rate. Table 20 shows the pairwise comparison matrix of the growth subcriteria. Similar to what was discussed in the previous section, the consistency condition of the calculation is checked and tabulated in Table 21. Finally, all subcriteria are normalized and tabulated in Table 22. These tables can be found in the Appendix. Next, there are two subcriteria considered for the market: P/B and P/E. Table 23 shows the pairwise comparison matrix of the market subcriteria; the consistency condition of the market subcriteria is checked and tabulated in Table 24. Finally, Table 25 shows the normalized weight of all subcriteria. (See Appendix for these tables.) Three subcriteria were considered for risk: financial, market, and systematic risk. Table 26 shows the pairwise comparison matrix of the risk subcriteria. Next, the consistency condition of the calculation was checked (Table 27). Finally, Table 28 shows the normalized weights of all subcriteria. (See Appendix.)

Internal relations of Main criteria

An advantage of ANP/FANP over other MCDM techniques is that the internal relations among criteria are considered, which are shown in Table 10. For example, a relation exists between growth and profitability. Next, all criteria were compared using a pairwise comparison matrix (Table 11). Next, calculation consistency is tabulated in Table 12; Table 13 shows the normalized weights of the criteria.

Table 10 Internal relations among main criteria
Full size table
Table 11 Pairwise comparison matrix of related criteria
Full size table
Table 12 Inconsistency test for the pairwise comparison matrix of related criteria
Full size table
Table 13 Normalized weights of related criteria
Full size table

Weighting the alternatives with regard to subcriteria

Here, the weighting process for alternatives based on each subcriterion is discussed. All alternatives (A1–A10) are compared based on each subcriterion to determine their importance. Since the structure of the tables is similar, the tables for earnings per share are shown in the main text while the rest appear in the Appendix.

Profitability subcriteria

Table 14 shows the pairwise comparison matrix of alternatives based on earnings per share. Then, Table 15 shows the inconsistency results for the pairwise comparison matrix of alternatives based on earnings per share. Finally, Table 16 shows the normalized weights of alternatives.

Table 14 Pairwise comparison matrix of alternatives based on earnings per share
Full size table
Table 15 Inconsistency test for the pairwise comparison matrix of alternatives based on earnings per share
Full size table
Table 16 Normalized weights of alternatives based on earnings per share
Full size table

Table 29 shows the pairwise comparison matrix of alternatives based on net profit margin. Table 30 shows the inconsistency test for the pairwise comparison matrix of alternatives based on net profit margin. Table 31 shows the normalized weights of all alternatives. Table 32 shows the pairwise comparison matrix of alternatives based on return on assets, Table 33 the inconsistency test results, and Table 34 the normalized weights of alternatives based on return on assets. These can be found in the Appendix.

Growth subcriteria

Here, the comparison process of alternatives based on the growth subcriteria is considered. Table 35 shows the pairwise comparison matrix of alternatives based on the earnings per share growth rate. Table 36 shows the inconsistency test for the pairwise comparison matrix, and Table 37 shows the normalized weights of alternatives based on the earnings per share growth rate. Similarly, Table 38 shows the pairwise comparison matrix of alternatives based on the net profit margin. Table 39 shows the inconsistency test of the pairwise comparison matrix, and Table 40 shows the normalized weights of the alternatives. Table 41 shows the pairwise comparison matrix of alternatives based on revenue growth rate, Table 42 the calculated inconsistency values, and Table 43 the normalized weights of the alternatives. (See Appendix for all abovementioned tables.)

Market subcriteria

Table 44 shows the pairwise comparison matrix of alternatives based on P/B, Table 45 shows the consistency result, and Table 46 shows the normalized weights of the alternatives. Table 47 shows the pairwise comparison matrix of alternatives based on P/E, Table 48 the consistency results, and Table 49 the normalized weights of alternatives. (See Appendix.)

Risk subcriteria

Table 50 shows the pairwise comparison matrix of alternatives based on financial risk, Table 51 presents the consistency results, and Table 52 shows the normalized weights of the alternatives. Table 53 shows the pairwise comparison matrix of alternatives based on market risk, and Table 54 shows the consistency test results. Table 55 shows the normalized weights of alternatives, Table 56 the pairwise comparison matrix of alternatives based on systematic risk, and Table 57 the consistency test outputs. Table 58 shows the normalized weights of alternatives. (See Appendix.)

Results obtained using super decisions software

The pairwise comparison matrices and comparative results of alternatives based on each subcriterion were entered into Super Decisions software for the final calculations. Table 17 shows the final ranking of criteria. As shown, market, profitability, growth, and risk are the most important criteria for portfolio selection. Similarly, Table 18 shows the final ranking of the subcriteria. Finally, all alternatives were compared based on each subcriterion. Table 19 shows the final ranking of alternatives. Based on the results, an investor is advised to invest in A6; other alternatives include A7, A2, A4, A8, A1, A5, A3, A9, and A10. Figure 3 displays the results.

Table 17 Ranking of criteria
Full size table
Table 18 Ranking of subcriteria
Full size table
Table 19 Ranking of alternatives
Full size table
Fig. 3
figure 3

Ranking of portfolios

Full size image

Conclusion

Portfolio selection is an important topic in financial engineering. There are different approaches for assessing and selecting portfolios, including financial models and MCDM techniques, among others. Although these models are well developed in the literature, the important role of input data should not be ignored. Therefore, using real data in portfolio selection is recommended. To address this concern, this study used real data from the TSE. Specifically, the developed model and the required calculations were verified using outputs obtained from real TSE data. Specific criteria were developed, and an FANP model was applied for portfolio selection. In this process, first, a literature review was conducted to investigate portfolio selection criteria. Next, the developed criteria were examined with regard to their importance and priority using a Likert-type questionnaire administered to experts. Finally, an FANP model was applied to prioritize the considered portfolios.

This study has some implications for research. Importantly, MCDM techniques should be included in portfolio selection. This is supported by previous studies. Aouni et al. (2018), for example, investigated portfolio selection methods that went beyond mean and variance. Likewise, the present study aimed to provide a new approach for considering different criteria in portfolio selection. It is clear that the classic portfolio selection model developed by Markowitz (1952) cannot accommodate extra criteria beyond return and risk (Aouni et al. 2018).

This research also has implication for practitioners, decision-makers, and managers. The process of identifying criteria, determining their importance, applying them using FANP, and analyzing the results can be considered a step-by-step procedure for assessing and selecting portfolios. Importantly, this method can be applied to other real-world problems. Meanwhile, for industry, this study’s developed measures, research framework, and method can be used by engineers, managers, and investors to choose the best available industrial stock portfolios.

In future research, other MCDM models can be considered for portfolio selection, and the results can be compared with those of the present study. In addition, factor analysis and confirmatory factor analysis can be applied to develop specific criteria for portfolio selection. Finally, future studies can use flexible decision-support systems (e.g., MCDM-based software) for the concurrent consideration of all portfolio selection criteria.