Combined approach to estimate the depth of the magma surface in a shallow conduit at Aso volcano, Japan

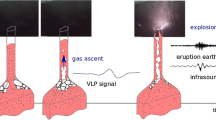
Abstract

Open-vent volcanoes provide opportunities to perform various methods of observation that can be used to study shallow plumbing systems. The depth of the magma–air interface in the shallow portion of the conduit can be used as an indicator of the volcanic activity of open-vent volcanoes. Although there are many methods used to estimate the depth, most of them cannot constrain the depth to a narrow range due to other unknown parameters. To constrain the depth more accurately, we combine two methods commonly used for estimating the depth of the magma–air interface. They consider the acoustic resonant frequency and the time delay of arrivals between the seismic and infrasound signals of explosions. Both methods have the same unknown parameters: the depth of the magma–air interface and the sound velocity inside the vent. Therefore, these unknowns are constrained so that both the observed resonant frequency and time delay can be explained simultaneously. We use seismo-acoustic data of Strombolian explosions recorded in the vicinity of Aso volcano, Japan, in 2015. The estimated depths and the sound velocities are 40–200 m and 300–680 m/s, respectively. The depth range is narrower than that of a previous study using only the time delay of arrivals. However, only a small amount of the observed data can be used for the estimation, as the rest of the data cannot provide realistic depths or sound velocities. In particular, a wide distribution of the observed time delay data cannot be explained by our simple assumptions. By considering a more complicated environment of explosions, such as source positions of explosions distributed across the whole surface of a lava pond in the conduit, most of the observed data can be used for estimation. This suggests that the factor controlling the observed time delay is not as simple as generally expected.

Graphic abstract

Introduction

Open-vent volcanoes provide a suitable environment for studying the complex magma supply system in shallow conduits. At these volcanoes, we can obtain time series data that directly reflect the source conditions of eruptions, such as infrasound, ejected material, volcanic gas temperature, and gas composition, as well as typically used data, such as seismic signals and ground surface deformation (e.g., Ripepe et al. 2009; Aiuppa et al. 2010; Andronico et al. 2013; Valade et al. 2016). Such multifaceted information contributes to a more vivid description of where the eruption is occurring and its characteristics.

The depth of the magma–air interface can be an important indicator of eruptive activities at open-vent volcanoes. This depth reflects the magma supply or the pressure in the plumbing system (Ripepe et al. 2005; Spina et al. 2015). By monitoring the level of the lava lake and ground surface deformation at Kilauea, the interaction between the summit reservoir and the flank eruption was shown (Patrick et al. 2015, 2019). In addition, the change in this depth can be a precursor of a major eruption. For example, a rise in the level of the lava lake was observed prior to the paroxysmal event at Villarrica volcano (Johnson et al. 2018b). This case implies that the monitoring of the magma–air interface depth can help to predict the next eruptive activity.

However, accurately constraining the depth of a magma–air interface is a challenging task. Although the best approach is to measure this depth from the crater rim directly, this is not possible at most volcanoes, because the magma surface in the conduit is not visible. In many cases, various records obtained at the time of the Strombolian explosions, such as the arrival-time delay between seismic and infrasound signals (Hagerty et al. 2000; Ruiz et al. 2006; Petersen and McNutt 2007; Sciotto et al. 2013; Richardson et al. 2014), the arrival-time delay between infrasound and thermal signals (Ripepe et al. 2002; Gurioli et al. 2014), the peak frequency and Q value of infrasound signals (Johnson et al. 2018a, b; Watson et al. 2019, 2020), the peak frequency and overtones of infrasound signals (Fee et al. 2010), the ballistic trajectories (Dürig et al. 2015; Tsunematsu et al. 2019), and the ejection velocity of particles (Taddeucci et al. 2012; Cigala et al. 2017; Salvatore et al. 2020), have been used to estimate this depth. The methods to estimate the depth of the magma–air interface using these records have some unknown parameters other than the depth. Such unknowns make it difficult to determine the depth itself accurately. It is a critical problem in understanding the situation inside the vent and predicting eruptive activity. In particular, if observed data show the time evolution during the eruptive period, it is not easy to judge which parameter effectively influences the time evolution of the data among the multiple unknowns. For example, the sound velocity in the vent is one of the unknown parameters required for the estimation using the peak frequency or the arrival time of infrasound signals (e.g., Johnson et al. 2018a). The sound velocity depends on the temperature of the gas and gas mass fraction (Morrissey and Chouet 2001). The change in the observed peak frequency or arrival time of the infrasound can be derived from either the change in depth or that in sound velocity. In one study, the change in the sound velocity was considered the primary cause of the variation in the observed data on the premise that the depth does not change (Ripepe et al. 2001). Other studies suggested that the depth must change with time, since the change in the observed data cannot be explained only by the change in the sound velocity (Sciotto et al. 2013; Richardson et al. 2014).

The uncertainty of the estimated depth of the magma–air interface may be improved by combining more than two methods already used in the literature. A multiparametric geophysical data set allows the estimation of the depth of the magma–air interface by such a combination of different methods. If Strombolian explosions occur, two methods can be applied to estimate the depth: one uses the peak frequency of infrasound signals, and the other uses the time delay of the arrivals of seismo-acoustic signals (Sciotto et al. 2013; Richardson et al. 2014). Both of these methods have the same unknowns: the depth of the magma–air interface and the sound velocity inside the vent. In some previous studies, when the sound velocity was given as a value inferred from the gas temperature at the vent, similar depths were estimated from both methods (Sciotto et al. 2013; Richardson et al. 2014). This suggests that the sound velocity can also be constrained by integrating these two methods.

In this study, we aim to accurately determine the depth of the magma–air interface by combining the two abovementioned methods for Aso volcano, Japan. At Aso volcano, the depth was previously estimated to be <400 m using the time delay of the arrivals of seismo-acoustic signals of Strombolian explosions (Ishii et al. 2019). However, the reliability of the estimated depth in this previous study is low, because the sound velocity inside the vent could not be uniquely determined. According to Yokoo et al. (2019), the infrasound signals observed at the volcano have a spectral structure with a distinct peak, suggesting acoustic resonance in the space of the conduit above the magma–air interface. Yokoo et al. (2019) pointed out that the depth of the magma–air interface can be estimated from the peak frequency of infrasound signals based on the results of the numerical simulation of propagating infrasound signals. Therefore, it is expected that the depth and the sound velocity that satisfy both the time delay of the signal arrivals (Ishii et al. 2019) and the peak frequency of the infrasound (Yokoo et al. 2019) can be constrained simultaneously. This combined method can make the uncertainty of the estimated depth small and lead to a more realistic understanding of the situation inside the vent. This method has the potential to be applied to the data recorded at any open-vent volcanoes (e.g., Villarrica, Etna, and Cotopaxi) in which (1) a clear peak frequency of infrasound signals suggesting conduit resonance is observed and (2) explosion events and associated seismic and infrasound signals are repeatedly observed.

Data

Seismo-acoustic data were acquired around the Nakadake 1st crater of Aso volcano. The magmatic eruption started at the crater in November 2014 and lasted until May 2015. Frequent Strombolian explosions and ash emissions were observed during this period overall (Yokoo and Miyabuchi 2015). We focused on the activity in April 2015, when Strombolian explosions occurred at a rate of once a few minutes (Ishii et al. 2019). The seismic and infrasound data used in this study were recorded at the stations of the observation network of Kyoto University nearest the active vent. A short-period seismometer (vertical component) and a low-frequency microphone were installed at stations KAF and ACM, respectively (Fig. 1a). Both stations were located on the western rim of the crater, $\sim$300 m from the vent. The sampling rate of the data was 100 Hz. We selected a total of 9 h of data when explosions were apparent in surveillance camera images and extracted 318 seismo-acoustic signals associated with explosions (Ishii et al. 2019). As shown in Fig. 1c, these infrasound signals are mainly composed of an approximately 0.5-Hz component derived from acoustic resonance in the conduit (Yokoo et al. 2019). This 0.5-Hz component is amplified at the explosion and superimposed by 2-Hz and 15-Hz components (Fig. 1c). The 15-Hz component typically had a time delay in the arrival time from those of the other components (Ishii et al. 2019). High-frequency seismic signals emerge $\sim$1 s prior to the arrival of the high-frequency infrasound signals (Fig. 1b).

Fig. 1

Station locations and observed signals. a Topographic map around the active crater of Aso volcano. The seismic station (KAF) and infrasound station (ACM) are located on the crater rim $\sim$300 m from the vent (black cross). During the eruptive period, a surveillance camera was also installed on the rim (white square) and captured an image every 20 s. b Seismic and c infrasound signals were sampled at a rate of 100 Hz. When a Strombolian explosion occurred, the seismic signal arrived prior to the infrasound signal. Two arrows show the arrivals of the seismic signal and high-frequency infrasound component ($\sim$15 Hz). The background of the infrasound signals is composed of a low-frequency component ($\sim$0.5-Hz) derived from acoustic resonance inside the vent (Yokoo et al. 2019). d, e Cross sections between the vent and stations. $L_\text {s}$ and $L_\text {i}$ are the propagation paths of the seismic and infrasound signals from the source of explosion toward the stations (Eqs. (2), (3))

Methods

We combined two methods commonly used to estimate the depth of the magma–air interface d: the first method uses the peak frequency of the infrasound signals $f_\text {0}$, and the second method uses the time delay of the arrivals between the seismic and infrasound signals $\Delta t$. Since both methods share the same unknown parameters, the depth of the magma–air interface d and sound velocity inside vent c, these two unknowns can be constrained by combining these two methods. The following subsections detail each method and how to combine them to determine the depth.

Peak frequency of infrasound signals

The first method assumes that the dominant frequency component of the infrasound signals is caused by resonance in the space of the conduit above the magma–air interface. This space of the conduit acts as a pipe resonator. The length of the pipe estimated from the observed resonant frequency can be assumed to be equivalent to the depth of the magma–air interface. The infrasound signals recorded at Aso volcano represent a distinct peak frequency ($\sim$0.5 Hz; Fig. 2a) throughout periods of the eruptive episode. This peak can be interpreted as the fundamental resonant frequency of a closed pipe (one end is closed and the other open; Yokoo et al. 2019). The resonant frequency of such a pipe is mainly controlled by its length, shape (e.g., cylinder, frustum, or horn), and sound velocity in the fluid-filled pipe. When estimating the length of the pipe from the peak frequency, it is common to assume both the shape and the sound velocity appropriately. Simple shapes such as a cylinder (Johnson et al. 2018b) or a Bessel horn (Richardson et al. 2014) are often used, because analytical solutions of resonant frequency exist for these shapes (Kinsler et al. 1999; Fletcher and Rossing 1998). On the other hand, the sound velocity in the pipe is usually inferred from a range of temperatures (over several hundred degrees) between the magma and the gas emissions from the vent. Thus, the sound velocity should change within a range of several hundred meters per second. Such a variation in the sound velocity can influence the reliability of the depth estimation. Watson et al. (2019) investigated the sensitivity of the infrasound signal to the temperature profile within the crater and suggested that the variation in the sound velocity has a smaller influence than the variation in the crater geometry. However, determining the appropriate sound velocity inside the vent is still a problem to solve. In this study, both the magma–air interface depth and the sound velocity were treated as unknown parameters, whereas the shape was assumed first, as described in the procedure below.

Fig. 2

Observed infrasound spectrum and distribution of its frequency ratio. a Amplitude spectra of the infrasound signals, calculated with 10-min waveforms. Gray lines show amplitude spectra provided from the data every 10 min of the 9-h subject period, and the black line is a smoothed spectrum of their average. The distinct peak is shown at $\sim$0.5 Hz ($f_\text {0}$), and some additional peaks exist at higher frequencies. The prominent peak among them is $\sim$2 Hz, corresponding to overtone $f_\text {1}$ of the acoustic resonance. b Distribution of the observed frequency ratio ($f_\text {1}/f_\text {0}$) and theoretical relationship between the frequency ratio and frustum radius ratio. The observed frequency ratio was calculated from the average amplitude spectrum of a (Additional file 3). The PDF of the frequency ratio is shown as a histogram. The black line is a theoretical relationship between the frequency ratio ($f_\text {1}/f_\text {0}$) and the radius ratio of the frustum of the open and closed ends ($a_\text {o}/a_\text {c}$), according to Ayers et al. (1985). The main four bins of the $f_\text {1}/f_\text {0}$ histogram correspond to $a_\text {o}/a_\text {c}$ values of 0.35, 0.43, 0.55, and 0.72 (dots and a cross on the black line). These values suggest that the shape of the space in the conduit widens as the depth increases. The PDF values of the four bins were used as weighting coefficients for the final summation of the results

The shape of the pipe can be constrained from the frequency of the overtones of infrasound signals. The spectrum of observed infrasound signals shows several peaks at frequencies higher than the fundamental frequency of 0.5 Hz (Fig. 2a). The peak at 2 Hz is especially noticeable whenever various surficial phenomena are observed (Yokoo et al. 2019). However, this 2-Hz component is not consistent with the first overtone of a closed cylindrical pipe with a fundamental frequency of 0.5 Hz. For a closed cylindrical pipe, the frequency of the first overtone $f_\text {1}$ is three times the fundamental frequency $f_\text {0}$ in theory. To yield both the observed frequencies of the fundamental and the first overtone, other pipe shapes must be considered. One candidate is a conical frustum (one end is closed). In this case, the frequency ratio between the first overtone and the fundamental mode ($f_\text {1}/f_\text {0}$) depends on the ratio of the radii of the open and closed ends ($a_{\text {o}}/a_{\text {c}}$). The theoretical resonant frequency f of such a conical frustum is represented as follows (Ayers et al. 1985):

$$\begin{aligned} \tan \Bigg ({\pi \frac{f}{f_{\text {open}}}}\Bigg )=\frac{1}{1-a_{\text {o}}/a_{\text {c}}}\Bigg (\pi \frac{f}{f_{\text {open}}}\Bigg ), \end{aligned}$$

(1)

where $f_{\text {open}}$ is the fundamental frequency for the open pipe and equals c/2l (l is the slant height of the frustum and c is the sound velocity; inset in Fig. 2b). Note that the notations are different from those of Ayers et al. (1985) (here, we replace B and $f_\text {0}$ in Eq. (6) of Ayers et al. (1985) with $a_{\text {o}}/a_{\text {c}}$ and $f_{\text {open}}$, respectively). By calculating the fundamental resonant frequency $f_\text {0}$ and the first overtone $f_\text {1}$ from this formula, it is found that $f_\text {1}/f_\text {0}$ is uniquely determined by $a_{\text {o}}/a_{\text {c}}$ alone, independent of vertical pipe length and sound velocity. The relationship of $f_\text {1}/f_\text {0}$ and $a_{\text {o}}/a_{\text {c}}$ according to Eq. (1) is shown in Fig. 2b. The distribution of the observed $f_\text {1}/f_\text {0}$ was calculated by reflecting the shape of the average amplitude spectrum of the 10-min window (Fig. 2a; Additional file 3). The distribution of $f_\text {1}/f_\text {0}$ indicates that $a_{\text {o}}/a_{\text {c}}$ is mostly in the range of 0.35–0.72 (Fig. 2b). Therefore, we assume four pipe shapes in this range of $a_{\text {o}}/a_{\text {c}}$ to estimate the depth of the magma–air interface. Considering that the radius of the vent on the crater floor was 25 m (Yokoo et al. 2019), the radii of the closed end of the four frustums were 35, 46, 58, and 71 m.

To understand the behavior of acoustic resonance in a volcano, we performed 3-D numerical simulations of infrasound signals. Assuming the pipe shape to be a frustum, we obtained the relationship among the two unknowns (the length of the pipe and sound velocity in the pipe) and the fundamental resonant frequency $f_\text {0}$. In a setting where a frustum pipe is connected to a flat plane (Additional file 2: Fig. S2–3a) and the sound velocity in the pipe is equivalent to that in the air (Additional file 2: Fig. S2–2), the computed $f_\text {0}$ roughly matches the theoretical solutions (Eq. (1); Fig. 3a; Additional file 2: Fig. S2–4a). However, assuming that the sound velocity inside the vent is higher than that outside the vent due to high temperatures (and assuming the density of the gas is lower than that outside the vent), the $f_\text {0}$ values provided by the simulation are lower than those expected from the theoretical solution (Fig. 3a; Additional file 2: Fig. S2–4d). Moreover, considering the actual case at Aso volcano, where a frustum pipe is situated at the center of the crater floor (Additional file 2: Fig. S2–3b), the computed $f_\text {0}$ becomes lower than that in the case of the flat plane (Fig. 3b). We used this computed relationship among the pipe length, the sound velocity, and $f_\text {0}$ instead of the theoretical solutions to estimate the depth of the magma–air interface. This relationship can be described as $f_\text {0} = {\mathcal {F}}(d, c)$, where the pipe length is d and the sound velocity in the pipe is c. The detailed settings and results of the numerical simulation are provided in Additional file 2.

Fig. 3

Frequency ratio of the fundamental resonant frequency between the theoretical values and numerical simulation results. The theoretical frequencies are calculated from Eq. (1). The simulations were performed under two conditions (Additional file 2: Figs. S2–3): a a frustum pipe is connected to a flat plane, and b a frustum pipe is situated at the center of the crater floor of Aso volcano. These figures show the cases, where the closed radius of the frustum ($a_\text {c}$) is 58 m. The sound velocities inside the vent were assumed to be 400 m/s, 600 m/s, 800 m/s, and $c_\text {air}$ (1-D profiles of the velocities are shown in Additional file 2: Fig. S2–2). At the high velocity inside the vent, the computed fundamental frequency is lower than the theoretical value (a, Additional file 2: Fig. S2–4d). The computed fundamental frequency with topography becomes slightly lower than that with a flat plane (b). The pipe lengths, indicated by the white-filled circles, cannot produce any overtone peaks of the amplitude spectra. c Amplitude spectra obtained from the simulations when $c = 600$ m/s and $a_\text {c} = 58$ m (with the volcanic topography). The black line shows the spectrum when the pipe length is 150 m, and the thin gray line shows the spectrum when the pipe length is 25 m. The spectral structure of the 150-m pipe is very similar to the observed structure (Fig. 2a). However, a very short pipe cannot make a clear two-peaked spectral structure such as that observed

An additional notable finding from the results of the simulations is that a short pipe cannot produce distinct overtones. Figure 3c shows the spectra of the simulated short and long pipes (25 and 150 m), where the sound velocity in the pipe is 600 m/s. The spectrum of the long pipe has a clear two-peaked structure similar to the observation (Fig. 2a). On the other hand, the short pipe yields ambiguous peaks that are far from the observed peaks. Only the length of the pipe whose spectral structure satisfies the following two conditions is used for the estimation: (1) the relative amplitude of overtone $f_\text {1}$ to that of the fundamental frequency $f_\text {0}$ is comparable to that observed, and (2) the minimal amplitude between $f_\text {0}$ and $f_\text {1}$ is small enough to form a two-peaked structure.

Time delay of arrivals of seismo-acoustic signals

The second method uses the time delay of arrivals between seismic and infrasound signals. The procedure of this method follows Ishii et al. (2019), who supposed that seismic and infrasound sources are colocated at the magma–air interface and that high-frequency seismic and infrasound signals (Fig. 1b, c) arise at the same time. Some studies assumed different source depths for the seismic and infrasound signals considering that the formation of a gas slug or the ascent of a slug before the explosion causes a low-frequency seismic signal (e.g., Ripepe et al. 2001; Harris and Ripepe 2007). However, the seismic signals observed at Aso volcano have a main energy of approximately 2–15 Hz. High-frequency seismic signals are generally regarded as signals related to the explosion itself (e.g., Harris and Ripepe 2007). At Aso volcano, the frequency range of 10–13 Hz is considered to be related to the explosion (Zobin and Sudo 2017). Therefore, this study assumes the colocated source of seismic and infrasound signals. The arrival times of seismic signals were manually determined using both the raw waveform and the high-pass filtered (>10 Hz) waveform (Additional file 1). The infrasound signal originating from the explosion is considered to be the component of 15 Hz (Ishii et al. 2019). Therefore, as in the case of seismic signals, the arrival time of the infrasound signal is comprehensively determined from the raw waveform and the >10 Hz high-pass filtered waveform (Additional file 1).

The time delay of the arrivals observed at the station ($\Delta t$) can be described as follows:

$$\begin{aligned} \Delta t = \frac{d}{c}+\frac{L_\text {i}-d}{c_\text {air}}-\frac{L_\text {s}}{v_\text {p}}. \end{aligned}$$

(2)

This equation shows that the time delay is derived from the different travel times between the seismic and infrasound signals. The path lengths of the seismic and infrasound signals are $L_\text {s}$ and $L_\text {i}$, respectively (Fig. 1d, e). These lengths are calculated from 1-m resolution digital elevation model (DEM) data of Aso volcano. The sound velocity in the air $c_\text {air}$ is determined from the 1-D profile of the sound velocity used for the numerical simulation (Additional file 2: Figs. S2–2). The initial phase of the seismic wave is assumed to be the P-wave, so its propagation velocity $v_\text {p}$ is 2.7 km/s (Tsutsui et al. 2003). By substituting these values into Eq. (2), it can represent a relationship between the two unknowns (the depth of the magma–air interface d and sound velocity inside the vent c) and observed $\Delta t$. This relationship can be described as $\Delta t = {\mathcal {G}}(d, c)$.

Combining the two methods

In this workflow, thus far, the relationship of the two unknown parameters, the depth of the magma–air interface d and the sound velocity inside the vent c, was acquired by each of the two methods ($f_\text {0}={\mathcal {F}}(d, c)$ and $\Delta t ={\mathcal {G}}(d, c)$). Both unknowns were then estimated by combining these relationships following three steps. First, the sound velocity inside the vent is described as a function of the depth and the fundamental frequency, $c = {\mathcal {F}}^{-1}(d, f_\text {0})$, by rearranging the relationship obtained from the numerical simulation. Then, by substituting this function into Eq. (2), a combined equation that is a function of only the depth and the observed parameters (the fundamental frequency $f_\text {0}$ and the time delay of the signal arrivals $\Delta t$) is obtained. Finally, this combined equation is solved for the depth of the magma–air interface when a pair of $f_\text {0}$ and $\Delta t$ values is given. The sound velocity is also determined by substituting the depth into the above function ${\mathcal {F}}^{-1}$. Only depths of <1000 m are considered a realistic range for Aso volcano. The sound velocity is limited to 300–800 m/s. This velocity range contains velocities calculated from the gas mass fraction reported for Strombolian explosions (0.67–0.94; Patrick 2007) and the temperature of magma and gas at Aso volcano (Ishii et al. 2019). The distribution of the pairs of observed parameters ($f_\text {0}$ and $\Delta t$) is shown as a probability density function (PDF) in Fig. 4a. This PDF is normalized so that the sum is 1. This distribution reflects the distribution of observed $\Delta t$ and the normalized spectral structure of the fundamental peak $f_\text {0}$, which is calculated from infrasound signals in a 40-s window for each event. The depth and sound velocity are calculated from all the pairs of $f_\text {0}$ and $\Delta t$ included in the area shown in Fig. 4a. The observed pairs included in the colored arcuate areas in Fig. 4b, c can provide realistic depths and sound velocities. The PDF value of each observed pair (Fig. 4a) is given to the depth and sound velocity estimated from that pair (see Additional file 3). The observed pair with a large PDF value provides highly probable depth and sound velocity results at the explosion. The magma–air interface depths are estimated using the four frustums (Fig. 2b), and the estimated results are then weighted and added together. The weighting coefficient of each shape is determined from the observed distribution of $f_\text {1}/f_\text {0}$ (Fig. 2b).

Fig. 4

PDF distribution of observed parameters and areas where the solutions exist for the combined equation. a PDF distribution of observed parameters ($f_\text {0}$ and $\Delta t$). This PDF is normalized so that the sum is 1. The PDF distribution of $f_\text {0}$ is centered at $\sim$0.5 Hz. The spectral structure of the amplitude spectrum of $f_\text {0}$ for each event is reflected in this distribution. The PDF distribution of the $\Delta t$ axis shows the variation in $\Delta t$ of all events. b, c The range of the observed parameters ($f_\text {0}$ and $\Delta t$), which can provide realistic depths and sound velocities inside the vent (colored arcuate areas). The colors show the values of estimated b depth and c sound velocity. These colored arcuate areas are narrow compared with the observed PDF distribution (gray contours). When the observed parameters included in the uncolored areas are substituted into the combined equation, the equation does not produce appropriate solutions. These figures show the cases in which the closed radius of the frustum pipe ($a_\text {c}$) is 58 m

Results

The two unknowns, the depth of the magma–air interface d and the sound velocity inside the vent c, are constrained by combining the two abovementioned methods. Estimated results were obtained as the 2-D PDF in a coordinate space of the depth and velocity (Fig. 5). The distribution of the 2-D PDF reflects the variation in the observed parameters (Additional file 3). We obtained four PDF distributions by assuming four frustum pipes. The individual PDF distributions for the four pipes show similar features (Fig. 5a–d); large PDF values are distributed at shallower depths (<200 m) and in wide ranges of the sound velocities. Then, we weighted and added these values using the coefficients determined from the distribution of the observed frequency ratio (Fig. 5e). The total PDF value in the area surrounded by the white line in Fig. 5e is equivalent to half the whole area. This suggests that magma–air interface depths and sound velocities within this area correspond to high probabilities. The depth range, including this area, was estimated to be 40–200 m (Fig. 5e). Previous research using only the time delay of signal arrivals estimated a wide range of 0–400 m (the area enclosed by a thin gray line in Fig. 5e; Ishii et al. 2019). Compared with that range, our estimated range is more limited. The corresponding shallower and deeper limits change by $\sim$40 m and $\sim$200 m, respectively. On the other hand, the sound velocity inside the vent is broadly distributed (300–680 m/s) over the assumed range (300–800 m/s) and cannot be strictly constrained in a narrower range. However, larger PDF values (brighter-colored area in Fig. 5e) are concentrated at lower velocities.

Fig. 5

2-D PDFs of two estimated unknown parameters. These unknowns are the depth of the magma–air interface and the sound velocity inside the vent. a–d PDFs assuming four frustum pipe radii ($a_\text {c}=$ 35, 46, 58, and 71 m, respectively). The results generally indicate that large PDF values are distributed at shallower depths (<200 m) and over wide sound velocity ranges. e Summed PDFs of these four results. The four PDF values are multiplied by the weighting coefficient of each shape, as determined from the observed PDF of $f_\text {1}/f_\text {0}$ (Fig. 2b) at the time of summation. The total PDF value in the region surrounded by a white line is equivalent to half the whole area. This region is at a depth of 40–200 m and a sound velocity of 300–680 m/s. The thin gray line is the estimated range from the previous study using only the time delay of arrivals (Ishii et al. 2019)

Discussion

Validity of the estimated depth and sound velocity results

The depth of the magma–air interface in the conduit at Aso volcano was estimated by the proposed method using both the peak frequency of infrasound signals and the time delay of arrivals between the seismic and infrasound signals (Fig. 5e). Our estimation constrains depths within a narrower range (40–200 m) than those of the previous research that considered only the time delay of the signal arrivals (0–400 m; Ishii et al. 2019). The deeper limit is approximately 200 m shallower than that in the previous study. The surficial phenomena observed during the eruptive period suggest that the deeper limit of the previous study (400 m) may be too deep. During the explosions, dispersion of incandescent bombs from the vent was usually observed. If the source of explosion had been deep in the conduit, bombs could not have reached up to the outside of the vent. The shallow depths of 40–200 m obtained in this study are more consistent with the actual surficial phenomena. In addition, the shallower limit of the estimated range is approximately 40 m deeper than that in the previous study. Since short-length (several tens of meters) pipes cannot produce the overtone of infrasound signals as observed (Fig. 3c), we eliminated the possibility of such shallow depths. In fact, the magma head in the vent was never visible from the crater rim during the eruptive period in 2014–2015. Therefore, the depth of the magma–air interface was most likely not very shallow. Tsunematsu et al. (2019) estimated the depth to be 11–13 m using ballistic trajectories at Aso volcano. Since such a shallow depth should not provide acoustic resonance, this result might be an underestimation. Tsunematsu et al. (2019) proposed a possible scenario in which the depth of explosion is different from the depth where the magma fragments begin to form parabolic trajectories. In this scenario, the fragments initially rise with the gas from the explosion source. Then, they are released from the gas flow and scattered in parabolic trajectories in the shallow region where the conduit widens. Although the diameter widening of the conduit in the shallow region has not been confirmed from our study, the discrepancy between our result and Tsunematsu et al. (2019) can support the scenario in which the depth of fragments scattering and that of explosion are different. Our constrained depths are also consistent with depths reported at other volcanoes with Strombolian explosions (e.g., <180 m at Stromboli and <130 m at Villarrica; Ripepe et al. 2002; Johnson et al. 2018b).

With this approach, the sound velocity inside the vent can be estimated during the depth of the magma–air interface estimation. The estimated velocities are broadly distributed in the assumed range (300–680 m/s; Fig. 5e). These velocities agree with those inferred from some observed temperatures. When Stromboli explosions occurred, the temperatures were measured by a thermal camera. The temperatures of the gas emissions from the vent and the bombs that landed around the vent were $\sim$100 $^\circ$C and 130–200 $^\circ$C, respectively. Although molten magma is hot (1000–1100 $^\circ$C), the temperature of the magma’s top cools in the air and can drop to <500 $^\circ$C, according to the deformation experiments of scoriae collected at Aso volcano (Namiki et al. 2018). If the gas–magma mixture in the resonant space of the conduit is as high as 100–500$^\circ$C, the sound velocity is 350–600 m/s given that the gas mass fraction is 0.67–0.94 (Patrick 2007). These velocities are equivalent to our estimated velocities. In addition, the velocity results with large PDF values seem to be slower (Fig. 5). This finding may imply that the average temperature in the vent normally tends to be relatively low and that it rises temporarily.

Validity of the assumed pipe shapes

In this study, some pipe shapes are assumed using the overtone of infrasound signals to constrain the depth and sound velocity inside the vent. The shape that could explain the observed overtones is a conical frustum flaring inside. This suggests that the use of overtone components of infrasound signals is an effective tool in constraining the pipe shape as previous work pointed out (Fee et al. 2010). It is difficult to judge if the assumed shape is realistic, because we could not observe the inside of the vent during the eruptive period. Some studies have reported that the horizontal scale of the internal cavity (pipe) can be larger than the diameter of the vent at the ground surface (e.g., Palma et al. 2008; Fee et al. 2010). Therefore, our assumed shape is not always unrealizable. However, this method simplifies the shape so much that it cannot be argued that our determined shape is the unique candidate. Determining the shape is not the main point of this study, so we will not discuss it further here, but determining the shape properly will still be an issue. When focusing on determining the crater shape, it may be useful to determine more realistic shape by iterative calculation to approach the observed frequency peaks or waveforms following Watson et al. (2019, 2020).

Interpretation of the variation in the time delay of signal arrivals

One of the notable problems to discuss is that only a small number of pairs of the observed parameters ($f_\text {0}$ and $\Delta t$) can be used for the estimation. The colored areas in Fig. 4b, c show the ranges of $f_\text {0}$ and $\Delta t$, where the solutions for the combined equation take realistic values (<1000 m and 300–800 m/s for the depth and sound velocity). However, these colored areas are significantly smaller than the distribution of the PDF of the observed $f_\text {0}$ and $\Delta t$. Therefore, most explosive events used in this study do not have any solutions. The total PDF value of the observed pairs ($f_\text {0}$ and $\Delta t$) included in the colored area becomes nothing more than $\sim$0.1. In particular, the observed $\Delta t$ varies from −0.15 s to 2.84 s, more widely distributed than the colored areas (Fig. 4). This wide distribution may suggest that $\Delta t$ is sensitive to some parameters other than the depth and sound velocity. Therefore, the distribution of observed $\Delta t$ should be explained rationally from the other aspects. Although the PDF of $f_\text {0}$ also seems to result in a widespread distribution, this is not essential because this distribution reflects the spectral structure of infrasound signals (Fig. 4a).

What can cause this wide distribution of the observed $\Delta t$? Common factors of variation in $\Delta t$ are the reading error of the signal arrivals or the fluctuation in the sound velocity outside the vent due to a change in wind or temperature. Since it is not easy to read the arrival time from noisy data, the accuracy of reading the time delay remains debatable. However, it is probably true that the time delay varies by about 2 s (Additional file 1). Even if the sound velocity in the air changes by ±20 m/s, only a $\sim$0.1 s variation in $\Delta t$ can occur, because the path length of the infrasound signal outside the vent is as short as 290 m (Fig. 1e). Therefore, such a wide distribution cannot be reproduced with only these errors.

Here, we consider a case in which the source position of the explosion changes horizontally along the magma–air interface for each event. We implicitly made two assumptions for the estimation of the depth in the method section. One is that the source of the explosion is located in the center of the conduit. Another is that the seismic signal generated at the source propagates to the station by a unique velocity. However, these assumptions may be oversimplifications. Therefore, we consider a slightly complicated situation of explosions that can occur everywhere on the surface of a lava pond inside the conduit, such as an example of Erebus volcano (Jones et al. 2008). In this case, the assumptions are modified to (1) the sources of the explosion are distributed over the entire surface of the lava pond and (2) the seismic signal generated at the source first propagates through the lava pond and then in the ground (Fig. 6). The propagation velocities are different between the lava pond and ground. When the source is located at a distance of r from the center of the lava pond and the propagation velocity of the seismic signal in the lava pond is $v_\text {p0}$ (Fig. 6), Eq. (2) can be rewritten as

$$\begin{aligned} \Delta t = \frac{\sqrt{d^2+r^2}}{c}+\frac{L_\text {i}-d}{c_\text {air}}-\left( \frac{a_\text {c}-r}{v_\text {p0}}+\frac{L'_\text {s}}{v_\text {p}} \right) . \end{aligned}$$

(3)

The first and third terms of Eq. (2), representing the travel times of the infrasound signals inside the vent and seismic signals, have been rewritten. The radius of the lava pond is identical to the radius of the closed end of the frustum pipe ($a_\text {c}$). The path length of the seismic signal between the margin of the lava pond and the station is indicated by $L'_\text {s}$.

Fig. 6

Schematic model of the shallow conduit of Aso volcano. Inside the active vent, a lava pond exists. The space above its magma–air interface is the shape of a frustum pipe and acts as a resonant pipe. The radius of the closed end of the frustum pipe $a_\text {c}$ is identical to that of the lava pond. Strombolian explosions occur at the surface of the lava pond. At the time of an explosion, seismic and infrasound signals are generated simultaneously at the source of explosion (SRC). The seismic signal propagates through the lava pond at a velocity of $v_\text {p0}$ and then propagates toward the station STA from the margin of the lava pond at P-wave velocity. The infrasound signal propagates through the air. The source position is expressed by a distance r from the center of the lava pond. We assumed that the sources are distributed across the entire surface of the lava pond (($0\le r \le a_\text {c}$)

When the depth and sound velocity are estimated using Eq. (3) instead of Eq. (2), the range of $\Delta t$, which can provide realistic depths and sound velocities, depends on the horizontal position of the source. For simplicity, the source positions are set at two endpoints along a radial line toward the station KAF, at the center and the margin of the lava pond ($r=0$ and $a_\text {c}$). For example, if the radius of the lava pond ($a_\text {c}$) is 58 m and the seismic propagation velocity in the lava pond ($v_\text {p0}$) is very low (here, as an example, the velocity is set to 23 m/s), the two arcuate colored areas in Fig. 7a represent the ranges of the observed parameters ($f_\text {0}$ and $\Delta t$) that can provide realistic solutions for the two sources ($r=0$ and 58). The change in the source position ($0\le r \le 58$) can reproduce the observed parameters ($f_\text {0}$ and $\Delta t$) in the area between the two arcs. Focusing on a case where $f_\text {0}=0.5$ Hz to simplify our discussion, the values of $\Delta t$ decrease when the source moves from the margin to the center (Fig. 7a). The lower bound increases as $v_\text {p0}$ increases, while the upper bound of $\Delta t$ does not change with $v_\text {p0}$ (black circles in Fig. 7a, b). Consequently, $v_\text {p0}$ increases, and the range between these bounds becomes narrower (Fig. 7c). Therefore, when $v_\text {p0}$ is small enough, the change in the source position may explain the wide distribution in the observed $\Delta t$.

Fig. 7

Ranges of the observed parameters that can provide realistic solutions for two source positions. a, b The colored arcuate areas show the ranges of the observed parameters ($f_\text {0}$ and $\Delta t$) with realistic solutions of the combined equation, assuming that the source positions of the explosions are at the center ($r = 0$) and the margin ($r = 58$) of the lava pond. The colors show the values of the estimated depth, as in Fig. 4b. The gray contours show the PDF distribution of the observed parameters (Fig. 4). Here, two cases are shown, where the seismic propagation velocities $v_\text {p0}$ are a 23 m/s and b 100 m/s. For simplicity, focusing on a case of $f_\text {0} = 0.5$ Hz (dotted line), $\Delta t$ when the source is at the center is smaller than that when the source is at the margin. If the source position changes within $0\le r \le 58$, the range of $\Delta t$ between the upper and lower bounds (black circles) can be reproduced in our model. c Ranges of $\Delta t$ between the bounds. The range narrows as $v_\text {p0}$ increases. However, the upper bound remains the same with increasing $v_\text {p0}$. The range also depends on the assumed radius of the lava pond $a_\text {c}$

However, no matter how much $v_\text {p0}$ changes, the observed large $\Delta t$ (>1 s) cannot fall between those two bounds. For example, if the same condition in Fig. 7a is applied ($a_\text {c} = 58$ m and $v_\text {p0} = 23$ m/s), the range of $\Delta t$ explained by the horizontal change in the source position extends from -1.59 to 1.06 s given $f_\text {0}=0.5$ Hz (Fig. 8b). Although the range is wide enough, the absolute values of $\Delta t$ included in this range are relatively small compared to the observed distribution of $\Delta t$ (Fig. 8c). The fraction of the PDF of $\Delta t$ within this range against the PDF in the whole range (dark-colored area/whole area of the distribution in Fig. 8c) reaches only $\sim$0.6 at most (Fig. 8h). This suggests that considering only the horizontal source position cannot explain all the variations in the observed $\Delta t$.

Fig. 8

Redefinition of the time delay of the arrivals of seismo-acoustic signals. a Seismic and infrasound waveforms and their arrivals. $\Delta t$ is the time delay between the seismic and high-frequency ($\sim$15 Hz) infrasound signals. $\Delta t'$ is that between the seismic and low-frequency ($\sim$2 Hz) infrasound signals. b Range of the time delay explained by the horizontal change in the source position when the seismic propagation velocity $v_\text {p0}$ is 23 m/s (same as Fig. 7c). c PDF distribution of the observed $\Delta t$ and d that of the observed $\Delta t'$ when $f_\text {0} = 0.5$ Hz. A case with $v_\text {p0}$ = 100 m/s is shown in e, f, and g. When $v_\text {p0}$ = 23 m/s, the range of time delays explained by the horizontal change in the source position is wide, as shown in b. Although the upper half of the distribution of $\Delta t$ is not included within the range of b (c), most of the distribution of $\Delta t'$ is included in this range (d). On the other hand, if $v_\text {p0}$ = 100 m/s, both distributions of $\Delta t$ and $\Delta t'$ cannot be completely included in the range of the time delays explained by the horizontal source change (f, g). h The fraction of the PDF of time delay explained by the horizontal change in source position against the PDF of time delay in the whole range (which means dark-colored area/whole area of the distribution in c, d, f, g). This fraction increases as the seismic propagation velocity $v_\text {p0}$ decreases. If $v_\text {p0} < 23$ m/s, the fraction becomes $\sim$0.9 for all four cases of the lava pond’s radii

To understand the wide distribution of observed $\Delta t$ more properly, we reconsider the definition of the time delay of signal arrivals. As mentioned in the method section, we assumed that high-frequency seismic and infrasound signals ($\sim$15 Hz) arise at the same time from the source of explosion on the magma surface. The waveforms of infrasound signals show that the low-frequency component ($\sim$2 Hz) arrives $\sim$0.3 s before the arrival of the high-frequency component (Fig. 8a, Ishii et al. 2019). Since such a low-frequency component can be derived from the swelling of the magma surface before an explosion (Delle Donne and Ripepe 2012; Goto et al. 2014), Ishii et al. (2019) assumed that no explosion occurred at the time of the low-frequency component excitation and that the seismic signal was synchronized with only the high-frequency component. However, here, we assumed that the arrival of this low-frequency infrasound and that of the high-frequency seismic signal have the same phases. The time delay of arrivals between the low-frequency infrasound and the high-frequency seismic signals is described as $\Delta t'$ (Fig. 8a). $\Delta t'$ becomes shorter than $\Delta t$, so that the distribution of observed $\Delta t'$ shifts in the negative direction of the time-delay axis compared with that of $\Delta t$ (Fig. 8d, g). This shift allows the majority of the observed $\Delta t'$ values to fall within the range of the time delay explained by the horizontal change in the source position. If $v_\text {p0}$ is <23 m/s, the fraction of the PDF of observed $\Delta t'$ within the range (dark-colored area/whole area of the distribution in Fig. 8d) becomes $\sim$0.9 for all four cases of the lava pond radius considered ($a_\text {c}=$ 35, 46, 58, and 71 m; Fig. 8h). Therefore, by assuming that the low-frequency infrasound signals are generated at the same time as the seismic excitation, the wide distribution of the time delay can be attributed to the change in the horizontal source position. However, the mechanism by which these seismic and infrasound signals are generated at the same time is still unclear. More detailed research will be needed to propose a specific source model in future work.

The seismic propagation velocity in the lava pond $v_\text {p0}$ needs to be low, several tens of meters per second, to explain the wide distribution of the observed time delay (Fig. 8h). A high-porosity medium could allow the seismic wave (P-wave) velocity to decrease to such low values (Dibble 1994). At Aso volcano, the uppermost portion of the magma column in the conduit would be a high-porosity (>0.7) foam layer (Namiki et al. 2018). Thus, it can realize a seismic velocity through the lava pond of several tens of meters per second.

Re-estimation of depth and sound velocity

Based on the above discussions, we estimated the depths and sound velocities inside the vent again by applying three modified assumptions: the consideration of the horizontal source positions, the low velocity of the seismic propagation in the lava pond, and the redefinition of the time delay of arrivals ($\Delta t'$). Ten sources are set along the same radial direction on the lava pond surface for convenience, and the estimated results of the depths and velocities for all the sources are summed. The seismic propagation velocity was assumed to be 23 m/s in the lava pond (Fig. 8h). As a result, the re-estimated magma–air interface depths and velocities are 40–200 m and 300–780 m/s, respectively (Fig. 9). This range of depths is the same as the range estimated before modifying the assumptions (Fig. 5e). Although the range of sound velocity extends slightly toward higher velocities than that shown in Fig. 5e, the features of the PDFs, such as the broad distribution and the bias toward low velocities, are similar. Since the number of observed pairs that used for the estimation increased, their total PDF value reaches $\sim$0.5. The total is less than $\sim$1 but more significant than before modification.

Fig. 9

Re-estimated 2-D PDF distribution of the estimated magma–air interface depth and sound velocity. The total PDF value in the region surrounded by a black line is equivalent to half the whole area. This region is at a depth of 40–200 m and a sound velocity of 300–780 m/s. The thin gray line shows the estimated range from the previous study using only the time delay of arrivals (Ishii et al. 2019). The dashed gray line is the estimated range of Fig. 5e. The pattern of this PDF distribution is very similar to that in Fig. 5e

The reasons why the total PDF value used for the estimation does not attain $\sim$1 are below. The first reason is the procedural problem in assuming the location of the source. For convenience, we assumed that only ten discrete sources are set. The space between the sources is not small enough, resulting in some events that do not have solutions. However, if the spacing is too small, the depth and sound velocity may not be uniquely determined from one observed pair ($f_\text {0}$ and $\Delta t'$). The second reason is that the colored areas with realistic solutions do not extend to the high-frequency $f_\text {0}$ area ($f_\text {0}>0.6$ Hz; Fig. 7a). However, it is not necessary to explain the spread of the PDF distribution in the $f_\text {0}$ axis direction, because the PDF distribution reflects the spectral structure of the infrasound signal (Fig. 4a). The final reason is that some events have long time delays that are impossible for our model to capture. No clear feature is common among the waveforms of these events, so we cannot determine why such long delays arise at this point. One possibility is that the time delay may appear to be long, because the initial phases of the infrasound signals are relatively small or unclear compared to typical events (Fig. 10).

Fig. 10

Example waveforms of seismo-acoustic signals. These waveforms have a a short time delay and b a long time delay of the arrivals. Dashed lines are the arrival times read manually. The solid line shows the time 1.12 s before the infrasound arrival. The maximum value of the time delay that can be reproduced by our model is 1.12 s. However, the time delay of example b seems to be longer than 1.12 s. Perhaps the initial phase of the infrasound signal was not excited well, causing the time delay to appear to be extended

Conclusions

We estimated the depth of the magma–air interface and the sound velocity inside the vent at Aso volcano simultaneously by combining two conventional methods: one considers the peak frequency of infrasound signals, and the other considers the time delay of arrivals of seismo-acoustic signals. The estimated depth is 40–200 m, which is a narrower range than the estimation of Ishii et al. (2019). In addition, the sound velocity is constrained to 300–680 m/s. However, only a part of the observed events was used for estimation due to the wide distribution of the time delay of the signal arrivals. We found that the wide distribution can be explained by incorporating the specific condition of the explosion into the model and defining the time delay of the signal arrivals appropriately. This suggests that the studied explosions were more complicated than expected. In particular, the observed time delay of arrivals may significantly reflect the complexity of the eruptive situation. However, in practice, it is better to first estimate the depth without considering such complexity of the explosion and then include it to explain the variation in observed values, if necessary. By applying the proposed method to temporal data in future work, it will be possible to estimate the time evolution of the depth of the magma–air interface in a conduit as in Richardson et al. (2014). This approach can be used to help to predict changes in eruption styles and to understand the shallow feeding system of open-vent volcanoes.