Abstract
We present the GFZ candidate field models for the \(13{\mathrm{th}}\) Generation International Geomagnetic Reference Field (IGRF-13). These candidates were derived from the Mag.num.IGRF13 geomagnetic core field model, which is constrained by Swarm satellite and ground observatory data from November 2013 to August 2019. Data were selected from magnetically quiet periods, and the model parameters have been obtained using an iteratively reweighted inversion scheme approximating a robust modified Huber norm as a measure of misfit. The root mean square misfit of the Mag.num.IGRF13 model to Swarm and observatory data is in the order of 3–5 nT for mid and low latitudes, with a maximum of 44 nT for the satellite east component data at high latitudes. The time-varying core field is described by order 6 splines and spherical harmonic coefficients up to degree and order 20. We note that the temporal variation of the core field component of the Mag.num.IGRF13 model is strongly damped and shows a smooth secular variation that suits well for the IGRF, where secular variation is represented as constant over 5-year intervals. Further, the external field is parameterised by a slowly varying part and a more rapidly varying part controlled by magnetic activity and interplanetary magnetic field proxies. Additionally, the Euler angles of the magnetic field sensor orientation are co-estimated. A widely discussed feature of the geomagnetic field is the South Atlantic Anomaly, a zone of weak and decreasing field strength stretching from southern Africa over to South America. The IGRF and Mag.num.IGRF13 indicate that the anomaly has developed a second, less pronounced eastern minimum at Earth’s surface since 2007. We observe that while the strong western minimum continues to drift westwards, the less pronounced eastern minimum currently drifts eastward at Earth’s surface. This does not seem to be linked to any eastward motion at the core–mantle boundary, but rather to intensity changes of westward drifting flux patches contributing to the observed surface field. Also, we report a sudden change in the secular variation measured at two South Atlantic observatories around 2015.0, which occurred shortly after the well-known jerk of 2014.0.

Similar content being viewed by others
Introduction
The observed geomagnetic field is a superposition of the dominating field generated in Earth’s outer core (the main field), remanent fields originating in the lithosphere, various contributions from electric current systems in the ionosphere and magnetosphere, and secondary fields that are induced mainly in the mantle. Geomagnetic core field models serve a wide variety of purposes, from practical applications such as navigation to scientific applications such as studies of core dynamo processes deep inside the Earth (e.g., Hulot et al. 2015). A widely used model in civil and scientific applications is the International Geomagnetic Reference Field (IGRF) that is updated every 5 years by the International Association of Geomagnetism and Aeronomy (IAGA). Here, we introduce the Mag.num.IGRF13 core field model (thereafter called Mag.num) that serves as parent for GFZ’s IGRF-13 candidate models, i.e. for a definitive model for epoch 2015.0 (DGRF 2015), a model for 2020.0 (IGRF 2020), and a prediction of the secular variation from 2020 to 2025 (SV). Data selection and processing are described in the data section, followed by the description of the modelling method and how the IGRF candidates were obtained from the parent model.
The South Atlantic Anomaly (SAA) is an area of low geomagnetic field intensity, strong westerly declination, and of a complex spatial pattern of inclination. The SAA has been developing since at least the 1600s in the South African region and has moved westward over the South Atlantic (Mandea et al. 2007; Hartmann and Pacca 2009). Its minimum is currently located over South America (Terra-Nova et al. 2017). The SAA is caused by magnetic flux patches at the core–mantle boundary (CMB) with magnetic flux opposite to the flux of the dominating dipole field direction in the Southern hemisphere.
The growth of the SAA might play an important role for the ongoing dipole decay (e.g. Bloxham and Gubbins 1985; Finlay et al. 2016a) and the magnetic field’s shielding is clearly reduced in that area (e.g. Heirtzler et al. 2002; Domingos et al. 2017). Some studies propose that it has an influence on climate and sea level change through an increased inflow of radiation energy in this weak field area (De Santis et al. 2012; Campuzano et al. 2018). Moreover, the SAA has been suggested as indicator for an impending field reversal or excursion (Gubbins 1987; De Santis et al. 2013; Tarduno et al. 2015). Note, however, that recent palaeomagnetic modelling results indicate that similar weak field structures in the vicinity of the South Atlantic occurred several times in the past 100,000 years and did not directly lead to excursions (Shah et al. 2016; Brown et al. 2018; Panovska et al. 2019). Here, we examine the most recent geomagnetic field development in the SAA region based on geomagnetic observatory data and the Mag.num model.
Data
Satellite data selection
Level 1B data of the three Swarm satellites were included from the beginning of the mission on 27th November 2013, up to 3rd August 2019, using baseline 05 as provided by ESA. These data are provided at 1 Hz temporal resolution, and have been sub-sampled to intervals of at least 20 seconds. In the following, low latitude refers to regions between \(\pm \, 55\) solar magnetic (SM) latitude. For these regions, data are rotated into the SM coordinate system. For the complementary high-latitude regions, data are expressed in the Earth-centred Earth-fixed North, East, Centre (NEC) coordinate system.
We apply the following selection criteria:
-
The z-component of the interplanetary magnetic field (IMF-\(B_z\)) is positive.
-
The large-scale magnetospheric field MMA_SHA_2F (Hamilton 2013) Swarm Level 2 product and its time derivative are lower than 40 nT and 40 nT/day, respectively.
-
Various quality flags indicate valid magnetic field and attitude information.
Additionally, only nighttime data are selected for low-latitude regions such that
-
Local time is between \(23\!\!:\!\!00\) and \(05\!\!:\!\!00\).
-
The sun is below the horizon at 100 km above Earth’s reference radius of 6371.2 km, corresponding to ionospheric altitudes.
These data selection criteria closely follow the approach of Lesur et al. (2008, 2010); Mandea et al. (2012); Rother et al. (2013).
Satellite difference data
Apart from the satellite vector measurements themselves, the along-track and cross-track differences between Swarm A and C can be used as a source of magnetic field information. External field contributions are notably reduced in these data, and we take advantage of this fact to construct a starting model for the iterative modelling process for Mag.num.
As described in the method section below, the coefficients of the final Mag.num model are obtained by inverting solely the vector field measurements themselves, not their differences.
The velocity of the Swarm satellites is sufficiently constant to calculate along-track differences for all three satellites using pairs of data with a constant temporal separation of 20 seconds. However, the estimation of cross-track differences requires a variable temporal separation to keep the inter-satellite distance constant. For a given data point i and the chosen distance \(D_0\), the paired data point j is found by minimising the following functional \(\phi \):
where \(f=5\) is a weighting factor, and \(D_{ij}\) and \(dt_{ij}\) are the actual distance and temporal separation between the two data points. Choosing \(D_0=160\) km leads to a time separation of about 20s.
In total, we used about 5.2 million cross-track and along-track difference data. Outliers caused by data gaps have been removed, leading to a rejection of \(12 \%\) of the original data set.
Observatory data selection
Additionally, we use observatory hourly mean values (HMV), spanning the period between January 2013 and July 2019, to better constrain secular variation. These data are distributed by ESA as Swarm AUX_OBS (baseline 01, version 20) (Macmillan and Olsen 2013), and are based on data stored at INTERMAGNET (https://www.intermagnet.org/) and the World Data Centre Edinburgh (http://www.wdc.bgs.ac.uk/).
Observatory data are selected to reduce external field contributions by applying the following criteria:
-
The Dst index (in form of the Swarm auxiliary data product AUX_Dst_2) is between \(\pm \, 30\) nT.
-
Local time is between \(23\!\!:\!\!00\) and \(05\!\!:\!\!00\).
-
The sun is below the horizon at 100 km above Earth’s reference radius of 6371.2 km.
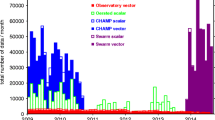
Obvious individual outliers were manually removed after a few iterations, as soon as the observatory offsets and external field parameters have converged. The temporal coverage of the selected observatory HMV is shown in Fig. 1.
Temporal data coverage of the observatory HMV after data selection in modified Julian days since 2000.0 from 2012-12-31 to 2019-06-27. Additional file 1: Table S1 links the observatory numbers to observatory names and locations
Method
Parameterisation
In the source-free region, the magnetic field can be described as the negative gradient of a scalar potential V associated with sources of internal and external origin, i.e.
where
and
Here, \(Y_{l}^{m}(\theta ,\phi )\) are the Schmidt semi-normalised spherical harmonics (SH) of degree l and order m, \(\theta , \phi , r\) and a are the geocentric co-latitude, longitude, satellite altitude and model reference radius, respectively, and \(g_l^m\) and \(q_l^m\) are the Gauss coefficients. We use the convention that negative orders are associated with \(\sin (|m|\phi )\) terms; whereas, positive orders (\(m\ge 0\)) are associated with \(\cos (m\phi )\) terms.
The internal sources consist of the time-varying core magnetic field, the quasi-static lithospheric field, and induced fields. The spatial signals of the core and lithospheric fields overlap, and we assume that the core magnetic field’s temporal evolution can be resolved up to SH degree and order \(L_i=20\) (c.f. Eq. 3). This temporal evolution is parametrised using order 6 B-splines basis functions \(\psi ^6_{i}(t)\) (de Boor 1978) which we define on the interval from December 31, 2012 to January 1st, 2020. This implies that the boundary nodes are not directly constrained by data. Overall, the time dependence of the Gauss coefficients is then given by
where \(g_{lj}^m\) are a set of spline coefficients for each Gauss coefficient \(g_l^m\). Here, we use a half-year knot separation, and \(N_t=9\) spline functions are used to represent each Gauss coefficient. Further, we set the reference radius of this large-scale field to \(a=3485~km\), the radius of the outer core. This choice has no influence on the inversion as we do not apply a regularisation constraint on the Gauss coefficients in spectral domain. For the core and the static SH degrees 21 to 30, the reference radius is set to the mean Earth radius of \(a=6371.2~km\). We do not aim to model the lithospheric field, and we subtract the Swarm auxiliary lithospheric field model (AUX_LIT_2) provided by ESA for SH degrees from 25 to 80 from the satellite data to avoid aliasing from unmodelled short wavelength field. We further co-estimate the remaining constant offsets for observatory data, so called observatory biases (Langel et al. (1982); see also Mandea and Langlais (2002); Macmillan and Thomson (2003)), which account for the unmodelled static lithospheric field of smaller spatial scales (Additional file 1: Table S1). Note, however, that due to the previous subtraction of the lithospheric field model, these biases do not reflect the full deviations from the core field. Moreover, induced fields are parameterised with one SH coefficient (degree one and order zero), and assumed to be proportional to the induced part, \(\text {MMA}_i\), of the Swarm MMA index (Hamilton 2013). The corresponding coefficient \(g_{1,j}^{0,\text {MMA}}\) serves as a scaling factor, and is estimated in \(N_e=14\) 6-month intervals such that
where \({{\mathcal {H}}}_j(x)=x, t \in [t_j,t_{j+1}]\) and is zero otherwise. For observatory data, we use a similar parameterisation, but the \(I_{st}\) index is used instead of the \(\text {MMA}_i\) index. The \(I_{st}\) index represents the induced part of the \(D_{st}\) index, and is derived using a 1D mantle conductivity profile as described by Maus and Weidelt (2004).
The external field is separated into a slowly varying part which is assumed to be constant over 30-day time intervals, and a more rapidly varying part. Concerning the slowly varying part, it is separated into a component that is described in Geocentric Solar Magnetic Coordinates (GSM) and another component that is described in Solar Magnetic (SM) coordinates. Both components are assumed to be large scale, and we use a maximum SH degree \(l=1\) such that
where \({{\mathcal {R}}}_{\text {GSM}}\) and \({{\mathcal {R}}}_{\text {SM}}\) are matrices rotating vectors defined in GSM and SM reference frames into the geocentric Earth fixed reference frame, respectively. Regarding the more rapidly varying part, it is separated into a component that scales with the Y-component of the Interplanetary Magnetic Field (IMF By) at a temporal resolution of 60 minutes, and another component that scales with the external part of the Swarm MMA index, \(\text {MMA}_e\), varying with the temporal resolution of one Swarm orbit, i.e. 90 minutes (Hamilton 2013). These components are completely described in SM coordinates, and given by
where the scaling coefficients \(q_{1j}^{m\,\,\text {MMA}}\), \(q_{1j}^{-1\,\,\text {IMF}}\), and \(q_{2j}^{0\,\,\text {MMA}}\) are assumed to be constant on 30-day time intervals. The external field coefficients were estimated independently for satellite and observatory data. For the latter, we additionally impose that \(q_{1j}^{0\,\,\text{SM}}=0\) to avoid co-linearities with the observatory crustal offsets. Also, we use the \(E_{st}\) index instead of the \(\text {MMA}_e\) index, analogous to Eq. 6.
In addition, the rotation angles between magnetic field vectors in the sensor reference frame and the satellite coordinate system are co-estimated in bins of fixed length (Rother et al. 2013). A bin-size of 27 days gives a good trade-off between maximising goodness-of-fit and minimising temporal variability of the estimated Euler angles. At low-latitude regions (between \(\pm \, 55\) solar magnetic latitude, see "Satellite data selection" section), however, the number of data per bin is not sufficient, and the local time selection criterion has been loosened for the purpose of Euler angle estimation in order to obtain a sufficient number of data (Rother et al. 2013). Any remaining bins with less than 1000 data points are ignored.
Iterative inversion scheme
The relationship between magnetic field vector measurements and the Gauss coefficients is linear and can be expressed as
where \({\mathbf {d}}\) is the data vector, \({\mathbf {m}}\) is the vector of Gauss coefficients, and \({\mathbf {G}}\) is the matrix linking the data to the Gauss coefficients according to Eqs. 2-8.
Due to unmodelled physical signals in the data, which will be considered as noise here, this equation cannot be solved directly. Instead, the Gauss coefficients are determined by minimising
where \({\mathbf {W}}\) contains the estimated data weights \(w_i\). Here, we neglect any cross-correlations between data errors and assume that \({\mathbf {W}}\) is diagonal.
Data weights should ideally represent the noise associated with data. The least-square fit yields the maximum likelihood solution if the data noise follows a Gaussian distribution. Here, we account for non-Gaussian noise distributions with larger tails, i.e. larger data outliers, using a modified Huber norm (Morschhauser et al. 2014; Lesur et al. 2015). In practice, this norm is approximated using iteratively re-weighted least-squares (Farquharson and Oldenburg 1998), and the weight of data point \(d_i\) at iteration \(j+1\) is given by
where \(\sigma _i\) corresponds to the assumed standard deviation (see Table 1), \({\mathbf {m}}^j\) refers to the estimated Gauss coefficients at iteration j, and \(k_i\) and \(a_i\) are parameters that account for the expected variability among different data subsets for this norm. In particular, this norm is based on a Gaussian distribution for data residuals lower or equal than \(k_i\), and \(a_i\) controls the shape of the underlying distribution’s tail such that lower values will have a larger tail. These parameters are chosen such that they represent the distribution of residuals from a preliminary model using an L2 norm (Table 1).
Noise, i.e. unmodelled signals in the data, will lead to an unstable model which will show unrealistically strong spatial and temporal field variations when downward continued. Therefore, we regularise our model by damping the third time derivative of the radial field component at Earth’s core radius c, i.e. by additionally minimising
over the whole time interval from beginning (\(t_1\)) to end (\(t_2\)) of the model. Further, the temporal end points of the model are explicitly damped to avoid oscillations due to the lack of data near the end points, by minimising
at times \(t=t_1\) and \(t=t_2\), i.e. both the second and first derivatives of the radial field at the temporal start and end points of the model. The damping parameters are often chosen such that the data misfit corresponds to the estimated noise level. Here, we choose a rather high damping parameter to obtain a smoothed model that suits well to IGRF’s constant secular variation within 5-year intervals, unlike a model that follows rapid SV variations more closely.
As described above, Mag.num is derived using a robust norm which is approximated using an iterative algorithm (Farquharson and Oldenburg 1998). Further, the estimation of Euler angles also introduces non-linearities, and requires an iterative inversion scheme (Rother et al. 2013). As starting model for the iterative process, we decided to use a model which entirely relies on Swarm satellite difference data (see data Section). The parameterisation of this Delta-model does not include any external fields as they are largely eliminated by considering differences only. As a result, the damping of the third time derivative (Eq. 12) was significantly reduced. Overall, the Delta model turned out to be a suitable and efficient starting model as it effectively reduces external field contributions and allows to reduce the number of required iterations.
IGRF-13 candidate models
The GFZ candidate model for DGRF-13 is a snapshot at epoch 2015.0 of the Mag.num parent model, truncated to degree and order 13. This epoch fully lies within the Mag.num time interval and is well covered by satellite and observatory data. Concerning the candidate for IGRF-13 at epoch 2020.0, data coverage did not reach the year 2020, still, we use a snapshot of Mag.num at 2020. This snapshot is a direct forecast which is considered relatively robust since temporal oscillations in the model have been strongly damped. Secular variation is not yet predictable by means of modelling. Therefore, we decided for a simple and conservative choice: the SV for 2020 to 2025 is approximated by the SV given by Mag.num at epoch 2019.0. This choice is justified by the good data coverage at this epoch. As an example, our secular variation prediction of \(g_1^0\) and \(g_2^0\) is shown in Fig. 2 (open red circle) along with the SV of the Mag.num parent model (purple line). For comparison, we also show SV as obtained from IGRF-12, with its predicted SV for 2015–2020 and the previous values calculated as linear 5-year SV from the main field coefficients (blue circles, see eq. 2 in Thébault et al. 2015). Mag.num is explicitly designed to describe the SV variabilities as they can be represented by IGRF. However, we note that the actual SV is more variable which is illustrated by the CHAOS model (grey line, Finlay et al. 2016b) that shows considerable non-linearities even within 5-year intervals. Our candidate models are compared to all other candidate models and the final IGRF-13 products by Alken et al. (2020a).
Two examples from low-degree coefficients (\(g_1^0\) and \(g_2^0\)) showing the secular variation from IGRF-12 (values for 1997.5 to 2012.5 calculated as linear SV from the adjacent main field coefficients), the Mag.num parent model and the more variable CHAOS-6 model. The red circle indicates our chosen value as predicted secular variation for the coefficients for 2020 to 2025, taken to be the SV of the parent model at epoch 2019.0
Model characteristics and validation
Geomagnetic power spectra
Geomagnetic power spectra for main field (MF), secular variation (SV) and secular acceleration (SA) are commonly used to compare different geomagnetic field models. In Fig. 3, the spectra from the Mag.num IGRF parent model for 2015.0 are shown in comparison to those of CHAOS6-x9 (Finlay et al. 2016). There is a close agreement between the models, both with respect to the MF and SV spectra. The much stronger regularisation of Mag.num, i.e. its weaker temporal variability, is reflected by a less energetic SA at low degrees (2–4) than that of CHAOS. The higher power at high SV and SA degrees (above 8) is of no concern as these degrees are not considered for the IGRF candidate models.
Data misfit and residuals
In Figs. 4 and 5, we show statistics and maps of the input satellite data residuals (after data selection and filtering) to the Mag.num IGRF parent model. The number of data, the mean of the residuals and the root mean square (rms) misfit between the data and the model are given in Table 2.
Histograms of the residuals for the three components X, Y, Z at low and mid latitudes in geocentric solar ecliptic coordinates for Swarm satellites Alpha (A, left), Bravo (B, middle) and Charlie (C, right) for the entire time of Mag.num. A Gaussian distribution corresponding to the calculated standard deviation (sd) of each distribution is indicated as black line. The distribution’s mean, skewness and excess kurtosis are given in the top right of each panel
As seen in Fig. 4, the distributions of residuals are close to but not fully Gaussian, all with positive excess kurtosis between 0.95 and 2.26. All have a nearly zero mean with very small skewness, indicating that no systematic biases are present for any of the components or satellites. The mapping of residuals in Fig. 5 confirms that the data are fit similarly well over all longitudes. For low and mid latitudes, the satellite data misfit amounts to no more than 3.2 nT for all components (Table 2). Higher residuals at high geomagnetic latitudes are expected as the high-latitude input data are more strongly influenced by external field signals, which should not be fit by the core field model. The average misfit here ranges from 14.1 nT in Z to 44.1 nT in the Y component (Table 2), and there are slight biases towards negative values in the X and Z and towards positive values in the Y component. The absolute average misfit of the additional satellite data that have been used for the Euler angle determination is slightly larger, but in the same order of magnitude as the input data, also with nearly zero mean. These data have not been used for the inversion of the core field model, and hence may serve as an independent benchmark. For the observatory data, the average misfit at low and mid latitudes lies between 3.6 and 5.1 nT, reaching up to 12.9 nT at high latitudes (Table 2). The mean and root mean square misfits for each observatory are given in Additional file 1: Table S1.
Comparison to independent observatory data
GFZ operates and supports a number of geomagnetic observatories (Korte et al. 2009; Matzka et al. 2010; Matzka 2016; Morschhauser et al. 2017), including geomagnetic observatories in the SAA region, e.g., Tristan da Cunha (TDC) (Matzka et al. 2009, 2011) and Saint Helena (SHE) (Korte et al. 2009) at \(15.87^\circ \)S and \(36.91^\circ \)S geocentric latitude, respectively. Both observatories are certified members of the INTERMAGNET global network. TDC was installed in 2009 and had to be relocated in 2018 due to contamination by noise. The Swarm AUX_OBS dataset does not contain TDC data after October 2016, and new data only exist since November 2018. SHE was installed in 2007, and data were recently re-calibrated to account for the effects of strong gradients in the crustal magnetic field on Saint Helena. SHE data are not contained in Swarm AUX_OBS, and hence were not used to construct the Mag.num model. We compare these two data sets with field predictions from Mag.num.
In particular, we calculate monthly mean values (MM) from calibrated hourly mean value (HMV) data of both observatories, and convert to geocentric coordinates. To approximate secular variation, finite differences are calculated based on these monthly means by
where \(MM_{t+6}\) is the value 6 months after the time of interest and \(MM_{t-6}\) the value 6 months before. This was done to avoid seasonal effects. The resulting approximated secular variation is shown in Fig. 6 and indicated by blue dots. For low-latitude observatories such as SHE and TDC, all components, and particularly the X (geocentric North), are affected by the magnetospheric ring current. Therefore, we additionally subtract the monthly mean values of the ring current magnetic field as predicted by the CHAOS6-x9 magnetospheric field model (Finlay et al. 2016b) from the estimated \(SV_t\) value. This results in much smoother estimates of secular variation (red dots). We note that a secular variation pulse (geomagnetic jerk) is observed in 2014 and is visible in the Y and Z components of both observatories. This jerk has been first reported by Torta et al. (2015), and was responsible for poor predictions of the SV in the IGRF-12 model. Additionally, a less prominent, but sudden change in secular variation is also observed in early 2015 for the Y component of both observatories, just 1 year after the jerk of 2015.0. No sudden changes in SV are observed later on.
Secular variation as derived from annual differences of observatory monthly means of a Tristan da Cunha (TDC) and b Saint Helena (SHE) geomagnetic observatories of the geocentric North (X), East (Y) and Vertical (Z) component (blue points). In addition, the external field description from the CHAOS6-x9 model was used to remove contributions of the magnetospheric ring current (RC), as shown by the red points. The black solid lines show the Mag.num IGRF parent model. The dashed lines are predictions from the CHAOS-6x9 model for comparison
Figure 6 shows how Mag.num (black solid line) and CHAOS6-x9 (black dashed line) fit the data of both observatories from 2015 to 2020. The good fit between Mag.num and this independent observatory data set, not included in the construction of the model, serves as a validation of the Mag.num secular variation estimates over this interval of time. The fact that Mag.num, unlike CHAOS-x9, does not fit the more rapid variations, such as the 2014 jerk, is expected and in agreement with the model’s design for low temporal variability.
Recent evolution of the South Atlantic Anomaly
At Earth’s surface
The South Atlantic Anomaly (SAA) is characterised by a longitudinally elongated minimum at Earth’s surface. The minimum of the SAA has been drifting westwards from the south-western coast of Africa in 1700 to its present position over Brazil (Hartmann and Pacca 2009). In recent years, the development of a second, eastern minimum within the SAA at Earth’s surface has been observed at around 5\(^{\circ }\) W, 40\(^{\circ }\) S (see also Fig. 7) and it was first reported by Terra-Nova et al. (2019). Figure 7a, b illustrate the SAA and the two minima in field intensity F as predicted by Mag.num at Earth’s surface for epochs 2013.0 and 2020.0, respectively. The (field intensity) isodynamic lines of the values at the saddle points (24.48 and 24.06 \(\mu \)T, respectively) between the minima are marked in black. In addition, Fig. 7c shows the field for epoch 2020.0 at the reference satellite altitude of 450 km. The best-fit great circle arc connecting the time-averaged (from 2013.0 to 2020.0) locations of the two minima and of the saddle point at Earth’s surface is also shown (red line).
Magnetic field intensity in the South Atlantic and South America with the two minima of the SAA (symbols) and the contour line going through the saddle point between them (black line) at Earth’s surface for a 2013.0 and b 2020.0 from the Mag.num model. White contour lines are given at every \(0.5\mu \text {T}\). The same is shown for a satellite altitude of 450 km in (c) with regular black contour lines every \(\mu \) T. The red line is the time average great circle fitted to the set of minima and saddle points from 2013.0 to 2020.0. Profiles of field intensity along this great circle are shown for Earth’s surface and satellite altitude from 2013.0 to 2020.0 in (d)
The locations of SAA main minimum (top left), saddle point (top right) and second minimum (bottom left) for all IGRF candidate models are shown as an indication of the robustness of the results from our Mag.num model (blue cross). Minima and saddle point have been determined from a 0.05\(^\circ \) grid and in some cases the same value is found on two or more grid points
Realistic model uncertainties cannot be derived directly from standard spherical harmonic models. To estimate the robustness of the second minimum and the reliability of the following analysis based on the Mag.num model, we compared the results from all IGRF candidate models for the locations of SAA minima and saddle point. Figure 8 shows close agreement among all models, with the different results falling within ±0.1\(^\circ \) of latitude and mostly ± 0.4\(^\circ \) of longitude from the average location for all three points. The Mag.num results lie well within this range in all cases. The sharp main minimum seems most robustly resolved, while uncertainties in longitude are somewhat larger for the flatter saddle point and second minimum, but still well separated in all models. Figure 7d shows the intensity profiles along the red line of panels a–c for the two reference altitudes and the two epochs, indicating the intensity evolution of the SAA. Due to geometric attenuation with distance from the source, i.e. the geodynamo in Earth’s core, a plateau, but no clear second minimum, is observed at the typical satellite altitude of 450 km (see Fig. 7c, d). To study the evolution of the SAA over a longer time scale, we plot the longitudes of the SAA minima and of the saddle point between them as predicted by the IGRF model from 1900.0 and 2020.0 in the 5-year IGRF intervals (Fig. 9). The western, main minimum is depicted by cyan circles. The secondary minimum (light blue triangles) and the saddle point (green triangles) are not present before 2005.0. In addition, the corresponding predictions by Mag.num are shown by black, purple, and orange solid lines with an annual resolution for the epochs 2013.0 to 2020.0, and the magenta line shows the longitude of the main minimum at 450 km altitude. According to Fig. 9, the western intensity minimum keeps drifting westward at a nearly constant rate of about 0.2 \(^{\circ }\)/year (since 1940 at a nearly constant latitude of around 26\(^{\circ }\)S). The new eastern minimum comes into existence between 2005 and 2010 (our best estimate is the year 2007) and drifts eastward with an average rate of 0.25\(^{\circ }\)/year at a latitude of about 41\(^{\circ }\)S. The saddle point, on the other hand, is moving westward at about 0.9\(^{\circ }\)/year close to 40\(^{\circ }\)S, contributing considerably to the growth of the area of the eastern minimum from 2013 to 2020 (see Fig. 7a, b). The drifts of western minimum and saddle point most likely continue according to both the Mag.num and also the final IGRF-13 (Alken et al. 2020b) predictions, as shown by the red squares and blue crosses, respectively. The drift of the eastern minimum has already slowed down in recent years, and the models predict that it will not drift further eastward in the next 5 years. The field strength in the eastern minimum decreased faster, by about \(0.5 \, \upmu \text {T}\) over the 7 years from 2013 to 2020, compared to less than half of that in the western minimum (Fig. 7d). However, we note that with values around 23.5 both Mag.num and IGRF-13 predict values similar as today for the eastern minimum in 2025. The field intensity of the western minimum, on the other hand, lies at 22.25 \(\upmu \)T in 2020 according to Mag.num and will further decrease to about 22.1 \(\upmu \)T according to both Mag.num and IGRF-13.
At the core–mantle boundary
The SAA is associated with reverse flux patches (RFPs) at the core–mantle boundary (Fig. 10a), but Terra-Nova et al. (2017) showed that it is not straightforward to link RFPs and the SAA minimum. Their analysis suggests that the location of the surface intensity minimum is determined by the combined influence of reverse and normal flux patches. Here, we restrict ourselves to a qualitative analysis of the RFPs at the core–mantle boundary. Downward continued maps of the radial field at the CMB derived from Mag.num predictions show four–five RFPs (positive Z, reddish colours) in the area from 0\(^{\circ }\) to 60\(^{\circ }\) S and 80\(^{\circ }\) W to 20\(^{\circ }\) E (Fig. 10). With the exception of a nearly stationary RFP near the tip of South America (c.f. RFP 1 in Table 3, see also next section) and a similarly stationary strong normal flux patch at the West coast of Africa (c.f. NFP 1 in Table 3, see also next section) all of them have drifted westward by a few degrees over the 7 years. The eastern local minimum at Earth’s surface (ca. 0\(^\circ \) N, 40\(^\circ \) S) is located above an area of weak normal flux at the CMB. Its apparent eastward drift seems to be caused mostly by the intensification of the RFP to its east (under southern Africa) compared to weaker changes of the RFP in the middle of the Atlantic and the normal patch south of that.
Linking the CMB and surface observations
Under the assumption of a source-free mantle, the surface field intensity expression of the South Atlantic Anomaly (SAA) is connected to the flux pattern at the CMB by the Laplace equation, and the mantle acts as a wavelength-dependent filter.
Finlay et al. (2020) used an analytical method to identify the features at the CMB that relate to the observed SAA minima at the surface. Here, we follow a more qualitative approach by tracking the field minima of the SAA down to the CMB. For this purpose, we investigate the field morphology at different levels within the mantle as predicted by Mag.num. We note that this analysis does not provide any physical interpretation, but is rather a discussion of downward continuation of a potential field as described by the Laplace equation.
Intensity (F, a–c) and vertical component (Z, d–f) for three depths, namely the reference Earth surface radius (0 km), 1600 km, and 2400 km. Several extrema in both field components are labelled and further information about them is given in Table 3. The black line in (a) is the contour line through the saddle point, the black line in (d) indicates the magnetic equator, and the red line in (a, d) indicates the great circle profile as shown in Fig. 7
In Fig. 11, we show the field intensity (F) (panels a–c) and the vertical field component (Z) (panels d–f) in 2020, both at levels of the Earth’s reference surface radius (panels a and d), at 1600 km (b and e), and at 2400 km (c and f) depth. Additional file 2: Figure S1 provides a more detailed view with a comparison of F in 2013 and 2020, and Z in 2020, all at levels of 0, 800, 1600, 2000, 2400 km and at the CMB depth of 2886.2 km. In maps showing F (Fig. 11a–c, Additional file 2: Figure S1), minima (blue) and maxima (orange) are labelled by numbers 1–7. In maps showing Z, patches are numbered 1–10, with normal flux patches (NFP, \(Z < 0\)) shown in green and blue, and reversed flux patches (RFP, \(Z > 0\)) shown in orange. Note that, as expected, some patches merge or disappear with increasing distance from the CMB. Table 3 lists information about the labelled extrema in F and flux patches in Z for the investigated depths, in particular including changes in their locations and strengths from 2013 to 2020.
Minimum 1 corresponds to the westward drifting main minimum of the SAA and is visible throughout the mantle. Looking at Z, it is linked to RFP 1 and its extension to the north. Minimum 2 corresponds to the eastward drifting, new eastern minimum in the SAA. It is also visible throughout the mantle, and grows to a northeast–southwesterly elongated zone of low F at 2400 km depth that also includes minimum 7. This zone is spatially linked to RFP 2, 7 and 8 at the CMB (see Additional file 2: Figure S1, the latter two have merged at 2400 km). We further note that RFP 5 and NFP 6 cancel out at 1600 km and above, leading to the rather flat area of F in the centre of our map at 1600 km depth (Fig. 11b). Interestingly, the new eastern minimum (2) is significantly larger in area and lower in F than the main minimum (1) at depths of 800–2400 km, i.e. throughout the mantle. Following table 3, minimum 2 reaches a value in F as low as 1363 nT at 2000 km depth, less than 10% of F at all other considered depth levels. Regarding the development of field strength of minimum 2 from 2013 to 2020 (c.f. Table 3), we observe a decrease in F at depths down to 2000 km (i.e. a deeper minimum in 2020 than 2013). Overall, F in minimum 2 decreased faster than in minimum 1, by at least a factor of 2 (dF in Table 3). Note, however, that the interpretation of weak F as an anomaly becomes less suitable with depth due to the increasing complexity of the field towards the CMB.
We expect that minimum 2 will probably either disappear with time, or it will grow (as it currently does) and then, controlled by the underlying westward drifting minimum, automatically turn into a westward drifting feature. The fast decrease of F in the eastern minimum 2 suggests that the latter scenario could be more likely. In this scenario, the region of anomalously low geomagnetic field strength stays in the South Atlantic region despite the general westward trend of the geomagnetic field, by a mechanism of formation of new minima of geomagnetic field strength at the eastern edge of the South Atlantic Anomaly.
Conclusions
We have presented Mag.num, the GFZ parent model for IGRF-13, derived using Swarm satellite and ground observatory data. The modelling method closely follows that of earlier developments (in particular the GRIMM models, see Lesur et al. 2008; Rother et al. 2013). A main modification is that an interim model based on Swarm along- and cross-track differences is used as a starting model for the iterative modelling process. This starting model has minimum external field influence and reduces the required number of iterations. Considering that the IGRF consists only of snapshots in 5-year intervals, we present a strongly regularised model version. This model does not reproduce rapid secular variation changes such as the jerk around 2014.0 and the sudden change in secular variation around 2015.0 that we report here for the South Atlantic observatories on the islands St. Helena and Tristan da Cunha. We chose the Mag.num parent model secular variation at epoch 2019.0 as estimate for the secular variation from 2020 to 2025.
Using the IGRF and Mag.num, we investigated the recent evolution of the SAA and in particular a second, less pronounced eastern minimum which has developed since 2007. A plateau is found in field intensity above the eastern minimum at satellite altitude, but due to the attenuation with increasing distance from the source no clear minimum is seen there. Contrary to the movement of the pronounced western minimum and the SAA as a whole, which have clearly and continuously drifted westward over the past decades, the eastern minimum has drifted slightly eastward at Earth’s surface. However, an analysis of the magnetic flux distribution at the CMB revealed that all reverse flux patches drift slightly westward, and the apparent eastward drift at Earth’s surface must be a result of intensity changes of different flux patches. Our investigation of magnetic field maps at 0, 800, 1600, 2000 2400 km depths and at the CMB for 2013 and 2020 provides a comprehensive description of the geomagnetic field variation in the SAA region between the CMB and Earth’s surface, as well as in time. The secondary eastern minimum is found to be a relatively weak surface expression of a remarkable subsurface area of weak intensity. At depths between 800 km and 2400 km, this eastern low intensity area is more pronounced than the intensity low associated with the western main minimum of the SAA at Earth’s surface. Additionally, the field intensity in the eastern minimum and the associated subsurface field has decreased faster from 2013 to 2020 than the intensity in and below the western main minimum of the SAA. The eastern minimum’s current eastward drift at Earth surface, however, seems to be an ephemeral feature of the magnetic field, caused by waxing and waning, rather than eastwards drifting field structures closer to the geodynamo source in the core. The formation of new minima of geomagnetic field strength at the South Atlantic Anomaly’s eastern edge provides a mechanism to keep the South Atlantic Anomaly more or less stationary despite the westward drift of the geomagnetic field.
Mag.num models, including less strongly regularised versions with higher temporal variability, are maintained and updated with most recent data on a regular basis. Mag.num model coefficients are available at https://www.gfz-potsdam.de/magmodels/.
Availability of data and materials
The satellite and observatory data used to generate the Mag.num models are available from the European Space agency at the website https://earth.esa.int/web/guest/swarm/data-access. The model coefficients are available at https://www.gfz-potsdam.de/magmodels/.
Abbreviations
- IGRF:
-
International geomagnetic reference field
- IAGA:
-
International Association of Geomagnetism and Aeronomy
- GFZ:
-
German Research Centre for Geosciences
- DGRF:
-
Definitive geomagnetic reference field
- SV:
-
Secular variation
- SAA:
-
South Atlantic Anomaly
- SM:
-
Solar magnetic coordinate system
- GSM:
-
Geocentric solar magnetic coordinates
- NEC:
-
North, East, Centre local coordinate system
- IMF:
-
Interplanetary magnetic field
- HMV:
-
Hourly mean values
- SH:
-
Spherical harmonics
- ESA:
-
European Space Agency
- MMA:
-
Fast-Track magnetospheric model
- MF:
-
Main field
- TDC:
-
Tristan da Cunha
- SHE:
-
Saint Helena
- RC:
-
Ring current
- INTERMAGNET:
-
International Real-time Magnetic Observatory Network
- CMB:
-
Core–Mantle Boundary
- RFP:
-
Reverse flux patches
- NFP:
-
Normal flux patches
- GRIMM:
-
GFZ Reference internal magnetic model
References
Alken P, Thébault E, Beggan CD, Aubert J, Baerenzung J, Brown WJ, Califf S, Chulliat A, Cox GA, Finlay CC, Fournier A, Gillet N, Hammer MD, Holschneider M, Hulot G, Korte M, Lesur V, Livermore PW, Lowes FJ, Macmillan S, Nair M, Olsen N, Ropp G, Rother M, Schnepf NR, Stolle C, Toh H, Vervelidou F, Vigneron P, Wardinski I (2020a) Evaluation of candidate models for the 13th generation International Geomagnetic Reference Field. Earth Planets Space. https://doi.org/10.1186/s40623-020-01281-4
Alken P, Th́ebault E, Beggan CD, Amit H, Aubert J, Baerenzung J, Bondar TN, Brown W, Califf S, Chambodut A, Chulliat A, Cox G, Finlay CC, Fournier A, Gillet N, Grayver A, Hammer MD, Holschneider M, Huder L, Hulot G, Jager T, Kloss C, Korte M, Kuang W, Kuvshinov A, Langlais B, Ĺeger JM, Lesur V, Livermore PW, Lowes FJ, Macmillan S, Mound JE, Nair M, Nakano S, Olsen N, Pav́on-Carrasco FJ, Petrov VG, Ropp G, Rother M, Sabaka TJ, Sanchez S, Saturnino D, Schnepf NR, Shen X, Stolle C, Tangborn A, Tøffner-Clausen L, Toh H, Torta JM, Varner J, Vervelidou F, Vigneron P, Wardinski I, Wicht J, Woods A, Yang Y, Zeren Z, Zhou B (2020b) International Geomagnetic Reference Field: the thirteenth generation. Earth Planets Space. https://doi.org/10.1186/s40623-020-01288-x
Bloxham J, Gubbins D (1985) The secular variation of the Earth’s magnetic field. Nature 317:777–781
Brown MC, Korte M, Holme R, Wardinski I, Gunnarson S (2018) Earth’s magnetic field is probably not reversing. Proc Nat Acad Sci 115:5111–5116
Campuzano SA, De Santis A, Pavón-Carrasco FJ, Osete ML, Qamili E (2018) New perspectives in the study of the Earth’s magnetic field and climate connection: the use of transfer entropy. PloS ONE 13(11):e0207270
de Boor C (1978) A Practical Guide to Splines. Springer, New York
De Santis A, Qamili E, Wu L (2013) Toward a possible next geomagnetic transition? Nat Hazards Earth Syst Sci 13:3395–3403
De Santis A, Qamili E, Spada G, Gasperini P (2012) Geomagnetic South Atlantic Anomaly and global sea level rise: a direct connection? J Atmos Solar Terres Phys 74:129–135
Domingos J, Jault D, Pais M, Mandea M (2017) The South Atlantic Anomaly throughout the solar cycle. Earth Planet Sci Lett 473:154–163
Farquharson CG, Oldenburg DW (1998) Non-linear inversion using general measures of data misfit and model structure. Geophys J Int 134(1):213–227
Finlay CC, Aubert J, Gillet N (2016a) Gyre-driven decay of the Earth’s magnetic dipole. Nat Commun 7:10422. https://doi.org/10.1038/ncomms10422
Finlay CC, Olsen N, Kotsiaros S, Gillet N, Toeffner-Clausen L (2016b) Recent geomagnetic secular variation from Swarm and ground observatories as estimated in the CHAOS-6 geomagnetic field model. Earth Planets Space 68:112. https://doi.org/10.1186/s40623-016-0486-1
Finlay CC, Kloss C, Olsen N, Hammer MD, Tøffner-Clausen L, Grayver A, Kuvshinov A (2020) The CHAOS-7 geomagnetic field model and observed changes in the South Atlantic Anomaly. Earth Planets Space 72:12. https://doi.org/10.1186/s40623-020-01252-9
Gubbins D (1987) Mechanism for geomagnetic polarity reversals. Nature 326:167–169
Hamilton B (2013) Rapid modelling of the large-scale magnetospheric field from Swarm satellite data. Earth Planets Space 65:1295–1308. https://doi.org/10.5047/eps.2013.09.003
Hartmann GA, Pacca IG (2009) Time evolution of the South Atlantic Magnetic Anomaly. Ann Braz Acad Sci 81:243–255
Heirtzler JR, Allen JH, Wilkinson DC (2002) Ever-present South Atlantic Anomaly damages spacecraft. Eos Trans Am Geophys Union 83(15):165–169. https://doi.org/10.1029/2002EO000105
Hulot G, Sabaka TJ, Olsen N, Fournier A (2015) The present and future geomagnetic field. In: Schubert G (ed) Treatise on geophysics, vol 5, 2nd edn. Elsevier, New York, pp 33–78
Korte M, Mandea M, Linthe H-J, Hemshorn A, Kotzé P, Ricaldi E (2009) New geomagnetic field observations in the South Atlantic Anomaly region. Ann Geophys 52:65–81
Langel RA, Estes RH, Mead GD (1982) Some new methods in geomagnetic field modeling applied to the 1960–1980 epoch. J Geomagnet Geoelectric 34(6):327–349
Lesur V, Wardinski I, Rother M, Mandea M (2008) GRIMM: the GFZ Reference Internal Magnetic Model based on vector satellite and observatory data. Geophys J Int 173:382–394. https://doi.org/10.1111/j.1365-246X.2008.03724.x
Lesur V, Olsen N, Thomson A (2010) Geomagnetic core field models in the satellite era. In: Mandea M, Korte M (eds) Geomagnetic observations and models, IAGA book series, vol 5. Springer, Berlin, pp 277–294
Lesur V, Rother M, Wardinski I, Schachtschneider R, Hamoudi M, Chambodut A (2015) Parent magnetic field models for the IGRF-12 GFZ-candidates. Earth Planets Space 67:87. https://doi.org/10.1186/s40623-015-0239-6
Macmillan S, Olsen N (2013) Observatory data and the Swarm mission. Earth Planets Space 65(11):1355–1362. https://doi.org/10.5047/eps.2013.07.011
Macmillan S, Thomson A (2003) An examination of observatory biases during the Magsat and Ørsted missions. Phys Earth Planet Inter 135:97–105. https://doi.org/10.1016/S0031-9201(02)00209-1
Mandea M, Langlais B (2002) Observatory crustal magnetic biases during MAGSAT and Ørsted satellite missions. Geophys Res Lett 29:15. https://doi.org/10.1029/2001GL013693
Mandea M, Korte M, Mozzoni D, Kotzé P (2007) The magnetic field changing over the Southern African continent—a unique behaviour. S Afr J Geol 110:193–202
Mandea M, Panet I, Lesur V, De Viron O, Diament M (2012) The Earth’s fluid core: recent changes derived from space observations of geopotential fields. PNAS 1:1. https://doi.org/10.1073/pnas.1207346109
Matzka J (2016) Geomagnetic observatories. J Large Scale Res Facil 2:A83. https://doi.org/10.17815/jlsrf-2-136
Matzka J, Olsen N, Fox Maule C, Pedersen LW, Berarducci A, Macmillan S (2009) Geomagnetic observations on Tristan da Cunha. Ann Geophys 52(1):97–105
Matzka J, Chulliat A, Mandea M, Finlay CC, Qamili E (2010) Geomagnetic observations for main field studies: from ground to space. Space Sci Rev 155:29–64. https://doi.org/10.1007/s11214-010-9693-4
Matzka J, Husøy B-O, Berarducci A, Wright D, Pedersen LW, Stolle C, Repetto R, Genin L, Merenyi L, Green J (2011) The geomagnetic observatory on Tristan da Cunha: setup, operation and experiences. Data Sci J 10:IAGA151–IAGA158. https://doi.org/10.2481/dsj.IAGA-22
Maus S, Weidelt P (2004) Separating the magnetospheric disturbance magnetic field into external and transient internal contributions using a 1D conductivity model of the Earth. Geophys Res Lett 31:12. https://doi.org/10.1029/2004GL020232
Morschhauser A, Lesur V, Grott M (2014) A spherical harmonic model of the lithospheric magnetic field of Mars. J Geophys Res Planets 119(6):1162–1188
Morschhauser A, Brando Soares G, Haseloff J, Bronkalla O, Protásio J, Pinheiro K, Matzka J (2017) The magnetic observatory on Tatuoca, Belém, Brazil: history and recent developments. Geosci Instrum Method Data Syst 6:367–376. https://doi.org/10.5194/gi-6-367-2017
Panovska S, Korte M, Constable CG (2019) One hundred thousand years of geomagnetic field evolution. Rev Geophys 57:12. https://doi.org/10.1029/2019RG000656
Rother M, Lesur V, Schachtschneider R (2013) An algorithm for deriving core magnetic field models from the Swarm data set. Earth Planet Space 65:1223–1231. https://doi.org/10.5047/eps.2013.07.005
Shah J, Koppers AAP, Leitner M, Leonhardt R, Muxworthy AR, Heunemann C, Bachtadse V, Ashley JAD, Matzka J (2016) Palaeomagnetic evidence for the persistence or recurrence of geomagnetic main field anomalies in the South Atlantic. Earth Planet Sci Lett 441:113–124. https://doi.org/10.1016/j.epsl.2016.02.039
Tarduno JA, Watkeys MK, Huffman TH, Cottrell RD, Blackman EG, Wendt A, Scribner CA, Wagner CL (2015) Antiquity of the South Atlantic Anomaly and evidence for top-down control on the geodynamo. Nat Commun 6:7865. https://doi.org/10.1038/ncomms8865
Terra-Nova F, Amit H, Hartmann GA, Trindade RIF, Pinheiro KJ (2017) Relating the South Atlantic Anomaly and geomagnetic flux patches. Phys Earth Planet Inter 266:39–53
Terra-Nova F, Amit H, Choblet G (2019) Preferred locations of weak surface field in numerical dynamos with heterogeneous core-mantle boundary heat flux: consequences for the South Atlantic Anomaly. Geophys J Int 217:1179–1199. https://doi.org/10.1093/gji/ggy519
Thébault E, Finlay CC, Beggan C, Alken P, Aubert J, Barrois O, Bertrand F, Bondar T, Boness A, Brocco L, Canet E, Chambodut A, Chulliat A, Coisson P, Civet F, Du A, Fournier A, Fratter I, Gillet N, Hamilton B, Hamoudi M, Hulot G, Jager T, Korte M, Kuang W, Xavier L, Langlais B, Leger J-M, Lesur V, Lowes F (2015) International Geomagnetic Reference Field: the 12th generation. Earth Planets Space 67(1):79. https://doi.org/10.1186/s40623-015-0228-9
Torta JM, Pavón-Carrasco FJ, Marsal S, Finlay CC (2015) Evidence for a new geomagnetic jerk in 2014. Geophys Res Lett 42(19):7933–7940
Acknowledgements
ESA is acknowledged for operating the Swarm satellite mission and providing access to the Swarm data and data products. The results presented in this paper partly rely on data collected at magnetic observatories. We thank the national institutes that support them and INTERMAGNET for promoting high standards of magnetic observatory practice (http://www.intermagnet.org). Vincent Lesur is acknowledged for the development of earlier versions of the geomagnetic field modelling code.
Funding
Open Access funding enabled and organized by Projekt DEAL.. Open Access funding enabled and organized by Projekt DEAL. The study has been supported partly by Swarm DISC activities funded by ESA contract No. 4000109587 and by institutional funding.
Author information
Authors and Affiliations
Contributions
MR derived all models and provided most of the figures for the manuscript. JM and AM provided the additional observatory data and carried out comparisons of model predictions to these data. FV contributed to model validations. JM provided the detailed analysis linking the core field to the surface. All authors discussed aspects of modelling and decided together on how to obtain the GFZ candidate models. MK, together with AM and CS guided the writing of the manuscript, to which all authors contributed. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors have no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Additional file 1.
List with locations and local bias estimates for the geomagnetic observatories used in the modelling.
Additional file 2.
Field intensity for 2013.0 and 2020.0 and vertical component for 2020.0 in the SAA region at 6 levels from Earth’s surface down to the CMB.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rother, M., Korte, M., Morschhauser, A. et al. The Mag.num core field model as a parent for IGRF-13, and the recent evolution of the South Atlantic Anomaly. Earth Planets Space 73, 50 (2021). https://doi.org/10.1186/s40623-020-01277-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40623-020-01277-0