Improvements and validation of the IRI UP method under moderate, strong, and severe geomagnetic storms

Abstract

This work describes several important improvements made to the International Reference Ionosphere UPdate (IRI UP) method, and a careful validation of its performances under disturbed conditions. The IRI UP method has been improved developing an algorithm capable to properly filter wrongly autoscaled ionosonde data to be assimilated, avoiding the use of these in the assimilation process. Furthermore, the preliminary quality check used to choose the variogram model in the Universal Kriging method has been replaced with a new quality check routine (NQCR), based on statistical tests carried out using the variables Q₁, Q₂, and cR, built on variogram’s residuals. NQCR objectively identifies the best variogram model from which to get more reliable effective indices maps to be ingested in the IRI model to obtain updated foF2 and hmF2 maps. IRI UP has been applied on 30 different time intervals, between January 1, 2004, and December 31, 2016, characterized by moderate, strong, and severe geomagnetic conditions, over the European region. A statistical comparison between IRI UP and IRI at the truth sites located at Fairford (51.7°N, 1.5°W, UK) and San Vito (40.6°N, 17.8°E, Italy), for foF2 and hmF2, has been performed. From the statistical validation clearly emerges how IRI UP, for foF2, performs significantly better than IRI, for each of the 30 geomagnetic storms considered. Regarding hmF2, IRI UP performances are lower than those for foF2, although still better than IRI ones. In the light of the results achieved in this investigation, the IRI UP method represents an interesting approach to Space Weather forecast in the ionospheric domain.

Introduction

Space Weather events can significantly affect the functioning of radio systems, with effects that can be rapid (immediately after the event) or delayed (a few days after the event). High-frequency (HF) point-to-point communications exploit the terrestrial ionosphere and represent a valid and complementary alternative to satellite communications. The ionosphere is a complex dynamic propagation environment, and this makes HF communications problematic even during not so intense Space Weather events, because of its intrinsic variability (e.g., Kouris et al. 1998; Kouris and Fotiadis 2002). Extreme events occurring on the Sun, such as flares and coronal mass ejections, produce important variations of the corpuscular (solar wind) and electromagnetic [ultraviolet (UV) and X-ray emissions] component arriving on the Earth, which have a deep impact on the magnetosphere–ionosphere–atmosphere system (Zolesi and Cander 2014). As a consequence of such events, under particular conditions [i.e., when the north-south component Bz of the Interplanetary Magnetic Field is orientated southward (Bz < 0)], moderate, strong, and severe geomagnetic storms can occur giving rise to ionospheric storms, since the dynamics and structure of the ionosphere are significantly affected by the geomagnetic activity (Buonsanto 1999). Under ionospheric storm conditions, empirical climatological models, like the International Reference Ionosphere (IRI) model (Bilitza et al. 2014, 2017; Bilitza and Reinisch 2008), are not able to properly predict the ionospheric behavior, in particular during severe geomagnetic storms, as recently demonstrated for instance by Pignalberi et al. (2016). Moreover, ionospheric storms give rise to an abnormal behavior of the HF operative band, with important repercussions on the reliability of radio communications at both regional and global scale. In these circumstances, in order to select the best frequencies to be used for HF communications, timely and accurate information about the ionospheric channel is required. That is why, as established by the IRI community (Bilitza et al. 2011, 2014, 2017), real-time space-sparse ionosonde data should be used in conjunction with climatological models in order to get a picture of the ionospheric plasma variability as near as possible to the real conditions.

Currently, this is made possible thanks to the modern ionospheric stations which are equipped with software that provides, in almost real time, the electron density profile and the ionospheric characteristics among which, from the radio propagative point of view, the most important are the critical frequency of the F2 ionospheric layer, foF2, and the propagation factor M(3000)F2.

Assimilating F2 layer characteristics and electron density profiles, obtained from ionosonde measurements, into background ionospheric models, it was possible to develop nowcasting models which have been repeatedly proved to be effective in providing a better comprehensive specification of the ionosphere (Angling and Khattatov 2006; Thompson et al. 2006; Decker and McNamara 2007; McNamara et al. 2007, 2008, 2010, 2011; Nava et al. 2011; Shim et al. 2011; Galkin et al. 2012; Pezzopane et al. 2011, 2013; Pietrella 2015; Pignalberi et al. 2018a, b).

Nowcasting models provide foF2, M(3000)F2, hmF2, and electron density maps, which have great value from the operative point of view, because their use is aimed at maximizing the reliability and availability of HF services, especially under very disturbed ionospheric conditions as those occurring during geomagnetic and ionospheric storms.

In the light of these considerations, it is easy to understand how important is to supply maps as reliable as possible. To this regard, a method, called International Reference Ionosphere UPdate (IRI UP), has been recently developed by Pignalberi et al. (2018a, b) as a valid alternative to both the Simplified Ionospheric Regional Model UPdating (SIRMUP) model (Zolesi et al. 2004; Tsagouri et al. 2005) and the IRI-SIRMUP-P (ISP) model (Pezzopane et al. 2011, 2013).

The IRI UP method, which has the potentiality to work over any area where an appropriate number of autoscaled ionosonde measurements are available, assimilates ionosonde foF2 and M(3000)F2 data and, relying on the Universal Kriging geostatistical interpolation technique (Kitanidis 1997), produces maps of effective values IG_12eff of the 12-months smoothed ionospheric index IG₁₂ [derived by the IG index as calculated by Liu et al. (1983)], and maps of effective values R_12eff of the 12-month smoothed sunspots number R₁₂ (Houminer et al. 1993).

IG_12eff and R_12eff maps are then taken as input by the IRI climatological model to update the ionospheric background, thus providing an instantaneous two-dimensional (2-D) mapping of foF2 and M(3000)F2 and, hence, of hmF2 in the region of application. Its validation was early conducted for a case study taking into account only the severe St. Patrick geomagnetic storm occurred on March 17, 2015 (Pignalberi et al. 2018a, b).

It must be kept in mind that the goodness of IRI UP nowcasting maps depends mainly on two important issues: (a) foF2 and M(3000)F2 data, autoscaled in some reference stations, constitute a discrete dataset which must be as reliable as possible because this dataset is used to compute the values of IG_12eff and R_12eff at each reference station; (b) the Kriging interpolation method which, starting from the discrete values of IG_12eff and R_12eff, provides IG_12eff and R_12eff nowcasting maps over the area under consideration, depends crucially on the choice of the variogram model which fits the experimental one. Therefore, in order to get a proper interpolation and consequently reliable IG_12eff and R_12eff maps, it is extremely important that selected variogram models have a good quality.

With regard to these two issues, in the work of Pignalberi et al. (2018a, b), the reliability of foF2 and M(3000)F2 autoscaled data was based on a quality check of ionograms: for the reference stations equipped with the Automatic Real-Time Ionogram Scaler with True height analysis (ARTIST) software (Reinisch and Huang 1983; Reinisch et al. 2005; Galkin and Reinisch 2008), only ionograms with a Confidence Score (CS) greater than 75 (see http://www.ursi.org/files/CommissionWebsites/INAG/web-73/confidence_score.pdf) were selected; for the reference stations equipped with the Autoscala software (Scotto and Pezzopane 2002, 2008; Pezzopane and Scotto 2005, 2007; Scotto 2009; Scotto et al. 2012), a careful visual inspection was adopted to select the reliable ionograms. Furthermore, to avoid unrealistic IG_12eff and R_12eff maps, a preliminary quality check of the variogram model, based on the exponent s of the power variogram model was also implemented.

In this paper, which represents the continuation of the work of Pignalberi et al. (2018a, b), the authors extended the investigation about the IRI UP method performance under disturbed geomagnetic conditions, selecting 30 time intervals characterized by moderate, strong, and severe geomagnetic storms occurred from January 1, 2004, to December 31, 2016. The validation of the IRI UP method is carried out comparing the IRI UP performance with the one of the IRI model with the STORM option “ON,” at the two truth sites of Fairford (51.7°N, 1.5°W, UK) and San Vito (40.6°N, 17.8°E, Italy).

Moreover, an appropriate filter (F) was implemented in the IRI UP method to automatically discard those ionosonde data clearly wrong (spikes) which, once assimilated, would affect negatively the ionospheric modeling. Its application turned out to be more effective than CS and visual inspection methods.

In addition, a new quality check routine (NQCR), based on statistical tests carried out using the statistical variables Q₁, Q₂, and cR, built on the residuals [differences between the observed (experimental variogram) and the modeled (variogram model) semivariance values], has also been proposed with the intention of replacing the quality check based on the exponent s of the power variogram model. This allowed to select more objectively, and with a more acceptable degree of confidence, the “best” variogram model to be used.

The data used and periods under study are presented in “Data used and periods under study” section. The description of the F algorithm implemented in the IRI UP method is provided in “Description of the filter implemented to select ionosonde data” section. A recall to the Kriging interpolation method is outlined in “The Kriging interpolation method: a brief recall” section. The description of the NQCR procedure is provided in “On the choice of the best variogram model in the Universal Kriging procedure: a new quality check routine (NQCR)” section. The validation of the IRI UP method and results obtained applying the NQCR procedure are the subject of “Validation of IRI UP method including the F algorithm and the NQCR procedure: some results” section. The discussion about the results and possible future developments is given in “Discussion, conclusions, and future developments” section.

Data used and periods under study

The data used in this study consist of: (a) A_p geomagnetic index data (Rostoker 1972); (b) K_p geomagnetic index data (Menvielle and Berthelier 1991); (c) foF2 and M(3000)F2 data.

Geomagnetic indices were downloaded from the OMNIWeb Data Explorer—NASA site at https://omniweb.gsfc.nasa.gov/form/dx1.html.

foF2 and M(3000)F2 data were downloaded from the interactive ionogram scaling software, SAO Explorer, developed at the University of Massachusetts Lowell Center for Atmospheric Research (UMLCAR) (http://ulcar.uml.edu/SAO-X/SAO-X.html) (Khmyrov et al. 2008; Reinisch and Galkin 2011).

In particular, foF2 and M(3000)F2 values from Rome and Gibilmanna were autoscaled from the ionograms recorded by an AIS-INGV ionosonde (Zuccheretti et al. 2003), and those from Warsaw were autoscaled from the ionograms recorded by a VISRC2 ionosonde (Pezzopane et al. 2009).

The ARTIST system was instead applied to autoscale foF2 and M(3000)F2 data from the ionograms recorded by digisondes (Bibl and Reinisch 1978) installed in the remaining ionospheric stations.

Table 1 provides an overview of the ionospheric stations considered, highlighting the ionosonde type, the autoscaling software, and the state of the station. The state “assimilated” means that foF2 and M(3000)F2 hourly values are assimilated to update the background model, while the state “used as test site” indicates that foF2 and M(3000)F2 hourly values are used only to test the IRI UP performance. The ionospheric stations available for data assimilation are listed for each year in Table 2. Figure 1 shows the geographical distribution of the ionospheric stations under consideration.

Table 1 European ionosonde network involved in the study

Table 2 Ionosonde stations temporal availability

Fig. 1

European ionosonde network involved in the study. Geographical distribution of the ionospheric stations listed in Table 1

The IRI UP performance was evaluated at the testing stations of Fairford and San Vito over 30 time intervals characterized by geomagnetic storms occurred between January 1, 2004, and December 31, 2016. Such period embraces part of the past 23rd solar cycle (August 1996–December 2008) and the current one. A_p daily mean values > 50 and K_p maximum values > 5⁺ (see https://www.spaceweatherlive.com/en/help/the-kp-index), as recorded during the main phase day of the storm, are the thresholds adopted to discard minor storms, thus selecting only the moderate, strong, and severe ones.

Specifically, each time interval was selected considering the day before the main phase of the storm (which in the selected cases is always a quiet day), the day of the main phase, and the next 4 days of the recovery phase, for a total number of 6 days for each time interval. Nevertheless, when the storm is characterized by substorms with A_p daily mean > 50, then from the last substorm occurred, 4 days of the recovery phase are further considered; this means that, in these cases, the period under study can be characterized by more than 6 days. Some information about the geomagnetic storms considered in this study is summarized in Table 3.

Table 3 Storm time periods analyzed in this study

Description of the filter implemented to select ionosonde data

Instead of reading the CS index from SAO files (Khmyrov et al. 2008), and visually inspecting the ionograms autoscaled by Autoscala, a new algorithm (F) was implemented in the IRI UP method to select ionosonde data. This has a dual objective: (a) to improve the level of reliability of assimilated data; (b) to speed up the selection process of data which are going to be assimilated.

The way the F algorithm works is as follows. In order to understand whether a value of foF2 or M(3000)F2 at a given hour hr [foF2_hr and M(3000)F2_hr, respectively] has been correctly autoscaled, foF2 and M(3000)F2 data, autoscaled in the previous 15 days at the same considered hour, are taken into account to calculate the mean values $\bar{m}_{{fo{\text{F}}2,hr,15{\text{prevdays}}}}$ and $\bar{m}_{{M(3000){\text{F}}2,hr,15{\text{prevdays}}}}$ and the corresponding standard deviations sd_{foF2,hr,15predays} and sd_{M(3000)F2,hr,15predays}. Specifically, standard deviations are calculated when time series have a number N of available data greater than 5; otherwise, they are fixed to 0.5 MHz and 0.15 for foF2 and M(3000)F2, respectively.

Subsequently, if sd_{foF2,hr,15predays} ≥ 0.5 MHz, foF2_hr is considered reliable if the following inequalities are fulfilled

$$\bar{m}_{{fo{\text{F}}2,hr,15{\text{prevdays}}}} - 5sd_{{fo{\text{F}}2,hr,15{\text{prevdays}}}} \le fo{\text{F}}2_{hr } \le \bar{m}_{{fo{\text{F}}2,hr,15{\text{prevdays}}}} + 5sd_{{fo{\text{F}}2,hr,15{\text{prevdays}}}} ;$$

(1)

otherwise, if sd_{foF2,hr,15predays} < 0.5 MHz, foF2_hr is considered reliable if the following inequalities are fulfilled

$$\bar{m}_{{fo{\text{F}}2,hr,15{\text{prevdays}}}} - 5\left( {0.5} \right) \le fo{\text{F}}2_{hr } \le \bar{m}_{{fo{\text{F}}2,hr,15{\text{prevdays}}}} + 5\left( {0.5} \right).$$

(2)

The inequalities (2) are considered because it may happens that when very quiet days occur, the previous 15 days are characterized by foF2 values very close to each other; in these cases, the value of sd_{foF2,hr,15predays} would be too small and, consequently, the inequalities (1) would constitute a too selective filter.

The values of foF2_hr considered reliable are then used to calculate IG_12eff values at the hour hr in the corresponding assimilated ionosonde station (Pignalberi et al. 2018a, b).

Likewise, if sd_{M(3000)F2,hr,15predays} > 0.15, M(3000)F2_hr is considered reliable if the following inequalities are fulfilled

$$\bar{m}_{{M(3000){\text{F}}2,hr,15{\text{prevdays}}}} - 5sd_{{M(3000){\text{F}}2,hr,15{\text{prevdays}}}} \le M\left( {3000} \right)F2_{hr} \le \bar{m}_{{M(3000){\text{F}}2,hr,15{\text{prevdays}}}} + 5sd_{{M(3000){\text{F}}2,hr,15{\text{prevdays}}}} ;$$

(3)

otherwise, if sd_{M(3000)F2,hr,15predays} < 0.15, M(3000)F2_hr is considered reliable if the following inequalities are fulfilled

$$\bar{m}_{{M(3000){\text{F}}2,hr,15{\text{prevdays}}}} - 5\left( {0.15} \right) \le fo{\text{F}}2_{hr } \le \bar{m}_{{M(3000){\text{F}}2,hr,15{\text{prevdays}}}} + 5\left( {0.15} \right).$$

(4)

As already said for foF2, the inequalities (4) replace the inequalities (3) which would constitute a too selective filter.

The values of M(3000)F2_hr considered reliable are then used to calculate R_12eff at the hour hr (Pignalberi et al. 2018a, b).

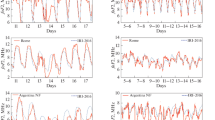
The aim of the proposed F algorithm is to remove spikes, that is values of foF2 and M(3000)F2 which are evidently wrongly autoscaled. Figure 2 shows an example of the effectiveness of the filter applied on foF2 and M(3000)F2 data recorded at Fairford over the period October 24–29, 2016 (storm number 30 of Table 3).

Fig. 2

Example of application of the F algorithm. foF2 and M(3000)F2 time series for the period October 24–29, 2016 (storm number 30 of Table 3) before (a, c, respectively) and after (b, d, respectively), applying the F algorithm. Red arrows indicate spikes which are then discarded by the F algorithm

The Kriging interpolation method: a brief recall

In this section some basic concepts concerning the Kriging Interpolation Method (KIM) are recalled and, at the same time, the fundamental notions on which the experimental variogram is based are provided, in order to improve the understanding of next sections.

The KIM estimates the value $\hat{z}({\mathbf{x}}_{ 0} )$ at a given point x₀ through a linear combination of n measurements of the variable z taken at locations with spatial coordinates ${\mathbf{x}}_{ 1} ,\,{\mathbf{x}}_{ 2} ,\, \ldots ,\,{\mathbf{x}}_{n} ,$ i.e.,

$$\hat{z}({\mathbf{x}}_{ 0} ) = \sum\limits_{i = 1}^{n} {\lambda_{i} z({\mathbf{x}}_{i} )} ,$$

(5)

where the bold letter stands for the array of coordinates of the measurements locations.

Therefore, the problem consists in selecting a set of coefficients λ₁, λ₂, …, λ_n that fulfill the conditions of unbiasedness and minimum variance (see for details Pignalberi et al. 2018a, b).

The fundamental brick of the KIM is the experimental variogram from which it is possible to get indications about the spatial correlations between the measurements.

Generally speaking, if we consider a relatively small number n of measurements z(x₁), z(x₂), …, z(x_n) as it can be assumed in this investigation (because the number of reference stations is at most 12), it is possible to form $\frac{n(n - 1)}{2}$ pairs of measurements, to define the distance of each pair $h_{k}$ = |x_k − x_k′|, and hence the corresponding semivariance $\gamma (h_{k} )$ as follows

$$\gamma (h_{k} ) = \frac{1}{2}\left[ {z({\mathbf{x}}_{k} ) - z({\mathbf{x}}_{k}^{{\prime }} )} \right]^{2} ,$$

(6)

where k = 1, …, $\frac{n(n - 1)}{2}$ refers to each pair of measurements.

The plot formed by the $\frac{n(n - 1)}{2}$ points of coordinates ($h_{k}$, $\gamma (h_{k} )$) constitutes the experimental variogram.

For cases where a huge number n of measurements is considered, it would be better to arrange the $\frac{n(n - 1)}{2}$ pairs of measurements in K bins having all the same width $W = \frac{{h_{\rm{max} } - h_{\rm{min} } }}{K},$ being $h_{\rm{min} }$ and $h_{\rm{max} }$ the absolute minimum and maximum distance among the $\frac{n(n - 1)}{2}$ pairs of measurements.

The lower and upper limit of each bin is defined through an iterative procedure which starts from h_min (the lower limit of the first bin) and ends with h_max (the upper limit of the last bin). For example, the first, second, third and last bins correspond to the intervals [$h_{\rm{min} }$, $h_{\rm{min} }$ + W), [$h_{\rm{min} }$ + W, $h_{\rm{min} }$ +2W), [$h_{\rm{min} }$ + 2W,$h_{\rm{min} }$ + 3W) and [$h_{\rm{min} }$ + (K − 1)W, $h_{\rm{max} }$], respectively.

As each bin can contain a different number, N_K, of pairs of measurements, the distance pertinent to each bin is then defined as the average value, $\bar{h}_{K}$, of the distances h_k “falling” inside the bin

$$\bar{h}_{K} = \frac{{\sum\nolimits_{k = 1}^{{N_{K} }} {h_{k} } }}{{N_{K} \, }}.$$

(7)

As a consequence, the semivariance associated with a given bin is the average value of the semivariances γ(h_k) “falling” inside that bin

$$\bar{\gamma }_{K} = \frac{{\sum\nolimits_{k = 1}^{{N_{K} }} {\gamma (h_{k} )} }}{{N_{K} }} = \frac{1}{{2(N_{K} )}}\sum\limits_{k = 1}^{{N_{K} }} {\left[ {z({\mathbf{x}}_{k} ) - z({\mathbf{x}}_{k}^{{\prime }} )} \right]^{2} } ;$$

(8)

the plot obtained with the K points (one for each bin) of coordinates ($\bar{h}_{K}$, $\bar{\gamma }_{K}$) constitutes the experimental variogram.

It is hence possible to “build” an experimental variogram based on the assimilated measurements recorded in the reference stations. It depends essentially on how the reference stations are distributed over the considered area. Data assimilation from many reference stations located close to each other is important to catch the small-scale spatial structures, because it populates the part of the variogram near the origin. The assimilation of data from reference stations placed far from each other is instead fundamental for the description of the large-scale spatial behavior.

Once the variogram is “built,” there is the need to find a mathematical function which fits the experimental data. The mathematical expressions that can be used to fit the experimental variogram correspond to five commonly used variogram models: linear and power (non-stationary models), gaussian, spherical, and exponential (stationary models).

The distinction between stationary and non-stationary models depends on their behavior at distances comparable to the size of the domain. When the experimental variogram presents a steady trend around a value, called sill (σ²), as the distance increases, it is possible to define a length scale, called range (α), at which the sill is obtained. α describes the spatial scale from which two measurements of the variable are no longer correlated. The variogram models characterized by the parameters σ² and α are called stationary. The value at the origin, γ(0) = c₀, indicates a discontinuity because the experimental variogram does not converge to zero as the distance decreases. The parameter c₀, called nugget, is a term describing how well the microscale variability is represented. The mathematical functions describing the various variogram models are the following:

• 1. Linear:

  $$\gamma (h) = c_{0} + \vartheta h,$$

  (9)

  where $\vartheta$ > 0 is the slope;

• 2. Power:

  $$\gamma (h) = c_{0} + \vartheta h^{s} ,$$

  (10)

  where $\vartheta$ > 0 is the scale and 0 < s < 2 is the exponent;

• 3. Gaussian:

  $$\gamma (h) = c_{0} + (\sigma^{2} - c_{0} )\left[ {1 - e^{{ - \left( {\frac{7h}{4\alpha }} \right)^{2} }} } \right],$$

  (11)

  exhibiting a parabolic behavior around the origin;

• 4. Spherical:

  $$\gamma (h) = \left\{ {\begin{array}{*{20}l} {c_{0} + (\sigma^{2} - c_{0} )\left[ {\frac{3h}{2\alpha } + \frac{1}{2}\left( {\frac{h}{\alpha }} \right)^{3} } \right]} \hfill & {{\text{for}}\,0 \, \le \, h \, \le \, \alpha } \hfill \\ {\sigma^{2} } \hfill & {\text{for}\,h > \alpha } \hfill \\ \end{array} \text{,}} \right.$$

  (12)

  exhibiting a linear behavior around the origin;

• 5. Exponential:

  $$\gamma (h) = c_{0} + (\sigma^{2} - c_{0} )\left[ {1 - e^{{ - \left( {\frac{3h}{\alpha }} \right)}} } \right],$$

  (13)

  exhibiting a linear behavior around the origin.

It is important to keep in mind that each variogram model embeds, with a different degree of reliability, the information concerning the small- and large-scale behavior of the parameter under study. That is why the selection of the variogram model plays a fundamental role in determining the quality and reliability of the prediction map over the area under consideration.

The observation at the point of coordinate x₀ can be represented as

$$z({\mathbf{x}}_{ 0} ) = m({\mathbf{x}}_{ 0} ) + \varepsilon ({\mathbf{x}}_{ 0} ),$$

(14)

where m(x₀) is the deterministic part of z(x₀) representing the large-scale spatial variability, while ε(x₀) is the stochastic part of z(x₀) which describes, particularly for stationary variogram models, the small-scale spatial variability. In the Ordinary Kriging method, m(x₀) = m, i.e., it is a constant which does not depends on the spatial coordinates. Since the electron density presents values at mid-low latitudes higher than the ones at mid-high latitudes, there exists a latitudinal spatial gradient characterizing the ionospheric characteristics which we are going to describe. This fact makes the Universal Kriging method (UKM) particularly suitable to describe the variability of the ionospheric characteristics under study, because UKM takes into account also the spatial gradients by means of additional terms, so that the term m(x₀), also called drift part, is written as

$$m({\mathbf{x}}_{ 0} ) = \sum\limits_{j = 1}^{p} {f_{j} ({\mathbf{x}}_{ 0} )\beta_{j} } ,$$

(15)

where f₁(x₀),…., f_p(x₀) are functions of spatial coordinates generally known, and β₁,…, β_p are the so called drift coefficients, which are usually unknown.

In our specific case the term m(x₀) is written as:

$$m\left( {{\mathbf{x}}_{0} } \right) \, = A + \varphi_{0} \cdot\,B + \lambda_{0} \cdot\,C,$$

(16)

being φ₀ and λ₀ the longitude and latitude of the point x₀, which are known, while the coefficients A, B, and C must be determined. The combination of Eq. (15) with Eq. (16) gives f₁(x_i) = 1, f₂(x_i) = φ₀, and f₃(x_i) = λ₀.

Combining Eq. (14) with Eq. (15), we get

$$z({\mathbf{x}}_{ 0} ) = \sum\limits_{j = 1}^{p} {f_{j} ({\mathbf{x}}_{ 0} )\beta_{j} } + \varepsilon ({\mathbf{x}}_{ 0} ).$$

(17)

With regard to the issue dealing with the stochastic part ε(x₀), being the topic out of the context of this work, we invite the interested reader to refer to Section 3.3 of Pignalberi et al. (2018a) and to Kitanidis (1997).

On the choice of the best variogram model in the Universal Kriging procedure: a new quality check routine (NQCR)

As already explained by Pignalberi et al. (2018a, b), reliable foF2, M(3000)F2, and hmF2 maps can be obtained when the IRI model is updated with a realistic IG_12eff and R_12eff representation. Such representation is obtained applying the UKM on a discrete set of IG_12eff and R_12eff values, obtained at the locations of selected reference stations. It must be pointed out that the UKM provides a variogram model which, in principle, should be the one that best fits the experimental variogram (i.e., the variogram built on the discrete set of IG_12eff and R_12eff values).

Therefore, the problem of how to choose among the possible variogram models described in “The Kriging interpolation method: a brief recall” section is of crucial importance, because this choice greatly affects the goodness of the IG_12eff and R_12eff maps and, consequently, the capability of delivering an accurate and trustworthy foF2, M(3000)F2, and hmF2 modeling. To this regard, in the work of Pignalberi et al. (2018a, b) a routine for the preliminary quality check of the variogram model, based on the evaluation of the exponent s (0 < s < 2) of the power variogram model, was developed in the IRI UP method.

In cases for which s is close to 0, the variogram model is an approximately straight horizontal line, while in cases for which s tends to 2 the variogram model has an approximately parabolic behavior at both small and large scales (Kitanidis 1997). For s ≪ 1 the semivariance does not vary with the distance, as it should be expected; therefore, these cases correspond to unrealistic situations which would lead to unrealistic maps of IG_12eff and R_12eff. For this reason, for the preliminary quality check of the variogram model, we have set a very low threshold value for s (s_thrs = 0.1) discarding those variograms for which s < s_thrs. Examples of variogram models and related maps of IG_12eff and R_12eff discarded by the IRI UP method are shown in Fig. 3. The meaning of the associated statistics parameters Q₁, Q₂, and cR written in the legend will be clarified in the next sections.

Fig. 3

Examples of discarded effective index variograms and maps. Examples of discarded variogram models (linear (top left), Gaussian (bottom left)), with corresponding maps of IG_12eff (top right) and R_12eff (bottom right), on March 20, 2015, at 16:00 UT

It should be noted that s < s_thrs does not provide an objective criterion, because s_thrs is the same for each variogram model. That is why in this work the IRI UP method has been updated by the NQCR procedure to choose the best variogram model, through appropriate statistical tests.

Q ₁ statistics

Residuals are the differences between observations and model predictions. In statistical modeling (regression, time series, analysis of variance, and geostatistics), the parameter estimation and the model validation depend heavily on the examination of residuals.

We can define the variable

$$Q_{1} = \frac{1}{n - 1}\sum\limits_{k = 2}^{n} {\varepsilon_{k} } ,$$

(18)

where n is the number of observations and $\varepsilon_{k} = \frac{{\delta_{k} }}{{S_{k} }}$ are the normalized residuals, being δ_k the common residuals and S_k the variance of their distribution. It can be proven (see Kitanidis 1997) that Q₁ is a statistical variable which follows the normal distribution with a probability density function (PDF) given by

$$f(Q_{1} ) = {\kern 1pt} \frac{1}{{\sqrt {\frac{2\pi }{n - 1}} }}e^{{ - \left( {\frac{{Q_{1}^{2} }}{{\frac{2}{n - 1}}}} \right)}} ,$$

(19)

with a mean value m = 0 and a variance $\sigma^{2} = \frac{1}{n - 1}.$

Therefore, we have a probability of about 95% that Q₁ is ranged in the interval

$$- \,2\sigma < Q_{1} < + 2\sigma \quad {\text{i}} . {\text{e}} .\quad \left| {Q_{1} } \right| < \frac{2}{{\sqrt {n - 1} }},$$

(20)

and a probability of about 68% that Q₁ is ranged in the interval

$$- \,\sigma < Q_{1} < + \sigma \quad {\text{i}} . {\text{e}} .\quad \left| {Q_{1} } \right| < \frac{1}{{\sqrt {n - 1} }}.$$

(21)

An example of the PDF and the cumulative probability function (CPF) of the variable Q₁, obtained for n = 12, is shown in Fig. 4.

Fig. 4

Probability density function and cumulative probability function for the Q₁ variable. Example of PDF (solid blue line) and CPF (solid green line) for Q₁, for n = 12. Red and black arrows (corresponding to red and black dashed vertical lines) indicate, respectively, the thresholds ± 1σ and ± 2σ. Black and red dashed horizontal lines represent the values referred to the CPF corresponding to the conditions (20) and (21) which, for the considered case, provide, respectively, the numerical solutions − 0.60 < Q₁ < + 0.60 and − 0.30 < Q₁ < + 0.30

When the condition (20) is fulfilled, the variogram model under examination is accepted and it is significant from the statistical point of view with a probability of about 95%; this implies that there exists a 5% of probability to accept an incorrect variogram model. However, a 5% cutoff is customary in statistics. Therefore, when (20) is met, we can assume that the variogram model has passed the Q₁ statistical test.

Q ₂ statistics

Another test that can be carried out to test the goodness of the variogram model is that relying on the statistical variable Q₂ defined as

$$Q_{2} = \frac{1}{n - 1}\sum\limits_{k = 2}^{n} {\varepsilon_{k}^{2} } .$$

(22)

It can be proven (see Kitanidis 1997) that Q₂ is a statistical variable whose PDF is

$$f(Q_{2} ) = \frac{{(n - 1)^{{\frac{n - 1}{2}}} Q_{2}^{{\frac{n - 3}{2}}} e^{{ - \left[ {\frac{{(n - 1)Q_{2} }}{2}} \right]}} }}{{2^{{\frac{n - 1}{2}}} \varGamma \left( {\frac{n - 1}{2}} \right)}},$$

(23)

with a mean value m → 1, for n → $\infty$, and a variance $\sigma^{2} = \frac{2}{n - 1}$.

An example of the PDF and CPF of the variable Q₂, obtained for n = 12, is shown in Fig. 5.

Fig. 5

Probability density function and cumulative probability function for the Q₂ variable. Example of PDF and CPF for Q₂ for n =  12. The black dashed horizontal lines intersect the CPF at the two points of coordinates (L, 0.025) and (U, 0.975), while the red dashed horizontal lines intersect the CPF at the two points of coordinates (L^1st, 0.25) and (U^3rd, 0.75), where L^1st and U^3rd identify the first and third quartile, respectively. As a consequence, the black and red arrows mark the intervals of the variable Q₂ corresponding to a statistical significance of 95% and 50%, respectively

Therefore, according to Fig. 5, if the value of Q₂ given by Eq. (22) is included in the interval

$$L < Q_{2} < U,$$

(24)

the variogram model under examination is significant from the statistical point of view with a probability of 95%. When this condition is met, we could say that the variogram model has passed the Q₂ statistical test to the usual confidence level of 5%, in the sense that there exists, however, a 5% probability that an incorrect variogram model is accepted.

It is worth noting that the form of PDF and CPF depends on the number n of assimilated ionosonde data and, consequently, the same stands for the values of the two thresholds (L, U) and (L^1st, U^3rd).

The cR criterion

The residuals are particularly important in evaluating how closely the variogram model fits the data, since smaller residuals imply a better fit. To construct stable (i.e., less affected by random error) criteria for the choice of the best variogram model, we may also use the stabilized geometric mean of the residuals’ variance (S_k), subject to the constraint Q₂ = 1 (see Kitanidis 1997), i.e., the parameter

$$cR = e^{{\left( {\frac{1}{n - 1}\sum\nolimits_{k = 2}^{n} {\ln (S_{k}^{2} )} } \right)}} .$$

(25)

The condition

$$cR = {\text{ minimum}},$$

(26)

allows to choose among the various variogram models.

Q ₁, Q ₂, and cR statistical test: some results

The statistical criteria (20), (24), and (26) described in the previous sections constitute the NQCR procedure implemented in the IRI UP method.

For the selection of the “best” variogram model, one could be tempted to consider only the cR criterion, leaving out the criteria (20) and (24). Nevertheless, from a preliminary investigation conducted over a large number of variogram models, we realized that if only the cR criterion were applied, several variogram models which do not satisfy the criteria (20) and/or (24) would be accepted.

For these reasons, we decided to proceed to the selection of the variogram through an iterative procedure that NQCR applies following the flowchart depicted in Fig. 6. The figure shows just an example of how the NQCR procedure can be applied on each of the epochs (dd/mm/yyyy/hh) listed in Table 3 and illustrates, in general terms, the various steps carried out in order to select that variogram model which, to an acceptable degree of confidence, fits the data more reliably than the other ones.

Fig. 6

NQCR procedure flowchart. Flowchart representing the main steps of the NQCR procedure

Figure 7 shows some examples of spherical and linear variogram models which have met the requirements (20), (24), and (26) and that therefore have been selected to get a statistically significant IG_12eff, and R_12eff modeling and, consequently, a reliable mapping of foF2 and M(3000)F2 and, hence, of hmF2. Note that the variograms reported in Fig. 7, matching the requirements (20), (24), and (26), automatically fulfill also the previous quality check s < s_thrs.

Fig. 7

Examples of effective index variograms and maps passing the NQCR selection procedure. (top left) Example of spherical variogram model which has passed the NQCR procedure and (top right) corresponding map of IG_12eff on October 16, 2016, at 12:00 UT. (bottom left) Example of linear variogram model which has passed the NQCR procedure and (bottom right) corresponding map of R_12eff on March 17, 2015, at 11:00 UT

Some examples of Q₁, Q₂, and cR time series, for linear and spherical variogram models used to obtain IG_12eff and R_12eff maps, are shown in Figs. 8 and 9, respectively. For the Q₁ statistical test, each case exceeding the threshold (20) is rejected, as well as for the Q₂ statistical test each case not included in the interval (24) is refused. Note that the epochs characterized by the greatest values of cR are those following the main phase of the storm.

Fig. 8

Q₁, Q₂, and cR time series for IG_12eff, for selected storms and variogram models. Q₁, Q₂, and cR time series for a linear and b spherical variogram models for IG_12eff corresponding to the severe geomagnetic storms listed in Table 3 as number 12 (left) and 27 (right). The continuous and dashed black lines in Q₁ and Q₂ plots represent the threshold values as highlighted at the top of the figure

Fig. 9

Q₁, Q₂, and cR time series for R_12eff, for selected storms and variogram models. Same as Fig. 8, but for R_12eff

Blue, red and green dots represent the values of Q₁, Q₂, and cR, respectively, computed by Eqs. (18), (22), and (25). We want to stress once again here the fact that for the Q₁ and Q₂ statistics the thresholds depend on the number n of foF2 and M(3000)F2 values available in the reference stations which, at a given hour, have been considered according to the criteria described in “Description of the filter implemented to select ionosonde data” section. Obviously, the value of n can be different from epoch to epoch because, at a given moment, it is possible that a station is not working and/or the ionospheric characteristics of a station are wrongly autoscaled.

This explains why the continuous black lines representing the Q₁ and Q₂ thresholds in Figs. 8 and 9 are not flat. The implementation of the NQCR procedure constitutes then an important difference with respect to the preliminary quality check based only on the exponent s for which, whatever is the epoch and variogram model under study, the threshold value s_thrs is not a function of n but it is fixed to 0.1.

Validation of IRI UP method including the F algorithm and the NQCR procedure: some results

The IRI UP method, embedding the F algorithm and the NQCR procedure, as described, respectively, in “Description of the filter implemented to select ionosonde data” and “On the choice of the best variogram model in the Universal Kriging procedure: a new quality check routine (NQCR)” sections, has been systematically tested over the 30 disturbed time intervals listed in Table 3, in order to investigate its performance during moderate, strong, and severe geomagnetic storms.

For each epoch, the testing procedure follows four steps:

• 1. the variogram models which have passed the Q₁ and Q₂ statistical tests (as, for example, those fitting the IG_12eff and R_12eff experimental variograms of Fig. 7) and the cR criterion are considered;

• 2. applying the UKM for each selected variogram model, IG_12eff and R_12eff maps are calculated over the European area depicted in Fig. 1;

• 3. foF2 and M(3000)F2 maps are calculated giving as input to the IRI model the IG_12eff and R_12eff maps calculated in 2); then, applying the empirical formula which relates hmF2 to foF2 and M(3000)F2 (Bilitza et al. 1979), also hmF2 maps are obtained;

• 4. from foF2 and hmF2 maps, values at the truth sites of Fairford and San Vito are extracted and compared with corresponding measurements.

For each storm the following statistical parameters are calculated:

$${\text{Root}}\,{\text{Mean}}\,{\text{Square}}\,{\text{Error}},\,{\text{RMSE}}_{X} = \sqrt {\frac{{\sum\nolimits_{i = 1}^{N} {(X_{\text{modeled},i} - X_{\text{ionosonde},i} )^{2} } }}{N}} ,$$

(27)

where N is the number of epochs that constitute the considered storm, $X$ stands for foF2 or hmF2, the subscript modeled stands for IRI UP or IRI predicted values (the IRI model is considered with the storm option “ON”), while the subscript ionosonde refers to values recorded by the ionosonde;

$${\text{Normalized}}\,{\text{Root}}\,{\text{Mean}}\;{\text{Square}}\,{\text{Error}},\quad {\text{NRMSE}}_{X} = \frac{{{\text{RMSE}}_{X} }}{{\bar{X}_{\text{ionosonde}} }},$$

(28)

where $\bar{X}_{\text{ionosonde}}$ is the arithmetic mean over time of X_ionosonde values;

$${\text{Pearson}}\,{\text{Correlation}}\,{\text{Coefficient}},\,\rho_{X} = \frac{{{\text{cov}}(X_{{{\text{modeled}},}} X_{\text{ionosonde}} )}}{{\sigma_{{X_{\text{modeled}} }} \sigma_{{X_{\text{ionosonde}} }} }},$$

(29)

where cov() is the covariance, while $\sigma_{{X_{\text{modeled}} }}$ and $\sigma_{{X_{\text{ionosonde}} }}$ are the standard deviations;

$${\text{Mean}}\,{\text{Delta}},{\text{MD}}_{X} = \frac{{\sum\nolimits_{i = 1}^{N} {(X_{{{\text{modeled}},i}} - X_{{{\text{ionosonde}},i}} )} }}{N}.$$

(30)

In addition, also the percentage of discarded maps is calculated:

$$\% {\text{discarded}} = \frac{{{\text{totalmaps}} - {\text{goodmaps}}}}{\text{totalmaps}},$$

(31)

where goodmaps is the number of IG_12eff or R_12eff maps passing the first two steps of the NQCR procedure, i.e., Q₁, and Q₂ tests, and totalmaps is the total potential number of maps.

Figures 10 and 11 show some examples of comparison between IRI and IRI UP, in terms of the aforementioned statistical quantities carried out at Fairford and San Vito for each storm listed in Table 3, for both foF2 and hmF2.

Fig. 10

Statistical parameters calculated at testing stations for foF2, for each storm time period. Trend of statistical parameters defined by Eqs. (27)–(30) related to foF2 for Fairford (left) and San Vito (right). The gap between storms number 2 and 5 at Fairford is due to the lack of ionosonde data

Fig. 11

Statistical parameters calculated at testing stations for hmF2, for each storm time period. Same as Fig. 10 but for hmF2

Figure 12 shows, for each storm individually and for the whole group of storms, the percentage of discarded variogram models calculated by Eq. (31).

Fig. 12

Percentage of variogram models discarded by the NQCR procedure. Percentage of discarded variogram models for (top) each storm listed in Table 3 and (bottom) all storms as a whole, for (left) foF2 and (right) hmF2. On the top panels the percentage of the linear model is not visible because hidden by the power model

Finally, the MD_X quantities provided by Eq. (30), taken as absolute values (to avoid that positive and negative values around zero could cancel each other), have been used to calculate the following mean value:

$${\text{Mean}}({\text{MD}}_{X} \,{\text{Absolute}}\,{\text{Value}}),\,{\text{MMD}}_{X } {\text{AV}} = \sum\limits_{j = 1}^{30} {\frac{{\left| {{\text{MD}}_{X,j} } \right|}}{30}} .$$

(32)

Tables 4 and 5 summarize the statistical results calculated by Eqs. (27)–(29) and Eq. (32) at the truth sites of Fairford and San Vito for foF2 and hmF2, respectively, in the following three cases: (a) IRI UP method running with a fixed variogram model (like in Pignalberi et al. 2018a) and considering only those cases passing the first two steps of the NQCR procedure, namely Q₁ and Q₂ tests; (b) IRI background model; (c) IRI UP method embedding the complete NQCR procedure.

Table 4 Statistical validation of foF2 as modeled by IRI UP and IRI

Table 5 Statistical validation of hmF2 characteristic as modeled by IRI UP and IRI

The winning percentage of each variogram model is computed for each single storm and for the complete storm set, evaluating the following parameters

$$\%_{{{\text{single}}\_{\text{storm}},i}} = \frac{{n_{{{\text{ss}},i}} }}{{N_{\text{ss}} }},$$

(33)

$$\%_{{{\text{all\_storms}},i}} = \frac{{\sum\nolimits_{{{\text{ss}} = 1}}^{30} {n_{{{\text{ss}},i}} } }}{{\sum\nolimits_{{{\text{ss}} = 1}}^{30} {N_{\text{ss}} } }},$$

(34)

where i is the index running on the 5 possible variogram models, ss is the index running on the considered storms, n_ss,i is the number of times the i variogram model is declared as the “winner” by the NQCR for the storm ss, and N_ss is the total number of epochs included in each single storm ss.

Figures 13a and 14a show the winning percentage of each variogram model for each single storm, for IG_12eff and R_12eff, respectively; Figs. 13b and 14b show the same percentage for the complete storm set.

Fig. 13

Percentage of IG_12eff variogram models declared winners by the NQCR procedure. a Winning percentages related to each IG_12eff variogram model, for each single storm, after applying the NQCR procedure sketched in Fig. 6; b same as a but considering all storms listed in Table 3 as a whole

Fig. 14

Percentage of R_12eff variogram models declared winners by the NQCR procedure. Same as Fig. 13 but for R_12eff

Discussion, conclusions, and future developments

In this investigation the IRI UP method was upgraded by applying the F algorithm and the NQCR procedure to select the best variogram model.

The F algorithm described by Eqs. (1)–(4) has proven to be very effective in disregarding ionosonde data which, once assimilated, would affect badly the modeling of IG_12eff and R_12eff, leading to unrealistic foF2 and M(3000)F2 maps and, consequently, to unlikely hmF2 maps (Pignalberi et al. 2018a, b). It must be noted that considering five standard deviations and thresholds values for the standard deviation equal to 0.5 MHz, for foF2, and 0.15, for M(3000)F2, are subjective choices, aiming to remove especially those measurements which are clearly out of range (spikes), as shown in Fig. 2.

Using residuals it is possible to define the statistical parameters Q₁ and Q₂ along with their PDF and CPF, which are sketched in Figs. 4 and 5, respectively, for a number of reference stations equal to 12. In these figures, the two thresholds |σ| and |2σ| for Q₁, and [L–U] and [L^1st–U^3rd] for Q₂, have been deliberately taken very different from each other, to highlight how the choice of the threshold value can have an important impact on the number of discarded variogram models. In fact, in Figs. 8 and 9, for the storm number 12 (August 23–28, 2005), it clearly emerges that the number of rejected variogram models is relatively large when the threshold is lowered from |2σ| to |σ| (for the statistical test Q₁) and from [L–U] to [L^1st–U^3rd] (for the statistical test Q₂). The threshold effect is however much less evident in the case of the storm number 27 (October 6–11, 2015), for which a limited number of variograms are discarded when reducing the threshold.

This is probably due to the different numbers of available reference stations used in the assimilation, which for the period October 6–11, 2015 (n = 12), is larger than that for the period August 23–28, 2005 (n = 8), thus allowing a better representation of the spatial gradients over the area under study.

When the distribution of semivariance values calculated through Eq. (6) is such that the experimental variogram cannot be adequately represented by any of the variogram models defined in “The Kriging interpolation method: a brief recall” section, we are forced to discard the variogram modeling because it would lead to unrealistic maps. Figure 3 shows some examples of discarded variogram models for IG_12eff and R_12eff; in these two cases the fitting function is an approximately straight horizontal line whatever is the considered variogram model, and the corresponding maps are not able to reproduce IG_12eff and R_12eff values over the reference stations. This is due to the very large nugget values (c₀ = 34.8 for IG_12eff and c₀ = 98.6 for R_12eff) describing the microscale variability. This implies that colored dots, marking the reference stations, are in contrast with the colors characterizing the regions around the reference stations, which means that the maps are not realistic since do not match the measured data.

On the other hand, if in Fig. 3 we look at the statistical parameters related to these two experimental variograms, the associated values of Q₁ (0.49 for IG_12eff, 0.37 for R_12eff) and Q₂ (0.91 for IG_12eff, 1.07 for R_12eff) are such that the two experimental variograms do not pass the Q₁ and Q₂ statistical test defined in “Q₁ statistics” and “Q₂ statistics” sections, and hence, they must be rejected along with their corresponding maps.

On the contrary, when the nugget effect is not so relevant and the distribution of semivariance values can be well described by most variogram models, the experimental variograms produce realistic maps. This is what happens for the case shown in Fig. 7 where the null nugget effect (c₀ = 0 for IG_12eff and R_12eff), and the associated values of Q₁ (0.22 for IG_12eff, 0.49 for R_12eff) and Q₂ (0.98 for IG_12eff, 0.76 for R_12eff) are such that the two experimental variograms pass both the Q₁ and the Q₂ statistical test. In this case, the corresponding maps show IG_12eff and R_12eff values, over the reference stations, compatible with those of the regions close to the reference stations.

The preliminary quality check based on the exponent s sets always the same threshold value s_thrs = 0.1 whatever is the epoch and variogram model under study, without taking into account that the goodness of the variogram model depends also on the number n of available ionosonde data which are going to be considered in the UKM. This significant limitation characterizing the first version of IRI UP is overcome because, through the NQCR procedure, the quality check now depends on the n value that can change from epoch to epoch. Moreover, another essential aspect that should be considered when NQCR is applied is that, from a scientific point of view, “winning” variogram models are more reliable than the ones which have passed only the s ≥ s_thrs test. As it is easy to realize looking at Figs. 8 and 9, the number of variogram models discarded by the NQCR procedure depends on the established thresholds values. As a general rule, if, at a given epoch, the number of reliable ionosonde data to be assimilated is relatively large, we can choose a more selective threshold, thus providing ionospheric characteristics maps with a high confidence level. In the event that the number of reliable ionosonde data is lower, we have to increase the threshold and in this case a map can be provided, but at a lower confidence level. It is clear that when there are very few reliable data to be assimilated, we cannot provide a statistically significant updated map. In this case the IRI UP method is not applicable and we rely on the IRI background map.

IRI UP and IRI prediction maps of the ionospheric characteristics foF2 and M(3000)F2, relative to 30 geomagnetic storms occurred between January 1, 2004, and December 31, 2016, are used to generate IRI UP and IRI prediction maps of hmF2 using Bilitza et al. (1979). The values of foF2 and hmF2 extracted at the two truth sites of Fairford and San Vito from the corresponding IRI UP and IRI prediction maps have been compared with the measurements, to compare IRI UP and IRI performance.

The obtained results confirm those shown in Pignalberi et al. (2018a, b) for the St. Patrick geomagnetic storm; in fact, as shown in Figs. 10 and 11, as well as in Tables 4 and 5, they indicate that IRI UP performs significantly better than IRI, for all the 30 considered cases.

Moreover, results of Tables 4 and 5 show that when IRI UP is applied deciding a priori the variogram model, and then considering only those cases passing the first two steps of the NQCR procedure, a clear difference among the various variogram models does not emerge.

In fact, NRMSE values for foF2 and hmF2 range, respectively, between 9.14 and 9.40% and between 10.83 and 11.31% at Fairford and between 9.36 and 9.74% and between 10.19 and 10.64% at San Vito, while MMD_X AV values for foF2 and hmF2 range, respectively, between 0.137 and 0.152 MHz and between 7.361 and 7.479 km at Fairford and between 0.083 and 0.090 MHz and between 7.469 and 8.162 km at San Vito.

When the IRI UP method runs with the complete NQCR procedure, its performance shows a noticeable improvement at the considered truth sites, for both foF2 and hmF2. In fact, in this case, NRMSE values for foF2 and hmF2 are 8.25% and 10.44% at Fairford and 8.70% and 8.62% at San Vito, while MMD_X AV values for foF2 and hmF2 are 0.122 MHz and 6.844 km at Fairford and 0.084 MHz and 6.959 km at San Vito.

NRMSE and MMD_X AV values obtained by the IRI UP method embedding the NQCR procedure, systematically smaller than the ones obtained by both the IRI UP method running with a fixed variogram model and the IRI model, prove that the NQCR procedure embedded in the IRI UP method is effective in providing more precise and accurate results.

In general, from Figs. 10 and 11 it emerges that IRI UP performs slightly better for foF2 than for hmF2. This happens for different reasons:

• 1. foF2 assimilated data are generally more reliable than the corresponding M(3000)F2 data. This is mostly due to the fact that ionograms can be characterized by multiple reflections of the F2 layer, and when this happens an autoscaling program can be misled and the second-order reflection can be identified as the real trace; in this case the foF2 value is usually not affected by a significant error, while the M(3000)F2 is significantly wrongly scaled (Scotto and Pezzopane 2008);

• 2. the spherical harmonic expansion used by IRI to describe the foF2 and M(3000)F2 spatial behavior (see Eq. (1) in Pignalberi et al. 2018a) stops when the maximum order of the harmonics is equal to 76, for foF2, and to 49, for M(3000)F2, which means that foF2 maps present a higher spatial resolution than M(3000)F2 ones;

• 3. hmF2 is calculated applying the empirical formula of Bilitza et al. (1979), and this implies that the error characterizing hmF2 depends on the errors relative to foF2, M(3000)F2, foE (the E-layer critical frequency), and R_12eff.; therefore, the error propagation leads to an error associated with hmF2 which is intrinsically larger than that of foF2;

• 4. last but not least, foF2 predictions are based on the IG_12eff index, which is an ionospheric index because it is “built” just starting from foF2 values recorded at several ionospheric stations (Liu et al. 1983), while M(3000)F2 predictions, which come into play to calculate hmF2, are not based on an ionospheric index, but on R_12eff.

Another positive aspect of the IRI UP method is that the experimental variogram has a higher spatial variability the larger is the number n of data assimilated from the reference stations, so that corresponding maps are statistically more reliable and are not discarded. This situation is clear from the results of Fig. 12 where, for each kind of variogram model, a decreasing trend of the number of discarded maps is observed starting from the storm number 17, corresponding to 2012, i.e., the year from which the number of available ionospheric stations maximizes (see Table 2).

It is also to be noted that stationary variogram models (gaussian, spherical, and exponential) are more sensitive than non-stationary ones to the number n of assimilated data; this is probably due to their more complex mathematical formulation which requires a greater value of n to represent more adequately the spatial correlations between measurements, for every spatial scale. In fact, considering all storms as a whole, it results that percentages of rejected stationary variograms for foF2 (Fig. 12c) and hmF2 (Fig. 12d) are greater than those related to non-stationary variograms (linear and power). This result is probably due to the cumulative effect of the first 16 storms listed in Table 3, which are relative to years characterized by a low value of n. Nevertheless, in Fig. 12a, b, the trend observed starting from the storm number 17, corresponding to the years for which n is increased (n = 12), suggests that the percentages of stationary and non-stationary discarded variogram models may converge to similar values as the number of stations increases.

The winning percentages shown in Figs. 13b and 14b indicate that among the linear, power, spherical, and exponential variogram models there is not a clear predominance of one model over another, and that the gaussian variogram model shows the higher percentages, ≈ 40% and 29%, for IG_12eff and R_12eff, respectively. This fact is surprising, because if we consider Fig. 12 the Gaussian model is the one most rejected. This means that the Gaussian variogram model passes more difficult the Q₁ and Q₂ statistical tests, but when this happens, it is more likely to be the best according to the NQCR procedure. A fact that clearly emerges also when each single storm is considered (Figs. 13a, 14a).

It is worth noting that the achieved results have been obtained without explicitly considering the hour of the day. In fact, with regard to the future developments, a very important aspect that will have to be considered is that ionospheric characteristics depend inherently on the hour of the day. At the solar terminator (hours around sunrise and sunset), regardless of the large-scale latitudinal spatial gradients, the electron density spatial distribution manifests also large longitudinal gradients on small spatial scales. On the contrary, under ionospheric stationary conditions (hours around noon and midnight) the electron density spatial distribution does not show large longitudinal differences and hence the ionospheric variability is characterized by small gradients on both large and small spatial scale. These considerations imply that the choice of the variogram model should depend on the hour of the day.

In principle, using the UKM method described in “The Kriging interpolation method: a brief recall” section, the large-scale spatial behavior of the considered ionospheric characteristic is represented by the term m of Eq. (14), which allows to characterize also those sectors that are far from reference stations where the data assimilation takes place, without necessarily using non-stationary variogram models (Pignalberi et al. 2018a, b).

This means that stationary variogram models (Gaussian, spherical, and exponential) could describe better the situations at the sunrise and sunset hours, when the ionospheric characteristic shows large gradients on small spatial scale.

Vice versa, in the hours around noon, when the small-scale spatial gradients are not so important, non-stationary variogram models (linear and power) are likely more indicated.

In the light of these considerations, a careful and detailed study, aimed to investigate how the hour of the day affects the choice of the variogram model, is of crucial importance to get useful clues in order to improve further the goodness of the variogram model selection and consequently the quality of prediction maps of the main ionospheric characteristics.

The results achieved in this investigation prove, however, that reliable and trustworthy updated maps of the main ionospheric characteristics can be provided with a satisfactory degree of confidence, especially under moderate, strong and severe geomagnetic storm conditions. This means that IRI UP method, embedding the F algorithm and the NQCR procedure, represents an interesting approach to Space Weather forecast in the ionospheric domain, for any region characterized by an adequately distributed network of ionosondes.