Background

Only three native ungulate species occur across Patagonian forests, arid grasslands, and shrub steppes: two cervids (Southern pudu, Pudu pudu, and South Andean huemul, Hippocamelus bisulcus) and one camelid (guanaco, Lama guanicoe; Mattioli 2011). Among them, the guanaco is the largest and most abundant species, as well as the one with the highest potential economic impact (Franklin et al. 1997). Guanacos range from Peru to Tierra del Fuego (Franklin 1983; Redford and Eisenberg 1992), although 90% of guanaco populations occur in Argentina (Franklin 1982), mainly throughout Patagonia (Puig 1995).

Despite the guanaco’s flexible social behavior (Franklin 1983) and ecophysiological adaptations to harsh environments (Franklin and Fritz 1991), populations have declined in numbers and geographic range (Franklin 1982; Puig 1995; Baldi et al. 2010). This decline has been attributed primarily to intense and uncontrolled hunting (Franklin 1982; Cunazza et al. 1995; Donadio and Buskirk 2006) and competition with introduced wild and domestic herbivores, such as the European hare (Lepus europaeus; Garrido 1985) and domestic sheep (Ovis aries; Puig et al. 1997; Baldi et al. 1997, 2001, 2004).

It is thought that Santa Cruz, the southernmost continental province of Argentine Patagonia, contains the largest guanaco population (Baldi et al. 2006). The suspected important contribution of this region to overall numbers contrasts with the paucity of available information about guanaco density and its spatial variation (Baldi et al. 2010). The only population estimation of guanacos in Santa Cruz is that of Amaya et al. (2001), who calculated a total of 223,847 guanacos based on strip counts along 2,800 km of aerial transects. Moreover, global population numbers are derived on the basis of densities reported in other parts of Patagonia (<600,000 individuals, about 90% in Argentina; IUCN 2014), where local guanaco densities were often below 2 ind/km2 (Baldi et al. 2010). Excluding the Patagonian survey by Amaya et al. (2001), deemed unreliable by IUCN (2013), density estimates used to calculate global guanaco numbers come from local studies or surveys over relatively small regions (e.g., Baldi et al. 1997, 2001; Puig et al. 1997, 2003) that show considerable variation in guanaco density. Given this heterogeneity and the expected influential contribution of Santa Cruz populations (Baldi et al. 2006), estimates of population size in Patagonia could substantially depart from figures currently accepted after obtaining more reliable estimates of guanaco numbers in Santa Cruz. Moreover, large-scale surveys can help quantify spatial variation in guanaco density.

Most density estimates of guanaco across Patagonia have been derived from strip count methods over relatively small areas. A key limitation of this technique is that it does not allow the estimation of animals missed within the sampled area. In contrast, distance sampling yields an estimate of missed guanacos, an objective estimate of the detection band along line transects, more accurate density estimates and their variances, and the possibility of extrapolating densities outside the area effectively surveyed (Buckland et al. 2001; Thomas et al. 2010).

In Santa Cruz, sheep ranching has been the prevalent land use since the late 1800s when European settlers arrived to the southern Patagonia (Soriano and Paruelo 1990). From the beginning, guanacos were generally perceived by ranchers as a pest and competitors of sheep for forage. On the other hand, guanacos have the potential of becoming an important economic source of complementary income to sheep ranching on a sustainable basis because of its wool (Franklin 1983; Sacchero et al. 2006), meat (Soto et al. 1991; Franklin et al. 1997), leather (Ojeda and Mares 1982), appeal for ecotourism, and as a game species (Franklin et al. 1997; MACS 2002).

The sustainability of potential guanaco exploitation should be based not only on sound population estimates, but also on a well-designed monitoring protocol for measuring population size before starting any extractive activity and assessing its potential impact later on (Di Stefano 2001). Statistically powerful monitoring programs (Steidl et al. 1997) can help detect early trends in guanaco abundance, despite noise in the survey data associated with seasonal variations or unavoidable errors in field sampling (Gibbs and Melvin 1997; Elzinga et al. 2001). Statistical power is critical in the design phase of monitoring wildlife populations (Taylor and Gerrodette 1993).

In this paper, we report spatial variation in estimates of guanaco population size for Santa Cruz obtained with distance sampling techniques on data from an extensive, large-scale road survey. We also propose a population monitoring protocol to detect temporal changes in guanaco population size. Such a protocol has the potential to be an important management tool for detecting further declines in guanaco populations due to unsustainable sheep ranching or potentially unsustainable ill-planned extraction of guanacos in Patagonia (Montes et al. 2006; Rey et al. 2009).

Methods

Study area

Santa Cruz province (46° to 53° S; 65° to 73° W, Figure 1a) expands over 245,865 km2 and accounts for 6.5% of the land area of Argentina (González and Rial 2004). With the exception of a western strip of Andean influence, this region is a cold semi-desert covered by shrub-steppes, where climate shows a marked gradient, with mean annual rainfall decreasing from west (800 mm) to east (down to 100 mm in some places) and mean annual temperatures decreasing from northeast to southwest in the range 5 to 10°C (Oliva et al. 2004). Aridity precludes shifting from sheep ranching to more profitable cattle ranching. Sheep overstocking (Golluscio et al. 1998) and overgrazing of mesic sites (Mazzoni and Vázquez 2004) has lead to widespread steppe degradation (León and Aguiar 1985). Unsustainable use of rangelands has resulted in land abandonment in 60% of the Santa Cruz province (Borrelli and Cibils 2005). A recent socioeconomic trend to resume sheep ranching has been reported but, unfortunately, practices responsible for previous damages to the steppe are being adopted again (Andrade 2005).

Figure 1
figure 1

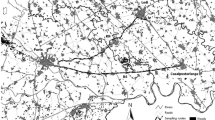
Guanaco geographic range, study area, and roads surveyed. a Former and present guanaco distribution throughout South America (adapted from Franklin et al. 1997) and study area, Santa Cruz province in southern Argentine Patagonia. b Initial stratification in 12 regions, based on productivity (three NDVI categories: low, medium, and high) and topography (two categories: flat and rugged terrain). The surveyed roads are shown.

Full size image

Guanaco social units

Guanacos are sexually monomorphic and aggregate in social groups during the breeding season (Sarno and Franklin 1999) and winter (Franklin 1983). The spatial distribution of individuals is strongly influenced by a mating system of resource defense polygyny, a territorial system wherein males compete for access to resources required by females (Franklin 1983; Young and Franklin 2004a). Guanacos can be found in three basic social units: family groups (a male with a group of females and young less than 1 year old called 'chulengos'), male groups composed mostly of non-breeding males, and solitary territorial males. There is a fourth potential social unit, female groups, observed during intensive studies in Torres del Paine National Park, Chile (Ortega and Franklin 1995). We did not consider this social unit because it may be less common (8% of all social units; Ortega and Franklin 1995) and could also include young (Bank et al. 2003) making them difficult to distinguish from family groups without closer examination. Pedrana et al. (2009) showed that only solitary males and family groups with chulengos could be unequivocally identified when conducting large-scale road surveys. This is because sex determination of every individual by their primary sexual characters is time consuming and hence impractical when, as it was our case, observers in a single vehicle had to survey thousands of kilometers during one breeding season. These difficulties increase for distant animals. Pedrana et al. (2009) also suggested that identification of male groups was challenging because an unknown proportion of family groups may have not contained chulengos.

When the goal is estimating population density, the relevant information is group size whereas recording group composition is of secondary importance. However, stratification helps to increase the precision of density estimates (Thomas et al. 2010) and, as social units differ in mean group size (Pedrana et al. 2009), social units represent a form of stratification that we considered during the survey design. Therefore, we opted to produce separate density estimates for three observable social units: breeding groups (defined as groups with detected chulengos), non-breeding groups (groups without chulengos or with undetected chulengos), and solitary animals. Guanaco contacts that could not be clearly assigned to any of these categories were placed in a fourth class called undetermined. A correct assignment of an observable group to a guanaco social unit could be possible (Franklin and Fritz 1991) but would require unavailable observation time, as in abundance surveys completing data collection in a period as short as possible (ideally a snapshot) is a priority. Finally, we also estimated density after pooling together all guanaco contacts.

Field surveys

The size, coloration, and behavior of guanacos make them easily detectable at distances of several hundred meters in the open Patagonian steppes where grasses and shrubs are generally <1 m high (Puig 1995). The prevalence of these conditions in the study area satisfies the key assumption of distance sampling methodology that all individuals that were on the road were detected (Bibby et al. 1992; Buckland et al. 2001; Thomas et al. 2010).

Road surveys were conducted from a vehicle during two consecutive birthing/breeding seasons (November 2004 to February 2005 and December 2005 to January 2006) in periods that lasted no more than 70 days per season. Given the extent of the area to be covered, we obtained data intensively, surveying during whole days with good visibility except periods within 1 h around twilight. Data were collected mostly at a speed of 20 km/h, by the driver and one observer, who exchanged their positions or were replaced every 2 h. Guanacos usually did not respond to our vehicle (with the exception of those that were on the road), so the distance sampling assumption that guanacos moved at much lower speeds than observers was also satisfied. A given road stretch was surveyed only during one breeding season and, in most cases, during a single day. All types of public roads were surveyed, although unpaved roads with scarce traffic (<10 vehicles/day) dominated (90%) the road network in Santa Cruz. When guanacos were detected, we stopped the vehicle, recorded group size (with binoculars when needed), and assigned the group to one of our three observable social units. We recorded the distance to the animal or the group center with a laser range finder (Leica LRF 1200 Rangemaster), thus fulfilling the distance sampling requirement of exact distance measurements. We also recorded our bearing relative to north obtained from the inertial compass reading of a GPS unit and the angle of the animal relative to our bearing. The perpendicular distance of contacts to the survey line was calculated from these data (Buckland et al. 2001).

Survey design

During the design of the study and in order to account for the expected regional variation in guanaco density associated with major environmental variability, stratified random sampling (Levy and Lemeshow 1999) was performed to establish which road segments would be surveyed each year (Figure 1b). We divided the study area into 12 geographical regions or strata, based on the combination of two environmental variables (Normalized Difference Vegetation Index, or NDVI, and mean slope) that we expected could influence the frequency of contacts with guanaco. Indeed, both variables accounted for guanaco distribution in Santa Cruz (Pedrana et al. 2010). NDVI was used because vegetation productivity could be an important driver of guanaco abundance, and mean slope because guanacos could prefer plains to rugged areas and their detectability could be affected by terrain irregularity. Further details about data sources and procedures are given by Travaini et al. (2007). We divided the values of mean NDVI into three classes and mean slope into two classes, which generated six possible environmental combinations. We selected the two largest polygons from each combination as seeds (12 seeds) and formed the final area by assigning the remaining polygons of a particular class to the closest seed.

Using vector coverage of roads, we randomly selected road segments, defined as complete or fractions of stretches between crossroads, up to a total length of 4,500 km during the first season (Figure 1b). To ensure that all strata would be properly sampled, 1,500 km were equally distributed among the 12 survey strata (125 km in each stratum in order to guarantee a minimum sampling effort in strata that could potentially cover small areas), and 3,000 km were subsequently allocated proportionally to the area of each stratum. During the second season, we randomly selected road segments not surveyed in the previous year up to completing a total of 8,141 km covered during the study (Figure 1b). Each road segment was surveyed just once, and segments surveyed in different years were typically hundreds of kilometers apart. The combination of randomization, exhaustive replication across strata and a balanced distribution among major environmental gradients led us to obtain abundance estimates representative for the whole study area. Again, environmental stratification helped to reduce the variance of density estimates (Thomas et al. 2010). Overall, our design allowed us to extrapolate density values beyond the sampled area and apply them to the whole extent of each stratum, i.e., to environmentally similar areas (Thomas et al. 2010), under the assumption that guanaco density tends to be homogeneous under similar ecological conditions.

Environments along and around roads seldom form a perfect random sample of ecosystems present in a region (Hawbaker et al. 2005; Bi et al. 2011). Using elevation as a proxy for environmental variation, we examined the extent to what mean altitude in 1 km cells overlapping roads (n = 23,230) differed from mean altitude in cells across Santa Cruz (n = 222,726), after excluding cells above 1,000 m which make up 8.6% of the study area. Along roads, frequencies expressed as proportions and computed for five 200 m classes of altitude between 0 and 1,000 m, ordered from low to high elevations, were as follows: 0.41, 0.31, 0.14, 0.11, and 0.03. Such values do not depart much from corresponding proportions of available elevations: 0.31, 0.30, 0.15, 0.15, and 0.09. This further suggests that major environmental variation across Santa Cruz was adequately captured by our road transects.

Abundance

Pedrana et al. (2010) modeled guanaco distribution in Santa Cruz using environmental predictors. Predicted probabilities of guanaco occurrence were divided in three classes and were plotted on a map (Figure 2). Assuming that predicted probabilities of detection are a positive function of guanaco abundance, this map can be read as a map with areas of expected low, medium, and high relative abundance of guanacos. Abundance estimates were calculated for each observable social unit, and for all guanaco contacts pooled together, within each area of expected relative abundance of guanacos and then for the whole study area. As predictions of guanaco occurrence were not made for water bodies, forests, areas above the treeline, and other habitats unsuitable for guanaco (Pedrana et al. 2010), the area for which abundance was estimated (222,545 km2; Table 1) was 91% of the surface of Santa Cruz province.

Figure 2
figure 2

Distribution of road surveys for monitoring guanaco populations. Shading shows the expected relative abundance of guanacos assuming it is a positive function of the probability of guanaco occurrence. Probabilities of occurrence calculated by Pedrana et al. (2010) were divided in three classes: <0.4, 0.4 to 0.6, and >0.6. Lines denote one realization of the possible location of 30-km sampling units needed for monitoring guanaco numbers under a hypothetical objective of detecting a 50% population change in the next 10 years, with α = 0.3 and a minimum power of 1-β = 0.8. a Example of 40 randomly placed sampling units required for detecting a population increase. b Example of 80 randomly placed sampling units needed to detect a population decrease.

Full size image
Table 1 Sampling effort and sightings across classes of expected relative abundance of guanacos
Full size table

Line transect data were analyzed using program DISTANCE 5.0 (Buckland et al. 2001; Thomas et al. 2010). Estimates of guanaco densities were done by fitting a detection function to the perpendicular distances of guanaco groups to the survey line (Buckland et al. 2001). We pooled records across all transects and years within each area of guanaco relative abundance to estimate the detection function g(x) for each social unit in order to attain the required minimum number of observations (Buckland et al. 2001). Although detectability varies among transects, the property of 'pooling robustness' ensures the reliability of abundance estimates when all data were analyzed together (Buckland et al. 2001; Thomas et al. 2010). Pooling helps even out fluctuations in guanaco density across surveyed transects as well as chance fluctuations in guanaco distribution (Fewster et al. 2005). Considering the extent of each area of guanaco relative abundance, density estimates were converted into estimates of population size. DISTANCE allows for identification of outlying observations at extreme distances, or sighting clumping, and suggests appropriate levels of truncation and grouping for fitting the detection function. We used the Akaike Information Criterion (AIC; Burnham and Anderson 1998) to choose the best competing model (key function + adjustment terms) for the detection function.

Monitoring program

We estimated the power of different monitoring designs to detect changes in guanaco population size with the aid of software MONITOR (Thomas and Krebs 1997; Gibbs and Ene 2010). MONITOR uses Monte Carlo simulations (Manly 1997) to model count surveys (encounter rate in our case) over time and generates detection rates derived from route-regression analyses (Geissler and Sauer 1990; Gibbs and Melvin 1997). This simulation procedure is useful for evaluating the trade-offs between sampling effort, logistical constraints, and power to detect trends (Gibbs et al. 1998; Field et al. 2005). To estimate power, we supplied the program with initial estimates of encounter rates and its variance for each scenario, that is, each combination of effect size (a pre-established percent increase or decrease in population size over a given period), time interval, class of guanaco relative abundance, and social unit. Monitoring output was defined in terms of sampling effort, survey frequency, and type I error. We arbitrarily defined sampling effort as the number of 30-km transects, but equally valid results could be obtained with shorter or longer transects. Based on our experience, a 30-km transect usually takes about 2 h to be completed, and 2 h was also the interval we used to switch observer and driver during field work. Additionally, random 30-km segments could be selected from the vector data of road coverage more easily than longer segments because distances between nodes of the road network were often >30 km. For each scenario, we estimated one value of statistical power after 1,000 replications. To select scenarios that we considered suitable for the design of a monitoring program, we set the minimum acceptable power at (1-β) = 0.80 (Di Stefano 2001), i.e., the highest probability of failing to detect an actual trend in guanaco abundance was 0.20.

As initial values, the program requires estimates of the mean and coefficient of variation of encounter rates which we derived empirically from our results.

Results

Guanaco abundance

We surveyed 8,141 km, approximately 93% of the public road network length in Santa Cruz. We recorded 991 contacts with guanaco social units that totaled 5,965 individuals (Table 1). Excluding contacts classified as undetermined, most guanacos were in groups, equally divided between breeding groups (47% of total contacts), and non-breeding groups (47%). The remaining 6% were solitary individuals (Table 1).

After considering competing detection functions, the Hazard-Rate key, with two-parameter cosine adjustment terms, was selected for all types of guanaco social units except solitary individuals, for which a function with four parameters was the most parsimonious. We truncated distance data at 500 m in all models except those for solitary individuals that were truncated at 600 m (Table 2), in order to attain a robust line transect analysis after the elimination of outliers (Buckland et al. 2001). Our truncation distance closely satisfied g(w) ≈ 0.15, where g(w) is the detection function at the truncation distance w (Table 2). After truncation, the number of contacts used to estimate guanaco density in each observable social unit is shown in Table 2. Within truncation distances, sightings at distance zero accounted for 9.4% of contacts, whereas a further 31.1% of contacts were made within 50 m of the survey line. The band 0 to 50 m was the modal class in a uniform distribution of distance classes at 50-m intervals. Within the modal class, mean (±SD) perpendicular distance to contacts was 24 ± 12 m.

Table 2 Density and population size
Full size table

We estimated a mean density of 4.79 ind/km2 with a coefficient of variation of 20% (Table 2). As expected, density estimates increased with the predicted probability of guanaco occurrence defined by Pedrana et al. (2010) as classes of expected relative abundance. Overall mean density greatly varied from areas with expected low relative abundance (1.12 ind/km2) to areas with expected high relative abundance (7.74 ind/km2; Table 2). Across social units, the highest value of mean density was found for breeding groups (2.23 ind/km2), which was a 34% higher than that for non-breeding groups (1.67 ind/km2; Table 2). High density values were also associated with high variances, which for breeding groups were about twice as high as for non-breeding groups or solitary guanacos (Table 2).

As classes of relative abundance were built with distribution models based on environmental predictors (Pedrana et al. 2010), assuming that guanaco densities fall within the confidence intervals shown in Table 2 in similar environments, we estimated a total guanaco population of 1,066,600 individuals in Santa Cruz (95% CI 727,800 to 1,563,200). Half of the estimated population size would appear in the form of breeding groups (Table 2). There was a remarkable match (a difference of only 1.33%) between estimates of guanaco population size obtained by summing up the estimated abundances for each guanaco social unit (N = 1,052,436 individuals) and those obtained after pooling all guanaco contacts together, although the confidence of the estimates using the former approach was lower (95% CI 489,900 to 2,594,200; Table 2).

Population monitoring

Detection of changes in guanaco population size over a 10-year period, either an increase or a decrease, would require considerable monitoring effort (Table 3). This effort grows significantly if a population trend in shorter periods, such as 5 years, is to be detected (Table 3). For instance, annual surveys of 40 30-km transects would be necessary for detecting a 50% increase in total guanaco abundance during the next 10 years, keeping α = 0.2 (Figure 2a). Detecting a 50% decrease in 10 years would require surveying twice as many transects every year (Figure 2b). The sampling effort required to detect a 50% increase during the next 5 years would be 80 transects. Finally, if we want to detect a 50% decrease within 5 years, we should relax type I error to α = 0.3 and survey 90 transects every year. Otherwise, sampling effort would increase over 120 transects (Table 3). Monitoring efforts for specific combinations of strata of predicted probability of guanaco occurrence and types of guanaco groups range from 20 to >120 transects (Table 3).

Table 3 Sampling effort needed to monitor guanaco population trends in Santa Cruz province, southern Patagonia
Full size table

Discussion

Our results confirm the expectation that a relatively high density of guanacos could be found in Santa Cruz (Baldi et al. 2010), where no comprehensive survey of abundance had been carried out before. Comparison with previously published figures for Santa Cruz is difficult because both ecological conditions and estimation methods used in available studies were quite different. For example, Manero et al. (1986), based on a single 119-km transect, estimated a summer density of 0.37 to 0.94 ind/km2 for an unspecified area located in central Santa Cruz, which would correspond to a region with medium-high predicted probabilities of guanaco occurrence (Pedrana et al. 2010) and for which our density estimates were 5 to 8 times higher. The estimates of Manero et al. (1986) were based on an encounter rate of 0.28 ind/km, a value much larger than the detection rate we estimated in the medium and high abundance areas (0.11 and 0.19 ind/km, respectively). The low values reported by Manero et al. (1986) were contemporary with intensive sheep ranching and associated yearly culling of chulengos during the 1970s, but were also not derived from distance sampling which could also help explain this marked discrepancy.

Our density estimates (1.1 to 7.7 ind/km2) fall within the range of values reported elsewhere in Patagonia. In northern areas, densities are also highly variable (1.0 to 13.9 ind/km2; Puig et al. 1997), and extreme values over 40 ind/km2 have been calculated (Puig et al. 2008). The same pattern can be found in central Patagonia where densities ranged between 0.6 and 8.8 ind/km2 (e.g., Saba and Battro 1987; Baldi et al. 1997; Marino and Baldi 2008). Variability in higher latitudes outside Santa Cruz, including Tierra del Fuego, varied in a narrower range (0.3 to 4.7 ind/km2; Raedeke 1982; Bonino and Fernández 1994; Ortega and Franklin 1995; Montes et al. 2000). In general, guanaco densities were lower in areas of high primary productivity if sheep occur in high density (Montes et al. 2000; Baldi et al. 2001, 2004), and our results agree with this pattern as we found high guanaco densities in areas with low sheep abundance identified by Pedrana et al. (2010).

In summary, guanaco density has been reported for about a dozen localities throughout Patagonia, generally very small in size as compared with Santa Cruz (e.g., Saba and Battro 1987; Ortega and Franklin 1995; Baldi et al. 1997; Puig et al. 1997). Baldi et al. (2010) suggested that guanaco density is rarely higher than 2 ind/km2 in northern and central Patagonia, which would be consistent with the global population estimate of <600,000 individuals that is currently accepted (Franklin et al. 1997; Baldi et al. 2010, IUCN 2013). In agreement with the contrasting densities reported in the studies listed above, our results reveal large spatial variations in guanaco density, with the difference between extreme estimates being sevenfold within Santa Cruz. This pattern can be unveiled only through extensive, large-scale surveys covering major environmental gradients. As published average guanaco densities for Patagonia are extrapolations based on densities calculated over areas much smaller than Santa Cruz, the risk exists that large-scale variation in density is missing, introducing biases in population size estimates for the whole guanaco geographic range. Indeed, our estimates of population size in Santa Cruz, even when the lower endpoint of 95% confidence intervals was used, are as large or larger than estimates of global guanaco population size (Baldi et al. 2010; IUCN 2013), suggesting that these deserve revision. Large-scale surveys that use distance sampling techniques could produce more accurate estimates of guanaco density, population size, and its variation than estimated based on strip transects over relatively small areas.

A critical assumption of distance sampling in our road surveys was that the distribution of guanacos is independent of roads (Thomas et al. 2010). The assumption of independence would be violated if guanacos were closer or farther from roads than expected from a uniform or a random distribution. This possibility is entirely dependent on guanaco behavior and requires hypotheses about the underlying mechanism. Pedrana et al. (2010) found low probabilities of detecting guanacos from roads within 20 km of the few small cities that occur in Santa Cruz, and hypothesized that this pattern could represent a response to hunting from roads. This observation could be in agreement with the hypothesis by Donadio and Buskirk (2006) that recurrent exposure to hunting alters foraging and, consequently, guanacos could avoid these disturbed sites. However, >95% of our survey was conducted far away from cities, in depopulated areas and with scanty traffic during most of the year. In general, we did not notice any consistent avoidance behavior of guanacos in response to our presence, namely, a stopped car with people pointing instruments to them, even at close distances. Although the repulsion hypothesis seems unlikely in Santa Cruz, if road avoidance by guanacos were a general pattern, it would have contributed to underestimate currently accepted density and numbers of guanaco across Patagonia.

Another possibility is that guanacos were attracted to roads. No specific mechanistic hypothesis has been formally forwarded in this regard, but the potential presence of good quality forage at road verges, perhaps as a result of disturbance associated with road maintenance, could be one of them. This hypothesis predicts a concentration of guanaco observations at distance zero, i.e., the road verge, where the hypothesized valuable resource should occur. This prediction was rejected because <10% of observations were recorded on the road, whereas the modal distance class for all social units was 0–50 m, where guanacos were foraging on regular steppe vegetation. Moreover, in most sites, we were unable to detect major differences in the abundance or composition of plants at road verges as compared with surrounding vegetation, although examining this edge effect requires specific studies. Without surveys along truly random lines (randomly placed straight lines away from roads or smaller tracks) and without a plausible mechanistic explanation for the high frequency of guanaco sightings within 50 m, the hypothesis of guanaco attraction to roads and the hypothesis or a mere decrease in guanaco detectability with distance to roads cannot be distinguished with our data. Considering existing evidence, we assume that the distribution of guanacos was independent of roads over most of the road network in Santa Cruz, and preliminarily conclude that biases in our density estimates due to the violation of this assumption are implausible.

In Patagonia, two alternative survey methods could be used to test the assumption that guanaco distribution is independent of roads, but it is unclear that these methods would allow extensive distance sampling over large regions. Horseback distance sampling has a number of disadvantages: rugged terrain could hardly be sampled, surveying areas far away from human habitation would be unfeasible (with the consequent bias), and it would be difficult to cover large regions during a short session. Aircraft distance sampling would solve some of these problems and therefore is desirable but, on the other hand, logistic costs of aerial surveys make them much more expensive than road surveys (Travaini et al. 2007).

A second concern regarding randomization of transects was pointed out by Fewster et al. (2005): the full enumeration of sources of variation in detectability is generally impossible for animals because of factors such as habitat, sighting conditions, and observer experience and alertness. Survey design should ensure that all transects in the study area have the same probability of being included in the sample. We think that our distribution of road segments among 2 years of study was suitable considering the logistic and time constraints imposed by the large area to be covered. Moreover, as guanacos exhibit quite sedentary habits and long-distance movements are rare even for migratory individuals (Mueller et al. 2011), separation between segments surveyed in different years further ensure independence of observations.

Interest in sustainable use of the guanaco has increased in Argentina and Chile. National strategies are concerned with evaluating, conserving, and restoring wild populations in Argentina (Puig 1992; Baldi et al. 2006), Chile (Soto 1993; Skewes and Soto 2003), Bolivia (Velasco et al. 1992), Ecuador (Paucar 1992), Paraguay (Ríos 1992), and Perú (Hoces 1992). Large-scale assessments of variation in density, such as the one we present here, are a valuable tool for developing management plans that integrate conservation and sustainable exploitation of guanaco populations (Baldi et al. 1997). Our estimation of guanaco population size in Santa Cruz is only half the number of sheep currently raised in this province (2,607,000 heads; INDEC 2011), which is also the maximum number of sheep stocked in the province during the last decade (INDEC 2009). More than 60% of Santa Cruz area, including the central basaltic highlands, interspersed with marine and continental sediments of variable susceptibility to erosion in the lowlands, has a sheep carrying capacity of 5–20 ind/km2 (Pablo Peri, personal communication). This low stocking rate corresponds to areas heavily overgrazed in the past where sustainable sheep ranging is no longer possible (Golluscio et al. 1998). Precisely, we estimated the highest guanaco abundances there (7.74 ind/km2) suggesting that in such arid and degraded shrub-steppes, guanacos could be viewed as an opportunity for sustainable development based upon a profitable natural resource (Sacchero et al. 2006).

Guanaco densities vary across space and over time, depending on natural (Puig et al. 1997) and human factors (Baldi et al. 2001, 2004). This variability should be considered in any extractive activity and subsequent commercial use of populations. In our view, knowledge of sex and age composition as well as other demographic parameters is incompatible with the quick assessment of group composition imposed by surveying a very large area in a few months. This could be attempted by several teams working simultaneously in different parts of the area, as guanaco demographic details would be needed before planning any extractive activity in a local population. Survey techniques that can derive sex ratio and age structure of a population are advantageous, as these provide potential insight into recent history, current status, and future population trends (Dimmick and Pelton 1996). Sex ratios and age classes are necessary for modeling guanaco populations and for determining harvest rates (Franklin and Fritz 1991, Fritz and Franklin 1994; Franklin et al. 1997), but are not essential when only estimating population size and trends, which requires at most a quick assignment of contacts to social units. Failure to estimate reliable sex ratios of guanaco populations from road-survey data is not uncommon, as assignment of contacts to social units on the sole basis of guanaco behavioral traits is not always reliable (Pedrana et al. 2009). In applications where one needs to know sex and age structure, this problem can be minimized, if not overcome, if surveys are conducted towards the end of the birth season when chulengos are abundant. In addition, with training and experience, sexes can be identified even at moderate distance by morphological characteristics (testes/vulva, penis/mammary gland, and body shape) and behavioral cues, as demonstrated by field studies with a more acceptable 3 to 5% unclassified animals (Franklin and Fritz 1991, Fritz and Franklin 1994; Ortega and Franklin 1995; Sarno and Franklin 1999; Young and Franklin 2004b). Methodological improvements by guanaco researchers and managers need to be made to substantially increase the reliability of field identification of guanaco sexes and social groups.

Monitoring guanacos in Santa Cruz could be wrongly considered unaffordable by wildlife managers if not evaluated within a cost-benefit analysis. The economic cost of well interspersed survey transects throughout the territory, developed by a team of three experienced observers during 10 to 15 days, should be counterbalanced against the potential economic benefit of direct income derived from guanaco products and the large conservation benefits arising from land use diversification. Additionally, considering the relatively predictable guanaco local distribution due to male territorial fidelity over the years, the effect of management practices on guanaco populations could be easily surveyed and monitored to evaluate trends (Young and Franklin 2004a). The sustained yield harvesting of guanaco wool and/or meat, complementary or supplementary to sheep ranching, may be the most effective way to conserve guanacos (Fritz and Franklin 1994) and other wildlife, if land owners acknowledge the potential economic return of this species. Diversifying land uses and adopting sustainable forms of guanaco exploitation should be the shared objectives of Argentine wildlife agencies, as a potential mechanism pursuing both the reduction of the ecological damage of sheep overgrazing and the socioeconomic improvement of rural communities in Patagonia rangelands.

Conclusions

Our results show that Santa Cruz contains a large population of guanacos and confirms that guanaco density tends to be higher in areas with low sheep density. Estimates of population size of nearly one million individuals exceed currently accepted estimates for the guanaco geographic range which suggest that the latter need to be revised. Guanaco density shows considerable variation across large-scale environmental gradients. Therefore, detecting a 50% population change within 10 years would require annual surveys of up to 80 30-km road transects evenly distributed across areas with relatively homogeneous environmental conditions. Yet, large-scale road surveys, combined with distance sampling techniques, can be recommended as a cost-effective method to monitor guanaco population trends over large regions. Considering the growing interest in sustainable use of guanaco populations, monitoring is needed to quantify its effects, to inform management, and to plan conservation measures in less abundant or declining populations.