Introduction

Geothermal energy has emerged as a clean alternative source of renewable energy for electric power generation and other direct uses (Wu and Li 2020). The enormous amount of energy stored in geothermal systems makes them an important renewable and sustainable energy source (Nieva et al. 2018; Gutiérrez-Negrín et al. 2020). Among the geothermal systems today exploited, hydrothermal systems stand out for their storage capability of hot fluids, which are used for the generation of electricity (Thien et al. 2015). The chemical composition of liquid and steam (gas) phases of geothermal fluids provides useful information on hydrogeological processes, thermal and recharge conditions of reservoirs, and underground flow patterns (Nicholson 1993). Within these applications, the reliable estimation of reservoir temperatures is a crucial task to evaluate the energy potential of geothermal resources (Gutiérrez-Negrín 2019). To carry out this task, several chemical geothermometers have been proposed for the prediction of deep equilibrium temperatures in geothermal systems (Guo et al. 2017). Chemical geothermometers are low-cost tools used for predicting reservoir temperatures in the early exploration and exploitation stages (Yan-guang et al. 2017). Solute geothermometers are mostly recommended for the prediction of reservoir temperatures in liquid-dominated reservoirs, LIQDR (Verma et al. 2008), whereas gas geothermometers are predominantly suggested for the calculation of reservoir temperatures in vapour-dominated (VAPDR) reservoirs (García-López et al. 2014).

The gas chemistry of geothermal fluids has been applied not only for the estimation of geothermal reservoir temperatures but also to elucidate water–rock interaction processes (Pang, 2001). The direct escape from deep magmatic sources, and the occurrence of gas–gas and gas–mineral reactions may explain the consumption and production of gases in these systems (Minissale et al. 1997).

The equilibria attainment among gas species is considered as a fundamental thermodynamic basis for gas geothermometry. This physicochemical process has been widely studied for the prediction of reservoir temperatures in LIQDR and VAPDR using the composition of vapour (or gas) samples collected from wells and fumaroles. To our knowledge, Ellis (1957) was the first geochemist to point out that gases in magmatic steam might be used to estimate reservoir temperatures. The first gas geothermometer is attributed to Tonani (1973) who found some relationships among geothermometric models, and the composition of geothermal gases.

From these studies, numerous gas geothermometers have been proposed based upon the analysis of gas-phase compositions, and the thermodynamic study of gas–gas and gas–mineral equilibria reactions. A comprehensive review on gas geothermometers has not been published yet in indexed journals, although some efforts have been conducted in compiling some of the geothermometers most commonly used (e.g. Henley et al. 1985; Nicholson 1993; Powell 2000; Powell and Cumming 2010). In this work, an update compilation of the most commonly used gas geothermometers is reported in Table 1. Most of these geothermometers may be roughly grouped as follows:

  • Simple equations calibrated with databases of gas-phase compositions of fluids collected from geothermal wells;

  • Complex grid-numerical geothermometers that calculate reservoir temperatures and other key parameters (e.g. the steam excess, the distribution coefficients of gases between liquid and steam, etc.); and

  • Geothermometric equations derived from fluid–rock interaction experiments.

Table 1 Updated compilation of gas geothermometers reported in the literature for determining geothermal reservoir temperatures
Full size table

Although these geothermometers have been proposed for the prediction of geothermal temperatures, their generalized application has been limited by the following issues:

  1. 1.

    The significant statistical differences among the temperature estimates predicted by a group of gas geothermometers;

  2. 2.

    The scarcity of the gas-phase compositions at lower temperature levels (between 90 and 150 °C) which has hindered the proposal of new improved equations;

  3. 3.

    The limited intervals of the gas composition and temperature for the application of the geothermometric equations;

  4. 4.

    The scarcity of geochemometric studies for the evaluation of the temperature estimates and their uncertainties; and

  5. 5.

    The lack of practical computer programs to estimate reservoir temperatures by using a wide variety of concentration units, and the complicated calculations involved in some equations.

To address the referred issues (1–3), geochemical databases with representative compositions of gas and/or steam phases from LIQDR and VAPDR are required. Considering the complex nature of the gas–mineral equilibria processes, it is also necessary to explore new regression tools based on artificial intelligence techniques for calibrating multivariate gas geothermometers, and so, to predict reservoir temperatures with a better accuracy. Among these techniques, the artificial neural networks (ANN) have been used in solving multivariate problems in Earth sciences (Poulton, 2001). For example, in geothermal studies, the use of ANN has been applied for (i) the development of Na–K geothermometers (Díaz-González et al. 2008; and Serpen et al. 2009); (ii) the prediction of mass and heat transport in geothermal wells (Bassam et al. 2010; Álvarez del Castillo et al. 2012; Porkhial et al. 2015); and (iii) the optimization of geothermal power plants (Arslan and Yetik 2011), among others.

One of the latest ANN applications reported for geothermal studies was conducted by Pérez-Zárate et al. (2019) who performed a preliminary study to evaluate ANNs for the prediction of geothermal temperatures using gas-phase compositions from which the present research work has been comprehensively completed.

To evaluate the uncertainties of gas geothermometers (the issue referred as 4), a limited number of geochemometric studies have been reported (e.g. D’Amore and Panichi 1980; Arnórsson et al. 2006; García-López et al. 2014). These studies stated that the prediction efficiency of gas geothermometers is affected by several error sources, such as gas sampling errors, analytical errors, coefficient errors, and the total propagated errors, associated with the calculation of temperatures (e.g. Kacandes and Grandstaff 1989; García-López et al. 2014).

The availability of new computer programs to calculate reservoir temperatures (the issue referred as 5) still constitutes a current necessity for the geothermometric studies. Computer programs to apply solute geothermometers in estimating temperatures are widely available for the study of geothermal systems (e.g. Verma et al. 2008; Spycher et al. 2016), whereas for the gas geothermometry, these programs are rarely shared in the literature. A short listing of open-source programs commonly used in gas geothermometry is included in Table 2. To fulfil the constraints (1–5), the development of new improved gas geothermometers and computer programs are still claimed by the geothermal industry.

Table 2 A listing of software reported in the technical literature for computing geothermal reservoir temperatures
Full size table

To address a reliable prediction of geothermal reservoir temperatures, new improved gas geothermometers and a practical computer program called GaS_GeoT have been developed in this work. GaS_GeoT was calibrated for the reliable prediction of reservoir temperatures in LIQDR and VAPDR for a temperature interval between 170 and 374 °C.

To evaluate the prediction efficiency of the new gas geothermometers in geothermal wells, an updated worldwide geochemical database containing gas-phase compositions of fluids were compiled. The prediction efficiency of these geothermometers was compared against twenty-five existing gas geothermometers (listed in Table 3). Details of this geochemometric study are also outlined in this work.

Table 3 Existing gas geothermometers reported in the geothermal literature which were used in the present work
Full size table

Work methodology

A comprehensive computational methodology was developed to achieve the following research objectives (Fig. 1a, b): (i) to evaluate ANNs based on a Multi-Criteria Decision Analysis (MCDA) for selecting optimal prediction models that enable new improved gas geothermometers to be developed; (ii) to create a new computer program for the effective use of the new gas geothermometers; (iii) to evaluate the prediction efficiency of the new gas geothermometers using the gas-phase compositions from well samples collected in LIQDR and VAPDR; and (iv) to compare the temperature estimates inferred from new gas geothermometers with those temperatures predicted by some existing geothermometers. In order to address these research goals, six computational modules were structured:

  • GasGeo_ANN: To carry out the optimal evaluation and selection of ANN architectures by using a novel application of the MCDA method;

  • GasGeo_Eq: To describe the new gas geothermometer equations developed and their applicability conditions;

  • GasGeo_Lit: To select twenty-five existing gas geothermometers for carrying out statistical comparison analyses;

  • GasChemT_Wells: To compile a new Worldwide Geochemical Database (NWGDB) containing gas-phase compositions, and bottom-hole temperatures (BHTm) measured in geothermal wells;

  • GasGeoT_Calc: To describe the calculation of geothermal reservoir temperatures by using the new and existing gas geothermometers, and the operation of the new computer program (GaS_GeoT); and

  • GasGeo_Geochem: To perform a comprehensive geochemometric analysis among the temperature estimates (predicted from all the geothermometers) and the bottom-hole temperature measurements (BHTm).

Fig. 1
figure 1figure 1

a Schematic flow diagram showing the work methodology used in this study. b Schematic flow diagram used by the MCDA method for the ranking and optimal selection of thirty-nine ANN architectures that correlate BHTm and gas-phase compositions

Full size image

A summary of these computational modules is described as follows:

GasGeo_ANN

A previous evaluation study of ANNs to predict geothermal reservoir temperatures was preliminarily conducted by Pérez-Zárate et al. (2019), which constitutes the foundational basis of the present research work. 455 ANN architectures were originally trained to predict reservoir temperatures using three Worldwide Geochemical Sub-databases (WG_SubDB1: q1 = 527; WG_SubDB2: q2 = 498; and WG_SubDB3: q3 = 97) containing gas-phase (CO2, H2S, CH4, and H2) compositions of geothermal fluids as input variables. According to Fig. 2, a multilayer perceptron model was used for the design of these ANNs using the conventional matrix notation (Eq. 1) for the determination of the ANN output (or target):

$$Y = {\text{BHT}}_{{{\text{ANN}}}} = LW \cdot f\left[ {IW \cdot X + b_{1} } \right] + b_{2} ,$$
(1)

where X is the input variable, and IW and b1 represent the matrix and the vector of coefficients between the input and hidden layers. LW and b2 are the layer weighting coefficients and the vector of coefficients between the hidden and output layers, and f corresponds to an activation function for the hidden layer.

Fig. 2
figure 2

Schematic diagram showing the conceptual model of a multilayer perceptron with three-layers, and a summary of the fundamental equations used by applying the Levenberg–Marquardt algorithm: Eq. (1.1) error vector; Eq. (1.2) cost function, where W is the vector of all the weights and biases and q is the total number of samples or patters; Eq. (1.3) where j is the jth element of the gradient; Eq. (1.4) the gradient in matrix form; Eq. (1.5) Jacobian matrix, where p is the total number of neurons; Eq. (1.6) iterative update of weights using the LM algorithm, where wt+1 is the next weight, wt is the current weight, μ is the learning rate factor, and I is the identity matrix

Full size image

A full description of the multilayer perceptron model is reported by Pérez-Zárate et al. (2019), and schematically summarized in Fig. 2 by listing the fundamental equations used for adjusting weighting and bias coefficients in the learning process of each ANN layer (referred as Eqs. 1.1–1.6). Such a perceptron model was solved by creating several Matlab numerical scripts that were previously reported (https://github.com/ANNGroup/GasG-Scripts-ANNs.git).

For the learning process of ANNs, the well-known Levenberg–Marquardt algorithm (LM), the hyperbolic tangent function, and the linear function were applied. All the ANNs were characterized by an input layer, one hidden layer, and an output layer. For the input and output layers, the data were normalized between -1 and 1, whereas for the hidden layer, the number of neurons varied from 1 to 35. Input data sets were randomly divided into training (80%), validation (10%), and testing (10%). From this study, thirty-nine ANNs were preliminarily reported as the most acceptable prediction models to correlate multivariate relationships among gas-phase compositions and BHT data (referred as ANN-1 to ANN-39 in Pérez-Zárate et al. 2019).

By using traditional evaluation metrics based on small differences and acceptable correlation coefficients between measured (BHTm) and simulated (BHTANN) temperatures, six ANNs were proposed as the ‘better prediction models’ (cited as ANN-12, ANN-13, ANN-22, ANN-25, ANN-33, and ANN-38 in the same paper). Although acceptable results were obtained from these earlier prediction models, some applicability problems were later identified in two ANNs that used a small data set for the learning process (WG_SubDB3: q3 = 97, which was used for the ANN-33 and ANN-38 models). The low representativeness of this sub-data set was lastly reflected on very limited intervals of applicability.

A generalization problem was therefore identified in the final development stage of new gas geothermometers, which may affect the future application of these tools in geothermometric studies for the geothermal prospection and exploitation. To correct these problems, a new evaluation methodology based on a novel MCDA method was applied for the optimal selection of the most reliable ANNs among the thirty-nine architectures previously proposed (Fig. 1b). The MCDA method was used, for the first time in the ANN literature, to comprehensively evaluate the efficiency of these ANN prediction models by utilizing the evaluation results derived from the following:

  1. I.

    The analysis Case 1 (AC1) described by the global learning processes of three sub-databases (WG_SubDB1, WG_SubDB2, and WG_SubDB3) applying the thirty-nine ANNs (pre-selected) and the following statistical metrics: the number of data used by each sub-database (q1 = 527; q2 = 498 and q3 = 97), the correlation coefficients (r) obtained between measured (BHTm) and simulated (BHTANN) temperatures for the training, validation, and testing stages, and the residuals calculated between measured and predicted temperatures (RMSE, MAE, and MAPE);

  2. II.

    The analysis Case 2 (AC2) described by the application of the thirty-nine ANNs to the largest sub-database (q1 = 527), as a generalization case, using the same statistical residuals between measured and predicted temperatures (RMSE, MAE, and MAPE); and

  3. III.

    The analysis Case 3 (AC3) described by the application of the thirty-nine ANNs to the same sub-database (q1 = 527) but strongly restricted by the applicability conditions of each ANN prediction model, using the same residuals between measured and predicted temperatures.

To apply the MCDA, it was necessary to normalize the resulting thirteen statistical metrics (Table 4). The normalization was performed either to minimize or maximize the evaluation metrics using the methodology proposed by Dincer and Acar (2015).

Table 4 A summary of the thirty-nine ANNs (proposed by Pérez-Zárate et al., 2019) for determining reservoir temperatures
Full size table

For example, in the particular case of the residual errors (RMSE, MAE, and MAPE), the best efficiency of the ANN prediction models would be given when these metrics achieve lower values, whereas for the linear correlation coefficient (r), higher values would be desirable. For the statistical residual (SRi), or the minimization obtained during the global learning and application processes of the ANNs, normalized data were calculated by using the RMSE, MAE, and MAPE results and the following equation:

$${\text{Normalized }}\;{\text{Data}}_{i} = \frac{{SR_{{{\text{max}}}} - SR_{i} }}{{SR_{{{\text{max}}}} - SR_{{{\text{min}}}} }} \times 10$$
(2)

whereas for the maximization, the normalized data was determined by using the following equation:

$${\text{Normalized}}\; {\text{Data}} _{i} = \frac{{SP_{i} - SP_{{{\text{min}}}} }}{{SP_{{{\text{max}}}} - SP_{{{\text{min}}}} }} \times 10,$$
(3)

where SPi are the statistical regression parameters: n (the data number used by each database) and r, the correlation coefficients, which were obtained from the training, validation, and testing of the ANNs.

The MCDA is suggested as an optimized method for the integral evaluation of various statistical metrics among predictor models using different scenarios to achieve a specific objective function (Adem and Geneletti 2018). To apply the MCDA, the Multi-Attribute Value Theory (MAVT) algorithm was used (Santoyo-Castelazo 2011; Santoyo-Castelazo et al. 2011; Santoyo-Castelazo and Azapagic 2014; Estévez et al. 2018). This algorithm required the determination of partial value functions, and the estimation of weighting factors for each evaluation metric. The global value function V(s) which represents the total score to be obtained by any ANN architecture in each scenario s is calculated as follows:

$$V\left( s \right) = \mathop \sum \limits_{i = 1}^{E} w_{i} u\left( s \right),$$
(4)

where wi and u(s) are the weighting factors used by the evaluation metric, and the value function which provides the metric efficiency for each ANN architecture and scenario, respectively; and E is the total number of the evaluation metrics.

Wang et al. (2009) suggested the use of variable weighting factors by considering the importance of the scenarios assumed on the predictor model efficiency. To apply the MCDA method, Santoyo-Castelazo and Azapagic (2014) suggested the use of a sensitivity analysis to determine the ranking score of prediction models based on different scenarios that enable indicators (or statistical metrics) to be varied under certain weighting criterion. In this work, the sensitivity analysis was applied for evaluating the prediction efficiency of each ANN model in the calculation of reservoir temperatures using four different scenarios (S), where thirteen statistical metrics were comprehensively analysed by assigning the following weighting criteria:

  • (S-1) Equal weighting factors assigned to the statistical metrics computed for the three analysis cases already postulated: AC1 (global learning processes); AC2 (the generalization case); and AC3 (the applicability restrictions imposed by each ANN model), i.e. AC1 = AC2 = AC3, Fig. 1b; see Additional file 1: Table S1.

  • (S-2) Greater weighting factors assigned to the seven statistical metrics computed for the AC1 (global learning processes) in comparison with equal weighting values assumed for the metrics of the AC2 and AC3, i.e. AC1 > (AC2 = AC3), Fig. 1b; see Additional file 1: Table S2.

  • (S-3) Greater weighting factors assigned to the three statistical metrics computed for the AC2 (the generalization case) in comparison with equal weighting values assumed for the metrics of the AC1 and AC3, i.e. AC2 > (AC1 = AC3), Fig. 1b; see Additional file 1: Table S3.

  • (S-4) Greater weighting factors assigned to the three statistical metrics computed from the AC3 (the restricted case of the applicability conditions) in comparison with equal weighting values assumed for the metrics of the AC1 and AC2, i.e. AC3 > (AC1 = AC2), Fig. 1b; see Additional file 1: Table S4.

After applying the MCDA (by means of the algorithm represented in Fig. 1b), the best ANN architectures were optimally selected and used for the development of the new gas geothermometers. A summarized description of the ranking score obtained by each ANN together with the optimal selection results are reported in Table 5. A full report containing all MCDA calculations obtained for the thirty-nine ANNs is reported in Additional file 1: Tables S1 to S4.

Table 5 Ranking score and optimal selection of the eight ANN architectures using the MCDA method
Full size table

GasGeo_Eq

This module was created to describe the new gas geothermometer equations inferred from the best ANNs (from here referred as GasG1 to GasG8), and their applicability conditions. Table 6 summarizes the eight ANNs that were optimally selected for the development of the new gas geothermometer equations. The number of neurons used for the three layers of the ANNs (input, hidden, and output) are included. The input variables used by each ANN are also reported, including their relative contribution (in %) obtained from the sensitivity analysis (Garson 1991). Weighting and bias coefficients of the optimal ANNs are reported in Table 7. These coefficients were used for the development of each gas geothermometer (GasGi, i = 1 to 8) by using the following general equation (Eq. 5):

$${\text{BHT}}_{{{\text{GasG}}_{{\text{i}}} }} \left( {^\circ C} \right) = \left\{ {{ } \left[ { \frac{{\left( {\mathop \sum \nolimits_{j = 1}^{m} \left( {LW_{{\left( {m,n} \right)}} \cdot \left( {\frac{2}{{1 + {\text{exp}}\left( { - 2 \cdot \left( {\mathop \sum \nolimits_{k} IW_{{\left( {m,k} \right)}} \cdot X_{\left( k \right)} + b_{1\left( m \right)} } \right)} \right)}} - 1} \right)} \right) + b_{2\left( n \right)} } \right) + 1}}{2}} \right] \cdot \alpha } \right\} + 170,$$
(5)
Table 6 New improved gas geothermometers proposed in this research work
Full size table
Table 7 Weighting and bias coefficients of the best ANN models (new gas geothermometers: GasG1 to GasG8)
Full size table

where X is the input variable; IW and b1 represent the associated coefficients to the input–hidden layers of the ANN; and LW and b2 are the coefficients for the hidden–output layers. The subscripts k, m, and n refer to input, hidden, and output neurons, respectively, whereas α represents a normalization factor equal to 214 for the GasG1, GasG2, GasG6, and GasG8, and 193 for the remaining geothermometers (GasG3, GasG4, GasG5, and GasG7).

Considering the complexity of the Eq. (5), it is pertinent to assume that a future application of the eight geothermometric equations could be discouraged by users when compared with simple equations already proposed from the existing gas geothermometers (Table 3). To overcome this limitation, a computer program (GaS_GeoT) codified in Java object-oriented programming was created. This program was developed for the effective use of the new gas geothermometer equations for the calculation of geothermal temperatures from gas-phase compositions (CO2, H2S, CH4, and H2). GaS_GeoT and a quick user manual are available in the public server (https://github.com/ANNGroup/GaS_GeoT.git).

The applicability conditions of the new gas geothermometers (GasG1 to GasG8) are reported in Table 8. These limits are the min–max values of concentration and temperature used during the ANN learning processes. The gas concentrations must be given in mmol/mol units (dry-basis), whereas the temperature in °C.

The input variables for the GasG1–GasG5 and GasG8 are given by the natural logarithm values (dimensionless) because these equations use gas ratios, whereas for the GasG6 and GasG7, the input variables are directly given in mmol/mol units.

GasGeo_Lit

This module was created to carry out a comparison of prediction efficiencies among the new (GasG1 to GasG8) and existing gas geothermometers using their temperature estimates. Twenty-five existing gas geothermometers have been included in Table 3. The fundamental criteria for selecting these geothermometers were as follows: (i) the determination of temperatures as a direct function of gas concentrations; and (ii) the use of gas concentrations (CO2, H2S, CH4, H2, and N2) most commonly applied in geothermometric studies.

GasChemT_Wells

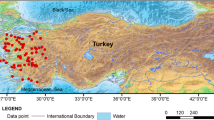
This module was created for compiling the NWGDB (nw = 265) with data that were not used in the ANN learning process. NWGDB contains compositions (in mmol/mol, dry-basis) of major (CO2 and H2S) and trace (H2, N2, CH4) geothermal gases, and BHT measurements (in °C) logged in wells from thirteen world geothermal fields (Fig. 3): (1) Berlin geothermal field (BGF), El Salvador (compiled from: Renderos 2002; n = 41: collected from a LIQDR); (2) Zunil geothermal field (ZGF), Guatemala (Giggenbach et al., 1992; n = 4: LIQDR); (3) Krafla geothermal field (KGF), Iceland (Stefánsson 2017; n = 8: LIQDR); (4) Kamojang geothermal field (KaGF), Indonesia (Laksminingpuri and Martinus 2013; n = 10: VAPDR); (5) Sibayak geothermal field (SGF), Indonesia (Abidin et al. 2005; n = 9: LIQDR); (6) Amiata geothermal field (AGF), Italy (Chiodini and Marini 1998; n = 4: VAPDR); (7) Larderello geothermal field (LGF), Italy (Chiodini and Marini 1998; n = 30: VAPDR); (8) Olkaria geothermal field (OGF), Kenya (Karingithi et al. 2010; Wamalwa 2015; n = 29: 13 data collected from a LIQDR and 16 from a VAPDR); (9) Cerro Prieto geothermal field (CPGF), Mexico (Nieva et al. 1982; Nehring and D’Amore 1984; n = 9: LIQDR); (10) Las Tres Virgenes geothermal field (LTVGF), Mexico (Verma et al. 2006; n = 4: LIQDR); (11) Los Azufres geothermal field (LAGF), Mexico (Nieva et al. 1985 and 1987; Santoyo et al., 1991; Arellano et al., 2005; Barragán et al., 2005, 2008, 2012; n = 36: 21 data collected from a LIQDR and 15 from a VAPDR; (12) Los Humeros geothermal field (LHGF), Mexico (López-Mendiola and Munguía, 1989; Tello et al., 2000; Arellano et al. 2003, 2015; n = 72: 60 data compiled from a LIQDR and 12 from a VAPDR); and (13) Palinpinon geothermal field (PGF), Philippines (D’Amore et al.1993; n = 9: LIQDR).

Fig. 3
figure 3

Location of the worldwide geothermal fields used for the creation of the new Geochemical Database (NWGDB). The updated world geothermal power generation is also shown

Full size image

To perform the analysis of prediction efficiency in new and existing gas geothermometers, the input data compiled in NWGDB were classified in two major groups: Group-1, LIQDR (g1 = 178), and Group-2, VAPDR (g2 = 87). A complete version of the NWGDB is reported in Additional file 1: Table S5.

GasGeoT_Calc

This module was created to describe the new computer program GaS_GeoT and the effective use of the new gas geothermometers (GasG1 to GasG8). The user interface and a calculation routine of geothermal reservoir temperatures by using GaS_GeoT are also described. Before running GaS_GeoT and to apply the twenty-five geothermometer equations (Table 3), the concentration units of the gas-phase compositions and the applicability conditions of each gas geothermometer were verified (Table 8).

To proceed with the calculation of the reservoir temperatures, all gas geothermometers were executed (see Fig. 1a). As one of the goals of this work was focused on the effective use of the new gas geothermometers (GasG1 to GasG8), the calculation process used by GaS_GeoT is schematically referred in five major sections of Fig. 4 and summarized as follows.

Fig. 4
figure 4

Schematic flow diagram and menu screens that show the execution of the computer program GaS_GeoT for the estimation of geothermal reservoir temperatures

Full size image
Fig. 5
figure 5

Results of a comparative analysis between measured (BHTm) and temperature estimates calculated for the new gas geothermometers (BHTGaS_GeoT). The plots a–d show the temperature results predicted by the new geothermometers for LIQDR wells, whereas the plots e–h] show the results for VAPDR. n* is the number of samples that fulfil the applicability conditions of each new gas geothermometer (Table 8). Dotted and dashed lines represent a hypothetical variability of the ± 10% and ± 20% with respect to the BHT mean value, respectively

Full size image
Table 8 Applicability conditions defined for the eight new gas geothermometers developed
Full size table

To open or upload the input data through the File option (menu 4.1 in Fig. 4), an Excel spreadsheet (with a filename extension: xlsx) is required. This file must contain eight columns: Column 1, Sample ID (numerical data: integer); Columns 2–4: Geothermal Well, Geothermal Field, and Country information, respectively (in alphanumerical format); and the Columns 5–8, to enter the gas-phase compositions of the gases CO2, H2S, CH4, and H2 in mmol/mol (dry-basis), respectively (numerical data in floating format).

In the Help option (menu 4.2 in Fig. 4), a template file with some input data examples is available as a useful query. A User’s Manual is also included in the Help option of the program, and the public server (https://github.com/ANNGroup/GaS_GeoT.git).

Two additional menu options appear in the main screen of GaS_GeoT: Validation and Geothermometers. The Validation menu option performs an input data validation for checking the existence of typographical mistakes in the CO2, H2S, CH4, and H2 compositions (menu 4.3 in Fig. 4). The Geothermometers menu option invokes a computer subroutine which will make either the total or partial selection of the gas geothermometers (GasG1 to GasG8) by checking their corresponding boxes (menu 4.4 in Fig. 4). After selecting the geothermometers, the calculation of temperatures is performed, and the GaS_GeoT will prompt the user to provide an output file name to print a report with the gas-phase compositions, and the temperature estimates calculated by the new gas geothermometers. An alternative output option is also requested by GaS_GeoT for displaying the output results on screen (option 4.5 in Fig. 4).

After applying GaS_GeoT and twenty-five existing geothermometers to the gas-phase composition of NWGDB (LIQDR g1 = 178 and VAPDR g2 = 87), an output file with all the temperature estimates is generated both to carry out the geochemometric evaluation, and to estimate the prediction efficiencies of the thirty-three gas geothermometers (Fig. 1a). A complete version of the output file is reported in Additional file 1: Tables S6 and S7, which contain the results obtained from the new and existing gas geothermometers, respectively.

GasGeo_Geochem

This module was developed to perform the geochemometric analyses using the temperature estimates obtained from new and existing gas geothermometers. To carry out these analyses, the following statistical metrics were applied: (1) Percent Difference, DIFF%; (2) Root Mean Square Error, RMSE; (3) Mean Absolute Error, MAE; (4) Mean Absolute Percentage Error, MAPE; and (5) the Difference Coefficient Ratio or statistical Theil's U test. As these metrics require the knowledge of actual bottom-hole temperatures, most of these were used as accuracy measures. The calculation equations used by these metrics are summarized in Table 9. RMSE, MAE, and MAPE metrics are interpreted as statistical residuals obtained between the bottom-hole temperatures (BHTm) and the temperature estimates predicted by any gas geothermometer, whereas the metrics DIFF% and Theil's U require a previous analysis. For example, when the DIFF% value is positive, the calculated temperature is greater than the BHTm of the respective geothermal well (which means an overestimation) and vice versa. Differences (DIFF%) either positive or negative ≤ 20% are assumed as acceptable estimates by considering the total propagated errors that are commonly quantified in some solute geothermometers (Verma and Santoyo 1997; García-López et al. 2014).

Table 9 Statistical metrics used for evaluating the prediction efficiency of gas geothermometers (new and existing)
Full size table

On the other hand, the statistical Theil's U is recommended for evaluating the prediction efficiency among several predictor models (Theil 1961). This metric was therefore used to evaluate the efficiency of the new geothermometers (GasG1 to GasG8) among other existing gas geothermometers. If the calculated values for the Theil's coefficient ratios are less than 1, it means that the errors obtained by the new geothermometers are lower than that those obtained from the existing geothermometers and vice versa (Álvarez del Castillo et al. 2012).

Results and discussion

After applying thirteen evaluation metrics and the MCDA, the thirty-nine ANNs were ranked (Table 5). Based on these optimization results, eight new gas geothermometers were successfully developed (Table 6): (1) GasG1 [ln(H2S/CO2), ln(CH4/CO2), ln(H2/CO2)]; (2) GasG2 [ln(CO2/CH4), ln(H2S/CH4), ln(H2/CH4)]; (3) GasG3 [ln(H2S/CO2), ln(CH4/CO2), ln(H2/CO2)]; (4) GasG4 [ln(CO2/CH4), ln(H2S/CH4), ln(H2/CH4)]; (5) GasG5 [ln(CO2/H2), ln(H2S/H2), ln(CH4/H2)]; (6) GasG6 [ln(CO2), ln(H2S), ln(CH4), ln(H2)]; (7) GasG7 [ln(CO2), ln(H2S), ln(CH4), ln(H2)]; and (8) GasG8 [ln(H2S/CO2), ln(CH4/CO2), ln(H2/CO2), ln(H2S), ln(H2S/H2)].

By considering the gas-phase compositions and the BHTm measurements compiled in the NWGDB (nw = 265), thirteen geothermal fields of the world (Berlin, Zunil, Krafla, Kamojang, Sibayak, Amiata, Larderello, Olkaria, Cerro Prieto, Las Tres Virgenes, Los Azufres, Los Humeros, and Palinpinon) were used for the geochemometric evaluation (see Additional file 1: Table S5). The geothermal reservoir temperatures estimated by applying the new gas geothermometers (GaS_GeoT) along with twenty-five existing geothermometers are reported in Additional file 1: Tables S6 and S7, respectively.

The prediction efficiency for all the gas geothermometers to determine reservoir temperatures was compared with measured BHTm values using the evaluation metrics (DIFF%, RMSE, MAE, MAPE, and Theil's U). A summary of the prediction efficiency results is reported in Table 10. A full version of this statistical comparison is also reported in Additional file 1: Tables S8 to S13.

Table 10 Summary of statistical results obtained from the geochemometric evaluation study of gas geothermometers
Full size table

Results for wells located in LIQDR

The reservoir temperatures estimated for the gas phase compositions from LIQDR using the new gas geothermometers (GasG1 to GasG8) and twenty-five existing gas geothermometers were statistically compared with the corresponding BHTs, and the obtained results are presented as rounded-off values in the following sections:

Analysis of the DIFF% metric

The percent difference (DIFF%) calculated from the temperature estimates by all the thirty-three gas geothermometers (new and existing) and BHTs shows better efficiencies by the newly gas geothermometers (GasG1 to GasG8) with 91 to 96% of the predicted temperatures falling within the limits of acceptance (DIFF% ± 20%; Table 10). This behaviour is clearly observed when the temperature estimates are plotted against the measured BHTs (Fig. 5a–d). However, only four existing geothermometers from the literature (ND84c, AG85b, AG85d, and AG85f) predicted 85 to 88% of the temperatures in the same acceptable limits (Table 10 and Fig. 6a–d). About 55–63% of the estimated reservoir temperatures are overestimated (with DIFF% ≤ 20%), 30–34% of the temperatures are underestimated (with DIFF% ≤ 20%), and 5–12% are equal (with DIFF% ≤ 1%), by the eight new gas geothermometers (GasG1 to GasG8), when compared to the BHTs, respectively (Table 10).

Arnórsson and Gunnlaugsson (1985) reported reservoir temperatures in some geothermal fields where the gas geothermometers may yield both under- and over-estimates for reservoir temperatures. Powell (2000) suggested that temperature underestimates may be due to the addition of un-equilibrated biogenic methane, whereas Barragán et al. (2000) stated that an overestimation of temperatures may derive from an excess of gases in total discharge of the wells.

Based on the DIFF% metric, the resulting ranking between 1st and 12th positions for the gas geothermometers under evaluation is occupied by GasG8, GasG3, GasG1, GasG7, GasG4, GasG2, GasG5, GasG6, AG85d, AG85b, ND84c, and AG85f, respectively.

Analysis of RMSE, MAE, and MAPE metrics

The RMSE values of the geothermometers vary between 32 and 136 (see Additional file 1: Table S9). The lowest values of RMSE ranging from 32 to 35 were obtained for the eight new gas geothermometers: GasG1 to GasG8 (Table 10). This systematic behaviour of RMSE replicates the better efficiency provided by the new gas geothermometers in comparison to those existing geothermometers, in predicting reservoir temperatures comparable to BHTm, which is clearly observed in Fig. 7a.

Moreover, all new gas geothermometers were characterized by the lowest values of MAE (ranging from 25 to 27), which also demonstrated that their temperature estimates have a better accuracy (Fig. 7b). With respect to the MAPE metric, small temperature differences between the temperature estimates and BHTs were also provided by the new gas geothermometers, which varied from 9 to 10 (Table 10). As MAPE represents an average value of absolute percentage errors, the lowest values calculated by the new gas geothermometers suggest a small better efficiency in predicting the reservoir temperatures, which is observed in Fig. 7c.

Based on the RMSE values, the resulting ranking between 1st and 12th positions for all the gas geothermometers was GasG3, GasG8, GasG5, GasG6, GasG7, GasG1, GasG2, GasG4, AG85b, AG85d, AG85f, and ND84c, respectively, whereas for the MAE and MAPE metrics, the first five positions corresponded to the new gas geothermometers with an order slightly different but consistent as the best geothermometric tools: GasG8, GasG5, GasG3, GasG7, and GasG4; and GasG5, GasG3, GasG8, GasG7, and GasG4, respectively (Table 10).

Analysis of the statistical Theil’s U test (LIQDR)

After analysing the Theil’s U results, the following inferences were accomplished: (1) the GasG3 geothermometer may be considered with confidence as the best predictor model among all other geothermometers because the Theil´s U values were systematically lower than 1; (2) it was also observed that the new geothermometers (GasG1 to GasG8) systematically provided the lowest errors in comparison with twenty-five existing geothermometers (Table 10); and (3) after comparing the prediction efficiency among the new gas geothermometers, the GasG3 exhibited Theil´s U lower values than 1 in comparison with those obtained for the remaining geothermometers (GasG1–GasG2 and GasG4–GasG8). A full description of the LIQDR results obtained for all the gas geothermometers under evaluation using the statistical evaluation metrics (DIFF%, RMSE, MAE, MAPE, and Theil´s U) is reported in Additional file 1: Tables S8 to S10.

Results for wells located in VAPDR

The prediction efficiency of the reservoir temperatures calculated in VAPDR samples using the thirty-three gas geothermometers (new and existing) was also compared with the actual BHT measurements.

Analysis of the DIFF% metric

Based on the percent difference (DIFF%) values calculated by the new gas geothermometers, a good prediction efficiency was observed with 78 to 85% of the predicted temperatures falling within the limits of acceptance (DIFF% ± 20%), as it is observed in Fig. 5e–h. Out of the total twenty-five gas geothermometers, four geothermometers (ND84b, ND84c, AG85f, and A98c) from the literature have shown statistical differences comparable to these new geothermometers with 79 to 85% (Table 10, and Fig. 6e–h). About 44–59% of the estimated reservoir temperatures are overestimated (with DIFF% ≤ 20%), 34–49% of the temperatures are underestimated (with DIFF% ≤ 20%), and 5–9% are equal (with DIFF% ≤ 1%), by the eight new gas geothermometers   (GasG1 to GasG8), when compared to the BHTs, respectively (Table 10).

Fig. 6
figure 6

Results of a comparative analysis between measured (BHTm) and temperature estimates calculated by four existing gas geothermometers (BHTGasGeo_Lit). The plots a–d show results of the ND84c, AG85b, Ag85d, and AG85f geothermometers obtained for LIQDR wells, whereas the plots e–h represent the results of the same geothermometers for VAPDR wells. Dotted and dashed lines represent a hypothetical variability of the ± 10% and ± 20% with respect to the BHT mean value, respectively

Full size image

According to these results, the new ranking between 1st and 12th positions for the gas geothermometers under evaluation was given by A98c, GasG3, GasG5, GasG1, ND84c, GasG2, GasG4, GasG8, ND84b, GasG6, AG85f, and GasG7, respectively. In this ranking, the prediction efficiency was actually very close between the geothermometers A98c and GasG3, differing in only two decimals of the applicability percentage (i.e. 85.1% for A98c, and 84.9% for GasG3; both percentages rounded-off as 85%). With these results, the gas geothermometer GasG3 systematically shows a high prediction efficiency similar to those results obtained for LIQDR systems.

Analysis of the RMSE, MAE, and MAPE metrics

The RMSE values calculated in VAPDR samples for all geothermometers showed a wider variability between 36 and 181 in comparison with those values estimated for LIQDR samples (see Additional file 1: Table S12). For the new gas geothermometers (GasG1 to GasG1), seven out of the eight (except GasG4) predict low values of RMSE ranging from 36 to 45 (Table 10 and Fig. 7d), whereas for the existing gas geothermometers, a wider interval of RMSE was calculated (from 39 to 181).

Fig. 7
figure 7

Results of the statistical metrics used to evaluate the prediction efficiency of the eight new gas geothermometers against four existing geothermometers of the literature. The a–c plots show the residual results obtained for LIQDR wells (RMSE, MAE, and MAPE), whereas the d–f plots show the same residuals for VAPDR wells

Full size image

In relation to the MAE metric, seven out of the eight new geothermometers were characterized by the lowest values ranging from 28 to 34, which also demonstrated that the temperature estimates predicted by the seven new geothermometers (except GasG4) are more accurate, as it is shown in Fig. 7e. Regarding the differences calculated in the MAPE values of the new gas geothermometers varied from 11 to 15 (Table 10 and Fig. 7f); which also suggest that seven out of eight geothermometers (except GasG4) provided a slight better efficiency.

Based on the integrated calculations obtained for all the metrics (RMSE, MAE, and MAPE), it was found that seven out of the eight new gas geothermometers show a better prediction efficiency to determine the reservoir temperatures in VAPDR gas samples. The resulting ranking between 1st and 12th positions according to RMSE was given by GasG3, GasG1 ND84c, A98c, GasG2, ND84b, AG85f, GasG6, GasG8, GasG7, GasG5, and GasG4, respectively, whereas for the MAE and MAPE metrics, the five positions corresponded to the new gas geothermometers: GasG3, GasG1, GasG2, GasG6, and GasG5.

Analysis of the statistical Theil’s U test (VAPDR)

After applying the Theil’s U results (Table 10), two interpretations are inferred: (1) it was systematically observed that the GasG3 predictor model (Theil’s U values lower than 1) is the most reliable and accurate gas geothermometer over the rest of the new geothermometers (GasG1–GasG2 and GasG4–GasG8); and (2) it was found that two (GasG1 and GasG3) out of the eight new geothermometers exhibited lower errors in estimating reservoir temperatures in comparison with those estimates predicted by the existing geothermometers.

A full description of the results obtained from the use of the thirty-three gas geothermometers in VAPDR systems is reported in Additional file 1: Tables S11 to S13.

As a final remark of this research work, it was demonstrated, for the first time, the effectiveness of the MCDA optimization method for ranking and selecting the most reliable ANN architectures to predict a dependent variable (BHTm) as a function of multiple independent variables (gas-phase compositions: CO2, H2S, CH4, and H2). We consider that this new evaluation proposal is actually innovating the evaluation methods commonly used in ANNs for evaluating their training, validation, and test stages, which typically rely on the simple use of the linear correlation coefficients (r) obtained between measured and simulated data.

With the optimal selection of the best predictor models used to correlate BHTm and gas-phase compositions, eight new improved gas geothermometers (GasG1 to GasG8) were successfully developed. Most of these new geothermometers provide reliable estimations of geothermal reservoir temperatures. We have also demonstrated that the prediction efficiency of these new geothermometric tools (mainly GasG1 and GasG3 geothermometers) exceeds the efficiency of those existing gas geothermometers available in the literature.

Conclusions

Eight new improved gas geothermometers (GasG1 to GasG8) based on an optimized selection of artificial neural networks by using the MCDA method were successfully developed for the reliable prediction of the geothermal reservoir temperatures. For an effective and practical use of these geothermometers, a new computer program GaS_GeoT was successfully developed. The evaluation of the efficiency of the new improved gas geothermometers in predicting the reservoir temperatures was successfully demonstrated for geothermal wells of LIQDR and VAPDR systems.

The new gas geothermometers (GasG1 to GasG8) provided the best prediction efficiencies for geothermal wells from LIQDR, whereas two out the eight (GasG1 and GasG3) demonstrated their best efficiency in predicting reservoir temperatures for VAPDR. Among the new gas geothermometers, the best geothermometric tool for predicting reservoir temperatures in LIQDR and VAPDR systems is the GasG3 geothermometer which uses the gas ratios: ln(H2S/CO2), ln(CH4/CO2), and ln(H2/CO2).

Out of the total twenty-five existing gas geothermometers, the most consistent geothermometers to predict reservoir temperatures comparable to those values inferred from the new geothermometers were as follows: (1) the ND84c, AG85b, AG85d, and AG85f geothermometers for LIQDR (which use CO2-H2S, CO2-H2, H2, and H2S concentrations); (2) the ND84b, ND84c, AG85f, and A98c geothermometers for VAPDR (which use CO2-H2, CO2-H2S, H2S, and H2S concentrations).

Taking in consideration the higher prediction efficiencies observed in predicting reservoir temperatures, the new gas geothermometers and the GaS_GeoT program may have the potential to become one of the most preferred geothermometric tools for the reliable estimation of the reservoir temperatures in geothermal prospection and exploitation.