Introduction

In real research programs, there are many new problems which lack empirical data. In these situations, we cannot obtain the probability distribution of the variables, and instead, we usually invite several experts to give their “belief degree” that each event will occur. The belief degree has a larger variance than the real probability because human beings usually overweight unlikely events (Kahneman and Tversky [1]) and human beings usually estimate a much wider range of values than the object actually takes (Liu [2]). In order to deal with these problems, Liu [3] put up the uncertainty theory in 2007 and refined [4] it in 2010. Nowadays, the uncertainty theory has become a new branch of mathematics for modeling nondeterministic phenomena.

Liu [5] proposed the concept of canonical Liu process in 2009. The canonical Liu process is a process with stationary and independent increments, and its every increment is a normal uncertain variable. It begins with time 0 and almost all sample paths are Lipschitz-continuous. Based on canonical Liu process, Liu [5] developed uncertain calculus to deal with differentiation and integration of an uncertain process. The concept of uncertain differential equations was proposed by Liu [6] in 2008. Uncertain differential equations have been widely applied in many fields such as uncertain finance (Liu [7], Yao [8]), uncertain optimal control (Zhu [9]), and uncertain differential game (Yang and Gao [10]).

The existence and uniqueness of an uncertain differential equation was studied by Chen and Liu [11] in 2010. An uncertain differential equation has a unique solution if its coefficients satisfy Lipschitz condition and linear growth condition. The definition of stability was given by Liu [5] in 2009. After that, Yao et al. [12] gave a sufficient condition for stability. An uncertain differential equation is stable if its coefficients satisfy the linear growth condition and the strong Lipschitz condition. Furthermore, Yao et al. [13] gave the concept of stability in mean for an uncertain differential equation and proved the sufficient and necessary condition for the linear uncertain differential equation being stable in mean. Based on those works, other types of stability were extended, like that, stability in moment (Sheng and Wang [14]), almost sure stability (Liu et al. [15]), and exponential stability (Sheng and Gao [16]).

Chen and Liu [11] figured out the analytic solution of the linear uncertain differential equation. Liu [17] and Yao [18] considered a spectrum of analytic methods to solve some special classes of nonlinear uncertain differential equations. Unfortunately, we cannot obtain the analytic solution of every uncertain differential equation. Then, it is sufficient to obtain the numerical results in most situations. Yao and Chen [19] found a way to transfer uncertain differential equations into a spectrum of ordinary differential equations. They put up a Yao-Chen formula to calculate the inverse distribution of solution at a given time. Based on the Yao-Chen formula, a numerical method was designed for giving the solution to uncertain differential equations via the Euler method. Yao [20] also studied the extreme value, first hitting time and time integral of solution of uncertain differential equations.

The Runge-kutta method is wide-used in solving ordinary differential equations, and it is more accurate than the Euler method. In this paper, we will present a way to solve uncertain differential equations with the Runge-Kutta method. The rest of the paper is organized as follows. The “Preliminaries” section presents some basic concepts and properties in uncertainty theory, including uncertain calculus, uncertain differential equations, and α-path. The “Runge-Kutta Method” section shows a new numerical method using the Runge-Kutta method. The “Numerical Experiments” section gives some numerical experiments to illustrate the new method and to calculate the uncertainty distribution, expected value, extreme value, and time integral of solution of the uncertain differential equation.

Preliminaries

Let ℒ be a σ-algebra on a nonempty set Γ. A set function is called an uncertain measure if it satisfies the following axioms: Axiom 1. (Normality Axiom) for the universal set Γ; Axiom 2. (Duality Axiom) for any event Λ; Axiom 3. (Subadditivity Axiom) For every countable sequence of events Λ 1,Λ 2, …, we have

The triplet is called an uncertainty space. Besides, Liu [5] defined the product uncertain measure on the product σ-algebra as follows in order to provide the operational law, Axiom 4. (Product Axiom) Let () be uncertainty spaces for k=1,2,…. The product uncertain measure is an uncertain measure satisfying

where Λ k are arbitrarily chosen events from for k=1,2,…, respectively.

An uncertain process is essentially a sequence of uncertain variables indexed by time. The study of the uncertain process was started by Liu [6] in 2008.

Definition 2.1.

(Liu [6]) Let T be a totally ordered set (e.g., time), and let () be an uncertainty space. An uncertain process is a function X t (γ) from to the set of real numbers such that {X t ∈B} is an event for any Borel set B of real numbers at each time t.

An uncertain process X t is said to have independent increments if

$$\begin{array}{@{}rcl@{}} X_{t_{0}},\,X_{t_{1}}-X_{t_{0}},\,X_{t_{2}}-X_{t_{1}},\,\ldots,\,X_{t_{k}}-X_{t_{k-1}} \end{array} $$

are independent uncertain variables where t 0 is the initial time and t 1,t 2,…,t k are any times with t 0<t 1<…<t k . An uncertain process X t is said to have stationary increments if, for any given t>0, the increments X s+t −X s are identically distributed uncertain variables for all s>0.

Definition 2.2.

(Liu [5]) An uncertain process C t is said to be a canonical Liu process if

  1. (i)

    C 0=0 and almost all sample paths are Lipschitz continuous;

  2. (ii)

    C t has stationary and independent increments;

  3. (iii)

    every increment C s+t −C s is a normal uncertain variable with uncertainty distribution

    $$\begin{array}{@{}rcl@{}} \Phi(x)=\left(1+\exp\left(\frac{-\pi x}{\sqrt{3}t}\right)\right)^{-1},\ x\in \mathfrak{R}. \end{array} $$

Definition 2.3.

(Liu [5]) Let X t be an uncertain process and let C t be a canonical Liu process. For any partition of closed interval [a,b] with a=t 1<t 2<…<t k+1=b, the mesh is written as

$$\begin{array}{@{}rcl@{}} \Delta=\max_{1\leq i\leq k}|t_{i+1}-t_{i}|. \end{array} $$

Then Liu integral of X t with respect to C t is defined as

$$\begin{array}{@{}rcl@{}} {\int_{a}^{b}}X_{t}\mathrm{d} C_{t}={\lim}_{\Delta\to 0}\sum_{i=1}^{k}X_{t_{i}}\cdot\left(C_{t_{i+1}}-C_{t_{i}}\right) \end{array} $$

provided that the limit exists almost surely and is finite. In this case, the uncertain process X t is said to be integrable.

Definition 2.4.

(Chen and Ralescu [21]) Let Z t be an uncertain process and let C t be a canonical Liu process. If there exist two uncertain processes μ t and σ t such that

$$\begin{array}{@{}rcl@{}} Z_{t}=Z_{0}+{\int_{0}^{t}} \mu_{s} ds +{\int_{0}^{t}} \sigma_{s} \mathrm{d} C_{s},\qquad \forall t\geq 0. \end{array} $$

Then Z t is called a Liu process with drift μ t and diffusion σ t . Furthermore, Z t has an uncertain differential

$$\begin{array}{@{}rcl@{}} \mathrm{d} Z_{t}=\mu_{t} \mathrm{d} t +\sigma_{t} \mathrm{d} C_{t}. \end{array} $$

Theorem 2.1.

(Liu [5]) Let h(t,c) be a continuously differentiable function. Then Z t =h(t,C t ) is a Liu process and has an uncertain differential

$$\begin{array}{@{}rcl@{}} \mathrm{d}Z_{t}=\frac{\partial h}{\partial t}\left(t,C_{t}\right)\mathrm{d} t+\frac{\partial h}{\partial c}\left(t,C_{t}\right)\mathrm{d} C_{t}. \end{array} $$

Definition 2.5.

(Liu [6]) Suppose C t is a canonical Liu process, and f and g are some given functions. Then

$$\begin{array}{@{}rcl@{}} \mathrm{d} X_{t}=f\left(t,X_{t}\right)\mathrm{d} t+g\left(t,X_{t}\right)\mathrm{d} C_{t} \end{array} $$

is called an uncertain differential equation. A solution is a Liu process X t that satisfies the above equation identically in t.

The existence and uniqueness theorem of solution of the uncertain differential equation was proved by Chen and Liu [11] under linear growth condition and Lipschitz continuous condition. More importantly, Yao and Chen [19] proved that the solution of an uncertain differential equation can be represented by a spectrum of ordinary differential equations.

Definition 2.6.

(Yao and Chen [19]) Let α be a number with 0<α<1. An uncertain differential equation

$$\begin{array}{@{}rcl@{}} \mathrm{d} X_{t}=f\left(t,X_{t}\right)\mathrm{d} t+g\left(t,X_{t}\right)\mathrm{d} C_{t} \end{array} $$

is said to have an α-path \(X_{t}^{\alpha }\) if it solves the corresponding ordinary differential equation

$$\begin{array}{@{}rcl@{}} \mathrm{d} X_{t}^{\alpha}=f\left(t,X_{t}^{\alpha}\right)\mathrm{d} t+\left|g\left(t,X_{t}^{\alpha}\right)\right|\Phi^{-1}(\alpha)\mathrm{d} t \end{array} $$

where Φ −1(α) is the inverse uncertainty distribution of standard normal uncertain variable, i.e.,

$$\begin{array}{@{}rcl@{}} \Phi^{-1}(\alpha)=\frac{\sqrt{3}}{\pi}\ln\frac{\alpha}{1-\alpha}. \end{array} $$

Theorem 2.2.

(Yao-Chen Formula [19]) Let X t and \(X_{t}^{\alpha }\) be the solution and α-path of the uncertain differential equation

$$\begin{array}{@{}rcl@{}} \mathrm{d} X_{t}=f\left(t,X_{t}\right)\mathrm{d} t+g\left(t,X_{t}\right)\mathrm{d} C_{t}. \end{array} $$

Then

Theorem 2.3.

(Yao and Chen [19]) Let X t and \(X_{t}^{\alpha }\) be the solution and α-path of the uncertain differential equation

$$\begin{array}{@{}rcl@{}} \mathrm{d} X_{t}=f\left(t,X_{t}\right)\mathrm{d} t+g\left(t,X_{t}\right)\mathrm{d} C_{t}. \end{array} $$

Then the solution X t has an inverse uncertainty distribution,

$$\begin{array}{@{}rcl@{}} \Psi_{t}^{-1}(\alpha)=X_{t}^{\alpha}. \end{array} $$

Runge-Kutta Method

Runge-Kutta method is an efficient method for solving ordinary differential equations. The widely used Runge-Kutta formula is a fourth-order formula. What we must notice is that there are many different fourth-order schemes and we just present one common form here. For an ordinary differential equation with initial value X 0

$$\begin{array}{@{}rcl@{}} \mathrm{d} X_{t}=F\left(t,X_{t}\right)\mathrm{d} t, \end{array} $$

the method uses the following formula

$$\begin{array}{@{}rcl@{}} X\left(t_{n+1}\right)=X\left(t_{n}\right)+\frac{1}{6}\left(k_{1}+2k_{2}+2k_{3}+k_{4}\right) \end{array} $$

where the k i are

$$\begin{array}{@{}rcl@{}} \begin{aligned} k_{1}&=hF\left(t_{n}, X_{n}\right),\\ k_{2}&=hF\left(t_{n}+\frac{1}{2}h, X_{n}+\frac{1}{2}hk_{1}\right),\\ k_{3}&=hF\left(t_{n}+\frac{1}{2}h, X_{n}+\frac{1}{2}hk_{2}\right),\\ k_{4}&=hF\left(t_{n}+h, X_{n}+hk_{3}\right), \end{aligned} \end{array} $$

and t n =n h. The step size h has been assumed to be constant for all steps.

Based on Theorem 2.2, we can design a Runge-Kutta method for uncertain differential equations. For an uncertain differential equation with initial value X 0,

$$\begin{array}{@{}rcl@{}} \mathrm{d} X_{t}=f\left(t, X_{t}\right)\mathrm{d} t+g\left(t,X_{t}\right)\mathrm{d} C_{t} \end{array} $$

and its α-path equations

$$\begin{array}{@{}rcl@{}} \mathrm{d} X_{t}^{\alpha}=f\left(t, X_{t}^{\alpha}\right)\mathrm{d} t+\left| g\left(t, X_{t}^{\alpha}\right)\right|\Phi^{-1}(\alpha)\mathrm{d} t, \end{array} $$

we can solve it with the method given below.

  1. Step 0:

    Fix a time s, an interation number N and a step length h=s/N. Set α=0 and i=0.

  2. Step 1:

    Set α←α+0.01.

  3. Step 2:

    Solve the corresponding ordinary differential equation

    $$\mathrm{d} X_{t}^{\alpha}=f\left(t, X_{t}^{\alpha}\right)\mathrm{d} t+\left| g\left(t, X_{t}^{\alpha}\right)\right|\Phi^{-1}(\alpha)\mathrm{d} t,\quad X_{0}^{\alpha}=X_{0} $$

with the Runge-Kutta method as follows

$$\begin{array}{@{}rcl@{}}</p><p class="noindent">X_{i+1}^{\alpha}=X_{i}^{\alpha}+\frac{1}{6}\left(k_{1}+2k_{2}+2k_{3}+k_{4}\right) \end{array} $$

where the k j ,j=1,2,3,4 are

$$\begin{array}{@{}rcl@{}} \begin{aligned} k_{1}&=h\left(f\left(t_{i},X_{i}^{\alpha}\right)+\left|g\left(t_{i},X_{i}^{\alpha}\right)\right|\Phi^{-1}(\alpha)\right),\\ k_{2}&=h\left(f\left(t_{i}+\frac{1}{2}h,X_{i}^{\alpha}+\frac{1}{2}hk_{1}\right)+\left|g\left(t_{i}+\frac{1}{2}h,X_{i}^{\alpha}+\frac{1}{2}hk_{1}\right)\right|\Phi^{-1}(\alpha)\right),\\ k_{3}&=h\left(f\left(t_{i}+\frac{1}{2}h,X_{i}^{\alpha}+\frac{1}{2}hk_{2}\right)+\left|g\left(t_{i}+\frac{1}{2}h,X_{i}^{\alpha}+\frac{1}{2}hk_{2}\right)\right|\Phi^{-1}(\alpha)\right),\\ k_{4}&=h\left(f\left(t_{i}+h,X_{i}^{\alpha}+hk_{3}\right)+\left|g\left(t_{i}+h,X_{i}^{\alpha}+hk_{3}\right)\right|\Phi^{-1}(\alpha)\right). \end{aligned} \end{array} $$
  1. Step 3:

    Set i←i+1.

  2. Step 4:

    Repeat Step 2 and Step 3 for N times, then we can obtain the \(X_{s}^{\alpha }\). Go back to Step 1 until α=0.99.

Then we can get the \(X_{s}^{\alpha }\) for every α, that is, we have a 99-table:

α

0.01

0.02

…

0.99

\(X_{s}^{\alpha }\)

\(X_{s}^{0.01}\)

\(X_{s}^{0.02}\)

…

\(X_{s}^{0.99}\)

According to Theorem 2.3, we have figured out the corresponding \(X_{s}^{\alpha }\) which satisfies . Then we obtain the inverse uncertainty distribution of X s .

Numerical Experiments

Based on the Runge-Kutta method, we will give some numerical experiments to calculate uncertainty distribution, expected value, extreme value and time integral of solution of uncertain differential equation.

Runge-Kutta Method for Uncertainty Distribution of Solution

For linear uncertain differential equation, Chen and Liu [11] proved an analytic solution. Let u 1t ,u 2t ,v 1t ,v 2t be integrable uncertain processes. Then the uncertain differential equation

$$\begin{array}{@{}rcl@{}} \mathrm{d} X_{t}=\left(u_{1t}X_{t}+u_{2t}\right)\mathrm{d} t+\left(v_{1t}X_{t}+v_{2t}\right)\mathrm{d} C_{t} \end{array} $$

has a solution

$$\begin{array}{@{}rcl@{}} X_{t}=U_{t}\left(X_{0}+{\int_{0}^{t}}\frac{u_{2s}}{U_{s}}\mathrm{d} s+{\int_{0}^{t}}\frac{v_{2s}}{U_{s}}\mathrm{d} C_{s}\right) \end{array} $$

where

$$\begin{array}{@{}rcl@{}} U_{t}=\exp\left({\int_{0}^{t}} u_{1s}\mathrm{d} s+{\int_{0}^{t}} v_{1s}\mathrm{d} C_{s}\right). \end{array} $$

We use Runge-Kutta method and method to solve the same linear uncertain differential equation and compare their accuracy.

Example 4.1.

Consider the following linear uncertain differential equation

$$\begin{array}{@{}rcl@{}} \mathrm{d} X_{t}=\left(m-aX_{t}\right)\mathrm{d} t+\sigma \mathrm{d} C_{t}, \qquad X_{0}=0, \qquad \sigma >0 \end{array} $$
((1))

and its α-path equation

$$\begin{array}{@{}rcl@{}} \mathrm{d} X_{t}^{\alpha}=\left(m-aX_{t}^{\alpha}+\sigma\Phi^{-1}(\alpha)\right)\mathrm{d} t. \end{array} $$

The analytic solution of Eq. (1) is

$$\begin{array}{@{}rcl@{}} X_{t}=\frac{m}{a}(1-\exp(-at))+\sigma \exp(-at){\int_{0}^{t}}\exp(as)\mathrm{d} C_{s}, \end{array} $$

and the inverse uncertainty distribution of X t is

$$\begin{array}{@{}rcl@{}} \Psi^{-1}_{t}(\alpha)=\left(\frac{m}{a}+\frac{\sigma}{a}\Phi^{-1}(\alpha)\right)(1-\exp(-at)). \end{array} $$

We choose the parameters as follows, m=5, a=1, σ=2, X 0=0, t=1,N=100. The curves are shown in Figs. 1 and 2. Figure 2 is in an enlarged view of Fig. 1.

Fig. 1
figure 1

The uncertainty distribution cure of Example 4.1

Full size image
Fig. 2
figure 2

An enlarged view of the uncertainty distribution cure of Example 4.1

Full size image

We add up the errors between the analytic solution and solutions of the two methods at the 99 points, the error of Runge-Kutta method is 0.9054, the errors of Euler method is 0.9146. We can see the error of Runge-Kutta method is less than the Euler method.

Example 4.2.

Consider the following linear uncertain differential equation

$$\begin{array}{@{}rcl@{}} \mathrm{d} X_{t}=u X_{t} \mathrm{d} t+v X_{t} \mathrm{d} C_{t},\qquad X_{0}=1 \end{array} $$
((2))

and its α-path is

$$\begin{array}{@{}rcl@{}} \mathrm{d} X^{\alpha}_{t}=\bigg(u X^{\alpha}_{t}+ |v X^{\alpha}_{t}|\Phi^{-1}(\alpha)\bigg)\mathrm{d} t. \end{array} $$

The analytic solution of Eq. (2) is

$$\begin{array}{@{}rcl@{}} X_{t}=X_{0}\exp\left(ut+vC_{t}\right), \end{array} $$

and the inverse uncertainty distribution of X t is

$$\begin{array}{@{}rcl@{}} \Psi^{-1}_{t}(\alpha)=X_{0}\exp\left(ut+v\Phi^{-1}(\alpha)\right). \end{array} $$

We choose the parameters as follows, u=0.1,v=1.25,X 0=1,t=1,N=100. The curves are shown in Figs. 3 and 4. The error of Runge-Kutta method is 3.6784, the errors of Euler method is 3.7146. We can see the error of Runge-Kutta method is less than the Euler method too.

Fig. 3
figure 3

The uncertainty distribution cure of Example 4.2

Full size image
Fig. 4
figure 4

An enlarged view of the uncertainty distribution cure of Example 4.2

Full size image

Example 4.3.

Let a be a real number. Consider a nonlinear uncertain differential equation

$$\begin{array}{@{}rcl@{}} \mathrm{d} X_{t}=\frac{a-X_{t}}{1-t}\mathrm{d} t +\mathrm{d} C_{t}, \qquad 0\leq t<1 \end{array} $$
((3))

with given initial value X 0=1.

The α-path of Eq. (3) is

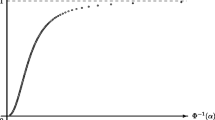
$$\begin{array}{@{}rcl@{}} \mathrm{d} X^{\alpha}_{t}=\left(\frac{a-X^{\alpha}_{t}}{1-t}+\Phi^{-1}(\alpha)\right)\mathrm{d} t. \end{array} $$

Set a=2, t=0.9 and N=1,000. The result is shown Fig. 5. And we can get that the expected value of solution is E[X t ]=1.6933.

Fig. 5
figure 5

The uncertainty distribution cure of Example 4.3

Full size image

Runge-Kutta Method for Extreme Value of Solution

Based on Yao-Chen formula, Yao [20] gave a formula to calculate extreme value of solution of an uncertain differential equation. Let X t and \(X_{t}^{\alpha }\) be the solution and α-path of the uncertain differential equation

$$\begin{array}{@{}rcl@{}} \mathrm{d} X_{t}=f\left(t,X_{t}\right)\mathrm{d} t+g\left(t,X_{t}\right)\mathrm{d} C_{t}. \end{array} $$

Then for any time s>0 and strictly increasing (decreasing) function J(x), the supremum

$$\begin{array}{@{}rcl@{}} \sup_{0\le t\le s}J(X_{t}) \end{array} $$

has an inverse uncertainty distribution

$$\begin{array}{@{}rcl@{}} \Psi_{s}^{-1}(\alpha)=\sup_{0\le t\le s}J\left(X_{t}^{\alpha}\right)\quad \left(\Psi_{s}^{-1}(\alpha)=\sup_{0\le t\le s}J\left(X_{t}^{1-\alpha}\right)\right); \end{array} $$

and the infimum

$$\begin{array}{@{}rcl@{}} \inf_{0\le t\le s}J(X_{t}) \end{array} $$

has an inverse uncertainty distribution

$$\begin{array}{@{}rcl@{}} \Psi_{s}^{-1}(\alpha)=\inf_{0\le t\le s}J\left(X_{t}^{\alpha}\right)\quad \left(\Psi_{s}^{-1}(\alpha)=\inf_{0\le t\le s}J\left(X_{t}^{1-\alpha}\right)\right). \end{array} $$

Example 4.4.

We continue the Example 4.3. Consider the supremum

$$\begin{array}{@{}rcl@{}} \sup_{0\leq t\leq s} \exp(-rt)(X_{t}-K) \end{array} $$

where r and K are real numbers.

The inverse uncertainty distribution of Equation of (4.4) is

$$\begin{array}{@{}rcl@{}} \Psi_{s}^{-1}(\alpha)=\sup_{0\leq t\leq s} \exp(-rt)\left(X_{t}^{\alpha}-K\right) \end{array} $$

for given times s>0. We choose the parameters r=0.02 and K=1. Based on Runge-Kutta method, the uncertainty distribution of extreme value at s=0.9 is shown in Fig. 6. And we can get

$$\begin{array}{@{}rcl@{}} \mathrm{E}\left[\sup_{0\leq t\leq s} \exp(-rt)(X_{t}-K)\right]=0.7936. \end{array} $$
Fig. 6
figure 6

The uncertainty distribution cure of extreme value at s=0.9

Full size image

Runge-Kutta Method for Time Integral of Solution

Based on Yao-Chen formula, Yao [20] gave a formula to calculate time integral of solution of an uncertain differential equation. Let X t and \(X_{t}^{\alpha }\) be the solution and α-path of the uncertain differential equation

$$\begin{array}{@{}rcl@{}} \mathrm{d} X_{t}=f\left(t,X_{t}\right)\mathrm{d} t+g\left(t,X_{t}\right)\mathrm{d} C_{t}. \end{array} $$

Then for any time s>0 and strictly increasing (decreasing) function J(x), the time integral

$$\begin{array}{@{}rcl@{}} {\int_{0}^{s}}J\left(X_{t}\right)\mathrm{d} t \end{array} $$

has an inverse uncertainty distribution

$$\begin{array}{@{}rcl@{}} \Psi_{s}^{-1}(\alpha)={\int_{0}^{s}}J\left(X_{t}^{\alpha}\right)\mathrm{d} t \quad \left(\Psi_{s}^{-1}(\alpha)={\int_{0}^{s}}J\left(X_{t}^{1-\alpha}\right)\mathrm{d} t\right). \end{array} $$

Example 4.5.

We continue the Example 4.3. Consider the time integral

$$\begin{array}{@{}rcl@{}} {\int_{0}^{s}} \exp(-rt)(X_{t}-K)\mathrm{d} t \end{array} $$
((4))

where r and K are real numbers.

The inverse uncertainty distribution of Equation of (4) is

$$\begin{array}{@{}rcl@{}} \Psi_{s}^{-1}(\alpha)={\int_{0}^{s}} \exp(-rt)\left(X_{s}^{\alpha}-K\right)\mathrm{d} t \end{array} $$

for given times s>0. We choose the parameters r=0.02 and K=1. Based on Runge-Kutta method, the uncertainty distribution of time integral at s=0.9 is shown in Fig. 7. And we can get

$$\begin{array}{@{}rcl@{}} \mathrm{E}\left[{\int_{0}^{s}} \exp(-rt)(X_{t}-K)\mathrm{d} t\right]=0.7156. \end{array} $$
Fig. 7
figure 7

The uncertainty distribution of time integral at s=0.9

Full size image

Conclusions

Uncertain differential equations have lots of applications in many fields especially in uncertain finance. Sometimes we just need the numerical solutions. This paper gave a Runge-Kutta method for solving uncertain differential equations, the extreme value and time integral of solution of uncertain differential equations. Examples in this paper proved that it is a more accuracy and effective method than the former algorithm.