Abstract
In this contribution, the accuracy and efficiency of various modeling assumptions and numerical settings in thermo-mechanical simulations of powder bed fusion (PBF) processes are analyzed. Thermo-mechanical simulations are used to develop a better understanding of the process and to determine residual stresses and distortions based on the temperature history. In these numerically very complex simulations, modeling assumptions are often made that reduce computational effort but lead to inaccuracies. These assumptions include the omission of the surrounding powder or the use of geometrically linearized material models. The numerical setting, in particular the temporal and spatial discretizations, can further lead to discretization errors. Here, a highly parallelized and adaptive finite element method based on the open source C++ library deal.II is validated and utilized, to investigate some of these modeling assumptions and to identify the required temporal and spatial discretizations for the simulation of PBF of Ti-6Al-4V. The insights initially gained on a simple wall-like geometry are transferred to a larger open rectangular profile where the results of a detailed simulation are compared with those of a more efficient one. The results for the efficient approach show a maximum deviation of \(\approx 8\%\) in the displacements and \(\approx 3.5\%\) in the residual stresses while significantly reducing the computational time.
Similar content being viewed by others
Introduction
Additive Manufacturing (AM) offers nearly unlimited design freedom during the construction process. One of the most widely used metal additive manufacturing techniques is Powder Bed Fusion (PBF) [1, 2]. During this manufacturing process, powder material is applied to a solid building platform and subsequently melted by a laser beam. This is repeated in a layer-wise fashion until the desired geometry is created. The final part is obtained after removing the solidified material from the building platform.
Major challenges in the AM process are the dimensional accuracy, the quality and the reproducibility of the manufactured part. Due to high thermal gradients in the beam vicinity residual stresses emerge which can lead to distortions, especially after removing the part from the building platform, and result in additional post-processing steps. Detailed explanations of the build-up of residual stresses can be found in [1] and [3]. In order to investigate these effects and to optimize PBF processes, thermo-mechanical finite element simulations have proven to be very beneficial.
In this manuscript a macroscopic thermo-mechanical process simulation of PBF of Ti-6Al-4V is introduced. This process simulation belongs to the intermediate-fidelity approaches, which consider the powder as a homogenized material and neglect melt pool dynamics, but explicitly represent the moving laser beam and the scan strategy. Even on this intermediate-fidelity level, the models and assumptions being made in literature differ. In [4,5,6,7] the coupling of thermal and mechanical quantities is considered in an one-way fashion neglecting the influence of deformation on the thermal response. In each time step the thermal problem is solved first and the obtained temperature field serves as input for the mechanical solution. In [8] the thermo-mechanical dissipation is taken into account, and in [9, 10] an operator-split approach is used. Riedlbauer et al. [11] investigated the performance of the monolitic and the adiabatic split approach for the nonlinear thermo-mechanical problem, whereby the adiabatic split was three times faster.
It is often assumed that geometrically linearized mechanical models are sufficient [5, 12,13,14]. These reduce the computational effort as compared to finite strain formulations [9, 15], but are limited to small strains. For deformations exceeding this limitation the obtained results show large deviations to its geometrically exact counterpart.
For the powder material and its properties different assumptions are made in literature. While some contributions include the surrounding powder to full extend in the simulation [16], others account for removed powder only by convection boundary conditions [12, 17]. Chiumenti et al. [18] compared the temperature differences of fully modeled powder to a substitute heat flux resulting in a maximum deviation of \(10\%\). In [19] the surrounding powder was omitted without compensation. The mechanical properties of powder are usually taken to be those of the solid material with a scaling factor. For the yield stress and the Young’s modulus scaling factors of 0.01 to \(-\)0.1 are widely used [9, 20, 21]. The scaling factor of the thermal expansion coefficient ranges from 0.0 to 1.0 [13, 22].
The constitutive laws used to represent the mechanical behavior of metal alloys, e.g. Ti-6Al-4V, also differ. Elastoplastic models are used which are either rate-dependent [8, 9, 14] or rate-independent without hardening [23, 24], with isotropic [25] or kinematic hardening [20]. In [8, 9] a temperature-dependent viscosity parameter is used which increases the rate-dependency with increasing temperature. In [8] a sensitivity analysis for different material properties of Ti-6Al-4V is carried out and the thermal expansion coefficient and the yield stress had the greatest influence. Denlinger et al. [24] presented an approach where stress relaxation above a critical temperature is accounted for by resetting certain quantities to zero. In [26] a transformation strain is introduced that accounts for this reset. In [9] the plastic strains are reset to zero and an increased viscosity accounts for stress relaxation when entering the mushy zone above \(80\%\) of the melting temperature. The evaluation of the material model is conducted in an incremental [23] or non-incremental fomulation [14].
Information about the finite element types used are rarely given. Lindgren [27] stated for welding simulations that the polynomial degree of the finite element shape functions used for the mechanical simulation model shall be one order higher than the one of the thermal element shape functions, since temperature increments directly become thermal strains but total strains are derivatives of the displacements. In [28] linear and quadratic shape functions are compared in terms of accuracy and run time for the simulation of selective laser melting processes using the finite cell method. A study on time integration schemes for thermal additive manufacturing simulations is conducted in [29]. For the spatially adaptive simulations in [14], correction terms are introduced to account for information loss during coarsening of the mesh. In [30], thermal and mechanical errors are estimated for single layer applications. Further spatial adaptivity techniques that adapt the mesh near the heat source are introduced in [4, 23, 31]. In [32] different time step sizes are used in different areas of the simulation domain for thermal selective laser sintering simulations of polymers.
In this manuscript, a detailed numerical analysis of various assumptions made in literature is performed. Influences of the modeling assumptions, as geometrically linear or nonlinear setting or the influence of the surrounding powder, are examined as well as the numerical setting including the element type, mesh size and time step size. This detailed analysis is made possible through the use of a highly parallelized simulation framework based on the C++ open source library deal.II [33, 34]. Spatial and temporal error indicators are introduced as adaptivity criteria. For a single wall example different settings are compared in terms of accuracy and computational effort. The insights gained are then transferred to a larger example and evaluated in detail. This paper is structured as follows. In section 2, the thermo-mechanical model is introduced, including all governing equations and material properties of Ti-6Al-4V. In the next section the numerical implementation, including the adaptive discretization in space and time is outlined. Validation and numerical results are presented in section 4, which compare the accuracy and computational effort of the various modeling and simulation settings. Finally, a conclusion is given and future steps are defined.
Thermomechanical process modeling
In the following, the thermo-mechanical equations, the constitutive models and the material properties of Ti-6Al-4V are summarized. The thermal and mechanical equations are weakly coupled and solved in a staggered approach, neglecting heat generated by deformation and plastic dissipation.
Thermal model
The unknown temperature field  \( [ ^{\circ }\hbox {C}]\) in the thermal domain
\( [ ^{\circ }\hbox {C}]\) in the thermal domain  is obtained by solving the nonlinear heat equation in an enthalpy form
is obtained by solving the nonlinear heat equation in an enthalpy form

Here, \(\dot{\{ \bullet \}}\) denotes the time derivative,  \( \left[ \frac{\hbox {kg}}{\hbox {m}^{3}}\right] \) the constant density,
\( \left[ \frac{\hbox {kg}}{\hbox {m}^{3}}\right] \) the constant density,  \( \left[ \frac{\hbox {W}}{\hbox {m}^{2}}\right] \) the heat flux and
\( \left[ \frac{\hbox {W}}{\hbox {m}^{2}}\right] \) the heat flux and  \( \left[ \frac{\hbox {W}}{\hbox {m}\,\hbox {K}}\right] \) the temperature-dependent thermal conductivity. Latent heat that is generated or absorbed during phase changes is accounted for by the change of the temperature-dependent specific enthalpy
\( \left[ \frac{\hbox {W}}{\hbox {m}\,\hbox {K}}\right] \) the temperature-dependent thermal conductivity. Latent heat that is generated or absorbed during phase changes is accounted for by the change of the temperature-dependent specific enthalpy  \( \left[ \frac{\hbox {J}}{\hbox {kg}}\right] \), see Fig. 1(a). The heat input Q \( \left[ \frac{\hbox {W}}{\hbox {m}^{3}}\right] \) introduced by the laser beam is approximated by a volumetric Gaussian distribution following the Goldak heat input model [35]
\( \left[ \frac{\hbox {J}}{\hbox {kg}}\right] \), see Fig. 1(a). The heat input Q \( \left[ \frac{\hbox {W}}{\hbox {m}^{3}}\right] \) introduced by the laser beam is approximated by a volumetric Gaussian distribution following the Goldak heat input model [35]

where the beam radius is denoted by  \( \left[ \hbox {m}\right] \), the beam power by
\( \left[ \hbox {m}\right] \), the beam power by  \( \left[ \hbox {W}\right] \) and the absorption coefficient by
\( \left[ \hbox {W}\right] \) and the absorption coefficient by  . The coordinates \(\xi _i\) belong to a local coordinate system with the origin in the center of the beam.
. The coordinates \(\xi _i\) belong to a local coordinate system with the origin in the center of the beam.
The boundary of the body  can be subdivided in the disjunct Dirichlet
can be subdivided in the disjunct Dirichlet  and Neumann
and Neumann  parts, where either the temperature or the heat flux due to radiation and convection is prescribed
parts, where either the temperature or the heat flux due to radiation and convection is prescribed


Here,  denotes the outward normal vector, an overbar \(\bar{\{ \bullet \}}\) prescribed quantities,
denotes the outward normal vector, an overbar \(\bar{\{ \bullet \}}\) prescribed quantities,  \( \left[ \frac{\hbox {W}}{\hbox {m}^{2}\hbox {K}}\right] \) the convection coefficient,
\( \left[ \frac{\hbox {W}}{\hbox {m}^{2}\hbox {K}}\right] \) the convection coefficient,  the gas temperature,
the gas temperature,  \( \left[ \frac{\hbox {W}}{\hbox {m}^{2}\hbox {K}^{4}}\right] \) the Stefan Boltzmann constant,
\( \left[ \frac{\hbox {W}}{\hbox {m}^{2}\hbox {K}^{4}}\right] \) the Stefan Boltzmann constant,  the emission coefficient and
the emission coefficient and  the ambient temperature.
the ambient temperature.
Mechanical model
In this subsection, the governing equations of the mechanical problem are presented. The linearized total strain is the symmetric gradient of the unknown displacements  . The balance of linear momentum is formulated in the mechanical domain
. The balance of linear momentum is formulated in the mechanical domain  and given with the required boundary conditions as
and given with the required boundary conditions as

Body forces and inertia terms are neglected. The mechanical Dirichlet and Neumann boundaries are denoted as  and
and  .
.  \( \left[ \hbox {m}\right] \) and
\( \left[ \hbox {m}\right] \) and  \( \left[ \hbox {Pa}\right] \) are the prescribed displacements and tractions. A thermo-elasto-viscoplastic material model is applied. The total strain is decomposed into elastic
\( \left[ \hbox {Pa}\right] \) are the prescribed displacements and tractions. A thermo-elasto-viscoplastic material model is applied. The total strain is decomposed into elastic  , viscoplastic
, viscoplastic  and thermal
and thermal  parts
parts

The thermal strain is obtained from the temperature-dependent coefficient of thermal expansion  \({\left[ \frac{\hbox {1}}{\textrm{K}}\right] }\), the reference temperature
\({\left[ \frac{\hbox {1}}{\textrm{K}}\right] }\), the reference temperature  and the second-order unit tensor
and the second-order unit tensor  . Neglecting thermal coupling, the free energy density
. Neglecting thermal coupling, the free energy density  reads
reads

with the internal hardening variable  , the temperature-dependent bulk modulus \(\kappa ( \vartheta )\) \( \left[ \hbox {Pa}\right] \), shear modulus \(\mu (\vartheta )\) \( \left[ \hbox {Pa}\right] \) and hardening modulus
, the temperature-dependent bulk modulus \(\kappa ( \vartheta )\) \( \left[ \hbox {Pa}\right] \), shear modulus \(\mu (\vartheta )\) \( \left[ \hbox {Pa}\right] \) and hardening modulus  \( \left[ \hbox {Pa}\right] \). The Cauchy stress
\( \left[ \hbox {Pa}\right] \). The Cauchy stress  \( \left[ \hbox {Pa}\right] \) and the hardening stress R \( \left[ \hbox {Pa}\right] \) are obtained as
\( \left[ \hbox {Pa}\right] \) and the hardening stress R \( \left[ \hbox {Pa}\right] \) are obtained as

where \(\{ \bullet \}^\text {vol}\) and \(\{\bullet \}^\text {dev}\) give the volumetric and deviatoric part of the second order tensor \(\{\bullet \}\), respectively. The von Mises yield criterion with isotropic hardening is applied

with the temperature-dependent yield stress  \( \left[ \hbox {Pa}\right] \). The evolutions of the viscoplastic strain
\( \left[ \hbox {Pa}\right] \). The evolutions of the viscoplastic strain  and the internal variable
and the internal variable  follow an associative flow rule of Perzyna type [36]
follow an associative flow rule of Perzyna type [36]

with the temperature-dependent viscosity parameter  \( \left[ \hbox {Pas}\right] \), the plastic multiplier \(\gamma \) and the Macauley brackets \(2 \langle \bullet \rangle = \bullet + |\bullet |\). In order to investigate the simplification error that is made while using this geometrically linear model, a corresponding geometrically nonlinear model based on the logarithmic strain space approach presented by Miehe in [37, 38] is introduced. Further information can be found in Appendix A.
\( \left[ \hbox {Pas}\right] \), the plastic multiplier \(\gamma \) and the Macauley brackets \(2 \langle \bullet \rangle = \bullet + |\bullet |\). In order to investigate the simplification error that is made while using this geometrically linear model, a corresponding geometrically nonlinear model based on the logarithmic strain space approach presented by Miehe in [37, 38] is introduced. Further information can be found in Appendix A.
Material properties
The thermal and thermo-mechanical properties of Ti-6Al-4V from [7, 39] are approximated by hyperbolic tangent functions as depicted in Fig. 1. The simulation introduces a one-way conversion from powder to melt and a bidirectional conversion between solid and melt. During these transformations latent heat is released or absorbed as indicated by the sudden increase of the specific enthalpy depicted in Fig. 1 (a). The latent heat is considered within a phase-change interval between the solidus and melting temperature.
Thermophysical and thermo-mechanical material properties of Ti-6Al-4V: specific enthalpy (a) and heat conductivity (b) [39], Young’s modulus (c), Poisson’s ratio (d), yield stress (e), viscosity parameter (f) and thermal expansion coefficient (g). The red and blue dashed lines indicate the pre-defined relaxation temperature  and melting temperature
and melting temperature  . Red crosses indicate points taken from [7]
. Red crosses indicate points taken from [7]
The thermal conductivities at room temperature of the two material phases solid/melt and powder differ significantly as shown in Fig. 1 (b). The material shows rather high values for the solid/melt phase which increase with temperature. In the powder phase, a low thermal conductivity of the material results in a stronger insulating effect. The yield stress and Young’s modulus decrease towards the melting temperature, and are held constant above. Following [9, 20] a scaling factor between the solid and powder Young’s modulus at room temperature of \(s=0.1\) is used. While the powder material is modeled to behave fully elastic, solid material and melt are modeled to be viscoplastic with a hardening coefficient  \( \left[ \hbox {Pa}\right] \) of \(\approx {5.0}\%\) of the respective Young’s modulus [40]. As Ti-6Al-4V shows rate-independent behavior for lower temperatures the viscosity parameter is set to
\( \left[ \hbox {Pa}\right] \) of \(\approx {5.0}\%\) of the respective Young’s modulus [40]. As Ti-6Al-4V shows rate-independent behavior for lower temperatures the viscosity parameter is set to  , resulting in the rate-independent limit case for the constitutive law presented in subsection 2.2. The rate-dependency increases with temperature, which is accounted for by an increase of the viscosity parameter. The subsequent decrease towards the melting temperature has to be seen in context with the stress relaxation where the relaxation temperature for Ti-6Al-4V is set to
, resulting in the rate-independent limit case for the constitutive law presented in subsection 2.2. The rate-dependency increases with temperature, which is accounted for by an increase of the viscosity parameter. The subsequent decrease towards the melting temperature has to be seen in context with the stress relaxation where the relaxation temperature for Ti-6Al-4V is set to  , indicated by the red dashed lines in the diagrams of Fig. 1. Further details on the stress and plastic strain relaxation are presented in subsection 3.3.
, indicated by the red dashed lines in the diagrams of Fig. 1. Further details on the stress and plastic strain relaxation are presented in subsection 3.3.
The isotropic thermal expansion coefficient  for solid and melt material increases with temperature. Temperature-related expansion and contraction of powder is neglected with regard to its porous structure. Therefore the reference temperature
for solid and melt material increases with temperature. Temperature-related expansion and contraction of powder is neglected with regard to its porous structure. Therefore the reference temperature  for the thermal strain computation in Eq. (6) is set to the melting temperature
for the thermal strain computation in Eq. (6) is set to the melting temperature  during phase change from powder to melt.
during phase change from powder to melt.
Numerical implementation
In the following, the discretizations in time and space of both the thermal and the mechanical problem are presented. The thermal and mechanical equations are solved in a staggered way. The discretizations in time and space are adaptive and various criteria, in particular to control the adaptivity in space, are introduced. Finally, the numerical integration of the material model including the consideration of stress and plastic strain relaxation in high temperature regions is described.
Discretization
In a first step the strong form of the nonlinear heat equation Eq. (1) is multiplied by an arbitrary test function  that satisfies the homogeneous Dirichlet boundary conditions, i.e.
that satisfies the homogeneous Dirichlet boundary conditions, i.e.  on
on  , and is integrated over the entire body
, and is integrated over the entire body  . After integrating by parts and applying the boundary conditions the so called weak form results
. After integrating by parts and applying the boundary conditions the so called weak form results

including capacity, external, conduction and source parts. Following the same procedure for the balance of linear momentum (5) with the mechanical test functions  , with
, with  on
on  , one obtains the weak form of the balance of linear momentum
, one obtains the weak form of the balance of linear momentum

with the internal and external parts.
The weak form of the nonlinear heat equation is discretized in time using finite differences with a two-stage S-DIRK scheme as presented in [41]. The time step size \(\Delta t\) indicates the time between two successive time steps \(t_n\) and \(t_{n+1}\). The discretization in space is done with the finite element method, using scalar-valued  and vector-valued ansatz functions
and vector-valued ansatz functions  for the unknown temperatures and displacements. The dimensionless factor \(\tau \) is introduced which relates the length that the laser beam travels within one time step to the beam radius
for the unknown temperatures and displacements. The dimensionless factor \(\tau \) is introduced which relates the length that the laser beam travels within one time step to the beam radius 

with the beam velocity  \( \left[ \frac{\hbox {m}}{\hbox {s}}\right] \). More details on the discretization in time and space can be found in Appendix B.
\( \left[ \frac{\hbox {m}}{\hbox {s}}\right] \). More details on the discretization in time and space can be found in Appendix B.
After discretization in time and space, Eq. (11) is represented by a scalar residual equation for each global degree of freedom I, the current time step \(t_{n+1}\) and Runge–Kutta stage k

The terms  are specified in the appendix, Eq. (35). Discretizing the mechanical Eq. (12) in space results in the discrete equilibrium of forces for each degree of freedom J
are specified in the appendix, Eq. (35). Discretizing the mechanical Eq. (12) in space results in the discrete equilibrium of forces for each degree of freedom J

with the internal and external forces defined in the appendix, Eq. (36). The nonlinear Eqs. (14) and (15) are solved by means of a Newton-Raphson scheme in a staggered-fashion. The temperature field  from Eq. (14) serves as input for Eq. (15) to compute the temperature-dependent material properties and the thermal strain following the latter part of Eq. (6).
from Eq. (14) serves as input for Eq. (15) to compute the temperature-dependent material properties and the thermal strain following the latter part of Eq. (6).
Adaptivity in time and space
The discrete points in time for which the systems of Eqs. (14) and (15) described above are solved are set adaptively. To capture the high process dynamics during exposure small time step sizes are chosen. In the cooling phase, starting as soon as the beam finishes scanning the current layer and ending when the next layer is applied, the temperature gradients decrease and the time step size is increased. This increase is accomplished based on the error measure obtained by the temporal integration in Eq. (31). From the spatially distributed errors at every Gauss point  a single scalar quantity is obtained for each time step
a single scalar quantity is obtained for each time step

where the total number of Gauss points in the thermal simulation is denoted by \(n_\text {a}^\vartheta \) and the values for the relative and absolute tolerances are set to \(\epsilon _r=0.001\) and \(\epsilon _a=0.001\), respectively. The time step size is adjusted based on this error measure as

The increase and decrease of the time step size are limited by the damping factors \(f_\text {max}=2.0\), which results in a maximum doubling of the time step size, and \(f_\text {min}=0.3\). In order to prevent oscillating time step sizes, a safety factor of \(f_\text {s} =0.85\) is used. The order of accuracy of the embedded Runge–Kutta scheme for the used two stage S-DIRK scheme equals \(q=1\). For further details on the choice of these values the reader is referred to [41].
For the spatial discretization adaptive hexahedral octree-based meshes are used. Consequently a preferably coarse initial mesh is chosen and refined in the desired regions. The element edge length in building direction of the initial mesh must be a \(2^x\)-multiple of the process layer height to enable the application of exactly one layer after x refinement steps. In octree meshes the refinement level difference of adjacent cells must not exceed 1.
During the manufacturing process, the laser beam moves within the building chamber, constantly changing the location where the largest gradients occur. An adaptive discretization in space is used to capture the high gradients in the region close to the energy input as accurately as possible while maintaining a similar computational effort throughout the simulation. The refinement and coarsening of the mesh for the thermo-mechanical simulation is carried out based on the following three criteria as depicted in Fig. 2.
Schematic representation of the spatial adaptivity. The coarse initial mesh (a) is first adapted based on the beam position (b). With the temperature distribution (c) the Kelly error indicator (d) is obtained. The equivalent viscoplastic strain distribution (e) is used for the mechanical error indicator (f). The indicators (d, f) are used for further refinement and coarsening. The elements with mechanical error indicator values \(\ge 0.8~ \mathfrak {e}^\text {m,max}\) are highlighted by a red outline
In the first step, during exposure periods all elements inside a radius of  around the current beam location which are known a-priori are refined. Secondly, the Kelly error indicator
around the current beam location which are known a-priori are refined. Secondly, the Kelly error indicator  as presented in [42] and implemented in the deal.II library is used, which returns a single scalar value for each cell that is a measure of the jump of the temperature gradient over the element faces. The error in the mechanical fields is approximated by the error indicator
as presented in [42] and implemented in the deal.II library is used, which returns a single scalar value for each cell that is a measure of the jump of the temperature gradient over the element faces. The error in the mechanical fields is approximated by the error indicator  , taking into account the stresses and plastic strains. The error indicator is similarly computed as the well known superconvergent patch recovery (SPR) [43, 44], where the superconvergence of certain points inside the finite element mesh is exploited. For each element the difference of a smoothed L2-projection \(\{\bullet \}^\text {L2}\) and the values computed at the quadrature points \(\{\bullet \}^{*}\) are evaluated for the stress and plastic strain. For efficiency the L2-projection is carried out using a lumped mass-matrix. The scalar product of these differences builds the mechanical error indicator
, taking into account the stresses and plastic strains. The error indicator is similarly computed as the well known superconvergent patch recovery (SPR) [43, 44], where the superconvergence of certain points inside the finite element mesh is exploited. For each element the difference of a smoothed L2-projection \(\{\bullet \}^\text {L2}\) and the values computed at the quadrature points \(\{\bullet \}^{*}\) are evaluated for the stress and plastic strain. For efficiency the L2-projection is carried out using a lumped mass-matrix. The scalar product of these differences builds the mechanical error indicator

for an element  . Elements are flagged for refinement and coarsening based on the thermal error and sequentially for refinement based on the mechanical error indicator. The flagging is executed if a threshold of \(80.0\%\) or \(20.0\%\) of the maximum error indicator is either exceeded or undercut. The refinement and coarsening procedure is carried out at every time step during exposure and every second time step when the beam is inactive. Figure. 2 (d, f) show the result of the Kelly and mechanical error indicator during the scan of a single line over three layers. The vicinity of the current beam location is refined. High values for the thermal Kelly error indicator
. Elements are flagged for refinement and coarsening based on the thermal error and sequentially for refinement based on the mechanical error indicator. The flagging is executed if a threshold of \(80.0\%\) or \(20.0\%\) of the maximum error indicator is either exceeded or undercut. The refinement and coarsening procedure is carried out at every time step during exposure and every second time step when the beam is inactive. Figure. 2 (d, f) show the result of the Kelly and mechanical error indicator during the scan of a single line over three layers. The vicinity of the current beam location is refined. High values for the thermal Kelly error indicator  are especially obtained in coarse elements at the melt pool boundary, lower values are obtained for the more refined elements around the beam center and regions with a uniform temperature distribution. For the mechanical error indicator
are especially obtained in coarse elements at the melt pool boundary, lower values are obtained for the more refined elements around the beam center and regions with a uniform temperature distribution. For the mechanical error indicator  high values are obtained at the boundaries between the first solidified layer and the building platform and between further solidified layers. Due to the stress relaxation at higher temperatures, small values for the mechanical error indicator are obtained in the vicinity of the beam center.
high values are obtained at the boundaries between the first solidified layer and the building platform and between further solidified layers. Due to the stress relaxation at higher temperatures, small values for the mechanical error indicator are obtained in the vicinity of the beam center.
During refinement a predefined maximum refinement level of r must not be exceeded, limiting the smallest element edge length.
Stress relaxation for high temperatures
In order to account for the softening and annealing behavior in high temperature regions, stress relaxation as presented in [24] is used. The mechanical constitutive model requires the time integration of the evolution equations of the internal variables (10) to compute the stresses in Eq. (8). Due to the layer-wise material application and the pronounced stress relaxation for temperatures close to the melting temperature, an incremental procedure to compute the stresses is applied. The resulting stresses in each time step \(t_{n+1}\) can be obtained by the stresses of the previous time step \(t_{n}\) and an updating term

The latter consists of two contributions that can be viewed as an update due to the change of strain and a temperature-related change of the underlying material properties.
For high temperatures, i.e. if the temperature of the solid material exceeds a predefined relaxation temperature \(\vartheta ^\text {relax}\), the stresses and plastic strains of the previous time step are reset to zero

As the total strain is unaltered, the current state at time step n is stress-free while maintaining the prevailing deformation. In [26] a similar approach is presented for a non-incremental formulation using a transformation strain that accounts for the relaxation.
Results and discussion
In the following section the numerical framework is first validated using experimental data obtained from literature. This includes the comparison of melt pool dimensions as width and depth [45] and maximum temperatures [46] for the thermal problem and residual von Mises stresses for the mechanical problem [47]. Further, two numerical examples are discussed, a simple wall-like geometry with 6 layers and a larger rectangular profile as depicted in Fig. 6. The small wall-like example is used to analyze the influences of numerical and modeling aspects, as time step size, element size and type, geometrically linear or nonlinear mechanical models and modeling of the powder material. Based on these results, an efficient simulation set-up is identified which is then compared in terms of accuracy and computational costs with a very accurate reference set-up by means of the larger example.
Thermal and mechanical validation
Thermal validation
Simulated melt pool dimensions for various process parameters and for single scan lines are compared to experimental results from [45]. The single scan lines are done on a \(30\,\upmu \hbox {m}\) thick powder layer on top of a solid plate of Ti-6Al-4V. The beam radius is  , the beam velocity is varied from
, the beam velocity is varied from  to \({1.2}\frac{\hbox {m}}{\hbox {s}}\) and the laser power from
to \({1.2}\frac{\hbox {m}}{\hbox {s}}\) and the laser power from  to \(300\,\hbox {W}\). The material parameters for Ti-6Al-4V are defined as in subsection 2.3. The initial and ambient temperature for radiation and convection are
to \(300\,\hbox {W}\). The material parameters for Ti-6Al-4V are defined as in subsection 2.3. The initial and ambient temperature for radiation and convection are  . Convection and radiation are considered on top of the exposed powder layer. The absorption coefficient is set to \(A=0.77\) [48]. For further details on the experimental setup the reader is referred to [45]. The experimentally determined and simulated melt pool dimensions are compared in Fig. 3. For the melt pool width a good overall agreement can be observed for both velocities and all investigated powers. Only in the cases with the highest line energies
. Convection and radiation are considered on top of the exposed powder layer. The absorption coefficient is set to \(A=0.77\) [48]. For further details on the experimental setup the reader is referred to [45]. The experimentally determined and simulated melt pool dimensions are compared in Fig. 3. For the melt pool width a good overall agreement can be observed for both velocities and all investigated powers. Only in the cases with the highest line energies  does the simulation overestimate the melt pool width. The largest deviations in the melt pool depth are also obtained for the highest investigated line energy at
does the simulation overestimate the melt pool width. The largest deviations in the melt pool depth are also obtained for the highest investigated line energy at  and
and  . For this parameter combination the melt pool depth and width are almost equal and thus the transition zone between the conduction and keyhole mode begins [49, 50]. Therefore, the presented simulation underestimates the melt pool depth and overestimates its width. Minor deviations can be observed for the melt pool depth for the lowest line energies of both examined velocities. The simulations overestimate the melt pool depth. This is attributed to the neglect of melt pool dynamics phenomena, recoil pressure and Marangoni convection in the model. A better agreement with the experiments would require an adjustment of the heat input model by adapting its size to the process parameters [51] or applying an anisotropic heat conduction coefficient as in [52].
. For this parameter combination the melt pool depth and width are almost equal and thus the transition zone between the conduction and keyhole mode begins [49, 50]. Therefore, the presented simulation underestimates the melt pool depth and overestimates its width. Minor deviations can be observed for the melt pool depth for the lowest line energies of both examined velocities. The simulations overestimate the melt pool depth. This is attributed to the neglect of melt pool dynamics phenomena, recoil pressure and Marangoni convection in the model. A better agreement with the experiments would require an adjustment of the heat input model by adapting its size to the process parameters [51] or applying an anisotropic heat conduction coefficient as in [52].
In a second validation step, the maximum temperatures for single line experiments conducted in [46] are compared to simulation results. Single lines are scanned on a solid building plate made of Ti-6Al-4V, without powder. The experimental measurements of the maximum temperatures were conducted using a CCD camera and further postprocessed as described in [46] for various process parameters. The beam radius is  , the initial temperature is
, the initial temperature is  and convection and radiation are again considered on the top surface of the powder with
and convection and radiation are again considered on the top surface of the powder with  . The same material parameter as described in subsection 2.3 are used. To account for the reduced absorptivity of solid material compared to the previous powder case, the absorption coefficient is reduced to
. The same material parameter as described in subsection 2.3 are used. To account for the reduced absorptivity of solid material compared to the previous powder case, the absorption coefficient is reduced to  [53]. The experimentally determined and simulated maximum temperatures are compared for different line energies in Fig. 4. The corresponding process parameter laser power and velocity are specified in Table 1. A good agreement (error in temperature \(\le 10\%\)) between the numerically predicted and the measured maximum temperatures can be observed for all investigated parameter settings, except for the cases with a laser power of \(50\,\hbox {W}\). These cases result in the three highest maximum temperatures, which are overestimated in the simulation. For this laser power, the maximum temperatures during exposure exceed the evaporation temperature of pure aluminum. Evaporation phenomena are neglected in the model, which might explain, that the maximum temperatures are overestimated in the simulations. In the postprocessing of the experimental results, it is assumed that the emissivity of the material is constant (calibrated at the solidification temperature). However, it is also mentioned that it changes with temperature [46]. This is not taken into account in the measurements and leads to larger uncertainties in the temperature measurements at higher temperatures. The red dashed line indicates the line energy of \(200\frac{\hbox {J}}{\hbox {m}}\) which is used in the numerical analysis in subsection 4.2.
[53]. The experimentally determined and simulated maximum temperatures are compared for different line energies in Fig. 4. The corresponding process parameter laser power and velocity are specified in Table 1. A good agreement (error in temperature \(\le 10\%\)) between the numerically predicted and the measured maximum temperatures can be observed for all investigated parameter settings, except for the cases with a laser power of \(50\,\hbox {W}\). These cases result in the three highest maximum temperatures, which are overestimated in the simulation. For this laser power, the maximum temperatures during exposure exceed the evaporation temperature of pure aluminum. Evaporation phenomena are neglected in the model, which might explain, that the maximum temperatures are overestimated in the simulations. In the postprocessing of the experimental results, it is assumed that the emissivity of the material is constant (calibrated at the solidification temperature). However, it is also mentioned that it changes with temperature [46]. This is not taken into account in the measurements and leads to larger uncertainties in the temperature measurements at higher temperatures. The red dashed line indicates the line energy of \(200\frac{\hbox {J}}{\hbox {m}}\) which is used in the numerical analysis in subsection 4.2.
Mechanical validation
For mechanical validation blind-hole-drilling measurements as conducted in [47] are compared to residual von Mises stresses obtained in the simulations. The measurements in [47] are performed in the middle of the top surface of a cube with side lengths of \(15\,\hbox {mm}\) that was scanned with a beam power of  and a velocity of
and a velocity of  . The layer thickness is
. The layer thickness is  and the hatch distance \(h={100}\,{\upmu \hbox {m}}\). With these process parameters, the laser covers a scan path of more than \(280\,\hbox {m}\) during the exposure. To reduce the computational effort the scanning of a smaller cross section of \(1.2\times 1.2\,\hbox {mm}^{2}\) over 10 layers is simulated. This simplification is also applied in the simulations done in [47] and is justifiable since the simulation results show an almost uniform stress distribution in the center cross section of the geometry, see Fig. 5(b). In the simulations the material parameters as given in subsection 2.3 are used without any adaptation. The initial temperature was set to
and the hatch distance \(h={100}\,{\upmu \hbox {m}}\). With these process parameters, the laser covers a scan path of more than \(280\,\hbox {m}\) during the exposure. To reduce the computational effort the scanning of a smaller cross section of \(1.2\times 1.2\,\hbox {mm}^{2}\) over 10 layers is simulated. This simplification is also applied in the simulations done in [47] and is justifiable since the simulation results show an almost uniform stress distribution in the center cross section of the geometry, see Fig. 5(b). In the simulations the material parameters as given in subsection 2.3 are used without any adaptation. The initial temperature was set to  and radiation and convection was considered on the top surface of the powder with
and radiation and convection was considered on the top surface of the powder with  . The bottom plate was mechanically constrained at the bottom surface. To reduce the influence of boundary effects due to the building plate and the free top surface the residual von Mises stresses on top of the fifth layer are averaged in a \(0.2\times 0.2\,\hbox {mm}^{2}\) area around the center of the cross section. The comparison of the simulated stresses with the experimental ones from [47] is given in Fig. 5(a). The numerically determined von Mises stress of \(381\,\hbox {MPa}\) is sufficiently close to the measured value of 421 MPa and within the experimental tolerance range from \({340}\,\hbox {MPa}\) - \(495\,\hbox {MPa}\). For comparison, the simulation results from [47] are also shown in Fig. 5. In that work no stress relaxation at high temperatures is conducted which results in the strong overestimation of the residual stress values.
. The bottom plate was mechanically constrained at the bottom surface. To reduce the influence of boundary effects due to the building plate and the free top surface the residual von Mises stresses on top of the fifth layer are averaged in a \(0.2\times 0.2\,\hbox {mm}^{2}\) area around the center of the cross section. The comparison of the simulated stresses with the experimental ones from [47] is given in Fig. 5(a). The numerically determined von Mises stress of \(381\,\hbox {MPa}\) is sufficiently close to the measured value of 421 MPa and within the experimental tolerance range from \({340}\,\hbox {MPa}\) - \(495\,\hbox {MPa}\). For comparison, the simulation results from [47] are also shown in Fig. 5. In that work no stress relaxation at high temperatures is conducted which results in the strong overestimation of the residual stress values.
Comparison of the simulated residual von Mises stress with the simulated and experimentally determined stresses from [47] (a). Von Mises stress distribution on top of the fifth layer (b). The black rectangle indicates the evaluation area
Numerical analysis of accuracy and efficiency
In the following subsection two numerical examples are used to investigate the influence of numerical and modeling aspects. Based on the findings of the first small wall-like example, a parameter set is determined which finds a good compromise between accuracy and computational effort. This is further illustrated in the open rectangular profile example. For both numerical examples the thermal process parameters are listed in Table 2.
Small wall-like geometry
In the first example the build of a wall consisting of a single line over six layers is simulated to study the displacement and von Mises stress evolution over the building process for various numerical settings and modeling assumptions. The scan path length is \(1.0\,\hbox {mm}\) and the layer height is given in Table 2. The wall is build on top of a \(1.3\,\hbox {mm}\) thick building platform with a total domain of \(1\,\hbox {mm} \times 2\,\hbox {mm}\) in the x-y plane, as depicted in Fig. 6(a). The scanning direction is the same for each layer. The cooling times for each layer before and after layer deposition are \(15\,\hbox {ms}\) and \(1\,\hbox {ms}\), respectively. Then the exposure starts again. The simulation is terminated after a final cooling time of \(100\,\hbox {ms}\).
Schematic illustration of both considered examples, where gray represents the solid building platform, red the applied powder layers and blue the geometry to be manufactured, e.g. the wall (a) and open rectangular profile (b), respectively. For the wall, the evaluation line Y denoted by the dotted orange line runs parallel to the y-axis on top of the second last layer. Point A is on top of the second layer in the middle of the wall. For the rectangular profile, point D is located at the end of the first scanning line on top of the first layer
The plate is mechanically constrained at the bottom and zero thermal fluxes at all boundaries are prescribed. Radiation and convection are neglected in the current example. The time step size is given by the factor \(\tau \), see Eq. (13), relating the process parameters velocity and laser beam radius to the time step size. Its value is held constant until the last of the six layers is scanned and successively increased based on the criterion discussed in subsection 3.2. This represents a rather conservative approach as adaptive time stepping between successive layers might lead to reduced time step numbers. In order to study the influence of the numerical setting, the time step size, the maximum spatial refinement level and the polynomial degree of the elements are varied. Further, the geometrically linear and nonlinear mechanical models and the powder model are altered. All considered cases are summarized in Table 3. The simulation run times and the von Mises stresses and displacements at the evaluation points after final cooling obtained for all numerical settings and modeling assumptions are compared to the most accurate reference setting, which is the computationally most expensive. Tables 7, 8, 9, 10, 11 and 12 in the in Appendix C summarize the results. Therefore, a relative error measure is introduced, that compares the result (stress, displacement) of the particular simulation \(\{\bullet \}\) with that of the accurate reference setting \(\{\bullet ^\star \}\) at a certain point at the end of the cooling phase in the following way

Temperature evolution (a), comparison of the displacements \(u_y\) (b, d) and the von Mises stress \(\sigma ^\text {vM}\) (c, e) for the geometrically nonlinear (black) and the geometrically linear setting (brown). The evaluation is carried out along the line Y as depicted in Fig. 6(a) after the final cooling (b, c) and over time at point A (a, d, e) where the curves start as soon as the melting temperature is firstly exceeded (conversion from powder to melt). The temperature distribution is the same for both settings
In a first step the difference between the geometrically linear and nonlinear mechanical models is investigated. Therefore, the results obtained for the geometrically linear setting are compared to the reference setting, while leaving all other parameters unchanged. As we are interested in the final deformation and residual stresses, we investigate the evolution of the von Mises stress and the displacements over time at point A, as depicted in Fig. 7 and Table 7. The curves of all presented plots start as soon as the temperature at the evaluated point exceeds the melting temperature for the first time, i.e. at the conversion from powder to melt. It is visible that the von Mises stress is reduced to zero when the relaxation temperature is exceeded, based on the procedure presented in section 3.3. In the subsequent exposure phases, the von Mises stress decreases due to the temperature-dependent material parameters. The displacements in y-direction (scanning direction) show that especially the phases in which the relaxation temperature is exceeded have the greatest influence on the final deformation due to stress relaxation. The influences of the exposure of the upper layers and the associated heating respectively thermal expansion are also visible in the displacement curves. The results for the displacements and stresses, depicted in Fig. 7 for the geometrically linear and nonlinear setting, show a maximum deviation of  ,
,  and
and  evaluated at point A. As the maximum total strains for the current example are below \(5\%\), the small strain assumption is valid. This might not hold true for different geometries and powder modeling assumptions as will be shown at the end of the subsection. The computational saving for the geometrically linearized approach is in the order of \(30\%\).
evaluated at point A. As the maximum total strains for the current example are below \(5\%\), the small strain assumption is valid. This might not hold true for different geometries and powder modeling assumptions as will be shown at the end of the subsection. The computational saving for the geometrically linearized approach is in the order of \(30\%\).
Comparison of the temperature (a), displacements \(u_y\) (b, d) and the von Mises stress \(\sigma ^\text {vM}\) (c, e) for different time step sizes. The evaluation is carried out along the line Y as depicted in Figure 6(a) after the final cooling (b, c) and over time (a, d, e) at point A
In the following, the increase of the time step size is investigated as a possible approach to reduce the computational effort. Six different time step sizes are considered here, \(\tau = 0.125,~ 0.25,~ 0.5,~ 1.0,~ 2.0,~ 5.0\). Further increasing the time step size would result in the melting temperature no longer being exceeded due to large errors in the predicted maximum temperature at each material point. In Fig. 8 (a), the temperature evolutions at point A are compared for the different time step sizes. For larger time steps the maximum temperatures are reduced, in particular for \(\tau = 5\). For small time steps \(\tau \le 1.0\) similar temperatures are obtained. The von Mises stresses evaluated along line Y and over time at point A (Fig. 8 (c) and (e)) show that increasing time step sizes lead to increasing deviations, but for \(\tau =0.5\) the final values at point A differ by just  to the smallest time step size. The displacements in y-direction evaluated along Y and at point A over time (Fig. 8 (b) and (d)) are most sensitive to larger time step sizes and show the strongest deviations. They are increasingly underestimated in comparison to the reference result. Time step sizes of \(\tau > 0.5\) (which is equivalent to \(0.1\,\hbox {ms}\)) yield unsatisfactory results with errors of
to the smallest time step size. The displacements in y-direction evaluated along Y and at point A over time (Fig. 8 (b) and (d)) are most sensitive to larger time step sizes and show the strongest deviations. They are increasingly underestimated in comparison to the reference result. Time step sizes of \(\tau > 0.5\) (which is equivalent to \(0.1\,\hbox {ms}\)) yield unsatisfactory results with errors of  evaluated at point A after cooling. The differences occur during the processing of the current and the following layer. Afterwards, the evolutions of the displacements are similar for all time step sizes, but shifted by the amount of the previous deviation. Evaluations of stresses and displacements at other points of the wall show the same behavior. When looking at the von Mises stress distribution in the y-z-plane depicted in Fig. 9, the stresses are not correctly captured anymore for values of \(\tau \ge 2.0 \). These deviations can be explained by the discrepancy between the temperature evolutions for these large time step sizes. The maximum temperatures are increasingly underestimated reducing the time span during which material points are above the relaxation temperature. The deviations of the displacements and stresses for small variations in the temperature evolutions (for \(\tau \le 1.0\)) are due to the changing mechanical boundary conditions during solidification. These differences result from the transition from melt to solid at slightly different points in times for different time discretizations (even if the temperatures are equal). With a smaller time step size this phase change is more accurately captured. This has a large influence on the residual stresses and also on the displacements in scanning direction. Due to the significant differences stresses and displacements, a time step size of \(\tau \le 0.5\) is recommended. With \(\tau = 0.5\) a reduction in computing time by \(65.9\%\) can be achieved compared to the smallest time step size, with marginal deviations in the temperatures and von Mises stress. For all further simulations a step size of \(\tau = 0.5\) is used.
evaluated at point A after cooling. The differences occur during the processing of the current and the following layer. Afterwards, the evolutions of the displacements are similar for all time step sizes, but shifted by the amount of the previous deviation. Evaluations of stresses and displacements at other points of the wall show the same behavior. When looking at the von Mises stress distribution in the y-z-plane depicted in Fig. 9, the stresses are not correctly captured anymore for values of \(\tau \ge 2.0 \). These deviations can be explained by the discrepancy between the temperature evolutions for these large time step sizes. The maximum temperatures are increasingly underestimated reducing the time span during which material points are above the relaxation temperature. The deviations of the displacements and stresses for small variations in the temperature evolutions (for \(\tau \le 1.0\)) are due to the changing mechanical boundary conditions during solidification. These differences result from the transition from melt to solid at slightly different points in times for different time discretizations (even if the temperatures are equal). With a smaller time step size this phase change is more accurately captured. This has a large influence on the residual stresses and also on the displacements in scanning direction. Due to the significant differences stresses and displacements, a time step size of \(\tau \le 0.5\) is recommended. With \(\tau = 0.5\) a reduction in computing time by \(65.9\%\) can be achieved compared to the smallest time step size, with marginal deviations in the temperatures and von Mises stress. For all further simulations a step size of \(\tau = 0.5\) is used.
In the next part, the spatial discretization is investigated. Hereby the effect of the refinement level  and the usage of elements with polynomial shape functions of degree \(p = 1\) or \(p = 2\) for the mechanical problem are investigated. The refinement level is directly coupled to the smallest element edge length of \(12.5\,{\upmu \hbox {m}}\), \({25.0}\,{\upmu \hbox {m}}\) and \({50.0}\,{\upmu \hbox {m}}\) for values of
and the usage of elements with polynomial shape functions of degree \(p = 1\) or \(p = 2\) for the mechanical problem are investigated. The refinement level is directly coupled to the smallest element edge length of \(12.5\,{\upmu \hbox {m}}\), \({25.0}\,{\upmu \hbox {m}}\) and \({50.0}\,{\upmu \hbox {m}}\) for values of  ,
,  and
and  , respectively.
, respectively.
Comparison of the temperature (a), displacements \(u_y\) (b, d) and the von Mises stress \(\sigma ^\text {vM}\) (c, e) for different refinement levels and polynomial degrees of the mechanical finite elements. The evaluation is carried out along the line Y as depicted in Fig. 6(a) after the final cooling (b, c) and over time at point A (a, d, e)
The temperatures at point A (Fig. 10 (a)) for all refinement levels are captured well, expect for minor deviations in the maximum temperatures during the initial melting cycle. The y-displacements and the von Mises stresses, evaluated at point A over time and along the line Y after the scanning process, are shown in Fig. 10 and Table 10. The results for meshes with linear elements, refinement level  , and with quadratic elements, refinement level
, and with quadratic elements, refinement level  , are in close agreement with the reference setting. Deviations of about
, are in close agreement with the reference setting. Deviations of about  to the reference case are obtained for linear elements with
to the reference case are obtained for linear elements with  for the displacements in y at point A after cooling. The largest deviations of
for the displacements in y at point A after cooling. The largest deviations of  and
and  are obtained for the displacements in y-direction for linear and quadratic elements with the coarsest mesh,
are obtained for the displacements in y-direction for linear and quadratic elements with the coarsest mesh,  . The von Mises stress values at point A after cooling for all considered spatial refinement levels and polynomial degrees of the mechanical elements show just minor deviations of
. The von Mises stress values at point A after cooling for all considered spatial refinement levels and polynomial degrees of the mechanical elements show just minor deviations of  to the reference setting. All investigated meshes are sufficient to capture the general distribution of stresses, as depicted in Fig. 11 for the y-z plane. With increasing element size more details of the stress distribution get suppressed, e.g. inter-layer details are lost for
to the reference setting. All investigated meshes are sufficient to capture the general distribution of stresses, as depicted in Fig. 11 for the y-z plane. With increasing element size more details of the stress distribution get suppressed, e.g. inter-layer details are lost for  , leading to blurred results as opposed to the reference. While the stress distribution for refinement level
, leading to blurred results as opposed to the reference. While the stress distribution for refinement level  and quadratic elements is similar as the reference solution, linear elements with the same spatial refinement seem to slightly underestimate the maximum von Mises stress at the building platform. For
and quadratic elements is similar as the reference solution, linear elements with the same spatial refinement seem to slightly underestimate the maximum von Mises stress at the building platform. For  the melted geometry differs from its more refined counterpart leading to differences in the stress distribution, especially in the vicinity of the powder-solid interface. A good compromise between accuracy and effort is obtained for a mesh with linear elements \(p=1\) and refinement levels of
the melted geometry differs from its more refined counterpart leading to differences in the stress distribution, especially in the vicinity of the powder-solid interface. A good compromise between accuracy and effort is obtained for a mesh with linear elements \(p=1\) and refinement levels of  and
and  . For
. For  , the displacement in scanning direction \(u_y\) and von Mises stress at point A differ from the reference solution by only
, the displacement in scanning direction \(u_y\) and von Mises stress at point A differ from the reference solution by only  and
and  , respectively. The computational effort is reduced by \( 95.1\%\) due to the use of linear elements (\(p=1\) and
, respectively. The computational effort is reduced by \( 95.1\%\) due to the use of linear elements (\(p=1\) and  ) as opposed to quadratic elements (\(p=2\) and
) as opposed to quadratic elements (\(p=2\) and  ). A further reduction in run time of \(59.8\%\) is reached for
). A further reduction in run time of \(59.8\%\) is reached for  , where the von Mises stress evolution shows similar deviations as the more refined case and the displacement error in y increases to
, where the von Mises stress evolution shows similar deviations as the more refined case and the displacement error in y increases to  compared to the reference setting at point A. For the numerical settings studied, the influence of the temporal discretization outweighs that of the spatial one. While larger time steps result in strong deviations, the results for all spatial discretizations generally correspond to the reference solution. The reduction of computational effort is remarkable for elements with linear shape functions as opposed to quadratic ones. As long as adaptive coarsening is conducted, h-refinement is computationally cheaper than an overall higher polynomial degree for the mechanical elements.
compared to the reference setting at point A. For the numerical settings studied, the influence of the temporal discretization outweighs that of the spatial one. While larger time steps result in strong deviations, the results for all spatial discretizations generally correspond to the reference solution. The reduction of computational effort is remarkable for elements with linear shape functions as opposed to quadratic ones. As long as adaptive coarsening is conducted, h-refinement is computationally cheaper than an overall higher polynomial degree for the mechanical elements.
 , \(p=1\) and
, \(p=1\) and 
Mechanical computation domain for studying the powder model (a). The evaluation points B and C are on top of the third powder layer on the front and right edges of the melted cross section. The displacements in scan direction at Point B (b) and transverse to the scan direction at point C (d) and the von Mises stress over time (c, e) for different mechanical computational domains are shown
To analyze the effects of the adaptive discretizations in time and space introduced in subsection 3.2, a reference simulation with a fixed time step size and a static spatial discretization using the geometrically non-linear setting was performed. The element edge length of the linear hexahedral elements is chosen to be equal to the smallest element edge length for the refinement level of  . A finer spatial discretization corresponding to the element edge length of
. A finer spatial discretization corresponding to the element edge length of  in the whole computational domain would lead to a total number of elements of above 1.6 million. A static time step size of
in the whole computational domain would lead to a total number of elements of above 1.6 million. A static time step size of  is used to match \(\tau =0.5\). The results for simulations with and without spatial and temporal adaptivity are compared to the reference setting as summarized in Table 4. For all settings the maximum errors in displacement in y and von Mises stress at point A are smaller than \(\pm 5.0\%\). Introducing an adaptive discretization in time results in a smaller increase in the error than the adaptive spatial discretization. One reason is that the time step size is only adaptively increased during cooling, but is similar during the scanning phase in all cases. Furthermore, spatial adaptivity requires the repeated projection of solution variables if the mesh is adapted, which leads to some inaccuracies. For the investigated simple geometry spatial adaptivity leads to greater time savings but for a different geometry or different process parameters with longer waiting times, the adaptive discretization in time might also reduce the computation time more strongly. To summarize, with the adaptive discretizations huge computational savings can be achieved, while minor deviations in the results of \(<\pm 5.0\%\) are observed.
is used to match \(\tau =0.5\). The results for simulations with and without spatial and temporal adaptivity are compared to the reference setting as summarized in Table 4. For all settings the maximum errors in displacement in y and von Mises stress at point A are smaller than \(\pm 5.0\%\). Introducing an adaptive discretization in time results in a smaller increase in the error than the adaptive spatial discretization. One reason is that the time step size is only adaptively increased during cooling, but is similar during the scanning phase in all cases. Furthermore, spatial adaptivity requires the repeated projection of solution variables if the mesh is adapted, which leads to some inaccuracies. For the investigated simple geometry spatial adaptivity leads to greater time savings but for a different geometry or different process parameters with longer waiting times, the adaptive discretization in time might also reduce the computation time more strongly. To summarize, with the adaptive discretizations huge computational savings can be achieved, while minor deviations in the results of \(<\pm 5.0\%\) are observed.
In the last study the influence of the powder model is evaluated. The powder is modeled as linear elastic with a small Young’s modulus. This is a very simplified assumption, especially during the cooling of the manufactured component. Therefore, the modeling of the surrounding powder is changed in two different ways: (i) the surrounding powder is partly omitted in the mechanical simulation or (ii) the elastic stiffness of the powder is decreased. The sensitivity of the results with respect to the powder model is analyzed and discussed. In the thermal simulation, the surrounding powder is completely taken into account, since the thermal conduction into the powder is not negligible [17], although it has a smaller conduction coefficient than the solid material. Partly excluding the surrounding powder in the mechanical simulation significantly reduces the number of elements and consequently the computing time. For both, the thermal and mechanical domain the size of the building platform remains unchanged, only the region of powder elements having mechanical degrees of freedom is varied. Simulations are conducted with a mechanical powder domain of \(x_\text {m} = 0.375\,\hbox {mm}\), \(y_\text {m} = 1.30\,\hbox {mm}\) and \(x_\text {m} = 0.25\,\hbox {mm}\), \(y_\text {m} = 1.20\,\hbox {mm}\) and compared to the reference setting (\(x_\text {m} = 1.0\,\hbox {mm}\), \(y_\text {m} = 2.0\,\hbox {mm}\)), see Fig. 12(a). The Young’s modulus of the powder is obtained by a scaling factor of  to the Young’s modulus of solid material at room temperature and increases to the value of solid/melt material at melting temperature. Additional evaluation points B and C are introduced which are located on the front and right edges of the wall to be built and on top of the third powder layer, in order to study effects at the boundary between solid and powder elements. In Fig. 12, the displacements in x and y and the von Mises stress at the points B and C are depicted over time for the three different mechanical simulation domains. The relative error after cooling and the run times are summarized in Table 11.
to the Young’s modulus of solid material at room temperature and increases to the value of solid/melt material at melting temperature. Additional evaluation points B and C are introduced which are located on the front and right edges of the wall to be built and on top of the third powder layer, in order to study effects at the boundary between solid and powder elements. In Fig. 12, the displacements in x and y and the von Mises stress at the points B and C are depicted over time for the three different mechanical simulation domains. The relative error after cooling and the run times are summarized in Table 11.
For both settings with reduced surrounding powder, the displacements at the points B and C increase slightly compared to the reference setting. Due to the lack of powder, during the heat expansion phase, the movement of the powder is less restricted and it can expand further. The subsequent contraction due to cooling is also stronger due to less powder preventing the contraction of the melt or solid. During the heat expansion phase, both reduced powder settings reach the same maximum displacement values.
The decrease of the von Mises stress values at the points B and C for a smaller powder region can be attributed, analogously to the displacements, to the absence of powder obstructing the thermal contraction of the wall during cooling. The final von Mises stress values for both settings with less surrounding powder are about  and
and  smaller than those of the reference setting at point B.
smaller than those of the reference setting at point B.
Similar results can be observed for simulations with the full powder domain but with a smaller scaling factor  for the Young’s modulus of powder, see Fig. 13 and Table 12. The results for
for the Young’s modulus of powder, see Fig. 13 and Table 12. The results for  and
and  are compared to those of the reference setting with
are compared to those of the reference setting with  . For all evaluation points the final von Mises stresses decrease significantly compared to the reference setting. Especially the points B and C, that are near the boundary of solid/melt and powder elements, show large differences up to
. For all evaluation points the final von Mises stresses decrease significantly compared to the reference setting. Especially the points B and C, that are near the boundary of solid/melt and powder elements, show large differences up to  , for
, for  . The thermal contraction of the cooling solid material is not so strongly hindered by powder with a lower Young’s moduli, leading to larger displacements in y, as can be seen in Fig. 13(c). This effect can also be observed for the points A and C but less prominent in Fig. 13(a) and (e). Since the maximum total strains increase with a decreasing scaling factor, for example to
. The thermal contraction of the cooling solid material is not so strongly hindered by powder with a lower Young’s moduli, leading to larger displacements in y, as can be seen in Fig. 13(c). This effect can also be observed for the points A and C but less prominent in Fig. 13(a) and (e). Since the maximum total strains increase with a decreasing scaling factor, for example to  for
for  , the validity of the geometrically linear mechanical model is reevaluated. Figure 14 and Table 8 compare the displacement in y and the von Mises stress over time at point B for
, the validity of the geometrically linear mechanical model is reevaluated. Figure 14 and Table 8 compare the displacement in y and the von Mises stress over time at point B for  . The displacement values at points A, B and C show small deviations of \(\le 2.0\%\) between the geometrically linear and nonlinear setting. For the von Mises stresses at point B larger deviations of up to
. The displacement values at points A, B and C show small deviations of \(\le 2.0\%\) between the geometrically linear and nonlinear setting. For the von Mises stresses at point B larger deviations of up to  are visible.
are visible.
It can be summarized that the modeling assumptions for the powder have a large influence on the mechanical results. Further a correlation of the validity of the geometrically linear assumption and the modeling assumption of the powder can be observed. For a scaling factor of  and for reduced surrounding powder domains total strain values \(\ge 5\%\) were obtained. Further studies and experimental validation have to be carried out to model the powder behavior more accurately.
and for reduced surrounding powder domains total strain values \(\ge 5\%\) were obtained. Further studies and experimental validation have to be carried out to model the powder behavior more accurately.
Open rectangular profile
The insights gained from the previous small scale example are now transferred to a larger geometry as presented in Fig. 6(b). This open rectangular profile consists of 20 scan lines over 21 layers. A cross-snake hatching pattern with a hatching space of \(h = 100\,\upmu \hbox {m}\) is chosen. In contrast to the previous example, radiation and convection are no longer neglected on the top surface. The temperature at the bottom of the building platform is fixed to \(\vartheta ^\text {D}=200^{\circ }\).
The manufacturing process is simulated using two different simulation settings as presented in Table 5. For reference the geometrically nonlinear setting is used with tri-quadratic shape functions for the mechanical simulation. The maximum refinement level is set to  resulting in a smallest element edge length of \(15\,\upmu \hbox {m}\). For the efficient setting linear elements with a maximum refinement level
resulting in a smallest element edge length of \(15\,\upmu \hbox {m}\). For the efficient setting linear elements with a maximum refinement level  (minimum element edge length of \(30\,\upmu \hbox {m}\)) are chosen. The time step size \(\tau =0.5\) is applied for both settings, as it was shown in the previous example that larger values have a strong negative influence on the accuracy of the results. The powder scaling factor is set to
(minimum element edge length of \(30\,\upmu \hbox {m}\)) are chosen. The time step size \(\tau =0.5\) is applied for both settings, as it was shown in the previous example that larger values have a strong negative influence on the accuracy of the results. The powder scaling factor is set to  for both settings.
for both settings.
The resulting temperature, von Mises stress and displacements in x and y are depicted in Fig. 15 for point D, see Fig. 6(b) for its position.
The temperatures except for the maximum temperatures in the first three melting cycles are captured very well with the efficient setting when compared to the reference setting, which is in agreement with the findings of the small scale example. A similar trend can be observed for the displacements in and perpendicular to scanning direction, \(u_x\) and \(u_y\) with deviations in the final displacements of  and
and  , respectively. The displacements in the scanning direction are more sensitive than those perpendicular to it, as it was also observed for the previous example. While the von Mises stresses during the exposure of the first few layers are overestimated for the efficient setting, the final von Mises stress is slightly smaller
, respectively. The displacements in the scanning direction are more sensitive than those perpendicular to it, as it was also observed for the previous example. While the von Mises stresses during the exposure of the first few layers are overestimated for the efficient setting, the final von Mises stress is slightly smaller  . The results at other points are similar. To summarize, the overall agreement of the final results of the efficient setting and the reference setting is fairly good, while the run time for the efficient setting was just \(\approx 2\%\) of that of the reference case.
. The results at other points are similar. To summarize, the overall agreement of the final results of the efficient setting and the reference setting is fairly good, while the run time for the efficient setting was just \(\approx 2\%\) of that of the reference case.
Conclusion
In this contribution a highly parallelized and adaptive finite element framework based on the open source C++ library deal.II was validated and utilized to simulate PBF processes. The effects of the numerical discretization and various modeling assumptions on the accuracy of the temperatures, displacements and stresses and on the computational effort are analyzed and discussed. The framework supports geometrically linear and nonlinear formulations. The latter makes use of the logarithmic strain space model introduced by Miehe [38]. In summary, the numerical study yielded the following results:
-
For the studied examples the geometrically linear setting was sufficient (differences of all compared quantities were less than \(4\%\) compared to the nonlinear setting).
-
The time step size was shown to be a sensitive parameter, especially for the displacements in scanning direction. A time step size of
 was used for the thermal and mechanical problem. Doubling the time step size led to errors in the displacements of up to \(\approx 45\%\).
was used for the thermal and mechanical problem. Doubling the time step size led to errors in the displacements of up to \(\approx 45\%\). -
A finite element mesh with six linear hexahedral elements over the melt pool width gave the most efficient and sufficiently accurate solution (reduction of computation time by \(\approx {97}\%\), error in von Mises stresses of \(\approx {-0.7}\%\)).
-
A strong influence of the powder parameters of the elastic powder model on the resulting displacements and stresses was observed. A lower Young’s modulus for the powder and the omission of the powder led to significantly lower stresses (up to \(\approx {70}\%\) lower).
Further steps include the extension of the presented parallelized and adaptive finite element framework by validated agglomeration approaches to bridge the gap to whole component simulations. This includes layer lumping techniques as well as powder substitute models. A hierarchical simulation environment for the PBF process is sought to gain a deeper process understanding.
Data Availability
The datasets used and/or analysed during the current study are available from the corresponding author on reasonable request.
Change history
20 November 2022
Missing Open Access funding information has been added in the Funding Note
References
Bartlett JL, Li X. An overview of residual stresses in metal powder bed fusion. Additive Manufac. 2019;27:131–49.
Seifi M, Salem A, Beuth J, Harrysson O, Lewandowski J. Overview of materials qualification needs for metal additive manufacturing. Jom. 2016;68(3):747–64.
Mercelis P, Kruth JP. Residual stresses in selective laser sintering and selective laser melting. Rapid Prototyping J. 2006;12(5):254–65.
Gouge M, Denlinger ER, Irwin J, Li C, Michaleris P. Experimental validation of thermo-mechanical part-scale modeling for laser powder bed fusion processes. Addit Manufact. 2019;29: 100771.
Parry LA, Ashcroft IA, Wildman RD. Understanding the effect of laser scan strategy on residual stress in selective laser melting through thermo-mechanical simulation. Addit Manufact. 2016;12:1–15.
Li C, Liu JF, Fang XY, Guo YB. Efficient predictive model of part distortion and residual stress in selective laser melting. Addit Manufact. 2017;17:157–68.
Tan P, Shen F, Li B, Zhou K. A thermo-metallurgical-mechanical model for selective laser melting of Ti6Al4V. Mater Design. 2019;168: 107642.
Xufei L, Lin X, Chiumenti M, Cervera M, Li JJ, Ma L, Wei L, Yunlong H, Huang W. Finite element analysis and experimental validation of the thermomechanical behavior in laser solid forming of Ti-6Al-4V. Addit Manufact. 2018;21:30–40.
Ganeriwala RK, Strantza M, King WE, Clausen B, Phan TQ, Levine LE, Brown DW, Hodge NE. Evaluation of a thermomechanical model for prediction of residual stress during laser powder bed fusion of Ti-6Al-4V. Addit Manufact. 2019;27:489–502.
Neil EH, Ferencz RM, Solberg JM. Implementation of a thermomechanical model for the simulation of selective laser melting. Comput Mech. 2014;54(1):33–51.
Riedlbauer D, Steinmann P, Mergheim J. Thermomechanical finite element simulations of selective electron beam melting processes: Performance considerations. Comput Mech. 2014;54(1):109–22.
Carraturo M, Jomo J, Kollmannsberger S, Reali A, Auricchio F, Rank E. Modeling and experimental validation of an immersed thermo-mechanical part-scale analysis for laser powder bed fusion processes. Addit Manufact. 2020;36: 101498.
Marques BM, Andrade CM, Neto DM, Oliveira MC, Alves JL, Menezes LF. Numerical analysis of residual stresses in parts produced by selective laser melting process. Procedia Manufact. 2020;47:1170–7.
Baiges J, Chiumenti M, Moreira CA, Cervera M, Codina R. An adaptive Finite Element strategy for the numerical simulation of additive manufacturing processes. Addit Manufact. 2020;37:1–22.
Denlinger ER, Gouge M, Irwin J, Michaleris P. Thermomechanical model development and in situ experimental validation of the Laser Powder-Bed Fusion process. Addit Manufact. 2017;16:73–80.
Denlinger ER, Vijay Jagdale GV, Srinivasan TE-W, Michaleris P. Thermal modeling of Inconel 718 processed with powder bed fusion and experimental validation using in situ measurements. Addit Manufact. 2016;11:7–15.
Li C, Gouge MF, Denlinger ER, Irwin JE, Michaleris P. Estimation of part-to-powder heat losses as surface convection in laser powder bed fusion. Addit Manufact. 2019;26:258–69.
Chiumenti M, Neiva E, Salsi E, Cervera M, Badia S, Moya J, Chen Z, Lee C, Davies C. Numerical modelling and experimental validation in Selective Laser Melting. Addit Manufact. 2017;18:171–85.
Strantza M, Ganeriwala RK, Clausen B, Phan TQ, Levine LE, Pagan D, King WE, Hodge NE, Brown DW. Coupled experimental and computational study of residual stresses in additively manufactured Ti-6Al-4V components. Mater Lett. 2018;231:221–4.
Parry LA, Ashcroft IA, Wildman RD. Geometrical effects on residual stress in selective laser melting. Addit Manufact. 2019;25:166–75.
Hodge NE. Towards improved speed and accuracy of laser powder bed fusion simulations via representation of multiple time scales. Addit Manufact. 2020;37: 101600.
Nils K, Fabian N, Hongxiao X, Vasily P. Thermo-mechanical Simulation of Additive Layer Manufacturing of Titanium Aerospace structures. LightMAT Conf. 2013;3:5.
Denlinger ER, Irwin J, Michaleris P. Thermomechanical Modeling of Additive Manufacturing Large Parts. J Manufact Sci Eng. 2014;136(6):9.
Denlinger ER, Heigel JC, Michaleris P. Residual stress and distortion modeling of electron beam direct manufacturing Ti-6Al-4V. Proc Instit Mech Eng B. 2015;229(10):1803–13.
Mirkoohi E, Sievers DE, Garmestani H, Liang SY. Thermo-mechanical modeling of thermal stress in metal additive manufacturing considering elastoplastic hardening. CIRP J Manuf Sci Technol. 2020;28:52–67.
Denlinger ER, Michaleris P. Effect of stress relaxation on distortion in additive manufacturing process modeling. Addit Manufact. 2016;12:51–9.
Lindgren LE. Finite element modeling and simulation of welding part 1: increased complexity. J Therm Stresses. 2001;24(2):141–92.
Carraturo M, Kollmannsberger S, Reali A, Auricchio F, Rank E. An immersed boundary approach for residual stress evaluation in selective laser melting processes. Addit Manufact. 2021;46: 102077.
Kollmannsberger S, Kopp P. On accurate time integration for temperature evolutions in additive manufacturing. GAMM Mitteilungen. 2021;44(4):1–14.
Ganeriwala RK, Hodge NE, Solberg JM. Towards improved speed and accuracy of laser powder bed fusion simulations via multiscale spatial representations. Addit Manufact. 2020;187: 110112.
Khan K, De A. Modelling of selective laser melting process with adaptive remeshing. Sci Technol Welding Joining. 2019;1718:391–400.
Soldner D, Mergheim J. Thermal modelling of selective beam melting processes using heterogeneous time step sizes. Computers Math Appl. 2019;78(7):2183–96.
Arndt D, Bangerth W, Blais B, Clevenger TC, Fehling M, Grayver AV, Heister T, Heltai L, Kronbichler M, Maier M, Munch P, Pelteret J-P, Rastak R, Thomas I, Turcksin B, Wang Z, Wells D. The deal.II library, version 9.2. J Numer Math. 2020;28(3):131–46.
Arndt D, Bangerth W, Davydov D, Heister T, Heltai L, Kronbichler M, Maier M, Pelteret J-P, Turcksin B, Wells D. The deal.II finite element library: design, features, and insights. Comput Math Appl. 2021;81:407–22.
Goldak J, Chakravarti A, Bibby M. A new finite element model for welding heat sources. Metallurgical Trans B. 1984;15(2):299–305.
Perzyna P. Thermodynamic theory of viscoplasticity. Adv Appl Mech. 1971;11:313–54.
Miehe C, Apel N, Lambrecht M. Anisotropic additive plasticity in the logarithmic strain space: modular kinematic formulation and implementation based on incremental minimization principles for standard materials. Computer Methods Appl Mech Eng. 2002;191(47–48):5383–425.
Miehe C, Lambrecht M. Algorithms for computation of stresses and elasticity moduli in terms of Seth-Hill’s family of generalized strain tensors. Commun Numer Methods Eng. 2001;17(5):337–53.
Riedlbauer D, Scharowsky T, Singer R, Steinmann P, Körner C, Mergheim J. Macroscopic simulation and experimental measurement of melt pool characteristics in selective electron beam melting of Ti-6Al-4V. Int J Advan Manufact Technol. 2017;88:1309–17.
Roberts IA. Investigation of residual stresses in the laser melting of metal powders in additive layer manufacturing. Wolverhampton: University of Wolverhampton; 2012.
Ellsiepen P, Hartmann S. Remarks on the Interpretation of Current Non-linear Finite-Element-Analyses as Differential-Algebraic Equations. Int J Numer Methods Eng. 2001;51:679–707.
Kelly DW, Gago JPSR, Zienkiewicz OC, Babuska I. A posteriori error analysis and adaptive processes in the finite element method: Part i-error analysis. Int J Numer Methods Eng. 1983;19(11):1593–619.
Zienkiewicz OC, Zhu JZ. The superconvergent patch recovery and a posteriori error estimates. Part 2: Error estimates and adaptivity. Int J Numer Methods Eng. 1992;33(7):1365–82.
Zienkiewicz OC, Zhu JZ. The superconvergent patch recovery and a posteriori error estimates. Part 1: The recovery technique. Int J Numer Methods Eng. 1992;33(7):1365–82.
Soylemez E. Modelling the Melt Pool of the Laser Sintered Ti6Al4V Layers with Goldak’s Double-Ellipsoidal Heat Source. In: 29th Annual International Solid Freeform Fabrication Symposium, pages 2018. p. 1721–36.
Yadroitsev I, Krakhmalev P, Yadroitsava I. Selective laser melting of Ti6Al4V alloy for biomedical applications: Temperature monitoring and microstructural evolution. J Alloys Compounds. 2014;583:404–9.
Xiao Z, Chen C, Zhu H, Zhiheng H, Nagarajan B, Guo L, Zeng X. Study of residual stress in selective laser melting of Ti6Al4V. Mater Design. 2020;193: 108846.
Mirkoohi E, Seivers DE, Garmestani H, Liang SY. Heat source modeling in selective laser melting. Materials. 2019;12(13):1–18.
King WE, Barth HD, Castillo VM, Gallegos GF, Gibbs JW, Hahn DE, Kamath C, Rubenchik AM. Observation of keyhole-mode laser melting in laser powder-bed fusion additive manufacturing. J Mater Process Technol. 2014;214(12):2915–25.
Khairallah SA, Anderson AT, Rubenchik A, King WE. Laser powder-bed fusion additive manufacturing: Physics of complex melt flow and formation mechanisms of pores, spatter, and denudation zones. Acta Materialia. 2016;108:36–45.
Makoana NW, Yadroitsava I, Möller H, Yadroitsev I. Characterization of 17–4ph single tracks produced at different parametric conditions towards increased productivity of lpbf systems-the effect of laser power and spot size upscaling. Metals. 2018;8:7.
Kollmannsberger S, Carraturo M, Reali A, Auricchio F. Accurate Prediction of Melt Pool Shapes in Laser Powder Bed Fusion by the Non-Linear Temperature Equation Including Phase Changes. Integrat Mater Manufact Innov. 2019;8(2):167–77.
Ye J, Khairallah SA, Rubenchik AM, Crumb MF, Guss G, Belak J, Matthews MJ. Energy Coupling Mechanisms and Scaling Behavior Associated with Laser Powder Bed Fusion Additive Manufacturing. Advan Eng Mater. 2019;21:7.
Irwin J, Michaleris P. A Line Heat Input Model for Additive Manufacturing. J Manuf Sci Eng Trans ASME. 2016;138(11):1–9.
Burkhardt C, Soldner D, Steinmann P, Mergheim J. An energetically consistent heat input model for additive manufacturing. PAMM. 2019;19(1):1–2.
Acknowledgements
The authors gratefully acknowledge the financial support by the German Science Foundation (DFG) within the Collaborative Research Center 814: Additive Manufacturing (subproject C3).
Funding
Open Access funding enabled and organized by Projekt DEAL. Funded by the Deutsche Forschungsgemeinschaft (DFG,German Research Foundation) - Project-ID 61375930 - SFB 814 - Additive Manufacturing TP C03.
Author information
Authors and Affiliations
Contributions
CB developed the concept, contributed the methodology, wrote the software and the original draft of the manuscript. JM and PS contributed to the writing, reviewed the manuscript, provided resources, project administration, funding acquisition and supervision. JM contributed to the methodology. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
A. Geometrically nonlinear setting
In the geometrically nonlinear setting, the deformation gradient is computed from the displacement field  as
as  . The right Cauchy–Green strain
. The right Cauchy–Green strain  is used to compute the logarithmic Hencky strain
is used to compute the logarithmic Hencky strain

where  and
and  denote the eigenvalues and the eigenvectors of the right Cauchy-Green strain, respectively. The logarithmic nature inherent to the Hencky strain allows to use the same additive constitutive laws for the geometrically nonlinear setting as for the geometrically linear one. Therefore Eq. (6) can be rewritten in terms of the Hencky strain as
denote the eigenvalues and the eigenvectors of the right Cauchy-Green strain, respectively. The logarithmic nature inherent to the Hencky strain allows to use the same additive constitutive laws for the geometrically nonlinear setting as for the geometrically linear one. Therefore Eq. (6) can be rewritten in terms of the Hencky strain as

The free energy density  as presented in Eq. (7) is redefined in terms of the Hencky strain
as presented in Eq. (7) is redefined in terms of the Hencky strain

The stress measure work conjugate to the Hencky strain is obtained as follows

The yield function (9) is re-expressed in terms of the logarithmic stress measure  and the evolution equations for the viscoplastic Hencky strain and the internal variable are similar and are integrated in the same manner as for the geometrically linear setting (10). Subsequently, the stress measure
and the evolution equations for the viscoplastic Hencky strain and the internal variable are similar and are integrated in the same manner as for the geometrically linear setting (10). Subsequently, the stress measure  has to be transferred back from the logarithmic space to the ’real world’ by multiplication with a fourth-order projection tensor. The resulting Piola–Kirchhoff stress
has to be transferred back from the logarithmic space to the ’real world’ by multiplication with a fourth-order projection tensor. The resulting Piola–Kirchhoff stress  is pushed forward to obtain the Cauchy stress
is pushed forward to obtain the Cauchy stress 

A similar transformation has to be applied to the tangent operator, for details see Miehe [38].
B. Discretization in time and space
In the following the discretization in time and space of the weak form is described in more detail. The weak form of the nonlinear heat equation given in (11) is discretized in time using finite differences. For each time step Eq. (11) is solved using a two-stage (\(s=2\)) S-DIRK scheme as presented in [41]. For each stage k the time derivative of the specific enthalpy is therefore approximated in the following way

The specific enthalpy at Runge–Kutta stage k is denoted by  and the starting value at stage k is given by
and the starting value at stage k is given by

For \(s=2\) and taking Eq. (27) into account these starting values are derived as

where  denotes the specific enthalpy value obtained in the previous time step and the coefficients \(a_{11}\) and \(a_{21}\) are taken from the Butcher tableau depicted in table 6. In summary, one obtains the following temporally discretized form of Eq. (11)
denotes the specific enthalpy value obtained in the previous time step and the coefficients \(a_{11}\) and \(a_{21}\) are taken from the Butcher tableau depicted in table 6. In summary, one obtains the following temporally discretized form of Eq. (11)

which is solved for the unknown temperature \(\vartheta _{n+1,k}\), and from this the enthalpy  is derived. For the here applied stiffly accurate approach with \(a_{2i}=b_i\) and \(a_{ij}=0\) for \(i<j\) the solution at time \(t_{n+1}\) coincides with the solution of the last stage. Besides the second order accurate solution of the presented 2-stage S-DIRK method, a first order accurate solution is obtained via the embedded stage with new coefficients \(\hat{b}_i\), see Table 6, and the same weighting factors \(a_{ij}\) and \(c_i\). From the difference of the two solutions an error measure
is derived. For the here applied stiffly accurate approach with \(a_{2i}=b_i\) and \(a_{ij}=0\) for \(i<j\) the solution at time \(t_{n+1}\) coincides with the solution of the last stage. Besides the second order accurate solution of the presented 2-stage S-DIRK method, a first order accurate solution is obtained via the embedded stage with new coefficients \(\hat{b}_i\), see Table 6, and the same weighting factors \(a_{ij}\) and \(c_i\). From the difference of the two solutions an error measure  is obtained at each point in space and time
is obtained at each point in space and time

which is used to adjust the time step size during no exposure.
The continuous moving heat input, as presented in Eq. (2), is analytically integrated within each time step [54] to obtain the incrementally averaged value

The local coordinates of the heat source term presented in Eq. (32) are substituted by \(\xi _1 = x_1\),  and \(\xi _3 = x_3\) for a beam traveling with the velocity
and \(\xi _3 = x_3\) for a beam traveling with the velocity  along the y-axis, respectively. The heat source term for the time step starting at \(t=t_0\) with a time step size
along the y-axis, respectively. The heat source term for the time step starting at \(t=t_0\) with a time step size  is obtained by
is obtained by

with the error function \({{\,\textrm{erf}\,}}\left( \bullet \right) \). This integration ensures that the entire region that is passed along the scan path within the current time step is assigned with the corresponding heat source without bypassing any points. The analytically integrated heat input is scaled [55] such that its amount is independent of the spatial discretization.
 , \(\tau =0.5\),
, \(\tau =0.5\),  and \(p=2\)
and \(p=2\) , \(\tau =0.5\),
, \(\tau =0.5\),  and \(p=2\)
and \(p=2\) ,
,  and \(p=2\)
and \(p=2\) and \(\tau =0.5\)
and \(\tau =0.5\)Equations (30) and (12) are now discretized in space by means of the finite element method. The temperature and displacement fields and their test functions are approximated elementwise by scalar-valued  or vector-valued ansatz functions
or vector-valued ansatz functions 

with  and
and  denoting the number of thermal and mechanical degrees of freedom per element, respectively. Following the Bubnov–Galerkin method, the same ansatz functions are used for the approximation of the test functions. The fully discretized capacity, external, conduction, and source parts of Eq. (11) can now be written as
denoting the number of thermal and mechanical degrees of freedom per element, respectively. Following the Bubnov–Galerkin method, the same ansatz functions are used for the approximation of the test functions. The fully discretized capacity, external, conduction, and source parts of Eq. (11) can now be written as

The local contributions of the \({n_{el}}\) elements are assembled into a global system of equations with the assembly operator  that assigns each contribution of the local degree of freedom i to the global degree of freedom I. Analogously the discrete internal and external force terms of the mechanical problem (12) are obtained
that assigns each contribution of the local degree of freedom i to the global degree of freedom I. Analogously the discrete internal and external force terms of the mechanical problem (12) are obtained

Results of the simple wall-like geometry at evaluation points A, B and C
In the following, the run times and the results obtained at the evaluation points A, B and C are summarized whereby each investigated modeling assumption and numerical setting is presented in separate tables. The simulations were run on 35 cores of an Intel(R) Xeon(R) CPU E5-2699 v4 @ 2.20GHz. The relative run times are always related to the numerically most expensive option of the corresponding table, while the error is derived from Eq. (21) with respect to the most accurate reference solution.
 , \(\tau =0.5\),
, \(\tau =0.5\),  and \(p=2\)
and \(p=2\) with geometrically nonlinear setting, full powder domain, \(\tau =0.5\),
with geometrically nonlinear setting, full powder domain, \(\tau =0.5\),  and \(p=2\).
and \(p=2\).Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Burkhardt, C., Steinmann, P. & Mergheim, J. Thermo-mechanical simulations of powder bed fusion processes: accuracy and efficiency. Adv. Model. and Simul. in Eng. Sci. 9, 18 (2022). https://doi.org/10.1186/s40323-022-00230-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40323-022-00230-y





 (a) and
(a) and  (b)
(b)











 for the geometrically nonlinear and linear setting
for the geometrically nonlinear and linear setting
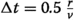 was used for the thermal and mechanical problem. Doubling the time step size led to errors in the displacements of up to
was used for the thermal and mechanical problem. Doubling the time step size led to errors in the displacements of up to