A new mortar formulation for modeling elastomer bedded structures with modal-analysis in 3D

Abstract

Background

It is a well-known fact that cross-laminated timber structures are sensitive to rumbling noises. These transmissions are best captured by a fully three-dimensional mathematical model. Since the discretization of such models with hexahedral elements in a conforming manner is highly complex, we chose the mortar method to reduce the algorithmic complexity for the mesh generation. Moreover we consider high-order finite elements in order to deal with the high aspect ratios in three-dimensionally resolved, cross-laminated walls and slabs. The geometric models and material specification was derived from a building information model.

Methods

This paper derives a new mortar formulation designed to replace an explicitely discretized elastomer with a new coupling condition. To this end, tailored Robin conditions are applied at the interface as coupling conditions instead of the more standard continuity constraints. Having demonstrated the suitability of the mortar method for high order finite elements, we proceed with the derivation of the dimensional reduced model with the new coupling condition and to show its stability by numerical experiments. We then test the performance of the new formulation on benchmark examples and demonstrate the engineering relevance for practical applications.

Results

The newly derived mortar formulation performs well. We tested the new formulation on fully three-dimensional examples of engineering relevance discretized by high-order finite elements up to degrees of p=10 and found the reproduction of both eigenvalues and eigenmodes to be accurate. Moreover, the mortar method allows for a significant reduction in the algorithmic complexity of mesh generation while simultaneously reducing the overall computational effort.

Conclusion

The newly derived modified mortar method for replacing an elastomer layer is not only an academically interesting variant but is capable of solving problems of practical importance in modal-analysis of cross-laminated timber structures.

Background

The main contribution of this paper is a new dimensionally reduced model which captures eigenvalues and eigenmodes of elastomeric coupled domains in timber structures. Dimensionally reduced models are very attractive from the computational point of view. There is no need to mesh the three dimensional but thin subdomain of the elastomer within our approach. However, new challenges arise such as the formulation of a suitable coupling condition and their numerical realization. Here we use a variant of the popular mortar finite element method [1]-[3]. Mortar methods can be analyzed within the abstract framework of saddlepoint problems and can be regarded as a domain decomposition technique. Firstly, coupled problems are teared, meshed and discretized separately resulting, in general, in non-matching meshes at the interfaces. Secondly, these independent subproblems are interconnected in a weak form by balance equations involving, e.g., the surface traction. Thus, these techniques provide a very flexible and computationally attractive setting to handle numerically coupled multi-physics problems. Mortar methods have been applied successfully in many engineering applications, such as, e.g., contact problems [4]-[7], dynamic and static structural analysis [8]-[10], flow problems [11]-[13] and coupled problems in acoustics [14],[15]. Further, the mortar method is used to simulate eigenvalue problems in [16],[17]. Most contributions deal only with first or second order approaches. Although the theory of high order mortar methods is well understood [18],[19], the implementation of higher order quadrature formulas on cut elements in 3D simulations is technical challenging. Here we apply high order, up to 20 in the polynomial degree, techniques to approximate eigenvalues and eigenmodes in cross laminated timber structures interconnected by thin elastomer structures.

Our motivation to derive such a formulation stems from the need to compute the modal-analysis which is a main part of vibro-acoustical-analysis. In order to control sound transmissions between slabs and walls, these components are often connected by elastomers which we firstly model by using the linear elasticity equation because of the very thin character. Due to the composition of timber constructions consisting of thin, layered and orthotropic material, we aim for a fully three-dimensional resolution of the slabs and walls. For this purpose, we use the p-version of the finite element method, as presented for example in [20]. Moreover, it is well suited for the computation of solid, but thin-walled structures because it is robust in terms of the large aspect ratios which arise naturally in fully three-dimensional models of plates and shells [21]. It also provides better accuracy and convergence properties than low-order finite elements. In addition, the p-version of the FEM has already been shown to lead to excellent results for the analysis of sound transition through timber floors [22].

However, the construction of conforming, three dimensional meshes, that are analysis-suitable, is non-trivial. In this paper, we utilize the mesh generation techniques presented in [23]. A conforming mesh of connected walls and slabs, increases the number of elements significantly, as a local mesh refinement, in only one of the components automatically spreads to the others.

These restrictions motivate the use of mortar methods allowing for an independent meshing of the individual building components, as the physically imperative coupling is carried out numerically at a later stage in a weak sense.

The mortar method was first introduced as a method to couple spectral elements with finite elements in [1] where the ansatz space was weakly constrained. The present contribution, however, views the mortar method in the more popular context of enforcing the coupling conditions by means of Lagrange multipliers, as introduced in [2], and thus resulting in a saddle point formulation.

The modeling of elastic interface boundary conditions has been the subject for low orders in [24]-[26]. Also the modeling of interface elements has been investigated in [27],[28], with a spring boundary condition in [29] and with a Robin-type condition in [30]. We built on the work of [31], which demonstrated the excellent applicability of the mortar method for problems in structural mechanics for discretizations of high orders. We extend this concept to elastomeric coupled domains. To this end, we enforce a non-standard Robin type condition at the interface by means of Lagrange multipliers instead of the continuity requirements. Robin type interface conditions have been used to glue nonconforming grids, see, e.g., [32]. The main difference to the current paper is that our coupling condition not only aims to glue two nonconforming grids together, but is also able to replace the whole explicit discretization of an elastomer. Therefore, it goes beyond a simple domain decompositon method, it provides also a dimensionally reduced model.

The contribution at hand is organized as follows: We start by presenting the problem setting in Section ‘Problem setting and conforming discretization’ and introduce the classical mortar method in Section ‘Mortar method’. In Section ‘Modeling of the elastomer’, we derive our new mortar coupling condition which is able to replace an explicitly discretized elastomer. In Section ‘Results and discussion’, we present our simulation results. Section ‘Results and discussion’ compares numerically the standard mortar method with the conforming high order method in the context of eigenvalue problems for a rigidly connected L-shaped wall-slab example. To establish a reference solution, we firstly compute the eigenvalues and eigenfunctions on a wall-slab configuration in a conforming discretization in Section ‘Results and discussion’. There we already investigate the effect of connecting walls and slabs with different elastomers on the eigenvalues and the eigenfunctions. We then test the new formulation on the same wall-slab configuration in Section ‘The new elastomeric coupled mortar formulation’. Section ‘Influence of the elastomer thickness’ analyses numerically the influence of the elastomer thickness on the new coupling condition. Furthermore a more complex and application relevant example is presented in Section ‘A complex example’. In Section ‘Conclusions’, we give some conclusion according to the numerical results showing the flexibility and robustness of the new mortar method for practical application.

Methods

Problem setting and conforming discretization

In this section, we provide a dimensionally reduced model, resulting in a modified mortar approach. In contrast to the classical mortar setting, we end up with a non-symmetric saddle-point formulation. The surface traction now enters as a spring into the coupling condition.

The eigenvalue problem under investigation is given by

(1)

where ρ is the density and the stress tensor σ and the linearized strain tensor ϵ are defined as

(2)

Furthermore denotes the Hookes tensor which is given by the material parameters. We have denoted the eigenvalues by ω to avoid a confusion with the Lagrange multiplier λ of the mortar method considered in Section ‘Mortar method’. The most important parameters are summarized in Table 1, for convenience. We will assume that the domain is bounded and polyhedral. In addition, we enforce Dirichlet boundary conditions on a non-trivial set Γ _D and homogeneous Neumann boundary conditions on Γ _N , where Γ _N ΓΓ _D =ø and Γ _D ∩Γ _N =∂ Ω.

Table 1 Parameter definitions

The variational formulation of (1) reads: Find the eigenvalues and the eigenfunctions uϵV(Ω):={u|u∈(H¹(Ω))³,u(Γ _D )=0} so that

(3)

We discretize Equation (3) using conforming finite elements of high order associated with a hexahedral mesh. As basis functions, we use hierarchical shape functions based on integrated Legendre polynomials [20],[33].

Mortar method

A mortar method is typically associated with a domain partitioning. Here, the domain Ω is decomposed into two non-overlapping subdomains Ω _m and Ω _s so that

The indices m and s correspond to the master and slave side, respectively. In our case, the wall is the slave domain and the slab is the mortar domain. We then define a common interface: Γ:=∂ Ω _s ∩∂ Ω _m and the Lagrange multiplier space by $M:={\left(H^{-\frac{1}{2}}\left(\Gamma \right)\right)}^3$ where $H^{-\frac{1}{2}}\left(\Gamma \right)$ is the dual space of . Here, we assume that and thus no modifications on ∂ Γ have to be taken into account. The primal space is defined by X:=V(Ω _m )×V(Ω _s ), where V(Ω _i ):={u|u∈(H¹(Ω _i ))³,u(Γ _D ∩∂ Ω _i )=0} with i∈{s,m}. We can now define our bilinear forms for the mortar method by

where <•,•> * denotes the duality pairing of ${\left(H^{\frac{1}{2}}\left(\Gamma \right)\right)}^3$ and ${\left(H^{-\frac{1}{2}}\left(\Gamma \right)\right)}^3$ and , are defined by

(4)

The eigenvalue problem (1) can then be written in the following variational form:

Find the eigenvalues , the eigenfunctions u∈X and λ∈M so that

(5)

Equation (5) now defines the saddle point problem arising from the mortar method. The Lagrange multiplier λ corresponds to the negative surface traction -σ n of Ω _s on the interface Γ, where n is the outward unit normal of Ω _s .

For the discretization of the primal variable of (5), we employ hexahedral finite elements of high order on each subdomain Ω _m ,Ω _s . The dual space is discretized by the trace space of the discrete primal space on Ω _s . This choice guarantees inf-sup stability [3],[34] and the mortar method for solving (5) can be written as

$$A(u,\lambda ;v,\mu )=\mathrm{\omega d}(u,v)$$

with A(u,λ;v,μ):=a(u,v)+b(v,λ)+b(u,μ).

The bilinearform A(•,•;•,•) fulfills the conditions of Remark 13.4 in [35], and thus the theory given in Section 8 of [35] ensures convergence of the discrete eigenvalues and eigenfunctions.

Modeling of the elastomer

The modeling of an elastomer for vibration isolation has been the subject in [36],[37]. These papers take many mechanical properties like strain and damping directly into account. Alternatively, the modal- and spectral-analysis can be realized by the modal superposition. In this case, the eigenmodes of the undamped system are required, and the damping is only taken into account in a postprocessing step. Thus, we neglect the damping. Moreover, the elastomer is modeled in terms of the linear elasticity equations because it is comparatively thin in one space direction [22]. This section will lay out a new modeling approach using a Robin type condition for the coupling, in order to replace an elastomer. This new coupling condition results in a dimensional reduced model which avoids the meshing of the three dimensional subdomain which corresponds to the elastomer. Our new coupling condition still yields a saddle point problem which fits into the implementational framework of mortar methods.

Modified mortar method using a Robin type condition

The goal of this modeling approach is to replace the elements representing the elastomer between the two components by a Robin type condition. The modeling idea is depicted in Figure 1. Because of the very thin elastomer layer, in our case 1.2[cm], we simplify the transversal shear in the elastomer and neglect the mass of the elastomer. We assume the elastomer to act linearly in z-direction on the solution between the slab and the wall. Without loss of generality, we assume the coordinate system of the mortar interface to be at z=0. Therefore, we define our displacement in the spirit of a Taylor series with z∈ [ 0,d], where d denotes the thickness of the elastomer as

$$u(x,y,z)=u_s(x,y)+\frac{z}{d}\left(u_m(x,y)-u_s(x,y)\right).$$

(6)

Figure 1

Modeling concept: thin layer (left) and interface formulation (right).

With this definition and with [ u]:=(u _m (x,y)−u _s (x,y)), the gradient of the displacement field at z=0 is given by

Now the linearized elastic strain reads

Further, we assume the following standard linear isotropic stress-strain relationship with the lamé parameters and to hold in the elastomer, i.e.,

As the interface is assumed to be aligned to z=0, the normal vector on Γ directed towards Ω _m is given by n= [ 0,0,1]^T. The fluxes are then explicitly given by

Equation (7) is the new coupling condition between displacements and surface traction in the strong form.

Note that in comparison to the standard mortar coupling condition u _s –u _m =0, we additionally obtain dependencies on the derivatives (u _s )_3,x,(u _s )_3,y,(u _s )_1,x,(u _s )_2,y, and the surface traction λ _s =-σ|_{z = 0}n interacts as a spring term with the displacement. The corresponding bilinear forms are now given by

with <•,•> being the scalar product and . We note that this scalar product on the dual space is realized within the discrete setting as a L²-surface integral. In contrast to the bilinear forms b(•,•) and $\tilde{b}(•,•)$ no basis functions being defined on different sides of the interface are associated with c(•,•). Both λ and μ are given by the mesh on the slave side, and thus a standard quadrature formula can be easily applied. For given surface tractions λ _i , the force equilibria of both bodies Ω _i reads

Neglecting the difference between –λ _s =σ|_z=0n and λ _m =σ|_z=dn, setting λ=λ _s and adding both equations we obtain

$$a(u,v)+b\left(v,\lambda \right)=\mathrm{\omega d}\left(u,v\right).$$

(8)

The new coupling condition Equation (7) in the weak form and Equation (8) leads to the dimensionally reduced model given by

$$\begin{array}{lllll}a(u,v)& +& b\left(v,\lambda \right)& =\mathrm{\omega d}(u,v)& ,v\in X\\ \tilde{b}\left(u,\mu \right)& -& \mathrm{\alpha c}\left(\lambda ,\mu \right)& =0& ,\mu \in M\end{array}$$

(9)

with the modeling parameter α defined as

Note that the parameters α and β can be directly computed from the properties of the elastomer. Replacing X by X _h and M by M _h gives the discrete version of Equation (9) yielding approximations ω _h of the eigenvalues.

Results and discussion

Comparison between conforming and mortar discretization

We now consider the example depicted in Figure 2. It resembles a rigidly supported wall connected to a slab on one side and clamped at the other side. The corresponding discretization is depicted in Figure 3. It consists of ten hexahedral elements in the conforming case and eight in the mortar case. At this stage, we do not model an elastomeric coupling yet but assign the material parameters for timber to all hexahedral elements.

Figure 2

L-shaped connection of a slab to a wall.

Figure 3

Hexahedral discretization: left conforming, right mortar.

The material parameters are given in Table 2, where Poisson's ratio and Young's module are denoted by ν and E, respectively.

Table 2 Elastomer properties for the simulations

The eigenvalues for a sequence of p-FEM computations with polynomial degree p∈{3,7,10,15} are depicted in Table 3 along with the differences between the conforming and the mortar discretization. The differences decrease for higher orders.

Table 3 Comparison of eigenfrequency of the L-shaped wall-slab configuration

Discrete modeling of the elastomer

In order to obtain a reference solution, the elastomer is discretely represented by a thin layer of hexahedral elements. The discretization is depicted in Figure 4, on the left. The green hexahedral elements in Figure 4 mark the elastomer. The material properties for typical elastomers are given in Table 2, where hard materials are listed first. The specific type of elastomer chosen in a practical application depends on the dead load to be expected on the elastomer. The corresponding eigenvalues of the system wall-elastomer-slab are given in Table 4. Eigenvalues corresponding to a direct connection of wall and slab are provided as well. It is readily apparent that, depending on the mode and the elastomer under contemplation, the eigenvalues of the system with an elastomer layer are about 5-35[ %] lower than without the elastomer. This is related to the fact that the coupling of the slab to the wall becomes weaker. Figure 5 illustrates the relative decay of each eigenvalue computed from the results depicted in Table 4.

Figure 4

Conforming (left) and mortar discretizations (right) of the structure whose geometry is described in Figure2. The thin elastomer layer is condensed into the mortar interface.

Figure 5

Dependence of the first eight eigenvalues of the elastomer (left) and relative decay with respect to no elastomer for the first 20 eigenvalues (right).

Table 4 Influence of the different elastomers on the eigenfrequencies given in [ H z ]

The new elastomeric coupled mortar formulation

We now test the new mortar model given by Equation (9) using the discretization depicted on the right-hand side of Figure 4. The results are compared to the classical, conforming discretization, as depicted on the left-hand side of Figure 4, where the elastomer was modeled explicitly, as described in Section ‘Results and discussion’.

Table 5 depicts the first eight eigenvalues obtained by the new mortar model along with the deviation in [%] from the eigenvalues of the explicitly modeled elastic layer whose results were given in Table 4. All computations are carried out with a polynomial degree of p=10. We observe that the new model is able to reproduce the eigenvalues to an accuracy of at least four per cent. Not only the eigenvalues but also the eigenmodes of the two different discretization models have to match closely. Figure 6 shows selected eigenvectors of Elastomer 5. The upper row provides the eigenvectors, as computed by an explicit modeling of the elastomer while the lower row represents the corresponding eigenvectors of the new mortar method. Obviously, different types of modes such as lateral and transversal shear modes as well as pure compression and traction modes are equally well represented. While in the upper row the elastomer undergoes severe deformations, these are approximated by the coupling conditions at the interface between wall and slab in the lower row. Note that the missing elements for the elastomeric layer result from the reduction of the dimension. Moreover, the sequence of the eigenmodes remains the same in both models.

Figure 6

Comparison between eigenmodes 1, 3, 4, 7. Top row: conforming, hexahedral discretization. Bottom row: new mortar method. Note that the greyscale shows the displacement.

Table 5 Eigenfrequencies given in [ H z ] for the new modeling approach along with the deviation in percent from the conforming discretization depicted on the left hand side of Figure 4

We also analyse the eigenmodes by a modal assurance criterion as it is described in [38]. This modal assurance criterion determines the correlation of the eigenmodes. For a good correlation, the resulting matrix should have a diagonal with values greater than 0.9. Values close to 0 mean a poor correlation. The modal assurance criterion matrices show very good results for all practically relevant elastomers investigated in this paper. We show exemplary the modal assurance criterion matrix for elastomer 5 in Table 6. A selection of the eigenmodes are depicted in Figure 6. This confirms the good results for the newly developed coupling condition. Furthermore, it is pointed out that the number of finite elements is reduced by one third even in this small example. Herein, the boundary conforming model required 12 hexahedral elements while only 8 hexahedral elements sufficed for the new mortar approach. However, and most importantly, the mesh generation is simpler using the reduced model in the sense that each wall or slab can now be meshed separately before the discretized components are glued back together.

Table 6 Modal assurance criterion for the modeling of Elastomer 5

Influence of the elastomer thickness

A key assumption of the new approach is that the displacement field varies only linearly in the direction perpendicular to the two opposite interface of the elastomer with adjacent structures. In order to investigate the validity of this assumption, we vary the thickness of the elastomer and show its influence on the corresponding eigenvalues.

Remark1.

At this point it is noted that the thickness of the elastomers for typical wall-slab configurations is below 3[ c m]. In practical applications, thicknesses range from 1[ c m] to 1.5[ c m].

The reference solution is again computed with the conforming finite element method. We perform our simulation with two further thicknesses of the elastomer. The first thickness is 3[ c m], which is the maximum relevant thickness and the second thickness is 4[ c m], which is beyond the typical application range. The results for the investigation for the two elastomer thicknesses are depicted in Table 7 and Table 8 respectively. The tables show the deviation in [%] between the new model and the explicitly modeled elastomer.

Table 7 Eigenfrequencies given in [ Hz ] for the conform and the new method with the corresponding deviation in [%] for the elastomer thickness 3[cm]

Table 8 Eigenfrequencies given in [ Hz ] for the conform and the new method with the corresponding deviation in [%] for the elastomer thickness 4[cm]

While it can be observed that the thicker the elastomer, the bigger the error, the error does not rise above engineering accuracy for practical applications. Table 9 and Table 10 show the model assurance criterion matrices for the eigenmodes for the corresponding 3[ c m] and 4[ c m] elastomer simulations.

Table 9 Modal assurance criterion for the modeling of Elastomer 5 with thickness 3[cm]

Table 10 Modal assurance criterion for the modeling of Elastomer 5 with thickness 4[cm]

A complex example

The good performance of the new mortar method carries over to larger examples of engineering relevance even if an orthotropic material law is used for the elastically connected building parts as these changes in the material parameters only have an influence on the tensor for the wood parts in the linear elasticity Equation (3). is then given according to [22] by

with

$$\begin{array}{l}{A}_{11}=\frac{E_x}{D_0}\left(1-{\nu }_{\mathit{\text{yz}}}^2\frac{E_z}{E_y}\right),A_{12}=A_{21}=\frac{E_y}{D_0}\left({\nu }_{\mathit{\text{xy}}}+{\nu }_{\mathit{\text{yz}}}{\nu }_{\mathit{\text{zx}}}\frac{E_z}{E_y}\right),\\ A_{13}=A_{31}=\frac{E_z}{D_0}\left({\nu }_{\mathit{\text{xy}}}{\nu }_{\mathit{\text{yz}}}+{\nu }_{\mathit{\text{zx}}}\right),A_{22}=\frac{\mathit{\text{Ey}}}{D_0}\left(1-{\nu }_{\mathit{\text{zx}}}^2\frac{E_z}{E_x}\right),\\ A_{23}=A_{32}=\frac{E_z}{D_0}\left({\nu }_{\mathit{\text{yz}}}+{\nu }_{\mathit{\text{xy}}}{\nu }_{\mathit{\text{zx}}}\frac{E_y}{E_x}\right),A_{33}=\frac{E_z}{D_0}\left(1-{\nu }_{\mathit{\text{xy}}}^2\frac{E_y}{E_x}\right)\end{array}$$

where

$$D_0=1-{\nu }_{\mathit{\text{yz}}}^2\frac{E_z}{E_y}-{\nu }_{\mathit{\text{xy}}}^2\frac{E_y}{E_x}-{\nu }_{\mathit{\text{xy}}}{\nu }_{\mathit{\text{yz}}}{\nu }_{\mathit{\text{zx}}}\frac{E_z}{E_x}-{\nu }_{\mathit{\text{zx}}}^2\frac{E_z}{E_x}.$$

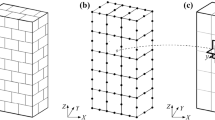
Figure 7 depicts a floor plan of a timber building along with a 2 1/2D submodel consisting of three rooms.

Figure 7

Detail of the ground floor plan considered for acoustical analysis.

This model forms the basis of the three-dimensional computational solid model comprising all conforming hexahedral elements depicted in Figure 8. Note that walls and slabs consist of several layers of wood, as depicted in Figure 9. The thickness of the layers is given in Table 11. Each layer is explicitly modeled with the characteristic, orthotropic material parameters of timber. We set the Young's moduli in fiber direction E _x =137•10⁶[N/m²], in-plane orthogonal E _y =1424•10⁶[N/m²], and perpendicular to the plane E _z =10211•10⁶[N/m²]. The Poisson's ratios are v _zx =0.035, v _yz =0.045, v _xy =0.037. In addition, we apply the shear moduli G _zx =459•10⁶[N/m²], G _yz =102•10⁶[N/m²] and G _xy =171•10⁶[N/m²]. The density is assumed to be ρ=450[k g/m³] for all layers. Although the individual layers have the same material properties, their fiber orientation in plane is orthogonal in adjacent layers in such a way that the orientation is equal on every other layer only. This situation is accurately resolved by the finite element mesh. The elastomer is situated only at the interface where the slab rests on the walls and possesses the isotropic material properties of Elastomer 5, as given in Table 2. The conforming model is depicted in Figure 8. In total, the mesh consists of 7578 hexahedral elements.

Figure 8

Conforming hexahedral discretization.

Figure 9

Wall types from left to right: Wall type 61, 85, 95 and slab 125.

Table 11 Layer thicknesses of walls and slab 125

The computational mesh for the mortar method is depicted in Figure 10. It consists of only 2475 hexahedral elements. It is evident how the components wall and slab were meshed independently of one another and are non-conforming at their interface. Not only does this greatly simplify the mesh generation process itself, it also avoids the generation of hexahedral elements due to continuity constraints at the interfaces of walls and/or slabs. A further reduction of hexahedral elements is possible by choosing mesh densities individually for all involved components. Also note that local refinements do not branch out to other walls. The elastomer where the slab rests on the walls is now modeled using the new mortar method given in Equation (8).

Figure 10

Non-conforming hexahedral discretization.

Table 12 also summarizes the comparison for the first eight eigenvalues and then selected higher eigenvalues up to one hundred. Note that the modeling error introduced by the new mortar approach remains below one per cent for all investigated eigenvalues. The error (in comparison to the conforming method) obtained when using the mortar method with the new coupling condition is comparable to the error obtained when using the standard mortar method. The upper row of Figure 11 depicts selected eigenvectors resulting from the conforming discretization given in Figure 8, while the lower half depicts the corresponding eigenvectors of the mortar discretization of Figure 10. All eigenvectors match within an accuracy which is considered sufficient for engineering applications.

Figure 11

Comparison between eigenmodes 1, 2, 3, 4. Top row: resulting from the conforming discretization corresponding to Figure 8, Bottom row: non-conforming discretization corresponding to Figure 10.

Table 12 Computed eigenfrequencies given in [ H z ]for the building example

Conclusions

The aim of this contribution was to model the behavior of eigenvalue problems of elastomerically supported, cross-laminated timber structures by means of an extended mortar method.

To this end, we first evaluated the applicability of the mortar method to the p-version of the finite element method of an eigenvalue problem for three-dimensional shell and plate-like structures. The deviation from a conformingly discretized, stiffly coupled wall-slab configuration for higher order p is below 1[ %] for all investigated eigenvalues. The eigenmodes likewise provided an excellent match within the required engineering tolerance. Secondly we derived a new coupling condition for the mortar method which is able to replace an explicit resolution of an elastomer. This new transmission condition is obtained from a dimension reduction. We then compared the eigenvalues and eigenmodes computed within this approach to the conformingly discretized wall-slab example, the wall now being connected to the slab by means of an elastomer. The resulting lowest eight eigenvalues of the two models correspond within a tolerance of less than 1[ %]. This accuracy is sufficient for the application at hand. We finally demonstrate that the good results obtained by the newly developed mortar variant also extend to larger examples of engineering relevance.

The practical motivation of using the new mortar method was to greatly simplify both the engineering modeling effort and the meshing process by dispensing with the need for a conformal element coupling between construction components like slabs and walls. An interesting side effect, however, was that it was also possible to significantly reduce the overall computational workload. The conforming model of the engineering example resulted in 7578 hexahedral elements while only 2475 hexahedral elements were needed for the mortar model. This reduction is due to the facts that: a) a component-wise mesh generation naturally introduces the possibility to choose local mesh densities, b) necessary refinements in other building components do not need to be respected and, accordingly, do not spread across interfaces, and c) at the interfaces of orthogonally coupled, laminated structures it was possible to avoid unnecessary hexahedral elements naturally due to the relaxed topological constraints, and d) it is not required to resolve the geometrically thin elastomer layer.