Introduction

China has been experiencing very rapid economic growth in recent decades, and its share of global gross domestic product had risen to 17.39% by the end of 2019; its growth has relied mainly on fossil fuels (coal and oil) that generate greenhouse CO2 (carbon dioxide) emissions and as a result China is now the largest carbon dioxide emitter in the world (Gregg et al., 2008; Guan et al., 2009; IEA, 2020). Given both its economic size and the level of its CO2 emissions, this country represents a particularly interesting case to analyse the relationship between economic growth and the environment. This is often understood in terms of the so-called environmental Kuznets curve (EKC) with its typical U-shape (as in the case of the original curve describing the relationship between income inequality and GDP (gross domestic product) per capita—see Kuznets, 1955). The basic idea is that emissions in countries in the early stages of development are low and therefore environmental qualities indicators are good; the subsequent industrialization process initially damages the environment, but as income per capita increases environmental legislation is introduced to reduce emissions and pollution (see Grossman & Krueger, 1991 and Shafik & Bandyopadhyay, 1992, among others).

The relationship between economic growth and CO2 emissions in China has been analysed in numerous papers using a variety of approaches (e.g. Du et al., 2012; Haisheng et al., 2005; Jalil & Mahmud, 2009; and Jalil & Feridun, 2011; Wang et al., 2011a, Wang et al., 2011b; Xie et al., 2018; Xu et al., 2014) as discussed in the literature review below. However, these have focused on factors that affect CO2 emissions or examined the evidence on the EKC, whilst the present study analyses the persistence of the two series and their linkages using fractional integration and cointegration methods, respectively.

Thus, its contribution is threefold. First, it improves on earlier works on the relationship between CO2 emissions and GDP in China by applying fractional integration and cointegration methods that are more general than those based on the classical stationary I(0) (integrated of order 0) v. non-stationary I(1) (integrated of order 1) dichotomy which had been previously used. In the standard framework the order of integration of the variables d can only be an integer, which is a rather restrictive assumption; the setup used in the present paper is instead much more general and flexible since this parameter is also allowed to take fractional values and as a result a much wider range of stochastic behaviours can be modelled. Whether a variable is stationary or not matters a great deal since in the former case the effects of shocks are only temporary whilst in the latter they are permanent and therefore a variable, if hit by a shock, will not revert to its long-run equilibrium, regardless of any policy measures. The more general framework used for the analysis in this paper also sheds light on intermediate cases when equilibrium is eventually restored, but deviations from it resulting from exogenous shocks are long-lived. Second, it is informative about both the dynamics and the long-run equilibrium, and it shows that both series of interest are highly persistent, but linked together in the long run. Thirdly, it provides important implications for both academics and policymakers. Specifically, to the former it suggests an interesting avenue for future research, namely investigating in greater depth the functional form of the relationship that has been established empirically in order to gain a better understanding of the issues of interest; to the latter it highlights the need for appropriate environmental policies during periods of economic growth. In particular, environmental innovation measures aimed at reducing carbon emissions, increasing energy efficiency and promoting green development have been shown also to provide growth opportunities for entrepreneurship in China (Chen & Lee, 2020; Zhang et al., 2017a, 2017b).

The layout of the paper is as follows. “Literature review” Section reviews the relevant literature. “Methodology” Section outlines the empirical framework. “Results and discussion” Section describes the data and discusses the empirical findings, while “Conclusions” Section offers some concluding remarks.

Literature review

Carbon dioxide (CO2) emissions are the main cause of climate change and global warming, and therefore they are among the most used indicators of environmental degradation (Apergis & Payne, 2009; Du et al., 2012; Lean & Smyth, 2010; Shahbaz et al., 2013, 2016; Tiwari et al., 2013). Higher CO2 levels in the Earth’s atmosphere are a serious issue as they can cause greenhouse effects and higher air temperature (Bacastow et al, 1985; Hofmann et al., 2009; IPCC, 2015; Liu et al., 2016). If the burning of fossil fuels continues, atmospheric CO2 concentration will double sometime during this century and air temperature will rise by 1.5–5 °C by 2100 (Baes et al., 1977; Kraaijenbrink et al., 2017; Mahlman, 1997). Carbon dioxide is associated with economic and other human activities, and accounts for three-quarters of Global Greenhouse Gas (GHG) emissions (Huaman & Jun, 2014; IPCC, 2015).

The linkage between economic growth and environmental degradation is examined in many studies providing mixed evidence. Some of them find that the relationship between CO2 emissions and economic growth is negative (Ajmi et al., 2015; Azomahou et al., 2006; Baek & Pride, 2014; Dogan & Aslan, 2017; Roca et al., 2001; Salahuddin et al., 2016), or that it is initially positive but then turns negative (Riti et al., 2017; Shahbaz et al., 2014, 2016). Other papers report instead a positive relationship (Ahmad & Du, 2017; Bakhsh et al., 2017; Chaabouni et al., 2016; Ma et al., 2016; Nasir & Rehman, 2011; Ozturk & Acaravci, 2013; Saidi & Mbarek, 2016). Some more recent research has used the autoregressive distributed lag (ARDL) model and a nonlinear version of the same to analyse the relationship between economic growth and CO2 emissions and has concluded that there is a positive long-term relationship between these two variables (Ahmad et al., 2018; Akalpler & Hove, 2019; Chen et al., 2019a, 2019b; Cosmas et al., 2019; Dong et al., 2018; Gill et al., 2018; Khan et al., 2019; Riti et al., 2017; Toumi & Toumi, 2019). Differences in terms of sample period, country-specific characteristics, model specifications, econometric methods and pollution indicators are possible reasons for the mixed results of those papers.

The environmental Kuznets curve (EKC), analogous to the inverted U-shaped curve originally used by Kuznets (1955) to model the relationship between income inequality and income levels, has become the most common framework to study the linkages between CO2 emissions and economic growth, either in single countries or in groups of countries. Early studies include Grossman and Krueger (1991, 1995), Stern and Common (2001) and Dinda (2004) and later Friedl and Getzner (2003), Dinda and Coondoo (2006) and Managi and Jena (2008). The results are mixed, some studies supporting the existence of an EKC (Ahmad, 2016; Ang, 2007; He & Richard, 2010; Iwata et al., 2010; Katz, 2015; Lau et al., 2014; López-Menéndez et al., 2014); others not finding any evidence for it (Jia et al., 2009; Liu et al., 2007a, 2007b; Magazzino, 2014a, 2014b, 2015; Pao et al., 2012; Riti & Shu, 2016); some reporting an N-shaped relationship (Kijima et al., 2010). Mikaylov et al. (2018) use a variety of cointegration methods (Johansen, ARDL, DOLS (dynamic ordinary least squares), FMOLS (fully modified ordinary least squares) and CCR (correlation regression estimator)) to test for the existence of an EKC in Azerbaijan and find that economic growth has a positive and statistically significant long-run effect on emissions which implies that the EKC hypothesis does not hold. Ru et al. (2018) apply a recently developed methodology based on the long-term growth rates (Stern et al., 2017) to model the income–emission relationship for four sectors (power, industry, residential, and transportation) and three difference types of pollutants (SO2 (sulfur dioxide), CO2, and BC (black carbon)); the analysis uses data for various countries from the global emission inventory developed at Peking University and finds that the results are both sector and pollutant specific. Barassi and Spagnolo (2012) estimate a VAR-GARCH (vector autoregression—generalized autoregressive conditional heteroskedastic) model and find evidence of both mean and volatility spillovers between per capita economic growth and carbon dioxide emissions in Canada, France, Italy, Japan, UK (United Kingdom) and USA (United States of America) over the period 1870–2005.

Panel studies supporting the validity of the EKC hypothesis include Martínez-Zarzoso and Bengochea-Morancho (2004) for 22 OECD countries; Farhani et al. (2014) for 10 Middle East and North African (MENA) countries; Gao and Zhang (2014) for 14 sub-Saharan African countries; Kasman and Duman (2015) for 15 countries which were Bulgaria, Croatia, Czech Republic, Estonia, Hungary, Iceland, Latvia, Lithuania, FYR of Macedonia, Malta, Poland, Romania, Slovak Republic, Slovenia, and Turkey; Pao and Tsai (2011) for Brazil, Russia, India and China; Osabuohien et al. (2014) for 50 African countries; Kim (2019) for newly industrialized Asian countries; Apergis and Payne (2009) for six Central American countries; Anastacio (2017) for Canada, the and Mexico.

Panel studies not finding evidence of an EKC include instead Onafowora and Owoye (2014) for Brazil, China, Egypt, Japan, Mexico, Nigeria, South Korea, and South Africa (only finding evidence of an EKC in Japan and South Korea); Mallick and Tandi (2015) for Bangladesh, India, Nepal, Pakistan, and Sri Lanka; Zoundi (2017) for 25 countries; Wang (2012) for 98 countries. These contradictory results reflect the issue of heterogeneity in the context of panels.

Among single country studies, the following support the existence of an EKC: Ozturk and Oz (2016) for Turkey; Latifa et al. (2014) for Algeria; Khan et al. (2019) and Shahbaz et al. (2012) for Pakistan; Sothan (2017) for Cambodia; Yazdi and Mastorakis (2014) for Iran; Saboori et al. (2016) for Malaysia; Can and Gozgor (2017) for France; Saboori et al. (2012) for Malaysia; Khalid (2014) for Mongolia; Shahbaz et al. (2015) for Portugal.

Those not finding any evidence for an EKC include Saleh and Abedi (2014) and Saboori and Soleymani (2011) for Iran; Ghosh et al. (2014) and Amin et al. (2012) for Bangladesh; Friedl and Getzner (2002) for Austria; Boopen and Vinesh (2011) for Mauritius; Alkhathlan et al. (2012) for Saudi Arabia; Saboori et al. (2012) for Indonesia; Dogan and Turkekul (2016) for the USA. In this case, differences in the results can be attributed to the different pollution indices, model specifications, estimation techniques and sample period used.

A few studies carry out fractional integration/cointegration methods to analyse CO2 emissions. For instance, Galeotti et al. (2009) implement such tests for 24 OECD (Organisation for Economic Cooperation and Development) countries and find only limited evidence supporting the EKC hypothesis. Barassi et al., 2018 use this approach to examine stochastic convergence of relative per capita CO2 emissions; according to their results this is relatively weak in the case of the OECD countries whilst there is stronger evidence in the case of the BRICS (Brazil, Russia, India, China, and South Africa); in addition, the former cannot be attributed to the presence of structural breaks. Gil-Alana et al. (2017) analyse the stochastic behaviour of CO2 emissions applying a long-memory approach with nonlinear trends and structural breaks to a long span of data for the BRICS and G7 countries (USA, UK, France, Italy, Germany, Japan and Canada). They conclude that shocks to CO2 emissions have permanent effects in most cases, except in Germany, the US and the UK. Compared to theirs the present paper, though considering only China rather than various countries, goes one step further since it also carries out fractional cointegration tests to establish whether there exist any long-run linkages between the growth rates of GDP and CO2 emissions.

Several other studies have focused on China given the size of its economy and the high level of its CO2 emissions. Some of them analyse the factors driving the latter, such as economies of scale, population and energy structure (Xie et al., 2018; Xu et al., 2014), and economic activity and energy intensity (Jalil & Mahmund, 2009; Liu et al., 2007a, 2007b; Zhang et al., 2009) (Wang et al., 2005). Using SDA (structural decomposition analysis) Peters et al. (2007) conclude that in China the growth in CO2 emissions from infrastructure construction, household consumption in cities, the urbanization process and lifestyle has been greater than the savings from efficiency improvements. On the other hand, Li and Wei (2015) find that the impact of the industrial structure on carbon dioxide emissions is gradually changing from positive to negative and that the main driver of the reduction of CO2 emissions in China is carbon intensity. Zhang et al. (2015) use SDA to investigate the factors that influence China's pollutants and conclude that increasing efficiency and intensity of emissions are important in reducing industrial pollution.

As for studies on the EKC in China, some find evidence for it (Haisheng et al., 2005; Jalil & Mahmud, 2009; and Jalil & Feridun, 2011); others do not (Du et al., 2012; Wang et al., 2011a, 2011b); others find an inverted N-shaped relationship between CO2 and GDP (Fang et al., 2019; Kang et al., 2016; Onafowora & Owoye, 2014) (Wang et al., 2019); some report the existence of an N trajectory (Dinda et al., 2000; Friedl & Getener, 2003; Lipford & Yandle, 2010; Martinez-Zarzoso & Begonchea-Morancho, 2004; Onafowora & Owoye, 2014). Finally, Riti et al. (2017) analyse the relationship between emissions, economic growth and energy consumption in China using a variety of econometric techniques such as ARDL, FMOLS and DOLS that produce similar results providing support for an EKC, but finding a different turning point compared to other studies.

The inconclusiveness of the results discussed above makes the design of appropriate environmental policies difficult for the Chinese authorities who have been under increasing pressure to deal more effectively with climate change issues. The aim of the present study is to obtain more robust evidence informing policy choices; this is achieved by applying fractional integration and cointegration methods whose features are outlined below.

Methodology

The order of integration of a time series is the differencing parameter required to make it stationary I(0). Specifically, a covariance stationary process [xt, t = 0, ± 1, …} is said to be I(0) if the infinite sum of all its autocovariances, defined as γu = E[(xt-Ext)(xt+u-Ext)] is = −finite, i.e.

$$\sum\limits_{u\, = \, - \infty \,}^{\infty } {\left| {\,\gamma_{u\,} } \right|} \,\,\,\, < \,\,\,\,\infty .$$
(1)

However, many processes do not satisfy (1); when the sum of the autocovariances is infinite, the process is said to exhibit long memory or long-range dependence, so-named because of the high degree of association between observations which are far apart in time. Within this category, the fractional integration or I(d) (integrated of order d) framework is one of the most widely used. Specifically, a process is said to be integrated of order d or I(d) if it can be represented as:

$$\,\,\,\,\,(1\,\, - \,\,L)^{d} x_{t} \,\,\,\, = \,\,\,\,u_{t} ,\,\,\,\,\,\,\,\,\,\,\,t\,\,\,\, = \,\,\,\,0\,,\,\, \pm 1\,,\,\,...\,,$$
(2)

where L is the lag operator (Lkxt = xt-k), and ut is I(0). One can use a Binomial expansion in Eq. (2) such that then, if d is fractional, xt can be expressed as

$$x_{t} \,\,\, = \,\,\,\,d\,x_{t - 1} \,\,\, - \,\,\,\,\frac{d(d\, - \,1)}{2}\,x_{t - 2} \,\,\,\, + \,\,\frac{d\,(d\, - 1)\,(d\, - \,2)}{6}\,\,x_{t - 2} \,\,\,\,\, + \,\,\,\,\,\,u_{t} \,\,\,\,\,\,.$$

In other words, xt is a function of all its past history, and the higher its value is, the higher is the level of dependence between observations distant in time. Thus, the parameter d measures the degree of persistence of the series. A very interesting case occurs when d belongs to the interval (0.5, 1), which implies non-stationary but mean-reverting behaviour, with shocks having transitory but long-lived effects. The fact that d might be a fractional value allows for a higher degree of flexibility compared to the standard models based on d = 0 for stationary series and d = 1 for non-stationary ones; in particular, it is more suitable to shed light on whether or not the series is mean-reverting, with shocks having longer lasting effects as the parameter d approaches 1. In a similar way, fractional cointegration allows to test for the existence of a long-run equilibrium relationships within a more general framework.

To estimate d for the individual series, we use the Whittle function in the frequency domain (Dahlhaus, 1989) following the procedure described in Robinson (1994) (see also Gil-Alana & Robinson, 1997). The bivariate analysis is based on the concept of fractional cointegration, and uses the two-step approach of Engle and Granger (1987) extended to the fractional case as in Cheung and Lai (1993) and Gil-Alana (2003) as well as the FCVAR (fractional cointegration vector autoregressive) model proposed by Johansen and Nielsen (2010, 2012).

The latter approach is an extension of the CVAR (Cointegrated Vector AutoRegressive) model (Johansen, 1996) to the fractional case, and it allows for series that are integrated of order d and cointegrate with order d–b, with b > 0. It considers the following model:

$$\Delta^{b} X_{t} \,\,\, = \,\,\,\,\alpha \,\beta^{^{\prime}} \,L_{b} X_{t} \,\,\,\, + \,\,\,\,\sum\limits_{i = 1}^{k} {\Gamma_{i} \,L_{b}^{i} \,X_{t} \,\,\,\,\, + } \,\,\,\,\varepsilon_{t} ,\,\,\,\,\,\,\,\,\,\,\,t\,\,\,\, = \,\,\,\,1\,,\,\,2\,,\,\,...\,,$$
(3)

where \(\,L_{b} \, = \,\,\,(1\,\, - \,\Delta \,^{b} )\) and ∆ is the first difference operator, i.e. (1–L), and Xt is the vector of the time series under examination. Β is a matrix whose columns are the cointegrating relationships in the system, that is to say the long-run equilibria, while Γi is the parameter that governs the short-run behaviour of the variables. The coefficients in α represent the speed of adjustment to the long-run equilibrium in response to temporary deviations from it and the short-run dynamics of the system.

Results and discussion

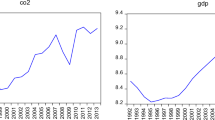
We use quarterly data on real GDP and CO2 emissions in China, from 1978 to 2015, obtained from the Eikon database, which merges data from different sources into a single platform. Figure 1 contains plots of these two series, both of which appear to be upward trended, and also, as additional information, of CO2 intensity (kg per kg of oil equivalent energy use), for the period 1971–2015 (source: the World Bank)—this series is also upward trended but has started to decline most recently.

Fig. 1
figure 1

Time series plots

Full size image

As a first step we examine the orders of integration of the two individual series under examination, i.e. of the logs of CO2 emissions and real GDP, respectively. For this purpose, we consider the following model:

$$y_{t} \,\,\, = \,\,\,\,\alpha \,\,\, + \,\,\,\,\beta \,t\,\,\,\, + \,\,\,\,x_{t} \,,\,\,\,\,\,\,\,\,\,(1\,\, - \,B)^{d} x_{t} \,\,\,\, = \,\,\,\,u_{t} ,\,\,\,\,\,\,\,\,\,\,\,t\,\,\,\, = \,\,\,\,1\,,\,\,2\,,\,\,...\,,$$
(4)

and test the null hypothesis:

$$H_{o} :\,\,\,\,d\,\,\,\, = \,\,\,\,d_{o} ,$$
(5)

in (4) for do-values of − 2, − 1.99, …. − 0.01, 0, 0,01, …, 1.99 and 2 under two alternative assumptions for the I(0) error term ut, namely that it follows a white noise and a weakly autocorrelated process as in the exponential spectral model of Bloomfield (1973), respectively. The latter fits extremely well in the framework suggested by Robinson (1994) and it is stationary for all values unlike the AR (autoregressive) case (see e.g. Gil-Alana, 2004). As for the deterministic terms, we consider the three cases of (i) no terms, (i) a constant, and (iii) a constant and a linear time trend, and choose the specification with statistically significant coefficients. The results are displayed in Table 1.

Table 1 Estimates of d on the individual series. Parametric approach
Full size table

The two individual series appear to be highly persistent. In the case of white noise residuals the estimated values of d are 1.87 and 1.92, respectively, for the log CO2 and log GDP series, and a significant positive time trend is found in the latter case. When allowing for autocorrelation, the estimated values are 1.91 and 1.82, and the null hypothesis of I(2) (integrated of order 2) behaviour cannot be rejected since the 95% confidence intervals include the value of 2 for both series. These values indicate high persistence with shocks having permanent or long-lasting effects both on the levels and the growth rates of the series.

Table 2 displays the estimates of d using the “local” Whittle semi-parametric approach of Robinson (1995). It is semi-parametric in the sense that no specific model is assumed for the I(0) error term. This method (Robinson, 1995) was later extended and improved by Phillips and Shimotsu (2005) and Abadir et al. (2007) among others, but the latter approaches require other user-chosen parameters in addition to the bandwidth and the results are very sensitive to those. When using this method, the estimates must be in the range (− 0.5, 0.5), and therefore we carry out the analysis using the second differences. The null of I(0) behaviour cannot be rejected in any case regardless of the bandwidth parameter. Thus, both the parametric and semi-parametric results indicate that the two series are non-stationary with orders of integration around 2 with shocks having permanent effects and producing changes in the level-trend structure of the data.

Table 2 Estimates of d on the individual series. Semi-parametric approach
Full size table

Next we examine the possibility of fractional cointegration by using in the first instance the method suggested by Gil-Alana (2003), which is an extension of the Engle and Granger (1987) approach to the fractional case. Thus, in the first step, we test for the order of integration of the two variables (in first differences). Since the previous results imply that they are I(1), in the second step, we regress one variable against the other and test whether the residuals are integrated of order d–b, these two parameters corresponding to the orders of integration of the two variables of interest. We display in Tables 3 and 4 the results for the two cases of uncorrelated and autocorrelated errors for three different estimation approaches for the coefficients in the regression model:

Table 3 Cointegrating regression using first differenced data
Full size table
Table 4 FCVAR results for the growth rate series
Full size table

(i) OLS (ordinary least squares) in the time domain, i.e.

$$\frac{{\sum\limits_{t = 1}^{T} {(1\, - \,L)\,\log \,CO2_{t} \,(\,1 - \,L)\,\log \,GDP_{t} } }}{{\sum\limits_{t = 1}^{T} {\left( {(\,1 - \,L)\,\log \,GDP_{t} } \right)^{2} } }};$$
(6)

(ii) OLS in the frequency domain, i.e.

$$\frac{{\sum\limits_{j = 0}^{T - 1} {I_{{(1\, - \,L)\,\log \,CO2_{t} \,(\,1 - \,L)\,\log \,GDP_{t} }} } }}{{\sum\limits_{j = 0}^{T - 1} {I_{{\left( {(\,1 - \,L)\,\log \,GDP_{t} } \right)}} } }},$$
(7)

where λj = 2πj/T, j = 1, …, T are the Fourier frequencies, and where for arbitrary sequences, wt and vt, we define the cross periodogram and periodogram, respectively, as

\(I_{wv\,} (\lambda )\,\,\, = \,\,\,\,\omega_{w} (\lambda )\,\,\omega_{v} ( - \lambda )^{T} \,;\) and \(I_{w} (\lambda )\,\,\, = \,\,\,I_{w\,w} (\lambda )\,\,,\)

with \(\omega (\lambda )\,\) being the discrete Fourier transform of wt: \(\omega_{w} (\lambda )\,\,\, = \,\,\,\,\frac{1}{{\sqrt {2\,\pi \,T} \,}}\,\sum\limits_{t = 1}^{T} {w_{t} \,e^{i\,\lambda \,t} } \,;\)

(iii) finally, we also employ a NBLS (narrow band least squares) estimator, which is related to the band estimator proposed by Hannan (1963), and which is given by

$$\frac{{\sum\limits_{j = 0}^{m} {s_{j} \,{\text{Re}} \,\left[ {I_{(1 - L)\log \,GDP\,\,(1 - L)\,\log \,CO2} \,(\lambda_{j} )\,} \right]} \,}}{{\sum\limits_{j = 0}^{m} {s_{j} \,\,I_{(1 - L)\log \,GDP} } (\lambda_{j} )}}\,,$$
(8)

where 1 ≤ m ≤ T/2, sj = 1 for j = 0, T/2 and sj = 2 otherwise, the motivation for this third approach being that, since cointegration is a long-run phenomenon, when estimating the slope coefficient in the regression model once might be concentrating only on the low frequencies, which are those corresponding to the long-run, hence neglecting information about the high frequencies, which might distort the estimation results (see Gil-Alana & Hualde, 2009).

In the first of these cases, the estimated values of d are 0.83 and 0.87, respectively, and while the I(1) hypothesis cannot be rejected with autocorrelated errors, it is rejected in favour of I(d, d < 1) with white noise residuals, i.e. in the latter case we find mean reversion and fractional cointegration, though with a very slow rate of adjustment; however, when using the frequency domain least squares estimator, the values are much smaller, providing evidence of fractional cointegration in the two cases of uncorrelated and autocorrelated errors; finally, when using the NBLS estimator in (7) the estimates are very sensitive to the choice of the bandwidth parameter and with m = (T)0.5 the null of standard cointegration, i.e. d = b = 1, cannot be rejected. Thus, the results seem to be very sensitive to the estimation method used for the cointegrating regression and the bandwidth parameter, but in all cases there is a reduction in the degree of integration in the long-run equilibrium relationship.

Given the lack of robustness of the above results, we also apply the FCVAR method of Johansen and Nielsen (2010, 2012), first under the assumption that d = b, these two parameters being the order of (fractional) integration of the individual series, which implies that the cointegrating errors will be I(d–b) = I (0). Their estimated order of integration is 1.024, which supports the hypothesis of classical cointegration, with the individual series being I(1) and the cointegrating errors I(0). Further, the null d = b cannot be rejected by means of a LR (likelihood ratio) test, which again implies standard cointegration. This finding is in contrast to the previous test results, which implied that standard cointegration should be rejected in favour of fractional cointegration (i.e. d–b > 0), and suggests that the earlier tests might be biased in favour of higher degrees of integration because of the method used for the estimation of the coefficients in the cointegrating regression (see Gil-Alana, 2003; Gil-Alana & Hualde, 2009). Classical cointegration between the two series, is also supported by the tests of Johansen (1988, 1996) and Johansen and Juselius (1990) (these test results are not reported for reasons of space). Therefore, there is evidence of a stable long-run equilibrium relationship between the growth rates of CO2 emissions and real GDP in China, implying long run co-movement between the two variables.

Concerning the implications of our findings in the context of existing research, one should notice that the previous literature predominantly focused on the causal relationship between energy consumption and economic growth, the determinants of CO2 emissions or the EKC hypothesis, whereas the present study provides novel evidence on the persistence and the link between the growth rates of CO2 emissions and real GDP in China. As for the limitations of our analysis, it should be stressed that it does not investigate the functional form of the equilibrium relationship that has been identified, and also the possible presence of non-linearities and structural breaks; future work could examine these issues by carrying out appropriate tests. Seasonal patterns and turning points could also be relevant in this context and should be a special focus of attention in future research.

Conclusions

This paper has analysed the relationship between the logarithms of CO2 emissions and real GDP in China by applying fractional integration and cointegration methods. These are more general than the standard methods based on the dichotomy between stationary and non-stationary series, allow for a much wider variety of dynamic processes, and provide information about the persistence and long-memory properties of the series and thus on whether or not the effects of shocks are long-lived. For all these reasons, our study makes a novel contribution to the literature. In particular, the univariate results indicate that the two series are non-stationary and highly persistent, their orders of integration being around 2, whilst the cointegration tests (using both standard and fractional techniques) imply that there exists a long-run equilibrium relationship between the two variables in first differences, i.e. their growth rates are linked together in the long run.

Our results also have important policy implications. Specifically, they suggest to policymakers the need for environmental policies aimed at reducing emissions during periods of economic growth: if China wants to be on a sustainable development path, decisive environmental policies appear to be necessary. In particular, the Chinese government should adopt more environmental innovation measures, especially to increase energy efficiency through energy consumption restructuring, to promote social awareness of the advantages of a low-carbon economy and of environmental protection, and to ensure the implementation of environmental protection legislation and compliance; this type of green development also offers new opportunities for entrepreneurship.