Abstract
The behavior of any complex dynamic system is a natural result of the interaction between the components of that system. Important examples of these systems are biological models that describe the characteristics of complex interactions between certain organisms in a biological environment. The study of these systems requires the use of precise and advanced computational methods in mathematics. In this paper, we discuss a prey–predator interaction model that includes two competitive predators and one prey with a generalized interaction functional. The primary presumption in the model construction is the competition between two predators on the only prey, which gives a strong implication of the real-world situation. We successfully establish the existence and stability of the equilibria. Further, we investigate the impact of the memory measured by fractional time derivative on the temporal behavior. We test the obtained mathematical results numerically by a proper numerical scheme built using the Caputo fractional-derivative operator and the trapezoidal product-integration rule.
Similar content being viewed by others
1 Highlights
-
A fractional-order predator–prey system is proposed.
-
The local behavior of the solution is studied.
-
An efficient numerical scheme is used for investigating the solution of the fractional system.
-
Some graphical representations with their biological interpretations are provided.
-
The numerical method also works to solve other similar problems in mathematical biology.
2 Introduction
Mathematical modeling of the real-world phenomenon is a potent tool for predicting some ecological and biological components. The validity of this mathematical approximation depends on the model itself. The crucial component that describes the interaction between different species in a certain environment is the interaction functional. There are many types of these functionals in the literature. Each one describes a specific manner of intermingling between two species. More precisely, let us assume that \(x(t)\) and \(y(t)\) are the densities of the prey and predator populations at the time t, respectively. One of the first interaction functionals is the Holling I interaction functional \(\mathit{ax}(t)y(t)\), where a is the hunting (predation) rate of the prey population by a predator. This functional response is one of the most used tools in the literature. For instance, we refer to [27, 29–38, 42, 43, 49–51]. The issue with this interaction functional is the unboundedness of the consumption of the prey by a predator, which is inconsistent with the actual conditions in nature. To fix this defect, Holling [26] constructed the saturated functional response \(\frac{\mathit{ax}(t)y(t)}{1+\mathit{at}_{h} x(t)}\), where \(t_{h}\) is the average handling time of prey by a predator. This functional resolves the unboundedness of the prey consumption by a predator. There are many other functional responses in the literature. In each case a specific manner on the intermingling between two species has been assumed.
The following items are some related examples:
-
Holling III interaction functional \(\frac{a(x(t))^{2} y(t)}{1+\mathit{at}_{h} (x(t))^{2}}\) [30].
-
Generalized Holling III interaction functional \(\frac{a(x(t))^{2} y(t)}{1+b x(t)+ c (x(t))^{2}}\) [32].
-
Beddington–DeAngelis interaction functional \(\frac{\mathit{ax}(t) y(t)}{1+b x(t)+ c y(t)}\) [28].
-
Ratio-dependent interaction functional \(\frac{\mathit{ax}(t) y(t)}{ x(t)+ y(t)}\) [42, 55].
-
Hassel–Varley interaction functional \(\frac{\mathit{ax}(t) y(t)}{1+b x(t)+ c y(t)}\) [6].
Here all the parameters are assumed to be positive. The reason for this great diversity in functionals is due to the variety of environmental conditions in the problem. Some of the factors that influence the selection of these parameters are the behavior of the prey and predator, and the studied area. For the last factor, many components play a crucial role such as rivers (water availability), food (for the prey), and the density of prey and predator. Overall, the functional selection depends on many factors.
The predator–prey models with three species have been attracted many researchers. In the environment the intermingling is not limited to just two populations, but interactions can be defined between more than two species in one single place. The scientists interested in this point of view have put efforts to model such complex interactions in the last few decades. We can take as an example two types of prey and one predator [15], where the predator has the capability of hunting both prey populations. Moreover, in prey–predator–superpredator models [35] the predator feeds the prey only, and the superpredator feeds both prey and predator. In some models, we study the interaction between two predators and one prey model where two types of predators are fed the same prey. Due to the intrinsic nature of the predators, there will always be a constant struggle to capture this one prey. In real situations, it is seen that one predator determines its own hunting territory. The presence of other predators in such territories is entirely unacceptable. This situation is called competition. The models in which competition is found have also received much attention in many research papers such as [2, 38]. In this paper, we are interested in studying the intermingling and competition between two competitive predators on one prey with a generalized class of interaction functionals in the presence of the time-fractional derivative. In [14], it is highlighted that the fractional-time derivative explains the memory effect of a dynamical system, where the order of the derivative is called the memory rate, and the kernel of the factional derivative is called the memory function. This point of view has been applied in many disciplines such as mathematics, engineering, signal proceeding, mechanics, and especially in mathematical biology [12, 20–24, 39–41, 44]. By summarizing all the previously mentioned components let us focus on the following time-fractional formulation with a generalized consumption functional:
where \(\frac{d^{\delta }}{\mathit{dt}^{\varepsilon }}\) represents Caputo’s derivative in terms of time, which is defined by
The conditions on the functionals f and g are defined as
- \((A_{1})\):
-
\(f(0)=0\), \(g(0)=0\),
- \((A_{2})\):
-
\(f'(x)>0\), \(g'(x)>0\) for \(x>0\).
In model (1), \(x(t)\), \(y(t)\), and \(z(t)\) are the densities of prey, first predator, and other predator populations at time t, respectively. We assume that the prey population reproduces logistically with the increasing rate r and the carrying capacity of the space k, \(e_{1}\) and \(e_{2}\) are respectively the conversion rate of the prey biomass into the first predator population and the diversion of the prey biomass into the second predator biomass, \(\mu _{1}\) and \(\mu _{2}\) are the mortality rates of the first and second predators, respectively, β (resp., γ) is the competition rate of the first predator with the second one (resp., of the second predator with the first one). The functionals f and g are respectively the interaction functionals for the first and second predator populations with the prey population. In the literature, there are a few papers that deal with a generalization of an interaction functional in a three-species model; we refer, for instance, to [29, 37, 45, 49–51], which give an additional motivation to our research. Furthermore, it is been also applied in understanding some epidemiological interactions; we refer, for example, to [3, 4, 16, 17, 31, 36, 46–48]. In nature the interaction between animals is affected by many factors, such as the weather, animal nature, environmental structure, natural resources (water, food), which can affect the interaction between the three studied populations. Hence it is wise to consider a wide class of interaction functionals, which provides a wide choice of applications of the obtained results in predicting the evolution of the species. For more reading about some recent methods of modeling ecological interactions, we refer the readers to [52, 53]. The applicability of model (1) is an additional motivation for us to present this paper. There are many functionals compatible with conditions \((A_{1})\) and \((A_{2})\), including Holling I–III interaction functional. Also, numerous other functionals fit with these functionals (we consider only the functional f, and the same can be assumed for the functional g):
-
\(f(x)=a\sqrt{x}\) [1],
-
\(f(x)=\frac{a\sqrt{x}}{1+\mathit{at}_{h} \sqrt{x}}\) [5],
-
\(f(x)=\mathit{ax}^{\alpha }\) (\(0<\alpha <1\)) [54],
-
\(f(x)=\frac{\mathit{ax}}{1+b\sqrt{x}+\mathit{cx}}\) [8],
-
\(f(x)=\frac{\mathit{ax}^{\alpha }}{1+\mathit{at}_{h} x^{\alpha }}\) [9].
This demonstrates the broad class of interaction functionality that we can consider in this study. For further details, e see [7, 10, 11, 13]. Based on the above-mentioned mathematical and biological backgrounds, the paper is structured as follows:
-
In Sect. 2, we offer some tools that will be useful in dealing with the fractional operator.
-
Sect. 3 is devoted to the mathematical investigation of model (1), where the asymptotic behavior of the solutions is investigated.
-
Sect. 4 offers a numerical scheme for the fractional system (1). The graphical representations of the solution for different parameters are also involved.
-
The concluding section of the paper is intended to highlight the biological meanings of the acquired numerical results.
3 Mathematical analysis and asymptotic behavior of the solution
3.1 Equilibria of the model
In this subsection, we determine the local behavior of system (1). First, we determine the equilibria of system (1), which are the solutions of the following system:
As a first remark, we deduce that system (2) has the following particular cases:
-
(i)
\(O=(0,0,0)\), which represents the extinction of the three populations.
-
(ii)
\(\Gamma _{0}=(k,0,0)\), which implies the extinction of two types of predators. The point is called the predator-free equilibrium (PFE).
-
(iii)
Searching for the first predator-free equilibrium (FPFE) as \(\Gamma _{1}=(x_{1} ,0,z_{1} )\), we insert \(y=0\). By replacing this result in the third equation of system (2) we get \(x_{1}=g^{-1} (\frac{\mu _{2}}{e_{2}} )\), where \(g^{-1}\) is the reciprocal function of g, which exists since g is a bijective function. Substituting this last result into the first equation of (2) yields
$$ z_{1}=\frac{\mathit{rx}_{1} e_{2}}{\mu _{2}} \biggl(1-\frac{x_{1}}{k} \biggr), $$which is positive if \(x_{1}< k\). Summarizing all the results, we can conclude that FPFE \(\Gamma _{1}=(x_{1},0,z_{1})\) exists if \(x_{1}< k\).
-
(iv)
Seeking for the second predator-free equilibrium (SPFE) \(\Gamma _{1}=(x_{2}, y_{2} ,0)\) by replacing \(z=0\) in (2). By substituting this result into the second equation of system (2) we get \(x_{2}=f^{-1} (\frac{\mu _{1}}{e_{1}} )\), where \(f^{-1}\) is the inverse function of f, which exists since f is a bijective function. Taking this last result along with the first equation of (2), we get
$$ y_{2}=\frac{\mathit{rx}_{2} e_{1}}{\mu _{1}} \biggl(1-\frac{x_{2}}{k} \biggr), $$which is biologically relevant if \(x_{2}< k\). Summarizing all the results, we can deduce that SPFE \(\Gamma _{2}=(x_{2},y_{2},0)\) exists if \(x_{2}< k\).
Remark 1
It is assumed that both functional f and g are increasing in x. From \(x_{2}\) and \(x_{1}\), if \(\lim_{x \rightarrow +\infty } f(x)=a\) (resp., \(\lim_{x \rightarrow +\infty } g(x)=b\)), then another condition on the parameters arises, \(\frac{\mu _{1}}{e_{1}}< a\) (resp., \(\frac{\mu _{2}}{e_{2}}< b\)), which is a necessary condition for having a solution for the equation \(f(x)=\frac{\mu _{1}}{e_{1}}\) (resp., \(g(x)=\frac{\mu _{2}}{e_{2}}\)). This feature can be seen in the Holling II–III interaction functional.
-
(v)
Now we are in a position to seek the coexistence equilibrium, which is the positive solution of the following system:
$$ \begin{gathered} 0=\mathit{rx}\biggl(1-\frac{x}{k} \biggr)-f(x) y - g(x) z, \\ 0=e_{1} f(x) -\mu _{1} -\beta z, \\ 0=e_{2} g(x) - \mu _{2} -\gamma y .\end{gathered} $$(3)From \(e_{2} g(x) - \mu _{2} -\gamma y =0\) we obtain
$$ y=\frac{e_{2}}{\gamma }g(x)-\frac{\mu _{2}}{\gamma }. $$(4)Moreover, from \(e_{1} f(x) -\mu _{1} -\beta z=0\) we find that
$$ z=\frac{e_{1}}{\beta }f(x)-\frac{\mu _{1}}{\beta }. $$(5)Substituting (4) and (5) into the first equation of (3), we get \(F_{1} (x)=F_{2} (x)\), where
$$ F_{1} (x)= \mathit{rx}\biggl(1-\frac{x}{k}\biggr),\qquad F_{2} (x)= f(x) g(x) \biggl( \frac{e_{2}}{\gamma }+ \frac{e_{1}}{\beta } \biggr)- \biggl( \frac{\mu _{2}}{\gamma }f(x)+ \frac{\mu _{1}}{\beta }g(x) \biggr). $$Some straightforward calculations suggest that
$$ F_{1} (0)=F_{1} (k)=0, \qquad F_{1} (x)= \textstyle\begin{cases} >0 &\text{for } x< \frac{k}{2}, \\ < 0& \text{for } x> \frac{k}{2}. \end{cases} $$To guarantee at least one nontrivial intersection between two curves of the functionals \(F_{1}\) and \(F_{2}\), we introduce the following assumption:
$$ F_{1} (\tilde{x})>F_{2} (\tilde{x}), \qquad F_{2} (k)>0\quad \text{with } \tilde{x}=\max \{x_{1},x_{2} \}, $$which it can be rewritten as
$$\begin{aligned} (H_{1}): \quad &\tilde{x}< k,~e_{2} >e_{2} ^{*} := \frac{f(k) g(k) (\frac{e_{2}}{\gamma }+ \frac{e_{1}}{\beta } )- ( \frac{\mu _{2}}{\gamma }f(k)+\frac{\mu _{1}}{\beta }g(k) )}{\beta f(k)g(k)}-e_{1} \gamma , \\ &r>r_{E}:= \frac{k [f(\tilde{x}) g(\tilde{x}) (\frac{e_{2}}{\gamma }+ \frac{e_{1}}{\beta } )- ( \frac{\mu _{2}}{\gamma }f(\tilde{x})+\frac{\mu _{1}}{\beta }g(\tilde{x}) ) ]}{\tilde{x}(k-\tilde{x})}. \end{aligned}$$Under condition \((H_{1})\), we get the existence of at least one nonnegative solution of system (3).
Remark 2
-
(i)
If \(\tilde{x}>k\), then system (3) has no solution.
-
(ii)
The condition \(F_{1} (\tilde{x})>F_{2} (\tilde{x})\) came from the fact that \(F_{1} '(0)=- ( \frac{\mu _{2}}{\gamma }f(0)+ \frac{\mu _{1}}{\beta }g(0) )<0\) (thus we can have \(F_{1} '(\upsilon )<0\) for υ sufficiently small).
3.2 Asymptotic behavior of (1)
In this part, we are interested in determining the asymptotic stability of the equilibria obtained in the previous section.
Remark 3
Consider the following fractional-order system:
where \(\varepsilon \in (0,1)\), \(A\in \mathbb{R}^{i\times i}\), and \(\varphi \in C^{1}(\mathbb{R}^{i},\mathbb{R}^{i})\) with \(D\varphi (0)=0\). For the time-fractional-order derivative, the concept of the local stability is very different from the first-order derivative, where in this case, we have an expansion of the stability region in comparison with the first-order derivative.
Let \((x,y,z)\) be an equilibrium for system (1). The Jacobian matrix of system (1) at \((x,y,z)\) is expressed as
At the predator-free equilibrium the Jacobian matrix (7) reduces into
The Jacobian matrix (8) has the eigenvalues \(\vartheta _{1}=-r<0\), \(\vartheta _{2}=e_{1} f(k)-\mu _{1}\), and \(\vartheta _{3}=e_{2} g(k) -\mu _{2} \). Hence
and
which means that the eigenvalues \(\vartheta _{i}\), \(i=1,2,3\), satisfy \(|\arg (\vartheta _{i})|>\frac{\varepsilon \pi }{2}\) if and only if \(x<\bar{x}:=\min \{x_{1} ,x_{2}\}\); in this case the predator-free equilibrium is locally stable, and it is unstable for \(x>\bar{x}\). We summarize the obtained results in the following lemma.
Lemma 1
The predator-free equilibrium is locally stable if \(x<\bar{x}\) and unstable if \(x>\bar{x}\).
Now we analyze the linear stability of FPFE point of \(\Gamma _{1}\). The Jacobian matrix corresponding to the equilibrium FPFE is evaluated as
As a first look, we can deduce that \(\vartheta _{2}= e_{1} f(x_{1} )-\mu _{1} -\beta z_{1}\) is an eigenvalue of the Jacobian matrix (9). By replacing the explicit formula of \(z_{1}\) we obtain \(\vartheta _{2}= e_{1} f(x_{1} )-\mu _{1} - \frac{\beta \mathit{rx}_{1} e_{2}}{\mu _{2}} (1-\frac{x_{1}}{k} )\). Obviously, if \(e_{1} f(x_{1} )-\mu _{1}<0\) (equivalent to \(x_{1} < x_{2}\)), then \(|\arg (\vartheta _{2})|>\frac{\varepsilon \pi }{2}\). Now we presume that if \(e_{1} f(x_{1} )-\mu _{1}>0\) (equivalent to \(x_{1} >x_{2}\)), then
Under the condition \(\vartheta _{2}>0\), we get \(|\arg (\vartheta _{2})|<\frac{\varepsilon \pi }{2}\). This means that FPFE is an unstable equilibrium point. Besides, from \(\vartheta _{2}>0\) we conclude that \(|\arg (\vartheta _{2})|<\frac{\varepsilon \pi }{2}\). This means that two remaining eigenvalues of the Jacobian matrix (9) determine the stability (resp., instability) of this equilibrium. Note that these significant eigenvalues are the eigenvalues of the matrix
To determine the nature of the eigenvalues of the reduced matrix (10), we define the characteristic equation of (10) as
where
where \(A=-2+\frac{g'(x_{1})x_{1} e_{2}}{\mu _{2}}\). To determine the sign of \(\Lambda _{1}\), the following results arise.
Lemma 2
Assuming \(x_{1} < k\), we obtain the following results:
-
(i)
\(\Lambda _{1}\leq 0\) if (\(-1\leq A\leq 0\)) or (\(A>0\) and \(k\leq k_{1} :=\frac{Ax_{1}}{1+A}\)) or (\(A<-1\) and \(k\leq k_{1} \)).
-
(ii)
\(\Lambda _{1} >0\) if (\(A>0\) and \(k< k_{1}\)) or (\(A<-1\) and \(k> k_{1} \)).
Proof
The proof can be easily deduced from the explicit formula of Λ. □
From Lemma 2, we can see that \(\Lambda _{1} \leq 0\) next to \(\Lambda _{2}>0\) gives \(|\arg \{\vartheta _{1,2}\}|>\frac{\varepsilon \pi }{2}\), which means that this equilibrium is stable. Now assume that \(\Lambda _{1} >0\) (which means that the second assumption of Lemma 2 holds). In this situation, (11) admits two complex roots of \(\vartheta _{\pm }=a_{1} \pm a_{2} i\), \(a_{1}, a_{2} \in \mathbb{R}\). Then these roots satisfy
To guarantee the stability of the equilibrium, we must have \(\tan ^{2} ( \arg \{ \vartheta _{i} \} ) > \tan ^{2} ( \frac{\varepsilon \pi }{2} ) \), \(i=1,2\), which implies that
Obviously, it is unstable for \(r>r^{*}\). Hence we resume the stability conditions for the equilibrium \((x_{1},0,z_{1})\) by the following theorem.
Theorem 1
If \(x_{1}< k\), then we have:
-
(i)
If \(x_{1} > x_{2}\) and \(r< r_{1}\), then the FPFE is unstable.
-
(ii)
For (\(x_{1} < x_{2}\) or (\(x_{1} > x_{2}\) and \(r>r_{1}\))), under condition (i) in Lemma 2, we get the local stability of FPFE.
-
(iii)
(\(x_{1} < x_{2}\) or (\(x_{1} > x_{2}\) and \(r>r_{1}\))), condition (ii) in Lemma 2, and \(r< r^{*}\) give the local stability of FPFE.
-
(vi)
(\(x_{1} < x_{2}\) or (\(x_{1} > x_{2}\) and \(r>r_{1}\))), condition (ii) in Lemma 2, and \(r>r^{*}\) imply that FPFE is unstable.
To study the stability of the SPFE of \(\Gamma _{2}\), we construct the Jacobian matrix
Obviously, \(\vartheta _{3}= e_{2} g(x) -\mu _{2} -\gamma y_{2}\) is an eigenvalue of the Jacobian matrix (12). Replacing \(y_{2}=\frac{\mathit{rx}_{2} e_{1}}{\mu _{1}} (1-\frac{x_{2}}{k} )\) in \(\vartheta _{3}\), we obtain \(\vartheta _{3}= e_{2} g(x_{2}) -\mu _{2} - \frac{\gamma \mathit{rx}_{2} e_{1}}{\mu _{1}} (1-\frac{x_{2}}{k} )\). Obviously, if \(e_{2} g(x_{2}) -\mu _{2}<0\) (equivalent to \(x_{1} >x_{2}\)), then \(|\arg (\vartheta _{3})|>\frac{\varepsilon \pi }{2}\). Now we suppose that \(e_{2} g(x_{2}) -\mu _{2}>0\) (equivalent to \(x_{1} < x_{2}\)). Then
For \(\vartheta _{3}>0\), we obtain \(|\arg (\vartheta _{3})|<\frac{\varepsilon \pi }{2}\), which means that SPFE is unstable. In fact, for \(\vartheta _{3}>0\), we get \(|\arg (\vartheta _{3})|<\frac{\varepsilon \pi }{2}\). This means that the other two eigenvalues of the Jacobian matrix (12) determine the stability (resp., instability) of this equilibrium. These eigenvalues are the eigenvalues of the matrix
The nature of the eigenvalues of the reduced matrix (13) can be determined through the quadratic equation
where
where \(B=1-\frac{f'(x_{2})x_{2} e_{2}}{\mu _{1}}\).
To prove the positivity of \(\Xi _{1}\), we use the following lemma.
Lemma 3
Let \(x_{2} < k\). Then:
-
(i)
\(\Xi _{1}\leq 0\) if (\(-1\leq B\leq 0\)) or (\(B>0\) and \(k\leq k_{2} :=\frac{1+B}{Bx_{1}}\)) or (\(B<-1\) and \(k\geq k_{1} \)).
-
(ii)
\(\Xi _{1} >0\) if (\(A>0\) and \(k> k_{2}\)) or (\(A<-1\) and \(k< k_{2} \)).
Proof
Form the explicit formula of Ξ we can determine its positivity. The proof is completed. □
From Lemma 2, we can see that \(\Xi _{1} \leq 0\) and \(\Xi _{2}>0\) lead to \(|\arg \{\vartheta _{1,2}\}|>\frac{\varepsilon \pi }{2}\), and hence the SPFE is stable. Now assume that \(\Lambda _{1} >0\) (which means that the second assumption of Lemma 3 holds). In this case, equation (14) has complex roots \(\vartheta _{\pm }=b_{1} \pm b_{2}\), \(b_{1} b_{2} \in \mathbb{R}\). Then we get
To ensure the stability of SPFE, we must have \(\tan ^{2} ( \arg \{ \vartheta _{i} \} ) > \tan ^{2} ( \frac{\varepsilon \pi }{2} ) \), \(i=1,2\), which implies that
and it is unstable for \(r>r^{**}\). We summarize the obtained results in the following theorem.
Theorem 2
Let \(x_{2}< k\). Then:
-
(i)
If \(x_{1} < x_{2}\) and \(r< r_{2}\), then the SPFE is unstable.
-
(ii)
If ((\(x_{1}>x_{2}\)) or (\(x_{1} < x_{2}\) and \(r>r_{2}\))) and condition (i) in Theorem 1is satisfied, then the SPFE is stable.
-
(iii)
((\(x_{1}>x_{2}\)) or (\(x_{1} < x_{2}\) and \(r>r_{2}\))), condition (ii) in Theorem 1, and \(r< r^{**}\) imply that the SPFE is stable.
-
(vi)
((\(x_{1}>x_{2}\)) or (\(x_{1} < x_{2}\) and \(r>r_{2}\))), condition (ii) in Theorem 1, and \(r>r^{**}\) imply that the SPFE is unstable.
Now we are in a position to focus on studying the local behavior of the coexistence equilibrium. For this equilibrium, we suppose that assumption \((H_{1})\) holds. The Jacobian matrix at this equilibrium is expressed as
The characteristic equation associated with Jacobian (16) is
where
Let
Using the Routh–Hurwitz stability criterion for fractional calculus defined in [19], we get the stability conditions for the nontrivial equilibrium.
Theorem 3
The positive equilibrium is stable if one of the following assumptions holds:
-
(i)
\(D>0\), \(\Phi _{2}>0\), \(\Phi _{0}>0\), \(\Phi _{2}\Phi _{1}>\Phi _{0}\).
-
(ii)
\(D<0\), \(\Phi _{2}\geq 0\), \(\Phi _{1}\geq 0\), \(\Phi _{0}\geq 0\), and \(\varepsilon <\frac{2}{3}\).
4 Numerical analysis of system (1)
4.1 A numerical scheme
The main purpose of this section is to numerically solve the following fractal problem:
By applying the fundamental theorem of fractional calculus on (1) we get
Letting \(t=t_{n}=n\hslash \) in (18), we arrive at
Now we can approximate the function \({P}(t, V(t))\) by the following linear approximation:
with the notation \(V_{i}= V(t_{i})\).
By substituting Eq. (20) into (19) and applying some algebra (for more detail, see [18]) we get
with
Using the numerical method presented in formula (21) to solve problem (1), we obtain the following iterative schemes:
where
4.2 Applications and graphical representations
4.2.1 Example 1
In this section, we numerically investigate system (1) to ensure the obtained results in the previous sections. First, we choose the functional f to be a Holling II interaction functional \(f(x)=\frac{\mathit{ax}}{1+\mathit{at}_{h} x}\). Then \(f^{-1}(x)=\frac{x}{a(1-t_{h} x)}\), and based on Remark 3.1 for the existence of \(x_{2}\), we must have \(\frac{\mu _{1}}{e_{1}}<\frac{1}{t_{h}}\), and the functional g to be a Holling I interaction functional.
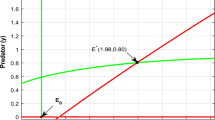
Figure 1 We consider the following parameters:
For these values, we obtain the local stability of FPFE. Indeed, these values satisfy \(x_{1} =x_{2}\) and \(\Lambda _{1}= -1.309<0\) (condition (i) in Lemma 2), which means that condition (ii) in Theorem 2 holds.
Figure 2 We consider the following parameters:
For these values, we get the local stability of the SPFE \(\Gamma _{2} =(0.0497,0.0346,0)\). More precisely, these values satisfy \(r< r_{1} = 1.12\), which means that \(\Gamma _{1} =(0.3,0,0.145)\) is unstable and satisfy the second condition of Theorem 3 (\(x1>x2\) and \(\Psi _{1}=0.148>0\)), which means that the SPFE is stable.
Figure 3 We set the following values of parameters:
Figure 4 We consider
and multivalues of the memory rate. In this example, we realize the effect of the memory on the stability of SPFE. More precisely, this figure highlights that the memory has a huge influence on the condition of the stability obtained in (15), which shows a great agreement between the theoretical findings and numerical ones, and thus we conclude the efficiency of the obtained numerical method.
4.2.2 Example 2
In this example, we consider another behavior of the prey population known by herd behavior (see [1, 34, 56]). In fact, we consider the functionals \(f(x)=a x^{\alpha }\) and \(g(x)=b x^{\alpha }\), where \(0<\alpha <1\) represents the herd shape rate. Thus \(f^{-1} (x)= (\frac{x}{a} )^{\frac{1}{\alpha }}\) and \(g^{-1} (x)= (\frac{x}{b} )^{\frac{1}{\alpha }}\). For the graphical representations, we take the following values of parameters.
Figure 5 In this figure, we consider the values
These values provide the local stability of the SPFE.
Figure 6 We considered the same values as in Fig. 5, except \(\alpha =0.8\). This leads to the instability of the SPFE and the occurrence of oscillations of the solution.
Figure 7 In this figure, we have taken
These values provide the instability of the FPFE.
Figure 8 In this figure, we consider the following choices:
These values provide the instability of the SPFE.
Figure 9 We consider the values
For these values, we have studied the effect of the memory rate on the stability of the SPFE.
Figure 10 The following values are used in numerical simulations
Using these values, we can investigate the effect of the memory rate on the stability of the FPFE.
5 Conclusions
In this research, we studied an ecological model with two predators fighting on one prey with a generalized functional response. The reason behind considering a comprehensive generalized class of functional interaction is to model the diversity in predator–prey interaction with the environment. These interactions can be affected by many factors, such as the environment and the adaptation of the three species. In the first section, we studied the existence of the equilibria of system (1), where we can have many equilibrium points next to the predator-free equilibrium. By analyzing the existence of the equilibria we obtained that these populations may have many scenarios. They include the extinction of three populations, two types of predators, the extinction of each population of predators, and finally the coexistence of the three populations. For the coexistence stage, we provided some conditions on the model parameters for the existence of this equilibrium. To determine which scenario will prevail, we have utilized the local asymptotic stability using the Jacobian matrix. Further, we proposed a numerical scheme to find an approximate solution of the fractional-derivative system (1), which is based on the trapezoidal product-integration rule. For the application part, we have utilized two examples. The first example models the interaction of the three populations in the case of the solitary behavior for the prey population. We obtained an excellent agreement between the mathematical results and graphical representation, which proves the accuracy of the obtained approximations by proposed iterative schemes. In fact, in the case of the extinction of the second predator, two sceneries may happen. The first case is to stabilize on the SPFE as it has been highlighted in Fig. 1 for the prey solitary behavior (PSB) of the prey population. Moreover, Fig. 5 displays the case of the prey herd behavior (PHB). The second case corresponds to the instability of the SPFE and the presence of oscillations. The numerical simulations for this case have been plotted in Fig. 7, and also Fig. 8 for PHB. The same remark is obtained for the extinction of the first predator population, presented in Figs. 2, 3, 7, in different cases (the stability and instability of SPFE). Furthermore, the effect of the memory rate measured by the time-fractional derivative order ε is established numerically in Figs. 4, 9, 10. In these figures, we proved that the memory rate can destabilize the equilibrium states, which demonstrates the importance of considering it in the model construction, where in the real-world, the influence of the time-fractional-order derivative can represent the influence of these two populations on the hunting. Further, we can highlight that system (1) undergoes Hopf bifurcation at FPFE and SPFE at \(r=r^{*}\) for FPFE. Moreover, at \(r=r^{**}\) system undergoes Hopf bifurcation for FPFE. The oscillatory behaviors generated by these equilibria are presented in Figs. 3, 4, 6, 7, 8, 9. For more detail about the proof, we refer to the readers to [25]. Based on the obtained results in this contribution, the diversity of the ecological systems can be measured by the choice of the functional response.
Availability of data and materials
Not applicable.
References
Ajraldi, V., Pittavino, M., Venturino, E.: Modelling herd behaviour in population systems. Nonlinear Anal., Real World Appl. 12(4), 2319–2338 (2011)
Arditi, R., Abillon, J.M., Vieira Da Silva, J.: A predator-prey model with satiation and intraspecific competition. Ecol. Model. 5(3), 173–191 (1978)
Bessonov, N., Bocharov, G., Touaoula, T.M., Trofimchuk, S., Volpert, V.: Delay reaction–diffusion equation for infection dynamics. Discrete Contin. Dyn. Syst., Ser. B 24(5), 2073–2091 (2019)
Boudjema, I., Touaoula, T.M.: Global stability of an infection and vaccination age-structured model with general nonlinear incidence. J. Nonlinear Funct. Anal. 2018(33), 1–21 (2018)
Braza, A.P.: Predator–prey dynamics with square root functional responses. Nonlinear Anal., Real World Appl. 13, 1837–1843 (2012)
Chen, X., Du, Z.: Existence of positive periodic solutions for a neutral delay predator–prey model with Hassell–Varley type functional response and impulse. Qual. Theory Dyn. Syst. 17(1), 67–80 (2017)
Dai, Y., Zhao, Y., Sang, B.: Four limit cycles in a predator–prey system of Leslie type with generalized Holling type III functional response. Nonlinear Anal., Real World Appl. 50, 218–239 (2019)
Djilali, S.: Herd behaviour in a predator–prey model with spatial diffusion: bifurcation analysis and Turing instability. J. Appl. Math. Comput. 58, 125–149 (2018)
Djilali, S.: Impact of prey herd shape on the predator–prey interaction. Chaos Solitons Fractals 120, 139–148 (2019)
Djilali, S.: Pattern formation of a diffusive predator–prey model with herd behavior and nonlocal prey competition. Math. Methods Appl. Sci. (2019). https://doi.org/10.1002/mma.6036
Djilali, S.: Effect of herd shape in a diffusive predator–prey model with time delay. J. Appl. Anal. Comput. 9(2), 638–654 (2019)
Djilali, S., Ghanbari, B.: The influence of an infectious disease on a prey–predator model equipped with a fractional-order derivative. Adv. Differ. Equ. 2021, 20 (2021)
Djilali, S., Touaoula, T.M., Miri, S.E.H.: A heroin epidemic model: very general non linear incidence, treat-age, and global stability. Acta Appl. Math. 152(1), 171–194 (2017)
Du, M., Wang, Z., Hu, H.: Measuring memory with the order of fractional derivative. Sci. Rep. 3, 3431 (2013). https://doi.org/10.1038/srep03431
Elettreby, M.F.: Two-prey one-predator model. Chaos Solitons Fractals 39(5), 2018–2027 (2009)
Frioui, M.N., Miri, S.E.-H., Touaoula, T.M.: Unified Lyapunov functional for an age-structured virus model with very general nonlinear infection response. J. Appl. Math. Comput. 58(5–6), 47–73 (2017)
Frioui, M.N., Touaoula, T.M., Ainseba, B.E.: Global dynamics of an age-structured model with relapse. Discrete Contin. Dyn. Syst., Ser. B 25(6), 2245–2270 (2020)
Garrappa, R.: Numerical solution of fractional differential equations: a survey and a software tutorial. Mathematics 6(2), 1–16 (2018)
Ghanabri, B., Djilali, S.: Mathematical and numerical analysis of a three-species predator–prey model with herd behavior and time-fractional-order derivative. Math. Methods Appl. Sci. (2019). https://doi.org/10.1002/mma.5999
Ghanbari, B.: On approximate solutions for a fractional prey–predator model involving the Atangana–Baleanu derivative. Adv. Differ. Equ. 2020, 679 (2020)
Ghanbari, B.: On the modeling of the interaction between tumor growth and the immune system using some new fractional and fractional-fractal operators. Adv. Differ. Equ. 2020, 585 (2020)
Ghanbari, B.: A fractional system of delay differential equation with nonsingular kernels in modeling hand-foot-mouth disease. Adv. Differ. Equ. 2020, 536 (2020)
Ghanbari, B.: On novel nondifferentiable exact solutions to local fractional Gardner’s equation using an effective technique. Math. Methods Appl. Sci. (2020). https://doi.org/10.1002/mma.7060
Ghanbari, B., Atangana, A.: Some new edge detecting techniques based on fractional derivatives with non-local and non-singular kernels. Adv. Differ. Equ. 2020, 435 (2020)
Ghanbari, B., Djilali, S.: Mathematical and numerical analysis of a three-species predator–prey model with herd behavior and time fractional-order derivative. Math. Methods Appl. Sci. 43(4), 1736–1752 (2020)
Holling, C.S.: The functional response of invertebrate predator to prey density. Mem. Entomol. Soc. Can. 45, 3–60 (1965)
Huang, J., Gong, Y., Ruan, S.: Bifurcation analysis in a predator-prey model with constant-yield predator harvesting. Discrete Contin. Dyn. Syst., Ser. B 1(8), 2101–2121 (2013)
Hwang, T.-W.: Global analysis of the predator–prey system with Beddington–DeAngelis functional response. J. Math. Anal. Appl. 281(1), 395–401 (2001)
Jia, Y., Xue, P.: Effects of the self- and cross-diffusion on positive steady states for a generalized predator–prey system. Nonlinear Anal., Real World Appl. 32, 229–241 (2016)
Kar, T.K., Matsuda, H.: Global dynamics and controllability of a harvested prey–predator system with Holling type III functional response. Nonlinear Anal. Hybrid Syst. 1(1), 59–67 (2007)
Kuniya, T., Touaoula, T.M.: Global stability for a class of functional differential equations with distributed delay and non-monotone bistable nonlinearity. Math. Biosci. Eng. 17(6), 7332–7352 (2020)
Liu, X., Liu, Y., Li, Q.: Multiple bifurcations and chaos in a discrete prey–predator system with generalized Holling III functional response. Discrete Dyn. Nat. Soc. (2015). https://doi.org/10.1155/2015/245421
Ma, Z., Li, W., Zhao, Y., Wang, W., Zhang, H., Li, Z.: Effects of prey refuges on a predator-prey model with a class of functional responses: the role of refuges. Math. Biosci. 218(2), 73–79 (2009)
Martina, I., Venturino, E.: Shape effects on herd behaviour in ecological interacting population models. Math. Comput. Simul. (2017). https://doi.org/10.1016/j.matcom.2017.04.009
Mbava, W., Mugisha, J.Y.T., Gonsalves, J.W.: Prey, predator and super-predator model with disease in the super-predator. Appl. Math. Comput. 297, 92–114 (2017)
Michel, P., Touaoula, T.M.: Asymptotic behavior for a class of the renewal nonlinear equation with diffusion. Math. Methods Appl. Sci. 36(3), 323–335 (2013)
Moghadas, S.M., Corbett, B.D.: Limit cycles in a generalized Gause-type predator–prey model. Chaos Solitons Fractals 37(5), 1343–1355 (2008)
Persson, L.: Behavioral response to predators reverses the outcome of competition between prey species. Behav. Ecol. Sociobiol. 28, 101–105 (1991)
Rezazadeh, H.: New solitons solutions of the complex Ginzburg–Landau equation with Kerr law nonlinearity. Optik 167, 218–227 (2018)
Rezazadeh, H., Inc, M., Baleanu, D.: Solutions for variants of (3 + 1)-dimensional Wazwaz–Benjamin–Bona–Mahony equations. Front. Phys. 8, 332 (2020)
Rezazadeh, H., Mirhosseini-Alizamini, S.M., Eslami, M., Rezazadeh, M., Abbagari, S.: New optical solitons of nonlinear conformable fractional Schrödinger–Hirota equation. Optik 172, 545–553 (2018)
Sen, M., Banerjee, M., Morozov, A.: Bifurcation analysis of a ratio-dependent prey–predator model with the Allee effect. Ecol. Complex. 11, 12–27 (2012)
Song, Y., Yuan, S.: Bifurcation analysis in a predator–prey system with time delay. Nonlinear Anal., Real World Appl. 7, 265–284 (2006)
Srivastava, H.M., Baleanu, D., Machado, J.A.T., Osman, M.S., Rezazadeh, H., Arshed, S., Gunerhan, H.: Traveling wave solutions to nonlinear directional couplers by modified Kudryashov method. Phys. Scr. 95(7), 075217 (2020)
Tao, Y., Wang, X., Song, X.: Effect of prey refuge on a harvested predator–prey model with generalized functional response. Commun. Nonlinear Sci. Numer. Simul. 16(2), 1052–1059 (2011)
Touaoula, T.M.: Global dynamics for a class of reaction–diffusion equations with distributed delay and Neumann condition. Commun. Pure Appl. Anal. 19(5), 2473–2490 (2018)
Touaoula, T.M.: Global stability for a class of functional differential equations (application to Nicholson’s blowflies and Mackey–Glass models). Discrete Contin. Dyn. Syst. 38(9), 4391–4419 (2018)
Touaoula, T.M., Frioui, M.N., Bessonov, N., Volpert, V.: Dynamics of solutions of a reaction-diffusion equation with delayed inhibition. Discrete Contin. Dyn. Syst. 13(9), 2425–2442 (2018)
van Leeuwena, E., Brannstrom, A., Jansen, V.A.A., Dieckmann, U., Rossberg, A.G.: A generalized functional response for predators that switch between multiple prey species. J. Theor. Biol. 328, 89–98 (2013)
Wang, S., Ma, Z., Wang, W.: Dynamical behavior of a generalized eco-epidemiological system with prey refuge. Adv. Differ. Equ. 2018, 244 (2018)
Wang, Z., Xie, Y., Lu, J., Li, Y.: Stability and bifurcation of a delayed generalized fractional-order prey–predator model with interspecific competition. Appl. Math. Comput. 347, 360–369 (2019)
Xie, Y., Wang, Z., Lu, J., Li, Y.: Stability analysis and control strategies for a new SIS epidemic model in heterogeneous networks. Appl. Math. Comput. 383, 125381 (2020)
Xie, Y., Wang, Z., Meng, B., Huang, X.: Dynamical analysis for a fractional-order prey–predator model with Holling III type functional response and discontinuous harvest. Appl. Math. Lett. 106, 106342 (2020)
Xu, C., Yuan, S., Zhang, T.: Global dynamics of a predator-prey model with defense mechanism for prey. Appl. Math. Lett. 62, 42–48 (2016)
Xu, R., Gan, Q., Ma, Z.: Stability and bifurcation analysis on a ratio-dependent predator–prey model with time delay. J. Comput. Appl. Math. 230, 187–203 (2009)
Zhang, F., Li, Y., Li, C.: Hopf bifurcation in a delayed diffusive Leslie–Gower predator–prey model with herd behavior. Int. J. Bifurc. Chaos 29(4), 1950055 (2019)
Acknowledgements
S. Djilali is partially supported by the DGRSDT of Algeria No. C00L03UN130120200004. We also thank the anonymous referees for their suggestions, which were significantly helpful in improving the presentation of the paper.
Funding
This research work is not supported by any funding agencies.
Author information
Authors and Affiliations
Contributions
Both authors contributed equally and significantly in writing this paper. Both authors have read and approved the final paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Djilali, S., Ghanbari, B. Dynamical behavior of two predators–one prey model with generalized functional response and time-fractional derivative. Adv Differ Equ 2021, 235 (2021). https://doi.org/10.1186/s13662-021-03395-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-021-03395-9