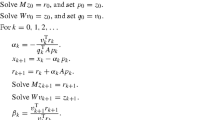1 Introduction

It is well known that linear matrix equations play crucial roles in control theory and related areas. Indeed, certain problems concerning analysis and design of control systems (e.g., existence of solutions or controllability/observability of the system) are converted to properties of associated matrix equations; see, for example, [1, Chs. 12–13] and [2]. Such matrix equations are particular cases of or closely related to the generalized Sylvester matrix equation

$$ AXB+CXD = E, $$
(1)

where \(A,B,C,D,E\) are given matrices, and X is an unknown matrix. This equation includes the equation \(AXB=E\), the Lyapunov equation \(AX+XA^{T} = E\), the (continuous-time) Sylvester equation \(AX+XB=E\), and the Kalman–Yakubovich equation or the discrete-time Sylvester equation \(AXB+X = E\). The generalized Sylvester equation naturally arises in robust control, singular system control, neural network, and statistics; see, foe example, [3, 4]. An important particular case of (1), the Sylvester equation, also has applications to image restoration and numerical methods for implicit ordinary differential equations; see, for example, [5, 6].

Let us discuss how to solve (1) via the direct Kronecker linearization. We can convert the matrix equation (1) into a vector–matrix equation by taking the vector operator \(\operatorname {vec}(\cdot )\) so that (1) is reduced to \(Px = b\), where

$$\begin{aligned} P = B^{T}\otimes A+D^{T}\otimes C,\qquad x = \operatorname {vec}X,\qquad b = \operatorname {vec}E. \end{aligned}$$

Here the symbol ⊗ denotes the Kronecker product. Thus Eq. (1) has a unique solution if and only if P is nonsingular. However, if the dimensions of matrices are large, then it will lead to computational difficulty, and so this approach is only applicable for small-dimensional matrices. For more information about analytical methods for solving such linear matrix equations, see, for example, [1, Ch. 12], [7, Ch. 4], and [8, Sect. 7.1]. Another technique is transforming the coefficient matrix into a Schur or Hessenberg form via an orthogonal transformation; see [9, 10].

For large matrix systems, iterative methods for solving matrix equations have received much attention. There are several ideas to formulate an iterative procedure for solving Eq. (1) and particular cases, for example, block successive overrelaxation [11], matrix sign function [12], block recursion [13, 14], Krylov subspace [15, 16], and truncated low-rank methods [17]. A group of iterative methods, called Hermitian and skew-Hermitian splitting (HSS) methods, relies on the fact that every square complex matrix can be written as the sum of its Hermitian and skew-Hermitian parts. Recently, there are several variants of HSS, namely, the generalized modified HSS (GMHSS) method [18], the accelerated double-step scale splitting (ADSS) method [19], the preconditioned HSS (PHSS) method [20], and the four-parameter positive skew-Hermitian splitting (FPPSS) method [21]. The idea of conjugate gradient (CG) also leads to several finite-step procedures to obtain the exact solution of the linear matrix equations. The principle of CG is constructing an orthogonal basis from the gradient of the associated quadratic function, consisting of vectors in the direction that approaches the fastest the exact solution. There are several variants of CG to solve such linear matrix equations, for example, the generalized conjugate direction (GCD) method [22], the conjugate gradient least-squares (CGLS) method [23], and generalized product-type methods based on biconjugate gradient (GPBiCG) method [24]. See more information in a survey [8] and references therein.

A group of gradient-based iterative algorithms relies on the ideas of hierarchical identification principle and minimization of quadratic norm-error functions; see, for example, [25–31]. Convergence analysis for such algorithms depends on the Frobenius norm \(\lVert \cdot \rVert _{F}\), the spectral norm \(\lVert \cdot \rVert _{2}\), the spectral radius \(\rho {(\cdot )}\), and the condition number \(\kappa {(\cdot )}\) of the associated iteration matrix. Let us focus on the following iterative algorithms to approximate the unique solution of Eq. (1) when all \(A,B,C,D\) are square matrices.

Algorithm 1.1

([32])

The gradient iterative algorithm (GI) for (1):

$$\begin{aligned} &X_{1}(k) = X(k-1) +\tau A^{T} \bigl[E-AX(k-1)B-CX(k-1)D \bigr]B^{T}, \\ &X_{2}(k) = X(k-1) + \tau C^{T} \bigl[E-AX(k-1)B-CX(k-1)D \bigr]D^{T}, \\ &X(k) = \frac{1}{2} \bigl(X_{1}(k)+X_{2}(k) \bigr). \end{aligned}$$

If we choose the convergence factor τ such that

$$\begin{aligned} \tau = \bigl(\lVert A \rVert _{2}^{2} \lVert B \rVert _{2}^{2}+\lVert C \rVert _{2}^{2} \lVert D \rVert _{2}^{2} \bigr)^{-1} \quad\text{or}\quad \tau = \bigl( \lVert A \rVert _{F}^{2} \lVert B \rVert _{F}^{2} + \lVert C \rVert _{F}^{2} \lVert D \rVert _{F}^{2} \bigr)^{-1}, \end{aligned}$$
(2)

then \(X(k)\) converges to the exact solution for any initial values \(X_{1}(0)\) and \(X_{2}(0)\). Numerical simulations in [25] reveal that Algorithm 1.1 is more efficient than the B-Q algorithm [12]. In [33], Algorithm 1.1 was shown to be applicable if

$$\begin{aligned} 0< \tau < \frac{2}{ \lVert A \rVert _{2}^{2} \lVert B \rVert _{2}^{2}+\lVert C \rVert _{2}^{2} \lVert D \rVert _{2}^{2} }, \end{aligned}$$
(3)

so that the range of τ is wider than that of (2).

Algorithm 1.2

([33])

The least-squares iterative algorithm (LSI) for (1):

$$\begin{aligned} &X_{1}(k) = X(k-1) +\mu \bigl(A^{T}A \bigr)^{-1}A^{T} \bigl(E-AX(k-1)B-CX(k-1)D \bigr)B^{T} \bigl(BB^{T} \bigr)^{-1}, \\ &X_{2}(k) = X(k-1) + \mu \bigl(C^{T}C \bigr)^{-1}C^{T} \bigl(E-AX(k-1)B-CX(k-1)D \bigr)D^{T} \bigl(DD^{T} \bigr)^{-1}, \\ &X(k) = \frac{1}{2} \bigl(X_{1}(k)+X_{2}(k) \bigr). \end{aligned}$$

To make Algorithm 1.2applicable for any initial values \(X_{1}(0)\) and \(X_{2}(0)\), the convergence factor μ must satisfy \(0<\mu <4\).

There are many iterative algorithms for the Sylvester equation. The first solver is the gradient iterative algorithm (GI), introduced by Ding and Chen [32]. Niu et al. [34] introduced the relaxed gradient iterative algorithm (RGI), that is, GI with relaxation parameter \(\omega \in (0,1)\). Wang et al. [35] modified the GI algorithm in such a way that the information \(X_{1}(k)\) has been fully considered to update \(X(k-1)\); the result is called the MGI algorithm. Recently, Tian et al. introduced JGI [36, Algorithm 4], AJGI1 [36, Algorithm 5], and AJGI2 [36, Algorithm 6] algorithms based on GI and the idea of extracting the diagonal part from each coefficient matrix. Moreover, there are other iterative methods for solving the generalized coupled Sylvester matrix equations; see, for example, [37, 38].

In this paper, we introduce an iterative method for solving the generalized Sylvester equation (1), for which matrices \(A,B,C,D,E\) are not necessarily square. Our algorithm is based on gradients and hierarchical identification principle. This algorithm consists of only one parameter, the convergence factor θ, and the only initial value. To perform a convergence analysis of the algorithm, we use analysis on a complete metric space, together with matrix analysis. We convert the matrix iteration process to a first-order linear difference vector equation with matrix coefficient. Then we apply the Banach contraction principle to show that the proposed algorithm converges to the unique solution for any initial value if and only if \(0< \theta < 2/\lVert P \rVert _{2}^{2}\). The range of the parameter is wider than those of [25, 33]. The convergence rate of the proposed algorithm is governed by the spectral radius of the associated iteration matrix. We also discuss error estimates; in particular, the error at each iteration becomes smaller than the previous one. The fastest convergence factor is determined so that the spectral radius of the iteration matrix is minimal. Moreover, we make convergence analysis of gradient-based iterative algorithms for the equation \(AXB=C\), the Sylvester equation, and the Kalman–Yakubovich equation. We also provide numerical simulations to illustrate our results for the matrix equation (1) and the Sylvester equation. We compare the efficiency of our algorithm with the direct Kronecker linearization and recent algorithms, namely, GI, LSI, RGI, MGI, JGI, AJGI1, and AJGI2 algorithms.

The rest of the paper is organized as follows. We derive a gradient-based iterative algorithm in Sect. 2. We then analyze the convergence of the algorithm in Sect. 3. Iterative algorithms for particular cases of (1) are investigated in Sect. 4. We illustrate and discuss numerical simulations of the algorithm in Sect. 5. Finally, we conclude the work in Sect. 6.

2 Deriving a gradient-based iterative algorithm for the generalized Sylvester matrix equation

We denote by \(\mathbb{M}_{m,n}\) the set of \(m\times n\) real matrices and set \(\mathbb{M}_{n} := \mathbb{M}_{n,n}\). In this section, we derive an iterative algorithm based on gradients to find a matrix \(X \in \mathbb{M}_{n,p}\) satisfying

$$\begin{aligned} AXB + CXD = E. \end{aligned}$$
(4)

Here we are given \(A,C \in \mathbb{M}_{m,n}\), \(B,D \in \mathbb{M}_{p,q}\), and \(E \in \mathbb{M}_{m,q}\), where \(m,n,p,q \in \mathbb{N}\) are such that \(mq=np\).

Recall that equation (4) has a unique solution if and only if the square matrix \(P = B^{T} \otimes A +D^{T} \otimes C\) is invertible. In this case, the (vector) solution is given by \(\operatorname {vec}X = P^{-1} \operatorname {vec}E\).

To derive an iterative procedure for solving (4), we recall the hierarchical identification principle from [33]. Define two matrices

$$ M := E-CXD \quad\text{and}\quad N := E-AXB. $$

In view of (4), we would like to solve two subsystems

$$ AXB = M \quad\text{and}\quad CXD = N. $$
(5)

We will minimize the following quadratic norm-error functions:

$$ L_{1}(X) := \lVert AXB - M \rVert ^{2}_{F}\quad \text{and}\quad L_{2}(X) := \lVert CXD-N \rVert ^{2}_{F}. $$
(6)

Now we deduce their gradients as follows:

$$\begin{aligned} \frac{\partial }{\partial X}L_{1} (X)& = \frac{\partial }{\partial X} \operatorname {tr}\bigl[(AXB-M)^{T}(AXB-M) \bigr] \\ &= \frac{\partial }{\partial X} \operatorname {tr}\bigl(XBB^{T} X^{T} A^{T} A \bigr)- \frac{\partial }{\partial X}\operatorname {tr}\bigl(X^{T} A^{T} M B^{T} \bigr) - \frac{\partial }{\partial X}\operatorname {tr}\bigl(BM^{T} AX \bigr) \\ &= \bigl(A^{T} A \bigr)^{T} X \bigl(BB^{T} \bigr) + A^{T} A X BB^{T} - A^{T} M B^{T} - \bigl(BM^{T} A \bigr)^{T} \\ &= 2A^{T}(AXB-M)B^{T}. \end{aligned}$$
(7)

Similarly, we have

$$\begin{aligned} \frac{\partial }{\partial X}L_{2} (X) = 2C^{T}(CXD-N)D^{T}. \end{aligned}$$
(8)

Let \(X_{1} (k)\) and \(X_{2} (k)\) be the estimates or iterative solutions of system (5) at iteration k. We introduce a step-size parameter \(\tau \in \mathbb{R}\) and a relaxation parameter \(\omega \in (0,1)\). We can derive recursive formulas for \(X_{1}(k)\) and \(X_{2}(k)\) from the gradient formulas (7) and (8) as follows:

$$\begin{aligned} X_{1}(k) &= X(k-1) + \tau (1- \omega ) A^{T} \bigl[M-AX(k-1)B \bigr]B^{T} \\ &= X(k-1) + \tau (1- \omega ) A^{T} \bigl[E-AX(k-1)B-CXD \bigr]B^{T}, \\ X_{2}(k) &= X(k-1) + \tau \omega C^{T} \bigl[N-CX(k-1)D \bigr]D^{T} \\ &= X(k-1) + \tau \omega C^{T} \bigl[E-AXB-CX(k-1)D \bigr]D^{T}. \end{aligned}$$

By the hierarchical identification principle the unknown variable X is replaced by its estimates at iteration \(k-1\). Instead of taking the arithmetic mean of \(X_{1}(k)\) and \(X_{2}(k)\) as in Algorithm 1.1, our algorithm computes the weighted arithmetic mean \(\omega X_{1}(k)+(1- \omega )X_{2}(k)\). By introducing the parameter \(\theta = \tau \omega (1-\omega )\) we get the following iterative algorithm.

Algorithm 2.1

Input \(A,C \in \mathbb{M}_{m,n}\), \(B,D \in \mathbb{M}_{p,q}\), and \(E \in \mathbb{M}_{m,q}\). Set \(A'=A^{T}\), \(B'=B^{T}\), \(C'=C^{T}\), and \(D'=D^{T}\). Choose an initial matrix \(X(0) \in \mathbb{M}_{n,p}\). For each \(k=0,1,2, \dots \) until End, do:

$$\begin{aligned} &F(k) = E-AX(k)B - CX(k)D, \\ &X(k+1) = X(k) + \theta \bigl[ A' F(k) B' + C' F(k) D' \bigr]. \end{aligned}$$

Note that our algorithm avoids duplicate computations by introducing \(F(k)\) at each iteration. To stop the process, we can impose a stopping rule such as \(\lVert F(k) \rVert _{F} < \epsilon \) or \(\lVert F(k) \rVert _{F} / \lVert E \rVert _{F} < \epsilon \), where ϵ is a chosen permissible error. The convergence of Algorithm 2.1 relies on the convergence factors θ, which will be determined in the next section. Note that the algorithm requires only one parameter and one initial value and uses less computing time than other gradient-based algorithms mentioned in Introduction.

3 Convergence analysis of the algorithm

In this section, we analyze the convergence of Algorithm 2.1. We convert the matrix iteration process to a first-order linear difference vector equation with contraction matrix as the coefficient. It follows that the contraction reflects the convergence criteria, convergence rate, and error estimates of the algorithm.

To analyze this algorithm, we recall useful facts in matrix analysis.

Lemma 3.1

(e.g. [7])

For any matrices A and B of conforming dimensions, we have

  1. (i)

    \(\lVert A^{T} A \rVert _{2} = \lVert A \rVert _{2}^{2}\);

  2. (ii)

    \(\lVert AB \rVert _{F} \leqslant \lVert A \rVert _{2} \lVert B \rVert _{F}\);

  3. (iii)

    if A is symmetric, then \(\lVert A \rVert _{2} = \rho (A)\);

  4. (iv)

    \(\lVert A \otimes B \rVert _{2} = \lVert A \rVert _{2} \lVert B \rVert _{2}\).

3.1 Convergence criteria

From Algorithm 2.1 we start with considering the error matrix

$$\begin{aligned} \widehat{X}(k) = X(k)-X. \end{aligned}$$

We will show that \(\widehat{X}(k) \to 0\) or, equivalently, \(\operatorname {vec}{\widehat{X}(k)} \to 0\) as \(k \to \infty \). Now we convert the matrix iteration process to a first-order linear difference vector equation with matrix coefficient. Indeed, we have

$$\begin{aligned} F(k) &= (AXB+CXD)- AX(k)B - CX(k)D \\ &= -A \widehat{X}(k) B - C \widehat{X}(k) D, \end{aligned}$$

and thus

$$\begin{aligned} \operatorname {vec}{F(k)} = - \bigl(B^{T} \otimes A + D^{T} \otimes C \bigr) \operatorname {vec}{ \widehat{X}(k)} = - P \operatorname {vec}{\widehat{X}(k)}. \end{aligned}$$

It follows that

$$\begin{aligned} \operatorname {vec}{\widehat{X}(k+1)} &= \operatorname {vec}\bigl\{ \widehat{X}(k) + \theta \bigl[ A^{T} F(k) B^{T} + C^{T} F(k) D^{T} \bigr] \bigr\} \\ &= \operatorname {vec}{\widehat{X}(k)} + \theta \bigl[ \operatorname {vec}\bigl(A^{T} F(k) B^{T} \bigr) + \operatorname {vec}\bigl(C^{T} F(k) D^{T} \bigr) \bigr] \\ &= \operatorname {vec}{\widehat{X}(k)} + \theta P^{T} \operatorname {vec}{F(k)} \\ &= \operatorname {vec}{\widehat{X}(k)} - \theta P^{T} P \operatorname {vec}{\widehat{X}(k)} \\ &= P_{\theta }\operatorname {vec}{\widehat{X}(k)}, \end{aligned}$$
(9)

where \(P_{\theta } = I_{np} - \theta P^{T} P\). Denoting \(u(k)= \operatorname {vec}{\widehat{X}(k)}\) for \(k \in \mathbb{N}\), we obtain a first-order linear difference vector equation, as desired.

Note that iteration (9) is also the Picard iteration

$$\begin{aligned} u(k+1) = Tu(k),\quad k \in \mathbb{N}, \end{aligned}$$
(10)

where T is the self-mapping on \(\mathbb{R}^{n}\) defined by \(Tx = P_{\theta } x\). We will find some properties of T yielding that the iteration converges to the fixed point \(u^{*}=0\) of T for arbitrary initial point \(u(0)\). In fact, this can be guaranteed by the Banach contraction principle:

Theorem 3.2

(e.g., [39, Sect. 5.1])

Let \((\mathbb{X},d)\) be a nonempty complete metric space. Let \(T: \mathbb{X}\to \mathbb{X}\) be a contraction, that is, there is a constant \(\alpha \in [0,1)\) such that

$$\begin{aligned} d(Tx,Ty) \leqslant \alpha d(x,y)\quad \forall x,y \in \mathbb{X}. \end{aligned}$$

Then T has a unique fixed point \(x^{*}\). The following estimates are equivalent and describe the convergence rate:

  1. (i)

    \(d(x_{n+1},x^{*}) \leqslant \alpha d(x_{n},x^{*})\);

  2. (ii)

    prior estimate: \(d(x_{n},x^{*}) \leqslant \frac{\alpha ^{n}}{1-\alpha } d(x_{1},x_{0})\);

  3. (iii)

    posterior estimate: \(d(x_{n+1},x^{*}) \leqslant \frac{\alpha }{1-\alpha } d(x_{n+1},x_{n})\).

Now we look for some conditions on \(P_{\theta }\) making the mapping T a contraction. For each \(x \in \mathbb{R}^{n}\), we have by Lemma 3.1 that

$$\begin{aligned} \lVert Tx \rVert _{F} = \lVert P_{\theta }x \rVert _{F} \leqslant \lVert P_{\theta } \rVert _{2} \lVert x \rVert _{F} = \rho (P_{\theta }) \lVert x \rVert _{F}. \end{aligned}$$

The last equality holds since \(P_{\theta }\) is a symmetric matrix. It follows that

$$\begin{aligned} \lVert Tx-Ty \rVert _{F} = \bigl\lVert T(x-y) \bigr\rVert _{F} \leqslant \rho (P_{\theta }) \lVert x-y \rVert _{F} \quad\forall x,y \in \mathbb{R}^{n}. \end{aligned}$$

Thus, if \(\rho (P_{\theta }) <1\), then T is a contraction relative to the metric induced by \(\lVert \cdot \rVert _{F}\). Note that further characterizations of matrix contractions, involving (induced) matrix norms, are given, for example, in [40]. Since \(P_{\theta }\) is a symmetric matrix, all its eigenvalues are real, and thus

$$\begin{aligned} \rho (P_{\theta }) = \operatorname {max}\bigl\lbrace \bigl\vert 1-\theta \lambda _{ \min } \bigl(P^{T}P \bigr) \bigr\vert , \bigl\vert 1- \theta \lambda _{\operatorname {max}} \bigl(P^{T}P \bigr) \bigr\vert \bigr\rbrace . \end{aligned}$$
(11)

It follows that \(\rho (P_{\theta })<1\) if and only if

$$ 0< \theta \lambda _{\min } \bigl(P^{T}P \bigr)< 2 \quad\text{and} \quad0< \theta \lambda _{\max } \bigl(P^{T}P \bigr)< 2. $$
(12)

Since P is invertible and \(P^{T}P\) is positive semidefinite, we have that \(P^{T}P\) is positive definite and \(\lambda _{\min }(P^{T}P)>0\). The positive definiteness of \(P^{T} P\) and Lemma 3.1(i) imply

$$\begin{aligned} \lambda _{\max } \bigl(P^{T}P \bigr) = \bigl\lVert P^{T} P \bigr\rVert _{2} = \lVert P \rVert _{2}^{2}. \end{aligned}$$

Hence condition (12) holds if and only if

$$\begin{aligned} 0 < \theta < \frac{2}{\lVert P \rVert _{2}^{2}}. \end{aligned}$$
(13)

Therefore, if (13) holds, then the sequence \(X(k)\) generated by Algorithm 2.1 converges to the solution of (4) for any initial value \(X(0)\).

Conversely, suppose that θ does not satisfy (13). The above discussion implies that \(\rho (P_{\theta }) \geqslant 1\), that is, there is an eigenvalue λ of \(P_{\theta }\) such that \(|\lambda | \geqslant 1\). We can choose an eigenvector \(v \in \mathbb{R}^{n}-\{0\}\) such that \(P_{\theta } v = \lambda v\). The Picard iteration (10) with initial point \(u(0)=v\) yields

$$\begin{aligned} u(k) = T^{k} u(0) = T^{k} v = \lambda ^{k} v \nrightarrow 0. \end{aligned}$$

Thus \(\widehat{X}(k) \nrightarrow 0\) or \(X(k) \nrightarrow X\).

We summarize a necessary and sufficient condition for the convergence criteria as follows.

Theorem 3.3

Let \(\theta \in \mathbb{R}\) be given. Then the sequence \(X(k)\) generated by Algorithm 2.1converges to the solution of (4) for any initial value \(X(0)\) if and only if θ satisfies (13).

Thus, if \(\theta \leqslant 0\) or \(\theta \geqslant \frac{2}{\lVert P \rVert _{2}^{2}}\), then Algorithm 2.1 is not applicable for some initial values.

3.2 Convergence rate and error estimates

We now apply the Banach contraction principle to analyze the convergence rate and error estimates of Algorithm 2.1. Note that the error at each step of the associated Picard iteration is equal to that of the original matrix iterative algorithm. Indeed, for any \(k \in \mathbb{N}\cup \{0\}\), we have

$$\begin{aligned} &\bigl\lVert u^{(k)}- u^{*} \bigr\rVert _{F} = \bigl\lVert \operatorname {vec}{\widehat{X}(k)} \bigr\rVert _{F} = \bigl\lVert \widehat{X}(k) \bigr\rVert _{F} = \bigl\lVert X(k)-X \bigr\rVert _{F}, \\ &\bigl\lVert u^{(k+1)}- u^{(k)} \bigr\rVert _{F} = \bigl\lVert \operatorname {vec}{ \widehat{X}(k+1)} - \operatorname {vec}{\widehat{X}(k)} \bigr\rVert _{F} \\ &\phantom{\bigl\lVert u^{(k+1)}- u^{(k)} \bigr\rVert _{F} }= \bigl\lVert \widehat{X}(k+1) - \widehat{X}(k) \bigr\rVert _{F} = \bigl\lVert X(k+1)-X(k) \bigr\rVert _{F}. \end{aligned}$$

Thus by Theorem 3.2(i) we obtain

$$\begin{aligned} \bigl\lVert X(k+1) - X \bigr\rVert _{F} \leqslant \rho (P_{\theta }) \bigl\lVert X(k) - X \bigr\rVert _{F}. \end{aligned}$$
(14)

It follows inductively that for each \(k \in \mathbb{N}\),

$$\begin{aligned} \bigl\lVert X(k) - X \bigr\rVert _{F} \leqslant \rho ^{k}(P_{\theta }) \bigl\lVert X(0) - X \bigr\rVert _{F}. \end{aligned}$$
(15)

Hence \(\rho (P_{\theta })\) describes how fast the approximate solutions \(X(k)\) converge to the exact solution X. The smaller the spectral radius, the faster \(X(k)\) goes to X. In that case, since \(\rho (P_{\theta }) <1\), if \(\lVert X(k) - X \rVert _{F} \neq 0\), then

$$\begin{aligned} \bigl\lVert X(k+1) - X \bigr\rVert _{F} < \bigl\lVert X(k) - X \bigr\rVert _{F}. \end{aligned}$$
(16)

Moreover, from the prior and posterior estimates in Theorem 3.4 we obtain the bounds

$$\begin{aligned} &\bigl\lVert X(k)-X \bigr\rVert _{F} \leqslant \frac{\rho ^{k}(P_{\theta })}{1-\rho (P_{\theta })} \bigl\lVert X(1)-X(0) \bigr\rVert _{F}, \end{aligned}$$
(17)
$$\begin{aligned} &\bigl\lVert X(k+1)-X \bigr\rVert _{F} \leqslant \frac{\rho (P_{\theta })}{1-\rho (P_{\theta })} \bigl\lVert X(k+1)-X(k) \bigr\rVert _{F}. \end{aligned}$$
(18)

we summarize our discussion in the following theorem.

Theorem 3.4

Suppose that the parameter θ is chosen as in Theorem 3.3so that the sequence \(X(k)\) generated by Algorithm 2.1converges to X for any initial value. Then we have:

  • The convergence rate of the algorithm is governed by the spectral radius (11).

  • The error estimates \(\lVert X(k+1) - X \rVert _{F}\) compared to the previous step and the first step are provided by (14) and (15), respectively. In particular, the error at each iteration gets smaller than the (nonzero) previous one, as in (16).

  • The prior estimate (17) and the posterior estimate (18) hold.

From (11), if the eigenvalues of \(\theta P^{T}P\) are close to 1, then the spectral radius of the iterative matrix is close to 0, and hence the errors \(\widehat{X}(k)\) converge faster to 0.

Remark 3.5

The convergence criteria and the convergence rate of Algorithm 2.1 depend on \(A,B,C,D\) but not on E. However, the matrix E can be used for a stopping criteria.

The following proposition determines the iteration number for which the approximated solution \(X(k)\) is close to the exact solution X so that \(\lVert X(k)-X \rVert _{F} < \epsilon \).

Proposition 3.6

According to Algorithm 2.1, for each given error \(\epsilon >0\), we have \(\lVert X(k)-X \rVert _{F} < \epsilon \) after \(k^{*}\) iterations for any

$$\begin{aligned} k^{*} > \frac{\log {\epsilon } - \log {\lVert X(0)-X \rVert _{F}}}{\log \rho (P_{\theta })}. \end{aligned}$$
(19)

Proof

From estimate (15) we have

$$\begin{aligned} \bigl\lVert X(k)-X \bigr\rVert _{F} \leqslant \rho ^{k} (P_{\theta }) \bigl\lVert X(0)-X \bigr\rVert _{F} \to 0\quad \text{as } k \to \infty . \end{aligned}$$

This precisely means that for each given \(\epsilon >0\), there is \(k^{*} \in \mathbb{N}\) such that for all \(k \geqslant k^{*}\),

$$\begin{aligned} \rho ^{k} (P_{\theta }) \bigl\lVert X(0)-X \bigr\rVert _{F} < \epsilon . \end{aligned}$$

Taking logarithms, we have that this condition is equivalent to (19). Thus, if we run Algorithm 2.1\(k^{*}\) times, then we get \(\lVert X(k)-X \rVert _{F} < \epsilon \), as desired. □

3.3 Optimal parameter

We now discuss the fastest convergence factors for Algorithm 2.1.

Theorem 3.7

Let \(0 < \theta < \frac{2}{\lVert P \rVert _{2}^{2}}\). Denote κ as the condition number of the matrix P. Then the optimal value of θ for which Algorithm 2.1is applicable for any initial value is determined by

$$ \theta _{\mathrm{opt}} = \frac{2}{\lambda _{\min }(P^{T}P)+\lambda _{\max }(P^{T}P)}. $$
(20)

In this case the spectral radius of the iteration matrix is given by

$$ \rho (P_{\theta _{\mathrm{opt}}}) = \frac{\lambda _{\max }(P^{T}P)-\lambda _{\min }(P^{T}P)}{\lambda _{\max }(P^{T}P)+\lambda _{\min }(P^{T}P)} = \frac{\kappa ^{2} -1}{\kappa ^{2} +1}. $$
(21)

Proof

Theorem 3.3 tells us that the convergence of the algorithm implies (13). The convergence rate of the algorithm is the same as that of the linear iteration (9) and thus is governed by the spectral radius (11). Hence we would like to minimize the spectral radius \(\rho (P_{\theta })\) subject to condition (13). Putting \(a = \lambda _{\min }(P^{T}P)\) and \(b=\lambda _{\max }(P^{T}P)\), we make the following optimization:

$$ \min_{0< \theta < \frac{2}{b}} \bigl\lbrace \operatorname {max}\bigl\lbrace \vert 1-a \theta \vert , \vert 1-b \theta \vert \bigr\rbrace \bigr\rbrace . $$

The minimality is reached at \(\theta _{\mathrm{opt}}= 2/(a+b)\), so that the minimum value of \(\rho (P_{\theta })\) is equal to \((b-a)/(b+a)\). □

From Theorem 3.7, Algorithm 2.1 has a fast convergence if the condition number of P is close to 1 or, equivalently, \(\lambda _{\max }(P^{T}P)\) is close to \(\lambda _{\min }(P^{T}P)\).

4 Iterative algorithms for particular cases of the generalized Sylvester equation

In this section, we discuss iterative algorithms for solving interesting particular cases of the generalized Sylvester equation.

4.1 The equation \(AXB = E\)

Assume that the equation \(AXB = E\) has a unique solution or, equivalently, the square matrix \(Q :=B^{T} \otimes A\) is invertible. In the particular case where A and B are square matrices, this condition is reduced to the invertibility of both A and B. The following algorithm is proposed to find the solution X.

Algorithm 4.1

Set \(A'=A^{T}\) and \(B'=B^{T}\). Choose \(X(0) \in \mathbb{M}_{n,p}\). For each \(k=0,1,2, \dots \) until End, do:

$$\begin{aligned} X(k+1) = X(k) + \theta A' \bigl(C-AX(k)B \bigr)B'. \end{aligned}$$

Note that \(Q^{T} Q = BB^{T} \otimes A^{T} A\) by the mixed-product property of the Kronecker product. Since Q is invertible, so is \(Q^{T} Q\). It follows that \(A^{T} A\) and \(BB^{T}\) are positive definite. Thus

$$\begin{aligned} \lambda _{\min } \bigl(Q^{T} Q \bigr) = \lambda _{\min } \bigl(A^{T} A \bigr) \lambda _{ \min } \bigl(BB^{T} \bigr) = \lambda _{\min } \bigl(A^{T} A \bigr) \lambda _{\min } \bigl(B^{T} B \bigr), \end{aligned}$$

and, similarly, \(\lambda _{\max } (Q^{T} Q) = \lambda _{\max }(A^{T} A) \lambda _{\max }(B^{T} B)\). Now we obtain the following:

Corollary 4.2

Assume that the equation \(AXB =E\) has a unique solution. Let \(\theta \in \mathbb{R}\). Then we have:

  1. 1)

    Algorithm 4.1is applicable for any initial value \(X(0)\) if and only if

    $$ 0 < \theta < \frac{2}{\lVert A \rVert ^{2}_{2} \lVert B \rVert ^{2}_{2}}. $$
  2. 2)

    The convergence rate of the iteration is governed by the spectral radius

    $$\begin{aligned} &\rho \bigl( I_{np} - \theta Q^{T} Q \bigr)\\ &\quad = \operatorname {max}\bigl\lbrace \bigl\vert 1- \theta \lambda _{\min } \bigl(A^{T} A \bigr) \lambda _{\min } \bigl(B^{T} B \bigr) \bigr\vert , \bigl\vert 1 - \theta \lambda _{\max } \bigl(A^{T} A \bigr) \lambda _{\max } \bigl(B^{T} B \bigr) \bigr\vert \bigr\rbrace . \end{aligned}$$
  3. 3)

    The optimal convergence factor for which Algorithm 4.1is applicable for any initial value is given by

    $$ \theta _{\mathrm{opt}} = \bigl[\lambda _{\min } \bigl(A^{T} A \bigr) \lambda _{\min } \bigl(B^{T} B \bigr) + \lambda _{\max } \bigl(A^{T} A \bigr) \lambda _{\max } \bigl(B^{T} B \bigr) \bigr]^{-1} /2. $$

4.2 The Sylvester equation

Suppose that \(m=n\) and \(p=q\). Assume that the Sylvester equation

$$\begin{aligned} AX + XD = E \end{aligned}$$
(22)

has a unique solution. This condition is equivalent to the invertibility of the Kronecker sum \(D^{T} \oplus A := D^{T} \otimes I_{n} + I_{p} \otimes A\), or all possible sums of eigenvalues of A and D are nonzero.

Algorithm 4.3

Set \(A'=A^{T}\) and \(D'=D^{T}\). Choose \(X(0) \in \mathbb{M}_{n,p}\). For each \(k=0,1,2, \dots \) until End, do:

$$\begin{aligned} &F(k) = E - AX(k) - X(k)D, \\ &X(k+1) = X(k) + \theta \bigl[ A' F(k) + F(k)D' \bigr]. \end{aligned}$$

Corollary 4.4

Assume that the equation \(AX+XD =E\) has a unique solution X. Then the iterative sequence \({X(k)}\) generated by Algorithm 4.3converges to X for any initial value \(X(0)\) if and only if

$$ 0 < \theta < \frac{2}{\lVert D^{T} \oplus A \rVert _{2}^{2}}. $$

Error estimates and the optimal convergence factor for Algorithm 4.3 can also be obtained from Theorem 2.1 when B and C are the identity matrices.

Remark 4.5

If A and D are positive semidefinite, then \(\lVert D^{T} \oplus A \rVert _{2}\) is reduced to \(\lVert A \rVert _{2} + \lVert D \rVert _{2}\).

4.3 The Kalman–Yakubovich equation

Suppose that \(m=n\) and \(p=q\). Assume that the Kalman–Yakubovich equation

$$\begin{aligned} AXB + X = E \end{aligned}$$
(23)

has a unique solution. This condition is equivalent to the invertibility of \(B^{T} \otimes A + I_{np}\) or, equivalently, to that all possible products of eigenvalues of A and B are not equal to −1.

Algorithm 4.6

Set \(A'=A^{T}\) and \(B'=B^{T}\). Choose \(X(0) \in \mathbb{M}_{n,p}\). For each \(k=0,1,2, \dots \) until End, do:

$$\begin{aligned} &F(k) = E-AX(k)B - X(k), \\ &X(k+1) = X(k) + \theta \bigl[ A' F(k) B' + F(k) \bigr]. \end{aligned}$$

Corollary 4.7

Assume that the equation \(AXB+X =E\) has a unique solution X. The iterative sequence \({X(k)}\) generated by Algorithm 4.6converges to X for any initial value \(X(0)\) if and only if

$$ 0 < \theta < \frac{2}{\lVert B^{T} \otimes A + I_{n^{2}} \rVert ^{2}_{2}}. $$

Remark 4.8

If A and B are positive semidefinite, then \(\lVert B^{T} \otimes A + I_{n^{2}} \rVert _{2}\) is reduced to \(\lVert A \rVert _{2} \lVert B \rVert _{2} +1\).

5 Numerical simulations

In this section, we report numerical results illustrating the effectiveness of Algorithm 2.1. We consider matrix systems from small dimensions (say, \(2\times 2\)) to large dimensions (say, \(120\times 120\)). We investigate the effect of changing convergence factors (see Example 5.1) and initial points (Example 5.2). We compare the performance of the algorithm to the direct Kronecker linearization (Example 5.1) and recent iterative algorithms (Example 5.3). We show that Algorithm 2.1 is still effective when dealing with a nonsquare problem (see Example 5.4). To measure errors at step k of the iteration, we consider the following relative error:

$$\begin{aligned} \frac{\lVert AX(k)B+CX(k)D-E \rVert _{F}}{\lVert E \rVert _{F}}. \end{aligned}$$

All iterations have been carried out on the same PC environment: MATLAB R2018a, Intel(R) Core(TM) i7-6700HQ CPU @ 2.60 GHz 2.60 GHz, RAM 8.00 GB. To measure the computational time (in seconds) taken for a program, we use the tic and toc functions in MATLAB and abbreviate CT for it. The readers are recommended to consider both reported errors and CTs while comparing the performance of any algorithms.

Example 5.1

Consider the equation \(AXB+CXD=E\), where \(A,B,C,D,E,X\) of sizes \(100\times 100\) are given by

$$\begin{aligned} &A = \operatorname {tridiag}(-1,2,-1),\qquad B=\operatorname {tridiag}(6,4,-1), \qquad C = \operatorname {tridiag}(1,2,3), \\ &D =\operatorname {tridiag}(4,2,-5),\qquad E=\operatorname {heptadiag}(2,-22,16,92,36,-58,-42). \end{aligned}$$

We run Algorithm 2.1 with five convergence factors; one of them is the optimal convergence factor \(\theta _{\mathrm{opt}} = 6.5398\text{e-}04\), determined by Theorem 3.7. According to (13), the range of appropriate θ is given by \(0<\theta <2/\lVert P \rVert _{2}^{2} \approx 6.5398\text{e-}04\) (in this case, \(\lambda _{\min }(P^{T} P) \approx 0\)), that is, Algorithm 2.1 is applicable for every chosen θ. The result after 100 iterations is presented by Fig. 1 and Table 1. From the relative error plot versus iteration time in Fig. 1 we see that the optimal convergence factor gives the fastest convergence. Table 1 shows that the computational times with the five convergence factors are significantly less than that of the direct method \(\operatorname {vec}X = P^{-1} \operatorname {vec}E\). The relative errors after 100 iterations are very small in comparison with the dimensions of the coefficient matrices.

Figure 1
figure 1

Relative errors for Example 5.1

Full size image
Table 1 Relative error and computational time for Example 5.1
Full size table

Example 5.2

In this example, we consider the equation \(AXB+CXD = E\) with different sizes of matrices, say, \(2\times 2\), \(10\times 10\), \(100\times 100\), and \(120\times 120\). For each case, we take \(A = \operatorname {tridiag}(7,-2,5)\), \(B = \operatorname {tridiag}(1,6,8)\), \(C = \operatorname {tridiag}(3,-9,1)\), \(D = \operatorname {tridiag}(9,-2,5)\), and \(E = \operatorname {heptadiag}(34,21,99,8,252,-9,135)\) of corresponding sizes. We denote by \(\operatorname {ones}(n)\) the \(n \times n\) matrix that contains 1 at every position. For each \(n \in \{2, 10, 100, 120\}\), we run Algorithm 2.1 with distinct initial candidates:

$$\begin{aligned} &X_{1} = 0.1\times \operatorname {ones}(n),\qquad X_{2} = 0.2\times \operatorname {ones}(n), \qquad X_{3} = 0.5\times \operatorname {ones}(n), \\ &X_{4} = 1.2\times \operatorname {ones}(n),\qquad X_{5} = 1.5\times \operatorname {ones}(n),\qquad X_{6} = 2\times \operatorname {ones}(n). \end{aligned}$$

We run 50 iterations for the matrices of dimensions \(2\times 2\) and \(10\times 10\), whereas we run 100 iterations for large dimensions \(100\times 100\) and \(120\times 120\). The optimal convergence factors θ for each case are provided in Table 2. The computational times and errors reported in Table 2 show that our algorithm is satisfactorily applicable for all initial candidates and different sizes of coefficient matrices.

Table 2 Relative error and computational time for Example 5.2
Full size table

Example 5.3

We consider the equation \(AX+XB = C\) with three cases of coefficient matrix sizes, namely \(2\times 2\), \(10 \times 10\), and \(100 \times 100\). We set

$$\begin{aligned} A_{0} = \begin{bmatrix} 1 & 2 \\ -3 & 4 \end{bmatrix},\qquad B_{0} = \begin{bmatrix} 8 & 0 \\ -5 & -6 \end{bmatrix}\quad \text{and}\quad Z = \begin{bmatrix} 2 & 3 \\ -6 & 9 \end{bmatrix}. \end{aligned}$$

For each \(n \in \{2,10,100\}\), we consider the coefficient matrices \(A=A_{0} \otimes I_{n/2}\), \(B=B_{0} \otimes I_{n/2}\), and \(X^{*}=Z \otimes I_{n/2}\) together with initial condition \(X(0) = 10^{-6} \times \operatorname {ones}(n)\). We compare Algorithm 2.1 with GI [25], RGI [34], MGI [35], JGI [36, Algorithm 4], AJGI1 [36, Algorithm 5], AJGI2 [36, Algorithm 6], and LSI [33] algorithms.

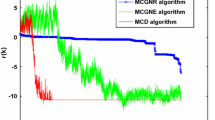
We run 50 iterations for dimension \(2\times 2\), 100 iterations for dimension \(10\times 10\), and 200 iterations for dimension \(100\times 100\). The relative error and the computational time in Table 3 reveal that our algorithm well performs comparing to the other algorithms. Figure 2 displays the error plots of the first 100 iterations for each case; \(2\times 2\) (a), \(10\times 10\) (b), and \(100\times 100\) (c). We can see that our algorithm gives the fastest convergence.

Figure 2
figure 2

Natural logarithm relative errors for Example 5.3

Full size image
Table 3 Relative error and computational time for Example 5.3
Full size table

Example 5.4

We consider the generalized Sylvester matrix equation with rectangular unknown matrix \(X\in M_{50,100}\). Let \(A,C\in M_{50}\) and \(B,D\in M_{100}\) be defined by \(A = \operatorname {tridiag}(-1,2,-1)\), \(B = \operatorname {tridiag}(1,4,-3)\), \(C = \operatorname {tridiag}(3,-1,2)\), and \(D = \operatorname {tridiag}(3,5,7)\). The exact solution is given by \(X^{*} = \tilde{X}\otimes I_{10}\), where

$$\begin{aligned} \tilde{X} = \begin{bmatrix} 1 & 3 & -5 & 9 & 5 & 7 & 4 & -6 & 9 & 10 \\ 2 & -8 & 9 & -7 & 4 & 5 & -6 & 1 & 2 & 3 \\ 2 & 3 & 5 & 7 & 9 & -8 & -5 & 0 & 1 & 2 \\ 6 & 9 & -8 & 7 & 5 & 4 & -2 & 0 & 3 & 6 \\ -8 & -9 & 6 & 5 & -1 & 2 & 0 & 3 & -4 & -7 \end{bmatrix}. \end{aligned}$$

The constant matrix E is determined by \(E=AX^{*}B+CX^{*}D\).

We compare Algorithm 2.1 (\(\theta _{\mathrm{opt}} = 6.4000\text{e-}05\)) and the algorithms compatible with nonsquare matrices, that is, GI [25], RGI [34], and MGI [35], with 100 iterations. The relative error at terminal iteration and the computational time of each algorithm and of the direct method are shown in Table 4, whereas Fig. 3 displays the error plots. Both of them reveal the effectiveness in performance of our algorithm. The computational times of GI-opt and GI are less than those of RGI and MGI. The reason that GI-opt takes little more time than GI is that our algorithm needs more time to compute \(\theta _{\mathrm{opt}}\) in Theorem 3.7. On the other hand, Algorithm 2.1 obtains a significantly better error than GI algorithm.

Figure 3
figure 3

Relative errors for Example 5.4

Full size image
Table 4 Relative error and computational time for Example 5.4
Full size table

6 Conclusion

We propose a gradient-based iterative algorithm (Algorithm 2.1) for solving the rectangular generalized Sylvester matrix equation (4) and its famous particular cases. Theorem 3.3 informs us that the parameter θ must be chosen properly to have the proposed algorithm applicable for any initial matrices. Moreover, we determine the optimal convergence factors, which makes the algorithm reach the fastest convergence rate. The asymptotic convergence rate of the algorithm is governed by the spectral radius of \(I_{np} - \theta P^{T} P\). If the eigenvalue \(\theta P^{T}P\) is close to 1, then the algorithm converges faster in the long run. The numerical simulations reveal that our algorithm is suitable for both small and large matrix systems, both square and nonsquare problems, and any initial points. In addition, the algorithm always gives the effective performance comparing to the errors obtained from recent methods, namely, GI, RGI, MGI, JGI, AJGI1, AJGI2, and LSI algorithms. There are two reasons that cause our algorithm to perform well. The first reason is that the algorithm requires only one parameter and one initial value, and avoids duplicated computations. The second is that the convergence factor is chosen by an optimization method.