1 Introduction

Infectious diseases are spread by pathogenic microorganisms. These diseases can transmit from one person to another or from animals or birds. Despite all the advancement in medicine to control the disease, it is still a major threat to the community. Major causes of infectious diseases are: change in human behavior, use of antibiotic drugs in larger and denser cities. Mathematical models for the infectious diseases are the major tools to study the process through which diseases spread in a population [1–3]. These models are used for the predictions about the future to evaluate strategies to control the disease. First-time authors of [4], formulated a simple model in 1927 that described the connection between “susceptible, infected, and recovered individuals in a population abbreviated as SIR” given by

$$ \textstyle\begin{cases} \frac{dx}{d\mathrm{t}}=\alpha N-\delta x(\mathrm{t}) y(\mathrm{t})-a x( \mathrm{t}), \\ \frac{dy}{d\mathrm{t}}=\delta x(\mathrm{t})y(\mathrm{t})-(\beta +a+b)y( \mathrm{t}), \\ \frac{dz}{d\mathrm{t}}=\beta y(\mathrm{t})- a z(\mathrm{t}), \end{cases} $$
(1)

where α is the birth rate, \(N=x(\mathrm{t})+y(\mathrm{t})+z(\mathrm{t})\), a represents the unrelated death rate, b is a disease-related death rate, δ is infectious rate, and β is the removal rate. Further, x stands for the density of susceptible, y for infected, and z for recovered individuals, respectively. Onward of the said model has been investigated very well, see [5–8].

Riemann, Liouville, Euler, and Fourier have made a significant contribution in the eighteenth century in the area mentioned above. Various aspects of mathematical modeling may not be well described via ordinary calculus since derivatives of noninteger order are in fact definite integrals that provide accumulation. The concerned accumulation includes the corresponding integer counterpart as a special case. Further such operators permit greater freedom in degree as compared to integer order (for details, see [9–21]). In the said area, by considering different aspects, great work has been done in [12–14]. Differential operator with noninteger order has not been uniquely defined. There are several definitions in the literature. On the basis of kernels, there are two concepts. One definition involving a singular kernel is often called power law, while the second one contains nonsingular kernel of exponential and Mittag-Leffler type. The differential operators involving Mittag-Leffler and exponential type kernel have been recently introduced by Atangana, Baleanu, Caputo, and Fabrizo (see [19, 22–25]). This derivative exhibits the singular kernel by a nonsingular kernel [20, 21, 26–29]. Since the differential and integral operators of ABC type are nonlocal and nonsingular, such operators reduce the complication in numerical analysis of many problems. Further in some problems, the mentioned operators play excellent roles in description of many hereditary and memory terms. Therefore, the mentioned operators have been considered in the recent time in an increasing way for investigating physical and biological problems. In this regard, a number of methods available in literature have been applied to compute solutions under these derivatives. To compute the approximate and analytical solution, a famous decomposition method was used as the best tool for many problems. Therefore, in this article, we utilize Laplace Adomian decomposition method (LADM) for the series solution of SIR model (1) under ABC derivative. We consider the biological model (1) and use the ABC derivative for the model with order μ such that \(\mu \in (0,1]\) as given by

$$ \textstyle\begin{cases} {}^{ABC}\mathcal{D}^{\mu }_{0}(x)(\mathrm{t})=\alpha N-\delta x( \mathrm{t}) y(\mathrm{t})-a x(\mathrm{t}), \\ {}^{ABC}\mathcal{D}^{\mu }_{0}(y)(\mathrm{t})=\delta x(\mathrm{t}) y( \mathrm{t})-(\beta +a+b) y(\mathrm{t}), \\ {}^{ABC}\mathcal{D}^{\mu }_{0}(z)(\mathrm{t})=\beta y(\mathrm{t})-a z( \mathrm{t}) \end{cases} $$
(2)

under the condition

$$ x(0)=N_{1},\qquad y(0)=N_{2} ,\qquad z(0)=N_{3}. $$

Then, we get the results in the form of an analytical solution of the SIR model. Moreover, we exhibit the approximate solution for distinct fractional order \(\mu \in (0,1]\). In addition, we study some results about the qualitative analysis and stability analysis for the concerned model. Further, the right-hand sides of model (2) vanish at zero as for the general problem in [20], Theorem 3.1. Via fixed point theory and nonlinear analysis, we establish some results regarding the existence and stability of solution. Then, we compute the required series solution via the proposed method for model (2).

2 Auxiliary results

We recall some fundamental results here.

Definition 1

Let \(\phi \in \mathcal{H}^{1}(0,\tau )\) and \(\mu \in (0,1]\), then the ABC derivative is defined as

$$ {}^{\mathcal{ABC}}\mathcal{D}_{0}^{\mu }\bigl(\phi (\mathrm{t})\bigr)= \frac{\mathcal{ABC}(\mu )}{(1-\mu )} \int _{0}^{\mathrm{t}} \frac{d}{d\theta }\phi (\theta )E_{\mu } \biggl[\frac{-\mu }{1-\mu }(t- \theta )^{\mu } \biggr]\,d \theta . $$
(3)

Here, \(E_{\mu }\) is known as a Mittag-Leffler function.

Definition 2

The fractional integral of ABC is

$$ {}^{\mathcal{AB}}\mathcal{I}_{0}^{\mu }\bigl(\phi (\mathrm{t})\bigr)= \frac{(1-\mu )}{\mathcal{ABC}(\mu )}\phi (\mathrm{t})+ \frac{\mu }{\mathcal{ABC}(\mu )\Gamma (\mu )} \int _{0}^{\mathrm{t}}\phi ( \theta ) (\mathrm{t}-\theta )^{\mu -1}\,d\theta , $$
(4)

while \(\mathcal{ABC}(\mu )\) is a normalization constant with \(\mathcal{ABC}(0)=1\), \(\mathcal{ABC}(1)=1\).

Definition 3

“The Laplace transform of the \(\mathcal{ABC}\) derivative of a function \(\phi (\mathrm{t})\)” is defined by

$$ \mathscr{L} \bigl[{}^{\mathcal{ABC}}\mathcal{D}_{0}^{\mu }\phi ( \mathrm{t}) \bigr]=\frac{\mathcal{ABC}(\mu )}{s^{\mu }(1-\mu )+\mu } \bigl[s^{\mu }\bigl[\phi ( \mathrm{t})\bigr]-s^{\mu -1}\phi (0) \bigr]. $$
(5)

Lemma 1

For \(0<\mu <1\), the solution of the problem

$$ \begin{gathered} {} {}^{\mathcal{ABC}}\mathcal{D}^{\mu }_{0} \phi (\mathrm{t})=g( \mathrm{t}),\quad \mathrm{t}\in [0,T], \\ \phi (0)=\phi _{0}, \end{gathered} $$

is provided by

$$ \phi (\mathrm{t})=\frac{(1-\mu )}{\mathcal{ABC}(\mu )}g(\mathrm{t})+ \frac{\mu }{\mathcal{ABC}(\mu )\Gamma (\mu )} \int _{0}^{\mathrm{t}}( \mathrm{t}-\theta )^{\mu -1}g( \theta )\,d\theta . $$
(6)

Definition 4

The operator \(\varphi _{k}: Y\rightarrow Y\) for \(k=1,2,3\) defined as

$$ \textstyle\begin{cases} {}^{\mathcal{ABC}}\mathcal{D}^{\mu }_{0}x(\mathrm{t})=\chi _{1}(x,y,z)( \mathrm{t}), \\ {}^{\mathcal{ABC}}\mathcal{D}^{\mu }_{0}y(\mathrm{t})=\chi _{2}(x,y,z)( \mathrm{t}), \\ {}^{\mathcal{ABC}}\mathcal{D}^{\mu }_{0}z(\mathrm{t})=\chi _{3}(x,y,z)( \mathrm{t}), \end{cases} $$
(7)

is Hyers–Ulam (HU) stable if, for any positive number \(c_{l}\) (\(l=1,2,3,\ldots 9\)), \(\Lambda _{l}\) (\(l=1,2,3\)) and for every solution \((\widehat{x},\widehat{y},\widehat{z})\in Y\) obeying the relation

$$ \textstyle\begin{cases} \Vert {x}-\widehat{x} \Vert \leq \Lambda _{1}, \\ \Vert {y}-\widehat{y} \Vert \leq \Lambda _{2}, \\ \Vert {z}-\widehat{z} \Vert \leq \Lambda _{3}, \end{cases} $$
(8)

with \(({x},{y},{z})\in Y\) of (7), the following hold:

$$ \textstyle\begin{cases} \Vert {x}-\widehat{x} \Vert \leq c_{1}\Lambda _{1}+c_{2}\Lambda _{2}+c_{3} \Lambda _{3}, \\ \Vert {y}-\widehat{y} \Vert \leq c_{4}\Lambda _{1}+c_{5}\Lambda _{2}+c_{6} \Lambda _{3}, \\ \Vert {z}-\widehat{z} \Vert \leq c_{7}\Lambda _{1}+c_{8}\Lambda _{2}+c_{9} \Lambda _{3}. \end{cases} $$
(9)

Definition 5

If \(\delta _{l}\) for \(l=1,2,3, \ldots n\) are eigenvalues of the matrix \(\mathcal{N}\), then the spectral radius is denoted as \(\Theta (\mathcal{N})\) and is defined as

$$ \Theta (\mathcal{N})=\max \bigl\{ \vert \delta _{l} \vert , \text{for } l=1,2,\ldots n\bigr\} . $$

Moreover, if \(\Theta (\mathcal{N})< 1\), this implies that \(\mathcal{N}\) tends to zero.

Theorem 1

For the operator \(\varphi _{k}: Y\rightarrow Y\) for \(k=1,2,3\), such that

$$ \textstyle\begin{cases} \Vert \varphi _{1}(x,y,z)-\varphi _{1}(\widehat{x},\widehat{y}, \widehat{z}) \Vert \leq c_{1} \Vert x-\widehat{x} \Vert +c_{2} \Vert y-\widehat{y} \Vert +c_{3} \Vert z-\widehat{z} \Vert , \\ \Vert \varphi _{2}(x,y,z)-\varphi _{2}(\widehat{x},\widehat{y}, \widehat{z}) \Vert \leq c_{4} \Vert x-\widehat{x} \Vert +c_{5} \Vert y-\widehat{y} \Vert +c_{6} \Vert z-\widehat{z} \Vert , \\ \Vert \varphi _{3}(x,y,z)-\varphi _{3}(\widehat{x},\widehat{y}, \widehat{z}) \Vert \leq c_{7} \Vert x-\widehat{x} \Vert +c_{8} \Vert y-\widehat{y} \Vert +c_{9} \Vert z-\widehat{z} \Vert , \\ \forall (x,y,z),\quad (\check{x},\check{y},\check{z})\in Y, \end{cases} $$
(10)

and the matrix

$$ \mathcal{N}= \begin{pmatrix} c_{1} & c_{2} &c_{3} \\ c_{4} & c_{5}&c_{6} \\ c_{7} &c_{8} &c_{9} \end{pmatrix} $$
(11)

tends to zero, then (7) is Hyers–Ulam stable.

3 Qualitative results for the proposed model (2)

In this part of the manuscript, we study qualitative results for problem (2). Here, we express right-hand sides of (2) as follows:

$$\begin{aligned}& \chi _{1}(\mathrm{t},x,y,z) = \alpha N-\delta x(\mathrm{t}) y( \mathrm{t})-a x(\mathrm{t}), \\& \chi _{2}(\mathrm{t},x,y,z) = \delta x(\mathrm{t}) y(\mathrm{t})-( \beta +a+b)y(\mathrm{t}), \\& \chi _{3}(\mathrm{t},x,y,z) = \beta y(\mathrm{t})-a z(\mathrm{t}). \end{aligned}$$
(12)

We select

$$\begin{aligned} \mathbf{M}_{j}= \sup _{A[d, b_{j}]} \bigl\Vert \varphi _{1}(\mathrm{t},x,y,z) \bigr\Vert \end{aligned}$$
(13)

such that

$$ A[d, b_{j}]=[\mathrm{t}-d, \mathrm{t}+d]\times [\mathrm{t}-b_{j}, \mathrm{t}+b_{j}]=B\times B_{j}\quad \text{for } j=1,2,3. $$

The concerned norm may be defined as

$$ \Vert \mathbf{Y} \Vert =\sup_{\mathrm{t}\in [\mathrm{t}-d, \mathrm{t}+b]} \bigl\vert \phi (\mathrm{t}) \bigr\vert . $$
(14)

Then the Picard operator is given as

$$ \mathbf{T}:A(B, B_{1}, B_{2}, B_{3})\rightarrow A(B, B_{1}, B_{2}, B_{3}). $$
(15)

We present the following theorem.

Theorem 2

In view of the Banach contraction theorem under the Picard operator as defined in (15), there exists at most one solution to the considered model (2).

Proof

In this regard, applying \({}^{\mathcal{AB}}\mathcal{I}^{\mu }\) on model (2), we obtain

$$ \textstyle\begin{cases} x(\mathrm{t})-x(0) = {}^{\mathcal{AB}}\mathcal{I}^{\mu }[ \chi _{1}(\mathrm{t},x,y,z)], \\ y(\mathrm{t})-y(0) = {}^{\mathcal{AB}}\mathcal{I}^{\mu }[\chi _{2}( \mathrm{t},x,y,z)], \\ z(\mathrm{t})-z(0) = {}^{\mathcal{AB}}\mathcal{I}^{\mu }[\chi _{3}( \mathrm{t},x,y,z)]. \end{cases} $$
(16)

Using Lemma 1 and writing (16) in a simple form, one has

$$ \mathbf{Y}(\mathrm{t})=\mathbf{Y}_{0}(\mathrm{t})+ \bigl[\Phi \bigl( \mathrm{t}, \mathbf{Y}(\mathrm{t})\bigr)-\Phi _{0}( \mathrm{t}) \bigr] \vartheta (\mu )+\bar{\vartheta }(\mu ) \int _{0}^{\mathrm{t}} ( \mathrm{t}-\zeta )^{\mu -1}\Phi \bigl(\zeta , \mathbf{Y}(\zeta )\bigr)\,d\zeta , $$
(17)

where

$$ \vartheta (\mu )=\frac{(1-\mu )}{\mathcal{ABC}(\mu )},\qquad \bar{\vartheta }( \mu )=\frac{\mu }{\mathcal{ABC}(\mu )\Gamma (\mu )}, $$

and

$$ \begin{gathered} \mathbf{Y}(\mathrm{t})= \textstyle\begin{cases}x(\mathrm{t}), \\ y(\mathrm{t}), \\ z(\mathrm{t}), \end{cases}\displaystyle \qquad \mathbf{Y}_{0}(\mathrm{t})= \textstyle\begin{cases}x(0), \\ y(0), \\ z(0), \end{cases}\displaystyle \qquad \Phi \bigl(\mathrm{t}, \mathbf{Y}(\mathrm{t})\bigr)= \textstyle\begin{cases}\chi _{1}(\mathrm{t},x,y,z), \\ \chi _{2}(\mathrm{t},x,y,z), \\ \chi _{3}(\mathrm{t},x,y,z), \end{cases}\displaystyle \\ \Phi _{0}(\mathrm{t})= \textstyle\begin{cases}\chi _{1}(0, x(0), y(0), z(0)), \\ \chi _{2}(0, x(0), y(0), z(0)), \\ \chi _{3}(0, x(0), y(0), z(0)). \end{cases}\displaystyle \end{gathered} $$
(18)

Using (17) and (18), the operator in (15) is defined as follows:

$$ \mathbf{T}\mathbf{Y}(\mathrm{t})=\mathbf{Y}_{0}( \mathrm{t})+ \bigl[ \Phi \bigl(\mathrm{t}, \mathbf{Y}(\mathrm{t})\bigr)-\Phi _{0}(\mathrm{t}) \bigr] \vartheta (\mu )+\bar{\vartheta }(\mu ) \int _{0}^{\mathrm{t}}(\mathrm{t}- \zeta )^{\nu -1} \Phi \bigl(\zeta , \mathbf{Y}(\zeta )\bigr)\,d\zeta . $$
(19)

Thus, the model under our study satisfies the result

$$\begin{aligned}& \Vert \mathbf{Y} \Vert \leq \max \{d_{1}, d_{2}, d_{3}\}, \end{aligned}$$
(20)
$$\begin{aligned}& \begin{aligned}[t] & \bigl\Vert T \mathbf{Y}(\mathrm{t})-\mathbf{Y}_{0}(\mathrm{t}) \bigr\Vert \\ &\quad =\sup_{ \mathrm{t}\in B} \biggl\vert \Phi \bigl(\mathrm{t}, \mathbf{Y}(\mathrm{t})\bigr) \vartheta (\mu )+\bar{\vartheta }(\mu ) \int _{0}^{\mathrm{t}}(\mathrm{t}- \zeta )^{\mu -1}\Phi \bigl(\xi , \mathbf{Y}(\zeta )\bigr)\,d\zeta \biggr\vert \\ &\quad \leq \sup_{\mathrm{t}\in B}\vartheta (\mu ) \bigl\vert \Phi \bigl(\mathrm{t}, \mathbf{Y}(\mathrm{t})\bigr) \bigr\vert +\sup _{\mathrm{t}\in B}\bar{\vartheta }(\mu ) \int _{0}^{\mathrm{t}}(\mathrm{t}-\zeta )^{\mu -1} \bigl\vert \Phi \bigl(\zeta , \mathbf{Y}(\zeta )\bigr) \bigr\vert \,d\zeta \\ &\quad \leq \vartheta (\mu )\mathbf{M}+\bar{\vartheta }(\mu ) \mathrm{t}^{ \mu }_{0}\mathbf{M}d, \quad\mathbf{M}=\max \{ \mathbf{M}_{j}\} \text{ for } j=1,2,3, \mathrm{t}_{0}= \max \{\mathrm{t}\in B\} \\ &\quad < d\mathbf{M}\leq \max \{d_{1}, d_{2}, d_{3}\}=\bar{d},\quad \text{where } d= \frac{(\Gamma (\mu )+ \mu \mathrm{t}^{\mu }_{0})}{\mathcal{ABC}(\mu )\Gamma (\mu )}, \end{aligned} \end{aligned}$$
(21)

such that

$$ d< \frac{\bar{d}}{\mathbf{M}}. $$

On further simplification, one has

$$\begin{aligned} \Vert \mathbf{T}\mathbf{Y}_{1}- \mathbf{T}\mathbf{Y}_{2} \Vert =\sup_{ \mathrm{t}\in B} \vert \mathbf{Y}_{1}-\mathbf{Y}_{2} \vert . \end{aligned}$$
(22)

To compute (22), we proceed as follows:

$$\begin{aligned} \Vert \mathbf{T}\mathbf{Y}_{1}-\mathbf{T} \mathbf{Y}_{2} \Vert =&\sup_{ \mathrm{t}\in B} \biggl\vert \vartheta (\mu ) \bigl(\Phi \bigl(\mathrm{t}, \mathbf{Y}_{1}(\mathrm{t}) \bigr)-\Phi \bigl(\mathrm{t}, \mathbf{Y}_{2}( \mathrm{t})\bigr) \bigr) \\ &{}+\bar{\vartheta }(\mu ) \int _{0}^{\mathrm{t}}(\mathrm{t}-\zeta )^{\nu -1} \bigl( \Phi \bigl(\zeta , \mathbf{Y}_{1}(\zeta )\bigr)-\Phi \bigl(\zeta , \mathbf{Y}_{2}( \zeta )\bigr) \bigr)\,d\zeta \biggr\vert , \\ \leq& \vartheta (\mu )k \Vert \mathbf{Y}_{1}-\mathbf{Y}_{2} \Vert + \bar{\vartheta }(\mu )k\mathrm{t}^{\mu } \Vert \mathbf{Y}_{1}-\mathbf{Y}_{2} \Vert ,\quad \text{with } k< 1 \\ \leq& \bigl\{ \vartheta (\mu )k+\bar{\vartheta }(\mu )\mathrm{t}^{\mu } k \bigr\} \Vert \mathbf{Y}_{1}-\mathbf{Y}_{2} \Vert , \\ \leq& d k \Vert \mathbf{Y}_{1}-\mathbf{Y}_{2} \Vert . \end{aligned}$$
(23)

As Φ is a contraction, so we have \(kd<1\), thus T is a contraction. Therefore, our concerned problem (18) has the required solution. □

4 Stability results

Theorem 3

If \(d<1 \) holds, then the matrix \(\mathcal{N}\) also converging to zero is Hyers–Ulam stable.

Proof

Taking any two solutions \((x,y,z)\), \((\widehat{x},\widehat{y},\widehat{z})\), we have

$$\begin{aligned} & \bigl\Vert \chi _{1}(x,y,z)-\chi _{1}(\widehat{x},\widehat{y}, \widehat{z}) \bigr\Vert \\ &\quad \leq \bigl[ \bigl\vert \Phi \bigl(\mathrm{t}, \mathbf{(x,y,z)}( \mathrm{t})\bigr)-\Phi \bigl(\mathrm{t}, \mathbf{(\widehat{x},\widehat{y},\widehat{z})}(\mathrm{t})\bigr) \bigr\vert \bigr] \vartheta (\mu ) \\ &\qquad {}+\bar{\vartheta }(\mu ) \int _{0}^{\mathrm{t}} (\mathrm{t}-\zeta )^{\mu -1} \bigl\vert \Phi \bigl(\zeta , \mathbf{(x,y,z)}(\zeta )\bigr)-\Phi \bigl(\zeta , \mathbf{(\widehat{x},\widehat{y},\widehat{z})}(\zeta )\bigr) \bigr\vert \,d\zeta \\ &\quad \leq \vartheta (\mu )k \bigl[ \Vert x-\widehat{x} \Vert + \Vert y- \widehat{y} \Vert + \Vert z- \widehat{z} \Vert \bigr] \\ &\qquad {}+\bar{\vartheta }(\mu ) \mathrm{t}^{\mu }k \bigl[ \Vert x- \widehat{x} \Vert + \Vert y- \widehat{y} \Vert + \Vert z-\widehat{z} \Vert \bigr] \\ &\quad \leq \bigl(\vartheta (\mu )+\bar{\vartheta }(\mu ) \mathrm{t}^{\mu } \bigr)k \Vert x-\widehat{x} \Vert \\ &\qquad {}+ \bigl(\vartheta (\mu )+\bar{\vartheta }(\mu ) \mathrm{t}^{\mu } \bigr)k \Vert y-\widehat{y} \Vert \\ &\qquad {}+ (\vartheta (\mu )+\bar{\vartheta }(\mu ) \mathrm{t}^{\mu }k \Vert z- \widehat{z} \Vert \\ &\quad \leq c_{1} \Vert x-\widehat{x} \Vert +c_{2} \Vert y- \widehat{y} \Vert +c_{3} \Vert z- \widehat{z} \Vert . \end{aligned}$$
(24)

In the same fashion, one has

$$ \begin{gathered} \bigl\Vert \chi _{2}(x,y,z)-\chi _{2}(\widehat{x},\widehat{y}, \widehat{z}) \bigr\Vert \leq c_{4} \Vert x-\widehat{x} \Vert +c_{5} \Vert y- \widehat{y} \Vert +c_{6} \Vert z-\widehat{z} \Vert , \\ \bigl\Vert \chi _{3}(x,y,z)-\chi _{3}(\widehat{x}, \widehat{y},\widehat{z}) \bigr\Vert \leq c_{7} \Vert x-\widehat{x} \Vert +c_{8} \Vert y-\widehat{y} \Vert +c_{9} \Vert z- \widehat{z} \Vert , \end{gathered} $$
(25)

where

$$ c_{i}= \bigl(\vartheta (\mu )+\bar{\vartheta }(\mu ) \mathrm{t}^{\mu } \bigr)k\quad \text{for each }i=1,2,\ldots,9. $$

Now, the matrix \(\mathcal{N}\) given by

$$ \mathcal{N}= \begin{pmatrix} c_{1} & c_{2} &c_{3} \\ c_{4} & c_{5}&c_{6} \\ c_{7} &c_{8} &c_{9} \end{pmatrix} $$
(26)

converges to zero. Hence, the system is Hyers–Ulam stable. □

5 Analytical results for the proposed model

Here, we are going to apply LADM to obtain general results for the considered model (2).

$$ \textstyle\begin{cases} \mathcal{L}[x(\mathrm{t})]=\frac{x(0)}{s}+ \frac{s^{\mu }(1-\mu )+\mu }{s^{\mu }\mathcal{ABC}(\mu )}\mathcal{L}[ \alpha N-\delta x(\mathrm{t}) y(\mathrm{t})- ax(\mathrm{t})], \\ \mathcal{L}[y(\mathrm{t})]=\frac{y(0)}{s}+ \frac{s^{\mu }(1-\mu )+\mu }{s^{\mu }\mathcal{ABC}(\mu )}\mathcal{L}[ \delta x(\mathrm{t}) y(\mathrm{t})-(\beta +a+b) y(\mathrm{t})], \\ \mathcal{L}[z(\mathrm{t})]=\frac{z(0)}{s}+ \frac{s^{\mu }(1-\mu )+\mu }{s^{\mu }\mathcal{ABC}(\mu )}\mathcal{L}[ \beta y(\mathrm{t})-a z(\mathrm{t})]. \end{cases} $$
(27)

Now, we are going to consider \(x(\mathrm{t})\), \(y(\mathrm{t})\), \(z(\mathrm{t})\) in terms of infinite series as follows:

$$ x(\mathrm{t})=\sum_{q=0}^{\infty }x_{q}( \mathrm{t}),\qquad y(\mathrm{t})= \sum_{q=0}^{\infty }y_{q}( \mathrm{t}),\qquad z(\mathrm{t})=\sum_{q=0}^{\infty }z_{q}( \mathrm{t}). $$
(28)

We resolve nonlinear terms as follows:

$$ x(\mathrm{t})y(\mathrm{t})=\sum _{q=0}^{\infty } A_{q} (x,y), $$
(29)

where \(A_{q}(x,y)\) can be defined as

$$ A_{q}(x,y)=\frac{1}{q!}\frac{d^{q}}{d\lambda ^{q}} \Biggl[\sum _{j=0}^{p} \lambda ^{j}x_{j}( \mathrm{t})\sum_{j=0}^{p}\lambda ^{j}y_{j}( \mathrm{t}) \Biggr]\Bigg|_{\lambda =0}. $$

Hence, by using (28) and (29), our system (27) becomes

$$ \textstyle\begin{cases} \mathcal{L} [\sum_{q=0}^{\infty }x_{q}(\mathrm{t}) ]= \frac{x(0)}{s}+\frac{s^{\mu }(1-\mu )+\mu }{s^{\mu }\mathcal{ABC}(\mu )} \mathcal{L} [\alpha N-\delta \sum_{q=0}^{\infty }A_{q}(x,y)-a\sum_{q=0}^{\infty }x_{q} ], \\ \mathcal{L} [\sum_{q=0}^{\infty }y_{q}(\mathrm{t}) ]= \frac{y(0)}{s}+\frac{s^{\mu }(1-\mu )+\mu }{s^{\mu }\mathcal{ABC}(\mu )} \mathcal{L} [\delta \sum_{q=0}^{\infty }A_{q}(x,y)-(\beta +a+b) \sum_{q=0}^{\infty }y_{q} ], \\ \mathcal{L} [\sum_{q=0}^{\infty }z_{q}(\mathrm{t}) ]= \frac{z(0)}{s}+\frac{s^{\mu }(1-\mu )+\mu }{s^{\mu }\mathcal{ABC}(\mu )} \mathcal{L} [\beta \sum_{q=0}^{\infty }y_{q}-a\sum_{q=0}^{\infty }z_{q} ]. \end{cases} $$
(30)

Upon comparing terms wise (30), one has

$$ \textstyle\begin{cases} \mathcal{L}[x_{0}(\mathrm{t})]=N_{1},\qquad \mathcal{L}[y_{0}(\mathrm{t})]=N_{2},\qquad \mathcal{L}[z_{0}(\mathrm{t})]=N_{3}, \\ \mathcal{L}[x_{1}(\mathrm{t})]= \frac{s^{\mu }(1-\mu )+\mu }{s^{\mu }\mathcal{ABC}(\mu )}\mathcal{L} [ \alpha N-\delta A_{0}(x,y)-a N_{1} ], \\ \mathcal{L}[y_{1}(\mathrm{t})] = \frac{s^{\mu }(1-\mu )+\mu }{s^{\mu }\mathcal{ABC}(\mu )}\mathcal{L} [ \delta A_{0}(x,y)-(\beta +a+b)N_{2} ], \\ \mathcal{L}[z_{1}(\mathrm{t})] = \frac{s^{\mu }(1-\mu )+\mu }{s^{\mu }\mathcal{ABC}(\mu )}\mathcal{L} [ \beta N_{2}-a N_{3} ], \\ \mathcal{L}[x_{2}(\mathrm{t})]= \frac{s^{\mu }(1-\mu )+\mu }{s^{\mu }\mathcal{ABC}(\mu )}\mathcal{L} [ \alpha N-\delta A_{2}(x,y)-a x_{1} ], \\ \mathcal{L}[y_{2}(\mathrm{t})] = \frac{s^{\mu }(1-\mu )+\mu }{s^{\mu }\mathcal{ABC}(\mu )}\mathcal{L} [ \delta A_{q}(x,y)-(\beta +a+b) y_{1} ], \\ \mathcal{L}[z_{2}(\mathrm{t})] = \frac{s^{\mu }(1-\mu )+\mu }{s^{\mu }\mathcal{ABC}(\mu )}\mathcal{L} [ \beta y_{1}-a z_{1} ], \\ \vdots \\ \mathcal{L}[x_{q+1}(\mathrm{t})]= \frac{s^{\mu }(1-\mu )+\mu }{s^{\mu }\mathcal{ABC}(\mu )}\mathcal{L} [ \alpha N-\delta A_{q}(u,x)-a x_{q} ], \\ \mathcal{L}[y_{q+1}(\mathrm{t})] = \frac{s^{\mu }(1-\mu )+\mu }{s^{\mu }\mathcal{ABC}(\mu )}\mathcal{L} [ \delta A_{q}(x,y)-(\beta +a+b)y_{q} ], \\ \mathcal{L}[z_{q+1}(\mathrm{t})] = \frac{s^{\mu }(1-\mu )+\mu }{s^{\mu }\mathcal{ABC}(\mu )}\mathcal{L} [ \beta y_{q}-a z_{q} ], \quad q\geq 0. \end{cases} $$
(31)

Simplifying the Laplace transform in (31), we get

$$ \textstyle\begin{cases} x_{0}(\mathrm{t})=N_{1},\qquad y_{0}(\mathrm{t})=N_{2},\qquad z_{0}( \mathrm{t})=N_{3}, \\ x_{1}(\mathrm{t})= (\alpha N-\delta N_{1} N_{2}-a N_{1} ) (1-\mu +\frac{\mu \mathrm{t}^{\mu }}{\Gamma (\mu )} ), \\ y_{1}(\mathrm{t})= (1-\mu + \frac{\mu \mathrm{t}^{\mu }}{\Gamma (\mu )} ) (\delta N_{1}N_{2}-( \beta +a+b)N_{2} ), \\ z_{1}(\mathrm{t})= (\beta N_{1}-a N_{3} ) (1-\mu + \frac{\mu \mathrm{t}^{\mu }}{\Gamma (\mu )} ), \\ x_{2}(\mathrm{t})= (1-\mu + \frac{\mu \mathrm{t}^{\mu }}{\Gamma (\mu )} )\alpha N- ((\delta N_{2}+ \alpha )(\alpha N-\delta N_{1} N_{2}-\alpha N_{1}) ) [ (1- \mu +\frac{\mu \mathrm{t}^{\mu }}{\Gamma (\mu )} ) ]^{2}, \\ y_{2}(\mathrm{t})= ((\delta N_{1}-a-\beta -b)(\delta N_{1} N_{2}+(a+b- \beta )N_{2})\\ \hphantom{y_{2}(\mathrm{t})=}{}+\delta N_{2}(\alpha N-\delta N_{1}N_{2}-\alpha N_{1}) ) [ (1-\mu +\frac{\mu \mathrm{t}^{\mu }}{\Gamma (\mu )} ) ]^{2}, \\ z_{2}(\mathrm{t})= [1-\mu + \frac{\mu \mathrm{t}^{\mu }}{\Gamma (\mu )} ]^{2} (\beta ( \delta N_{1}N_{2}-(\beta +a+b)N_{2})-a(\beta N_{1}-aN_{3}) ), \end{cases} $$

and so on.

In this way, the reaming terms may be computed. Finally, the required solutions can be expressed as follows:

$$ x(\mathrm{t})=\sum_{k=0}^{\infty }x_{k}( \mathrm{t}),\qquad y(\mathrm{t})=\sum_{k=0}^{\infty }y_{k}( \mathrm{t}),\qquad z(\mathrm{t})=\sum_{k=0}^{\infty }z_{k}( \mathrm{t}), $$
(32)

6 Computational results

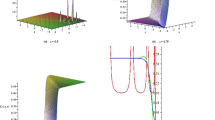
In this section of the paper, our computational results about a series solution of the concerned model are represented. To obtain the main goal, we apply LADM for the solution corresponding to the values given in Table 1. In view of Table 1, we exhibit the results, which are represented in (32) for different fractional order in the following Figs. 1–3 using Matlab. Figures 1–3 show the graphs for the population of three compartments (susceptible, infected, and recovered) for distinct values of μ. One can observe that as we increase the values of μ, the corresponding solutions converge to the solution at integer order. Moreover, with passage of time the population of the susceptible class is decreasing when starts from 0.1 in given time of 250 days under proper cure or vaccination. The decreasing process of a class is different at different fractional order, while the density of infected papulation is decreasing in given time of 250 days. Hence, the recovered class is increasing with passage of time. As we observe, for different values of μ, the distinct trajectories are obtained as exhibited in Figs. 1–3. Increasing or decreasing (growth or decay) process is somewhat greater at small fractional order values as compared to those of greater fractional order.

Figure 1
figure 1

Dynamical behavior of “susceptible papulation” corresponding to various values of μ

Full size image
Figure 2
figure 2

Dynamical behavior of “infected papulation” corresponding to various values of μ

Full size image
Figure 3
figure 3

Dynamical behavior of “recovered papulation” corresponding to various values of μ

Full size image
Table 1 Parameters and their numerical values in model (2)
Full size table

7 Concluding remarks

We have discussed LADM for a biological model of the SIR model using the ABC operator. Also, we developed some results about the qualitative theory and Hyers–Ulam stability analysis. The methodology utilized here for dynamical problems under ABC operator of derivative is very rarely applied in the literature. Further on providing some graphs of approximate results, we have illustrated the procedure. The mentioned tool may be used in the future to handle more complicated problems under the aforementioned operator.