1 Introduction

An elastic beam is an important element needed in structures like buildings, bridges, ships, and aircrafts. The deformations of the beam can be modeled (see, e.g., [2]) by the fourth-order Navier boundary value problem

$$\begin{aligned} \textstyle\begin{cases} \omega ^{(4)}(t)=h(t,\omega (t),\omega ^{\prime \prime }(t)), & 0< t< 1, \\ \omega (0)=\omega (1)=\omega ^{\prime \prime }(0)=\omega ^{\prime \prime }(1)=0, \end{cases}\displaystyle \end{aligned}$$
(1.1)

where \(h:[0,1]\times \mathbb{R}\times \mathbb{R\rightarrow R}\) is continuous.

Aftabizadeh [3] studied problem (1.1) under the restriction that h is bounded on \([0,1]\times \mathbb{R}\times \mathbb{R}\). By using a topological degree method he proved the existence and uniqueness of a solution. In [4] (see also [5]) the authors established the existence of a solution for problem (1.1) by means of the lower and upper solutions method. Differently from this method, Dang et al. [1] investigated problem (1.1) by reducing it to an operator equation and using some easily verified conditions. In [6] the authors studied the existence of a solution of a fourth-order differential equation boundary value problem by proving a new fixed point result based on a new distance structure called the extended Branciari b-distance.

Motivated by the novel approach presented in [1], our purpose is generalization of their results to the frame of fractional differentiation. More precisely, we address the question of existence and uniqueness of solutions of the following problem:

$$\begin{aligned} \textstyle\begin{cases} D^{\alpha }(D^{\beta }\omega )(t)=h(t,\omega (t),D^{\beta }\omega (t)), & 0< t< 1, \\ \omega (0)=\omega (1)=D^{\beta }\omega (0)=D^{\beta }\omega (1)=0, \end{cases}\displaystyle \end{aligned}$$
(1.2)

where \(\alpha,\beta \in (1,2]\), \(D^{\alpha }\) and \(D^{\beta }\) are the standard Riemann–Liouville differentiation, and the real function h is supposed to be continuous on \([0,1]\times \mathbb{R\times R}\) and satisfying some appropriate conditions.

For \(\alpha =\beta =2\), we recover the results obtained in [1].

In the literature, various mathematical procedures have been considered by scientists through different research-oriented aspects of fractional differential equations. In particular, the fixed point theory has been used very extensively to find solutions of such equations. For instance, in [7] the authors studied the existence of solutions to nonlinear Volterra–Fredholm integral equations of certain types and to nonlinear fractional differential equations of the Caputo type by using the technique of a fixed point with numerical experiment in an extended b-metric space. On the other hand, in [8] the authors established some new fixed-point theorems, which extend and unify several existing results in the literature. As application of their results, they have proved the existence and uniqueness of solutions to some fractional and integer-order differential equations. In [9] the authors established the existence and uniqueness of solutions of boundary value problems for a nonlinear fractional differential equation by means of a fixed point problem for an integral operator. The conditions for the existence and uniqueness of a fixed point for an integral operator are derived via b-comparison functions on complete b-metric spaces. Our approach in the present study consists in applying the Banach fixed point theorem.

Our paper is organized as follows. In Sect. 2, we establish key inequalities on the Green operator functions. In Sect. 3, by reducing problem (1.2) to an operator equation we prove the existence, uniqueness, and positivity of a solution. We propose an approximation process of this solution. We provide some examples at the end of Sect. 3.

2 Preliminaries and lemmas

For the convenience of the reader, we recall some basic definitions and known results related to fractional calculus [10, 11].

Definition 2.1

Let \(\omega: ( 0,\infty ) \rightarrow \mathbb{R} \) be a measurable function. The Riemann–Liouville fractional integral of order \(\gamma >0\) for ω is defined as

$$\begin{aligned} I^{\gamma }\omega (t):=\frac{1}{\Gamma ( \gamma ) }\int _{0}^{t} ( t-y ) ^{\gamma -1}\omega ( y ) \,dy,\quad t>0, \end{aligned}$$

where Γ is the Euler gamma function.

Definition 2.2

Let \(\omega: ( 0,\infty ) \rightarrow \mathbb{R} \) be a measurable function. The Riemann–Liouville fractional derivative of order \(\gamma >0\) for ω is defined as

$$\begin{aligned} D^{\gamma }\omega (t):=\frac{1}{\Gamma ( n-\gamma ) } \biggl( \frac{d}{dt} \biggr) ^{n} \int _{0}^{t} ( t-y ) ^{n-\gamma -1} \omega ( y ) \,dy= \biggl( \frac{d}{dt} \biggr) ^{n}I^{n- \gamma }\omega (t), \end{aligned}$$

where \(n=[\gamma ]+1\), and \([\gamma ]\) is the integer part of γ.

Lemma 2.3

Let \(\delta >0\) and \(\omega \in C ( 0,1 ) \cap L^{1} ( 0,1 ) \). Then we have

  1. (i)

    For \(0<\gamma <\delta \), \(D^{\gamma }I^{\delta }\omega =I^{\delta -\gamma }\omega \) and \(D^{\delta }I^{\delta }\omega =\omega \);

  2. (ii)

    \(D^{\gamma }\omega (t)=0\) if and only if \(\omega (t)=c_{1}t^{\gamma -1}+c_{2}t^{\gamma -2}+\cdots +c_{m}t^{ \gamma -m}\), \(c_{i}\in \mathbb{R} \), \(i=1,\dots,m\), where m is the smallest integer greater than or equal to γ.

  3. (iii)

    Assume that \(D^{\gamma }\omega \in C ( 0,1 ) \cap L^{1} ( 0,1 ) \). Then

    $$\begin{aligned} I^{\gamma }D^{\gamma }\omega ( t ) =\omega (t)+c_{1}t^{ \gamma -1}+c_{2}t^{\gamma -2}+ \cdots+c_{m}t^{\gamma -m}, \end{aligned}$$

    \(c_{i}\in \mathbb{R} \), \(i=1,\ldots,m\), where m is the smallest integer greater than or equal to γ.

Lemma 2.4

([12])

For \(\gamma \in (1,2]\) and \(\varphi \in C([0,1],\mathbb{R})\), the unique solution of

$$\begin{aligned} \textstyle\begin{cases} D^{\gamma }\omega ( t ) +\varphi (t)=0, &0< t< 1, \\ \omega (0)=\omega (1)=0,\end{cases}\displaystyle \end{aligned}$$
(2.1)

is

$$\begin{aligned} \omega (t)= \int _{0}^{1}G_{\gamma } ( t,y ) \varphi ( y ) \,dy, \end{aligned}$$
(2.2)

where

$$\begin{aligned} G_{\gamma } ( t,y ):= \frac{1}{\Gamma ( \gamma ) }\textstyle\begin{cases} [ t ( 1-y ) ]^{\gamma -1}- ( t-y ) ^{ \gamma -1} & \textit{for }0\leq y\leq t\leq 1, \\ [ t ( 1-y ) ]^{\gamma -1} & \textit{for }0\leq t\leq y \leq 1.\end{cases}\displaystyle \end{aligned}$$
(2.3)

Proof

To make the argument complete and self-contained, we reproduce this short proof. By means of Lemma 2.3 we can equivalently reduce (2.1) to

$$\begin{aligned} \omega (t)=c_{1}t^{\gamma -1}+c_{2}t^{\gamma -2}- \frac{1}{\Gamma ( \gamma ) } \int _{0}^{t} ( t-y ) ^{\gamma -1} \varphi ( y ) \,dy,\quad\text{for some }c_{1},c_{2}\in \mathbb{R}. \end{aligned}$$
(2.4)

From the conditions \(\omega (0)=0\) and \(\omega (1)=0\) we get

$$\begin{aligned} c_{2}=0\quad \text{and}\quad c_{1}=\frac{1}{\Gamma ( \gamma ) }\int _{0}^{1} ( 1-y ) ^{\gamma -1}\varphi ( y ) \,dy. \end{aligned}$$

Substituting \(c_{1}\) and \(c_{2}\) into (2.4), we obtain (2.2). □

Throughout the paper, for \(\gamma \in (1,2]\) and \(\varphi \in C([0,1],\mathbb{R})\), we denote

$$\begin{aligned} \begin{aligned} &M_{\gamma }:=\frac{1}{\gamma \Gamma ( \gamma +1 ) }\biggl( \frac{\gamma -1}{\gamma } \biggr)^{\gamma -1}\quad\text{and}\\ & \mathcal{G}_{\gamma }\varphi (t):= \int _{0}^{1}G_{\gamma } ( t,y ) \varphi (y) \,dy\quad \text{for }0\leq t\leq 1. \end{aligned} \end{aligned}$$
(2.5)

Remark 2.5

Let \(\gamma \in (1,2]\).

  1. (i)

    Note that \((t,y)\rightarrow G_{\gamma }(t,y)\) is a nonnegative continuous function on \([ 0,1 ] \times [ 0,1 ] \).

  2. (ii)

    For \(\varphi \in C([0,1],\mathbb{R})\), the function \(t\rightarrow \mathcal{G}_{\gamma }\varphi (t)\) is continuous on \([0,1]\).

Lemma 2.6

Let \(\alpha,\beta \in (1,2]\) and \(\varphi \in C([0,1],\mathbb{R})\). Then

$$\begin{aligned} \Vert \mathcal{G}_{\alpha }\varphi \Vert \leq M_{\alpha } \Vert \varphi \Vert \quad\textit{and}\quad \bigl\Vert \mathcal{G}_{ \beta } ( \mathcal{G}_{\alpha }\varphi ) \bigr\Vert \leq M_{\alpha }M_{\beta } \Vert \varphi \Vert , \end{aligned}$$
(2.6)

where \(\Vert \varphi \Vert := \underset{t\in [ 0,1]}{\max } \vert \varphi (t) \vert \).

Proof

From (2.5) and Remark 2.5 we have

$$\begin{aligned} \bigl\vert \mathcal{G}_{\gamma }\varphi (t) \bigr\vert \leq \Vert \varphi \Vert \psi (t), \end{aligned}$$
(2.7)

where

$$\begin{aligned} \psi (t):= \int _{0}^{1}G_{\alpha } ( t,y ) \,dy. \end{aligned}$$

By using (2.3) and a simple computation we get

$$\begin{aligned} \psi (t)=\frac{1}{\Gamma ( \alpha +1 ) }t^{\alpha -1}(1-t). \end{aligned}$$

Since \(\Vert \psi \Vert =\psi (\frac{\alpha -1}{\alpha })=M_{\alpha }\), from (2.7) we deduce that

$$\begin{aligned} \bigl\vert \mathcal{G}_{\gamma }\varphi (t) \bigr\vert \leq M_{ \alpha } \Vert \varphi \Vert \quad\text{for }t\in [ 0,1]. \end{aligned}$$

Hence

$$\begin{aligned} \Vert \mathcal{G}_{\alpha }\varphi \Vert \leq M_{\alpha } \Vert \varphi \Vert \quad\text{and}\quad \bigl\Vert \mathcal{G}_{ \beta } ( \mathcal{G}_{\alpha }\varphi ) \bigr\Vert \leq M_{\beta }M_{\alpha } \Vert \varphi \Vert . \end{aligned}$$

The proof is completed. □

3 Existence results and iterative method

For \(\alpha,\beta \in (1,2]\) and \(M>0\), we let

$$\begin{aligned} \mathcal{D}_{M}=\bigl\{ (t,y,z)\in \mathbb{R}^{3}: 0\leq t \leq 1, \text{ } \vert y \vert \leq MM_{\alpha }M_{\beta }, \vert z \vert \leq MM_{\alpha }\bigr\} \end{aligned}$$

and denote by

$$\begin{aligned} \mathbb{B}_{M}:=\bigl\{ \theta \in C\bigl([0,1],\mathbb{R}\bigr): \Vert \theta \Vert \leq M\bigr\} . \end{aligned}$$

Theorem 3.1

Let \(h\in C([0,1]\times \mathbb{R}\times \mathbb{R},\mathbb{R)}\). Assume that there exist \(M>0\) and \(L_{i}>0\) \((i=1,2)\) such that

  1. (i)

    \(\vert h(t,y,z) \vert \leq M\) for all \((t,y,z)\in \mathcal{D}_{M}\).

  2. (ii)

    \(\vert h(t,y_{2},z_{2})-h(t,y_{1},z_{2}) \vert \leq L_{1} \vert y_{2}-y_{1} \vert +L_{2} \vert z_{2}-z_{1} \vert \) for all \((t,y_{i},z_{i})\in \mathcal{D}_{M}\), \(i=1,2\).

  3. (iii)

    \(q:=L_{1}M_{\alpha }M_{\beta }+L_{2}M_{\alpha }<1\).

Then problem (1.2) admits a unique continuous solution ω with \(D^{\beta }\omega \in C([0,1],\mathbb{R)}\) satisfying

$$\begin{aligned} \Vert \omega \Vert \leq MM_{\alpha }M_{\beta } \quad\textit{and}\quad \bigl\Vert D^{\beta }\omega \bigr\Vert \leq MM_{\alpha }. \end{aligned}$$
(3.1)

Proof

Let \(\varphi \in C([0,1],\mathbb{R})\) and set

$$\begin{aligned} T\varphi (t):=h\bigl(t,\mathcal{G}_{\beta } ( \mathcal{G}_{\alpha } \varphi ) (t),-\mathcal{G}_{\alpha }\varphi (t)\bigr),\quad t\in [ 0,1]. \end{aligned}$$
(3.2)

Assume that ω is a continuous solution of problem (1.2) with \(D^{\beta }\omega \in C([0,1]\mathbb{)}\). Then by Lemma 2.4 the function \(\varphi (t):=h(t,\omega (t),D^{\beta }\omega (t))\) is a fixed point of the operator T.

Conversely, if φ is a fixed point of the operator T, then again by Lemma 2.4

$$\begin{aligned} \omega (t):=\mathcal{G}_{\beta } ( \mathcal{G}_{\alpha }\varphi ) (t) \end{aligned}$$
(3.3)

is a continuous solution of problem (1.2) with \(D^{\beta }\omega (t)=-\mathcal{G}_{\alpha }\varphi (t)\in C([0,1] \mathbb{)}\). So, problem (1.2) is reduced to a fixed point problem for T.

Since \(h\in C([0,1]\times \mathbb{R}\times \mathbb{R},\mathbb{R)}\), it is clear from Remark 2.5 that Tφ is continuous on \([0,1]\).

Due to Lemma 2.6, for \(\varphi \in \mathbb{B}_{M}\), we have

$$\begin{aligned} \Vert \mathcal{G}_{\alpha }\varphi \Vert \leq MM_{ \alpha }\quad\text{and}\quad \bigl\Vert \mathcal{G}_{\beta } ( \mathcal{G}_{\alpha }\varphi ) \bigr\Vert \leq MM_{\alpha }M_{ \beta }. \end{aligned}$$
(3.4)

Hence, for \(t\in [ 0,1]\), \((t,\mathcal{G}_{\beta } ( \mathcal{G}_{\alpha }\varphi ) (t),- \mathcal{G}_{\alpha }\varphi (t))\in \mathcal{D}_{M}\), and by assumption (i) we have \(T(\mathbb{B}_{M})\subset \mathbb{B}_{M}\).

We claim aim that T is a contraction on \(\mathbb{B}_{M}\). Indeed, for \(\varphi _{1},\varphi _{2}\in \mathbb{B}_{M}\), by assumption (ii) and Lemma 2.4 we have

$$\begin{aligned} \bigl\vert T\varphi _{2}(t)-T\varphi _{1}(t) \bigr\vert &= \bigl\vert h\bigl(t,\mathcal{G}_{\beta } ( \mathcal{G}_{\alpha }\varphi _{2} ) (t),-\mathcal{G}_{\alpha }\varphi _{2}(t)\bigr)-h\bigl(t, \mathcal{G}_{\beta } ( \mathcal{G}_{\alpha }\varphi _{1} ) (t),-\mathcal{G}_{\alpha } \varphi _{1}(t)\bigr) \bigr\vert \\ &\leq L_{1} \bigl\vert \mathcal{G}_{\beta } ( \mathcal{G}_{ \alpha }\varphi _{2} ) (t)-\mathcal{G}_{\beta } ( \mathcal{G}_{\alpha }\varphi _{1} ) (t) \bigr\vert +L_{2} \bigl\vert \mathcal{G}_{\alpha }\varphi _{1}(t)-\mathcal{G}_{\alpha } \varphi _{2}(t) \bigr\vert \\ &=L_{1} \bigl\vert \mathcal{G}_{\beta } \bigl( \mathcal{G}_{\alpha }( \varphi _{2}-\varphi _{1}) \bigr) (t) \bigr\vert +L_{2} \bigl\vert \mathcal{G}_{\alpha }( \varphi _{1}-\varphi _{2}) (t) \bigr\vert \\ &\leq (L_{1}M_{\alpha }M_{\beta }+L_{2}M_{\alpha }) \Vert \varphi _{2}-\varphi _{1} \Vert . \end{aligned}$$

Since \(q:=L_{1}M_{\alpha }M_{\beta }+L_{2}M_{\alpha }<1\), we deduce that T is a contraction operator on \(\mathbb{B}_{M}\). Hence there exists a unique \(\varphi \in \mathbb{B}_{M}\) such that

$$\begin{aligned} \varphi (t)=h\bigl(t,\mathcal{G}_{\beta } ( \mathcal{G}_{\alpha } \varphi ) (t),-\mathcal{G}_{\alpha }\varphi (t)\bigr)\quad\text{for }t \in [ 0,1]. \end{aligned}$$

So, problem (1.2) admits a unique solution \(\omega (t):=\mathcal{G}_{\beta } ( \mathcal{G}_{\alpha }\varphi ) (t) \in C([0,1],\mathbb{R})\) satisfying (3.1). □

Remark 3.2

Theorem 3.1 extends Theorem 1 in [1] to the fractional setting.

To establish the positivity of solution of problem (1.2), for \(M>0\), we denote

$$\begin{aligned} \mathcal{D}_{M}^{+}=\bigl\{ (t,y,z)\in \mathbb{R}^{3}: 0\leq t\leq 1, 0\leq y\leq MM_{\alpha }M_{\beta }, -MM_{\alpha }\leq z \leq 0\bigr\} . \end{aligned}$$

Corollary 3.3

Let h be a continuous function on \([0,1]\times \mathbb{R}\times \mathbb{R}\). Assume that there exist \(M>0\) and \(L_{i}>0\) \((i=1,2)\) such that

  1. (i)

    \(0\leq h(t,y,z)\leq M\) for all \((t,y,z)\in \mathcal{D}_{M}^{+}\).

  2. (ii)

    \(\vert h(t,y_{2},z_{2})-h(t,y_{1},z_{2}) \vert \leq L_{1} \vert y_{2}-y_{1} \vert +L_{2} \vert z_{2}-z_{1} \vert \) for all \((t,y_{i},z_{i})\in \mathcal{D}_{M}^{+}\), \(i=1,2\).

  3. (iii)

    \(q:=L_{1}M_{\alpha }M_{\beta }+L_{2}M_{\alpha }<1\).

Then problem (1.2) admits a unique nonnegative continuous function ω satisfying

$$\begin{aligned} 0\leq \omega (t)\leq MM_{\alpha }M_{\beta }\quad\textit{for }t\in [ 0,1]. \end{aligned}$$
(3.5)

Theorem 3.4

(Iterative method)

Under the assumptions of Theorem 3.1, consider the iterative process defined by

$$\begin{aligned} \varphi _{0}\in \mathbb{B}_{M}\quad \textit{and}\quad \varphi _{k+1}(t):=h\bigl(t, \mathcal{G}_{\beta } ( \mathcal{G}_{\alpha }\varphi _{k} ) (t),- \mathcal{G}_{\alpha } \varphi _{k}(t)\bigr). \end{aligned}$$
(3.6)

The sequence \((\mathcal{G}_{\beta } ( \mathcal{G}_{\alpha }\varphi _{k} ) )_{k\geq 0}\) converges uniformly to ω, the unique solution of problem (1.2), and we have

$$\begin{aligned} \bigl\Vert \mathcal{G}_{\beta } ( \mathcal{G}_{\alpha }\varphi _{k} ) -\omega \bigr\Vert \leq M_{\alpha }M_{\beta } \frac{q^{k}}{(1-q)} \Vert \varphi _{1}-\varphi _{0} \Vert , \end{aligned}$$
(3.7)

where \(q:=L_{1}M_{\alpha }M_{\beta }+L_{2}M_{\alpha }<1\).

Proof

From the proof of Theorem 3.1 we know that the sequence \((\varphi _{k})_{k\geq 0}\) converges to a unique \(\varphi \in \mathbb{B}_{M}\) satisfying \(T(\varphi )=\varphi \), and we have

$$\begin{aligned} \Vert \varphi _{k}-\varphi \Vert \leq \frac{q^{k}}{1-q} \Vert \varphi _{1}-\varphi _{0} \Vert . \end{aligned}$$
(3.8)

By using Lemma 2.6 we deduce

$$\begin{aligned} \bigl\Vert \mathcal{G}_{\beta } ( \mathcal{G}_{\alpha }\varphi _{k} ) -\omega \bigr\Vert &= \bigl\Vert \mathcal{G}_{\beta } ( \mathcal{G}_{\alpha }\varphi _{k} ) -\mathcal{G}_{ \beta } ( \mathcal{G}_{\alpha }\varphi ) \bigr\Vert \\ &= \bigl\Vert \mathcal{G}_{\beta }\bigl(\mathcal{G}_{\alpha }( \varphi _{k}- \varphi )\bigr) \bigr\Vert \\ &\leq M_{\alpha }M_{\beta } \Vert \varphi _{k}-\varphi \Vert \\ &\leq M_{\alpha }M_{\beta }\frac{q^{k}}{1-q} \Vert \varphi _{1}- \varphi _{0} \Vert . \end{aligned}$$

Hence the sequence \((\mathcal{G}_{\beta } ( \mathcal{G}_{\alpha }\varphi _{k} ) )_{k\geq 0}\) converges uniformly to ω, and inequality (3.7) holds. □

Remark 3.5

Theorem 3.4 extends Theorem 3 in [1] to the fractional setting.

Example 3.6

Let \(\alpha =\beta =\frac{3}{2}\), and consider the problem

$$\begin{aligned} \textstyle\begin{cases} D^{\frac{3}{2}}(D^{\frac{3}{2}}\omega ) ( t ) =e^{\omega (t)},& 0< t< 1, \\ \omega (0)=\omega (1)=D^{\frac{3}{2}}\omega (0)=D^{\frac{3}{2}} \omega (1)=0.\end{cases}\displaystyle \end{aligned}$$
(3.9)

In this example, \(M_{\alpha }=M_{\beta }=\frac{8}{27}\frac{\sqrt{3}}{\sqrt{\pi }}\) and \(f(t,y,z)=e^{y}\). To ensure assumption (i) in Theorem 3.1, we have to choose \(M>0\) such that

$$\begin{aligned} e^{\frac{64}{243\pi }M}\leq M. \end{aligned}$$

This holds, for example, with \(M=2\).

On the other hand, in \(\mathcal{D}_{2}=\{(t,y,z)\in \mathbb{R}^{3}: 0\leq t\leq 1, \vert y \vert \leq \frac{128}{243\pi }, \vert z \vert \leq \frac{16}{27} \frac{\sqrt{3}}{\sqrt{\pi }}\}\), since

$$\begin{aligned} f_{y}^{\prime }=e^{y}\quad \text{and}\quad f_{z}^{\prime }=0, \end{aligned}$$

we have

$$\begin{aligned} \bigl\vert f_{y}^{\prime } \bigr\vert \leq 2. \end{aligned}$$

Hence assumption (ii) in Theorem 3.1 is satisfied with \(L_{1}=2\) and \(L_{2}=1\). Also, we have \(q:=L_{1}M_{\alpha }M_{\beta }+L_{2}M_{\alpha }\approx 0.457 21<1\). Thus by Theorem 3.1 problem (3.9) admits a unique continuous solution ω satisfying

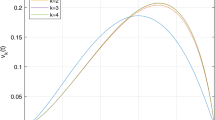
$$\begin{aligned} \Vert \omega \Vert \leq \frac{128}{243\pi }\quad\text{and}\quad \bigl\Vert D^{\frac{3}{2}}\omega \bigr\Vert \leq \frac{16}{27} \frac{\sqrt{3}}{\sqrt{\pi }}. \end{aligned}$$

Take the initial approximation \(\varphi _{0}(t)=1\). Some iterations of \(\omega _{k}(t):=\mathcal{G}_{\frac{3}{2}} ( \mathcal{G}_{\frac{3}{2}}\varphi _{k} ) (t)\) are presented in Fig. 1.

Figure 1
figure 1

Graphs of the successive approximation of ω

Full size image

Example 3.7

For \(\alpha =\frac{4}{3}\) and \(\beta =\frac{5}{3}\), consider the problem

$$\begin{aligned} \textstyle\begin{cases} D^{\frac{4}{3}}(D^{\frac{5}{3}}\omega ) ( t ) =t\omega (t)+t^{2}(D^{\frac{5}{3}}\omega (t))^{2}+1,& 0< t< 1, \\ \omega (0)=\omega (1)=D^{\frac{5}{3}}\omega (0)=D^{\frac{5}{3}} \omega (1)=0.\end{cases}\displaystyle \end{aligned}$$
(3.10)

In this example, \(M_{\alpha }=\frac{3}{4\Gamma ( \frac{7}{3} ) }(\frac{1}{4})^{\frac{1}{3}}\), \(M_{\beta }=\frac{3}{5\Gamma ( \frac{8}{3} ) }(\frac{2}{5})^{\frac{2}{3}}\), and \(f(t,y,z)=ty+t^{2}z^{2}+1\).

Assumption (i) in Theorem 3.1 will hold if we choose \(M>0 \) such that

$$\begin{aligned} MM_{\alpha }M_{\beta }+M^{2}M_{\alpha }^{2}+1 \leq M. \end{aligned}$$

We can verify that \(M=2\) is a suitable candidate. On the other hand, since

$$\begin{aligned} f_{y}^{\prime }=t\quad \text{and}\quad f_{z}^{\prime }=2t^{2}z, \end{aligned}$$

it follows that for \((t,y,z)\in \mathcal{D}_{2}=\{(t,y,z)\in \mathbb{R}^{3}: 0\leq t\leq 1, \vert y \vert \leq 2M_{\alpha }M_{\beta }, \vert z \vert \leq 2M_{\alpha }\}\),

$$\begin{aligned} \bigl\vert f_{y}^{\prime } \bigr\vert \leq 1\quad \text{and}\quad \bigl\vert f_{z}^{ \prime } \bigr\vert \leq 4M_{\alpha } \leq 2. \end{aligned}$$

So assumption (ii) in Theorem 3.1 is satisfied with \(L_{1}=1\) and \(L_{2}=2\). Also, we have \(q:=L_{1}M_{\alpha }M_{\beta }+L_{2}M_{\alpha }\approx 0.879 55<1\).

Hence problem (3.10) admits a unique continuous solution ω satisfying

$$\begin{aligned} \Vert \omega \Vert \leq 2M_{\alpha }M_{\beta }\quad \text{and}\quad \bigl\Vert D^{\frac{5}{3}}\omega \bigr\Vert \leq 2M_{\alpha }. \end{aligned}$$

This solution can be approximate by the sequence \(\omega _{k}(t):\mathcal{G}_{\frac{5}{3}} ( \mathcal{G}_{\frac{4}{3}}\varphi _{k} ) (t)\) with \(\varphi _{0}(t)=1\). Some iterations are presented in Fig. 2.

Figure 2
figure 2

Graphs of the successive approximation of ω

Full size image