Abstract
This paper presents an absolutely stable noniterative difference scheme for solving a general class of singular perturbation problems having left, right, internal, or twin boundary layers. The original two-point second-order singular perturbation problem is approximated by a first-order delay differential equation with a variable deviating argument. This delay differential equation is transformed into a three-term difference equation that can be solved using the Thomas algorithm. The uniqueness and stability analysis are discussed, showing that the method is absolutely stable. An optimal estimate for the deviating argument is obtained to take advantage of the second-order accuracy of the central finite difference method in addition to the absolute stability property. Several problems having left, right, interior, or twin boundary layers are considered to validate and illustrate the method. The numerical results confirm that the deviating argument can stabilize the unstable discretized differential equation and that the new approach is effective in solving the considered class of singular perturbation problems.
Similar content being viewed by others
1 Introduction
Singular perturbation problems (SPPs), also known as stiff, arise very frequently in various areas of applied science, such as fluid mechanics, heat transfer, materials science, chemical and electrical engineering, superconductor theory, and chemical reactor systems [1–9]. It is a well-known fact that SPPs exhibit stiff internal or boundary layers as the singular perturbation parameter approaches zero [10–49]. As this happens, the stiffness ratio increases and the classical numerical methods become inadequate for solving such problems over standard locally uniform meshes, where nonphysical oscillations emerge in the numerical solution due to the stability restriction on the step-size. An interesting collection of examples of exotic numerical solutions of singular perturbation problems obtained using inadequate numerical discretization schemes can be found in [10]. The construction of special-purpose numerical methods for ensuring convergence regardless of the value of the perturbation parameter was first raised in [11, 12] using fitting factor (stabilization term) and fitting mesh (layer adapted mesh) techniques. It is well known that depending on the behavior of the differential operator coefficients in SPPs, the solutions exhibit a boundary layer, twin boundary-layers, or interior layer [3, 4, 13–18]. A variety of numerical and semianalytical numerical methods for solving different classes of SPPs exhibiting a boundary layer, twin boundary-layers, or interior layer can be found in [18–49]. In all of these SPP classes, a priori information about the location of the layers is used to construct appropriate numerical methods for SPPs. And consequently, the numerical methods developed for SPPs have different numerical integration algorithms depending on the location of the layers. The purpose of this paper is to present a noniterative absolutely stable difference scheme for solving a general class of SPPs having left, right, internal, or twin boundary layers. The method does not depend on asymptotic expansions and needs no prior information about the location of the layers, and so it is designed to be suitable for the practicing engineers and applied mathematicians who need a practical tool for solving SPPs (see, for example, [15, 38] for asymptotic techniques, designed for a similar purpose). The method depends on replacing the original two-point second-order SPP by a first-order approximate delay differential equation with a variable deviating argument. This delay differential equation is transformed into a three-term difference equation that can be solved using the Thomas algorithm [50]. The stability analysis of the method is discussed showing that the method is absolutely stable under a certain condition on the deviating argument whereas there is no stability restriction on the step-size. An optimal estimate for the deviating argument is obtained to take advantage of the second-order accuracy of the central finite difference method [48, 50] in addition to the absolute stability property [19, 28, 48–50]. Several problems having left, right, interior, or twin boundary layers are considered to validate and illustrate the method. To analyze the effect of the deviating argument on the solution accuracy, the maximum absolute solution error is presented in tables and figures for constant and variable deviating argument values. The numerical results confirm that the deviating argument can stabilize the unstable discretized differential equation and that the new approach is effective in solving the considered class of singular perturbation problems.
2 Description of the method
Consider the following linear SPP:
with BCs
where \(0 < \varepsilon \ll 1\), a, b, A and B are given constants, and \(p(x)\), \(q(x)\) and \(r(x)\in C^{1}(x)\), \(x \in [a,b]\). Moreover, we assume that \(q(x) \ge 0\) for all \(x \in [a,b]\). Under these assumptions, problem (1) has a unique solution with boundary or interior layers [13–49]. The interval \([a,b]\) is divided into N subintervals \([x_{i},x_{i + 1}]\), \(i = 0,1,2,\ldots,N - 1\), each of length h, i.e., \(h = (b - a)/N\) and \(x_{i} = a + ih\). For the sake of simplicity, we use \(p_{i} = p(x_{i})\), \(q_{i} = q(x_{i})\), \(r_{i} = r(x_{i})\), \(y_{i - 1} = y(x_{i - 1})\), \(y_{i + 1} = y(x_{i + 1})\), \(y'_{i} = y'(x_{i})\). Dividing Eq. (1) by −ε and letting \(\omega = 1/\varepsilon \) results in
Let \(\delta _{i} = \delta (x_{i})\) be a positive variable deviating argument (\(0 < \delta _{i} \ll 1\)). Then by using the Taylor expansion about the point \(x_{i}\), we have
By substituting Eq. (3) into Eq. (2), we have
Now, applying standard forward and centered finite difference formulas for \(y'_{i}\) in Eq. (4) results in
Again, using the Taylor expansion and the standard backward finite difference, we obtain:
By substituting Eq. (6) into Eq. (5), we get the following difference equation:
where
The difference Eq. (7) and the two BCs in (1) results in a tridiagonal system that can be easily solved using the Thomas algorithm to obtain the unknowns \(y_{1}\) to \(y_{N - 1}\).
2.1 Thomas algorithm
A brief description of the Thomas algorithm [50], is presented as follows.
In this algorithm, the solution of the difference Eq. (7) can be written as
where \(W_{i}\) and \(T_{i}\) are to be determined. From Eq. (12) we have
and substituting (12) and (13) into (7), we get
Comparing (14) and (12) results in
Starting with initial conditions \(W_{0} = 0\) and \(T_{0} = y_{0} = A\), the values of \(W_{i}\) and \(T_{i}\) for \(i = 1,2,\ldots,N - 1\) are computed in a forward process, from Eqs. (15)–(16), and then \(y_{i}\) is computed in a backward process, from Eq. (12), using the BC \(y_{N} = B\).
3 Uniqueness and stability analysis
In this section, the uniqueness and stability condition of the proposed algorithm for the difference Eq. (7) is analyzed.
Theorem 1
The numerical scheme\(E_{i}y_{i - 1} + F_{i}y_{i} + G_{i}y_{i + 1} \cong H_{i}\)defined in (7)–(11) results in a unique stable solution provided
Proof
The existence of a unique solution to the tridiagonal system results from establishing that the tridiagonal coefficient matrix of the system is diagonally dominant. It is clear that \(E_{i}\) in (8) and \(G_{i}\) in (10) are nonnegative when \(\frac{2}{h\delta _{i}} + \frac{\omega p_{i}}{2h} \ge 0\) and \(\frac{2}{h\delta _{i}} - \frac{\omega p_{i}}{2h} \ge 0\), respectively. These inequalities are verified if the condition \(\delta _{i} \le \frac{4}{\omega \vert p_{i} \vert }\) is verified. Following this condition, \(F_{i}\) is negative and verifies the inequality \(\vert F_{i} \vert \ge \vert G_{i} \vert + \vert E_{i} \vert = \frac{4}{h\delta _{i}}\). Thus, under condition (17), the tridiagonal coefficient matrix is diagonally dominant, and the numerical scheme has a unique solution.
For stability analysis, suppose that a small numerical error \(\tau _{i - 1}\) was introduced in the calculation of \(W_{i - 1}\) so that it yields an approximate value \(\tilde{W}_{i - 1}\) such that
Then, from (18) and (15), we have
Thus, the numerical scheme defined by (7)–(11) results in a unique stable solution under condition (17). □
Now, if we chose \(\delta _{i} = \frac{4}{\omega \vert p_{i} \vert }\), then for the left-end boundary layers, \(p_{i} < 0\), we have \(E_{i} = 0\), and the present scheme is reduced to a stable forward integration scheme. Also, on the other hand, for the right-end boundary layers, \(p_{i} > 0\), we have \(G_{i} = 0\), and the present scheme is reduced to a stable backward integration scheme. Moreover, in the above two cases, the propagation error in (20) has vanished.
Moreover, at \(p_{i} = 0\), for twin-boundary layers or internal layers, or at \(h \le \frac{2}{\omega \Vert p_{i} \Vert _{\infty }}\), we set \(\delta _{i} = 2h \le \frac{4}{\omega \vert p_{i} \vert }\), and the present scheme is reduced to the standard central finite difference scheme (CFD) in [48, 50]. Thus, to take advantage of the second-order accuracy of the standard central finite difference scheme in addition to the absolute stability property, \(\delta _{i}\) can be selected according to
The stability in CFD is controlled by the step-size restriction whereas the present scheme is absolutely stable without any restrictions on the step-size.
These details are combined in the following algorithm:
3.1 Algorithm steps
Step I: compute
-
\(h = (b - a)/(N)\),
-
\(x = (a:h:b)\)
Step II: set \(xx = 0\), \(\mathrm{index} = 0\), \(w = 1/\varepsilon \)
-
Set \(W = [0,0,\ldots,0]\), \(T[0,0,\ldots,0]\) where the vector length is N
-
Set \(T(1) = A\), \(W(1) = 0\)
Step II: while \(xx \le b - h\), compute
-
(i)
\(xx = x(\mathrm{index})\);
-
(ii)
\(p = p(xx)\); \(q = q(xx)\); \(r = r(xx)\)
-
(iii)
\(\delta = \min (4/(w*\mathrm{abs}(p + 1E - 16)), 2h)\)
-
(iv)
\(E(\mathrm{index}) = 2/h + \delta wp/(2h)\)
-
(v)
\(G(\mathrm{index}) = 2/h - \delta wp/(2h)\)
-
(vi)
\(F(\mathrm{index}) = 4/h - \delta wq\)
-
(vii)
\(H(\mathrm{index}) = - \delta wf\)
-
(viii)
\(\mathrm{index} = \mathrm{index} + 1\)
Step III: Do Steps (i) and (ii) for \(\mathrm{index}2 = 1,2,3,\ldots,N - 1\)
-
(i)
Compute \(W(\mathrm{ind}) = - \frac{G(\mathrm{index}2)}{G(\mathrm{index}2) + E(\mathrm{index}2)*W(\mathrm{index}2 - 1)}\)
-
(ii)
Compute \(T(\mathrm{ind}) = \frac{F(\mathrm{index}2)*T(\mathrm{index}2 - 1) - H(\mathrm{index}2)}{G(\mathrm{index}2) + E(\mathrm{index}2)*W(\mathrm{index}2 - 1)}\)
Step IV: Compute the solution
-
(i)
set \(\mathrm{Sol} = [0,0,\ldots,0]\), where the vector length is \(N - 2\)
-
(ii)
Set \(\mathrm{Sol}(N) = B\)
-
(iii)
Compute \(\mathrm{Sol}(\mathrm{index}2 - 1) = W(\mathrm{index}2 - 1)*\mathrm{Sol}(\mathrm{index}2) + T(\mathrm{index}2 - 1)\) where \(\mathrm{index}2 = N,N - 1,\ldots,3,2,1\)
This algorithm is easily adaptable in any mathematical environment. We present the Matlab code in Appendix A.
4 Numerical results
To demonstrate the applicability of the method, we consider in the following several problems having left, right, interior, or twin boundary layers. These problems have been discussed in the literature and their approximate solutions are available for comparison.
4.1 Left-end boundary-layer problems
Example 1
Consider the following SPBVP [2, 7, 13–15, 38]
with BCs \(y(0)=1\) and \(y(1)=1\). The exact solution is given by
where and .
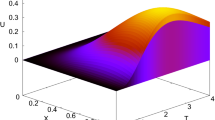
The solution errors are listed in Table 1 for \(\varepsilon=10^{-3}\) and \(\varepsilon=10^{-4}\) at \(h=0.001\). The solutions for \(\varepsilon=10^{-4}\) using the present absolutely stable central difference (ASCD) and the standard CFD schemes are presented in Fig. 1.
The solution of Example 1 for \(\varepsilon=10^{-4}\) using the ASCD and CFD schemes
Example 2
Consider the following SPBVP [7, 13–15, 38]
with BCs \(y (0) = 0\) and \(y (1) = 1\). The exact solution is given by
The solution errors are presented in Table 2 for \(\varepsilon=10^{-3}\) and \(\varepsilon=10^{-4}\) at \(h=0.001\). The solutions for \(\varepsilon=10^{-4}\) using the ASCD and CFD schemes are depicted in Fig. 2.
The solution of Example 2 for \(\varepsilon=10^{-4}\) using the ASCD and CFD schemes
Example 3
Consider the following SPBVP [47]
with BCs \(y (0) = 0\) and \(y (1) = 1\). The exact solution is given by
The solution errors are presented in Table 3 for \(\varepsilon=10^{-3}\) and \(\varepsilon=10^{-4}\) at \(h=0.001\). The solutions for \(\varepsilon=10^{-4}\) using the ASCD and CFD schemes are present in Fig. 3.
The solution of Example 3 for \(\varepsilon=10^{-4}\) using the ASCD and CFD schemes
The results in Tables 1, 2 and 3 show that at \(\delta_{i}=4/\omega|p_{i}|\) or \(\delta_{i}=\delta_{\mathrm{op}}=4/\omega|p_{i}|\), there is no propagation error with the Thomas algorithm (20). Also, at \(\varepsilon=10^{-3}\) the ASCD is reduced to the CFD scheme, where \(\delta_{\mathrm{op}}=2h\), and the results are identical. Although the ASCD stability is verified at \(\delta _{i} = 4/\omega \vert p_{i} \vert \), selecting \(\delta _{i} = \delta _{\mathrm{op}}\) takes advantage of the second-order accuracy of the CFD in addition to the absolute stability property depending on the step-size value. The solution obtained at \(\varepsilon=10^{-4}\) using the ASCD is more accurate than that obtained by CFD due to the absolute stability property of the ASCD, while the stability restriction of CFD results in nonphysical oscillations in the numerical solution as illustrated in Figs. 1, 2 and 3. Figure 4 shows the solution error of Example 3 at \(\varepsilon=10^{-4}\) using different values of the deviating argument \(\delta_{i}=k/\omega|p_{i}|\), \(k = 4, 3, 2, 1\). The results in Fig. 4 reveal that a more accurate solution is obtained at \(\delta_{i}=4/\omega|p_{i}|\). Moreover, Fig. 5 depicts the solution error of Example 3 at \(\varepsilon=10^{-4}\) using constant and variable deviating arguments \(\delta_{i}=4/\omega|p_{i}|_{\infty}\), \(\delta_{i}=4/\omega|p_{i}|\), respectively. Figure 5 reveals that a more accurate solution is obtained using a variable deviating argument \(\delta_{i}\).
The solution errors of Example 3 for \(\varepsilon=10^{-4}\) and different values of \(\delta_{i}\)
The solution errors of Example 3 for \(\varepsilon=10^{-4}\) using constant and variable deviating argument \(\delta_{i}\)
4.2 Right-end boundary-layer problems
Example 4
Consider the following SPBVP [2, 13]
with BCs \(y (0) = 1\) and \(y (1) = 0 \). The exact solution is given by
The solution errors are reported in Table 4 for \(\varepsilon=10^{-3}\) and \(\varepsilon=10^{-4}\) at \(h=0.001\). The numerical solution using the ASCD and CFD schemes for \(\varepsilon=10^{-4}\) are presented in Fig. 6.
The solution of Example 4 for \(\varepsilon=10^{-4}\) using the ASCD and CFD schemes
Example 5
Consider the following SPBVP
with BCs \(y (0) =1+ \exp(-(1+\varepsilon ) /\varepsilon )\) and \(y (1) =1+ \exp(-1) \). The exact solution is given by
The solution errors are presented in Table 5 for \(\varepsilon=10^{-3}\) and \(\varepsilon=10^{-4}\) at \(h=0.001\). The numerical solution using the ASCD and CFD schemes for \(\varepsilon=10^{-4}\) are given in Fig. 7.
The solution of Example 5 for \(\varepsilon=10^{-4}\) using the ASCD and CFD schemes
The results in Tables 4 and 5 and Figs. 6 and 7 show that the ASCD can handle problems with right-end boundary layers effectively as well as those with left-end boundary layers.
4.3 Internal or twin-boundary-layer problems
Example 6
Consider the following SPBVP [49] given by
with BCs \(y (-1) = 0\) and \(y (1) = 2\). The exact solution is given by
The solution errors are listed in Table 6 for \(\varepsilon=10^{-3}\) and \(\varepsilon=10^{-4}\) at \(h=0.001\). The numerical solutions using the ASCD and CFD schemes for \(\varepsilon=10^{-4}\) are presented in Fig. 8.
The solution of Example 6 for \(\varepsilon=10^{-4}\) using the ASCD and CFD schemes
Example 7
Consider the following SPBVP with twin boundary layer [40, 42]
with BCs \(y (0) =1\) and \(y (1) =1\). The exact solution is given by
The solution errors are listed in Table 7 for \(\varepsilon=10^{-3}\) and \(\varepsilon=10^{-4}\) at \(h=0.001\). The numerical solutions using the ASCD and CFD methods for \(\varepsilon=10^{-4}\) are presented in Fig. 9.
The solution of Example 7 for \(\varepsilon=10^{-4}\) using the ASCD and CFD schemes
The results in Table 6 and Fig. 8 show that the ASCD and CFD lead to stable and accurate results for the internal layer problem (26). The reason for absenting the stability restriction of CFD in solving internal layer problems is that the internal layer occurs at a turning point \(x = x_{\mathrm{in}}\) at which \(p(x_{\mathrm{in}}) = 0\). The results in Table 7 show that the solution obtained for the twin boundary layer problem (28) at \(\varepsilon=10^{-4}\) using the ASCD is more accurate than those of the CFD and thus is due to the absolute stability property of the ASCD, while for the CFD the stability restriction results in nonphysical oscillations in the numerical solution as shown in Fig. 9.
Figure 10 depicts the solution error of Example 7 for \(\varepsilon=10^{-4}\) using different values of the deviating argument \(\delta_{i}=k/\omega|p_{i}|\), \(k = 4, 3, 2, 1\). The results in Fig. 10 show that a more accurate solution is obtained at \(\delta_{i}=4/\omega|p_{i}|\). Figure 11 illustrates the solution error of Example 7 for \(\varepsilon=10^{-4}\) when adopting constant and variable deviating arguments \(\delta_{i}=4/\omega|p_{i}|_{\infty}\), \(\delta_{i}=4/\omega|p_{i}|\), respectively. Figure 11 reveals that a more accurate solution is obtained using a variable deviating argument.
The solution errors of Example 7 at \(\varepsilon=10^{-4}\) and different values of \(\delta_{i}\)
Solution errors of Example 7 at \(\varepsilon=10^{-4}\) using constant and variable deviating argument \(\delta_{i}\)
5 Conclusions
This paper presented an absolutely stable noniterative central difference scheme for solving a general class of SPPs having left, right, internal, or twin boundary layers. The original two-point second-order SPPs is approximated by a first-order delay differential equation with a variable deviating argument. This delay differential equation was transformed into a three-term difference equation that was solved using the Thomas algorithm. The stability analysis of the method is discussed showing that the method is absolutely stable under a certain condition on the deviating argument without stability restriction on the step-size. An optimal estimation for the deviating argument is obtained taking advantage of the second-order accuracy of the central finite difference method in addition to the absolute stability property. Several examples having left, right, interior, or twin boundary layers were considered to illustrate the method. To analyze the effect of the deviating argument on the solution accuracy, the maximum absolute error is reported in several tables and figures for constant and variable deviating argument values. The results confirm that the variable deviating argument results in more accurate results than the constant one. Moreover, the results reveal that the deviating argument can stabilize the unstable discretized differential equation and that the present method is effective in solving the considered class of SPPs.
References
Johnson, S.: Singular Perturbation Theory, Mathematical and Analytical Techniques with Applications to Engineering. Springer, Berlin (2005)
Bender, C.M., Orszag, S.A.: Advanced Mathematical Methods for Scientists and Engineers. McGraw-Hill, New York (1978)
Kevorkian, J., Cole, J.D.: Perturbation Methods in Applied Mathematics. Springer, New York (1981)
O’Malley, R.E.: Singular Perturbation Methods for Ordinary Differential Equations, vol. 89. Springer, New York (1991)
Roos, H.-G., Stynes, M., Tobiska, L.: Robust Numerical Methods for Singularly Perturbed Differential Equations. Springer Ser. Comput. Math. Springer, Berlin (2008)
El’sgol’ts, L.E., Norkin, S.B.: Introduction to the Theory and Application of Differential Equations with Deviating Arguments. Academic Press, New York (1973)
El-Zahar, E.R.: Applications of adaptive multi-step differential transform method to singular perturbation problems arising in science and engineering. Appl. Math. Inf. Sci. 9(1), 223–232 (2015)
Chamkha, A.J., Rashad, A.M., EL-Zahar, E.R., EL-Mky, H.A.: Analytical and numerical investigation of Fe3O4–water nanofluid flow over a moveable plane in a parallel stream with high suction. Energies 12(1), 1–18 (2019)
El-Zahar, E.R., Rashad, A.M., Seddek, L.F.: The impact of sinusoidal surface temperature on the natural convective flow of a ferrofluid along a vertical plate. Mathematics 7(11), 1014 (2019). https://doi.org/10.3390/math7111014
Franz, S., Roos, H.G.: The capriciousness of numerical methods for singular perturbations. SIAM Rev. 53(1), 157–173 (2011)
Il’in, A.M.: Differencing scheme for a differential equation with a small parameter affecting the highest derivative. Math. Notes Acad. Sci. USSR 6(2), 596–602 (1969)
Vulanović, R.: A uniform numerical method for quasilinear singular perturbation problems without turning points. Computing 41(1–2), 97–106 (1989)
Kadalbajoo, M.K., Reddy, Y.N.: Numerical solution of singular perturbation problems via deviating arguments. Appl. Math. Comput. 21(3), 221–232 (1987)
Reddy, Y.N., Reddy, K.A.: Numerical integration method for general singularly perturbed two-point boundary value problems. Appl. Math. Comput. 133, 351–373 (2002)
El-Zahar, E.R.: Approximate analytical solution of singularly perturbed boundary value problems in MAPLE. AIMS Math. 5(3), 2272–2284 (2020). https://doi.org/10.3934/math.2020150
Sangeetha, G., Thirupathi, P., Phaneendra, K.: Non-standard fitted operator scheme for singularly perturbed boundary value problem. J. Math. Comput. Sci. 10(4), 793–804 (2020)
Melesse, W.G., Tiruneh, A.A., Derese, G.A.: Uniform hybrid difference scheme for singularly perturbed differential-difference turning point problems exhibiting boundary layers. Abstr. Appl. Anal. 2020, Article ID 7045756 (2020)
Kaur, D., Kumar, V.: Numerical solution with special layer adapted meshes for singularly perturbed boundary value problems. In: Applied Mathematical Analysis: Theory, Methods, and Applications, vol. 383. Springer, Cham (2020)
El-Zahar, E.R., Machado, J.T., Ebaid, A.: A new generalized Taylor-like explicit method for stiff ordinary differential equations. Mathematics 7(12), 1154 (2019). https://doi.org/10.3390/math7121154
Rakmaiah, S., Phaneendra, K.: Numerical solution of singularly perturbed boundary value problems with twin boundary layers using exponential fitted scheme. Commun. Math. Appl. 10(4), 797–807 (2019)
Phaneendra, K., Lalu, M.: Gaussian quadrature for two-point singularly perturbed boundary value problems with exponential fitting. Commun. Math. Appl. 10(3), 447–467 (2019)
Dubey, R.K., Gupta, V.: A mesh refinement algorithm for singularly perturbed boundary and interior layer problems. Int. J. Comput. Methods 1950024 (2019). https://doi.org/10.1142/S0219876219500245
Geng, F., Tang, Z., Zhou, Y.: Reproducing kernel method for singularly perturbed one-dimensional initial-boundary value problems with exponential initial layers. Qual. Theory Dyn. Syst. 17(1), 177–187 (2018)
Wu, L., Ni, M., Lu, H.: Internal layer solution of singularly perturbed optimal control problem with integral boundary condition. Qual. Theory Dyn. Syst. 17(1), 49–66 (2018)
Mukherjee, K.: Parameter-uniform improved hybrid numerical scheme for singularly perturbed problems with interior layers. Math. Model. Anal. 23(2), 167–189 (2018)
Geng, F.Z., Qian, S.P.: A new numerical method for singularly perturbed turning point problems with two boundary layers based on reproducing kernel method. Calcolo 54(2), 515–526 (2017)
Sharp, N., Trummer, M.: A spectral collocation method for systems of singularly perturbed boundary value problems. Proc. Comput. Sci. 108, 725–734 (2017)
Cen, Z., Le, A., Xu, A.: A high-order finite difference scheme for a singularly perturbed reaction-diffusion problem with an interior layer. Adv. Differ. Equ. 2017(1), 202 (2017)
Geetha, N., Tamilselvan, A., Subburayan, V.: Parameter uniform numerical method for third order singularly perturbed turning point problems exhibiting boundary layers. Int. J. Appl. Comput. Math. 2(3), 349–364 (2016)
Volkov, V., Lukyanenko, D., Nefedov, N.: Asymptotic-numerical method for the location and dynamics of internal layers in singular perturbed parabolic problems. In: International Conference on Numerical Analysis and Its Applications, pp. 721–729. Springer, Cham (2016)
El-Zahar, E.R.: Piecewise approximate analytical solutions of high order singular perturbation problems with a discontinuous source term. Int. J. Differ. Equ. 2016, Article ID 1015634 (2016). https://doi.org/10.1155/2016/1015634
Atay, M.T., Cengizci, S., Eryilmaz, A.: SCEM approach for singularly perturbed linear turning mid-point problems with an interior layer. New Trends Math. Sci. 4(1), 115–124 (2016)
Phaneendra, K., Rakmaiah, S., Reddy, M.C.K.: Computational method for singularly perturbed boundary value problems with dual boundary layer. Proc. Eng. 127, 370–376 (2015)
Phaneendra, K., Rakmaiah, S., Reddy, M.C.K.: Numerical treatment of singular perturbation problems exhibiting dual boundary layers. Ain Shams Eng. J. 6(3), 1121–1127 (2015)
O’Riordan, E., Quinn, J.: A linearised singularly perturbed convection-diffusion problem with an interior layer. Appl. Numer. Math. 98, 1–17 (2015)
Geng, F.Z., Qian, S.P., Li, S.: A numerical method for singularly perturbed turning point problems with an interior layer. J. Comput. Appl. Math. 255, 97–105 (2014)
Shen, J., Han, M.: Canard solution and its asymptotic approximation in a second-order nonlinear singularly perturbed boundary value problem with a turning point. Commun. Nonlinear Sci. Numer. Simul. 19(8), 2632–2643 (2014)
El-Zahar, E.R., EL-Kabeir, S.M.M.: A new method for solving singularly perturbed boundary value problems. Appl. Math. Inf. Sci. 7(3), 927–938 (2013)
El-Zahar, E.R.: Approximate analytical solutions of singularly perturbed fourth-order boundary value problems using differential transform method. J. King Saud Univ., Sci. 25(3), 257–265 (2013)
Geng, F.Z., Qian, S.P.: Reproducing kernel method for singularly perturbed turning point problems having twin boundary layers. Appl. Math. Lett. 26(10), 998–1004 (2013)
Liu, C.S.: The Lie-group shooting method for solving nonlinear singularly perturbed boundary value problems. Commun. Nonlinear Sci. Numer. Simul. 17(4), 1506–1521 (2012)
Kadalbajoo, M.K., Arora, P., Gupta, V.: Collocation method using artificial viscosity for solving stiff singularly perturbed turning point problem having twin boundary layers. Comput. Math. Appl. 61(6), 1595–1607 (2011)
Attili, B.S.: Numerical treatment of singularly perturbed two point boundary value problems exhibiting boundary layers. Commun. Nonlinear Sci. Numer. Simul. 16(9), 3504–3511 (2011)
Wang, Y., Su, L., Cao, X., Li, X.: Using reproducing kernel for solving a class of singularly perturbed problems. Comput. Math. Appl. 61(2), 421–430 (2011)
Kumar, M., Mishra, H.K., Singh, P.: A boundary value approach for a class of linear singularly perturbed boundary value problems. Adv. Eng. Softw. 40(4), 298–304 (2009)
Kumar, M., Singh, P., Mishra, H.K.: An initial-value technique for singularly perturbed boundary value problems via cubic spline. Int. J. Comput. Methods Eng. Sci. Mech. 8(6), 419–427 (2007)
Qiu, Y., Sloan, D.M., Tng, T.: Numerical solution of singularly perturbed two-point boundary value problem using equidistribution: analysis of convergence. Appl. Math. Comput. 116, 121–143 (2000)
Greenspan, D., Cassulli, V., Horova, I.: Numerical analysis for applied mathematics, science and engineering. Acta Appl. Math. 37(3), 313–314 (1994)
Lopez, L.: Stability of a three-point scheme for linear second-order singularly perturbed BVPs with turning points. Appl. Math. Comput. 52(2–3), 279–300 (1992)
Burden, R.L., Faires, J.D.: Numerical Analysis. PWS. Kent Publishing Co., Boston (1989)
Acknowledgements
The authors would like to thank the referees for their valuable comments and suggestions which helped to improve the manuscript.
Availability of data and materials
Not applicable.
Funding
Not applicable.
Author information
Authors and Affiliations
Contributions
All authors have equal contributions in this paper. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors have no competing interests regarding the publication of this paper.
Appendix A
Appendix A
Clear all, format long Epsn=.001, a=0; b=1; w=1/Epsn; Alpha=0 %1+exp((-1-Epsn)/Epsn) Beta=1 %1+1/exp(1) h0=.01 Deltamax=2*h0 JJ=3.999 Ind=0; x=a; xx=0; hh=(a:h0:b) While xx<b-h0 Ind=Ind+1; x=hh (Ind+1); % f=0; p=-1; q=1; % f=-1-2*x; p=-1; q=0; % f=0; p=-(1-x/2); q=1/2; % f=-2/(x+1)*(log(2/(x+1))-1); p=-2; q=-2/(1+x); % f=-x-2.9995; p=f; q=0 % f=0; p=-1; q=0 % f=0; p=1; q=0 % f=0; p=1; q=1+epsp; % f=0; p=x; q=1; % f=0; p=-x; q=0 % p=0; q=1; f= -cos (pi*x)^2-2*epsp^2*pi^2*cos(2*pi*x) Delta=min(JJ/w/abs(p),Deltamax) If p==0; Delta=min(JJ/w/abs(p+1e-6),Deltamax);end; ALPHANEG(Ind)=(2/h0+Delta*w*p/2/h0); ALPHAPOS(Ind)=(2/h0-Delta*w*p/2/h0); ALPHAI(Ind)= -4/h0-Delta*w*q; BETA=-w*Delta*f; if (ALPHAI)>0 |(ALPHAPOS)<0|(ALPHANEG)<0| abs(ALPHAI)+.1<abs(ALPHAPOS)+abs(ALPHANEG), error ('not dominant'); end end % Thomas algorithm in Matlab environment subc = [ ALPHANEG';0;0]; supc = [0;0; ALPHAPOS']; diagc= [1; ALPHAI';1]; Bvector = [alpha; BETA';beta]; AAAA = spdiags ([subc diagc supc],-1:1, length (Bvector), length (Bvector)); YSOL=AAAA\Bvector;.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
El-Zahar, E.R., Alotaibi, A.M., Ebaid, A. et al. Absolutely stable difference scheme for a general class of singular perturbation problems. Adv Differ Equ 2020, 411 (2020). https://doi.org/10.1186/s13662-020-02862-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-020-02862-z