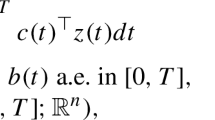Abstract
This work mainly investigates a class of convex interval-valued functions via the Katugampola fractional integral operator. By considering the p-convexity of the interval-valued functions, we establish some integral inequalities of the Hermite–Hadamard type and Hermite–Hadamard–Fejér type as well as some product inequalities via the Katugampola fractional integral operator. In addition, we compare our results with the results given in the literature. Applications of the main results are illustrated by using examples. These results may open a new avenue for modeling, optimization problems, and fuzzy interval-valued functions that involve both discrete and continuous variables at the same time.
Similar content being viewed by others
1 Introduction
Fractional calculus [1–21] is invariably important in almost all areas of mathematics and other natural sciences. Indeed, we can clearly realize that fractional operators have appeared in all fields of natural science and in fractional differential equations [22–35]. In particular, it has been used in the study of waves in liquids, propagation of sound, gravitational attraction, and vibrations of strings. Numerous significant definitions and concepts have been established for the investigation of the fractional operators, for instance, Riemann, Liouville, Caputo, Hadamard, Katugampola, Atangana–Baleanu operators, and so on. Some well-known operators have been utilized for finding the existence of solutions to the boundary value problems, fractional integrodifferential equations or inclusions were elaborated [36–40].
In the present scenario, numerous significant fractional derivative and integral operators are systematically and successfully analyzed with the assistance of fractional integral inequalities [41–50]. It is known that variants have many important applications in all parts of mathematics as well as in different areas of natural science. Among others, numerous sorts of variants, those conveying the names of Jensen, Hermite–Hadamard, Hardy, Ostrowski, Minkowski, and Opial et al., have a profound noteworthiness; also, they have an extraordinary effect in significant fields of research. Convexity [51–60] has received renewed attention in mathematical sciences, statistical theory, optimization theory, fixed point theory, and several other areas of science and technology. Over the years, convex sets and convex functions have been modified to a remarkable variety of convexities such as \(H_{p, q}\)-convexity [61–64], harmonic convexity [65], strong convexity [66, 67], Schur convexity [68, 69], quasi-convexity [70], generalized convexity [71], and so on. In particular, many inequalities can be found in the literature [72–93] via the convexity theory.
Recently, the following Hermite–Hadamard inequality [94], one of the famous distinguished classical inequalities, has gained much consideration.
Let \(\mathcal{Q}:\mathcal{I}\rightarrow \mathbb{R}\) be a convex function. Then the double inequality
holds for all \(e, f\in \mathcal{I}\) with \(f\neq e\). If \(\mathcal{Q}\) is concave, then both the inequalities in (1.1) hold in the reverse direction. Many generalizations, modifications, applications, refinements, and variants for Hermite–Hadamard inequality (1.1) can be found in the literature [95, 96].
The following weighted generalization of Hermite–Hadamard inequality (1.1) was derived by Fejér:
Due to the modification among the ideas of convexity, the refinements for double inequality (1.2) have been widely investigated by many researchers. To meet the development trend of this research field, we delineate a new scheme and future plan in the present framework. We consider the p-convex function which assumes a dynamic job in portraying the idea of the interval-valued function just as establishing several generalizations by employing the Katugampola fractional integral operator.
On the other hand, a long history that can be followed back to Archimede’s computation of the circumference of a circle has based on the theory of interval analysis. It fell into obscurity for a long time because of the dearth of utilities to different sciences. To the preeminence of our understanding, the substantial effort did not seem to this extent until the 1950s. In 1966, the first celebrated monograph concerned with interval analysis was written by Moore, who is famous as the founder of intervals, in order to compute the error bounds of the numerical solutions of a finite state machine. After his exploration, several researchers focused on studying the literature and applications of interval analysis in automatic error analysis, computer graphics, neural network output optimization, robotics, computational physics, and several other well-known areas in science and technology. Since then, several analysts have been broadly concentrated on and investigated the interval analysis and interval-valued functions in both mathematics and its applications.
The principal objective of this article is that we propose the notion of p-convex function for the interval-valued function. We also present the results concerning Hermite–Hadamard inequality, Fejér type inequality, and certain other related variants by employing p-convexity, which correlates with the Katugampola fractional integral operator. Finally, the repercussions of the employed technique depict the presentations for various existing outcomes. Results obtained by the novel approach disclose that the suggested scheme is very accurate, flexible, effective, and simple to use.
2 Preliminaries
For the basic notions and definitions on interval analysis, we use the literature [97].
Let \(\mathcal{M}\) be the space of all intervals of \(\mathbb{R}\) and \(\mathcal{D}\in \mathcal{M}\) be defined by
Then \(\mathcal{D}\) is said to be degenerate if \(\underline{\mathfrak{d}}=\bar{\mathfrak{d}}\). If \(\underline{\mathfrak{d}}>0\), then \(\mathcal{D}\) is said to be positive, and if \(\bar{\mathfrak{d}}<0\), then \(\mathcal{D}\) is said to be negative. We use \(\mathcal{M}^{+}\) and \(\mathcal{M}^{-}\) to symbolize the sets of all positive and negative intervals.
Let \(\eta \in \mathbb{R}\) and \(\eta \mathcal{D}\) be defined by
Then the addition \(\mathcal{D}_{1}+ \mathcal{D}_{2}\) and Minkowski difference \(\mathcal{D}_{1}- \mathcal{D}_{2}\) for \(\mathcal{D}_{1}, \mathcal{D}_{2}\in \mathcal{M}\) are defined by
and
respectively.
The inclusion relation “⊇” means that
Let \(\mathcal{I}\subseteq \mathbb{R}\) be an interval and \(\mathcal{Q}(z)=[\underline{\mathcal{Q}}(z),\bar{\mathcal{Q}}(z)]\) (\(z\in \mathcal{I}\)). Then \(\mathcal{Q}(z)\) is said to be Lebesgue integrable if \(\underline{\mathcal{Q}}(z)\) and \(\bar{\mathcal{Q}}(z)\) are measurable and Lebesgue integrable on \(\mathcal{I}\). Moreover, \(\int _{e}^{f}\mathcal{Q}(z)\,dz\) is defined by
Now, we introduce the concept of Katugampola fractional integral operator for interval-valued function.
Let \(q\geq 1\), \(c\in \mathbb{R}\), and \(\chi _{c}^{q}(e,f)\) be the set of all complex-valued Lebesgue integrable interval-valued functions \(\mathcal{Q}\) on \([e,f]\) for which the norm \(\|\mathcal{Q}\|\chi _{c}^{q}\) is defined by
for \(1\leq q<\infty \) and
Katugampola [98] presented a new fractional integral to generalize the Riemann–Liouville and Hadamard fractional integrals under certain conditions.
Let \(p, \delta >0\) and \(\mathfrak{J}\mathfrak{L}_{([e,f])}\) be the collection of all complex-valued Lebesgue integrable interval-valued functions on \([e,f]\). Then the interval left and right Katugampola fractional integrals of \(\mathcal{Q}\in \mathfrak{J}\mathfrak{L}_{([e,f])}\) with order \(\delta >0\) are defined by
and
respectively, where \(\varGamma (z)=\int _{0}^{\infty }\zeta ^{z-1}e^{-\zeta }\,d\zeta \) is the Euler gamma function [99].
In [100], Zhang and Wan presented a definition of the p-convex function as follows.
Definition 2.1
([100])
Let \(p\in \mathbb{R}\) with \(p\neq 0\). Then the interval \(\mathcal{I}\) is said to be p-convex if
for all \(e,f\in \mathcal{I}\) and \(\eta \in [0,1]\).
Definition 2.2
([100])
Let \(p\in \mathbb{R}\) with \(p\neq 0\) and \(\mathcal{I}\subseteq \mathbb{R}\) be a p-convex interval. Then the function \(\mathcal{Q}:\mathcal{I}\rightarrow \mathbb{R}\) is said to be a p-convex function if the inequality
holds for all \(e,f\in \mathcal{I}\) and \(\eta \in [0,1]\).
From Definition 2.2 we clearly see that the p-convexity reduces to classical convexity and harmonic convexity if \(p=1\) and \(p=-1\), respectively.
Next, we introduce a novel concept of interval p-convexity.
Definition 2.3
Let \(p\in \mathbb{R}\) with \(p\neq 0\) and \(\mathcal{I}\subseteq \mathbb{R}\) be a p-convex interval. Then the function \(\mathcal{Q}:\mathcal{I}\rightarrow \mathcal{M}^{+}\) is said to be a p-convex interval-valued function if
for all \(e,f\in \mathcal{I}\) and \(\eta \in [0,1]\). If the set inclusion (2.8) is reversed, then \(\mathcal{Q}\) is said to be a p-concave interval-valued function.
Remark 2.4
From Definition 2.3 we clearly see that
3 Results and discussions
In this section, we establish several Hermite–Hadamard type inequalities for the p-convex interval-valued functions by employing the Katugampola fractional integral operator. In what follows, we denote by \(\mathcal{QC}(\mathcal{I},\mathcal{M}^{+})\) the family of interval p-convex functions of the interval \(\mathcal{I}\).
Theorem 3.1
Let\(p, \delta >0\), \(e,f\in \mathcal{I}\)such that\(f>e\), \(\mathcal{Q}\in \mathfrak{J}\mathfrak{L}_{([e,f])}\). Then
if\(\mathcal{Q}\in \mathcal{QC}(\mathcal{I},\mathcal{M}^{+})\).
Proof
It follows from \(\mathcal{Q}\in \mathcal{QC}(\mathcal{I},\mathcal{M}^{+})\) that
for all \(x,y\in [e,f]\).
Let \(\eta \in [0,1]\), \(x^{p}=\eta e^{p}+(1-\eta )f^{p}\) and \(y^{p}=(1-\eta ) e^{p}+\eta f^{p}\). Then (3.2) leads to
Multiplying both sides (3.3) by \(\eta ^{\delta -1}\) and integrating the obtained result with respect to η over \((0,1)\), we have
and
Since \(\mathcal{Q}\in \mathcal{QC}(\mathcal{I},\mathcal{M}^{+})\), we get
and
Adding (3.7) and (3.8), we obtain
Multiplying both sides (3.9) by \(\eta ^{\delta -1}\) and integrating both sides of the obtained result with respect to η over \((0,1)\), we get
which completes the proof of Theorem 3.1. □
Remark 3.2
From Theorem 3.1 we clearly see that
-
(1)
Let \(\underline{q}=\bar{q}\). Then we get Theorem 2.1 [103].
-
(2)
If \(p=1\) and \(\underline{q}=\bar{q}\), then Theorem 3.1 reduces to the result given in [104].
-
(3)
If \(\delta =p=1\) and \(\underline{q}=\bar{q}\), then Theorem 3.1 becomes the result in [105].
Example 3.3
Let p be an odd number, \(\delta =\frac{1}{2}\), \(u\in [2,3]\), and \(\mathcal{Q}(u)=[2-u^{\frac{p}{2}},u^{\frac{p}{2}}+2]\). Then we clearly see that \(\mathcal{Q}\in \mathfrak{J}\mathfrak{L}_{([2,3])}\) and
Note that
Therefore,
and Theorem 3.1 is verified.
The next Theorem 3.4 gives the Hermite–Hadamard–Fejér type inequality for interval-valued p-convex functions.
Theorem 3.4
Let\(p,\delta >0\), \(e,f\in \mathcal{I}\)with\(f>e\), \(\mathcal{Q}\in \mathfrak{J}\mathfrak{L}_{([e,f])}\), and\(\mathcal{W}(x)=\mathcal{W}([e^{p}+f^{p}-x^{p}]^{\frac{1}{p}})\geq 0\)for\(x\in \mathcal{I}\). Then we have the Hermite–Hadamard–Fejér type inequality for interval-valuedp-convex functions as follows:
if\(\mathcal{Q}\in \mathcal{QC}(\mathcal{I},\mathcal{M}^{+})\).
Proof
Since \(\mathcal{W}\) is nonnegative, integrable, and p-symmetric with respect to \([\frac{e^{p}+f^{p}}{2} ]^{\frac{1}{p}}\), we get
Multiplying both sides of (3.4) by \(\eta ^{\delta -1}\mathcal{W} ( [\eta f^{p}+(1-\eta )u^{p} ]^{ \frac{1}{p}} )\), we have
Let \(u^{p}=\eta f^{p}+(1-\eta ) e^{p}\). Then one has
Therefore,
Multiplying both sides of (3.9) by \(\eta ^{\delta -1}\mathcal{W} ( [\eta f^{p}+(1-\eta )u^{p} ]^{ \frac{1}{p}} )\), we get
□
Remark 3.5
Theorem 3.4 leads to the conclusion that
-
(1)
Let \(\mathcal{W}(x)=1\). Then we get Theorem 3.1.
-
(2)
If \(\underline{q}=\bar{q}\) and \(\delta =1\), then we get Theorem 5 of [106].
-
(3)
Let \(\underline{q}=\bar{q}\) and \(\mathcal{W}(x)=p=\delta =1\). Then we get the classical Hermite–Hadamard inequality (1.1).
-
(4)
If \(\underline{q}=\bar{q}\) and \(\delta =1\), then we obtain the classical Hermite–Hadamard–Fejér type inequality (1.2).
Theorem 3.6
Let\(p, \delta >0\), \(e,f\in \mathcal{I}\)with\(f>e\), and\(\mathcal{Q}_{1}, \mathcal{Q}_{2}\in \mathfrak{J}\mathfrak{L}_{([e, f])}\). Then we have
if\(\mathcal{Q}_{1}, \mathcal{Q}_{2}\in \mathcal{QC}(\mathcal{I}, \mathcal{M}^{+})\), where
and
Proof
Let \(\eta \in [0,1]\). Then it follows from the assumption of Theorem 3.6 that
and
Analogously, we have
Adding (3.19) and (3.20), we obtain
Multiplying both sides of (3.21) by \(\eta ^{\delta -1}\) and integrating the obtained result with respect to η over \((0,1)\), we have
From (2.1) and (3.22), we have
and
Therefore, the desired result (3.14) follows from (3.22)–(3.24). □
Example 3.7
Let p be an odd number, \([e,f]=[0,2]\), \(\delta =\frac{1}{2}\), \(\mathcal{Q}_{1}(u)=[u^{p},4-e^{u^{p}}]\), and \(\mathcal{Q}_{2}(u)=[u^{p},3-u^{p}]\). Then \(\mathcal{Q}_{1},\mathcal{Q}_{2}\in \mathfrak{J}\mathfrak{L}_{([0,2])}\) and
Note that
Therefore, we have
It follows that
and Theorem 3.6 is verified.
Theorem 3.8
Let\(p, \delta >0\), \(e, f\in \mathcal{I}\)with\(f>e\), and\(\mathcal{Q}_{1},\mathcal{Q}_{2}\in \mathfrak{J}\mathfrak{L}_{([e,f])}\). Then
if\(\mathcal{Q}_{1}, \mathcal{Q}_{2}\in \mathcal{QC}(\mathcal{I}, \mathcal{M}^{+})\), where\(\varUpsilon _{1}(a,b)\)and\(\varUpsilon _{2}(a,b)\)are given in (3.15) and (3.16), respectively.
Proof
Let \(\eta \in [0,1]\). Then we clearly see that
Since \(\mathcal{Q}_{1},\mathcal{Q}_{2}\in \mathcal{QC} ([e,f], \mathcal{K}^{+} )\), we have
Multiplying both sides of (3.29) by \(\eta ^{\delta -1}\) and integrating the obtained result with respect to η over \((0,1)\), we have
On the other hand, making suitable substitution and applying (2.1), we obtain
4 Conclusion
We have proposed the concept of p-convexity for the interval-valued functions, established several novel Hermite–Hadamard type and Hermite–Hadamard–Fejér type inequalities for the p-convex interval-valued functions. Our results provided the interval-valued counterparts of the inequalities presented in [103, 106], and our ideas may lead to a lot of follow-up research.
References
Adil Khan, M., Begum, S., Khurshid, Y., Chu, Y.-M.: Ostrowski type inequalities involving conformable fractional integrals. J. Inequal. Appl. 2018, Article ID 70 (2018)
Adil Khan, M., Chu, Y.-M., Kashuri, A., Liko, R., Ali, G.: Conformable fractional integrals versions of Hermite–Hadamard inequalities and their generalizations. J. Funct. Spaces 2018, Article ID 6928130 (2018)
Adil Khan, M., Khurshid, Y., Du, T.-S., Chu, Y.-M.: Generalization of Hermite–Hadamard type inequalities via conformable fractional integrals. J. Funct. Spaces 2018, Article ID 5357463 (2018)
Chu, Y.-M., Adil Khan, M., Ail, T., Dragomir, S.S.: Inequalities for α-fractional differentiable functions. J. Inequal. Appl. 2017, Article ID 93 (2017)
Iqbal, A., Adil Khan, M., Ullah, S., Chu, Y.-M.: Some new Hermite–Hadamard-type inequalities associated with conformable fractional integrals and their applications. J. Funct. Spaces 2020, Article ID 9845407 (2020)
Khurshid, Y., Adil Khan, M., Chu, Y.-M.: Conformable integral inequalities of the Hermite–Hadamard type in terms of GG- and GA-convexities. J. Funct. Spaces 2019, Article ID 6926107 (2019)
Khurshid, Y., Adil Khan, M., Chu, Y.-M., Khan, Z.A.: Hermite–Hadamard–Fejér inequalities for conformable fractional integrals via preinvex functions. J. Funct. Spaces 2019, Article ID 3146210 (2019)
Rashid, S., Jarad, F., Chu, Y.-M.: A note on reverse Minkowski inequality via generalized proportional fractional integral operator with respect to another function. Math. Probl. Eng. 2020, Article ID 7630260 (2020)
Rashid, S., Jarad, F., Kalsoom, H., Chu, Y.-M.: On Pólya–Szegö and Ćebyšev type inequalities via generalized k-fractional integrals. Adv. Differ. Equ. 2020, Article ID 125 (2020)
Rashid, S., Jarad, F., Noor, M.A., Kalsoom, H., Chu, Y.-M.: Inequalities by means of generalized proportional fractional integral operators with respect another function. Mathematics 7(12), 1225 (2019)
Rashid, S., Noor, M.A., Noor, K.I., Chu, Y.-M.: Ostrowski type inequalities in the sense of generalized \(\mathcal{K}\)-fractional integral operator for exponentially convex functions. AIMS Math. 5(3), 2629–2645 (2020)
Cheng, J.-F., Chu, Y.-M.: Solution to the linear fractional differential equation using Adomian decomposition method. Math. Probl. Eng. 2011, Article ID 587068 (2011)
Cheng, J.-F., Chu, Y.-M.: On the fractional difference equations of order \((2, q)\). Abstr. Appl. Anal. 2011, Article ID 497259 (2011)
Cheng, J.-F., Chu, Y.-M.: Fractional difference equations with real variable. Abstr. Appl. Anal. 2012, Article ID 918529 (2012)
Jiang, Y.-J., Xu, X.-J.: A monotone finite volume method for time fractional Fokker–Planck equations. Sci. China Math. 62(4), 783–794 (2019)
Zhou, S.-H., Jiang, Y.-J.: Finite volume methods for N-dimensional time fractional Fokker–Planck equations. Bull. Malays. Math. Sci. Soc. 42(6), 3167–3186 (2019)
Pratap, A., Raja, R., Cao, J.-D., Alzabut, J., Huang, C.-X.: Finite-time synchronization criterion of graph theory perspective fractional-order coupled discontinuous neural networks. Adv. Differ. Equ. 2020, Article ID 97 (2020)
Liu, F.-W., Feng, L.-B., Anh, V., Li, J.: Unstructured-mesh Galerkin finite element method for the two-dimensional multi-term time-space fractional Bloch–Torrey equations on irregular convex domains. Comput. Math. Appl. 78(5), 1637–1650 (2019)
Huang, C.-X., Liu, L.-Z.: Sharp function inequalities and boundedness for Toeplitz type operator related to general fractional singular integral operator. Publ. Inst. Math. 92(106), 165–176 (2012)
Zhou, X.-S., Huang, C.-X., Hu, H.-J., Liu, L.: Inequality estimates for the boundedness of multilinear singular and fractional integral operators. J. Inequal. Appl. 2013, Article ID 303 (2013)
Wu, J., Liu, Y.-C.: Uniqueness results and convergence of successive approximations for fractional differential equations. Hacet. J. Math. Stat. 42(2), 149–158 (2013)
Rafeeq, S., Kalsoom, H., Hussain, S., Rashid, S., Chu, Y.-M.: Delay dynamic double integral inequalities on time scales with applications. Adv. Differ. Equ. 2020, Article ID 40 (2020)
Rashid, S., Ashraf, R., Noor, M.A., Noor, K.I., Chu, Y.-M.: New weighted generalizations for differentiable exponentially convex mapping with application. AIMS Math. 5(4), 3525–3546 (2020)
Rashid, S., İşcan, İ., Baleanu, D., Chu, Y.-M.: Generation of new fractional inequalities via n polynomials s-type convexity with application. Adv. Differ. Equ. 2020, Article ID 264 (2020)
Huang, C.-X., Guo, S., Liu, L.-Z.: Boundedness on Morrey space for Toeplitz type operator associated to singular integral operator with variable Calderón–Zygmund kernel. J. Math. Inequal. 8(3), 453–464 (2014)
Zhou, X.-S.: Weighted sharp function estimate and boundedness for commutator associated with singular integral operator satisfying a variant of Hörmander’s condition. J. Math. Inequal. 9(2), 587–596 (2015)
Huang, C.-X., Liu, L.-Z.: Boundedness of multilinear singular integral operator with a non-smooth kernel and mean oscillation. Quaest. Math. 40(3), 295–312 (2017)
Tan, Y.-X., Liu, L.-Z.: Weighted boundedness of multilinear operator associated to singular integral operator with variable Calderón–Zygmund kernel. Rev. R. Acad. Cienc. Exactas Fís. Nat., Ser. A Mat. 111(4), 931–946 (2017)
Hu, H.-J., Liu, L.-Z.: Weighted inequalities for a general commutator associated to a singular integral operator satisfying a variant of Hörmander’s condition. Math. Notes 101(5–6), 830–840 (2017)
Wang, J.-F., Chen, X.-Y., Huang, L.-H.: The number and stability of limit cycles for planar piecewise linear systems of node-saddle type. J. Math. Anal. Appl. 469(1), 405–427 (2019)
Wang, J.-F., Huang, C.-X., Huang, L.-H.: Discontinuity-induced limit cycles in a general planar piecewise linear system of saddle-focus type. Nonlinear Anal. Hybrid Syst. 33, 162–178 (2019)
Huang, C.-X., Yang, Z.-C., Yi, T.-S., Zou, X.-F.: On the basins of attraction for a class of delay differential equations with non-monotone bistable nonlinearities. J. Differ. Equ. 256(7), 2101–2114 (2014)
Huang, C.-X., Long, X., Huang, L.-H., Fu, S.: Stability of almost periodic Nicholson’s blowflies model involving patch structure and mortality terms. Can. Math. Bull. 63(2), 405–422 (2020)
Huang, C.-X., Zhang, H., Huang, L.-H.: Almost periodicity analysis for a delayed Nicholson’s blowflies model with nonlinear density-dependent mortality term. Commun. Pure Appl. Anal. 18(6), 3337–3349 (2019)
Cai, Z.-W., Huang, J.-H., Huang, L.-H.: Periodic orbit analysis for the delayed Filippov system. Proc. Am. Math. Soc. 146(11), 4667–4682 (2018)
Abdeljawad, T.: On conformable fractional calculus. J. Comput. Appl. Math. 279, 57–66 (2015)
Abdeljawad, T., Baleanu, D.: Monotonicity results for fractional difference operators with discrete exponential kernels. Adv. Differ. Equ. 2017, Article ID 78 (2017)
Hilfer, R.: Applications of Fractional Calculus in Physics. World Scientific, River Edge (2000)
Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations. Elsevier, Amsterdam (2006)
Podlubny, I.: Fractional Differential Equations. Academic Press, San Diego (1999)
Abbas Baloch, I., Chu, Y.-M.: Petrović-type inequalities for harmonic h-convex functions. J. Funct. Spaces 2020, Article ID 3075390 (2020)
Adil Khan, M., Chu, Y.-M., Khan, T.U., Khan, J.: Some new inequalities of Hermite–Hadamard type for s-convex functions with applications. Open Math. 15(1), 1414–1430 (2017)
Adil Khan, M., Hanif, M., Khan, Z.A., Ahmad, K., Chu, Y.-M.: Association of Jensen’s inequality for s-convex function with Csiszár divergence. J. Inequal. Appl. 2019, Article ID 162 (2019)
Adil Khan, M., Pečarić, J., Chu, Y.-M.: Refinements of Jensen’s and McShane’s inequalities with applications. AIMS Math. 5(5), 4931–4945 (2020)
Adil Khan, M., Wu, S.-H., Ullah, H., Chu, Y.-M.: Discrete majorization type inequalities for convex functions on rectangles. J. Inequal. Appl. 2019, Article ID 16 (2019)
Awan, M.U., Talib, S., Chu, Y.-M., Noor, M.A., Noor, K.I.: Some new refinements of Hermite–Hadamard-type inequalities involving \(\varPsi _{k}\)-Riemann–Liouville fractional integrals and applications. Math. Probl. Eng. 2020, Article ID 3051920 (2020)
Hu, X.-M., Tian, J.-F., Chu, Y.-M., Lu, Y.-X.: On Cauchy–Schwarz inequality for N-tuple diamond-alpha integral. J. Inequal. Appl. 2020, Article ID 8 (2020)
Khan, S., Adil Khan, M., Chu, Y.-M.: Converses of the Jensen inequality derived from the Green functions with applications in information theory. Math. Methods Appl. Sci. 43(5), 2577–2587 (2020)
Song, Y.-Q., Adil Khan, M., Zaheer Ullah, S., Chu, Y.-M.: Integral inequalities involving strongly convex functions. J. Funct. Spaces 2018, Article ID 6595921 (2018)
Wu, S.-H., Chu, Y.-M.: Schur m-power convexity of generalized geometric Bonferroni mean involving three parameters. J. Inequal. Appl. 2019, Article ID 57 (2019)
Adil Khan, M., Zaheer Ullah, S., Chu, Y.-M.: The concept of coordinate strongly convex functions and related inequalities. Rev. R. Acad. Cienc. Exactas Fís. Nat., Ser. A Mat. 113(3), 2235–2251 (2019)
Chu, Y.-M., Qiu, Y.-F., Wang, M.-K.: Hölder mean inequalities for the complete elliptic integrals. Integral Transforms Spec. Funct. 23(7), 521–527 (2012)
Chu, Y.-M., Wang, M.-K.: Optimal Lehmer mean bounds for the Toader mean. Results Math. 61(3–4), 223–229 (2012)
Chu, Y.-M., Wang, M.-K., Jiang, Y.-P., Qiu, S.-L.: Concavity of the complete elliptic integrals of the second kind with respect to Hölder means. J. Math. Anal. Appl. 395(2), 637–642 (2012)
Chu, Y.-M., Wang, M.-K., Qiu, S.-L.: Optimal combinations bounds of root-square and arithmetic means for Toader mean. Proc. Indian Acad. Sci. Math. Sci. 122(1), 41–51 (2012)
Qiu, S.-L., Ma, X.-Y., Chu, Y.-M.: Sharp Landen transformation inequalities for hypergeometric functions, with applications. J. Math. Anal. Appl. 474(2), 1306–1337 (2019)
Wang, M.-K., Chu, Y.-M.: Refinements of transformation inequalities for zero-balanced hypergeometric functions. Acta Math. Sci. 37B(3), 607–622 (2017)
Wang, M.-K., Chu, H.-H., Chu, Y.-M.: Precise bounds for the weighted Hölder mean of the complete p-elliptic integrals. J. Math. Anal. Appl. 480(2), Article ID 123388 (2019). https://doi.org/10.1016/j.jmaa.2019.123388
Wang, M.-K., Chu, Y.-M., Jiang, Y.-P.: Ramanujan’s cubic transformation inequalities for zero-balanced hypergeometric functions. Rocky Mt. J. Math. 46(2), 679–691 (2016)
Wang, M.-K., Chu, H.-H., Li, Y.-M., Chu, Y.-M.: Answers to three conjectures on convexity of three functions involving complete elliptic integrals of the first kind. Appl. Anal. Discrete Math. 14, 255–271 (2020)
Zhao, T.-H., Shi, L., Chu, Y.-M.: Convexity and concavity of the modified Bessel functions of the first kind with respect to Hölder means. Rev. R. Acad. Cienc. Exactas Fís. Nat., Ser. A Mat. 114(2), Article ID 96 (2020). https://doi.org/10.1007/s13398-020-00825-3
Wang, G.-D., Zhang, X.-H., Chu, Y.-M.: A power mean inequality for the Grötzsch ring function. Math. Inequal. Appl. 14(4), 833–837 (2011)
Wang, M.-K., He, Z.-Y., Chu, Y.-M.: Sharp power mean inequalities for the generalized elliptic integral of the first kind. Comput. Methods Funct. Theory 20(1), 111–124 (2020)
Wang, M.-K., Chu, Y.-M., Qiu, Y.-F., Qiu, S.-L.: An optimal power mean inequality for the complete elliptic integrals. Appl. Math. Lett. 24(6), 887–890 (2011)
Awan, M.U., Akhtar, N., Iftikhar, S., Noor, M.A., Chu, Y.-M.: New Hermite–Hadamard type inequalities for n-polynomial harmonically convex functions. J. Inequal. Appl. 2020, Article ID 125 (2020)
Zaheer Ullah, S., Adil Khan, M., Khan, Z.A., Chu, Y.-M.: Integral majorization type inequalities for the functions in the sense of strong convexity. J. Funct. Spaces 2019, Article ID 9487823 (2019)
Zaheer Ullah, S., Adil Khan, M., Chu, Y.-M.: Majorization theorems for strongly convex functions. J. Inequal. Appl. 2019, Article ID 58 (2019)
Chu, Y.-M., Wang, G.-D., Zhang, X.-H.: The Schur multiplicative and harmonic convexities of the complete symmetric function. Math. Nachr. 284(5–6), 653–663 (2011)
Chu, Y.-M., Xia, W.-F., Zhang, X.-H.: The Schur concavity, Schur multiplicative and harmonic convexities of the second dual form of the Hamy symmetric function with applications. J. Multivar. Anal. 105, 412–421 (2012)
Latif, M.A., Rashid, S., Dragomir, S.S., Chu, Y.-M.: Hermite–Hadamard type inequalities for co-ordinated convex and quasi-convex functions and their applications. J. Inequal. Appl. 2019, Article ID 317 (2019)
Zaheer Ullah, S., Adil Khan, M., Chu, Y.-M.: A note on generalized convex functions. J. Inequal. Appl. 2019, Article ID 291 (2019)
Chu, Y.-M., Long, B.-Y.: Sharp inequalities between means. Math. Inequal. Appl. 14(3), 647–655 (2011)
Chu, Y.-M., Wang, M.-K.: Inequalities between arithmetic-geometric, Gini, and Toader means. Abstr. Appl. Anal. 2012, Article ID 830585 (2012)
Chu, Y.-M., Wang, M.-K., Qiu, S.-L., Jiang, Y.-P.: Bounds for complete elliptic integrals of the second kind with applications. Comput. Math. Appl. 63(7), 1177–1184 (2012)
He, X.-H., Qian, W.-M., Xu, H.-Z., Chu, Y.-M.: Sharp power mean bounds for two Sándor–Yang means. Rev. R. Acad. Cienc. Exactas Fís. Nat., Ser. A Mat. 113(3), 2627–2638 (2019)
Qian, W.-M., Chu, Y.-M.: Sharp bounds for a special quasi-arithmetic mean in terms of arithmetic and geometric means with two parameters. J. Inequal. Appl. 2017, Article ID 274 (2017)
Qian, W.-M., He, Z.-Y., Chu, Y.-M.: Approximation for the complete elliptic integral of the first kind. Rev. R. Acad. Cienc. Exactas Fís. Nat., Ser. A Mat. 114(2), Article ID 57 (2020). https://doi.org/10.1007/s13398-020-00784-9
Qian, W.-M., He, Z.-Y., Zhang, H.-W., Chu, Y.-M.: Sharp bounds for Neumann means in terms of two-parameter contraharmonic and arithmetic mean. J. Inequal. Appl. 2019, Article ID 168 (2019)
Qian, W.-M., Xu, H.-Z., Chu, Y.-M.: Improvements of bounds for the Sándor–Yang means. J. Inequal. Appl. 2019, Article ID 73 (2019)
Qian, W.-M., Yang, Y.-Y., Zhang, H.-W., Chu, Y.-M.: Optimal two-parameter geometric and arithmetic mean bounds for the Sándor–Yang mean. J. Inequal. Appl. 2019, Article ID 287 (2019)
Qian, W.-M., Zhang, X.-H., Chu, Y.-M.: Sharp bounds for the Toader–Qi mean in terms of harmonic and geometric means. J. Math. Inequal. 11(1), 121–127 (2017)
Qian, W.-M., Zhang, W., Chu, Y.-M.: Bounding the convex combination of arithmetic and integral means in terms of one-parameter harmonic and geometric means. Miskolc Math. Notes 20(2), 1157–1166 (2019)
Qiu, Y.-F., Wang, M.-K., Chu, Y.-M., Wang, G.-D.: Two sharp inequalities for Lehmer mean, identric mean and logarithmic mean. J. Math. Inequal. 5(3), 301–306 (2011)
Wang, M.-K., Chu, Y.-M.: Landen inequalities for a class of hypergeometric functions with applications. Math. Inequal. Appl. 21(2), 521–537 (2018)
Wang, M.-K., Chu, Y.-M., Qiu, S.-L., Jiang, Y.-P.: Bounds for the perimeter of an ellipse. J. Approx. Theory 164(7), 928–937 (2012)
Wang, M.-K., Chu, Y.-M., Zhang, W.: Monotonicity and inequalities involving zero-balanced hypergeometric function. Math. Inequal. Appl. 22(2), 601–617 (2019)
Wang, M.-K., Chu, Y.-M., Zhang, W.: Precise estimates for the solution of Ramanujan’s generalized modular equation. Ramanujan J. 49(3), 653–668 (2019)
Wang, M.-K., Hong, M.-Y., Xu, Y.-F., Shen, Z.-H., Chu, Y.-M.: Inequalities for generalized trigonometric and hyperbolic functions with one parameter. J. Math. Inequal. 14(1), 1–21 (2020)
Wang, M.-K., Li, Y.-M., Chu, Y.-M.: Inequalities and infinite product formula for Ramanujan generalized modular equation function. Ramanujan J. 46(1), 189–200 (2018)
Wang, B., Luo, C.-L., Li, S.-H., Chu, Y.-M.: Sharp one-parameter geometric and quadratic means bounds for the Sándor–Yang means. Rev. R. Acad. Cienc. Exactas Fís. Nat., Ser. A Mat. 114(1), Article ID 7 (2020). https://doi.org/10.1007/s13398-019-00734-0
Wang, M.-K., Zhang, W., Chu, Y.-M.: Monotonicity, convexity and inequalities involving the generalized elliptic integrals. Acta Math. Sci. 39B(5), 1440–1450 (2019)
Yang, Z.-H., Qian, W.-M., Zhang, W., Chu, Y.-M.: Notes on the complete elliptic integral of the first kind. Math. Inequal. Appl. 23(1), 77–93 (2020)
Zhao, T.-H., Wang, M.-K., Chu, Y.-M.: A sharp double inequality involving generalized complete elliptic integral of the first kind. AIMS Math. 5(5), 4512–4528 (2020)
Adil Khan, M., Iqbal, A., Suleman, M., Chu, Y.-M.: Hermite–Hadamard type inequalities for fractional integrals via Green’s function. J. Inequal. Appl. 2018, Article ID 161 (2018)
Adil Khan, M., Mohammad, N., Nwaeze, E.R., Chu, Y.-M.: Quantum Hermite–Hadamard inequality by means of a Green function. Adv. Differ. Equ. 2020, Article ID 99 (2020)
Rashid, S., Noor, M.A., Noor, K.I., Safdar, F., Chu, Y.-M.: Hermite–Hadamard type inequalities for the class of convex functions on time scale. Mathematics 7(10), 956 (2019)
Chalco-Cano, Y., Flores-Franulič, A., Román-Flores, H.: Ostrowski type inequalities for interval-valued functions using generalized Hukuhara derivative. Comput. Appl. Math. 31(3), 457–472 (2012)
Katugampola, U.N.: A new approach to generalized fractional derivatives. Bull. Math. Anal. Appl. 6(4), 1–15 (2014)
Zhao, T.-H., Chu, Y.-M., Wang, H.: Logarithmically complete monotonicity properties relating to the gamma function. Abstr. Appl. Anal. 2011, Article ID 896483 (2011)
Zhang, K.-S., Wan, J.-P.: p-convex functions and their properties. Pure Appl. Math. 23(1), 130–133 (2007)
Costa, T.M.: Jensen’s inequality type integral for fuzzy-interval-valued functions. Fuzzy Sets Syst. 327, 31–47 (2017)
Liu, X.-L., Ye, G.-J., Zhao, D.-F., Liu, W.: Fractional Hermite–Hadamard type inequalities for interval-valued functions. J. Inequal. Appl. 2019, Article ID 266 (2019)
Toplu, T., Set, E., İşcan, İ., Maden, S.: Hermite–Hadamard type inequalities for p-convex functions via Katugampola fractional integrals. Facta Univ., Ser. Math. Inform. 34(1), 149–164 (2019)
Sarikaya, M.Z., Set, E., Yaldiz, H., Başak, N.: Hermite–Hadamard’s inequalities for fractional integrals and related fractional inequalities. Math. Comput. Model. 57, 2403–2407 (2013)
Fang, Z.-B., Shi, R.-J.: On the \((p,h)\)-convex function and some integral inequalities. J. Inequal. Appl. 2014, Article ID 45 (2014)
Kunt, M., İşcan, İ.: Hermite–Hadamard–Fejér type inequalities for p-convex functions. Arab J. Math. Sci. 23(2), 215–230 (2017)
Acknowledgements
The authors would like to express their sincere thanks to the editor and the anonymous reviewers for their helpful comments and suggestions.
Availability of data and materials
Not applicable.
Funding
The work was supported by the Natural Science Foundation of China (Grant Nos. 11971142, 61673169, 11871202, 11701176, 11626101, 11601485).
Author information
Authors and Affiliations
Contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Abdeljawad, T., Rashid, S., Khan, H. et al. On new fractional integral inequalities for p-convexity within interval-valued functions. Adv Differ Equ 2020, 330 (2020). https://doi.org/10.1186/s13662-020-02782-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-020-02782-y