1 Introduction

The fractional diffusion equation is derived by replacing the classical time or space derivatives with fractional derivative. This kind of equation has been widely applied in many scientific fields. For instance, physical, chemical, biology, mechanical engineering, signal processing and systems identification, electrical, control theory, finance, fractional dynamics, etc.; please see the references [1–8].

If we replace the classical space derivative with a space fractional derivative, we can obtain the space-fractional diffusion equation. This equation is generally used to describe some diffusion phenomena such as the super-diffusion, non-Gaussian diffusion, sub-diffusion, and so on; also refer to [9, 10]. In the past years, the direct problems for the space-fractional diffusion equation have been studied extensively, see [11–17]. In recent years, more and more people have been focusing on the inverse problems for this equation, which usually include parameter identification problem, inverse initial value problem, Cauchy problem, inverse heat conduction problem, inverse source problem, inverse boundary condition problem, and so on. At present, some works on the inverse problem of space-fractional diffusion problem have been published, see [18–21], etc.

In this paper, we consider the Riesz–Feller space-fractional backward diffusion problem

$$ \textstyle\begin{cases} u_{t}(x,t)={}_{x}D^{\alpha }_{\theta }u(x,t),\quad x\in R,0< t< T, \\ u(x,t)|_{x\rightarrow \pm \infty }=0,\quad 0< t\leq T, \\ u(x,T)=g(x),\quad x\in R, \end{cases} $$
(1)

where \(T>0\) is a constant, the space-fractional derivative \({}_{x}D^{\alpha }_{\theta }\) is the Riesz–Feller fractional derivative of order α (\(0<\alpha \leq 2\)) and skewness θ (\(|\theta |\leq \min \{\alpha , 2-\alpha \}\), \(\theta \neq \pm 1\)), its Fourier transform is defined in [22] as

$$ \mathcal{F}\bigl\{ {}_{x}D^{\alpha }_{\theta }f(x); \xi \bigr\} =-\psi ^{\theta }_{ \alpha }(\xi )\widehat{f}(\xi ), $$
(2)

with

$$ \psi ^{\theta }_{\alpha }(\xi )= \vert \xi \vert ^{\alpha }e^{i(\operatorname{sign} (\xi )) \theta \pi /2}= \vert \xi \vert ^{\alpha } \biggl( \cos \biggl( \frac{\theta \pi }{2} \biggr) +i\operatorname{sign}(\xi )\sin \biggl( \frac{\theta \pi }{2} \biggr) \biggr). $$
(3)

The Riesz–Feller fractional derivative is defined as [22]

$$\begin{aligned}& \begin{aligned}[b] {}_{x}D^{\alpha }_{\theta }f(x)={}& \frac{\varGamma (1+\alpha )}{\pi }\sin \frac{(\alpha +\theta )\pi }{2} \int ^{\infty }_{0} \frac{f(x+\zeta )-f(x)}{\zeta ^{1+\alpha }}\,d\zeta \\ &{}+\frac{\varGamma (1+\alpha )}{\pi }\sin \frac{(\alpha -\theta )\pi }{2} \int ^{\infty }_{0} \frac{f(x-\zeta )-f(x)}{\zeta ^{1+\alpha }}\,d\zeta ,\quad 0< \alpha < 2, \end{aligned} \end{aligned}$$
(4)
$$\begin{aligned}& {}_{x}D^{2}_{0} f(x)= \frac{d^{2}f(x)}{dx^{2}}, \quad \alpha =2. \end{aligned}$$
(5)

Meanwhile, for the convenience of numerical calculation, [23] also defined the Riesz–Feller fractional derivative \({}_{x}D^{\alpha }_{\theta }\) as

$$\begin{aligned}& \begin{aligned}[b] {}_{x}D^{\alpha }_{\theta }f(x)={}&{-} \frac{1}{\varGamma (1-\alpha )\sin (\alpha \pi )}\sin \frac{(\alpha -\theta )\pi }{2} \frac{d}{dx} \int ^{x}_{-\infty } \frac{f(\zeta )}{(x-\zeta )^{\alpha }}\,d\zeta \\ &{}-\frac{1}{\varGamma (1-\alpha )\sin (\alpha \pi )}\sin \frac{(\alpha +\theta )\pi }{2} \frac{d}{dx} \int ^{\infty }_{x} \frac{f(\zeta )}{(\zeta -x)^{\alpha }}\,d\zeta ,\quad 0< \alpha < 1, \end{aligned} \end{aligned}$$
(6)
$$\begin{aligned}& {}_{x}D^{1}_{\theta }f(x)=- \frac{1}{\pi }\cos \frac{\theta \pi }{2} \frac{d}{dx} \int ^{\infty }_{-\infty }\frac{f(\zeta )}{(x-\zeta )}\,d\zeta +\sin \frac{\theta \pi }{2}\frac{df(x)}{dx},\quad \alpha =1, \end{aligned}$$
(7)
$$\begin{aligned}& \begin{aligned}[b] {}_{x}D^{\alpha }_{\theta }f(x)={}&{-} \frac{1}{\varGamma (2-\alpha )\sin (\alpha \pi )}\sin \frac{(\alpha -\theta )\pi }{2} \frac{d^{2}}{dx^{2}} \int ^{x}_{- \infty }\frac{f(\zeta )}{(x-\zeta )^{\alpha -1}}\,d\zeta \\ &{}-\frac{1}{\varGamma (2-\alpha )\sin (\alpha \pi )}\sin \frac{(\alpha +\theta )\pi }{2} \frac{d^{2}}{dx^{2}} \int ^{\infty }_{x} \frac{f(\zeta )}{(\zeta -x)^{\alpha -1}}\,d\zeta , \quad 1< \alpha < 2, \end{aligned} \end{aligned}$$
(8)
$$\begin{aligned}& {}_{x}D^{2}_{0} f(x)=\frac{d^{2}f(x)}{dx^{2}},\quad \alpha =2. \end{aligned}$$
(9)

This fractional derivative has a wide range of applications in the theory of probability distribution, thermoelasticity [24], ecology [25], plasma physics [26], continuum mechanics [27], hydrology [28, 29], and finance, especially modeling for the high-frequency price dynamics in financial markets [30–32] and [7].

Let \(\delta >0\) be the measured error bound, given the final measured data \(g^{\delta }(x)\) with \(\|g^{\delta }(x)-g(x)\|_{L^{2}(R)}\leq \delta \), our purpose is to determine \(u(x,t)\) (\(0\leq t< T\)) from (1). We know that, as \(\alpha =2\), problem (1) is just the standard backward heat conduction problem (BHCP). This problem is ill-posed in the sense that the solution does not depend continuously on the given data, so the regularization method is required to overcome its ill-posedness and recover the stability of the solution. Up to now, some regularization methods have been presented and used to solve this problem. For example, Zheng et al. in [21] proposed the convolution and spectral regularized methods to solve the backward problem. Shi et al. [33] presented an a-posteriori parameter selection rule for the convolution regularized method and deduced the error estimate of logarithmic type. Cheng et al. [34] used an iteration method to deal with a similar inverse problem. Zhao et al. [35] applied a simplified Tikhonov method to research an inverse problem for space-fractional backward diffusion problem and derive the a-priori convergence estimate. For the case of \(\theta =0\), [36–38] respectively proposed the logarithmic, negative exponential, and fractional Tikhonov regularization methods to overcome the ill-posedness of the considered problem, and then based on the conditional stability and an a-posteriori regularized parameter choice rule, the authors derived the convergence estimates of logarithmic and double logarithmic types. [39, 40] used the spectral truncation method to solve the space-fractional heat conduction problem backward in time and obtained the optimal error estimation.

In ordinary Tikhonov regularization method, the penalty term commonly is added as \(\|u(x,t)\|^{2}_{L^{2}(R)}\). Instead of Tikhonov method, this paper adds the penalty term as \(\|u(x,0)\|^{2}_{H^{s}(R)}\) (\(0\leq s< p\), \(p>0\) is a constant) to construct a generalized Tikhonov regularization method (see Sect. 2) and derives the convergence estimates of logarithmic and double logarithmic types by adopting an a-posteriori selection rule of regularization parameter. Finally, we verify the computational effectiveness for our method by making the corresponding numerical experiments. Note that, as \(s=0\), our method becomes the simplified Tikhonov method in [35]. In [35], the authors mainly derived the optimal a-priori convergence estimate of regularized solution, but did not consider the a-posteriori convergence result. In this paper, we not only construct the generalized Tikhonov method to overcome the ill-posedness of the considered problem, but also derive the a-posteriori convergence estimate of our method. Meanwhile, by making the comparison we find that, under the a-posteriori choice rule of regularization parameter, the numerical simulation effect of our method is similar with the simplified Tikhonov method. Then the method given in this paper can be seen as an extension and supplement on the one in [35].

The remainder of this paper is arranged as follows. In Sect. 2, based on the conditional stability, we make a description for the construction procedure of our regularization method. The a-posteriori result of convergence estimate is shown in Sect. 3. Section 4 is devoted to the numerical implementations and the corresponding simulation results. Some conclusions are drawn in Sect. 5.

2 Conditional stability and regularization method

2.1 Conditional stability

Let \(f\in L^{2}(R)\), the Fourier and inverse Fourier transforms are defined as

$$\begin{aligned}& \widehat{f}(\xi ):=\frac{1}{\sqrt{2\pi }} \int _{-\infty }^{\infty }f(x)e^{i \xi x}\,dx,\quad \xi \in R, \end{aligned}$$
(10)
$$\begin{aligned}& f(x):=\frac{1}{\sqrt{2\pi }} \int _{-\infty }^{\infty }\widehat{f}( \xi )e^{-i\xi x}\,d\xi ,\quad x\in R. \end{aligned}$$
(11)

Take the Fourier transform of problem (1) with respect to x, then for \(\xi \in R\), the solution of problem (1) in the frequency domain can be expressed as follows:

$$ \widehat{u}(\xi ,t)=e^{\psi ^{\theta }_{\alpha }(\xi )(T-t)}\widehat{g}( \xi ). $$
(12)

Hence, the exact solution of problem (1) can be written by

$$ u(x,t)=\frac{1}{\sqrt{2\pi }} \int _{-\infty }^{\infty } e^{\psi ^{ \theta }_{\alpha }(\xi )(T-t)}\widehat{g}(\xi )e^{-i\xi x}\,d\xi . $$
(13)

From (13) we know that \(\psi ^{\theta }_{\alpha }(\xi )\) has a positive real part \(|\xi |^{\alpha }\cos \frac{\theta \pi }{2}\), as \(|\xi |\rightarrow \infty \), the function \(e^{|\xi |^{\alpha }(T-t)\cos \frac{\theta \pi }{2}}\) tends to infinity, hence problem (1) is ill-posed in the sense that the solution does not depend continuously on the given data. However, under certain additional condition, the continuous dependence of solution can be established, this is called the conditional stability [41].

Suppose that there exists a constant \(E>0\) such that the following a-priori bound holds:

$$ \bigl\Vert u(\cdot ,0) \bigr\Vert _{p}\leq E,\quad p>0. $$
(14)

Here, \(\|u(\cdot ,0)\|_{p}\) denotes the Sobolev space \(H^{p}\)-norm defined by

$$ \bigl\Vert u(\cdot ,0) \bigr\Vert _{p}= \biggl( \int _{-\infty }^{\infty } \bigl(1+\xi ^{2} \bigr)^{p} \bigl\vert \widehat{u}(\cdot ,0) \bigr\vert ^{2}\,d\xi \biggr)^{1/2}, $$
(15)

we know that, as \(p=0\), this is the \(L^{2}\)-norm. Throughout this paper, we denote by \(\|\cdot \|\) the \(L^{2}\)-norm.

In [42], under the assumption of the a-priori bound condition (14), the authors established the following condition stability by using the interpolation method:

$$ \bigl\Vert u(\cdot ,t) \bigr\Vert \leq \sqrt{2}E^{1-\frac{t}{T}} \bigl\Vert g(\cdot ) \bigr\Vert ^{ \frac{t}{T}} \biggl(\frac{1}{T\cos (\theta \pi /2)}\ln \frac{1}{ \Vert g(\cdot ) \Vert } \biggr)^{ \frac{-p (1-\frac{t}{T} )}{\alpha }}. $$
(16)

2.2 Regularization method

According to the expression of solution (13), in order to overcome the ill-posedness of the considered problem, a natural way is to eliminate the high frequency part (\(|\xi |\rightarrow +\infty \)) of function \(e^{|\xi |^{\alpha }(T-t)\cos \frac{\theta \pi }{2}}\) and construct a stable approximation solution for problem (1).

In what follows, based on the condition stability (16), we make a description for our regularization method. According to (13), for the fixed \(0\leq t< T\), the problem of seeking \(u(x,t)\) from (1) can be transformed into the operator equation

$$ K(t)u(x,t)=g(x), $$
(17)

and based on (12), \(\widehat{K}(t):L^{2}(R)\rightarrow L^{2}(R)\) is a linear bounded multiplication operator with \(\widehat{K}(t)=e^{-\psi ^{\theta }_{\alpha }(\xi )(T-t)}=e^{-|\xi |^{\alpha }(T-t) \cos (\frac{\theta \pi }{2} ) -i|\xi |^{\alpha }(T-t)\operatorname{sign}(\xi )\sin (\frac{\theta \pi }{2} )}\). By the basic calculation, we know that the adjoint operator of it can be written as \(\widehat{K^{*}}(t)=e^{-|\xi |^{\alpha }(T-t)\cos ( \frac{\theta \pi }{2} ) +i|\xi |^{\alpha }(T-t)\operatorname{sign}(\xi ) \sin (\frac{\theta \pi }{2} )}\).

Assume that the noisy data \(g^{\delta }\) satisfies

$$ \bigl\Vert g^{\delta }-g \bigr\Vert \leq \delta . $$
(18)

In order to get a stable solution to problem (1) with noisy data \(g^{\delta }\), we solve the variational problem

$$ \min_{u\in L^{2}(R)} \bigl\Vert K(t)u(x,t)-g^{\delta }(x) \bigr\Vert ^{2} +\mu \bigl\Vert u(x,0) \bigr\Vert ^{2}_{H^{s}(R)}, \quad 0\leq s< p, $$
(19)

where \(\mu >0\) plays a role of the regularization parameter, \(\delta >0\) denotes the measured error bound. By the Parseval identity and (12), this variational problem becomes minimizing the functional

$$ \min_{\widehat{u}\in L^{2}(R)} \bigl\Vert e^{-\psi ^{\theta }_{\alpha }( \xi )(T-t)} \widehat{u}(\xi ,t)-\widehat{g^{\delta }}(\xi ) \bigr\Vert ^{2} +\mu \biggl\Vert \bigl(1+ \vert \xi \vert ^{2} \bigr)^{s/2} \frac{e^{-\psi ^{\theta }_{\alpha }(\xi )(T-t)}}{e^{-\psi ^{\theta }_{\alpha }(\xi )T}}\widehat{u}(\xi ,t) \biggr\Vert ^{2}. $$
(20)

Denote \(\widehat{u}^{\delta }_{\mu }(\xi ,t)\) to be the solution of problem (20), then it satisfies the Euler equation

$$\begin{aligned}& \biggl(e^{-2 \vert \xi \vert ^{\alpha }(T-t)\cos (\frac{\theta \pi }{2} )} +\mu \bigl(1+ \vert \xi \vert ^{2} \bigr)^{s} \frac{e^{-2 \vert \xi \vert ^{\alpha }(T-t)\cos (\frac{\theta \pi }{2} )}}{e^{-2 \vert \xi \vert ^{\alpha }T\cos (\frac{\theta \pi }{2} )}} \biggr) \widehat{u}^{\delta }_{\mu }(\xi ,t) \\& \quad =e^{- \vert \xi \vert ^{\alpha }(T-t)\cos (\frac{\theta \pi }{2} ) +i \vert \xi \vert ^{\alpha }(T-t)\operatorname{sign}(\xi )\sin (\frac{\theta \pi }{2} )}\widehat{g^{\delta }}(\xi ). \end{aligned}$$
(21)

From (21), in the frequency domain the regularized solution \(\widehat{u}^{\delta }_{\mu }(\xi ,t)\) can be expressed as

$$ \widehat{u}^{\delta }_{\mu }(\xi ,t)= \frac{e^{\psi ^{\theta }_{\alpha }(\xi )(T-t)} \widehat{g^{\delta }}(\xi )}{1+\mu (1+ \vert \xi \vert ^{2})^{s}e^{2 T \vert \xi \vert ^{\alpha }\cos (\frac{\theta \pi }{2} )}}. $$
(22)

Thus, the regularization solution of problem (1) can be written as

$$ u^{\delta }_{\mu }(x,t)=\frac{1}{\sqrt{2\pi }} \int _{-\infty }^{\infty } \frac{e^{\psi ^{\theta }_{\alpha }(\xi )(T-t)} \widehat{g^{\delta }}(\xi )e^{-i\xi x}}{1+\mu (1+ \vert \xi \vert ^{2})^{s}e^{2 T \vert \xi \vert ^{\alpha }\cos (\frac{\theta \pi }{2} )}}\,d\xi . $$
(23)

Remark 2.1

Note that in (19) we add the penalty item in the sense of \(H^{s}\)-norm to construct the regularization solution (23). In fact, if we add the penalty item in the sense of \(L^{2}\)-norm, i.e., in the standard Tikhonov regularization method, the penalty item is added as \(\|u(x,t)\|^{2}_{L^{2}(R)}\), then the Tikhonov regularization solution can be expressed as

$$ u^{\delta }_{Tik\mu }(x,t)=\frac{1}{\sqrt{2\pi }} \int _{-\infty }^{ \infty } \frac{e^{\psi ^{\theta }_{\alpha }(\xi )(T-t)} \widehat{g^{\delta }}(\xi )e^{-i\xi x}}{1+\mu e^{2 (T-t)|\xi |^{\alpha }\cos (\frac{\theta \pi }{2} )}}\,d\xi . $$
(24)

In 2014, [35] modified (24) to construct a simplified Tikhonov regularization solution

$$ u^{\delta }_{STik\mu }(x,t)=\frac{1}{\sqrt{2\pi }} \int _{-\infty }^{ \infty } \frac{e^{\psi ^{\theta }_{\alpha }(\xi )(T-t)} \widehat{g^{\delta }}(\xi )e^{-i\xi x}}{1+\mu e^{2T|\xi |^{\alpha }\cos (\frac{\theta \pi }{2} )}}\,d\xi . $$
(25)

From (23), (24), and (25) we can find that, in order to overcome the ill-posedness of the considered problem (i.e., eliminate the high frequency part of function \(e^{|\xi |^{\alpha }(T-t)\cos \frac{\theta \pi }{2}}\)), the function \(\frac{e^{\psi ^{\theta }_{\alpha }(\xi )(T-t)} }{1+\mu (1+|\xi |^{2})^{s}e^{2 T|\xi |^{\alpha }\cos (\frac{\theta \pi }{2} )}}\) is a better “kernel” than \(\frac{e^{\psi ^{\theta }_{\alpha }(\xi )(T-t)} }{1+\mu e^{2 (T-t)|\xi |^{\alpha }\cos (\frac{\theta \pi }{2} )}}\) and \(\frac{e^{\psi ^{\theta }_{\alpha }(\xi )(T-t)} }{1+\mu e^{2T|\xi |^{\alpha }\cos (\frac{\theta \pi }{2} )}}\). Note that, as \(s=0\), our method becomes the simplified Tikhonov method, thus the method given in this paper can be seen as an interesting extension on the one in [35], which is similar to the generalized Tikhonov method in [43]. In 2012, [44] used a similar method to research a multidimensional inverse source problem for standard heat equation (\(\alpha =2\)). We point out that this method also can be extended to solve the multidimensional space-fractional backward diffusion problem. However, because the special process is similar to one-dimensional case, here we only consider problem (1).

3 Convergence estimate under an a-posteriori rule of the regularization parameter

This section adopts a kind of a-posteriori rule to select the regularization parameter μ. This idea comes from [33] and then derives the convergence estimate for the regularization method. On the general description for the a-posteriori selection rule of regularized parameter, we can see the discrepancy principle in [45].

We seek the regularization parameter μ by the equation

$$ \bigl\Vert u^{\delta }_{\mu }(x,T)-g^{\delta }(x) \bigr\Vert =h(\delta ). $$
(26)

Here, \(h(\delta )>\delta \) will be given later. The following two lemmas will be needed in the convergence estimate of a-posteriori type.

Lemma 3.1

Let\(\varrho (\mu )=\|u^{\delta }_{\mu }(x,T)-g^{\delta }(x)\|\)and\(0< h(\delta )<\|g^{\delta }\|\), then we have the following conclusions:

  1. (i)

    For\(\mu \in (0,+\infty )\), \(\varrho (\mu )\)is a continuous function;

  2. (ii)

    \(\lim_{\mu \rightarrow 0}\varrho (\mu )=0\);

  3. (iii)

    \(\lim_{\mu \rightarrow +\infty }\varrho (\mu )=\|g^{\delta }\|\);

  4. (iv)

    For\(\mu \in (0,+\infty )\), \(\varrho (\mu )\)is a strictly increasing function.

Proof

We can easily prove the conclusions of this lemma by taking

$$ \varrho (u)= \biggl\Vert \frac{\mu (1+ \vert \xi \vert ^{2})^{s}e^{2 T \vert \xi \vert ^{\alpha }\cos (\frac{\theta \pi }{2} )} \widehat{g^{\delta }}(\xi )}{1+\mu (1+ \vert \xi \vert ^{2})^{s}e^{2 T \vert \xi \vert ^{\alpha }\cos (\frac{\theta \pi }{2} )}} \biggr\Vert , $$
(27)

here we omit the detailed procedure. Lemma 3.1 means that, as \(0< h(\delta )<\|g^{\delta }\|\), equation (26) has a unique solution. □

Lemma 3.2

Assume that a-priori bound condition (14) is valid, then the regularized solution (23) combined with a-posteriori selection rule (26) determines that the regularization parameter\(\mu =\mu (\delta ,g^{\delta })\)satisfies\(\frac{1}{\mu }\leq \frac{D^{2}_{0}E^{2}}{4(h(\delta )-\delta )^{2}}\), here\(D_{0}\)is a positive constant.

Proof

From (26), there holds

$$\begin{aligned} h(\delta ) =& \biggl\Vert \frac{\mu (1+ \vert \xi \vert ^{2})^{s}e^{2 T \vert \xi \vert ^{\alpha }\cos (\frac{\theta \pi }{2} )} \widehat{g^{\delta }}(\xi )}{1+\mu (1+ \vert \xi \vert ^{2})^{s}e^{2 T \vert \xi \vert ^{\alpha }\cos (\frac{\theta \pi }{2} )}} \biggr\Vert \\ \leq& \biggl\Vert \frac{\mu (1+ \vert \xi \vert ^{2})^{s}e^{2 T \vert \xi \vert ^{\alpha }\cos (\frac{\theta \pi }{2} )} }{1+\mu (1+ \vert \xi \vert ^{2})^{s}e^{2 T \vert \xi \vert ^{\alpha }\cos (\frac{\theta \pi }{2} )}}\bigl( \widehat{g^{\delta }}( \xi )-\widehat{g}(\xi )\bigr) \biggr\Vert \\ &{}+ \biggl\Vert \frac{\mu (1+ \vert \xi \vert ^{2})^{s}e^{2 T \vert \xi \vert ^{\alpha }\cos (\frac{\theta \pi }{2} )} }{1+\mu (1+ \vert \xi \vert ^{2})^{s}e^{2 T \vert \xi \vert ^{\alpha }\cos (\frac{\theta \pi }{2} )}} \widehat{g}(\xi ) \biggr\Vert \\ \leq& \delta + \biggl\Vert \frac{\mu (1+ \vert \xi \vert ^{2})^{s}e^{ T \vert \xi \vert ^{\alpha }\cos (\frac{\theta \pi }{2} )} (1+ \vert \xi \vert ^{2})^{-\frac{p}{2}}(1+ \vert \xi \vert ^{2})^{\frac{p}{2}}e^{ T \vert \xi \vert ^{\alpha }\cos (\frac{\theta \pi }{2} )} }{1+\mu (1+ \vert \xi \vert ^{2})^{s}e^{2 T \vert \xi \vert ^{\alpha }\cos (\frac{\theta \pi }{2} )}} \widehat{g}(\xi ) \biggr\Vert \\ \leq& \delta +E\sup_{\xi \in R}B(\xi ). \end{aligned}$$
(28)

By the basic simplification and using the mean value inequality, it can be gotten that

$$\begin{aligned} B(\xi ) =& \frac{\mu (1+ \vert \xi \vert ^{2})^{s}e^{ T \vert \xi \vert ^{\alpha }\cos (\frac{\theta \pi }{2} )} }{1+\mu (1+ \vert \xi \vert ^{2})^{s}e^{2 T \vert \xi \vert ^{\alpha }\cos (\frac{\theta \pi }{2} )}}\bigl(1+ \vert \xi \vert ^{2}\bigr)^{-\frac{p}{2}} \\ =& \frac{\sqrt{\mu }(1+ \vert \xi \vert ^{2})^{-\frac{p}{2}} }{\frac{1}{\sqrt{\mu }}\cdot (1+ \vert \xi \vert ^{2})^{-s}e^{-T \vert \xi \vert ^{\alpha }\cos (\frac{\theta \pi }{2})} +\sqrt{\mu }e^{T \vert \xi \vert ^{\alpha }\cos (\frac{\theta \pi }{2})}} \\ \leq& \frac{\sqrt{\mu }}{2} \cdot \bigl(1+ \vert \xi \vert ^{2}\bigr)^{-\frac{p-s}{2}}. \end{aligned}$$
(29)

Since \(0\leq s< p\) and \(\lim_{|\xi |\rightarrow 0+}(1+|\xi |^{2})^{-\frac{p-s}{2}}=1\), \(\lim_{|\xi |\rightarrow +\infty }(1+|\xi |^{2})^{-\frac{p-s}{2}}=0\), then there exists \(D_{0}>0\) such that \(B(\xi )\leq D_{0}\sqrt{\mu }/2\). Now combining (28), we can derive the result of Lemma 3.2. □

Theorem 3.3

Suppose thatugiven by (13) is the exact solution of problem (1), \(u^{\delta }_{\mu }\)defined by (23) is the regularization solution. Let the exact datagand measured data\(g^{\delta }\)satisfy (18), and the a-priori bound (14) is satisfied.

  1. (i)

    If the regularization parameter is selected by a-posteriori rule (26) with\(h(\delta )=\delta +\delta ^{\frac{1-\gamma }{2}}\) (\(0<\gamma <1\)), then we have the following convergence estimate of logarithmic type:

    $$\begin{aligned} \bigl\Vert u^{\delta }_{\mu }(x,t)-u(x,t) \bigr\Vert \leq& \frac{DD^{2}_{0}E^{2}\delta ^{\gamma }}{4} +\sqrt{2}E^{1-\frac{t}{T}} \bigl(2\delta +\delta ^{\frac{1-\gamma }{2}} \bigr) ^{\frac{t}{T}} \\ &{}\times\biggl(\frac{1}{T\cos (\theta \pi /2)} \ln \frac{1}{(2\delta +\delta ^{\frac{1-\gamma }{2}})} \biggr) ^{ \frac{-p (1-\frac{t}{T} )}{\alpha }}. \end{aligned}$$
    (30)
  2. (ii)

    If the regularization parameter is chosen by a-posteriori rule (26) with\(h(\delta )=\delta +\sqrt{\delta }\ln \frac{1}{\delta }\), then we have the following convergence estimate of double logarithmic type:

    $$\begin{aligned} \bigl\Vert u^{\delta }_{\mu }(x,t)-u(x,t) \bigr\Vert \leq& \frac{DD^{2}_{0}E^{2}}{4 (\ln \frac{1}{\delta } )^{2}} + \sqrt{2}E^{1-\frac{t}{T}} \biggl(2 \delta +\sqrt{\delta } \ln \frac{1}{\delta } \biggr)^{\frac{t}{T}} \\ &{}\times \biggl( \frac{1}{T\cos (\theta \pi /2)} \ln \frac{1}{(2\delta +\sqrt{\delta }\ln \frac{1}{\delta })} \biggr) ^{ \frac{-p (1-\frac{t}{T} )}{\alpha }}, \end{aligned}$$
    (31)

    where\(D>0\)is a constant, \(D_{0}\)is given in Lemma 3.2.

Proof

Using the Parseval theorem, it is clear that

$$ \bigl\Vert u^{\delta }_{\mu }(\cdot ,t)-u( \cdot ,t) \bigr\Vert \leq \bigl\Vert \widehat{u^{\delta }_{\mu }}( \cdot ,t)-\widehat{u_{\mu }}(\cdot ,t) \bigr\Vert + \bigl\Vert \widehat{u_{\mu }}( \cdot ,t)-\widehat{u}(\cdot ,t) \bigr\Vert . $$
(32)

For \(\mu \in (0,1)\) and from (18), we get that

$$\begin{aligned} \bigl\Vert \widehat{u^{\delta }_{\mu }}( \cdot ,t)-\widehat{u_{\mu }}( \cdot ,t) \bigr\Vert =& \biggl\Vert \frac{e^{\psi ^{\theta }_{\alpha }(\xi )(T-t)} }{1+\mu (1+ \vert \xi \vert ^{2})^{s}e^{2 T \vert \xi \vert ^{\alpha }\cos (\frac{\theta \pi }{2} )}} \bigl(\widehat{g^{\delta }}(\xi )-\widehat{g}(\xi ) \bigr) \biggr\Vert \\ \leq& \frac{\delta }{\mu (e^{-(T-t) \vert \xi \vert ^{{\alpha }}\cos (\frac{\theta \pi }{2})}+(1+ \vert \xi \vert ^{2})^{s} e^{(T+t) \vert \xi \vert ^{\alpha }\cos (\frac{\theta \pi }{2})} )}. \end{aligned}$$
(33)

By the simple calculation, we notice that \(\lim_{|\xi |\rightarrow 0+}e^{-(T-t)|\xi |^{{\alpha }} \cos ( \frac{\theta \pi }{2})}+(1+|\xi |^{2})^{s}\times e^{(T+t)|\xi |^{\alpha } \cos (\frac{\theta \pi }{2})}=2\) and \(\lim_{|\xi |\rightarrow +\infty }e^{-(T-t)|\xi |^{{\alpha }} \cos ( \frac{\theta \pi }{2})}+(1+|\xi |^{2})^{s} e^{(T+t)|\xi |^{\alpha } \cos (\frac{\theta \pi }{2})} =+\infty \), then there exists a positive number D such that

$$ \bigl\Vert \widehat{u^{\delta }_{\mu }}( \cdot ,t)-\widehat{u_{\mu }}(\cdot ,t) \bigr\Vert \leq D\delta /\mu . $$
(34)

By (34) and Lemma 3.2, we get

$$ \bigl\Vert u^{\delta }_{\mu }(\cdot ,t)-u_{\mu }(\cdot ,t) \bigr\Vert \leq \frac{DD^{2}_{0}E^{2}\delta }{4(h(\delta )-\delta )^{2}}. $$
(35)

Now we give the estimate for the second term of (32). It is noticed that

$$\begin{aligned} \bigl\Vert K(t) \bigl(u_{\mu }(x,t)-u(x,t) \bigr) \bigr\Vert =& \biggl\Vert \frac{\mu (1+ \vert \xi \vert ^{2})^{s}e^{2T \vert \xi \vert ^{\alpha }\cos (\frac{\theta \pi }{2})} }{1+\mu (1+ \vert \xi \vert ^{2})^{s}e^{2T \vert \xi \vert ^{\alpha }\cos (\frac{\theta \pi }{2})}} \widehat{g}(\xi ) \biggr\Vert \\ \leq& \biggl\Vert \frac{\mu (1+ \vert \xi \vert ^{2})^{s}e^{2T \vert \xi \vert ^{\alpha }\cos (\frac{\theta \pi }{2})} }{1+\mu (1+ \vert \xi \vert ^{2})^{s}e^{2T \vert \xi \vert ^{\alpha }\cos (\frac{\theta \pi }{2})}} \bigl( \widehat{g^{\delta }}(\xi )-\widehat{g}(\xi )\bigr) \biggr\Vert \\ &{} + \biggl\Vert \frac{\mu (1+ \vert \xi \vert ^{2})^{s}e^{2T \vert \xi \vert ^{\alpha }\cos (\frac{\theta \pi }{2})} }{1+\mu (1+ \vert \xi \vert ^{2})^{s}e^{2T \vert \xi \vert ^{\alpha }\cos (\frac{\theta \pi }{2})}} \widehat{g^{\delta }}( \xi ) \biggr\Vert \\ \leq& \delta +h(\delta ). \end{aligned}$$
(36)

In addition, according to a-priori bound condition (14), we have

$$\begin{aligned}& \bigl\Vert u_{\mu }(x,t)-u(x,t) \bigr\Vert _{H^{p}(R)} \\& \quad = \biggl\Vert \bigl(1+ \vert \xi \vert ^{2} \bigr)^{ \frac{p}{2}} \frac{\mu (1+ \vert \xi \vert ^{2})^{s} e^{2T \vert \xi \vert ^{\alpha }\cos (\frac{\theta \pi }{2})} }{1+\mu (1+ \vert \xi \vert ^{2})^{s}e^{2T \vert \xi \vert ^{\alpha } \cos (\frac{\theta \pi }{2})}} e^{\psi ^{\theta }_{\alpha }(\xi )(T-t)}\widehat{g}(\xi ) \biggr\Vert \\& \quad \leq \biggl\Vert \bigl(1+ \vert \xi \vert ^{2}\bigr)^{\frac{p}{2}} \frac{\mu (1+ \vert \xi \vert ^{2})^{s} e^{2T \vert \xi \vert ^{\alpha }\cos (\frac{\theta \pi }{2})} }{1+\mu (1+ \vert \xi \vert ^{2})^{s}e^{2T \vert \xi \vert ^{\alpha } \cos (\frac{\theta \pi }{2})}} \widehat{u}(\xi ,0) \biggr\Vert \\& \quad \leq \bigl\Vert u(x,0) \bigr\Vert _{H^{p}(R)}\leq E. \end{aligned}$$
(37)

By the condition stability result (16), it can be gotten that

$$ \bigl\Vert u_{\mu }(x,t)-u(x,t) \bigr\Vert \leq \sqrt{2}E^{1-\frac{t}{T}} \bigl(\delta +h( \delta ) \bigr)^{\frac{t}{T}} \biggl(\frac{1}{T\cos (\theta \pi /2)} \ln \frac{1}{(\delta +h(\delta ))} \biggr) ^{ \frac{-p (1-\frac{t}{T} )}{\alpha }}. $$
(38)

Combining (35) with (38), we can derive that

$$\begin{aligned} \bigl\Vert u^{\delta }_{\mu }(x,t)-u(x,t) \bigr\Vert \leq& \frac{DD^{2}_{0}E^{2}\delta }{4(h(\delta )-\delta )^{2}} +\sqrt{2}E^{1- \frac{t}{T}} \bigl(\delta +h(\delta ) \bigr)^{\frac{t}{T}} \\ &{}\times\biggl( \frac{1}{T\cos (\theta \pi /2)} \ln \frac{1}{(\delta +h(\delta ))} \biggr) ^{\frac{-p (1-\frac{t}{T} )}{\alpha }}. \end{aligned}$$
(39)

Finally, for cases (i) and (ii), we can establish the corresponding convergence results (30) and (31), respectively. □

Remark 3.4

In the normal discrepancy principle [45], the regularization parameter μ is chosen by the equation \(\|u^{\delta }_{\mu }(x,T)-g^{\delta }(x)\|=\tau \delta \), here \(\tau >1\) is a constant. We find that, if we adopt this rule to select the regularization parameter, the convergence estimate of regularization solution can not be easily derived. In view of this, in order to establish the convergence result of regularized method, here we adopt a-posteriori rule (26) to select the regularization parameter, which is factually a modified version for the normal discrepancy principle.

4 Numerical simulations

This section does some numerical experiments to verify the convergence and stability of our method. Since the analytic solution of problem (1) is generally difficult to be expressed explicitly, here we solve the following direct problem to construct the final data \(g(x)\) by the finite difference method:

$$ \textstyle\begin{cases} u_{t}(x,t)={}_{x}D^{\alpha }_{\theta }u(x,t), \quad -a< x< a, 0< t< T, \\ u(-a,t)=u(a,t)=0, \quad 0\leq t\leq T, \\ u(x,0)=h(x), \quad -a< x< a, \end{cases} $$
(40)

where the Riesz–Feller fractional derivative \({}_{x}D^{\alpha }_{\theta }\) is defined by (6)–(9).

We choose \(a=5\), \(T=1\), denote \(\triangle t=\frac{T}{L}\) and \(\triangle x=\frac{2a}{M}\) to be the step sizes for time and space variables, respectively. The grid points in the time interval are labeled \(t_{l}=l\triangle t\), \(l=0, 1,2,\ldots ,L\), the grid points in the space interval are \(x_{i}=-a+i\triangle x\), \(i=0,1,2,\ldots ,M\), and setting \(u^{l}_{i}=u(x_{i},t_{l})\).

We approximate \(u_{t}\) at \((x_{i},t_{l})\) as follows:

$$ u_{t}(x_{i},t_{l}) \approx \frac{u^{l+1}_{i}-u^{l}_{i}}{\triangle t},\quad i=1,2, \ldots ,M-1, $$
(41)

and \({}_{x}D^{\alpha }_{\theta }u\) at \((x_{i},t_{l})\) is approximated as in [21]. The special scheme has four cases:

  1. (i)

    As \(0<\alpha <1\) and \(|\theta |\leq \alpha \),

    $$\begin{aligned}& {}_{x}D^{\alpha }_{\theta }u(x_{i},t_{l}) \approx - \frac{ (c_{+}\sum^{i}_{k=0}(-1)^{k} \binom{\alpha }{k}u^{l}_{i-k} +c_{-}\sum^{M-i}_{k=0}(-1)^{k}\binom{\alpha }{k}u^{l}_{i+k} )}{(\triangle x)^{\alpha }}, \\& \quad i=1,2,\ldots ,M-1. \end{aligned}$$
    (42)
  2. (ii)

    As \(\alpha =1\) and \(-1<\theta \leq 0\),

    $$\begin{aligned}& {}_{x}D^{\alpha }_{\theta }u(x_{i},t_{l}) \approx - \frac{\cos (\frac{\theta \pi }{2} ) (\sum^{i}_{k=1}\frac{u^{l}_{i-k}}{k(k+1)} +\sum^{M-i}_{k=1}\frac{u^{l}_{i+k}}{k(k+1)}-2u^{l}_{i} )}{\pi \triangle x}+ \sin \biggl(\frac{\theta \pi }{2} \biggr) \frac{u^{l}_{i}-u^{l}_{i-1}}{\triangle x}, \\& \quad i=1,2,\ldots ,M-1. \end{aligned}$$
    (43)
  3. (iii)

    As \(\alpha =1\) and \(0\leq \theta <1\),

    $$\begin{aligned}& {}_{x}D^{\alpha }_{\theta }u(x_{i},t_{l}) \approx - \frac{\cos (\frac{\theta \pi }{2} ) (\sum^{i}_{k=1}\frac{u^{l}_{i-k}}{k(k+1)} +\sum^{M-i}_{k=1}\frac{u^{l}_{i+k}}{k(k+1)}-2u^{l}_{i} )}{\pi \triangle x}+ \sin \biggl(\frac{\theta \pi }{2} \biggr) \frac{u^{l}_{i+1}-u^{l}_{i}}{\triangle x}, \\& \quad i=1,2,\ldots ,M-1. \end{aligned}$$
    (44)
  4. (iv)

    As \(1<\alpha <2\) and \(|\theta |\leq 2-\alpha \),

    $$\begin{aligned}& {}_{x}D^{\alpha }_{\theta }u(x_{i},t_{l}) \approx - \frac{ (c_{+}\sum^{i+1}_{k=0}(-1)^{k} \binom{\alpha }{k}u^{l}_{i+1-k} +c_{-}\sum^{M-i+1}_{k=0}(-1)^{k}\binom{\alpha }{k}u^{l}_{i-1+k} )}{(\triangle x)^{\alpha }}, \\& \quad i=1,2,\ldots ,M-1, \end{aligned}$$
    (45)

where \(c_{+}=\frac{\sin ((\alpha -\theta )\pi /2)}{\sin (\alpha \pi )}\), \(c_{-}=\frac{\sin ((\alpha +\theta )\pi /2)}{\sin (\alpha \pi )}\). Each case above combines with the boundary condition

$$ u^{l}_{0}=u^{l}_{M}=0,\quad l=1,2, \ldots ,L, $$
(46)

and the initial condition

$$ u^{0}_{i}=h(x_{i}),\quad i=0,1,2, \ldots ,M. $$
(47)

Thus, the final data is given by the initial condition

$$ g(x_{i})=u(x_{i},T)\approx u^{L}_{i},\quad i=0,1,2,\ldots ,M. $$
(48)

The measured data is chosen by the following random form:

$$ g^{\delta }(x)=g(x)+\varepsilon g(x) \bigl(2\operatorname{rand}\bigl(\operatorname{size}\bigl(g(x)\bigr)\bigr)-1\bigr), $$
(49)

with \(\delta =\varepsilon \|g\|\), here ε is the noisy level.

For the fixed \(0\leq t< T\), in order to make the sensitivity analysis for numerical results, we calculate the relative error defined by

$$ \epsilon (u)= \bigl\Vert u(x,t)-u^{\delta }_{\mu }(x,t) \bigr\Vert / \bigl\Vert u(x,t) \bigr\Vert . $$
(50)

In the computational procedure, we always take \(\triangle x=1/100\), \(\triangle t=1/10\text{,}000\), \(M=100\), \(L=10\text{,}000\), and \(\varepsilon =0.01\). The exact and regularized solutions are calculated by (13) and (23), respectively; the regularized parameter is chosen by a-posteriori rule (26) with \(h(\delta )=\delta +\delta ^{\frac{1-\gamma }{2}}\) (\(0<\gamma <1\)). We shall make a comparison for the computational results of regularized and exact solutions.

Example

In the direct problem (40), we take the initial distribution that satisfies \(h(x)\in L^{2}(R)\) with

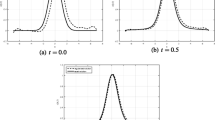
$$ h(x)= \textstyle\begin{cases} 2x+4, & -2\leq x\leq 0, \\ -2x+4, & 0\leq x\leq 2, \\ 0, &\text{others}. \end{cases} $$
(51)

Numerical results of exact and regularized solutions are shown in Figs. 1–3. For the fixed \(\alpha =0.5\), \(s=2\), \(\gamma =0.1\), \(\varepsilon =0.01\), Fig. 1 presents the numerical results for different θ at \(t=0.6\) and 0. Point line: exact solution; Star line: regularized solution with \(\theta =0\) and \(\mu =3.3433\mathrm{e}{-}04\); Loop line: regularized solution with \(\theta =0.01\) and \(\mu =3.3485\mathrm{e}{-}04\); Plus line: regularized solution with \(\theta =0.1\) and \(\mu =3.2330\mathrm{e}{-}04\); Diamond line: regularized solution with \(\theta =-0.01\) and \(\mu =3.3346\mathrm{e}{-}04\); Multiplication line: regularized solution with \(\theta =-0.1\) and \(\mu =3.0930\mathrm{e}{-}04\).

Figure 1
figure 1

At \(t=0.6\) and 0, \(\alpha=0.5\), \(s=2\), \(\gamma=0.1\), \(\varepsilon=0.01\): Exact and regularized solutions for different θ. Point: exact solution; Star line: regularized solution with \(\theta=0\) and \(\mu=3.3433\text{e}{-}04\); Loop: \(\theta=0.01\) and \(\mu=3.3485\text{e}{-}04\); Plus: \(\theta=0.1\) and \(\mu=3.2330\text{e}{-}04\); Diamond: \(\theta=-0.01\) and \(\mu=3.3346\text{e}{-}04\); Multiplication: \(\theta=-0.1\) and \(\mu=3.0930\text{e}{-}04\)

Full size image

For the fixed \(\alpha =1\), \(s=2\), \(\gamma =0.1\), \(\varepsilon =0.01\), Fig. 2 gives the numerical results for different θ at \(t=0.6\) and 0. Point line: exact solution; Star line: regularized solution with \(\theta =0\) and \(\mu =1.8960\mathrm{e}{-}04\); Loop line: regularized solution with \(\theta =0.01\) and \(\mu =1.9180\mathrm{e}{-}04\); Plus line: regularized solution with \(\theta =0.1\) and \(\mu =2.0983\mathrm{e}{-}04\); Diamond line: regularized solution with \(\theta =-0.01\) and \(\mu =1.9022\mathrm{e}{-}04\); Multiplication line: regularized solution with \(\theta =-0.1\) and \(\mu =1.9575\mathrm{e}{-}04\).

Figure 2
figure 2

At \(t=0.6\) and 0, \(\alpha=1\), \(s=2\), \(\gamma=0.1\), \(\varepsilon=0.01\): Exact and regularized solutions for different θ. Point: exact solution; Star: regularized solution with \(\theta=0\) and \(\mu=1.8960\text{e}{-}04\); Loop: \(\theta=0.01\) and \(\mu=1.9180\text{e}{-}04\); Plus: \(\theta=0.1\) and \(\mu=2.0983\text{e}{-}04\); Diamond: \(\theta=-0.01\) and \(\mu=1.9022\text{e}{-}04\); Multiplication: \(\theta=-0.1\) and \(\mu=1.9575\text{e}{-}04\)

Full size image

At \(t=0.6\) and 0, \(\alpha =1.5\), \(s=2\), \(\gamma =0.1\), \(\varepsilon =0.01\), numerical results for different θ are shown in Fig. 3. Point line: exact solution; Star line: regularized solution with \(\theta =0\) and \(\mu =2.8407\mathrm{e}{-}04\); Loop line: regularized solution with \(\theta =0.01\) and \(\mu =2.8439\mathrm{e}{-}04\); Plus line: regularized solution with \(\theta =0.1\) and \(\mu =2.9321\mathrm{e}{-}04\); Diamond line: regularized solution with \(\theta =-0.01\) and \(\mu =2.8389\mathrm{e}{-}04\); Multiplication line: regularized solution with \(\theta =-0.1\) and \(\mu =2.8831\mathrm{e}{-}04\).

Figure 3
figure 3

At \(t=0.6\) and 0, \(\alpha=1.5\), \(s=2\), \(\gamma=0.1\), \(\varepsilon=0.01\): Exact and regularized solutions for different θ. Point: exact solution; Star: regularized solution with \(\theta=0\) and \(\mu=2.8407\text{e}{-}04\); Loop: \(\theta=0.01\) and \(\mu=2.8439\text{e}{-}04\); Plus: \(\theta=0.1\) and \(\mu=2.9321\text{e}{-}04\); Diamond: \(\theta=-0.01\) and \(\mu=2.8389\text{e}{-}04\); Multiplication: \(\theta=-0.1\) and \(\mu=2.8831\text{e}{-}04\)

Full size image

Figures 1–3 show that the simulation effect of this method is feasible and acceptable in solving the considered problem. Meanwhile we can find that, for the fixed α, s, γ, ε, the numerical result becomes well as θ tends to zero.

At \(t=0\), we also investigate the influences of ε, α, s, and γ on the numerical result. For \(\alpha =1.5\), \(\theta =0\), \(s=2\), \(\gamma =0.2\), the relative errors for various ε are shown in Table 1. Table 1 shows that the better numerical result is the smaller ε becomes, this means the convergence of our method.

Table 1 At \(t=0\): \(\alpha=1.5\), \(\theta=0\), \(s=2\), \(\gamma=0.2\), the relative errors for various ε
Full size table

For \(\theta =0\), \(s=2\), \(\gamma =0.2\), \(\varepsilon =0.01\), the relative errors for various α are presented in Table 2. Table 2 indicates that the numerical procedure is stable to the fractional order α.

Table 2 At \(t=0\): \(\theta=0\), \(s=2\), \(\gamma=0.2\), \(\varepsilon=0.01\), the relative errors for various α
Full size table

For \(\alpha =1.5\), \(\theta =0\), \(\gamma =0.2\), \(\varepsilon =0.01\), the errors for various s are given in Table 3. Table 3 shows that the smaller s is taken, the better numerical results are. Meanwhile, as \(s=0\), our method becomes the simplified Tikhonov method, we find that, under the a-posteriori choice rule of regularization parameter, the calculated effect of our method is similar with the simplified Tikhonov method.

Table 3 At \(t=0\): \(\alpha=1.5\), \(\theta=0\), \(\gamma=0.2\), \(\varepsilon=0.01\), the relative errors for various s
Full size table

For \(\alpha =1.5\), \(\theta =0\), \(s=2\), \(\varepsilon =0.01\), the relative errors for various γ are shown in Table 4. From Table 4 we can note that the result becomes well as γ becomes small. Then, for the fixed α, θ, s, ε, in order to obtain the satisfied numerical result, γ should relatively be taken as a smaller positive number that belongs to the interval \((0,1)\).

Table 4 At \(t=0\): \(\alpha=1.5\), \(\theta=0\), \(s=2\), \(\varepsilon=0.01\), the relative errors for various γ
Full size table

5 Conclusions

A Riesz–Feller space-fractional backward diffusion problem is investigated. We firstly construct a generalized Tikhonov method to recover the continuous dependence of solution on the given final data. And then the convergence estimates of logarithmic and double logarithmic types for the regularized method are derived by adopting a-posteriori choice rules of regularization parameter. Finally, we verify the convergence and stability for the proposed method by making some numerical experiments.