1 Introduction

The soliton, which is one of the ubiquitous natural phenomena in daily life, has attracted much more attention due to its significant role in the physical and industrial applications like optical fibers [1], optical metamaterials [2, 3] and many others. Understanding the dynamics of soliton can lead to an extensive improvement in technology and industry. Therefore, a lot of intensive studies are devoted to the family of nonlinear Schrödinger (NLS) equation as it is the governing equation that describes the soliton propagation in many branches of science, e.g. nonlinear optics. Various powerful tools are developed to analyze the NLS models and to calculate their exact solutions. Such techniques include the extended trial function method [4], a modified simple equation method [5], the tanh–coth method [6, 7], the projective Riccati equations method [8], a new generalized exponential rational function method [9, 10], the Lie group method [11, 12], the Weierstrass elliptic function method [13], a new mapping method and a new auxiliary equation method [14].

The investigation of soliton pulse solutions with nonlinear chirping has become a fascinating research topic. The reason is that the chirped pulses can be valuable in many technical applications such as the design of fiber-optic amplifiers, optical pulse compressors and solitary wave-based communications links. Furthermore, the chirp is used in spread spectrum communications and some devices, e.g. sonar and radar. There are various studies that have been carried out to retrieve the chirped soliton solutions for different forms of NLS models in the presence of some effects like perturbations, the Kerr law or non-Kerr law nonlinearities and others. For more details, the reader is referred to Refs. [15–20].

Recently, many generalizations of the NLS equation were introduced depending on the physical situation. One interesting example is the Fokas–Lenells (FL) equation that appears in the area of nonlinear optical fibres. Since its first appearance nearly a decade ago [21], the model of the FL equation has been studied by some authors in the present time to obtain exact soliton solutions using several types of integration schemes. Among these approaches are the complex envelope function ansatz [22], the trial equation method [23], the extended trial function method [24], and the modified simple equation method [25]. Also we mention the three methods of the modified Kudryashov’s method, the \(\exp(-\psi(\eta))\)-expansion method, and the sine-Gordon expansion method [26]. Finally, we have the semi-inverse variational principle [27], the Riccati equation method [28], the generalized exponential function method [29], the mapping method [30], the modified extended direct algebraic method [31], and the Laplace–Adomian decomposition method [32].

This paper sheds light on the chirped soliton solutions of the FL equation. Perturbation terms of Hamiltonian type are present in the model with full nonlinearity. Thus, the FL equation proposed in this study takes the form

$$ iq_{t}+a_{1} q_{xx}+a_{2} q_{xt}+ \vert q \vert ^{2} (bq+i \sigma q_{x} )=i\bigl\{ \alpha q_{x}+\lambda\bigl( \vert q \vert ^{2n}q\bigr)_{x} +\mu\bigl( \vert q \vert ^{2n}\bigr)_{x} q \bigr\} , $$
(1)

where the dependent variable \(q(x, t)\) is a complex-valued function that denotes the soliton profile while the independent variables x and t indicate spatial and temporal variables. The first term in Eq. (1) stands for the temporal evolution. The terms \(a_{1}\) and \(a_{2}\) represent the coefficients of group velocity dispersion and spatio-temporal dispersion respectively. Then the fourth term accounts for the cubic nonlinearity and the fifth term refers to the nonlinear dispersion. The perturbation terms α, λ and μ on the right-hand side of Eq. (1) represent inter-modal dispersion, self-steepening effect, and nonlinear dispersion, respectively.

The authors in [23] investigated the chirped soliton solutions of the FL equation (1) in the absence of perturbation terms (i.e., \(\alpha=\lambda=\mu=0\)) whereas the studies in [24–32] were devoted to the chirp-free soliton solutions of Eq. (1). The present study concentrates thoroughly on the chirped optical solitons of Eq. (1) in the emergence of perturbation terms. The corresponding chirp is also retrieved for each of the optical pulses.

Now, we aim to deal with the model (1) via obtaining the traveling wave reduction. The paper is organized as follows. In the next section, we analyze the complex structure of Eq. (1) using the traveling wave hypothesis. In Sect. 3, the auxiliary equation method of two forms is applied to derive the chirped soliton solutions. Section 4 contains the graphical representations of some obtained soliton solutions. Our discussion and conclusion are presented in Sect. 5.

2 Mathematical analysis

To tackle the complex structure of Eq. (1), we use the traveling wave hypothesis of the form

$$ q(x,t)=u(\xi) e^{i(\phi(\xi)-\varOmega t)}, $$
(2)

where \(u(\xi)\) and \(\phi(\xi)\) are real functions of the traveling coordinate \(\xi=x-\nu t\). Here, ν is the group velocity while Ω is the frequency of the wave oscillation. The corresponding chirp is introduced by \(\delta\omega(x,t)=-\frac{\partial}{\partial x} [\phi(\xi)-\varOmega t ]=-\phi'(\xi)\).

Substituting the transformation (2) into Eq. (1), we obtain a system of equations for real and imaginary parts given as

$$\begin{aligned}& \begin{aligned}[b] &-(\alpha+\nu+a_{2} \varOmega)u' + 2(a_{1}-a_{2}\nu)u' \phi' + (a_{1}-a_{2}\nu )u \phi''\\&\quad+ \sigma u^{2}u' - \bigl((2n+1)\lambda+2n\mu \bigr)u^{2n} u'=0,\end{aligned} \end{aligned}$$
(3)
$$\begin{aligned}& \begin{aligned}[b]&(\alpha+\nu+a_{2} \varOmega)u \phi'+ \varOmega u+(a_{1}-a_{2}\nu)u'' - (a_{1}-a_{2}\nu)u \phi^{\prime2} \\&\quad+ b u^{3} -\sigma u^{3} \phi' + \lambda u^{2n+1}\phi'= 0,\end{aligned} \end{aligned}$$
(4)

where a prime denotes the derivative with respect to ξ. Equation (3) can be integrated after multiplying on u to induce

$$ \phi'=\frac{\alpha+\nu+a_{2} \varOmega}{2(a_{1}-a_{2}\nu)} - \frac{\sigma u^{2}}{4(a_{1}-a_{2}\nu)} + \frac{((2n+1)\lambda+2n\mu) u^{2n}}{(a_{1}-a_{2}\nu)(2n+2)}, $$
(5)

where the integration constant is taken to be zero. To ensure a closed form solution for the proposed model, we set \(n=1\). Thus, Eq. (5) reduces to

$$ \phi'= \frac{(\alpha+\nu+a_{2} \varOmega)}{2(a_{1}-a_{2}\nu)} + \frac {(3\lambda+2\mu-\sigma)u^{2}}{4(a_{1}-a_{2}\nu)}. $$
(6)

Accordingly, the resultant chirp can be addressed as

$$ \delta\omega(x,t)= -\frac{(\alpha+\nu+a_{2} \varOmega)}{2(a_{1}-a_{2}\nu )} - \frac{(3\lambda+2\mu-\sigma)u^{2}}{4(a_{1}-a_{2}\nu)} . $$
(7)

Now, substituting Eq. (6) into Eq. (4) leads to

$$ u''+\frac{c_{2}}{4}u+\frac{c_{4}}{2}u^{3}+ \frac{c_{6}}{16} u^{5}=0, $$
(8)

where

$$\begin{aligned}& c_{2}=\frac{(\alpha+\nu+a_{2} \varOmega)^{2}+4 \varOmega(a_{1}-a_{2}\nu )}{(a_{1}-a_{2}\nu)^{2}}, \end{aligned}$$
(9)
$$\begin{aligned}& c_{4}=\frac{(\lambda-\sigma)(\alpha+\nu+a_{2} \varOmega)+2b(a_{1}-a_{2}\nu )}{(a_{1}-a_{2}\nu)^{2}}, \end{aligned}$$
(10)
$$\begin{aligned}& c_{6}=\frac{(3\lambda+2\mu-\sigma)(\lambda-2\mu-3\sigma) }{(a_{1}-a_{2}\nu)^{2}}. \end{aligned}$$
(11)

Multiplying both sides of Eq. (8) by \(u'\) and integrating with respect to ξ, yields

$$ u^{\prime2}+2 c_{0}+\frac{c_{2}}{4}u^{2}+ \frac{c_{4}}{4}u^{4}+\frac{c_{6}}{48}u^{6}=0, $$
(12)

where \(c_{0}\) is the constant of integration.

It is worth to mention that Eq. (12) can be written in the integral form

$$ \pm(\xi-\xi_{0})= \int\frac{1}{\sqrt{-(2 c_{0}+\frac{c_{2}}{4}u^{2}+\frac {c_{4}}{4}u^{4}+\frac{c_{6}}{48}u^{6})}}\,\mathrm {d}u. $$
(13)

Taking the constant of integration to be zero, i.e. \(c_{0}=0\), Eq. (13) is reduced to the following form:

$$ \pm(\xi-\xi_{0})= \int\frac{1}{u\sqrt{-(\frac{c_{2}}{4}+\frac {c_{4}}{4}u^{2}+\frac{c_{6}}{48}u^{4})}}\,\mathrm {d}u. $$
(14)

According to Yomba [33], one can obtain different types of soliton solutions including bright, dark, and singular solitons.

3 Chirped soliton solutions

In this section, we demonstrate the exact analytic chirped soliton solutions of Eq. (1) with the existing conditions. Equation (12) can be written in the structure of a first-order nonlinear ODE of the form

$$ u^{\prime2}=l_{0} + l_{2}u^{2} + l_{4} u^{4} + l_{6} u^{6}=0, $$
(15)

or

$$ u^{\prime2}=r_{0} + r_{2}u^{2} + \frac{1}{2}r_{4} u^{4} + \frac{1}{3}r_{6} u^{6}=0, $$
(16)

where \(l_{i}\) and \(r_{i}\) (\(i=0, 2, 4, 6\)) are constants to be determined. It is well known that Eqs. (15) and (16) admit various types of solutions. Equation (15) has solutions in the form

$$ u(\xi)=\frac{1}{2} \biggl[-\frac{l_{4}}{l_{6}} \bigl(1\pm f(\xi) \bigr) \biggr]^{\frac{1}{2}}, $$
(17)

where the function \(f(\xi)\) can be expressed through the Jacobi elliptic functions [34] while Eq. (16) has a variety of solutions in terms of trigonometric and hyperbolic functions [35].

In what follows, the solutions of Eq. (12) will be extracted and then substituted into the relations (2) and (7) to display different forms of chirped soliton solutions and their associated chirping to Eq. (1). Comparing the coefficients of \(u^{j}\) (\(j=0, 2, 4, 6\)) in Eqs. (15) and (16) as given in [34, 35] to their corresponding in Eq. (12), the following cases of values for the constants \(c_{i}\) (\(i=0, 2, 4, 6\)) will be derived.

Case I. If \(c_{0}=\frac{9 c_{4}^{3} (m^{2}-1)}{16 c_{6}^{2} m^{2}}\), \(c_{2}=\frac{3 c_{4}^{2} (5m^{2}-1)}{4 c_{6} m^{2}}\), then one can find the Jacobi elliptic function solutions of Eq. (1) as

$$\begin{aligned}& q(x, t)= \sqrt{ -\frac{3 c_{4}}{c_{6}} \biggl(1\pm \operatorname {sn}\biggl(- \frac {c_{4}}{2m}\sqrt{-\frac{3}{c_{6}}}\xi \biggr) \biggr)} e^{i(\phi(\xi )-\varOmega t)}, \end{aligned}$$
(18)
$$\begin{aligned}& q(x, t)= \sqrt{ -\frac{3 c_{4}}{c_{6}} \biggl(1\pm\frac{1}{m} \operatorname {ns}\biggl(-\frac{c_{4}}{2m}\sqrt{-\frac{3}{c_{6}}}\xi \biggr) \biggr) } e^{i(\phi(\xi)-\varOmega t)}, \end{aligned}$$
(19)

where \(c_{4}>0\), \(c_{6}<0\) and \(0< m<1\) is the modulus of the Jacobi elliptic functions. As \(m\rightarrow1\), solution (18) reduces to the following chirped kink and anti-kink soliton solutions:

$$ q(x, t)= \sqrt{ -\frac{3 c_{4}}{c_{6}} \biggl(1\pm\tanh \biggl(- \frac {c_{4}}{2}\sqrt{-\frac{3}{c_{6}}}\xi \biggr) \biggr) } e^{i(\phi(\xi )-\varOmega t)}, $$
(20)

and solution (19) degenerates to a chirped singular soliton solutions in the form

$$ q(x, t)= \sqrt{ -\frac{3 c_{4}}{c_{6}} \biggl(1\pm\coth \biggl(- \frac {c_{4}}{2}\sqrt{-\frac{3}{c_{6}}}\xi \biggr) \biggr) } e^{i(\phi(\xi )-\varOmega t)}. $$
(21)

The corresponding chirping are expressed, respectively, by

$$\begin{aligned}& \delta\omega(x,t)= -\frac{(\alpha+\nu+a_{2} \varOmega)}{2(a_{1}-a_{2}\nu )} + \frac{ 3 c_{4} (3\lambda+2\mu-\sigma)}{4 c_{6} (a_{1}-a_{2}\nu)} \biggl[1\pm \tanh \biggl(-\frac{c_{4}}{2}\sqrt{-\frac{3}{c_{6}}}\xi \biggr) \biggr], \end{aligned}$$
(22)
$$\begin{aligned}& \delta\omega(x,t)= -\frac{(\alpha+\nu+a_{2} \varOmega)}{2(a_{1}-a_{2}\nu )} + \frac{ 3 c_{4} (3\lambda+2\mu-\sigma)}{4 c_{6} (a_{1}-a_{2}\nu)} \biggl[1\pm \coth \biggl(-\frac{c_{4}}{2}\sqrt{-\frac{3}{c_{6}}}\xi \biggr) \biggr]. \end{aligned}$$
(23)

Case II. If \(c_{0}=\frac{9 c_{4}^{3}}{16 c_{6}^{2} m^{2}}\), \(c_{2}=\frac{3 c_{4}^{2} (4m^{2}+1)}{4 c_{6} m^{2}}\), then this results in the Jacobi elliptic function solutions of Eq. (1) as

$$ q(x, t)= \sqrt{ -\frac{3 c_{4}}{c_{6}} \biggl(1\pm \operatorname {cn}\biggl( \frac {c_{4}}{2m}\sqrt{\frac{3}{c_{6}}}\xi \biggr) \biggr)} e^{i(\phi(\xi )-\varOmega t)}, $$
(24)

where \(c_{4}<0\), \(c_{6}>0\). As \(m\rightarrow1\), solution (24) reduces to the following chirped bright soliton solutions:

$$ q(x, t)= \sqrt{ -\frac{3 c_{4}}{c_{6}} \biggl(1\pm \operatorname {sech}\biggl( \frac {c_{4}}{2}\sqrt{\frac{3}{c_{6}}}\xi \biggr) \biggr)} e^{i(\phi(\xi )-\varOmega t)}, $$
(25)

and the chirp is given by

$$ \delta\omega(x,t)= -\frac{(\alpha+\nu+a_{2} \varOmega)}{2(a_{1}-a_{2}\nu )} + \frac{ 3 c_{4} (3\lambda+2\mu-\sigma)}{4 c_{6} (a_{1}-a_{2}\nu)} \biggl[1\pm \operatorname {sech}\biggl(\frac{c_{4}}{2}\sqrt{\frac{3}{c_{6}}}\xi \biggr) \biggr]. $$
(26)

Case III. If \(c_{0}=\frac{c_{4}^{3}}{3 c_{6}^{2}}\), \(c_{2}=\frac{3 c_{4}^{2}}{c_{6}}\), then this gives rise to the chirped dark soliton solution of Eq. (1) as

$$ q(x, t)=2 \sqrt{-\frac{2 c_{4} \tanh^{2} (\frac{\epsilon}{2}\sqrt {-\frac{c_{4}^{2}}{c_{6}}}\xi ) }{c_{6} (3+\tanh^{2} (\frac {\epsilon}{2}\sqrt{-\frac{c_{4}^{2}}{c_{6}}}\xi ) )}} e^{i(\phi(\xi)-\varOmega t)}, $$
(27)

and the chirped bright soliton solution of the form

$$ q(x, t)=2 \sqrt{-\frac{2 c_{4} \coth^{2} (\frac{\epsilon}{2}\sqrt {-\frac{c_{4}^{2}}{c_{6}}}\xi ) }{c_{6} (3+\coth^{2} (\frac {\epsilon}{2}\sqrt{-\frac{c_{4}^{2}}{c_{6}}}\xi ) )}} e^{i(\phi(\xi)-\varOmega t)}, $$
(28)

where \(c_{4}>0\), \(c_{6}<0\). The corresponding chirpings are given, respectively, by

$$\begin{aligned}& \delta\omega(x,t)=-\frac{(\alpha+\nu+a_{2} \varOmega)}{2(a_{1}-a_{2}\nu)} + \frac{ 2 c_{4} (3\lambda+2\mu-\sigma)\tanh^{2} (\frac{\epsilon }{2}\sqrt{-\frac{c_{4}^{2}}{c_{6}}}\xi ) }{c_{6} (a_{1}-a_{2}\nu) (3+\tanh^{2} (\frac{\epsilon}{2}\sqrt{-\frac{c_{4}^{2}}{c_{6}}}\xi ) )}, \end{aligned}$$
(29)
$$\begin{aligned}& \delta\omega(x,t)=-\frac{(\alpha+\nu+a_{2} \varOmega)}{2(a_{1}-a_{2}\nu)} + \frac{ 2 c_{4} (3\lambda+2\mu-\sigma)\coth^{2} (\frac{\epsilon }{2}\sqrt{-\frac{c_{4}^{2}}{c_{6}}}\xi ) }{c_{6} (a_{1}-a_{2}\nu) (3+\coth^{2} (\frac{\epsilon}{2}\sqrt{-\frac{c_{4}^{2}}{c_{6}}}\xi ) )} . \end{aligned}$$
(30)

Case IV. If \(c_{0}=0\), \(c_{2}=\frac{3 c_{4}^{2}}{c_{6}}\), then one can reach the chirped kink soliton solution of the form

$$ q(x, t)=\sqrt{-\frac{3 c_{4}}{c_{6}} \biggl(1+ \tanh \biggl( \frac {\epsilon}{2}\sqrt{-\frac{3c_{4}^{2}}{c_{6}}}\xi \biggr) \biggr)} e^{i(\phi(\xi)-\varOmega t)}, $$
(31)

and the chirped singular soliton solution

$$ q(x, t)=\sqrt{-\frac{3 c_{4}}{c_{6}} \biggl(1+ \coth \biggl( \frac {\epsilon}{2}\sqrt{-\frac{3c_{4}^{2}}{c_{6}}}\xi \biggr) \biggr)} e^{i(\phi(\xi)-\varOmega t)}, $$
(32)

where \(c_{4}>0\), \(c_{6}<0\). The corresponding chirping are given, respectively, by

$$\begin{aligned}& \delta\omega(x,t)=-\frac{(\alpha+\nu+a_{2} \varOmega)}{2(a_{1}-a_{2}\nu)} + \frac{ 3 c_{4} (3\lambda+2\mu-\sigma) (1+ \tanh (\frac {\epsilon}{2}\sqrt{-\frac{3c_{4}^{2}}{c_{6}}}\xi ) ) }{4 c_{6} (a_{1}-a_{2}\nu) } , \end{aligned}$$
(33)
$$\begin{aligned}& \delta\omega(x,t)=-\frac{(\alpha+\nu+a_{2} \varOmega)}{2(a_{1}-a_{2}\nu)} + \frac{ 3 c_{4} (3\lambda+2\mu-\sigma) (1+ \coth (\frac {\epsilon}{2}\sqrt{-\frac{3c_{4}^{2}}{c_{6}}}\xi ) ) }{4 c_{6} (a_{1}-a_{2}\nu) } . \end{aligned}$$
(34)

Case V. If \(c_{0}=0\), then this leads to the chirped soliton solutions of Eq. (1) as

$$\begin{aligned}& q(x, t)=2 \sqrt{-\frac{3 c_{2} c_{4} \operatorname {sech}^{2} (\frac{\sqrt {-c_{2}}}{2}\xi ) }{12c_{4}^{2} - c_{2} c_{6} (1+\epsilon\tanh (\frac{\sqrt{-c_{2}}}{2}\xi ) )^{2}}} e^{i(\phi(\xi )-\varOmega t)}, \end{aligned}$$
(35)
$$\begin{aligned}& q(x, t)=2 \sqrt{\frac{3 c_{2} c_{4} \operatorname {csch}^{2} (\frac{\sqrt {-c_{2}}}{2}\xi ) }{12c_{4}^{2} - c_{2} c_{6} (1+\epsilon\coth (\frac{\sqrt{-c_{2}}}{2}\xi ) )^{2}}} e^{i(\phi(\xi )-\varOmega t)}, \end{aligned}$$
(36)
$$\begin{aligned}& q(x, t)=\sqrt{-\frac{3 c_{2} \operatorname {sech}^{2} (\frac{\sqrt{-c_{2}}}{2}\xi ) }{3c_{4} - \epsilon\sqrt{3c_{2} c_{6}} \tanh (\frac{\sqrt {-c_{2}}}{2}\xi )}} e^{i(\phi(\xi)-\varOmega t)}, \end{aligned}$$
(37)
$$\begin{aligned}& q(x, t)= \sqrt{\frac{3 c_{2} \operatorname {csch}^{2} (\frac{\sqrt{-c_{2}}}{2}\xi ) }{3c_{4} - \epsilon\sqrt{3c_{2} c_{6}} \coth (\frac{\sqrt {-c_{2}}}{2}\xi )}} e^{i(\phi(\xi)-\varOmega t)}, \end{aligned}$$
(38)

where \(c_{6}<0\) in solutions (37) and (38).

$$\begin{aligned}& q(x, t)=\sqrt{- \frac{6 c_{2} \operatorname {sech}^{2} (\frac{\epsilon\sqrt {-c_{2}}}{2}\xi ) }{4\sqrt{M} - (2\sqrt{M}-3c_{4}) \operatorname {sech}^{2} (\frac{\epsilon\sqrt{-c_{2}}}{2}\xi )} } e^{i(\phi(\xi )-\varOmega t)}, \end{aligned}$$
(39)
$$\begin{aligned}& q(x, t)=\sqrt{- \frac{6 c_{2} \operatorname {csch}^{2} (\frac{\epsilon\sqrt {-c_{2}}}{2}\xi ) }{4\sqrt{M} + (2\sqrt{M}+3c_{4}) \operatorname {csch}^{2} (\frac{\epsilon\sqrt{-c_{2}}}{2}\xi )}} e^{i(\phi(\xi)-\varOmega t)}, \end{aligned}$$
(40)
$$\begin{aligned}& q(x, t)=\sqrt{- \frac{6 c_{2} }{2\epsilon\sqrt{M} \cosh (\sqrt {-c_{2}}\xi )+3 c_{4}} } e^{i(\phi(\xi)-\varOmega t)}, \end{aligned}$$
(41)

where \(M>0\).

$$ q(x, t)=\sqrt{- \frac{6 c_{2}}{2\epsilon\sqrt{-M} \sinh (\sqrt {-c_{2}}\xi ) + 3c_{4}} } e^{i(\phi(\xi)-\varOmega t)}, $$
(42)

where \(M<0\). Solutions (39) and (41) represent bright solitons while solutions (40) and (42) are singular solitons. In this case, \(M=\frac{3}{4}(3c_{4}^{2}-c_{2} c_{6})\), \(\epsilon=\pm1\) and \(c_{2}<0 \). The associated chirp can be written, respectively, as

$$\begin{aligned}& \delta\omega(x,t)=-\frac{(\alpha+\nu+a_{2} \varOmega)}{2(a_{1}-a_{2}\nu)} + \frac{ 3 c_{2} c_{4} (3\lambda+2\mu-\sigma)\operatorname {sech}^{2} (\frac {\sqrt{-c_{2}}}{2}\xi ) }{(a_{1}-a_{2}\nu) [12c_{4}^{2} - c_{2} c_{6} (1+\epsilon\tanh (\frac{\sqrt{-c_{2}}}{2}\xi ) )^{2} ]}, \end{aligned}$$
(43)
$$\begin{aligned}& \delta\omega(x,t)=-\frac{(\alpha+\nu+a_{2} \varOmega)}{2(a_{1}-a_{2}\nu)} - \frac{ 3 c_{2} c_{4} (3\lambda+2\mu-\sigma)\operatorname {csch}^{2} (\frac {\sqrt{-c_{2}}}{2}\xi ) }{(a_{1}-a_{2}\nu) [12c_{4}^{2} - c_{2} c_{6} (1+\epsilon\coth (\frac{\sqrt{-c_{2}}}{2}\xi ) )^{2} ]}, \end{aligned}$$
(44)
$$\begin{aligned}& \delta\omega(x,t)=-\frac{(\alpha+\nu+a_{2} \varOmega)}{2(a_{1}-a_{2}\nu)} + \frac{ 3 c_{2} (3\lambda+2\mu-\sigma)\operatorname {sech}^{2} (\frac{\sqrt {-c_{2}}}{2}\xi ) }{4(a_{1}-a_{2}\nu) [3c_{4} - \epsilon\sqrt {3c_{2} c_{6}} \tanh (\frac{\sqrt{-c_{2}}}{2}\xi ) ]}, \end{aligned}$$
(45)
$$\begin{aligned}& \delta\omega(x,t)=-\frac{(\alpha+\nu+a_{2} \varOmega)}{2(a_{1}-a_{2}\nu)} - \frac{ 3 c_{2} (3\lambda+2\mu-\sigma)\operatorname {csch}^{2} (\frac{\sqrt {-c_{2}}}{2}\xi ) }{4(a_{1}-a_{2}\nu) [3c_{4} - \epsilon\sqrt {3c_{2} c_{6}} \coth (\frac{\sqrt{-c_{2}}}{2}\xi ) ]}, \end{aligned}$$
(46)
$$\begin{aligned}& \delta\omega(x,t)=-\frac{(\alpha+\nu+a_{2} \varOmega)}{2(a_{1}-a_{2}\nu)} + \frac{ 3 c_{2} (3\lambda+2\mu-\sigma)\operatorname {sech}^{2} (\frac{\epsilon \sqrt{-c_{2}}}{2}\xi ) }{2(a_{1}-a_{2}\nu) [4\sqrt{M} - (2\sqrt{M}-3c_{4}) \operatorname {sech}^{2} (\frac{\epsilon\sqrt{-c_{2}}}{2}\xi ) ]}, \end{aligned}$$
(47)
$$\begin{aligned}& \delta\omega(x,t)=-\frac{(\alpha+\nu+a_{2} \varOmega)}{2(a_{1}-a_{2}\nu)} + \frac{ 3 c_{2} (3\lambda+2\mu-\sigma)\operatorname {csch}^{2} (\frac{\epsilon \sqrt{-c_{2}}}{2}\xi ) }{2(a_{1}-a_{2}\nu) [4\sqrt{M} + (2\sqrt{M}+3c_{4}) \operatorname {csch}^{2} (\frac{\epsilon\sqrt{-c_{2}}}{2}\xi ) ]}, \end{aligned}$$
(48)
$$\begin{aligned}& \delta\omega(x,t)=-\frac{(\alpha+\nu+a_{2} \varOmega)}{2(a_{1}-a_{2}\nu)} + \frac{ 3 c_{2} (3\lambda+2\mu-\sigma)}{2(a_{1}-a_{2}\nu) [2\epsilon\sqrt{M} \cosh (\sqrt{-c_{2}}\xi )+3 c_{4} ]}, \end{aligned}$$
(49)
$$\begin{aligned}& \delta\omega(x,t)=-\frac{(\alpha+\nu+a_{2} \varOmega)}{2(a_{1}-a_{2}\nu)} + \frac{ 3 c_{2} (3\lambda+2\mu-\sigma)}{2(a_{1}-a_{2}\nu) [2\epsilon\sqrt{-M} \sinh (\sqrt{-c_{2}}\xi ) + 3c_{4} ]}. \end{aligned}$$
(50)

4 Graphical interpretation

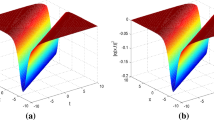
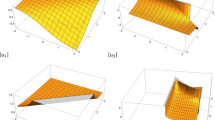
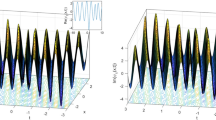
The chirped soliton solutions of the FL equation (1) are described graphically. Some of the obtained solutions are depicted by selecting different values of parameters to understand the physical meaning. In each figure, we display the 3D plot of the modulus and real part of optical solitons as well as the 2D plot of their corresponding chirp. For example, the plots of the modulus of chirped dark soliton solution (20) and the chirped singular soliton solution (21) are represented with different values of parameters in Figs. 1(a) and 2(a), respectively, where \(a_{1}=4\), \(a_{2}=1\), \(b=2\), \(\alpha=2\), \(\lambda=6\), \(\mu=1\), \(\nu=1\), \(\sigma=2\), \(\varOmega=3\). The real part and associated chirp of solutions (20) and (21) are illustrated in Figs. 1(b)–(c) and 2(b)–(c), respectively. Figure 3(a) demonstrates the plot of the modulus of chirped bright soliton solution (25) whereas the real part and corresponding chirping of solution (25) are shown in Fig. 3(b)–(c). We describe the modulus of chirped dark soliton solution (27) in Fig. 4(a). Its real part and corresponding chirping are presented in Fig. 4(b)–(c). The modulus of chirped bright soliton solution (28) is depicted in Fig. 5(a) while the real part and associated chirp of solution (28) are plotted in Fig. 5(b)–(c). Using different values of parameters, the modulus of chirped bright soliton solution (41) is shown in Fig. 6(a) and, its real part and corresponding chirping are presented in Fig. 6(b)–(c), where \(a_{1}=3\), \(a_{2}=-4\), \(b=2\), \(\alpha=-6\), \(\lambda=6\), \(\mu=1\), \(\nu=1\), \(\sigma=2\), \(\varOmega=-2\). Figure 7(a) displays the modulus of another type of chirped singular soliton given by (42). The real part and associated chirp of solution (42) are illustrated in Fig. 7(b)–(c).

Figure 1
figure 1

Chirped kink soliton solution (20) with \(a_{1}=4\), \(a_{2}=1\), \(b=2\), \(\alpha=2\), \(\lambda=6\), \(\mu=1\), \(\nu=1\), \(\sigma=2\), \(\varOmega=3\). (a) Modulus. (b) Real part. (c) Corresponding chirp

Full size image
Figure 2
figure 2

Chirped singular soliton solution (21) with \(a_{1}=4\), \(a_{2}=1\), \(b=2\), \(\alpha=2\), \(\lambda=6\), \(\mu=1\), \(\nu=1\), \(\sigma=2\), \(\varOmega=3\). (a) Modulus. (b) Real part. (c) Corresponding chirp

Full size image
Figure 3
figure 3

Chirped bright soliton solution (25) with \(a_{1}=2\), \(a_{2}=4\), \(b=2\), \(\alpha=2\), \(\lambda=6\), \(\mu=1\), \(\nu=1\), \(\sigma=1\), \(\varOmega=-3\). (a) Modulus. (b) Real part. (c) Corresponding chirp

Full size image
Figure 4
figure 4

Chirped dark soliton solution (27) with \(a_{1}=4\), \(a_{2}=1\), \(b=2\), \(\alpha=2\), \(\lambda=6\), \(\mu=1\), \(\nu=1\), \(\sigma=2\), \(\varOmega=3\). (a) Modulus. (b) Real part. (c) Corresponding chirp

Full size image
Figure 5
figure 5

Chirped bright soliton solution (28) with \(a_{1}=4\), \(a_{2}=1\), \(b=2\), \(\alpha=2\), \(\lambda=6\), \(\mu=1\), \(\nu=1\), \(\sigma=2\), \(\varOmega=3\). (a) Modulus. (b) Real part. (c) Corresponding chirp

Full size image
Figure 6
figure 6

Chirped bright soliton solution (41) with \(a_{1}=3\), \(a_{2}=-4\), \(b=2\), \(\alpha=-6\), \(\lambda=6\), \(\mu=1\), \(\nu=1\), \(\sigma=2\), \(\varOmega=-2\). (a) Modulus. (b) Real part. (c) Corresponding chirp

Full size image
Figure 7
figure 7

Chirped singular soliton solution (42) with \(a_{1}=4\), \(a_{2}=1\), \(b=2\), \(\alpha=2\), \(\lambda=6\), \(\mu=1\), \(\nu=1\), \(\sigma=2\), \(\varOmega=3\). (a) Modulus. (b) Real part. (c) Corresponding chirp

Full size image

5 Discussion and conclusion

Herein our target is to compare the results obtained here with corresponding results of some previous studies in the literature (e.g., [22–31]). The authors in [22, 23], for instance, utilized the trial equation method and the complex envelope function ansatz to examine the combined solitary wave and chirped soliton solutions of the FL equation (1) when perturbation terms are neglected (i.e., \(\alpha=\lambda=\mu=0\)). The studies in [24–31] implemented various types of methods and extracted different forms of exact solutions to Eq. (1), where the chirp-free soliton solutions are retrieved. In the present work we have investigated the chirped soliton solutions of the FL equation (1) by applying the auxiliary equation method with two forms. In addition to this, the associated chirp for each of the optical solitons is derived. We deduce from these discussions that the obtained chirped soliton solutions are new and the analysis in our paper is more general than the analysis in [22–31].

The current study discussed the chirped soliton solutions of the FL equation in the presence of Hamiltonian perturbation terms. The complex envelope traveling-wave hypothesis is invoked to reduce the governing model to an ODE. The resultant ODE is a first-order nonlinear ODE with six-degree terms. Hence, it is handled analytically using the auxiliary equation method with two structures. As a result, different types of chirped soliton solutions including bright, dark, kink and singular solitons are derived. Additionally, a set of combo optical soliton solutions are obtained as well. The associated chirp is also induced for each of these optical solitons. The graphical representations for some obtained chirped solitons are also exhibited by selecting suitable values of parameters.