1 Introduction

Investigation of explicit solutions for nonlinear evolution equations (NLEEs) is very important to understand complex nonlinear phenomena in plasma physics, nonlinear optics, fluid mechanics, and other scientific fields [1–4]. So far many techniques for constructing explicit solutions for NLEEs, such as the inverse scattering transformation [5], the bilinear method [6], Darboux transformation [7–10], Bäcklund transformation [11, 12], and the Lie group method [13, 14], have been developed. Among them, the bilinear method proposed by Hirota is an effective tool for solving NLEEs [6]. Based on the bilinear form, the N-soliton solutions for the NLEE can be obtained through algebraic procedure, and the N-soliton solutions are usually expressed in the Grammian or Wronskian determinant form [6, 15–17]. One of the advantages of deriving solutions in determinant form is that not only soliton solutions but also many other types of solutions, such as complexiton solutions [18, 19], rogue waves [20–24], lumps [25], and semi-rational solutions [26–30], can be derived. Another advantage is that one can get solutions of any order based on determinant solutions, and the expression of the solutions is very simple [6, 15–30]. Therefore, it is of great significance to construct solutions in terms of determinant for NLEEs. Recently, the interactions of various kind of nonlinear waves that are governed by many NLEEs have been studied [3, 4, 15–17, 26–31]. The soliton interactions are usually considered to be elastic for many integrable NLEEs, but the soliton interactions for certain NLEEs are found to be inelastic [15–17, 31]. Many novel interactions of fusion and fission of solitons and other kinds of nonlinear waves have also been investigated [3, 4, 26–30]. In this paper, we investigate the Grammian determinant solutions and the interactions of the obtained nonlinear waves for the following Bogoyavlenskii–Kadomtsev–Petviashvili (BKP) equation [32, 33]:

$$\begin{aligned} (4u_{xt}+u_{xxxy}+8u_{x}u_{xy}+4u_{xx}u_{y})_{x}+ \delta u_{yyy}=0,\quad \delta =\pm 1. \end{aligned}$$
(1.1)

BKP equation (1.1) is a modified version of the Calogero–Bogoyavlenskii–Schiff equation [34, 35]

$$\begin{aligned} 4u_{xt}+u_{xxxy}+8u_{x}u_{xy}+4u_{xx}u_{y}=0. \end{aligned}$$
(1.2)

Eq. (1.1) can also be regarded as a modification of the KP equation, which has various physical settings in nonlinear optics, Bose–Einstein condensate, and plasmas [36–38]. As in the case of the KP equation, BKP equation (1.1) is classified as the BKP-I equation when \(\delta =-1\) and the BKP-II equation when \(\delta =1\) [32, 33]. The Lax pairs, Darboux transformations, and explicit solutions for the BKP-II and BKP-I equations are constructed by using the singular manifold method respectively [32, 33]. In [39], soliton and periodic solutions for the BKP-II equation are derived by applying an extended tanh method. With symbolic computation, solitary wave and multi-front wave collisions for the BKP-II equation are investigated [40]. Through the Bell polynomials, soliton solutions, Bäcklund transformation, Lax pair, and conservation laws for the BKP-II equation are derived [41]. The nonlocal symmetry, Bäcklund transformation, and consistent Riccati expansion solvability for the BKP equation are obtained in [42]. Several bilinear forms, bilinear Bäcklund transformations, kink periodic solitary wave, and lump wave solutions for the BKP equation are presented by employing the binary Bell polynomials [43]. However, to the best of our knowledge, Grammian solutions for BKP equation (1.1) and their dynamics have not been reported.

It is easy to see that BKP equation (1.1) can be rewritten in the following form by employing the scaling transformation \(t\rightarrow \frac{1}{4}t\):

$$\begin{aligned} (u_{xt}+u_{xxxy}+8u_{x}u_{xy}+4u_{xx}u_{y})_{x}+ \delta u_{yyy}=0,\quad \delta =\pm 1. \end{aligned}$$
(1.3)

Through the dependent variable transformation

$$\begin{aligned} u=(\ln f)_{x}, \end{aligned}$$
(1.4)

Equation (1.3) can be transformed into the bilinear form

$$\begin{aligned} &\biggl(\frac{1}{3}D_{x}^{4}-\alpha D_{x}D_{s}+\delta D_{y}^{2}\biggr)f \cdot f=0, \end{aligned}$$
(1.5a)
$$\begin{aligned} &\biggl(\frac{2}{3}D_{x}^{3}D_{y}+D_{x}D_{t}+ \alpha D_{y}D_{s}\biggr)f\cdot f=0, \end{aligned}$$
(1.5b)

where α is an arbitrary constant, s is an auxiliary independent variable, \(D_{x},D_{y},D_{s}\), and \(D_{t}\) are the Hirota bilinear operators defined by [6]

$$\begin{aligned} D_{x}^{n_{1}}D_{y}^{n_{2}}D_{s}^{n_{3}}D_{t}^{n_{4}}(G \cdot F)={}&\biggl( \frac{\partial }{\partial x}-\frac{\partial }{\partial x'}\biggr)^{n_{1}}\biggl( \frac{\partial }{\partial y}-\frac{\partial }{\partial y'}\biggr)^{n_{2}}\biggl( \frac{\partial }{\partial s}-\frac{\partial }{\partial s'}\biggr)^{n_{3}}\biggl( \frac{\partial }{\partial t}-\frac{\partial }{\partial t'}\biggr)^{n_{4}} \\ & {} G(x,y,s,t)F\bigl(x',y',s',t' \bigr)\bigg|_{x'=x, y'=y,s'=s,t'=t}. \end{aligned}$$

The aim of the paper is to derive Grammian determinant solutions for the BKP equation by using the KP hierarchy reduction method which was first proposed by the Kyoto school [44]. The plan of this paper is as follows. In Sect. 2, soliton solutions in the Grammian determinant form for the BKP-II equation are constructed and soliton collisions are demonstrated graphically. In Sect. 3, lump-soliton solutions in the Grammian form for the BKP-I equation are obtained. In Sect. 4, the structures and the dynamics of the lump-soliton solutions for the BKP-I equation are discussed through graphs. Finally, some conclusions are given in Sect. 5.

2 Soliton solutions for the BKP-II equation in the Grammian determinant form

In this section, we derive Grammian determinant solutions for the BKP-II equation

$$\begin{aligned} (u_{xt}+u_{xxxy}+8u_{x}u_{xy}+4u_{xx}u_{y})_{x}+u_{yyy}=0. \end{aligned}$$
(2.1)

The main idea is to get solutions for Eq. (2.1) from the Grammian determinant solutions of the KP hierarchy under the reduction of the KP hierarchy. For this purpose, we first characterize the following result on the KP hierarchy [45].

Lemma 1

The bilinear equations

$$\begin{aligned} &\bigl(D_{x_{1}}^{4}-4D_{x_{1}}D_{x_{3}}+3D_{x_{2}}^{2} \bigr)\tau _{n}\cdot \tau _{n}=0, \end{aligned}$$
(2.2a)
$$\begin{aligned} &\bigl(D_{x_{1}}^{3} D_{x_{2}}+2D_{x_{2}}D_{x_{3}}-3D_{x_{1}} D_{x_{4}}\bigr) \tau _{n}\cdot \tau _{n}=0, \end{aligned}$$
(2.2b)

in the KP hierarchy admit determinant solutions

$$\begin{aligned} \tau _{n}=\det _{1\leq i,j\leq N}\bigl(m^{(n)}_{ij} \bigr), \end{aligned}$$
(2.3)

where the matrix element \(m^{(n)}_{ij}\) satisfies

$$\begin{aligned} \begin{aligned} &\partial _{x_{1}}m_{i,j}^{(n)}=\varphi _{i}^{(n)} \psi _{j}^{(n)}, \qquad \partial _{x_{2}}m_{i,j}^{(n)}=\bigl(\partial _{x_{1}} \varphi _{i}^{(n)}\bigr) \psi _{j}^{(n)}- \varphi _{i}^{(n)}\bigl(\partial _{x_{1}} \psi _{j}^{(n)}\bigr), \\ &\partial _{x_{3}}m_{i,j}^{(n)}=\bigl(\partial ^{2}_{x_{1}} \varphi _{i}^{(n)}\bigr) \psi _{j}^{(n)}+\varphi _{i}^{(n)}\bigl(\partial ^{2}_{x_{1}} \psi _{j}^{(n)}\bigr)-\bigl( \partial _{x_{1}} \varphi _{i}^{(n)}\bigr) \bigl( \partial _{x_{1}} \psi _{j}^{(n)}\bigr), \\ &\partial _{x_{4}}m_{i,j}^{(n)}=\bigl(\partial ^{3}_{x_{1}} \varphi _{i}^{(n)}\bigr) \psi _{j}^{(n)}-\bigl(\partial ^{2}_{x_{1}} \varphi _{i}^{(n)}\bigr) \bigl(\partial _{x_{1}} \psi _{j}^{(n)}\bigr)+\bigl(\partial _{x_{1}} \varphi _{i}^{(n)}\bigr) \bigl(\partial ^{2}_{x_{1}} \psi _{j}^{(n)}\bigr)-\varphi _{i}^{(n)} \bigl(\partial ^{3}_{x_{1}} \psi _{j}^{(n)} \bigr), \\ & m_{i,j}^{(n+1)}=m_{i,j}^{(n)}+\varphi _{i}^{(n)}\psi _{j}^{(n+1)}, \end{aligned} \end{aligned}$$
(2.4)

and \(\varphi _{i}^{(n)},\psi _{j}^{(n)}\) are arbitrary functions satisfying

$$\begin{aligned} \partial _{x_{k}}\varphi _{i}^{(n)}= \varphi _{i}^{(n+k)},\qquad \partial _{x_{k}}\psi _{j}^{(n)}=-\psi _{j}^{(n-k)},\quad k=1,2,3,4. \end{aligned}$$
(2.5)

In order to derive solutions for BKP-II equation (2.1), consider the functions \(\varphi _{i}^{(n)}, \psi _{j}^{(n)}\), and \(m_{i,j}^{(n)}\) defined by

$$\begin{aligned} & {\varphi }_{i}^{(n)}=p_{i}^{n}e^{\xi _{i}},\qquad {\psi }_{j}^{(n)}=(-q_{j})^{-n}e^{ \eta _{j}}, \\ & {m}_{i,j}^{(n)}=\delta _{ij}+ \int ^{x_{1}}{\varphi }_{j}^{(n)}{ \psi }_{i}^{(n)}\,dx_{1}=\delta _{ij}+ \frac{1}{p_{i}+q_{j}}\biggl(- \frac{p_{i}}{q_{j}}\biggr)^{n} e^{\xi _{i}+\eta _{j}}, \\ & \xi _{i}=p_{i}x_{1}+p_{i}^{2}x_{2}+p_{i}^{3}x_{3}+p_{i}^{4}x_{4},\qquad \eta _{j}=q_{j}x_{1}-q_{j}^{2}x_{2}+q_{j}^{3}x_{3}-q_{j}^{4}x_{4}, \end{aligned}$$

where \(p_{i},q_{j}\) are arbitrary constants, \(\delta _{ij}\) is the Kronecker delta notation. It is easy to verify that \(\varphi _{i}^{(n)}, \psi _{j}^{(n)}\), and \(m_{i,j}^{(n)}\) satisfy (2.4) and (2.5). By taking

$$\begin{aligned} x_{1}=x,\qquad x_{2}=y,\qquad x_{3}= \frac{4}{3\alpha }s,\qquad x_{4}=-2t, \end{aligned}$$

bilinear equations (2.2a)–(2.2b) are reduced to the bilinear form (1.5a)–(1.5b) of the BKP-II equation with \(\delta =1\). Therefore, we get the following theorem.

Theorem 1

BKP-II equation (2.1) admitsN-soliton solutions (1.4) with

$$\begin{aligned} f=\tau _{0}= \biggl\vert \delta _{ij}+ \frac{1}{p_{i}+q_{j}}e^{\xi _{i}+ \eta _{j}} \biggr\vert _{N\times N} \end{aligned}$$
(2.6)

and

$$\begin{aligned} \xi _{i}=p_{i}x+p_{i}^{2}y-2p_{i}^{4}t,\qquad \eta _{j}=q_{j}x-q_{j}^{2}y+2q_{j}^{4}t. \end{aligned}$$
(2.7)

According to Theorem 1, the one-soliton solutions for BKP-II equation (2.1) are given by taking \(N=1\). In this case,

$$\begin{aligned} f=1+\frac{1}{p_{1}+q_{1}}e^{\xi _{1}+\eta _{1}}, \end{aligned}$$

and the one-soliton solutions take the form

$$\begin{aligned} u= \frac{e^{\xi _{1}+\eta _{1}}}{1+\frac{1}{p_{1}+q_{1}}e^{\xi _{1}+\eta _{1}}}. \end{aligned}$$

When \(p_{1}+q_{1}>0\), we get the non-singular one-soliton solutions

$$\begin{aligned} u=\frac{p_{1}+q_{1}}{2}+\frac{p_{1}+q_{1}}{2}\tanh \biggl\{ \frac{1}{2} \biggl[\xi _{1}+\eta _{1}+\ln \biggl( \frac{1}{p_{1}+q_{1}} \biggr) \biggr] \biggr\} . \end{aligned}$$
(2.8)

From (2.8) we find that the one-soliton solution is a kink soliton. By taking \(N=2\), we derive

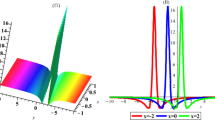
$$\begin{aligned} f={}& \begin{vmatrix} 1+\frac{1}{p_{1}+q_{1}}e^{\xi _{1}+\eta _{1}} & \frac{1}{p_{1}+q_{2}}e^{ \xi _{1}+\eta _{2}} \\ \frac{1}{p_{2}+q_{1}}e^{\xi _{2}+\eta _{1}} & 1+\frac{1}{p_{2}+q_{2}}e^{ \xi _{2}+\eta _{2}} \end{vmatrix} \\ ={}&1+\frac{1}{p_{1}+q_{1}}e^{\xi _{1}+\eta _{1}}+ \frac{1}{p_{2}+q_{2}}e^{\xi _{2}+\eta _{2}} \\ & {}+ \frac{(p_{1}-p_{2})(q_{1}-q_{2})}{(p_{1}+q_{1})(p_{1}+q_{2})(p_{2}+q_{1})(p_{2}+q_{2})} e^{\xi _{1}+\xi _{2}+\eta _{1}+\eta _{2}}. \end{aligned}$$

The two-soliton solutions can be written down from (1.4) and the above f. Similarly, the three-soliton solutions in the Grammian determinant form can be obtained. Figure 1 presents the interaction of the three solitons for BKP-II equation (2.1). As the figure shows, all the solitons are kink-type and the velocity and amplitude remain unchanged before and after the collision, and therefore the interaction of the three solitons is an elastic interaction.

Figure 1
figure 1

Interaction of three solitons for the BKP-II equation with parameters \(p_{1}=1, q_{1}=1.2, p_{2}=0.8, q_{2}=0.5, p_{3}=1.5, q_{3}=2\)

Full size image

3 Lump-soliton solutions for the BKP-I equation in the Grammian determinant form

Similar to Sect. 2, we can construct soliton solutions in the Grammian determinant form for the BKP-I equation

$$\begin{aligned} (u_{xt}+u_{xxxy}+8u_{x}u_{xy}+4u_{xx}u_{y})_{x}-u_{yyy}=0. \end{aligned}$$
(3.1)

Recently, Rao and his collaborators have proposed an effective method to derive semi-rational solutions for the third-type Davey–Stewartson equation, the multi-component long-wave-short-wave resonance interaction system, and the Fokas system [26–28]. In what follows, by using the method proposed by Rao, we present semi-rational solutions for the BKP-I equation in the following theorem.

Theorem 2

BKP-I equation (3.1) has semi-rational solutions (1.4) with

$$\begin{aligned} f=\tau _{0}, \quad\tau _{0}=\det _{1\leq i,j\leq N} \bigl(m^{(0)}_{ij}\bigr), \end{aligned}$$
(3.2)

where the matrix element is given by

$$\begin{aligned} m_{i,j}^{(0)}=e^{\xi _{i}+\xi ^{*}_{j}}\sum _{k=0}^{n_{i}}c_{ik}\biggl(p_{i} \frac{\partial }{\partial p_{i}}+\xi '_{i}\biggr)^{n_{i}-k} \sum _{l=0}^{n_{j}}c^{*}_{jl} \biggl(p^{*}_{j} \frac{\partial }{\partial p_{i}}+\xi ^{\prime *}_{j} \biggr)^{n_{j}-l} \frac{1}{p_{i}+p^{*}_{j}}+\gamma _{ij}c_{in_{i}}c^{*}_{jn_{j}}, \end{aligned}$$
(3.3)

\(p_{i},p_{j},c_{ik},c_{jl}\)are arbitrary complex constants, \(\gamma _{ij}\)are arbitrary real constants, and

$$\begin{aligned} \xi _{i}=p_{i}x+ip_{i}^{2}y-2ip_{i}^{4}t,\qquad \xi '_{i}=p_{i}x+2ip_{i}^{2}y-8ip_{i}^{4}t. \end{aligned}$$
(3.4)

Proof

Consider the functions \(\varphi _{i}^{(n)}, \psi _{j}^{(n)}\), and \(m_{i,j}^{(n)}\) defined by

$$\begin{aligned} &{\varphi }_{i}^{(n)}=A_{i}p_{i}^{n}e^{\xi _{i}},\qquad {\psi }_{i}^{(n)}=B_{j}(-q_{i})^{-n}e^{ \eta _{j}}, \\ &{m}_{i,j}^{(n)}=A_{i}B_{j} \biggl[ \gamma _{ij}+ \frac{1}{p_{i}+q_{j}}\biggl(-\frac{p_{i}}{q_{j}} \biggr)^{n} e^{\xi _{i}+\eta _{j}} \biggr], \\ &\xi _{i}=p_{i}x_{1}+p_{i}^{2}x_{2}+p_{i}^{3}x_{3}+p_{i}^{4}x_{4},\qquad \eta _{j}=q_{j}x_{1}-q_{j}^{2}x_{2}+q_{j}^{3}x_{3}-q_{j}^{4}x_{4}, \end{aligned}$$
(3.5)

where \(A_{i}\) and \(B_{j}\) are differential operators given by

$$\begin{aligned} A_{i}=\sum_{k=0}^{n_{i}}c_{ik} \biggl(p_{i}\frac{\partial }{\partial p_{i}}\biggr)^{n_{i}-k},\qquad B_{j}= \sum_{l=0}^{n_{j}}d_{jl} \biggl(q_{i} \frac{\partial }{\partial q_{i}}\biggr)^{n_{j}-l}, \end{aligned}$$

\(p_{i},q_{j},c_{ik}\), and \(d_{jl}\) are all arbitrary complex constants, \(\gamma _{ij}\) are arbitrary real constants. Obviously, \(\varphi _{i}^{(n)}, \psi _{j}^{(n)}\), and \(m_{i,j}^{(n)}\) satisfy (2.4) and (2.5). Therefore, \(\tau _{n}=\det _{1\leq i,j\leq N}(m^{(n)}_{ij})\) with (3.5) are solutions of bilinear equations (2.2a)–(2.2b). Noting that

$$\begin{aligned} & \biggl(p_{i}\frac{\partial }{\partial p_{i}}\biggr)p_{i}^{n}e^{\xi _{i}}=p_{i}^{n}e^{ \xi _{i}} \biggl(p_{i}\frac{\partial }{\partial p_{i}}+\xi '_{i}+n \biggr), \\ & \biggl(q_{i}\frac{\partial }{\partial q_{i}}\biggr) (-q_{j})^{-n}e^{\eta _{j}}=(-q_{j})^{-n}e^{ \eta _{j}} \biggl(q_{j}\frac{\partial }{\partial q_{j}}+\eta '_{j}-n \biggr), \end{aligned}$$

where

$$\begin{aligned} \xi '_{i}=p_{i}x_{1}+2p_{i}^{2}x_{2}+3p_{i}^{3}x_{3}+4p_{i}^{4}x_{4},\qquad \eta '_{j}=q_{j}x_{1}-2q_{j}^{2}x_{2}+3q_{j}^{3}x_{3}-4q_{j}^{4}x_{4}, \end{aligned}$$

the matrix element \(m^{(n)}_{ij}\) can be rewritten as

$$\begin{aligned} {m}_{i,j}^{(n)}={}&\biggl(-\frac{p_{i}}{q_{j}} \biggr)^{n} e^{\xi _{i}+\eta _{j}} \sum_{k=0}^{n_{i}}c_{ik} \biggl(p_{i}\frac{\partial }{\partial p_{i}}+\xi '_{i}+n \biggr)^{n_{i}-k} \\ &{}\times \sum_{l=0}^{n_{j}}d_{jl} \biggl(q_{i} \frac{\partial }{\partial q_{i}}+\eta '_{j}-n \biggr)^{n_{j}-l} \frac{1}{p_{i}+q_{j}}+\gamma _{ij}c_{in_{i}}d_{jn_{j}}. \end{aligned}$$

By applying the variable transformation

$$\begin{aligned} x_{1}=x,\qquad x_{2}=iy, \qquad x_{3}= \frac{4}{3\alpha }s,\qquad x_{4}=-2it, \end{aligned}$$

and taking

$$\begin{aligned} q_{i}=p_{j}^{*},\qquad d_{jl}=c^{*}_{jl}, \end{aligned}$$
(3.6)

we have \(\xi ^{\prime *}_{j}=\eta '_{j}\) and Eqs. (2.2a)–(2.2b) are reduced to the bilinear form (1.5a)–(1.5b) of the BKP-I equation with \(\delta =-1\). Setting \(f=\tau _{0}\), we get the semi-rational solutions for BKP-I equation (3.1) as given in Theorem 2.

The semi-rational solutions for the BKP-I equation consist of lumps and kink solitons to the equation. Therefore, we call them lump-soliton solutions. Taking \(\gamma _{ij}=0\) and by the gauge invariance of \(\tau _{n}\) function, we can get lump solutions for BKP-I equation (3.1). Moreover, in (3.3) we can normalize \(c_{i0}=1\) by a scaling of f, so we take \(c_{i0}=1\) hereafter. □

4 Discussion on the interactions between lumps and kink solitons

In this section, we investigate the dynamics of lump-soliton solutions for the BKP-I equation. It is shown that the fascinating phenomena of fusion and fission can be observed in the study of lump-soliton solutions for the equation.

4.1 Dynamics of one lump and one soliton

Taking \(N=1\) and \(n_{1}=1\) in (3.2), we can get the fundamental lump-soliton solutions for the BKP-I equation as

$$\begin{aligned} u=(\ln f)_{x}, \end{aligned}$$
(4.1)

where

$$\begin{aligned} f={}&e^{\xi _{1}+\xi ^{*}_{1}}\sum_{k=0}^{1}c_{1k} \biggl(p_{1} \frac{\partial }{\partial p_{1}}+\xi '_{1} \biggr)^{1-k} \sum_{l=0}^{1}c^{*}_{1l} \biggl(p^{*}_{1} \frac{\partial }{\partial p^{*}_{1}}+\xi ^{\prime *}_{1} \biggr)^{1-l} \frac{1}{p_{1}+p^{*}_{1}}+\gamma _{11}c_{11}c^{*}_{11} \\ ={}&\frac{e^{\xi _{1}+\xi ^{*}_{1}}}{p_{1}+p^{*}_{1}} \biggl[ \biggl( \xi '_{1}+c_{11}- \frac{p_{1}}{p_{1}+p^{*}_{1}} \biggr) \biggl(\xi ^{\prime *}_{1}+c^{*}_{11}- \frac{p^{*}_{1}}{p_{1}+p^{*}_{1}} \biggr) + \frac{p_{1}p^{*}_{1}}{(p_{1}+p^{*}_{1})^{2}} \biggr] \\ &{}+\gamma _{11}c_{11}c^{*}_{11}, \end{aligned}$$
(4.2)

\(\xi _{1}=p_{1}x+ip_{1}^{2}y-2ip_{1}^{4}t\), \(\xi '_{1}=p_{1}x+2ip_{1}^{2}y-8ip_{1}^{4}t\), \(c_{11}\) is an arbitrary complex constant. When \(\gamma _{11}=0\), the fundamental lump-soliton solutions reduce to lump solutions, therefore we take \(\gamma _{11}=1\). For the nonsingularity of u, \(p_{1}\) is not purely imaginary.

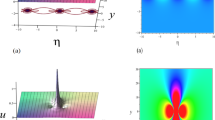
We observe the time evolution of the fundamental lump-soliton solutions (4.1) on the \(x-y\) plane. From Fig. 2(a) and Fig. 2(b), we can see that when \(t\ll 0\) this solution contains only one kink soliton and a lump appears from the kink soliton gradually. In Fig. 2(c), the lump separates from the kink soliton and then spreads along the opposite direction to the kink soliton. When \(t\gg 0\), this solution contains one kink soliton and one lump. In this case, the fundamental lump-soliton solution shows the fission phenomenon of a lump from a kink soliton. From Fig. 3(a) and Fig. 3(b), we can observe that this solution comprises one kink soliton and one lump when \(t\ll 0\). As time goes on, the lump moves towards the kink soliton and then collides with the kink soliton. After the collision, the lump merges with the kink soliton in Fig. 3(c). When \(t\ll 0\), the fundamental lump-soliton solution comprises only one kink soliton. In this case, solution (4.1) shows the fusion phenomenon of a lump into a kink soliton.

Figure 2
figure 2

Plot of a lump and a kink soliton fission with parameters \(p_{1}=0.3-0.4i, c_{11}=1, \gamma _{11}=1\)

Full size image
Figure 3
figure 3

Plot of a lump and a kink soliton fusion with parameters \(p_{1}=0.4+0.5i, c_{11}=1, \gamma _{11}=1\)

Full size image

4.2 Dynamics of multiple lump-soliton solutions

Taking \(N>1,n_{i}=1,\gamma _{ii}=1\) in (3.2), the multiple lump-soliton solutions for the BKP-I equation can be constructed. Considering the case of \(N=2\), the function f is given by

$$\begin{aligned} f= \begin{vmatrix} {m}_{11}^{(0)} & {m}_{12}^{(0)} \\ {m}_{21}^{(0)} & {m}_{22}^{(0)} \end{vmatrix}, \end{aligned}$$

where

$$\begin{aligned} {m}_{ij}^{(0)}=\frac{e^{\xi _{i}+\xi ^{*}_{j}}}{p_{i}+p^{*}_{j}} \biggl[ \biggl(\xi '_{i}+c_{i1}-\frac{p_{i}}{p_{i}+p^{*}_{j}} \biggr) \biggl(\xi ^{\prime *}_{j}+c^{*}_{j1}- \frac{p^{*}_{j}}{p_{i}+p^{*}_{j}} \biggr) +\frac{p_{i}p^{*}_{j}}{(p_{i}+p^{*}_{j})^{2}} \biggr]+ \gamma _{ij}c_{i1}c^{*}_{j1}, \end{aligned}$$
(4.3)

\(\xi _{i}\) and \(\xi '_{i}\) are given by (3.4), \(p_{1},p_{2},c_{11},c_{21}\) are arbitrary complex constants.

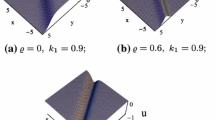
Now we observe the dynamical behaviors of the multiple lump-soliton solutions. From Fig. 4, we observe that two lumps emerge from two kink solitons gradually and then separate completely. This multiple lump-soliton solution comprises only two kink solitons when \(t\ll 0\) and evolves into two lumps and two kink solitons when \(t\gg 0\). From Fig. 5, we observe that two lumps move towards two kink solitons and then merge with the two kink solitons after the interaction. This solution comprises two lumps and two kink solitons when \(t\ll 0\) and reduces to two kink solitons when \(t\gg 0\). Therefore, Fig. 4 and Fig. 5 show the fission process of two lumps from two kink solitons and the fusion process of two lumps and two kink solitons respectively. However, from Fig. 6, we observe multiple lump-soliton solution which has different dynamics from those in Fig. 4 and Fig. 5. Obviously, the multiple lump-soliton solution is composed of one lump and two kink solitons all the time and there is no fission or fusion of the lump and the two kink solitons, but the amplitude and the propagation direction of the lump change after the collision. Therefore, the collision is an inelastic collision.

Figure 4
figure 4

Plot of two lumps and two kink solitons fission with parameters \(p_{1}=0.3-0.4i, p_{2}=0.5-0.6i, c_{11}=c_{21}=1, \gamma _{11}= \gamma _{22}=1, \gamma _{12}=\gamma _{21}=0\)

Full size image
Figure 5
figure 5

Plot of two lumps and two kink solitons fusion with parameters \(p_{1}=0.3+0.4i, p_{2}=0.5+0.6i, c_{11}=c_{21}=1, \gamma _{11}= \gamma _{22}=1, \gamma _{12}=\gamma _{21}=0\)

Full size image
Figure 6
figure 6

Plot of one lump and two kink solitons interaction with parameters \(p_{1}=0.3-0.4i, p_{2}=0.5+0.6i, c_{11}=c_{21}=1, \gamma _{11}= \gamma _{22}=1, \gamma _{12}=\gamma _{21}=0\)

Full size image

4.3 Dynamics of higher-order lump-soliton solutions

Taking \(N=1\) and \(n_{1}>1\) in (3.1), the higher-order lump-soliton solutions for the BKP-I equation can be derived. To demonstrate the interactions of the higher-order lump-soliton solutions, we set \(n_{1}=3\) to derive third-order lump-soliton solutions as

$$\begin{aligned} f={}&e^{\xi _{1}+\xi ^{*}_{1}} \biggl[\biggl(p_{1} \frac{\partial }{\partial p_{1}}+\xi '_{1}\biggr)^{3}+c_{11} \biggl(p_{1} \frac{\partial }{\partial p_{1}}+\xi '_{1} \biggr)^{2}+c_{12}\biggl(p_{1} \frac{\partial }{\partial p_{1}}+ \xi '_{1}\biggr)+c_{13} \biggr] \\ &{}\times \biggl[\biggl(p^{*}_{1}\frac{\partial }{\partial p^{*}_{1}}+\xi ^{\prime *}_{1}\biggr)^{3}+c^{*}_{11} \biggl(p^{*}_{1} \frac{\partial }{\partial p^{*}_{1}}+\xi ^{\prime *}_{1} \biggr)^{2}+c^{*}_{12}\biggl(p^{*}_{1} \frac{\partial }{\partial p^{*}_{1}}+\xi ^{\prime *}_{1}\biggr)+c^{*}_{13} \biggr] \frac{1}{p_{1}+p^{*}_{1}} \\ &{}+\gamma _{11}c_{13}c^{*}_{13}, \end{aligned}$$
(4.4)

where \(\xi _{i}\) and \(\xi '_{i}\) are given by (3.4), \(\gamma _{11}\) is nonzero real constant, \(c_{11},c_{12},c_{13}\) are arbitrary complex constants.

To illustrate the dynamics of the third-order lump-soliton solutions, the time evolution of the solution is plotted in Fig. 7 and Fig. 8. As Fig. 7 shows, three lumps arise from a kink soliton and then separate from the soliton gradually. As shown in Fig. 8, three lumps come to interact with a kink soliton and then fuse into the kink soliton completely. Therefore, the dynamics of these higher-order lump-soliton solutions is broadly analogous to that of fundamental lump-soliton solutions, which is shown in Fig. 2 and Fig. 3, but more lumps interact with a kink soliton.

Figure 7
figure 7

Plot of three lumps and a kink soliton fission with parameters \(p_{1}=0.5-0.4i, c_{11}=c_{12}=c_{13}=1, \gamma _{11}=1\)

Full size image
Figure 8
figure 8

Plot of three lumps and a kink soliton fusion with parameters \(p_{1}=0.5+0.4i, c_{11}=c_{12}=c_{13}=1, \gamma _{11}=1\)

Full size image

5 Conclusions

In this paper, we investigate the BKP equation by employing Hirota’s direct method and the KP hierarchy reduction method. N-soliton solutions in the Grammian determinant form for the BKP-II equation are derived and soliton collisions are illustrated through graphs. Lump-soliton solutions in the Grammian determinant form for the BKP-I equation are obtained and the dynamics of three subclasses of the solutions are shown graphically. The fundamental lump-soliton solutions describe the fission of a lump from a kink soliton and the fusion of a lump into a kink soliton. The dynamical behaviors of higher-order lump-soliton solutions are very similar to fundamental lump-soliton solutions, except that the higher-order lump-soliton solutions comprise more lumps interacting with a kink soliton. However, the multiple lump-soliton solutions possess more complex structures and dynamical behaviors than the fundamental lump-soliton solutions and higher-order lump-soliton solutions. When \(N=2\), the multiple lump-soliton solutions not only exhibit the fission of two lumps from two kink solitons and the fusion of two lumps into two kink solitons, but also the inelastic collision of one lump and two kink solitons. It should be noted that the interaction scenarios of nonlinear waves for NLEEs are diverse [3, 4, 15–17, 26–31]. In practice, the fusion and fission phenomena have been explored in some physical fields such as hydrodynamics, nuclear physics, and plasma physics [46, 47]. It is hoped that the obtained results will enrich the applications of NLEEs in nonlinear scientific fields.