1 Introduction

In this paper we consider the following time-fractional Black–Scholes (B–S) equation:

$$\begin{aligned} & \frac{\partial _{R}^{\alpha }V}{\partial \tau ^{\alpha }}+ \frac{1}{2}\bar{\sigma }^{2}(\tau )x^{2}\frac{\partial ^{2}V}{\partial x^{2}}+\bar{r}(\tau )x\frac{\partial V}{\partial x}- \bar{r}(\tau )V=0,\quad (x,\tau )\in \mathbb{R}^{+}\times [0,T ), \end{aligned}$$
(1.1)
$$\begin{aligned} & V(x,T)=\max \{ x-E,0 \}, \quad x\in \mathbb{R}^{+}, \end{aligned}$$
(1.2)
$$\begin{aligned} & V(0,\tau )=0, \quad \tau \in [0,T ), \end{aligned}$$
(1.3)

where V is the value of a European call option with strike price E and expiry date T, x is the asset price, r̄ is the risk-free interest rate, σ̄ is the volatility of the underlying asset, \(\frac{\partial _{R}^{\alpha }V}{\partial \tau ^{ \alpha }}\) is the right modified Riemann–Liouville derivative defined as

$$\begin{aligned} \frac{\partial _{R}^{\alpha }V}{\partial \tau ^{\alpha }}=\frac{1}{ \varGamma (1-\alpha )}\frac{\partial }{\partial \tau } \int _{\tau }^{T}\frac{V(x, \xi )-V(x,T)}{ (\xi -\tau )^{\alpha }}\,{\mathrm{d}} \xi,\quad 0< \alpha < 1. \end{aligned}$$

Here we assume that \(\bar{\sigma }^{2}(\tau )\geq \mu >0, \beta ^{*} \geq \bar{r}(\tau )\geq \beta >0\). We note that when the functions \(\bar{\sigma }(\tau )\) and \(\bar{r}(\tau )\) are constants, problem (1.1)–(1.3) reduces to the Wyss time-fractional Black–Schole equation [26].

There are a few analytical and numerical methods for the valuation of the time-fractional B–S equations. The analytical methods for the time-fractional B–S equations are usually based on integral transform methods [5, 12, 26], homotopy analysis methods [17], or wavelet based hybrid methods [11], etc. But the solutions obtained by analytical methods usually take the form of a convolution of some special functions or an infinite series with an integral, which makes them hard to calculate. Therefore, efficient numerical methods become essential. Zhang et al. [27] and Staelen and Hendy [7] developed implicit finite difference methods for pricing the barrier options under the Wyss’ time-fractional B–S equation. Golbabai and Nikan [8] also proposed a numerical approach based on the moving least-squares method to approximate the Wyss’ time-fractional B–S equation for pricing the barrier options. Chen [4] described a new operator splitting method for pricing American options under the Wyss’ time-fractional B–S equation. Song and Wang [23] presented an implicit difference method for the Jumarie time-fractional B–S equation. Koleva and Vulkov [15] derived a weighted finite difference scheme for the Jumarie time-fractional B–S equation. Kalantari and Shahmorad [13] used a Grünwald–Letnikov scheme to solve the Jumarie time-fractional B–S equation for pricing the American put option. But these papers only study the case that the exact solutions of the B–S equations are sufficiently smooth.

As discussed in [24], the exact solutions of the time-fractional B–S equations may exhibit singularity. Based on a priori information of the exact solution, Cen et al. [2] presented an integral discretization scheme on a priori graded mesh for the Wyss time-fractional B–S equation. When the coefficients of the time-fractional B–S equation are related to time τ, a priori information of the exact solution is difficult to obtain. In this paper, an adaptive moving mesh method is developed in order to deal with the possible singularity effectively for the time-fractional B–S equation. A finite difference method is used to discretize the time-fractional Black–Scholes equation and error analysis for the discrete scheme is derived. Then, an adaptive moving mesh based on a priori error analysis is established by equidistribution of a positive monitor function which involves the second-order time derivative of the computed solution. Numerical experiments are provided to validate the theoretical results.

The remainder of the paper is organized as follows. Some theoretical results on the continuous time-fractional B–S equation are described in Sect. 2. The discretization scheme is derived in Sect. 3. An adaptive algorithm is established in Sect. 4. Finally, numerical experiments are presented in Sect. 5.

Notation. Throughout the paper, C will denote a generic positive constant that is independent of the mesh. Note that C is not necessarily the same at each occurrence. To simplify the notation we set \(g_{i}^{j}=g(x_{i},t_{j})\) for any function g on the domain of definition. We use the (pointwise) maximum norm on the domain of definition Ω by \(\Vert \cdot \Vert _{\bar{\varOmega }}\).

2 The continuous problem

By using the change of variables \(t=T-\tau, u(x,t)=V(x,T-t)\) and the relationship between the Riemann–Liouville derivative and the Caputo derivative, it is shown in [2, 4] that the model can be reformulated into

$$\begin{aligned} & \frac{\partial ^{\alpha }u}{\partial t^{\alpha }}-\frac{1}{2}\sigma ^{2}(t)x^{2} \frac{\partial ^{2}u}{\partial x^{2}}-r(t)x\frac{\partial u}{\partial x}+r(t)u=0, \quad (x,t )\in \mathbb{R}^{+}\times (0,T ], \end{aligned}$$
(2.1)
$$\begin{aligned} & u(x,0)=\max \{ x-E,0 \}, \quad x\in \mathbb{R}^{+}, \end{aligned}$$
(2.2)
$$\begin{aligned} & u(0,t)=0, \quad t\in (0,T ], \end{aligned}$$
(2.3)

where \(\sigma (t)=\bar{\sigma }(T-t), r(t)=\bar{r}(T-t)\), and \(\frac{\partial ^{\alpha }u}{\partial t^{\alpha }}\) is the Caputo derivative defined as

$$\begin{aligned} \frac{\partial ^{\alpha }u}{\partial t^{\alpha }}=\frac{1}{\varGamma (1- \alpha )} \int _{0}^{t} (t-s )^{-\alpha } \frac{\partial u}{ \partial t}(x,s)\,\mathrm{d}s,\quad 0< \alpha < 1. \end{aligned}$$

The infinite domain \(\mathbb{R}^{+}\times (0,T]\) is truncated into \(\varOmega =(0,X)\times (0,T]\) for numerical calculation. The boundary conditions \(X=4E\) and \(u(X,t)=X-E e^{-rt}\) are chosen for the European call option based on Wilmott et al.’s estimate [25]. Normally, the error caused by this truncation can be neglected. Therefore, in the remaining of this paper we will consider the following time-fractional differential equation:

$$\begin{aligned} & Lu(x,t)=0, \quad(x,t)\in \varOmega, \end{aligned}$$
(2.4)
$$\begin{aligned} & u(x,0)=\max (x-E,0 ),\quad x\in [0,X], \end{aligned}$$
(2.5)
$$\begin{aligned} & u(0,t)=0,\qquad u(X,t)=X-E e^{-rt},\quad t\in [0,T], \end{aligned}$$
(2.6)

where

$$\begin{aligned} Lu(x,t)\equiv \frac{\partial ^{\alpha }u}{\partial t^{\alpha }}- \frac{1}{2}\sigma ^{2}(t)x^{2}\frac{\partial ^{2}u}{\partial x^{2}}-r(t)x \frac{ \partial u}{\partial x} +r(t)u. \end{aligned}$$
(2.7)

Let \(W^{1}_{t} ((0,T] )\) denote the space of functions \(w(t)\in C^{1} ( (0,T ] )\) such that \(w'\) is Lebesgue integrable in \((0,T ]\). The following result for the differential operator L can be obtained as Theorem 3 of [21] on the function space \(C(\bar{\varOmega })\cap W _{t}^{1} ( (0,T ] )\cap C_{x}^{2} ((0,X) )\).

Lemma 2.1

(Maximum principle)

Let \(u(x,t)\in C(\bar{\varOmega }) \cap W_{t}^{1} ( (0,T ] )\cap C_{x}^{2} ((0,X) )\). If \(Lu(x,t)\geq 0\)for \(x\in \varOmega \)with \(u(0,t)\geq 0,\ u(X,t) \geq 0\)for \(t\in (0,T]\)and \(u(x,0)\geq 0\)for \(x\in (0,X)\), then \(u(x,t)\geq 0\)for all \(x\in \bar{\varOmega }\).

By applying this maximum principle the following stability result can be obtained as Theorem 4 of [21].

Lemma 2.2

(Stability result)

The exact solution \(u(x,t)\)of problem (2.4)–(2.6) satisfies the following stability estimate:

$$\begin{aligned} \bigl\Vert u(x,t) \bigr\Vert _{\bar{\varOmega }}\leq X-Ee^{-rT}. \end{aligned}$$

Referring to [1, 2, 10, 18, 22, 24] it can be further seen that the time derivatives of the exact solution may blow up at \(t=0\), which complicates the construction of the discretization scheme.

3 Discretization scheme

Let \(\varOmega ^{K}= \{ 0=t_{0}< t_{1}<\cdots <t_{K}=T \} \) and \(\varOmega ^{N}= \{ 0=x_{0}< x_{1}<\cdots <x_{N}=X \} \). An approximation to the time-fractional derivative on \(\varOmega ^{K}\) can be obtained by the quadrature formula,

$$\begin{aligned} \frac{\partial ^{\alpha }u(x_{i},t_{j})}{\partial t^{\alpha }} & = \frac{1}{ \varGamma (1-\alpha )}\sum _{k=1}^{j} \int _{t_{k-1}}^{t_{k}} (t_{j}-s ) ^{-\alpha }\frac{\partial u(x_{i},s)}{\partial s}\,{\mathrm{d}}s \\ & \approx \frac{1}{\varGamma (2-\alpha )}\sum_{k=1}^{j} \bigl[ (t _{j}-t_{k-1} )^{1-\alpha }- (t_{j}-t_{k} )^{1-\alpha } \bigr]D_{t}^{-}u_{i}^{k}, \end{aligned}$$

where \(D_{t}^{-}u_{i}^{k}=\frac{u^{k}_{i}-u_{i}^{k-1}}{\triangle t _{k}}\) with \(\triangle t_{k}=t_{k}-t_{k-1}\).

Since the Black–Scholes differential operator becomes a convection-dominated when the volatility or the asset price is small, a piecewise uniform mesh \(\varOmega ^{N}\) is constructed as that in [3] for the spatial discretization to ensure the stability:

$$\begin{aligned} x_{i}= \textstyle\begin{cases} h, & i=1, \\ h[1+\frac{\mu }{\beta ^{*}}(i-1)], & i=2,\ldots,N, \end{cases}\displaystyle \end{aligned}$$
(3.1)

where

$$\begin{aligned} h=\frac{X}{1+\frac{\mu }{\beta ^{*}}(N-1)}. \end{aligned}$$

Then the mesh sizes \(h_{i}=x_{i}-x_{i-1}\) satisfy

$$\begin{aligned} h_{i}=\textstyle\begin{cases} h, & i=1, \\ \frac{\mu }{\beta ^{*}} h, & i=2,\ldots,N. \end{cases}\displaystyle \end{aligned}$$
(3.2)

On the piecewise uniform mesh \(\varOmega ^{N}\) we apply a central difference scheme to approximate the spatial derivatives.

Hence, combining the time discretization scheme with spatial discretization scheme we can derive the fully discretized scheme on \(\varOmega ^{N\times K}\equiv \varOmega ^{N}\times \varOmega ^{K}\) as follows:

$$\begin{aligned} & L^{N,K}U_{i}^{j}=0,\quad 1\leq i< N,\ 1\leq j \leq K, \end{aligned}$$
(3.3)
$$\begin{aligned} & U_{i}^{0}=\max (x_{i}-E,0 ), \quad0\leq i \leq N, \end{aligned}$$
(3.4)
$$\begin{aligned} & U_{0}^{j}=0,\qquad U_{N}^{j}=X-E e^{-rt_{j}},\quad 0\leq j\leq K, \end{aligned}$$
(3.5)

where \(U_{i}^{j}\) is the approximation solution of \(u(x_{i},t_{j})\),

$$\begin{aligned} L^{N,K}U_{i}^{j} ={} & \frac{1}{\varGamma (2-\alpha )} \sum_{k=1}^{j} \bigl[ (t_{j}-t_{k-1} )^{1-\alpha }- (t_{j}-t_{k} ) ^{1-\alpha } \bigr]D_{t}^{-}U_{i}^{k} \\ &{} -\frac{1}{2} \bigl(\sigma ^{j} \bigr)^{2}x_{i}^{2} \delta _{x}^{2}U _{i}^{j}-r^{j}x_{i}D^{0}_{x}U_{i}^{j}+r^{j}U_{i}^{j}, \end{aligned}$$
(3.6)

and

$$\begin{aligned} &\delta _{x}^{2}U_{i}^{j}= \frac{2}{h_{i}+h_{i+1}} \biggl(\frac{U_{i+1} ^{j}-U_{i}^{j}}{h_{i+1}}-\frac{U_{i}^{j}-U_{i-1}^{j}}{h_{i}} \biggr),\\ & D_{x}^{0}U_{i}^{j}= \frac{U_{i+1}^{j}-U_{i-1}^{j}}{h_{i}+h_{i+1}},\qquad D_{t}^{-}U_{i}^{j}= \frac{U_{i}^{j}-U_{i}^{j-1}}{\triangle t_{j}}. \end{aligned}$$

Next we show that the matrix associated with the discrete operator \(L^{N,K}\) is an M-matrix. Hence the scheme is maximum-norm stable.

Lemma 3.1

(Discrete maximum principle)

The operator \(L^{N,K}\)defined by (3.6) on the mesh \(\varOmega ^{N\times K}\)satisfies a discrete maximum principle, i.e. if \(v^{j}_{i}\)is a mesh function that satisfies \(v_{0}^{j}\geq 0,\ v^{j}_{N}\geq 0\ (0\leq j\leq K)\), \(v_{i}^{0}\geq 0\ (0\leq i \leq N) \)and \(L^{N,K}v^{j}_{i}\geq 0 \ (1 \leq i< N,\ 0< j \leq K)\), then \(v^{j}_{i}\geq 0\)for all \(i,j\).

Proof

Let

$$\begin{aligned} & a_{i,i-1}^{j}=-\frac{ (\sigma ^{j} )^{2}x_{i}^{2}}{ (h_{i}+h_{i+1} )h_{i}}+ \frac{r^{j}x_{i}}{h_{i}+h_{i+1}},\qquad a_{i,i+1}^{j}=-\frac{ (\sigma ^{j} )^{2}x_{i}^{2}}{ (h _{i}+h_{i+1} )h_{i+1}}- \frac{r^{j}x_{i}}{h_{i}+h_{i+1}}, \\ & a_{i,i}^{j}=\frac{ (\sigma ^{j} )^{2}x_{i}^{2}}{h_{i}h _{i+1}}+r^{j}+ \frac{ (\triangle t_{j} )^{-\alpha }}{\varGamma (2-\alpha )},\quad 1\leq i< N,\ 1\leq j\leq K, \end{aligned}$$

and

$$\begin{aligned} a_{i,i}^{k}={}&\frac{1}{\varGamma (2-\alpha )\triangle t_{k}} \bigl[ (t _{j}-t_{k-1} )^{1-\alpha }- (t_{j}-t_{k} )^{1-\alpha } \bigr] \\ &{} -\frac{1}{\varGamma (2-\alpha )\triangle t_{k+1}} \bigl[ (t_{j}-t _{k} )^{1-\alpha }- (t_{j}-t_{k+1} )^{1-\alpha } \bigr],\quad 1\leq k\leq j-1. \end{aligned}$$

By simple calculation we have

$$\begin{aligned} a_{i,i-1}^{j} & < -\frac{ (\sigma ^{j} )^{2}x_{1}x_{i}}{(h _{i}+h_{i+1})h_{i}} + \frac{r^{j}x_{i}}{h_{i}+h_{i+1}}= \frac{ [r ^{j}h_{i}- (\sigma ^{j} )^{2} x_{1} ]x_{i}}{(h_{i}+h _{i+1})h_{i}} \\ & = \frac{ [r^{j}\frac{\mu }{\beta ^{*}}- (\sigma ^{j} ) ^{2} ]hx_{i}}{(h_{i}+h_{i+1})h_{i}}\leq 0 \end{aligned}$$

for \(2\leq i< N\). It is easy to show

$$\begin{aligned} & a_{i,i+1}^{j}< 0,\qquad a_{i,i}^{j}>0,\quad 1 \leq i< N, \ 1\leq j\leq K, \\ & a_{i,i}^{k}=\frac{1}{\varGamma (1-\alpha )} \bigl[ (t_{j}-\xi _{k} )^{-\alpha }- (t_{j}- \xi _{k+1} )^{-\alpha } \bigr] \leq 0,\quad 1\leq k\leq j-1, \end{aligned}$$

and

$$\begin{aligned} & a_{1,1}^{j}+a_{1,2}^{j}>0,\quad 1\leq j\leq K, \\ & a_{i,i-1}^{j}+a_{i,i}^{j}+a_{i,i+1}^{j}+ \sum_{k=1}^{j-1}a_{i,i} ^{k}>0,\quad 1< i< N, \ 1\leq j\leq K, \\ & a_{N-1,N-1}^{j}+a_{N-1,N}^{j}>0,\quad 1\leq j\leq K, \end{aligned}$$

where \(\xi _{k}\in (t_{k-1},t_{k})\). Hence, it is easy to see that the matrix associated with \(L^{N,K}\) is a strictly diagonally dominant L-matrix, which means that it is an M-matrix. By applying the same argument as that in [14, Lemma 3.1], it is straightforward to obtain the result of our lemma. □

The next lemma gives us a useful formula for the truncation error.

Lemma 3.2

LetUbe the solution of the difference scheme (3.3)–(3.5) andube the exact solution of problem (2.4)–(2.6). Then we have the following truncation error estimates:

$$\begin{aligned} \bigl\vert L^{N,K} \bigl(u_{i}^{j}-U_{i}^{j} \bigr) \bigr\vert \leq {}& C\max_{1\leq k \leq j} (\triangle t_{k} )^{1-\alpha } \int _{t_{k-1}}^{t _{k}} \biggl\vert \frac{\partial ^{2} u}{\partial t^{2}}(x_{i},s) \biggr\vert \,{\mathrm{d}}s \\ &{} +C (h_{i}+h_{i+1} ) \int _{x_{i-1}}^{x_{i+1}} \biggl(x _{i}^{2} \biggl\vert \frac{\partial ^{4}u}{\partial x^{4}}(y,t_{j}) \biggr\vert +x _{i} \biggl\vert \frac{\partial ^{3}u}{\partial x^{3}}(y,t_{j}) \biggr\vert \biggr) \,\mathrm{d}y \end{aligned}$$

for \(1\leq i< N\)and \(1\leq j\leq K\), whereCis a positive constant independent of the mesh.

Proof

It follows from (3.3) and (3.6) that

$$\begin{aligned} \bigl\vert L^{N,K} \bigl(u_{i}^{j}-U_{i}^{j} \bigr) \bigr\vert = {}& \bigl\vert L^{N,K}u_{i} ^{j}-Lu(x_{i},t_{j}) \bigr\vert \\ \leq {}& \frac{1}{\varGamma (1-\alpha )}\sum_{k=1}^{j} \biggl\vert \int _{t_{k-1}} ^{t_{k}} (t_{j}-s )^{-\alpha } \biggl[D_{t}^{-}u_{i}^{k}- \frac{ \partial u}{\partial s}(x_{i},s) \biggr]\,{\mathrm{d}}s \biggr\vert \\ &{} +\frac{1}{2} \bigl(\sigma ^{j} \bigr)^{2}x_{i}^{2} \biggl\vert \delta _{x}^{2}u_{i}^{j}- \frac{\partial ^{2}u}{\partial x^{2}}(x_{i},t_{j}) \biggr\vert +r ^{j}x_{i} \biggl\vert D_{x}^{0}u_{i}^{j}- \frac{\partial u}{\partial x}(x _{i},t_{j}) \biggr\vert . \end{aligned}$$
(3.7)

For \(k< j\) we use an integration by parts as that in [24] to obtain

$$\begin{aligned} & \int _{t_{k-1}}^{t_{k}} (t_{j}-s )^{-\alpha } \biggl[D _{t}^{-}u_{i}^{k}- \frac{\partial u}{\partial s}(x_{i},s) \biggr]\,{\mathrm{d}}s \\ & \quad=-\alpha \int _{t_{k-1}}^{t_{k}} (t_{j}-s )^{-\alpha -1} \bigl[ (s-t_{k-1} )D_{t}^{-}u_{i}^{k}- \bigl(u(x_{i},s)-u(x _{i},t_{k-1}) \bigr) \bigr]\,{\mathrm{d}}s \\ &\quad =-\alpha \bigl[ (\gamma _{1}-t_{k-1} )D_{t}^{-}u_{i} ^{k}- \bigl(u(x_{i},\gamma _{1})-u(x_{i},t_{k-1}) \bigr) \bigr] \int _{t_{k-1}}^{t_{k}} (t_{j}-s )^{-\alpha -1}\,{\mathrm{d}}s \\ &\quad =-\alpha (\gamma _{1}-t_{k-1} ) \biggl[ \frac{\partial u}{ \partial t}(x_{i},\gamma _{2})- \frac{\partial u}{\partial t}(x_{i}, \gamma _{3}) \biggr] \int _{t_{k-1}}^{t_{k}} (t_{j}-s )^{- \alpha -1}\,{\mathrm{d}}s, \end{aligned}$$

where we have used the mean value theorem with \(\gamma _{1},\gamma _{2}, \gamma _{3}\in (t_{k-1},t_{k} )\). Hence, applying a Taylor formula with the integral form of the remainder we can obtain

$$\begin{aligned} &\biggl\vert \int _{t_{k-1}}^{t_{k}} (t_{j}-s )^{-\alpha } \biggl[D _{t}^{-}u_{i}^{k}- \frac{\partial u}{\partial s}(x_{i},s) \biggr]\,{\mathrm{d}}s \biggr\vert \\ & \quad\leq C \triangle t_{k} \int _{t_{k-1}}^{t_{k}} \biggl\vert \frac{\partial ^{2} u}{\partial t^{2}}(x_{i},s) \biggr\vert \,{\mathrm{d}}s \int _{t_{k-1}} ^{t_{k}} (t_{j}-s )^{-\alpha -1}\,{\mathrm{d}}s \\ & \quad\leq C (\triangle t_{k} )^{1-\alpha } \int _{t_{k-1}} ^{t_{k}} \biggl\vert \frac{\partial ^{2} u}{\partial t^{2}}(x_{i},s) \biggr\vert \,{\mathrm{d}}s \end{aligned}$$
(3.8)

for \(k< j\). Similarly, we have

$$\begin{aligned} &\biggl\vert \int _{t_{j-1}}^{t_{j}} (t_{j}-s )^{-\alpha } \biggl[D _{t}^{-}u_{i}^{j}- \frac{\partial u}{\partial s}(x_{i},s) \biggr]\,{\mathrm{d}}s \biggr\vert \\ & \quad= \biggl\vert \frac{\partial u}{\partial t}(x_{i},\gamma _{4})-\frac{ \partial u}{\partial t}(x_{i},\gamma _{5}) \biggr\vert \int _{t_{j-1}}^{t _{j}} (t_{j}-s )^{-\alpha }\,{\mathrm{d}}s \\ & \quad\leq C (\triangle t_{j} )^{1-\alpha } \int _{t_{j-1}} ^{t_{j}} \biggl\vert \frac{\partial ^{2}u}{\partial t^{2}}(x_{i},s) \biggr\vert \,{\mathrm{d}}s, \end{aligned}$$
(3.9)

where we also have used the mean value theorem with \(\gamma _{4},\gamma _{5}\in (t_{j-1},t_{j} )\). By applying Taylor’s formulas about \(x_{i}\) we also have

$$\begin{aligned} \biggl\vert \delta _{x}^{2}u_{i}^{j}- \frac{\partial ^{2}u}{\partial x^{2}}(x _{i},t_{j}) \biggr\vert \leq C (h_{i}+h_{i+1} ) \int _{x_{i-1}} ^{x_{i+1}} \biggl\vert \frac{\partial ^{4}u}{\partial x^{4}}(y,t_{j}) \biggr\vert \,{\mathrm{d}}y \end{aligned}$$
(3.10)

and

$$\begin{aligned} \biggl\vert D_{x}^{0}u_{i}^{j}- \frac{\partial u}{\partial x}(x_{i},t_{j}) \biggr\vert \leq C (h_{i}+h_{i+1} ) \int _{x_{i-1}}^{x_{i+1}} \biggl\vert \frac{ \partial ^{3}u}{\partial x^{3}}(y,t_{j}) \biggr\vert \,{\mathrm{d}}y. \end{aligned}$$
(3.11)

Combining (3.7) with (3.8)–(3.11) we have

$$\begin{aligned} &\bigl\vert L^{N,K} \bigl(u_{i}^{j}-U_{i}^{j} \bigr) \bigr\vert \\ & \quad\leq C\max_{1\leq k \leq j} (\triangle t_{k} )^{1-\alpha } \int _{t_{k-1}}^{t _{k}} \biggl\vert \frac{\partial ^{2} u}{\partial t^{2}}(x_{i},s) \biggr\vert \,{\mathrm{d}}s \\ & \qquad{}+C (h_{i}+h_{i+1} ) \int _{x_{i-1}}^{x_{i+1}} \biggl(x _{i}^{2} \biggl\vert \frac{\partial ^{4}u}{\partial x^{4}}(y,t_{j}) \biggr\vert +x _{i} \biggl\vert \frac{\partial ^{3}u}{\partial x^{3}}(y,t_{j}) \biggr\vert \biggr) \,\mathrm{d}y. \end{aligned}$$
(3.12)

From this we complete the proof. □

Based on the properties of the European option [2, 3, 25] we assume that the solution u satisfies the following regularities:

$$\begin{aligned} \biggl\vert x^{2}\frac{\partial ^{4} u}{\partial x^{4}} \biggr\vert \leq C,\qquad \biggl\vert x\frac{\partial ^{3} u}{\partial x^{3}} \biggr\vert \leq C \quad\text{for } (x,t ) \in \varOmega. \end{aligned}$$
(3.13)

Then applying the maximum principle and the truncation error estimates we have the following bound.

Theorem 3.3

LetUbe the solution of difference scheme (3.3)–(3.5) andube the exact solution of problem (2.4)–(2.6). Then, under the assumption (3.13) we have the following bound:

$$\begin{aligned} \Vert u-U \Vert _{\bar{\varOmega }^{N,K}} \leq C \max_{1\leq i\leq N, 1\leq j\leq K} ( \triangle t_{j} )^{1- \alpha } \int _{t_{j-1}}^{t_{j}} \biggl\vert \frac{\partial ^{2} u}{\partial t ^{2}}(x_{i},s) \biggr\vert \,{\mathrm{d}}s +CN^{-2}, \end{aligned}$$
(3.14)

whereCis a positive constant independent of the mesh.

4 Adaptive time meshes via equidistribution

Since the solution \(u(x,t)\) of the problem exhibits singularity at \(t=0\), one has to use adapted nonuniform time meshes which are fine inside the singular region and coarse in the outer region. To obtain such a mesh, we use the idea of equidistribution principle which has been applied to a wide range of practical problems (see, e.g. [6, 9, 16, 19, 20]). A mesh \(\varOmega ^{K}\) is said to be equidistributed, if

$$\begin{aligned} \int _{t_{j-1}}^{t_{j}}\bar{M}(s)\,\mathrm{d}s= \frac{1}{K} \int _{0}^{T} \bar{M}(s)\,\mathrm{d}s, \quad j=1,2, \dots, K, \end{aligned}$$
(4.1)

where \(\bar{M}(t)\) is called the monitor function. In accordance with the estimate (3.14) in Theorem 3.3, a piecewise constant function is chosen to be the monitor function \(M(x_{i},t)\), i.e.,

$$\begin{aligned} M(x_{i},t)=M_{i}^{j}=1+ \sqrt{ \bigl\vert \delta _{t}^{2}U_{i}^{j} \bigr\vert },\quad t\in (t_{j-1},t_{j} ), \end{aligned}$$
(4.2)

where

$$\begin{aligned} \delta _{t}^{2}U_{i}^{j}= \frac{2}{\triangle t_{j}+\triangle t_{j+1}} \biggl(\frac{U_{i}^{j+1}-U_{i}^{j}}{\triangle t_{j+1}}-\frac{U_{i} ^{j}-U_{i}^{j-1}}{\triangle t_{j}} \biggr),\quad 1\leq j< K. \end{aligned}$$

This type of monitor function has been used in some literature; see e.g., Das and Vigo-Aguiar [6], Gowrisankar and Natesan [9] and Kopteva et al. [16].

In order to solve the equidistribution problem (4.1), we construct the following iteration algorithm for the time discretization:

Step 1. Take the uniform mesh \(\varOmega ^{N,K,(0)}= \{ (x_{i},t_{j}^{(0)} ) \vert 0\leq i\leq N, 0\leq j\leq K \} \) as the initial mesh for the iteration and go to Step 2 with \(k=0\).

Step 2. Compute the discrete solution \(\{ U_{i}^{j,(k)} \} \) satisfying (3.3)–(3.5) with the help of the mesh \(\varOmega ^{N,K,(k)}= \{ (x_{i},t_{j}^{(k)} ) \vert 0\leq i\leq N, 0\leq j\leq K \} \). Set \(\triangle t_{j}^{(k)}=t_{j}^{(k)}-t_{j-1}^{(k)}\) for each j. Compute

$$\begin{aligned} \varPhi _{i}^{j,(k)}=\sum_{p=1}^{j} \triangle t_{p}^{(k)}M_{i}^{p,(k)}, \end{aligned}$$

and find \(i^{*}\) such that

$$\begin{aligned} \varPhi _{i^{*}}^{K,(k)}=\max_{1\leq i< N} \bigl\{ \varPhi _{i}^{K,(k)} \bigr\} , \end{aligned}$$

where \(M_{i}^{p,(k)}\) is the value of the monitor function computed at the pth interior node of the current mesh. We set \(M_{i}^{0,(k)}=M _{i}^{1,(k)}\) and \(M_{i}^{K,(k)}=M_{i}^{K-1,(k)}\).

Step 3. Choose a constant \(C_{0}>1\). The stopping criterion for the iteration algorithm is

$$\begin{aligned} \frac{ {\max_{1\leq j\leq K}\triangle t_{j}^{(k)}M_{i^{*}}^{j,(k)}}}{\varPhi _{i^{*}}^{K,(k)}}\leq \frac{C_{0}}{K}. \end{aligned}$$

If it holds true, then go to Step 5, else continue with Step 4.

Step 4. Set \(Y_{j}^{(k)}=j\varPhi _{i^{*}}^{K,(k)}/K\). Interpolate \((Y_{j}^{(k)},t_{j}^{(k+1)} )\) to \((\varPhi _{i^{*}} ^{j,(k)},t_{j}^{(k)} )\) by using the piecewise linear interpolation. Then generate a new mesh

$$\begin{aligned} \varOmega ^{N,K,(k+1)}=\left \{ \bigl(x_{i},t_{j}^{(k+1)} \bigr)|0 \leq i\leq N, 0\leq j\leq K\right . \bigr\} . \end{aligned}$$

Set \(k=k+1\) and return to Step 2.

Step 5. Set \(\varOmega ^{N,K,*}=\varOmega ^{N,K,(k)}\) and \(\{ U_{i}^{j,*} \} = \{ U_{i}^{j,(k)} \} \), then stop.

5 Numerical experiments

In this section we carry out numerical experiments for two test problems to indicate the efficiency and accuracy of our numerical scheme.

Example 5.1

A fractional differential equation with a known exact solution:

$$\begin{aligned} & \frac{\partial ^{\alpha }u}{\partial t^{\alpha }}-\frac{1}{2}\sigma ^{2}x^{2} \frac{\partial ^{2}u}{\partial x^{2}}-rx\frac{\partial u}{ \partial x}+ru=f(x,t),\quad (x,t)\in (0,1)\times (0,1], \\ & u(x,0)=e^{x}+x+1, \quad x\in (0,1), \\ & u(0,t)=t^{\alpha }+2, \qquad u(1,t)=t^{\alpha }+e+2,\quad t\in (0,1] \end{aligned}$$

with \(\sigma =0.1, r=0.06\) and \(0<\alpha <1\), where \(f(x,t)\) is chosen such that the exact solution is \(u(x,t)=t^{\alpha }+e^{x}+x+1\).

The maximum error is denoted by

$$\begin{aligned} e^{N,K}= {\max_{0\leq i\leq N, 0\leq j\leq K} \bigl\vert u_{i}^{j}-U_{i}^{j} \bigr\vert }, \end{aligned}$$

and the corresponding convergence rate is computed by

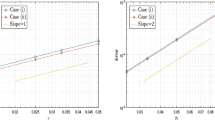
$$\begin{aligned} r^{N}=\log _{2} \bigl(e^{N,K}/e^{2N,2K} \bigr). \end{aligned}$$

The numerical results on an adaptive moving mesh for Example 5.1 are tabulated in Table 1. In order to aid the reader’s understanding of the mesh computed by the algorithm when solving Example 5.1, Fig. 1, which should be read from bottom to top, shows the time mesh after each iteration. Figure 2 represents the final computed time mesh for Example 5.1 with \(\alpha =0.2\), which shows that the mesh points are concentrated near \(t=0\).

Figure 1
figure 1

Evolution of the time mesh for Example 5.1 with \(\alpha =0.2\)

Full size image
Figure 2
figure 2

Final computed time mesh for Example 5.1 with \(\alpha =0.2\)

Full size image
Table 1 Error estimates and convergence rates for Example 5.1
Full size table

Example 5.2

A time-fractional Black–Scholes equation without a known exact solution:

$$\begin{aligned} & \frac{\partial ^{\alpha }u}{\partial t^{\alpha }}-\frac{1}{2}\sigma ^{2}(t)x^{2} \frac{\partial ^{2}u}{\partial x^{2}}-r(t)x\frac{\partial u}{\partial x}+r(t)u=0,\quad (x,t)\in (0,X)\times (0,T], \\ & u(x,0)=\max (x-E,0 ),\quad x\in (0,X), \\ & u(0,t)=0,\qquad u(X,t)=X-Ee^{-rt},\quad t\in (0,T], \end{aligned}$$

with parameters: \(\sigma =0.3(1+t), r=0.04(1+\sin t), E=10, T=1\) and \(X=40\).

The double mesh principle is used to estimate the errors and compute the experiment convergence rates. Set \(\bar{U}^{N,K}(x,t)\) be a linear interpolation of the approximated solution \(\{ U_{i}^{j} \} \) with spatial discretization parameter N and time discretization parameter K and \(\bar{U}^{N,K}(x_{i},t_{j})\) be the value of the function \(\bar{U}^{N,K}(x,t)\) at mesh point \((x_{i},t _{j})\). Then the maximum errors

$$\begin{aligned} e^{N,K}= {\max_{1\leq i\leq N, 1\leq j\leq K} \bigl\vert \bar{U}^{N,K}(x_{i},t_{j})- \bar{U}^{2N,2K}(x_{i},t_{j}) \bigr\vert }, \end{aligned}$$

and the convergence rates

$$\begin{aligned} r^{N}=\log _{2} \bigl(e^{N,K}/e^{2N,2K} \bigr) \end{aligned}$$

for Example 5.2 are listed in Table 2. The generation of adapted moving meshes after each iteration for the time discretization is depicted in Fig. 3. The final computed time mesh for the time-fractional Black–Scholes equation with \(\alpha =0.2\) is depicted in Fig. 4, which also shows that the mesh points are concentrated near \(t=0\). The computed option value U is depicted in Fig. 5, which shows that the numerical solution by our method is non-oscillatory.

Figure 3
figure 3

Evolution of the time mesh for Example 5.2 with \(\alpha =0.2\)

Full size image
Figure 4
figure 4

Final computed time mesh for Example 5.2 with \(\alpha =0.2\)

Full size image
Figure 5
figure 5

Computed option value U for Example 5.2 with \(\alpha =0.2\)

Full size image
Table 2 Error estimates and convergence rates for Example 5.2
Full size table

Tables 1 and 2 show that the computed solution converges to the exact solution on an adaptive moving mesh with first order accuracy and the numerical results do not depend strongly on the value of α, which supports the convergence estimate of Theorem 3.3. From these results we confirm that our method with an adaptive moving mesh is more accurate than the method on the uniform mesh.