1 Introduction

Compartmental models in epidemiology are well used to simplify mathematical modeling of infectious diseases [1]. Their origin is in the early 20th century, with an important early work being that by Kermack and McKendrick in 1927 [2]. The population is subdivided into three groups: susceptible, infectious and recovered, and the model is referred to as an SIR epidemic model. The model is applicable to infectious diseases such as measles, chickenpox, or mumps, where infection confers immunity.

For many important infections there is a significant incubation period during which an individual has been infected but is not yet infectious himself [3]. During this period the individual is in compartment E, known as the exposed term, and such models are called SEIR models. To express the distribution of incubation period, we consider age-structured SEIR framework. Let \(S(t)\), \(E(t)\), \(I(t)\), and \(R(t)\) be the fraction of susceptible, exposed, infectious, and recovered population at time t, respectively. Motivated by [4,5,6], consider a non-autonomous SEIR model of integro-differential type whose transmission rate is time-dependent:

$$\begin{aligned}& \frac{\mathrm {d}S(t)}{\mathrm {d}t} = \mu -\beta (t)S(t)I(t)-\mu S(t), \end{aligned}$$
(1a)
$$\begin{aligned}& E(t) =E_{0}P(t)\exp (-\mu t)+ \int _{0}^{t} \beta (t-u) S(t-u) I(t-u) P(u) \exp (-\mu u) \,\mathrm {d}u, \end{aligned}$$
(1b)
$$\begin{aligned}& \frac{\mathrm {d}I(t)}{\mathrm {d}t} = \int _{0}^{t} \beta (t-u)S(t-u)I(t-u)\bigl[-P _{u}(u)\bigr]\exp (-\mu u) \,\mathrm {d}u -(\gamma +\mu ) I(t), \end{aligned}$$
(1c)
$$\begin{aligned}& \frac{\mathrm {d}R(t)}{\mathrm {d}t} = \gamma I(t)-\mu R(t), \end{aligned}$$
(1d)

where \(1/\gamma \) is the mean period of infectiousness, \(P(u)\) is the probability of remaining incubated (assumed asymptomatic and not infectious) to time u from entering, and μ is the natural mortality. We consider a transmission rate as time-dependent function, \(\beta (t)\). Choosing time-dependent transmission rate is reasonable because, for example, the transmission rate could decay after some control measures for epidemic are introduced [7]. Also \(P_{u}\) denotes the derivative with respect to u. The initial conditions are given as \(S(0)=S_{0}\), \(E(0)=E _{0}\), \(I(0)=I_{0}\), \(R(0)=R_{0}\), and \(S_{0}+E_{0}+I_{0}+R_{0}=1\). In general, it is reasonable to assume that a function \(P:[0,\infty ) \rightarrow [0,1] \in \mathcal{L}^{1}\) is Lebesgue integrable, differentiable a.e., non-increasing, \(P(0)=1\), and \(\lim_{t\rightarrow \infty } P(t) = 0\) [8]. Additionally, let T be a continuous random variable of incubation period of some infectious diseases. If we know the distribution of incubation period heuristically, we can define P by

$$\begin{aligned} P(u)=\mathbb{P}(T>u)= 1-F(u), \end{aligned}$$
(2)

where F is a cumulative density function of random variable of infectious period T; P is called the survival function. Many previous studies have developed various survival functions P such as Dirac-delta [9, 10], exponential [11], gamma [12,13,14,15], Mittag-Leffler [16, 17], and joint [18, 19] types. In some cases, this framework of SEIR model can be simplified by a system of ordinary or fractional differential equations with various incubation period distribution (see Table 1).

Table 1 SEIR models generated by various distributions with delay effect in the previous papers
Full size table

Following these ideas, in this work, we construct an SEIR epidemic model, which is named Coxian-distributed SEIR model, to incorporate empirical incubation period distribution. Coxian distribution, as one of the phase-type distributions, can be considered as a mixture of hypo- and hyper-exponential distributions. The novelty of the distribution is the density in the class of all non-negative distribution functions [20] and so all types of incubation period are approximated by a Coxian distribution. A basic reproduction number, \(R_{0}\), was derived. Applying Lyapunov theory, we show that the basic reproduction number determines the global stability of equilibrium of our model with constant transmission rate. We also give an application illustrating how to use a Coxian-distributed SEIR model with empirical incubation period data. The limitation of the model is also discussed in the last section.

2 Derivation of Coxian-distributed SEIR model

A Coxian distribution with n phases is defined as the time until absorption into state 0, starting from state n, of the Markov process with discrete states in continuous time. A focal state, X, can be partitioned into n substates \(X_{n},\ldots,X_{1}\), each with independent dwell times that are exponentially distributed with rates \(\lambda _{i}\), \(i=n,n-1,\ldots,1\). Inflow into the state \(X_{n}\) can be described by a non-negative, integrable inflow rate \({I}_{X}(t)\). Particles that transition out of a substate \(X_{k}\) at time t transition into either a different substate \(X_{k-1}\) with probability \(\bar{p}_{k-1}\), or enter the recipient state \(X_{0}\) with probability \(p_{k-1}=1-\bar{p}_{k-1}\), for \(k=n,n-1,\ldots,1\). Then, Coxian-distributed random variable X [20] is the time until absorption in \(X_{0}\) starting from state n, and the probability density function \(f_{X}\) is given as \(f_{X}(t)=\mathbf{p} \exp {(t\mathbf{Q})}\mathbf{q}\) where

$$\begin{aligned} \begin{gathered} \mathbf{p} = \begin{bmatrix} 1&0& \ldots &0 \end{bmatrix} \in M_{1\times n}(\mathbb{R}), \\ \mathbf{Q} = \begin{bmatrix} -\lambda _{n}&\bar{p}_{n-1}\lambda _{n} & 0 & \ldots & \ldots &0 \\ 0&- \lambda _{n-1}&\bar{p}_{n-2}\lambda _{n-1}&0 & \ldots &0\\ \vdots &\vdots &\vdots &\ddots & \vdots &\vdots \\ 0& \ldots & \ldots & \ldots &-\lambda _{2}&\bar{p}_{1}\lambda _{2}\\ 0& \ldots & \ldots & \ldots &0&-\lambda _{1} \end{bmatrix} \in M_{n\times n}(\mathbb{R}), \\ \mathbf{q} =-\mathbf{Q1}= \begin{bmatrix} p_{n-1}\lambda _{n} &p_{n-2}\lambda _{n-1}& \ldots &p_{1}\lambda _{2} & \lambda _{1} \end{bmatrix} ^{\top }\in M_{n\times 1}(\mathbb{R}), \end{gathered} \end{aligned}$$
(3)

1 is an \(n\times 1\) vector of ones and Q is the transition rate matrix, \(0< p_{i}<1\) for \(i=1,2,\ldots,n-1\) and \(\lambda _{i}>0\) for \(i=1,2,\ldots,n\). The survival function P is given as

$$\begin{aligned} P(t)=\mathbf{p}\exp ({t\mathbf{Q}})\mathbf{1}. \end{aligned}$$
(4)

For convenience, define

$$ \hat{f}(t):= \int _{t}^{\infty }\exp (-\mu u)f_{X}(u) \,\mathrm {d}u \in (0,1). $$

Then, the Laplace transform \(\mathcal{L}\) of \(f_{X}\) is \(\hat{f}(0)\) from the definition of Laplace transform, and given explicitly by

$$\begin{aligned}{} [\mathcal{L}f_{X}](s)=\mathbf{p}(s\mathbf{I}- \mathbf{Q})^{-1} \mathbf{q} =\sum_{i=0}^{n-1} \Biggl[ a_{i} \prod_{j=1}^{n-i} \frac{ \lambda _{n+1-j}}{s+\lambda _{n+1-j}} \Biggr], \end{aligned}$$
(5)

where I is the \(n\times n\) identity matrix and \(a_{i}=p _{i}\prod_{j=1}^{n-1-i}\bar{p}_{j+i}\).

Derivation of Coxian-distributed SEIR model is as follows: assume that the infectious period is Coxian-distributed with the survival function (4) in the model (12). First, note that if we put the \(1\times n\) vector P as:

$$\begin{aligned} \mathbf{P}(t) &:=\mathbf{p}\exp (t\mathbf{Q})= \begin{bmatrix} P_{n}&P_{n-1}& \ldots &P_{2}&P_{1} \end{bmatrix} , \end{aligned}$$

where \(P_{i}\)’s are functions of t, then the survival function P is expressed as

$$\begin{aligned} P(t)=\sum_{i=1}^{n} P_{n}(t). \end{aligned}$$
(6)

Since \(\frac{\mathrm {d}[\exp {(t\mathbf{Q})}]}{\mathrm {d}t}= \exp {(t \mathbf{Q})}\mathbf{Q}\), \(\mathbf{P}'(t)=\mathbf{P}(t)\mathbf{Q}\) holds,

$$\begin{aligned} \begin{gathered} \frac{\mathrm {d}P_{n}}{\mathrm {d}t} = -\lambda _{n} P_{n}, \\ \frac{\mathrm {d}P_{i}}{\mathrm {d}t} = \bar{p}_{i}\lambda _{i+1}P_{i+1}- \lambda _{i}P_{i}, \quad \text{for } i=n-1,\ldots,1, \end{gathered} \end{aligned}$$
(7)

and

$$\begin{aligned} \frac{\mathrm {d}P(t)}{\mathrm {d}t}=\sum _{i=1}^{n}\frac{\mathrm {d}P _{i}(t)}{\mathrm {d}t}=-\lambda _{1} P_{1}(t)-\sum_{i=1}^{n-1}p_{i} \lambda _{i+1}P_{i+1}(t). \end{aligned}$$
(8)

Now, if we put (4) into (1b), then (1b) will have the form from (6):

$$ E(t)=\sum_{i=1}^{n} \int _{0}^{\infty }P_{i}(u) \beta (t-u) S(t-u) I(t-u) \exp (-\mu u) \,\mathrm {d}u. $$

So if we put

$$\begin{aligned} E_{i}(t)= \int _{0}^{\infty }P_{i}(u) \beta (t-u) S(t-u) I(t-u) \exp (- \mu u) \,\mathrm {d}u, \end{aligned}$$
(9)

for \(i=n,n-1,\ldots,1\) and differentiate (9) for each \(i=n,n-1,\ldots,1\), then (7) yields:

$$\begin{aligned} \begin{gathered} \frac{\mathrm {d}E_{n}(t)}{\mathrm {d}t} =\beta (t) S(t)I(t) - (\lambda _{n}+\mu ) E_{n}(t), \\ \frac{\mathrm {d}E_{i}(t)}{\mathrm {d}t} =\bar{p}_{i}\lambda _{i+1} E _{i+1}(t)-(\lambda _{i}+\mu )E_{i}(t), \quad i=n-1,\ldots,2,1, \end{gathered} \end{aligned}$$
(10)

and so substituting (8) into (1c) yields

$$ \begin{aligned} \frac{\mathrm {d}I(t)}{\mathrm {d}t}&= \int _{0}^{t} \beta (t-u)S(t-u)I(t-u) \Biggl[ \lambda _{1} P_{1}(u)+ \sum_{i=1}^{n-1}p_{i} \lambda _{i+1}P_{i+1}(u) \Biggr] \exp (-\mu u) \,\mathrm {d}u \\&\quad{} -( \gamma +\mu ) I(t),\end{aligned} $$

and (1c) becomes

$$\begin{aligned} \frac{\mathrm {d}I(t)}{\mathrm {d}t}=\lambda _{1} E_{1}(t)+\sum_{i=1}^{n-1} p_{i}\lambda _{i+1} E_{i+1}(t) - (\gamma +\mu )I(t). \end{aligned}$$
(11)

From (10) and (11), targeted n-chained Coxian-distributed SEIR model is derived from (1a)–(1d) when we put \(p_{0}=1\) as follows:

$$\begin{aligned} \begin{gathered} \frac{\mathrm {d}S(t)}{\mathrm {d}t} =\mu -\beta (t) S(t)I(t)-\mu S(t), \\ \frac{\mathrm {d}E_{n}(t)}{\mathrm {d}t} =\beta (t) S(t)I(t) - (\lambda _{n}+\mu )E_{n}(t), \\ \frac{\mathrm {d}E_{i}(t)}{\mathrm {d}t} =\bar{p}_{i}\lambda _{i+1} E _{i+1}(t)-(\lambda _{i}+\mu )E_{i}(t), \quad i=n-1,\ldots,2,1, \\ \frac{\mathrm {d}I(t)}{\mathrm {d}t} =\sum_{i=0}^{n-1} p_{i} \lambda _{i+1} E_{i+1}(t) - (\gamma +\mu )I(t), \\ \frac{\mathrm {d}R(t)}{\mathrm {d}t} =\gamma I(t)-\mu R(t), \end{gathered} \end{aligned}$$
(12)

with \(\sum_{i=1}^{n}E_{i}(t)=E(t)\). A schematic diagram for the model (12) is depicted in Fig. 1.

Figure 1
figure 1

Scheme of model (12)

Full size image

Basic properties of the model are as follows: the region

$$ \varOmega = \Biggl\{ (S,E_{n},E_{n-1}, \ldots,E_{1},I,R)\in \mathbb{R} ^{n+3}_{+}:S+ \sum_{j=1}^{n} E_{j}+I+R \equiv 1 \Biggr\} $$

is obviously positive-invariant. Also if the initial data \(S(0)\), \(E _{i}(0)\), \(I(0)\), and \(R(0)\) for \(i=n,n-1,\ldots,1\) are positive, then the solutions \(S(t)\), \(E_{i}(t)\), \(I(t)\), and \(R(t)\) of the model (12) are non-negative for all \(t>0\). Indeed, if we assume that there exists \(t_{1}>0\) such that \(S(t)>0\), \(E_{i}(t)>0\), \(I(t)>0\), \(R(t)>0\), \(i=n,n-1,\ldots,1\) in \(t \in [0,t_{1})\) and \(S(t_{1})\cdot \prod_{i=1} ^{n} E_{i}(t_{1}) \cdot I(t_{1}) \cdot R(t_{1})=0\) (i.e., one of the states is 0 at time \(t_{1}\)), then

$$ \frac{\mathrm {d}S(t)}{\mathrm {d}t}=\mu -\bigl(\zeta (t)+\mu \bigr) S(t)\ge -\bigl( \zeta (t)+ \mu \bigr)S(t). $$

When we take the force of infection \(\zeta (t)=\beta (t)I(t)\), we get that

$$ S(t_{1})\ge S(0) \exp \biggl\{ -\mu t_{1}- \int _{0}^{t_{1}}\zeta (u) \,\mathrm {d}u \biggr\} >0 $$

holds by Gronwall inequality. Similarly, it can be shown that \(E_{i}(t_{1})>0\), \(I(t_{1})>0\), and \(R(t_{1})>0\) for \(i=n,n-1,\ldots,1\), and this yields a contradiction.

3 The basic reproduction number, \(R_{0}\)

When the parameters are constant, we can compute the basic reproduction number. Assume the number of infectious humans is small in the early phase, i.e., \(S\approx 1\). Consider \(\beta (t)\equiv \bar{\beta }\). Define the average time that an individual remains in the exposed class becoming infectious without dying, P̂, as

$$ \hat{P}= \int _{0}^{\infty }\exp (-\mu u)P(u) \,\mathrm {d}u. $$

We note that μP̂ represents the probability that an exposed individual will die during the course of incubation, and so the probability of surviving the exposed class is \(1-\mu \hat{P}\). Note that since \(0 \le P(t)\le 1\) for \(t\ge 0\), the inequality

$$ 0\le \hat{P} \le \int _{0}^{\infty }\exp (-\mu u) \,\mathrm {d}u = 1/\mu $$

holds and so the probability μP̂ is well defined. From the definition of the basic reproduction number, we can represent this number, denoted by \(R_{0}\), as

$$ R_{0}=\bar{\beta } \cdot (1-\mu \hat{P})\cdot \frac{1}{\gamma +\mu }. $$

Since \(\mu \hat{P} = 1+\int _{0}^{\infty }\exp {(-\mu u)}P'(u) \,\mathrm {d}u\), integrating by parts and using the relation \(P'(t)=-f_{X}(t)\) in the usual sense, we get

$$ 1-\mu \hat{P} = \int _{0}^{\infty }\exp (-\mu u)f_{X}(u) \,\mathrm {d}u= \hat{f}(0) = [\mathcal{L}f_{X}](\mu ). $$

From (5), \(R_{0}\) is explicitly represented as

$$\begin{aligned} R_{0}=\frac{\bar{\beta }}{\gamma +\mu } \sum _{i=0}^{n-1} \Biggl[ a _{i} \prod _{k=1}^{n-i} \frac{\lambda _{n+1-k}}{\lambda _{n+1-k}+ \mu } \Biggr], \end{aligned}$$
(13)

where \(a_{i}=p_{i}\prod_{j=1}^{n-1-i}\bar{p}_{j+i}\). Note that if we ignore the demographic part, i.e., \(\mu =0\), then \(R_{0}\) is expressed as \(\bar{\beta }/\gamma \), as in the classical model.

4 Equilibria analysis for the case of constant transmission rate

Consider the case when \(\beta (t)=\bar{\beta }\), a positive constant. Model (12) has an equilibrium

$$\begin{aligned} \mathcal{E}^{d}=\bigl(S^{d},E_{n}^{d},E_{n-1}^{d}, \ldots,E_{1}^{d},I^{d},R ^{d} \bigr)=(1,0,0,\ldots,0), \end{aligned}$$
(14)

which is called the disease-free equilibrium. Now we prove the following result:

Theorem 1

The disease-free equilibrium, \(\mathcal{E}^{d}\), of model (12) is globally asymptotically stable in the domainΩif \(R_{0}\le 1\).

Proof

Consider the function

$$\begin{aligned} V=\sum_{j=1}^{n} w_{j} E_{j}+I, \end{aligned}$$

for positive constants \(w_{j}\), \(j=1,\ldots,n\), where

$$\begin{aligned} w_{j}=\sum_{l=1}^{j} \alpha _{l}^{j}\prod_{k=l}^{j} \frac{\lambda _{k}}{ \lambda _{k}+\mu }, \end{aligned}$$

with

$$ \alpha _{l}^{j}= \textstyle\begin{cases} p_{j-1} &\text{if }l=j, \\ p_{l-1}\prod_{\xi =l}^{j-1}\bar{p}_{\xi } &\text{otherwise, i.e., if }l=1,2,\ldots,j-1, \end{cases} $$

for fixed j. Then, we can observe that \(w_{n}={(\gamma +\mu )R_{0}}/ {\bar{\beta }}\). The derivative of V with respect to time t is given by

$$\begin{aligned} \begin{aligned}[b] \frac{\mathrm {d}V}{\mathrm {d}t} &=\sum _{j=1}^{n}w_{j} \frac{\mathrm {d}E _{j}}{\mathrm {d}t}+\frac{\mathrm {d}I}{\mathrm {d}t} \\ &=w_{n} \bigl[\bar{\beta }S(t)I(t)-(\lambda _{n}+\mu )E_{n}(t) \bigr]+ \sum_{j=1}^{n-1}w_{j} \bigl[\bar{p}_{j}\lambda _{j+1}E_{j+1}(t)-( \lambda _{j}+\mu )E_{j}(t) \bigr] \\ & \quad{} +\sum_{j=0}^{n-1}p_{j} \lambda _{j+1}E_{j+1}(t)-(\gamma +\mu )I(t) \\ &=w_{n}\bar{\beta }S(t)I(t)-(\gamma +\mu )I(t)+\sum _{j=2}^{n} \bigl[-w _{j}(\lambda _{j}+\mu )+w_{j-1}\bar{p}_{j-1}\lambda _{j}+p_{j-1}\lambda _{j} \bigr]E_{j}(t) \\ & \quad{} +\bigl[p_{0}\lambda _{1}-w_{1}( \lambda _{1}+\mu )\bigr]E_{1}(t), \end{aligned} \end{aligned}$$
(15)

by rearrangement. Moreover, since

$$\begin{aligned} p_{0}\lambda _{1}-w_{1}( \lambda _{1}+\mu )=p_{0}\lambda _{1}-p_{0} \lambda _{1}=0, \end{aligned}$$
(16)

we obtain

$$\begin{aligned} w_{j} &=\sum_{l=1}^{j} a_{l}^{j} \prod_{k=l}^{j} \frac{\lambda _{k}}{ \lambda _{k}+\mu } \\ &=a_{1}^{j}\prod_{k=1}^{j} \frac{\lambda _{k}}{\lambda _{k}+\mu }+a _{2}^{j}\prod _{k=2}^{j}\frac{\lambda _{k}}{\lambda _{k}+\mu }+\cdots +a_{j}^{j}\frac{\lambda _{j}}{\lambda _{j}+\mu } \\ &=\bar{p}_{j-1}\frac{\lambda _{j}}{\lambda _{j}+\mu }\underbrace{ \Biggl[a_{1}^{j-1}\prod_{k=1}^{j-1} \frac{\lambda _{k}}{\lambda _{k}+ \mu }+a_{2}^{j-1}\prod _{k=2}^{j-1}\frac{\lambda _{k}}{\lambda _{k}+ \mu }+\cdots +a_{j-1}^{j-1}\frac{\lambda _{j-1}}{\lambda _{j-1}+ \mu } \Biggr]}_{=\sum _{l=1}^{j-1}a_{l}^{j-1}\prod _{k=l}^{j-1}\frac{ \lambda _{k}}{\lambda _{k}+\mu }=w_{j-1}} \\ & \quad{} +a_{j}^{j}\frac{\lambda _{j}}{\lambda _{j}+\mu } \quad \bigl(\text{since }a_{k}^{j}=\bar{p}_{j-1} \cdot a_{k}^{j-1}\bigr) \\ &=\frac{\lambda _{j}}{\lambda _{j}+\mu } [\bar{p}_{j-1}w_{j-1} +p_{j-1} ], \end{aligned}$$

and so we can get the recurrence relation

$$\begin{aligned} w_{j}(\lambda _{j}+\mu )=w_{j-1}\bar{p}_{j-1}\lambda _{j}+p_{j-1} \lambda _{j}, \end{aligned}$$
(17)

for each \(j=2,3,\ldots,n\). Thus, if we substitute (16) and (17) into (15), we obtain

$$\begin{aligned} \frac{\mathrm {d}V}{\mathrm {d}t} &=w_{n}\bar{\beta }SI-(\gamma +\mu )I+ \sum _{j=2}^{n}\underbrace{ \bigl[-w_{j}(\lambda _{j}+\mu )+w_{j-1} \bar{p}_{j-1}\lambda _{j}+p_{j-1}\lambda _{j} \bigr]}_{\text{$=0$ by (17)}}E_{j} \\ & \quad{} +\underbrace{\bigl[p_{0}\lambda _{1}-w_{1}( \lambda _{1}+\mu )\bigr]}_{\text{$=0$ by (16)}}E_{1} \\ &=w_{n} \bar{\beta }SI-(\gamma +\mu )I \\ &\le w_{n}\bar{\beta }I-(\gamma +\mu )I \quad (\text{since }S\le 1\text{; equality holds iff }S=1) \\ &=(\gamma +\mu ) \biggl( \underbrace{w_{n}\frac{\bar{\beta }}{ \gamma +\mu }}_{=R_{0}}-1 \biggr)I \\ &=(\gamma +\mu ) (R_{0}-1)I\le 0 \quad \text{if }R_{0} \le 1. \end{aligned}$$

Therefore, \(V'\le 0\) if \(R_{0}\le 1\) and \(V'=0\) if and only if \(E_{n}=E_{n-1}=\cdots =E_{1}=I=0\). Also, substituting \(I=0\) into the equations for S and R shows that \(S\rightarrow 1\) and \(R\rightarrow 0\) as \(t\rightarrow \infty \). This means V is a Lyapunov function in the domain Ω. So from the LaSalle’s invariance principle, every solution to the equations in model (12), with initial conditions in Ω, approaches \(\mathcal{E}^{d}\) as \(t\rightarrow \infty \). Since Ω is positively invariant, the disease-free equilibrium \(\mathcal{E}^{d}\) is globally asymptotically stable in Ω if \(R_{0}\le 1\). □

Next we consider the endemic equilibrium, \(\mathcal{E}^{\ast }=(S^{ \ast },E_{n}^{\ast },\ldots,E_{1}^{\ast },I^{\ast },R^{\ast })\), whose components are all positive.

Proposition 2

The endemic equilibrium \(\mathcal{E}^{\ast }\)of model (12) exists uniquely when \(R_{0}>1\), and there is no endemic equilibrium otherwise.

Proof

Solving the algebraic system in (12) for fixed points gives

$$\begin{aligned}& \bar{\beta }S^{\ast }I^{\ast } = \mu \bigl(1-S^{\ast } \bigr), \end{aligned}$$
(18a)
$$\begin{aligned}& \bar{\beta }S^{\ast }I^{\ast } = (\lambda _{n}+\mu )E_{n}^{\ast }, \end{aligned}$$
(18b)
$$\begin{aligned}& E_{i}^{\ast } =\frac{1}{\lambda _{i}+\mu } \bar{p}_{i} \lambda _{i+1}E _{i+1}^{\ast }\quad \text{for }i=n-1,\ldots,2,1, \end{aligned}$$
(18c)
$$\begin{aligned}& I^{\ast } =\frac{1}{\gamma +\mu }\sum_{i=0}^{n-1}p_{i} \lambda _{i+1}E _{i+1}^{\ast }= \frac{1}{\gamma +\mu } \bar{\beta } S^{\ast }I^{ \ast }(1-\mu \hat{P}), \end{aligned}$$
(18d)
$$\begin{aligned}& R^{\ast } =\frac{\gamma }{\mu } I^{\ast }. \end{aligned}$$
(18e)

From (18a) and (18b),

$$\begin{aligned} E_{n}^{\ast }=\mu \bigl(1-S^{\ast }\bigr) \frac{1}{\lambda _{n}+\mu }, \end{aligned}$$
(19a)

and from (18c), we get \(E_{j}^{\ast }\) for \(j=n-1,n-2,\ldots,1\) recursively as

$$\begin{aligned} E_{j}^{\ast }=\mu \bigl(1-S^{\ast }\bigr) \frac{1}{\lambda _{j}+\mu } \prod _{k=j+1}^{n} \frac{\bar{p}_{k-1}\lambda _{k}}{\lambda _{k}+ \mu }. \end{aligned}$$
(19b)

Substituting (19a)–(19b) into (18d) yields

$$\begin{aligned} I^{\ast } &=\mu \bigl(1-S^{\ast } \bigr) \frac{1}{\gamma +\mu }\sum_{i=0}^{n-1}p _{i}\lambda _{i+1}E_{i+1}^{\ast }, \\ &=\mu \bigl(1-S^{\ast }\bigr) \frac{1}{\gamma +\mu } \\ &\quad{}\times \Biggl[ p_{0}\frac{ \lambda _{1}}{\lambda _{1}+\mu }\prod_{k=2}^{n} \frac{\bar{p}_{k-1} \lambda _{k}}{\lambda _{k}+\mu } + p_{1}\frac{\lambda _{2}}{\lambda _{2}+\mu }\prod _{k=3}^{n}\frac{\bar{p}_{k-1}\lambda _{k}}{\lambda _{k}+\mu }+\cdots + p_{n-1}\frac{\lambda _{n}}{\lambda _{n}+\mu } \Biggr] \\ &=\mu \bigl(1-S^{\ast }\bigr) \frac{1}{\gamma +\mu } \sum _{i=0}^{n-1} \Biggl[a_{i} \prod _{k=i+1}^{n} \frac{\lambda _{k}}{\lambda _{k}+ \mu } \Biggr] \\ &=\mu \bigl(1-S^{\ast }\bigr) \frac{1}{\gamma +\mu } \sum _{i=0}^{n-1} \Biggl[ a_{i} \prod _{k=1}^{n-i} \frac{\lambda _{n+1-k}}{\lambda _{n+1-k}+ \mu } \Biggr] \\ &=\frac{\mu }{\bar{\beta }} \bigl(1-S^{\ast }\bigr) R_{0}. \end{aligned}$$
(20)

Moreover, if we substitute (20) into (18a), then

$$\begin{aligned} I^{\ast }=\frac{\mu }{\bar{\beta }} (R_{0}-1), \end{aligned}$$

since \(S^{\ast }\neq 1\). Hence \(I^{\ast }>0\) if \(R_{0}>1\). Also, if \(I^{\ast }>0\), then \(0< S^{\ast }=1/R_{0}<1\) and \(R^{\ast }>0\) from (18e). Moreover, \(E_{i}\)’s are positive since \(1-S^{\ast }>0\). Conversely, if \(R_{0}\le 1\), then the model has no positive equilibrium. □

Finally, we claim the following:

Theorem 3

The endemic equilibrium, \(\mathcal{E}^{\ast }\), of model (12) is globally asymptotically stable in the interior ofΩif \(R_{0}>1\).

Proof

Motivated by [21], consider a Lyapunov function \(V_{e}\equiv V_{e}(S,I)\) given as

$$ V_{e} = V_{1e}+V_{2e}, $$

where

$$\begin{aligned}& V_{1e} =\hat{f}(0)\cdot G \biggl(\frac{S}{S^{\ast }} \biggr)+I^{ \ast }\cdot G \biggl(\frac{I}{I^{\ast }} \biggr), \\& V_{2e} =\bar{\beta }S^{\ast }I^{\ast } \int _{0}^{\infty }\hat{f}(u) \cdot G \biggl( \frac{S(t-u)I(t-u)}{S^{\ast }I^{\ast }} \biggr) \,\mathrm {d}u, \end{aligned}$$

and \(G(x)=x-1-\ln x\). Notice that \(V_{e}=0\) when \(S=S^{\ast }, E_{n}=E _{n}^{\ast },\ldots, R=R^{\ast }\) and \(V_{e}>0\) otherwise. Differentiating \(V_{1e}\) and \(V_{2e}\) with respect to time t yields

$$\begin{aligned} \frac{\mathrm {d}V_{1e}}{\mathrm {d}t} =& \hat{f}(0) \biggl(1-\frac{S ^{\ast }}{S(t)} \biggr) \bigl[\mu -\bar{\beta }S(t)I(t)- \mu S(t) \bigr] \\ &{} + \biggl(1-\frac{I^{\ast }}{I(t)} \biggr) \biggl[ \int _{0}^{\infty }\bar{ \beta }S(t-u)I(t-u)\exp (-\mu u)f_{X}(u) \,\mathrm {d}u-(\gamma +\mu )I(t) \biggr] \\ =&-\hat{f}(0) \cdot \mu \frac{(S(t)-S^{\ast })^{2}}{S(t)}+ \hat{f}(0)\cdot \bar{\beta }S^{\ast }I^{\ast }-\hat{f}(0)\cdot \bar{ \beta }S(t)I(t) \\ &{}- \hat{f}(0)\cdot \bar{\beta } \frac{{S^{\ast }} ^{2}}{S(t)} I^{\ast }+ \hat{f}(0) \cdot \bar{\beta } S^{\ast }I(t) \\ &{} + \int _{0}^{\infty }\bar{\beta }S(t-u) I(t-u)\exp (-\mu u)f_{X}(u) \,\mathrm {d}u -\frac{I(t)}{I^{\ast }} \int \bar{\beta } S^{\ast }I^{\ast }\exp (-\mu u)f_{X}(u) \,\mathrm {d}u \\ &{} -\frac{I^{\ast }}{I(t)} \int _{0}^{\infty }\bar{\beta }S(t-u) I(t-u) \exp (- \mu u)f_{X}(u) \,\mathrm {d}u \\ &{} + \int _{0}^{\infty }\bar{\beta }S^{ \ast }I^{\ast } \exp (-\mu u)f_{X}(u) \,\mathrm {d}u, \end{aligned}$$
(21)

due to relations (18a) and (18d), and

$$\begin{aligned} \begin{aligned}[b] \frac{\mathrm {d}V_{2e}}{\mathrm {d}t} &= \frac{\mathrm {d}}{\mathrm {d}t} \bar{\beta }S^{\ast }I^{\ast } \int _{0}^{\infty }\hat{f}(u)\cdot G \biggl( \frac{S(t-u)I(t-u)}{S^{\ast }I^{\ast }} \biggr) \,\mathrm {d}u \\ &=\hat{f}(0)\cdot \bar{\beta }S^{\ast }I^{\ast }\cdot G \biggl(\frac{S(t)I(t)}{S ^{\ast }I^{\ast }} \biggr)-\bar{\beta }S^{\ast }I^{\ast } \int _{0}^{ \infty }G \biggl(\frac{S(t-u)I(t-u)}{S^{\ast }I^{\ast }} \biggr) \,\mathrm {d}\hat{f}(u) \\ &=\hat{f}(0)\cdot \bar{\beta }S^{\ast }I^{\ast }\cdot G \biggl(\frac{S(t)I(t)}{S ^{\ast }I^{\ast }} \biggr) \\ & \quad{}-\bar{\beta }S^{\ast }I^{\ast } \int _{0}^{ \infty }G \biggl(\frac{S(t-u)I(t-u)}{S^{\ast }I^{\ast }} \biggr) \exp (-\mu u)f_{X}(u) \,\mathrm {d}u \\ &=\hat{f}(0)\cdot \bar{\beta } \biggl(S(t)I(t)-S^{\ast }I^{\ast }-S ^{\ast }I^{\ast }\cdot \ln \frac{S(t)I(t)}{S^{\ast }I^{\ast }} \biggr) \\ & \quad{} - \int _{0}^{\infty } \biggl[\bar{\beta }S(t-u)I(t-u)- \bar{\beta }S^{ \ast }I^{\ast }-\bar{\beta }S^{\ast }I^{\ast } \cdot \ln \frac{S(t-u)I(t-u)}{S ^{\ast }I^{\ast }} \biggr] \\ & \quad{}\times \exp (-\mu u)f_{X}(u) \,\mathrm {d}u \\ &=\hat{f}(0)\cdot \biggl(\bar{\beta }S(t)I(t)-\bar{\beta }S^{\ast }I ^{\ast }\cdot \ln \frac{S(t)I(t)}{S^{\ast }I^{\ast }} \biggr) \\ & \quad{} - \int _{0}^{\infty } \biggl[\bar{\beta }S(t-u)I(t-u)- \bar{\beta }S^{ \ast }I^{\ast }\cdot \ln \frac{S(t-u)I(t-u)}{S^{\ast }I^{\ast }} \biggr] \\ & \quad{}\times \exp (-\mu u)f_{X}(u) \,\mathrm {d}u. \end{aligned} \end{aligned}$$
(22)

Combining (21) and (22), we get

$$\begin{aligned} \frac{\mathrm {d}V_{e}}{\mathrm {d}t} &= \frac{\mathrm {d}V_{1e}}{\mathrm {d}t}+\frac{\mathrm {d}V_{2e}}{\mathrm {d}t} \\ &= -\hat{f}(0) \cdot \mu \frac{(S(t)-S^{\ast })^{2}}{S(t)}- \hat{f}(0)\cdot \bar{\beta }S^{\ast }I^{\ast } \biggl[\frac{S^{ \ast }}{S(t)}-2 \biggr] \\ & \quad{} - \int _{0}^{\infty }\bar{\beta }S^{\ast }I^{\ast } \biggl[\frac{S(t-u)I(t-u)}{S ^{\ast }I(t)} -\ln \frac{S(t-u)I(t-u)}{S(t)I(t)} \biggr]\exp (- \mu u)f_{X}(u) \,\mathrm {d}u \\ &= -\hat{f}(0) \cdot \mu \frac{(S(t)-S^{\ast })^{2}}{S(t)}- \hat{f}(0)\cdot \bar{\beta }S^{\ast }I^{\ast }\cdot G \biggl(\frac{S \ast }{S(t)} \biggr)+\hat{f}(0)\cdot \bar{\beta }S^{\ast }I^{\ast } \biggl[1- \ln \frac{S^{\ast }}{S(t)} \biggr] \\ & \quad{} - \int _{0}^{\infty }\bar{\beta }S^{\ast }I^{\ast } \cdot G \biggl(\frac{S(t-u)I(t-u)}{S ^{\ast }I(t)} \biggr)\exp (-\mu u)f_{X}(u) \,\mathrm {d}u \\ & \quad{} -\underbrace{ \int _{0}^{\infty }\bar{\beta }S^{\ast }I^{\ast } \biggl[ 1+ \ln \frac{S(t-u)I(t-u)}{S^{\ast }I(t)}-\ln \frac{S(t-u)I(t-u)}{S(t)I(t)} \biggr]\exp (-\mu u)f_{X}(u) \,\mathrm {d}u} _{=-\int _{0}^{\infty }\bar{\beta }S^{\ast }I^{\ast }\exp (-\mu u)f _{X}(u)[1-\ln \frac{S^{\ast }}{S(t)}] \,\mathrm {d}u =-\hat{f}(0)\cdot \bar{ \beta }S^{\ast }I^{\ast } [1-\ln \frac{S^{\ast }}{S(t)} ]} \\ &= -\hat{f}(0) \cdot \mu \frac{(S(t)-S^{\ast })^{2}}{S(t)}- \hat{f}(0)\cdot \bar{\beta }S^{\ast }I^{\ast }\cdot G \biggl(\frac{S \ast }{S(t)} \biggr) \\ & \quad{} - \int _{0}^{\infty }\bar{\beta }S^{\ast }I^{\ast } \cdot G \biggl(\frac{S(t-u)I(t-u)}{S ^{\ast }I(t)} \biggr) \exp (-\mu u)f_{X}(u) \,\mathrm {d}u \\ &\le 0, \end{aligned}$$

since \(G(x)\ge 0\) for all \(x>0\), and so the integrand of the last term is positive. Therefore, by the LaSalle’s principle, every solution to the equations of model (12) approaches the endemic equilibrium for \(R_{0}>1\). Thus the endemic equilibrium \(\mathcal{E}^{\ast }\) is globally asymptotically stable if \(R_{0}>1\). □

Theorems 1 and 3 indicate that the disease could be eliminated by maintaining the basic reproduction number less than unity, and conversely, when \(R_{0}\) is greater than unity, the disease persists in the epidemiological point of view.

5 An application

The 2009 epidemic of influenza H1N1 in Canada is investigated to explain the procedure of fitting an incubation period to our model. The procedure is summarized as follows: first, approximate the empirical distribution by a Coxian distribution, and second, investigate a Coxian-distributed SEIR model.

First, we approximate the empirical distribution of incubation period by a Coxian distribution, \(1-P\), as in (2). The empirical data of incubation period are captured from [22], and the data are fit to exponential and Coxian distributions, respectively. Unfortunately, there is no criterion for choosing the number of substates n. However, Akaike’s information criterion, AIC, gives the relative quality of statistical models for a given set of data [23], and so we choose n that makes the AIC smallest. Next, the human case data are fit to Coxian-distributed SEIR model. The report [24] is used for obtaining daily human case data. We normalized the model (12) as multiplying the human population. Since the duration of an epidemic is short relative to a human lifetime, we ignore the demographic effect, and so \(\mu =0\) is assumed. Since the rate of infection-related death is too small to be considered, we don’t consider the death from the epidemic. Motivated by [22], the mean duration of infectiousness \(1/\gamma \) is assumed as 7.1. We consider the initial time (\(t=0\)) as April 14 when the epidemic started. Since there are two turning points in April 29 and June 4 in the duration of epidemic, we assume that the transmission rate \(\beta (t)\) is the step function:

$$ \beta (t)= \textstyle\begin{cases} \beta _{0} &\text{for }t\in [0,15), \\ \beta _{1} &\text{for }t\in [15,53), \\ \beta _{2} &\text{for }t\in [53,\infty ), \end{cases} $$

and estimate \(\beta (t)\) by fitting between the case data and the cumulative prevalence, \(\int _{0}^{t} \{ \sum_{i=0}^{n-1}p_{i} \lambda _{i+1}E_{i+1}(u) \} \,\mathrm {d}u\), from the model by minimizing the sum of squared residuals of the corresponding data.

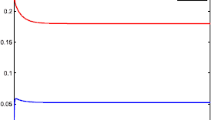
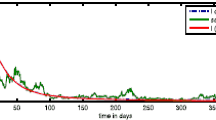
The left panel of Fig. 2 shows the result of fitting the empirical distribution of incubation period to a Coxian distribution with 12-chains, which is determined by AIC (corresponding \(\mathrm{AIC} =-36.3\)). We see that the fit curve explains the distribution of empirical incubation period well. The right panel of Fig. 2 illustrates the result of investigating Coxian-distributed SEIR model. Best fitted values of set of parameters are \(\beta _{0}=0.642\), \(\beta _{1}=0.252\), and \(\beta _{2}=0.131\) and so the basic reproduction number (13), \(R_{0}\) (\(=\beta _{0}/\gamma \)) is 4.561. To compare the result with the classical model, we fit the empirical distribution of incubation period to an exponential distribution and investigate the classical exponential SEIR model. In this case, AIC value of distribution fit is −33.3. The exponential model gives \(\beta _{0}=0.584\), \(\beta _{1}=0.234\) and \(\beta _{2}=0.133\) and so \(R_{0}\) is 4.146 in the first phase. From the example, we can see that a Coxian-distributed SEIR model can give nice fit results, and moreover, \(R_{0}\) can vary greatly when considering a realistic distribution. This result supports the fact that a common assumption for exponentially-distributed incubation period always underestimates the basic reproductive number of infection from onset data, and considering a realistic incubation period distribution is important to modeling epidemics [25].

Figure 2
figure 2

Results of fitting the empirical distribution of incubation period to a Coxian distribution with 12-chains (left), and to Coxian-distributed SEIR model with 12-chains (right)

Full size image

6 Discussion

Many previous works have strongly emphasized that modelers should be cautious for considering the intrinsic facts to classical frameworks when epidemic models for public health are proposed. In the study, we have derived an SEIR model based on Coxian distribution which approximates the distribution of the incubation period and performed mathematical analysis of the model.

In our analysis, we constructed the basic reproduction number which can be interpreted as the number of cases one case generates on average over its infectious period in a wholly susceptible environment. The model, which uses a constant transmission rate, was analyzed to obtain insights into its dynamical features. From the analysis, we found that the model has a globally asymptotically stable disease-free equilibrium whenever the basic reproduction number is less than unity and the model has a unique endemic equilibrium, which is globally asymptotically stable whenever the basic reproduction number exceeds unity. Thus, our basic reproduction number can also be interpreted as the asymptotic per generation of infection.

The model also has some limitations. First, several parameters are needed to fit empirical data, and this requires computational work. Secondly, loss of biological meaning could be caused by going out to the absorbing state without going through the whole chain of incubation. However, our model could be applicable when sufficient empirical information of the incubation period is given as shown in an application section. For example, it might enable us to describe the SEIR model of a particular type of distribution, like bimodal, that is not expressed in a conventional way, such as Plasmodium vivax malaria in temperate regions.