Efficient analytical techniques for solving time-fractional nonlinear coupled Jaulent–Miodek system with energy-dependent Schrödinger potential

Abstract

In this paper, we present analytical-approximate solution to the time-fractional nonlinear coupled Jaulent–Miodek system of equations which comes with an energy-dependent Schrödinger potential by means of a residual power series method (RSPM) and a q-homotopy analysis method (q-HAM). These methods produce convergent series solutions with easily computable components. Using a specific example, a comparison analysis is done between these methods and the exact solution. The numerical results show that present methods are competitive, powerful, reliable, and easy to implement for strongly nonlinear fractional differential equations.

1 Introduction and preliminaries

The term fractional calculus which involves fractional derivatives and fractional integral is nothing new. As stated in the letter L’Hospital wrote to Leibniz, in 1695, he asked him “what is the meaning of the expression $d^{n} y/dx^{n}$ when $n=1/2$?” Leibniz replied to the L’Hospital letter telling him that “$d^{1/2}x$ will be equal to $x\sqrt{dx:x}$.” In reality, this is an apparent paradox, from this evident paradox, one day useful consequences will be drawn [1,2,3,4]. Since then, mathematicians have investigated this concept, the like of Riemann–Liouville, Caputo–Hadamard, Erdélyi–Kober, Grünwald–Letnikov, Fourier, Marchaud, Riesz, and Weyl, to mention a few. Most of these derivatives are defined on the basis of the corresponding fractional integral in the Riemann–Liouville sense. Recently, fractional calculus has attracted the attention of researchers in the various field of natural science and engineering due to it wide applications in these various mention fields. The applications can be found in anomalous transport, control theory of dynamical systems, signal and image processing, nanotechnology, financial modeling, viscoelasticity, random walk, nanoprecipitate growth in solid solutions, modeling for shape memory polymers, and anomalous diffusion just to mention a few. We refer the reader to [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20] and the references therein for more details.

Nonlinear partial differential equations (NPDEs) have been attracting attention of engineers, physicists and mathematicians in recent years. Among such NPDEs, we have the Jaulent–Miodek system of equations which comes with energy-dependent Schrödinger potential [21]. These systems of equations are extensively used as a model in solving many real world problems in various fields of engineering and natural sciences; see [22,23,24,25] and the references therein for more details. Due to the momentous and special position these equations have in the above-mentioned fields, it is important to understand the solutions (both the analytic-approximate and the numerical solutions) to these nonlinear partial differential equations (NPDEs). Comprehensive mathematical analysis of the nonlinear fractional-order coupled Jaulent–Miodek equations are still under study and it plays an important role in many parts of science and engineering such as plasma physics [25] and condensed matter physics [26, 27].

There are several methods used in obtaining approximate solutions to linear and nonlinear FPDE such as the Adomian decomposition method (ADM) [28, 29], the homotopy-perturbation method (HPM) [30,31,32,33,34], the variational iteration method (VIM) [35], the q-homotopy analysis transform method (q-HATM) [36, 37], the fractional natural decomposition method (FNDM) [38], the fractional multi-step differential transformed method (FMsDTM) [39], the new iterartive method (NIM) [40,41,42] and the homotopy analysis method (HAM) [43,44,45,46]. In a recent development, [47,48,49,50,51,52,53], a modified homotopy analysis method was established which has potential applications in a wide range of systems of differential equations. This method provides a convenient way to ascertain the convergence of approximation series and even exact solutions. This modification is called a q-homotopy analysis method (q-HAM), we refer this method as one of the most efficient methods of obtaining analytical-approximate and exact solutions for nonlinear partial fractional differential equations as well as the classical type.

Nonlinear time-fractional coupled Jaulent–Miodek sytem of equations where $0<\alpha\leq1$, is defined as follows:

$$\begin{aligned}& \frac{{{\partial}^{\alpha}}u}{\partial{{t}^{\alpha}}}+\frac {{{\partial} ^{3}}u}{\partial{{x}^{3}}}+\frac{3}{2}v\frac{{{\partial }^{3}}v}{\partial{{x}^{3}}}+ \frac{9}{2}\frac{\partial v}{\partial x}\frac{{{\partial }^{2}}v}{\partial{{x}^{2}}}-6u\frac{\partial u}{\partial x}-6uv \frac{\partial v}{\partial x}-\frac{3}{2}\frac{\partial u}{\partial x}{{v}^{2}} =0, \\& \frac{{{\partial}^{\alpha}}v}{\partial{{t}^{\alpha}}}+\frac {{{\partial}^{3}}v}{\partial{{x}^{3}}}-6\frac{\partial u}{\partial x}v-6u\frac {\partial v}{\partial x}- \frac{15}{2}\frac{\partial v}{\partial x}{{v}^{2}} =0, \end{aligned}$$

(1)

which comes with energy-dependent Schrödinger potential [54,55,56]. Recently, the Sumudu transform homotopy-perturbation method (STHPM) [54], the Hermite wavelets method (HWM) and the optimal homotopy asymptotic method (OHAM) [57], the invariant subspace method [58], the q-homotopy analysis transform method (q-HATM) [59], and others [60,61,62] have been used to obtain approximate solutions of the nonlinear time-fractional Jaulent–Miodek system of equations.

In this paper, we present approximate solutions to time-fractional coupled Jaulent–Miodek equations using the residual power-series method (RSPM) and the q-homotopy analysis method (q-HAM). The paper is organized as follows. In Sect. 2, we explain residual power-series method (RSPM) and the q-homotopy analysis method (q-HAM), describe its convergence analysis, and we present example that shows reliability and efficiency of this method in order to obtain its stable numerical results. In Sect. 3, we obtain approximate solutions of the time-fractional nonlinear coupled Jaulent–Miodek system of equations using both the residual power-series method (RSPM) and the q-homotopy analysis method (q-HAM). In Sect. 4, we discuss the results obtained by RSPM and q-HAM, and Sect. 5 gives our conclusion.

Definition 1.1

The real function $f(t)$, $t>0$ is said to be in the space of $C_{\mu }$ ($\mu>0$) when there exists a real number p (>μ) such that $f(t)=t^{p}f_{1}(t)$ in which $f_{1}\in C[0,\infty)$ and it is said to be in the space of $C_{\mu}^{m}$ when $f^{(m)}\in C_{\mu}$, $m\in\aleph$ [3, 63].

Definition 1.2

The Riemann–Liouville fractional integral operator ($J^{\alpha}$) of order $\alpha\geq0$ of a function $f\in C_{\mu}$, $\mu\geq-1$ is defined as [3, 63]

$$ J^{\alpha}f(t)=\frac{1}{\varGamma(\alpha)} \int_{0}^{t}(t-\tau)^{\alpha-1}f(\tau)\,d\tau, \quad\alpha, t>0, $$

(2)

and $J^{0}f(t)=f(t)$, where Γ is the well-known Gamma function. Then the following properties hold for the function f:

$$f\in C_{\mu}, \qquad\mu\geq-1,\qquad\alpha, \beta\geq0\quad \text{and}\quad \lambda>-1. $$

Also, these general properties have been itemized as follows:

• (a) $J^{\alpha}J^{\beta}f(t)=J^{\alpha+\beta}f(t)$,

• (b) $J^{\alpha}J^{\beta}f(t)=J^{\beta}J^{\alpha}f(t)$,

• (c) $J^{\alpha}t^{\lambda}=\frac{\varGamma(\lambda +1)}{\varGamma(\lambda +1+\alpha)}t^{\lambda+\alpha}$.

Definition 1.3

The fractional derivative of a function f of order α in the Caputo sense, for $f\in C_{-1}^{m}$, $m\in\aleph\cup\{0\}$ is defined as [3]

$$ D^{m\alpha}f(t)=J^{m-\alpha}f^{(m)}(t)=\frac{1}{\varGamma(m-\alpha )}\int_{0}^{t}(t-\tau)^{m-\alpha-1}f^{(m)}( \tau)\,d\tau,\quad \alpha, t>0, $$

(3)

where $m-1<\alpha<m$ and the function f satisfies some defined properties as follows:

• (a) $D^{\alpha} ( af(t)+bg(t) ) =aD^{\alpha }f(t)+bD^{\alpha }g(t)$, $a,b\in\Re$,

• (b) $D^{\alpha}J^{\alpha}f(t)=f(t)$,

• (c) $J^{\alpha}D^{\alpha}f(t)=f(t)-\sum_{j=0}^{m-1}f^{(j)}(0) \frac{t^{j}}{j!}$, $t>0$.

2 Analysis of approximate methods

2.1 Algorithm and convergence of RPSM

Here, using the RPS method, series solutions for the Jaulent–Miodek system of equations are obtained. The RPS method [64,65,66,67,68] consists of expressing the solution of Eq. (1) as a fractional power-series expansion about the initial point $t=t_{0}$. It is worth mentioning that the proposed method can reduce the computational time and work as compared with other traditional techniques while maintaining the efficiency of the results obtained [69]. We have

$$ u(t,x)=\sum _{m=0}^{\infty}{\frac{D_{t}^{m\alpha }u_{m}(x,{{t}_{0}})}{\varGamma(m\alpha+1)}} {{ ( t-{{t}_{0}} ) }^{m\alpha}},\quad 0< \alpha\leq1, x\in[ a,b ] ,0\leq t< \Re, $$

(4)

and

$$ v(t,x)=\sum _{m=0}^{\infty}{\frac{D_{t}^{m\alpha }v_{m}(x,{{t}_{0}})}{\varGamma(m\alpha+1)}} {{ ( t-{{t}_{0}} ) }^{m\alpha}},\quad 0< \alpha\leq1, x\in[ a,b ] ,0\leq t< \Re. $$

(5)

The zeroth RPS approximate solutions of $u(t,x)$ and $v(t,x)$ can be written as follows:

$$\begin{aligned}& {{u}_{0}}(t,x)={{f}_{0}}(x)=f(x), \\& {{v}_{0}}(t,x)={{g}_{0}}(x)=g(x). \end{aligned}$$

(6)

Next, let $u_{k}(t,x)$ and $v_{k}(t,x)$ denote, respectively, the kth truncated series of $u(t,x)$ and $v(t,x)$ given as

$$\begin{aligned}& {{u}_{k}}(t,x)=\sum _{n=0}^{{k}}{{{f}_{n}}}(x) \frac{{{t}^{n\alpha}}}{\varGamma( 1+n\alpha) } , \end{aligned}$$

(7)

$$\begin{aligned}& {{v}_{k}}(t,x)=\sum _{n=0}^{{k}}{{{g}_{n}}}(x) \frac{{{t}^{n\alpha}}}{\varGamma(1+n\alpha) }. \end{aligned}$$

(8)

Substitution of the kth truncated series $u_{k}(t,x)$ and $v_{k}(t,x)$ of Eqs. (7) and (8) into the main equation Eq. (1) leads to the kth residual function denoted by $\operatorname{Res} u_{k}(t,x)$ and $\operatorname{Res} v_{k}(t,x)$ given by

$$\begin{aligned}& \begin{aligned}[b] \operatorname{Res}u_{k}(t,x) ={}&D_{t}^{\alpha }u(t,x)+(u_{k})_{xxx}(t,x)+ \frac{3 }{2}(v_{k})_{xxx}(t,x)v_{k}(t,x)+ \frac {9}{2}(v_{k})_{x}(t,x) (v_{k})_{xx}(t,x) \\ &- 6u_{k}(t,x) (u_{k})_{x}(t,x)-6{{u}_{k}}(t,x) (u_{k})_{x}(t,x)-6{{u}_{k}}(t,x){{v}_{k}}(t,x) (v_{k})_{x}(t,x) \\ &- \frac{3}{2}(u_{k})_{x}(t,x)v_{k}^{2}(t,x), \end{aligned} \hspace{-6pt} \\& \begin{aligned} \operatorname{Res}v_{k}(t,x) ={}&D_{t}^{\alpha }v(t,x)+(v_{k})_{xxx}(t,x)-6(u_{k})_{x}(t,x)v_{k}(t,x)-6u_{k}(t,x) (v_{k})_{x}(t,x) \\ &- \frac{15}{2}(v_{k})_{x}(t,x)v_{k}^{2}(t,x). \end{aligned} \end{aligned}$$

(9)

Also, we obtain

$$ \operatorname{Res}u(t,x)=\lim_{k\rightarrow\infty} \operatorname{Res}_{k}(t,x). $$

(10)

It is noticed that $\operatorname{Res}u(t,x)=0$ for all values of $x\in[ a,b]$. This means that $\operatorname{Res}u(t,x)$ is infinitely many times differentiable at $x=a$. Besides, $\frac {{{d}^{k}}}{d{{x}^{k-1}}}\operatorname{Res}u(0,x)=\frac {{{d}^{k}}}{d{{x}^{k-1}}}\operatorname{Res}u_{k}(0,x)=0$. In fact, this equation is a fundamental rule in RPS method in order to apply it on many linear and nonlinear problems. To obtain the kth approximate solutions, we consider Eqs. (7) and (8) and then we differentiate both sides of these equations with respect to independent variables x and t and then we substitute $t=0$ in order to find f and g constant parameters. After substituting these constant parameters in $u_{k}(t,x)$, we can obtain the kth truncated series and by putting it in Eq. (1), we get our favorite approximate solution. This procedure can be iterated for other arbitrary order of coefficients with RPS solutions of Eq. (1). Now, regarding the convergence of the above iteration scheme, we present the following theorem.

Theorem 2.1

If there exists a fixed constant $0< K<1$such that

$$\bigl\Vert {{u}_{n+1}} ( t,x ) \bigr\Vert \leq K \bigl\Vert {{u}_{n}} ( t,x ) \bigr\Vert $$

for all $n\in\mathbb{N}$and $0< t< R<1$, then the sequence of approximate solution converges to an exact solution.

Proof

For all $0< t< R<1$, we have

$$\begin{aligned} \bigl\Vert u(t,x)-{{u}_{n}}(t,x) \bigr\Vert =& \Biggl\Vert \sum _{i=n+1}^{\infty}{{{u}_{i}}(t,x)} \Biggr\Vert \\ \leq&\sum _{i=n+1}^{\infty}{ \bigl\Vert {{u}_{i}}(t,x) \bigr\Vert } \\ \leq& \bigl\Vert {f(x)} \bigr\Vert \sum _{i=n+1}^{\infty }{{{K}^{i}}} \\ =&\frac{{{K}^{n+1}}}{1-K} \bigl\Vert {f(x)} \bigr\Vert \overset{n\rightarrow \infty}{\longrightarrow}0. \end{aligned}$$

(11)

 □

2.2 Fundamentals of the q-HAM

Here, we give a brief analysis of the q-homotopy analysis method as applied to differential equations. Generally, we consider the following differential equation:

$$ \mathcal{N} \bigl[\mathcal {D}_{t}^{\alpha}w(t,x) \bigr]-f(t,x)=0, $$

(12)

where $\mathcal {D}_{t}^{\alpha}$ is the fractional derivative in time, $\mathcal{N}$ denotes the nonlinear operator, f is a given function and $w(t,x)$ is an unknown function. This is the the zeroth-order deformation equation

$$\begin{aligned} (1-nq)\mathcal{L} \bigl(\varphi(t,x;q)-w_{0}(t,x) \bigr)=qhH(t,x) \bigl(\mathcal{N}\bigl[\mathcal {D}_{t}^{\alpha}\varphi(t,x;q) \bigr]-f(t,x) \bigr), \end{aligned}$$

(13)

where $n\geqslant1$, $q\in[0,\frac{1}{n} ]$ denotes the so-called embedded parameter, $h\neq0$ is an auxiliary parameter, $H(t,x)$ is a non-zero auxiliary function, L is an auxiliary linear operator.

The following equations are obtained for $q=0$ and $q=\frac{1}{n}$, respectively:

$$ \varphi(t,x;0)=w_{0}(t,x) \quad\text{and}\quad\varphi\biggl(t,x; \frac {1}{n} \biggr)=w(t,x) . $$

(14)

So, starting from 0, as q approaches $\frac{1}{n}$, the solution $\varphi(t,x;q)$ varies from the initial guess $w_{0}(t,x)$ to the solution $w(t,x)$. We need to carefully choose $w_{0}(t,x)$, $\mathcal {L}$, h, $H(t,x)$ to ascertain the existence of the solution $\varphi (t,x;q)$ of Eq. (12) for $q\in[0,\frac{1}{n} ]$. The Taylor series expansion of $\varphi(t,x;q)$ gives

$$ \varphi(x,t;q)=w_{0}(t,x)+\sum_{m=1}^{\infty}w_{m}(t,x)q^{m}, $$

(15)

where

$$ w_{m}(t,x)=\frac{1}{m!}\frac{\partial^{m}\varphi (t,x;q)}{\partial q^{m}} \bigg|_{q=0}. $$

(16)

Assume that the auxiliary linear operator L, the initial guess $c_{0}$, the auxiliary parameter h and $H(t,x)$ are properly chosen such that the series Eq. (15) converges at $q=\frac{1}{n}$, then we have

$$ w(t,x)=w_{0}(t,x)+\sum_{m=1}^{\infty}w_{m}(t,x) \biggl(\frac{1}{n} \biggr)^{m}. $$

(17)

Let the vector $\vec{w}_{n}$ be defined as follows:

$$ \vec{w}_{n}= \bigl\{ w_{0}(t,x),w_{1}(t,x), \ldots,w_{n}(t,x) \bigr\} . $$

(18)

First, differentiate Eq. (13) m times with respect to the parameter q, then evaluate at $q=0$ and finally divide them by m!. We have what is known as the mth-order deformation equation [52, 70]

$$ \mathcal{L} \bigl[w_{m}(t,x)-\chi^{*}_{m}w_{m-1}(t,x) \bigr]=hH(t,x)\mathcal{R}_{m} (\vec{w}_{m-1} ), $$

(19)

with initial conditions

$$ w_{m}^{(k)}(0,x)=0,\quad k=0,1,2,\ldots,m-1, $$

(20)

where

$$ \mathcal{R}_{m} (\vec{w}_{m-1} )=\frac {1}{(m-1)!} \frac{\partial^{m-1} (\mathcal{N}[\mathcal {D}_{t}^{\alpha}\varphi(t,x;q)]-g(t,x) )}{\partial q^{m-1}} \bigg|_{q=0} $$

(21)

and

$$\begin{aligned} \chi^{*}_{m}=\left \{ \textstyle\begin{array}{l@{\quad}l} 0,& m\leqslant1, \\ n,&\text{otherwise}. \end{array}\displaystyle \right . \end{aligned}$$

(22)

3 Solutions of time-fractional coupled Jaulent–Miodek system of equations

This section presents application of the above approximate methods for obtaining solutions of the time-fractional coupled Jaulent–Miodek system of equations.

3.1 RPSM solution

Consider the following time-fractional coupled Jaulent–Miodek (JM) system of equations:

$$\begin{aligned}& \frac{\partial^{\alpha}u}{\partial t^{\alpha}}+\frac {\partial ^{3}u}{\partial x^{3}}+\frac{3}{2}v \frac{\partial^{3}v}{\partial x^{3}}+\frac{9}{2}\frac{\partial v}{\partial x} \frac{\partial^{2}v}{\partial x^{2}}-6u\frac{\partial u}{\partial x}-6uv\frac{\partial v}{\partial x}-\frac {3}{2} \frac{\partial u}{\partial x}v^{2}=0, \\& \frac{\partial^{\alpha}v}{\partial t^{\alpha}}+\frac{\partial ^{3}v}{\partial x^{3}}-6\frac{\partial u}{\partial x}v-6u \frac{\partial v}{\partial x}-\frac{15}{2}\frac{\partial v}{\partial x}v^{2}=0, \end{aligned}$$

(23)

subject to the initial conditions

$$ u(0,x)=f(x),\qquad v(0,x)=g(x). $$

(24)

The method reveals the solution of the problem as a fractional power series around the initial value $t=0$ as

$$\begin{aligned}& u(t,x)=\sum_{n=o}^{\infty}f_{n}(x) \frac{t^{n\alpha}}{\varGamma (1+n\alpha)}, \end{aligned}$$

(25)

$$\begin{aligned}& v(t,x)=\sum_{n=o}^{\infty}g_{n}(x) \frac{t^{n\alpha}}{\varGamma (1+n\alpha)}. \end{aligned}$$

(26)

Next, let $u_{k}(t,x)$ and $v_{k}(t,x)$ denote the kth truncated series of $u(t,x)$ and $v(t,x)$, respectively, we have

$$\begin{aligned}& u_{k}(t,x)=\sum_{n=o}^{k}f_{n}(x) \frac{t^{n\alpha}}{\varGamma (1+n\alpha)}, \end{aligned}$$

(27)

$$\begin{aligned}& v_{k}(t,x)=\sum_{n=o}^{k}g_{n}(x) \frac{t^{n\alpha}}{\varGamma (1+n\alpha)} . \end{aligned}$$

(28)

We define the kth residual functions as

$$\begin{aligned}& \begin{aligned}[b] \operatorname{Res} u_{k}(t,x) ={}& D_{t}^{\alpha }u(t,x)+(u_{k})_{xxx}(t,x)+ \frac{3}{2}(v_{k})_{xxx}(t,x)v_{k}(t,x)+ \frac {9}{2}(v_{k})_{x}(t,x) (v_{k})_{xx}(t,x)\hspace{-12pt} \\ &-6u_{k}(t,x) (u_{k})_{x}(t,x)-6u_{k}(t,x) (v_{k})_{x}(t,x)v_{k}(t,x)\\&- \frac {3}{2}(u_{k})_{x}(t,x)v_{k}^{2}(t,x), \end{aligned} \end{aligned}$$

(29)

$$\begin{aligned}& \begin{aligned}[b] \operatorname{Res} v_{k}(t,x) ={}& D_{t}^{\alpha }v(t,x)+(v_{k})_{xxx}(t,x)-6(u_{k})_{x}(t,x)v_{k}(t,x)-6u_{k}(t,x) (v_{k})_{x}(t,x) \\ &-\frac{15}{2}(v_{k})_{x}(t,x)v_{k}^{2}(t,x). \end{aligned} \end{aligned}$$

(30)

Since $\operatorname{Res}u(t,x)=0$ and $\lim_{k\rightarrow\infty }\operatorname{Res} u_{k}(t,x)=\operatorname{Res}u(t,x)$ for all $x\in I$ and $t\geq0$ [71, 72], $D_{t}^{m\alpha}\operatorname {Res}u(t,x)=0$, because the fractional derivative of a constant is 0 in the Caputo sense. Also, the fractional derivative $D_{t}^{m\alpha}\operatorname{Res}u(t,x)=0$ and $\operatorname {Res}u_{k}(t,x)$ is matching at $t=0$ for each $m=0,1,2,\ldots,k$. We first substitute $u_{k}(t,x)$ and $v_{k}(t,x)$ into Eq. (1) and find the fractional derivative formula $D_{t}^{(k-1)\alpha}\operatorname{Res}u(0,x)=0$ for $k=1,2,3$. Solving these algebraic equations gives the $f_{n}(x)$ and $g_{n}(x)$ coefficients.

For the first step, we consider $k=1$,

$$\begin{aligned}& u_{1}(t,x)=f(x)+f_{1}(x)\frac{t^{\alpha}}{\varGamma(\alpha +1)}, \end{aligned}$$

(31)

$$\begin{aligned}& v_{1}(t,x)=g(x)+g_{1}(x)\frac{t^{\alpha}}{\varGamma(\alpha+1)} , \end{aligned}$$

(32)

and

$$\begin{aligned}& \begin{aligned}[b]\operatorname{Res} u_{1}(0,x) ={}&f_{1}(x)-6f^{\prime}(x)f(x)- \frac {3}{2}f^{\prime }(x)g^{2}(x)-6f(x)g(x)g^{\prime}(x)+ \frac{9}{2}g^{\prime }(x)g^{\prime \prime}(x) \\ &+f^{(3)}(x)+\frac{3}{2}g^{(3)}(x)g(x), \end{aligned} \end{aligned}$$

(33)

$$\begin{aligned}& \operatorname{Res} v_{1}(0,x) =g_{1}(x)-6f^{\prime }(x)g(x)-6f(x)g^{\prime }(x)-\frac{15}{2}g^{2}(x)g^{\prime}(x)+g^{(3)}(x). \end{aligned}$$

(34)

Therefore

$$\begin{aligned}& f_{1}(x) =\frac{1}{2} \bigl( -2f^{(3)}+3g^{2}f^{\prime }+12ff^{\prime }+12fgg^{\prime(3)}g-9g^{\prime}g^{\prime\prime} \bigr) , \end{aligned}$$

(35)

$$\begin{aligned}& g_{1}(x) =\frac{1}{2} \bigl( 12gf^{\prime}+12fg^{\prime (3)}+15g^{2}g^{\prime} \bigr) , \end{aligned}$$

(36)

and

$$\begin{aligned}& \begin{aligned}[b] u_{1}(t,x) ={}&f(x)+\frac{t^{\alpha} ( 12f(x)f^{\prime }(x)+3f^{\prime }(x)g^{2}(x)+12f(x)g(x)g^{\prime}(x) ) }{2\varGamma(\alpha+1)} \\ &-\frac{t^{\alpha} (9g^{\prime}(x)g^{\prime\prime }(x)+2f^{(3)}(x)+3g(x)g^{(3)}(x) ) }{2\varGamma(\alpha+1)}, \end{aligned} \\& v_{1}(t,x) =g(x)+\frac{t^{\alpha} ( 12f^{\prime }(x)g(x)+12f(x)g^{\prime}(x)+15g^{2}(x)g^{\prime }(x)-2g^{(3)}(x) ) }{2\varGamma(\alpha+1)} . \end{aligned}$$

(37)

To obtain $f_{2}(x)$ and $g_{2}(x)$, we substitute the second truncated series,

$$\begin{aligned}& u_{2}(t,x) =f(x)+f_{2}(x)\frac{t^{2\alpha}}{\varGamma(2\alpha +1)}+f_{1}(x)\frac{t^{\alpha}}{\varGamma(\alpha+1)} , \end{aligned}$$

(38)

$$\begin{aligned}& v_{2}(t,x) =g(x)+g_{2}(x)\frac{t^{2\alpha}}{\varGamma(2\alpha +1)}+g_{1}(x)\frac{t^{\alpha}}{\varGamma(\alpha+1)} , \end{aligned}$$

(39)

into the second residual functions $\operatorname{Res}u_{2}(t,x)$ and $\operatorname{Res}v_{2}(t,x)$ and applying $D_{t}^{\alpha}$ on both sides for $t=0$ yields

$$\begin{aligned}& \begin{aligned}[b] \operatorname{Res} u_{2}(0,x) ={}&f_{2}(x)-f^{(6)}(x)+12f^{(4)}(x)g(x)^{2}+12f(x)f^{(4)}(x)+84f^{(3)}(x)g(x)g^{\prime }(x) \\ &+108f^{\prime\prime}(x)g^{\prime\prime}(x)g(x)+108f^{\prime \prime }(x)g^{\prime2}(x)- \frac{9}{4}^{\prime\prime2}f^{\prime\prime }(x)g^{4}(x) \\ &+18f^{\prime\prime2}-36f(x)^{2}f^{\prime\prime(3)}(x)f^{\prime 3}f^{\prime}(x)g^{\prime}(x)g(x)-252f(x)f^{\prime}(x)g^{\prime}(x)g(x) \\ &+225f^{\prime}(x)f^{\prime2}(x)g^{\prime}(x)g^{\prime\prime 2}-72f(x)f^{\prime2}+30f^{(3)}(x)f^{\prime(4)}(x)g(x) \\ &-54f(x)g(x)^{3}g^{\prime\prime2}g(x)g^{\prime\prime }(x)+72f(x)g^{\prime\prime2}-180f(x)g(x)^{2}g^{\prime 2}(x) \\ &-72f(x)^{2}g^{\prime2}(x)+102f(x)g^{(3)}(x)g^{\prime }(x)-3g^{(6)}(x)g(x)+ \frac{27}{2}g^{(4)}(x)g^{3}(x)\hspace{-12pt} \\ &-\frac{33}{2}g^{(3)}(x)^{2}+108g(x)^{2}g^{\prime\prime2}(x)+ \frac {135}{2}g^{\prime4}(x)+432g(x)g^{\prime2}(x)g^{\prime\prime}(x) \\ &-\frac{27}{2}g^{(5)}(x)g^{\prime(4)}(x)g^{\prime\prime (3)}(x)g(x)^{2}g^{\prime}(x), \end{aligned} \end{aligned}$$

(40)

$$\begin{aligned}& \begin{aligned}[b] \operatorname{Res} v_{2}(0,x) ={}&g_{2}(x)+12f^{(4)}(x)g(x)+30f^{(3)}(x)g^{\prime }(x)+36f^{\prime\prime}(x)f^{\prime\prime}(x)g^{\prime\prime 3}(x) \\ &-72f(x)f^{\prime\prime(3)}(x)f^{\prime2}g^{\prime\prime 3}(x)f^{\prime}(x)g^{\prime}(x)g(x)-144f(x)f^{\prime}(x)g^{\prime }(x) \\ &-72f^{\prime 2}(x)g(x)+12f(x)g^{(4)}(x)-126f(x)g(x)^{2}g^{\prime\prime 2}(x)g^{\prime \prime}(x) \\ &-252f(x)g(x)g^{\prime2}(x)-g^{(6)}(x)+24g^{(4)}(x)g(x)^{2}- \frac {225}{4}g(x)^{4}g^{\prime\prime }(x) \\ &+72g(x)g^{\prime\prime2}(x)-225g(x)^{3}g^{\prime 2}(x)+120g^{(3)}(x)g(x)g^{\prime}(x)+117g^{\prime2}g^{\prime\prime }(x), \end{aligned} \end{aligned}$$

(41)

and

$$\begin{aligned}& \begin{aligned}[b] f_{2}(x) ={}&f^{(6)}-12f^{(4)}g^{2}-12ff^{(4)}-84f^{(3)}gg^{\prime }+ \frac{9g^{4}f^{\prime\prime}}{4}+54fg^{2}f^{\prime\prime2}gg^{\prime \prime } \\ &-108gf^{\prime\prime}g^{\prime\prime}-108f^{\prime\prime} \bigl( g^{\prime} \bigr) ^{2} +72f^{2} \bigl( g^{\prime} \bigr) ^{2}-18 \bigl( f^{\prime\prime} \bigr) ^{2}+36f^{2}f^{\prime\prime(3)}gf^{\prime2} \bigl( f^{\prime} \bigr) ^{2} \\ &+252fgf^{\prime}g^{\prime3}f^{\prime}g^{\prime}-225f^{\prime }g^{\prime}g^{\prime\prime}+72f \bigl( f^{\prime} \bigr) ^{2}-30f^{(3)}f^{\prime(4)}g-72f \bigl( g^{\prime\prime} \bigr) ^{2} \\ &+54fg^{3}g^{\prime\prime(3)}g^{\prime2} \bigl( g^{\prime} \bigr) ^{2}+3g^{(6)}g+\frac{33}{2} \bigl( g^{(3)} \bigr) ^{2}-108g^{2} \bigl( g^{\prime\prime} \bigr) ^{2}, \end{aligned} \end{aligned}$$

(42)

$$\begin{aligned}& \begin{aligned}[b] g_{{2}}(x) ={}&{-}30f^{(3)}g^{\prime2}g^{\prime\prime3} \bigl( 6f^{\prime \prime}+25 \bigl( g^{\prime} \bigr) ^{2} \bigr) -9g^{\prime\prime } \bigl( 4f^{\prime\prime}+13 \bigl( g^{\prime} \bigr) ^{2} \bigr) -30g^{(3)}f^{\prime} \\ &+12f \bigl( 12f^{\prime}g^{\prime(4)} \bigr)+6g^{2} \bigl( 48f^{\prime}g^{\prime}+21fg^{\prime\prime(4)} \bigr) \\ &+12g \bigl( -f^{(4)}+6ff^{\prime\prime}+6 \bigl( f^{\prime} \bigr) ^{2}+21f \bigl( g^{\prime} \bigr) ^{2}-6 \bigl( g^{\prime\prime } \bigr) ^{2}-10g^{(3)}g^{\prime} \bigr) \\ &+g^{(6)}+\frac{225g^{4}g^{\prime\prime}}{4} . \end{aligned} \end{aligned}$$

(43)

Therefore

$$\begin{aligned}& \begin{aligned}[b] u_{{2}}(t,x) ={}&f(x)\\&+\frac{t^{\alpha} ( -2f^{(3)}(x)+12f(x) ( f^{\prime}(x)+g(x)g^{\prime}(x) ) +3g(x)^{2}f^{\prime (3)}(x)g(x)-9g^{\prime}(x)g^{\prime\prime}(x) ) }{2\varGamma (\alpha+1)}\hspace{-24pt} \\ &+\frac{1}{4\varGamma(2\alpha+1)}(4f^{(6)}(x)t^{2\alpha }-48f^{(4)}(x)g(x)^{2}t^{2\alpha}-48f(x)f^{(4)}(x)t^{2\alpha} \\ &-336f^{(3)}(x)g(x)t^{2\alpha}g^{\prime2\alpha}f^{\prime\prime }(x)g^{\prime\prime2\alpha}f^{\prime\prime}(x)g^{\prime 2}+9g(x)^{4}t^{2\alpha}f^{\prime\prime2}t^{2\alpha}f^{\prime\prime 2\alpha}f^{\prime\prime2} \\ &+144f(x)^{2}t^{2\alpha}f^{\prime\prime(3)}(x)t^{2\alpha}f^{\prime 3}t^{2\alpha}f^{\prime}(x)g^{\prime2\alpha}f^{\prime}(x)g^{\prime 2\alpha}f^{\prime}(x)g^{\prime}(x)g^{\prime\prime2}t^{2\alpha }f^{\prime2} \\ &+288f(x)t^{2\alpha}f^{\prime2}-120f^{(3)}(x)t^{2\alpha}f^{\prime (4)}(x)t^{2\alpha}-288f(x)t^{2\alpha}g^{\prime\prime2} \\ &+216f(x)g(x)^{3}t^{2\alpha}g^{\prime\prime2}g(x)t^{2\alpha }g^{\prime \prime2}t^{2\alpha}g^{\prime2}+720f(x)g(x)^{2}t^{2\alpha}g^{\prime 2} \\ &-408f(x)g^{(3)}(x)t^{2\alpha}g^{\prime(6)}(x)t^{2\alpha }-54g(x)^{3}g^{(4)}(x)t^{2\alpha}+66g^{(3)}(x)^{2}t^{2\alpha } \\ &-432g(x)^{2}t^{2\alpha}g^{\prime\prime2}-270t^{2\alpha}g^{\prime 4}\\&+54g^{(5)}(x)t^{2\alpha}g^{\prime(4)}(x)t^{2\alpha}g^{\prime \prime 2}g^{(3)}(x)t^{2\alpha}g^{\prime2\alpha}g^{\prime2}g^{\prime\prime}(x), \end{aligned} \end{aligned}$$

(44)

$$\begin{aligned}& v_{2}(t,x) =g(x)+\frac{t^{\alpha} ( 12g(x)f^{\prime }(x)+12f(x)g^{\prime(3)}(x)+15g(x)^{2}g^{\prime}(x) ) }{2\varGamma (\alpha+1)} \\& \phantom{v_{2}(t,x) =}+\frac{1}{4\varGamma(2\alpha +1)}(-48f^{(4)}(x)g(x)t^{2\alpha }-120f^{(3)}(x)g^{\prime}(x)t^{2\alpha}-144f^{\prime\prime }(x)g^{\prime \prime3}f^{\prime\prime}(x)t^{2\alpha} \\& \phantom{v_{2}(t,x) =}+288f(x)g(x)f^{\prime\prime(3)}(x)f^{\prime 2}f^{\prime }(x)g^{\prime }(x)t^{2\alpha}+576f(x)f^{\prime}(x)g^{\prime}(x)t^{2\alpha }+288g(x)f^{\prime2}t^{2\alpha} \\& \phantom{v_{2}(t,x) =}-48f(x)g^{(4)}(x)t^{2\alpha }+504f(x)g(x)^{2}g^{\prime\prime 2}g^{\prime \prime}(x)t^{2\alpha}+1008f(x)g(x)g^{\prime2}t^{2\alpha} \\& \phantom{v_{2}(t,x) =}+4g^{(6)}(x)t^{2\alpha }-96g^{(4)}(x)g(x)^{2}t^{2\alpha }+225g(x)^{4}g^{\prime\prime}(x)t^{2\alpha}-288g(x)g^{\prime\prime 2}t^{2\alpha} \\& \phantom{v_{2}(t,x) =}+900g(x)^{3}g^{\prime2}t^{2\alpha }-480g^{(3)}(x)g(x)g^{\prime }(x)t^{2\alpha}-468g^{\prime2}g^{\prime\prime}(x)t^{2\alpha}) . \end{aligned}$$

(45)

Applying the same procedure we finally calculated the following values:

$$\begin{aligned}& \begin{aligned}[b] u_{3}(t,x) ={}&f(x)+\frac{f_{1}(x)t^{\alpha}}{\varGamma(\alpha +1)}+\frac{f_{2}(x)t^{2\alpha}}{\varGamma(2\alpha+1)}+ \frac{t^{3\alpha}}{2\varGamma (\alpha+1)^{2}\varGamma(3\alpha+1)} \\ &\times\bigl(6\varGamma(\alpha+1)^{2}g(x)g_{2}(x)f^{\prime}(x)\\&+6 \alpha\varGamma(2\alpha)g_{1}(x)^{2}f^{\prime2}f_{2}(x)f^{\prime 2}f_{2}(x)g(x)g^{\prime 2}f(x)g_{2}(x)g^{\prime}(x) \\ &+24\alpha\varGamma(2\alpha)f_{1}(x)g_{1}(x)g^{\prime 2}g(x)^{2}f_{2}^{\prime2}f(x)g(x)g_{2}^{\prime}(x)+12 \alpha\varGamma(2\alpha)g(x)g_{1}(x)f_{1}^{\prime}(x)\hspace{-12pt} \\ &+24\alpha\varGamma(2\alpha)f_{1}(x)g(x)g_{1}^{\prime}(x)+24 \alpha\varGamma(2\alpha)f(x)g_{1}(x)g_{1}^{\prime 2}f(x)f_{2}^{\prime}(x) \\ &+24\alpha\varGamma(2\alpha)f_{1}(x)f_{1}^{\prime2}f_{2}^{(3)}(x)-3 \varGamma(\alpha+1)^{2}g_{2}(x)g^{(3)}(x) \\ &-9\varGamma(\alpha+1)^{2}g_{2}^{\prime}(x)g^{\prime\prime 2}g^{\prime}(x)g_{2}^{\prime \prime}(x)-18 \alpha\varGamma(2\alpha)g_{1}^{\prime}(x)g_{1}^{\prime \prime 2}g(x)g_{2}^{(3)}(x) \\ &-6\alpha\varGamma(2\alpha)g_{1}(x)g_{1}^{(3)}(x)\bigr), \end{aligned} \end{aligned}$$

(46)

$$\begin{aligned}& \begin{aligned}[b] v_{{3}}(t,x) ={}&g(x)+\frac{g_{1}(x)t^{\alpha}}{\varGamma(\alpha +1)}+\frac{g_{2}(x)t^{2\alpha}}{\varGamma(2\alpha+1)}+ \frac{t^{3\alpha}}{2\varGamma (\alpha+1)^{2}\varGamma(3\alpha+1)} \\ &\times\bigl(12\varGamma(\alpha+1)^{2}g_{2}(x)f^{\prime 2}f_{2}(x)g^{\prime 2}g(x)f_{2}^{\prime2}f(x)g_{2}^{\prime}(x)+24 \alpha\varGamma(2\alpha)g_{1}(x)f_{1}^{\prime}(x) \\ &+24\alpha\varGamma(2\alpha)f_{1}(x)g_{1}^{\prime 2}g(x)g_{2}(x)g^{\prime }(x)+30 \alpha\varGamma(2\alpha)g_{1}(x)^{2}g^{\prime 2}g(x)^{2}g_{2}^{\prime}(x) \\ &+60\alpha\varGamma(2\alpha)g(x)g_{1}(x)g_{1}^{\prime 2}g_{2}^{(3)}(x)\bigr). \end{aligned} \end{aligned}$$

(47)

3.2 q-HAM solution

Consider the same Eq. (23), we use initial approximations

$$\begin{aligned} u_{0}(t,x):=u(0,x)=f(x) \end{aligned}$$

and

$$\begin{aligned} v_{0}(t,x):=v(0,x)=g(x). \end{aligned}$$

We apply q-HAM and obtain the following:

$$\begin{aligned}& \begin{aligned}[b] \mathcal{R}_{m} (\vec{u}_{m-1} )={}& \mathcal {D}_{t}^{\alpha}u_{m-1}+u_{(m-1)xxx}+1.5\sum _{k=0}^{m-1}v_{k}v_{(m-1-k)xxx}+4.5 \sum_{k=0}^{m-1}v_{kx}v_{(m-1-k)xx} \\ &-6\sum_{k=0}^{m-1}u_{k}u_{(m-1-k)x}-6 \sum_{k=0}^{m-1}\sum _{j=0}^{k}u_{j}v_{k-j}v_{(m-1-k)x} \\ &-1.5\sum_{k=0}^{m-1}\sum _{j=0}^{k}v_{j}v_{k-j}u_{(m-1-k)x}, \end{aligned} \end{aligned}$$

(48)

$$\begin{aligned}& \begin{aligned}[b] \hat{\mathcal{R}}_{m} (\vec{v}_{m-1} )={}& \mathcal {D}_{t}^{\alpha}v_{m-1}+v_{(m-1)xxx}-6\sum _{k=0}^{m-1}v_{k}u_{(m-1-k)x}-6 \sum_{k=0}^{m-1}u_{kx}v_{(m-1-k)x} \\ &-7.5\sum_{k=0}^{m-1}\sum _{j=0}^{k}v_{j}v_{k-j}v_{(m-1-k)x}. \end{aligned} \end{aligned}$$

(49)

Therefore, we have the solution to the system for $m\geq1$

$$\begin{aligned}& u_{m}(t,x)=\chi^{*}_{m} u_{m-1}(t,x)+h J^{\alpha}\bigl[\mathcal{R}_{m} \bigl(\vec{u}_{m-1}(t,x) \bigr) \bigr], \end{aligned}$$

(50)

$$\begin{aligned}& v_{m}(t,x)=\chi^{*}_{m} v_{m-1}(t,x)+h J^{\alpha}\bigl[\hat{\mathcal{R}}_{m} \bigl( \vec{v}_{m-1}(t,x) \bigr) \bigr]. \end{aligned}$$

(51)

Hence, the expression of the series solutions by q-HAM are

$$\begin{aligned}& u(t,x;n;h)=U^{(M)}(t,x,n,h)=u_{0}(t,x)+\sum _{i=1}^{M}u_{i}(t,x;n;h) \biggl( \frac{1}{n} \biggr)^{i}, \end{aligned}$$

(52)

$$\begin{aligned}& v(t,x;n;h)=V^{(M)}(t,x,n,h)=v_{0}(t,x)+\sum _{i=1}^{M}v_{i}(t,x;n;h) \biggl( \frac{1}{n} \biggr)^{i}. \end{aligned}$$

(53)

The series solutions obtained in Eqs. (52) and (53) are appropriate solutions to the system Eq. (23) in terms of the convergence parameter h and n.

4 Numerical comparison

For numerical comparison purposes, we consider the system of equations 23 with different initial data.

4.1 Case I

We begin with a case where exact solutions are known when $\alpha=1$. Consider the following initial conditions:

$$\begin{aligned}& u(0,x) =f(x)=\frac{1}{8}\lambda^{2} \biggl( 1-4\sec h^{2} \biggl( \frac{ \lambda x}{2} \biggr) \biggr), \\& v(0,x) =g(x)=\lambda\sec h \biggl( \frac{\lambda x}{2} \biggr). \end{aligned}$$

(54)

The exact solutions of the problem ($\alpha=1$) are given by

$$\begin{aligned}& u(t,x) =\frac{1}{8}\lambda^{2} \biggl( 1-4\sec h^{2} \biggl( \frac{1}{2} \lambda\biggl( x+\frac{1}{2} \lambda^{2}t \biggr) \biggr) \biggr), \\& v(t,x) =\lambda\sec h \biggl( \frac{1}{2}\lambda\biggl( x+ \frac {1}{2}\lambda^{2}t \biggr) \biggr), \end{aligned}$$

(55)

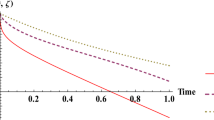
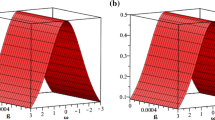
where λ is an arbitrary constant. The absolute errors for this Case I are reported in Tables 1, 2. In Figs. 1, 2, 3, 4, we present the graphical representation of the obtained results by RPSM, q-HAM and the exact solutions. We compare solutions, $(U^{(3)},V^{(3)})$, obtained by RPSM and q-HAM with the exact solutions by using different values of the parameters x and t.

Figure 1

Comparison for Case I: $u(t,x)$, $\lambda=0.5$, $\alpha =1$

Figure 2

Comparison for Case I: $v(t,x)$, $\lambda=0.5$, $\alpha =1$

Figure 3

RPSM vs. exact solution for Case I in 2D with $\lambda=0.5$, $\alpha=1$

Figure 4

q-HAM vs. exact solution for Case I in 2D with $\lambda =0.5$, $\alpha=1$

Table 1 Case I Comparison ($U^{(3)}$): RPSM, q-HAM with the exact solution

Table 2 Case I Comparison ($V^{(3)}$): RPSM, q-HAM with the exact solution

4.2 Case II

$$\begin{aligned}& u(0,x) =f(x)=e^{\gamma x}, \\& v(0,x) =g(x)=e^{\beta x}, \end{aligned}$$

(56)

where γ and β are arbitrary constant. Applying a similar procedure, the series solutions of RPSM are given by

$$\begin{aligned}& u_{1}(t,x)=\frac{t^{\alpha} (-12 \beta^{3} e^{2 \beta x}+3 (4 \beta +\gamma) e^{x (2 \beta+\gamma)}-2 \gamma^{3} e^{\gamma x}+12 \gamma e^{2 \gamma x} )}{2 \varGamma(\alpha+1)}+e^{\gamma x}, \\& v_{1}(t,x)=\frac{1}{2} e^{\beta x} \biggl( \frac{t^{\alpha} (-2 \beta ^{3}+12 (\beta+\gamma) e^{\gamma x}+15 \beta e^{2 \beta x} )}{\varGamma (\alpha+1)}+2 \biggr), \\& u_{2}(t,x) =t^{2\alpha} \bigl( 9 \bigl( 104\beta^{2}+20\beta \gamma +\gamma^{2} \bigr) e^{x(4\beta+\gamma)}\\& \phantom{u_{2}(t,x) =}+4 \bigl( 60\beta ^{6}e^{2\beta x}-774\beta^{4}e^{4\beta x}+\gamma^{6}e^{\gamma x}-60\gamma ^{4}e^{2\gamma x} \bigr) +108\gamma^{2}e^{3\gamma x} \bigr) \\& \phantom{u_{2}(t,x) =}/{\bigl(4\varGamma(2\alpha +1)\bigr)} \\& \phantom{u_{2}(t,x) =}+t^{2\alpha} \bigl( 18(2\beta+\gamma)(4\beta +5\gamma )e^{2x(\beta +\gamma)}\\& \phantom{u_{2}(t,x) =}-3 \bigl( 68\beta^{4}+101\beta^{3}\gamma +72\beta ^{2}\gamma ^{2}+28\beta\gamma^{3}+4\gamma^{4} \bigr) e^{x(2\beta+\gamma )} \bigr) \\& \phantom{u_{2}(t,x) =}/\bigl(4\varGamma(2\alpha+1)\bigr) \\& \phantom{u_{2}(t,x) =}+\frac{t^{\alpha}}{4\varGamma(\alpha +1)}-24\beta^{3}e^{2\beta x}+6(4\beta+ \gamma)e^{x(2\beta+\gamma)}-4\gamma^{3}e^{\gamma x}+e^{\gamma x}+24 \gamma e^{2\gamma x}, \\& v_{2}(t,x) =\frac{t^{2\alpha}e^{\beta x} ( 72(3\beta+\gamma )(7\beta +3\gamma)e^{x(2\beta+\gamma)}-24(\beta+\gamma)^{2} ( 2\beta ^{2}+\beta\gamma+2\gamma^{2} ) e^{\gamma x} ) }{4\varGamma (2\alpha+1)} \\& \phantom{v_{2}(t,x) =}+\frac{t^{2\alpha}e^{\beta x} ( 4\beta ^{6}-1332\beta ^{4}e^{2\beta x}+1125\beta^{2}e^{4\beta x}+144(\beta+2\gamma)^{2}e^{2\gamma x} ) }{4\varGamma(2\alpha+1)} \\& \phantom{v_{2}(t,x) =}+\frac{t^{\alpha}e^{\beta x} ( -4\beta ^{3}+24(\beta+\gamma )e^{\gamma x}+30\beta e^{2\beta x} ) }{4\varGamma(\alpha +1)}+e^{\beta x}. \end{aligned}$$

5 Conclusion

In this paper, we have employed efficient analytical techniques, called the residual power series method and the q-homotopy analysis method, to obtain approximate series solutions to the time-fractional coupled Jaulent–Miodek system of equations which comes with energy-dependent Schrödinger potential with different initial conditions. The numerical results are compared with the known exact solutions when $\alpha=1$. From our numerical results, see Tables 1, 2 and Figures 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, we demonstrate the fast convergence rate of the present methods even after computing a few iterations in solving a system of strongly nonlinear fractional differential equations. Although these methods are different, the results are similar and the resulting errors are comparable. Both methods are elegant and do not require any transformations, perturbations or discretization. Our numerical results further show that the methods are reliable, powerful and easy to implement when compared to other numerical and approximate methods. Since the time-fractional coupled Jaulent–Miodek system of equations is a complex system, the results prove that the present methods could be applied to various complex fractional linear and nonlinear models occurring in various fields of science and engineering, respectively.

Figure 5

RPSM vs. q-HAM for Case II for $U^{(2)}(t,x)$ with $\beta =0.1$, $\gamma=0.1$ and $\alpha=0.35$

Figure 6

RPSM vs. q-HAM for Case II for $U^{(2)}(t,x)$ with $\beta =0.1$, $\gamma=0.1$ and $\alpha=0.45$

Figure 7

RPSM vs. q-HAM for Case II for $U^{(2)}(t,x)$ with $\beta =0.1$, $\gamma=0.1$ and $\alpha=0.55$

Figure 8

RPSM vs. q-HAM for Case II for $U^{(2)}(t,x)$ with $\beta =0.1$, $\gamma=0.1$ and $\alpha=1$

Figure 9

RPSM vs. q-HAM for Case II for $V^{(2)}(t,x)$ with $\beta =0.1$, $\gamma=0.1$ and $\alpha=0.35$

Figure 10

RPSM vs. q-HAM for Case II for $V^{(2)}(t,x)$ with $\beta =0.1$, $\gamma=0.1$ and $\alpha=0.45$

Figure 11

RPSM vs. q-HAM for Case II for $V^{(2)}(t,x)$ with $\beta =0.1$, $\gamma=0.1$ and $\alpha=0.55$

Figure 12

RPSM vs. q-HAM for Case II for $V^{(2)}(t,x)$ with $\beta =0.1$, $\gamma=0.1$ and $\alpha=1$

Appendix

The components of the series solutions obtained by qHAM given in Eqs. (52) and (53) are obtained for Case I and Case II, successively below.

1.1 Case I

$$\begin{array}{c}\begin{array}{rl}{u}_1(t,x)=& {\chi }_1^{\ast }{u}_0(t,x)+h{J}^{\alpha }\left[{\mathcal{R}}_1({\overrightarrow{u}}_0(t,x))\right]\\ =& h{J}^{\alpha }[{\mathcal{D}}_t^{\alpha }{u}_0+u_{0xxx}+1.5v_0{v}_{0xxx}+4.5v_{0x}{v}_{0xx}]\\ & -h{J}^{\alpha }[6u_0{u}_{0x}+6u_0{v}_0{v}_{0x}+1.5v_0{v}_0{u}_{0x}]\\ =& -\frac{h{\lambda }^{5}tanh(\frac{\lambda x}{2}){sech}^2(\frac{\lambda x}{2})}{4\Gamma (\alpha +1)}{t}^{\alpha },\end{array}\hfill \\ \begin{array}{rl}{v}_1(t,x)=& {\chi }_1^{\ast }{v}_0(t,x)+h{J}^{\alpha }\left[{\hat{\mathcal{R}}}_1({\overrightarrow{v}}_0(t,x))\right]\\ =& h{J}^{\alpha }[{\mathcal{D}}_t^{\alpha }{v}_0+v_{0xxx}-6v_0{u}_{0x}-6u_0{v}_{0x}-7.5v_0{v}_0{v}_{0x}]\\ =& \frac{h{\lambda }^{4}tanh(\frac{\lambda x}{2})sech(\frac{\lambda x}{2})}{4\Gamma (\alpha +1)}{t}^{\alpha },\end{array}\hfill \\ u_2(t,x)={\chi }_2^{\ast }{u}_1(t,x)+h{J}^{\alpha }\left[{\mathcal{R}}_2({\overrightarrow{u}}_1(t,x))\right]\hfill \\ \phantom{u_2(t,x)}=n{u}_1+h{J}^{\alpha }[{\mathcal{D}}_t^{\alpha }{u}_1+u_{1xxx}+1.5v_0{v}_{1xxx}+1.5v_1{v}_{0xxx}+4.5v_{0x}{v}_{1xx}+4.5v_{1x}{v}_{0xx}]\hfill \\ \phantom{u_2(t,x)=}-h{J}^{\alpha }[6u_0{u}_{1x}+6u_1{u}_{0x}+6u_0{v}_0{v}_{1x}+6u_0{v}_1{v}_{0x}+6u_1{v}_0{v}_{0x}\hfill \\ \phantom{u_2(t,x)=}+1.5v_0{v}_0{u}_{1x}+1.5v_0{v}_1{u}_{0x}+1.5v_1{v}_0{u}_{0x}]\hfill \\ \phantom{u_2(t,x)}=(n+h)u_1+h{J}^{\alpha }[u_{1xxx}+1.5v_0{v}_{1xxx}+1.5v_1{v}_{0xxx}+4.5v_{0x}{v}_{1xx}+4.5v_{1x}{v}_{0xx}]\hfill \\ \phantom{u_2(t,x)=}-h{J}^{\alpha }[6u_0{u}_{1x}+6u_1{u}_{0x}+6u_0{v}_0{v}_{1x}+6u_0{v}_1{v}_{0x}+6u_1{v}_0{v}_{0x}\hfill \\ \phantom{u_2(t,x)=}+1.5v_0{v}_0{u}_{1x}+1.5v_0{v}_1{u}_{0x}+1.5v_1{v}_0{u}_{0x}]\hfill \\ \phantom{u_2(t,x)}=-\frac{h{\lambda }^5(n+h)tanh(\frac{\lambda x}{2}){sech}^2(\frac{\lambda x}{2})}{4\Gamma (\alpha +1)}{t}^{\alpha }-\frac{h^2{\lambda }^8(cosh(\lambda x)-2){sech}^4(\frac{\lambda x}{2})}{16\Gamma (2\alpha +1)}{t}^{2\alpha },\hfill \\ \begin{array}{rl}{v}_2(t,x)& ={\chi }_2^{\ast }{v}_1(t,x)+h{J}^{\alpha }\left[{\hat{\mathcal{R}}}_2({\overrightarrow{v}}_1(t,x))\right]\\ & =n{v}_1+h{J}^{\alpha }[{\mathcal{D}}_t^{\alpha }{v}_1+v_{1xxx}-6v_0{u}_{1x}-6v_1{u}_{0x}-6u_0{v}_{1x}-6u_1{v}_{0x}\\ & -7.5v_0{v}_0{v}_{1x}-7.5v_0{v}_1{v}_{0x}-7.5v_1{v}_0{v}_{0x}]\\ & =(n+h)v_1+h{J}^{\alpha }[v_{1xxx}-6v_0{u}_{1x}-6v_1{u}_{0x}-6u_0{v}_{1x}-6u_1{v}_{0x}\\ & -7.5v_0{v}_0{v}_{1x}-7.5v_0{v}_1{v}_{0x}-7.5v_1{v}_0{v}_{0x}]\\ & =\frac{h{\lambda }^4(h+n)tanh(\frac{\lambda x}{2})sech(\frac{\lambda x}{2})}{4\Gamma (\alpha +1)}{t}^{\alpha }+\frac{{\lambda }^7{h}^2(cosh(\lambda x)-3){sech}^3(\frac{\lambda x}{2})}{32\Gamma (2\alpha +1)}{t}^{2\alpha },\end{array}\hfill \\ \begin{array}{rl}{u}_3(t,x)=& {\chi }_3^{\ast }{u}_2(t,x)+h{J}^{\alpha }\left[{\mathcal{R}}_3({\overrightarrow{u}}_2(t,x))\right]\\ =& n{u}_2+h{J}^{\alpha }[{\mathcal{D}}_t^{\alpha }{u}_2+u_{2xxx}+1.5v_0{v}_{2xxx}+1.5v_1{v}_{1xxx}+1.5v_2{v}_{0xxx}\\ & +4.5v_{0x}{v}_{2xx}+4.5v_{1x}{v}_{1xx}+4.5v_{2x}{v}_{0xx}]\\ & -h{J}^{\alpha }[6u_0{u}_{2x}+6u_1{u}_{1x}+6u_2{u}_{0x}+6u_0{v}_0{v}_{2x}+6u_0{v}_1{v}_{1x}\\ & +6u_1{v}_0{v}_{1x}+6u_0{v}_2{v}_{0x}+6u_1{v}_1{v}_{0x}+6u_2{v}_0{v}_{0x}]\\ & -h{J}^{\alpha }[1.5v_0{v}_0{u}_{2x}+1.5v_0{v}_1{u}_{1x}+1.5v_1{v}_0{u}_{1x}\\ & +1.5v_0{v}_2{u}_{0x}+1.5v_1{v}_1{u}_{0x}+1.5v_2{v}_0{u}_{0x}]\\ =& (n+h)u_2+h{J}^{\alpha }[u_{2xxx}+1.5v_0{v}_{2xxx}+1.5v_1{v}_{1xxx}+1.5v_2{v}_{0xxx}\\ & +4.5v_{0x}{v}_{2xx}+4.5v_{1x}{v}_{1xx}+4.5v_{2x}{v}_{0xx}]\\ & -h{J}^{\alpha }[1.5v_0{v}_0{u}_{2x}+1.5v_1{v}_1{u}_{1x}+1.5v_1{v}_0{u}_{1x}\\ & +1.5v_0{v}_2{u}_{0x}+1.5v_1{v}_1{u}_{0x}+1.5v_2{v}_0{u}_{0x}]\\ =& -\frac{h{\lambda }^5{(h+n)}^{2}sinh(\lambda x){sech}^4(\frac{\lambda x}{2})}{8\Gamma (\alpha +1)}{t}^{\alpha }-\frac{h^2{\lambda }^8(h+n)(cosh(\lambda x)-2){sech}^4(\frac{\lambda x}{2})}{8\Gamma (2\alpha +1)}{t}^{2\alpha }\\ & +\left[\right(h^3{\lambda }^{11}[3\Gamma (2\alpha +1)(20cosh(\lambda x)-cosh(2\lambda x)-43)\\ & -2\Gamma {(\alpha +1)}^2(cosh(2\lambda x)+28cosh(\lambda x)-165)]tanh\left(\frac{\lambda x}{2}\right){sech}^6\left(\frac{\lambda x}{2}\right))\\ & /(1024\Gamma {(\alpha +1)}^2\Gamma (3\alpha +1))]t^{3\alpha },\end{array}\hfill \\ v_3(t,x)={\chi }_3^{\ast }{v}_2(t,x)+h{J}^{\alpha }\left[{\hat{\mathcal{R}}}_3({\overrightarrow{v}}_2(t,x))\right]\hfill \\ \phantom{v_3(t,x)}=n{v}_2+h{J}^{\alpha }[{\mathcal{D}}_t^{\alpha }{v}_2+v_{2xxx}-6v_0{u}_{2x}-6v_1{u}_{1x}-6v_2{u}_{0x}\hfill \\ \phantom{v_3(t,x)=}-6u_{0x}{v}_{2x}-6u_{1x}{v}_{1x}-6u_{2x}{v}_{0x}]\hfill \\ \phantom{v_3(t,x)=}-h{J}^{\alpha }[7.5v_0{v}_0{v}_{2x}+7.5v_0{v}_1{v}_{1x}+7.5v_1{v}_0{v}_{1x}\hfill \\ \phantom{v_3(t,x)=}+7.5v_0{v}_2{v}_{0x}+7.5v_1{v}_1{v}_{0x}+7.5v_2{v}_0{v}_{0x}]\hfill \\ \phantom{v_3(t,x)}=(n+h)v_2+h{J}^{\alpha }[v_{2xxx}-6v_0{u}_{2x}-6v_1{u}_{1x}-6v_2{u}_{0x}\hfill \\ \phantom{v_3(t,x)=}-6u_{0x}{v}_{2x}-6u_{1x}{v}_{1x}-6u_{2x}{v}_{0x}]\hfill \\ \phantom{v_3(t,x)=}-h{J}^{\alpha }[7.5v_0{v}_0{v}_{2x}+7.5v_0{v}_1{v}_{1x}+7.5v_1{v}_0{v}_{1x}\hfill \\ \phantom{v_3(t,x)=}+7.5v_0{v}_2{v}_{0x}+7.5v_1{v}_1{v}_{0x}+7.5v_2{v}_0{v}_{0x}]\hfill \\ \phantom{v_3(t,x)}=\frac{h{\lambda }^4{(h+n)}^{2}tanh(\frac{\lambda x}{2})sech(\frac{\lambda x}{2})}{4\Gamma (\alpha +1)}{t}^{\alpha }+\frac{{\lambda }^7{h}^2(h+n)(cosh(\lambda x)-3){sech}^3(\frac{\lambda x}{2})}{16\Gamma (2\alpha +1)}{t}^{2\alpha }\hfill \\ \phantom{v_3(t,x)=}+\left[\right(h^3{\lambda }^{10}[12\Gamma (2\alpha +1)(3cosh(\lambda x)-7)\hfill \\ \phantom{v_3(t,x)=}+\Gamma {(\alpha +1)}^2(cosh(2\lambda x)-92cosh(\lambda x)+147)]tanh\left(\frac{\lambda x}{2}\right){sech}^5\left(\frac{\lambda x}{2}\right))\hfill \\ \phantom{v_3(t,x)=}/(512\Gamma {(\alpha +1)}^2\Gamma (3\alpha +1))]t^{3\alpha }.\hfill \end{array}$$

1.2 Case II

$$\begin{aligned}& \begin{aligned} u_{1}(t,x)={}&\chi^{*}_{1} u_{0}(t,x)+h J^{\alpha}\bigl[\mathcal{R}_{1} \bigl(\vec{u}_{0}(t,x) \bigr) \bigr] \\ ={}&h J^{\alpha}\bigl[\mathcal{D}_{t}^{\alpha}u_{0} + u_{0xxx}+1.5v_{0}v_{0xxx}+4.5v_{0x}v_{0xx} \bigr] \\ &-h J^{\alpha}[6u_{0}u_{0x}+6u_{0}v_{0}v_{0x}+1.5v_{0}v_{0}u_{0x} ] \\ ={}&{-}\frac{h[3(\gamma+4\beta)e^{(\gamma+2\beta)x}-2(\gamma ^{3}e^{\gamma x}-6\gamma e^{2\gamma x}+6\beta^{3}e^{2\beta x})]}{2\varGamma (\alpha+ 1)} t^{\alpha}, \end{aligned} \\& \begin{aligned}v_{1}(t,x)&=\chi^{*}_{1} v_{0}(t,x)+h J^{\alpha}\bigl[\hat{\mathcal{R}}_{1} \bigl( \vec{v}_{0}(t,x) \bigr) \bigr] \\ &=h J^{\alpha}\bigl[\mathcal{D}_{t}^{\alpha}v_{0}+ v_{0xxx}-6v_{0}u_{0x}-6u_{0}v_{0x}-7.5v_{0}v_{0}v_{0x} \bigr] \\ &=-\frac{he^{\beta x}[12(\gamma+\beta)e^{\gamma x}-2\beta ^{3}+15\beta e^{2\beta x}]}{ 2\varGamma(\alpha+1)} t^{\alpha}, \end{aligned} \\& u_{2}(t,x)=\chi^{*}_{2} u_{1}(t,x)+h J^{\alpha}\bigl[\mathcal{R}_{2} \bigl(\vec{u}_{1}(t,x) \bigr) \bigr] \\& \phantom{u_{2}(t,x)}=n u_{1}+h J^{\alpha}\bigl[\mathcal{D}_{t}^{\alpha}u_{1} + u_{1xxx}+1.5v_{0}v_{1xxx}+1.5v_{1}v_{0xxx}+4.5v_{0x}v_{1xx}+4.5v_{1x}v_{0xx} \bigr] \\& \phantom{u_{2}(t,x)=}-h J^{\alpha}[6u_{0}u_{1x}+6u_{1}u_{0x}+6u_{0}v_{0}v_{1x}+6u_{1}v_{1}v_{0x}+6u_{1}v_{0}v_{0x}\\& \phantom{u_{2}(t,x)=}+1.5v_{0}v_{0}u_{1x}+1.5v_{1}v_{1}u_{0x}+1.5v_{1}v_{0}u_{0x} ] \\& \phantom{u_{2}(t,x)}=(n+h) u_{1}+h J^{\alpha}[u_{1xxx}+1.5v_{0}v_{1xxx}+1.5v_{1}v_{0xxx}+4.5v_{0x}v_{1xx}+4.5v_{1x}v_{0xx} ] \\& \phantom{u_{2}(t,x)=}-h J^{\alpha}[6u_{0}u_{1x}+6u_{1}u_{0x}+6u_{0}v_{0}v_{1x}+6u_{1}v_{1}v_{0x}+6u_{1}v_{0}v_{0x}\\& \phantom{u_{2}(t,x)=}+1.5v_{0}v_{0}u_{1x}+1.5v_{1}v_{1}u_{0x}+1.5v_{1}v_{0}u_{0x} ] \\& \phantom{u_{2}(t,x)=}=-\frac{h(n+h) [3(\gamma+4\beta)e^{(\gamma +2\beta )x}-2(\gamma^{3}e^{\gamma x}-6\gamma e^{2\gamma x}+6\beta^{3}e^{2\beta x}) ]}{2\varGamma(\alpha+ 1)} t^{\alpha}\\& \phantom{u_{2}(t,x)=}-\Bigl(3h^{2}e^{(\gamma+2\beta)x} \bigl[4\gamma ^{4}+28\gamma^{3}\beta +72\gamma^{2}\beta^{2}+101\gamma\beta^{3}-84\gamma\beta e^{(\gamma x)}\\& \phantom{u_{2}(t,x)=}-15\gamma\beta e^{(2\beta x)}+68\beta^{4}-78\beta ^{2}e^{(2\beta x)} \bigr]\\& \phantom{u_{2}(t,x)=}/\bigl(\varGamma(2\alpha+ 1)\bigr) \Bigr)t^{2\alpha} \\& \phantom{u_{2}(t,x)=}+\Bigl(h^{2} \bigl[4\gamma^{6}e^{(\gamma x)}-240\gamma^{4}e^{(2\gamma x)}+9\gamma^{2} \bigl(40e^{2(\gamma+\beta)x}+e^{(\gamma+4\beta )x}+48e^{3\gamma x} \bigr)\\& \phantom{u_{2}(t,x)=}+24\beta^{2} e^{2\beta x } \bigl(24e^{2\gamma x}+10\beta^{4}-129\beta^{2}e^{2\beta x } \bigr) \bigr]\\& \phantom{u_{2}(t,x)=}/\bigl(4\varGamma(2\alpha+ 1)\bigr)\Bigr) t^{2\alpha}, \\& \begin{aligned} v_{2}(t,x)={}&\chi^{*}_{2} v_{1}(t,x)+h J^{\alpha}\bigl[\hat{\mathcal{R}}_{2} \bigl( \vec{v}_{1}(t,x) \bigr) \bigr] \\ ={}&n v_{1}+h J^{\alpha}\bigl[\mathcal{D}_{t}^{\alpha}v_{1}+ v_{1xxx}-6v_{0}u_{1x}-6v_{1}u_{0x}-6u_{0}v_{1x}-6u_{1}v_{0x}\\ &-7.5v_{0}v_{0}v_{1x}-7.5v_{1}v_{1}v_{0x}-7.5v_{1}v_{0}v_{0x} \bigr] \\ ={}&(n+h) v_{1}+hJ^{\alpha}[v_{1xxx}-6v_{0}u_{1x}-6v_{1}u_{0x}-6u_{0}v_{1x}-6u_{1}v_{0x}\\ &-7.5v_{0}v_{0}v_{1x}-7.5v_{1}v_{1}v_{0x}-7.5v_{1}v_{0}v_{0x} ] \\ ={}&{-}\frac{h(n+h)e^{\beta x}[12(\gamma+\beta)e^{\gamma x}-2\beta ^{3}+15\beta e^{2\beta x}]}{ 2\varGamma(\alpha+1)} t^{\alpha}\\ &+\frac{h^{2}e^{\beta x}[-48e^{\gamma x}(\gamma^{4}+\beta^{4})+576\gamma ^{2}e^{2\gamma x}+4\beta^{6}-1332\beta^{4}e^{2\beta x}+1125\beta ^{2}e^{4\beta x}] }{4\varGamma(2\alpha+1)} t^{2\alpha} \\ &+\Bigl(6h^{2}e^{(\gamma+\beta)x}\bigl[6\beta e^{\gamma x}(4\gamma +\beta )-\gamma{\beta}\bigl(5\gamma^{2}+6\gamma{\beta}+5\beta^{2}\bigr)\\ &+3e^{2\beta x}(\gamma+3\beta)(3\gamma+7\beta)\bigr]\\ &/\varGamma(2\alpha+1) \Bigr)t^{2\alpha}. \end{aligned} \end{aligned}$$