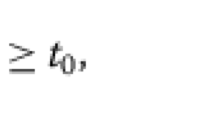Oscillations of differential equations with non-monotone deviating arguments

Abstract

The oscillatory behavior of the solutions to a differential equation with several non-monotone arguments and nonnegative coefficients is studied, and some new oscillation criteria are given. More precisely, sufficient conditions in terms of limsup and liminf are established, which essentially improve several known criteria existing in the literature. The results are illustrated by examples numerically solved in MATLAB.

1 Introduction

Consider the first-order linear differential equation with several variable deviating arguments of either delayed (DDE)

or advanced type (ADE)

where $p_{i}$, $q_{i}$, $1\leq i\leq m$, are functions of nonnegative real numbers, and $\tau _{i}$, $\sigma _{i}$, $1\leq i\leq m$, are functions of positive real numbers satisfying

$$ \tau _{i}(t)< t, \quad t\geq t_{0}\quad \text{and}\quad \lim_{t\rightarrow \infty }\tau _{i}(t)=\infty , \quad 1\leq i \leq m, $$

(1.1)

and

$$ \sigma _{i}(t)>t,\quad t\ge t_{0},\quad 1\leq i\leq m , $$

(1.2)

respectively.

By a solution of (E) or ($E'$) we mean a function absolutely continuous on $[t_{0},\infty )$ satisfying (E) or ($E'$) for almost all $t\geq t_{0}$.

A solution of (E) or ($E'$) is oscillatory if it is neither eventually positive nor eventually negative. If there exists an eventually positive or eventually negative solution, then the equation is nonoscillatory. An equation is oscillatory if all its solutions oscillate.

The problem of establishing sufficient conditions for the oscillation of all solutions of equations (E) or ($E'$) has been studied extensively. The reader is referred to [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23] and the references cited therein. Most of this work though involves the special case where the arguments are nondecreasing, while only a small fraction of these papers deal with the general case where the arguments are not necessarily monotone. See, for example, [1,2,3,4,5,6,7, 13, 14] and the references cited therein. The general case is significant not only from the mathematical standpoint, but for its applications in the real world as well. This is because there are always natural disturbances, for example, noise in communication systems, that affect all the parameters of the equation, and therefore the fair (from a mathematical point of view) monotone arguments become non-monotone almost always.

The objective of this paper is to derive new sufficient conditions for all solutions of (E) and ($E'$) to be oscillatory when the arguments are not necessarily monotone. Our results essentially improve several known criteria existing in the literature, which are briefly reviewed below for the reader’s convenience.

Throughout this paper, we are going to use the following notation:

$$ \begin{aligned} P(t) &:=\sum_{i=1}^{m} p_{i}(t), \qquad \alpha :=\liminf_{t\rightarrow \infty } \int _{\tau (t)}^{t}P(s)\,ds , \\ Q(t) &:= \sum_{i=1}^{m} q_{i}(t), \qquad \beta :=\liminf_{t\rightarrow \infty } \int _{t}^{\sigma (t)}Q(s)\,ds , \end{aligned} $$

and

$$ D(\omega ):=\textstyle\begin{cases} 0, & \text{if }\omega >1/e, \\ \frac{ 1-\omega -\sqrt{1-2\omega -\omega ^{2}}}{2}, & \text{if }\omega \in [ 0,1/e ] , \end{cases} $$

where $\tau (t):=\max_{1\leq i\leq m}\{\tau _{i}(t)\}$ and $\sigma (t):= \min_{1\leq i\leq m}\{\sigma _{i}(t)\}$.

1.1 DDEs (chronological review)

It follows from Remark 2.7.3 in [20] that if $\tau _{i}$, $1\leq i\leq m$, are nondecreasing and

$$ \limsup_{t\rightarrow \infty } \int _{\tau (t)}^{t}P(s)\,ds>1 , $$

(1.3)

then every solution of (E) oscillates. This result is similar to Theorem 2.1.3 [20] which is a special case of the result by Ladas, Lakshmikantham, and Papadakis [17].

In 1978, Ladde [19] and in 1982, Ladas and Stavroulakis [18] proved that if

$$ \alpha >\frac{1}{e}, $$

(1.4)

then every solution of (E) oscillates.

In 1984, Hunt and Yorke [11] proved that if $\tau _{i}$ are nondecreasing, $t-\tau _{i}(t)\leq \tau _{0}$, $1\leq i\leq m$, and

$$ \liminf_{t\rightarrow \infty }\sum_{i=1}^{m} p_{i}(t) \bigl( t-\tau _{i}(t) \bigr) >\frac{1}{e}, $$

(1.5)

then every solution of (E) oscillates.

Suppose that $\tau _{i}$, $1\leq i\leq m$, are not necessarily monotone. Set

$$ h_{i}(t):=\sup_{t_{0}\leq s\leq t}\tau _{i}(s)\quad \text{and}\quad h(t):= \max_{1\leq i\leq m}h_{i}(t), \quad t \geq t_{0}. $$

(1.6)

Clearly, $h_{i}$, h are nondecreasing and $\tau _{i}(t)\leq h_{i}(t) \leq h(t)< t$ for all $t\geq t_{0}$.

In 2016, Braverman, Chatzarakis, and Stavroulakis [1] proved that if, for some $r\in \mathbb{N}$,

$$ \limsup_{t\rightarrow \infty } \int _{h(t)}^{t}\sum_{i=1}^{m} p_{i}( \zeta )a_{r}\bigl(h(t),\tau _{i}(\zeta ) \bigr)\,d\zeta >1, $$

(1.7)

or

$$ \liminf_{t\rightarrow \infty } \int _{h(t)}^{t}\sum_{i=1}^{m} p_{i}( \zeta )a_{r}\bigl(h(t),\tau _{i}(\zeta ) \bigr)\,d\zeta >\frac{1}{e}, $$

(1.8)

where

$$\begin{aligned}& \begin{aligned} &a_{1}(t,s) :=\exp \biggl\{ \int _{s}^{t}P(\zeta )\,d\zeta \biggr\} , \\ &a_{r+1}(t,s) :=\exp \Biggl\{ \int _{s}^{t}\sum_{i=1}^{m} p_{i}(\zeta )a_{r}\bigl(\zeta ,\tau _{i}(\zeta ) \bigr)\,d\zeta \Biggr\} , \end{aligned} \end{aligned}$$

then every solution of (E) oscillates.

Several improvements have been made to the above conditions, see [3,4,5, 7] to arrive at the recent forms [4]

$$\begin{aligned}& \limsup_{t\rightarrow \infty } \int _{h(t)}^{t}P(s)\exp \biggl( \int _{\tau ( s ) }^{h(t)}P(u)\exp \biggl( \int _{\tau (u)} ^{u}W_{\ell }(\xi )\,d\xi \biggr) \,du \biggr)\,ds>1, \end{aligned}$$

(1.9)

$$\begin{aligned}& \limsup_{t\rightarrow \infty } \int _{h(t)}^{t}P(s)\exp \biggl( \int _{\tau ( s ) }^{h(t)}P(u)\exp \biggl( \int _{\tau (u)} ^{u}W_{\ell }(\xi )\,d\xi \biggr) \,du \biggr)\,ds>1-D(\alpha ), \end{aligned}$$

(1.10)

$$\begin{aligned}& \liminf_{t\rightarrow \infty } \int _{h(t)}^{t}P(s)\exp \biggl( \int _{\tau ( s ) }^{h(s)}P(u)\exp \biggl( \int _{\tau (u)} ^{u}W_{\ell }(\xi )\,d\xi \biggr) \,du \biggr)\,ds>\frac{1}{e}, \end{aligned}$$

(1.11)

where

$$ W_{\ell }(t):=P(t) \biggl[ 1+ \int _{\tau (t)}^{t}P(s)\exp \biggl( \int _{\tau ( s ) }^{t}P(u)\exp \biggl( \int _{\tau (u)} ^{u}W_{\ell -1}(\xi )\,d\xi \biggr) \,du \biggr)\,ds \biggr] $$

with

$$ W_{0}(t):=P(t) \biggl[ 1+ \int _{\tau (t)}^{t}P(s)\exp \biggl( \int _{\tau (s)}^{t}P(\omega )\exp \biggl( \lambda _{0} \int _{\tau ( \omega )}^{\omega }P(u)\,du \biggr)\,d\omega \biggr)\,ds \biggr], $$

where $\lambda _{0}$ is the smaller root of the transcendental equation $\lambda =e^{\alpha \lambda }$.

1.2 ADEs (chronological review)

For ($E'$), the dual condition of (1.3) is

$$ \limsup_{t\rightarrow \infty } \int _{t}^{\sigma (t)}Q(s)\,ds>1 , $$

(1.12)

where $\sigma _{i}$, $1\leq i\leq m$, are nondecreasing (see [20], paragraph 2.7).

In 1978, Ladde [19] and in 1982, Ladas and Stavroulakis [18] proved that if

$$ \beta >\frac{1}{e}, $$

(1.13)

then every solution of ($E'$) oscillates.

In 1990, Zhou [23] proved that if $\sigma _{i}(t)-t\leq \sigma _{0}$, $1\leq i\leq m$, and

$$ \liminf_{t\rightarrow \infty }\sum_{i=1}^{m} q_{i}(t) \bigl( \sigma _{i}(t)-t \bigr) >\frac{1}{e}, $$

(1.14)

then every solution of ($E'$) oscillates; see also [8, Corollary 2.6.12].

Suppose that $\sigma _{i}$, $1\leq i\leq m$, are not necessarily monotone. Set

$$ \rho _{i}(t):=\inf_{s\geq t}\sigma _{i}(s) \quad \text{and}\quad \rho (t):= \min_{1\leq i\leq m}\rho _{i}(t), \quad t\geq t_{0}. $$

(1.15)

Clearly, $\rho _{i}$, ρ are nondecreasing and $\sigma _{i}(t) \geq \rho _{i}(t)\geq \rho (t)>t$ for all $t\geq t_{0}$.

In 2016, Braverman, Chatzarakis, and Stavroulakis [1] proved that if, for some $r\in \mathbb{N}$,

$$ \limsup_{t\rightarrow \infty } \int _{t}^{\rho (t)}\sum_{i=1}^{m} q_{i}( \zeta )b_{r}\bigl(\rho (t),\sigma _{i}( \zeta )\bigr)\,d\zeta >1, $$

(1.16)

or

$$ \liminf_{t\rightarrow \infty } \int _{t}^{\rho (t)}\sum_{i=1}^{m} q_{i}( \zeta )b_{r}\bigl(\rho (t),\sigma _{i}( \zeta )\bigr)\,d\zeta >\frac{1}{e} , $$

(1.17)

where

$$ \begin{aligned} &b_{1}(t,s) :=\exp \biggl\{ \int _{t}^{s}Q(\zeta )\,d\zeta \biggr\} , \\ &b_{r+1}(t,s) :=\exp \Biggl\{ \int _{t}^{s}\sum_{i=1}^{m}q_{i}( \zeta )b _{r}\bigl(\zeta ,\sigma _{i}(\zeta )\bigr)\,d\zeta \Biggr\} , \end{aligned} $$

then every solution of ($E'$) oscillates.

Several improvements have been made to the above conditions, see [3,4,5, 7] to arrive at the recent forms [4]

$$\begin{aligned}& \limsup_{t\rightarrow \infty } \int _{t}^{\rho (t)}Q(s)\exp \biggl( \int _{\rho (t)}^{\sigma (s)}Q(u)\exp \biggl( \int _{u}^{\sigma (u)}S _{\ell }(\xi )\,d\xi \biggr) \,du \biggr)\,ds>1, \end{aligned}$$

(1.18)

$$\begin{aligned}& \limsup_{t\rightarrow \infty } \int _{t}^{\rho (t)}Q(s)\exp \biggl( \int _{\rho (t)}^{\sigma (s)}Q(u)\exp \biggl( \int _{u}^{\sigma (u)}S _{\ell }(\xi )\,d\xi \biggr) \,du \biggr)\,ds>1-D(\beta ), \\ \end{aligned}$$

(1.19)

$$\begin{aligned}& \liminf_{t\rightarrow \infty } \int _{t}^{\rho (t)}Q(s)\exp \biggl( \int _{\rho (s)}^{\sigma (s)}Q(u)\exp \biggl( \int _{u}^{\sigma (u)}S _{\ell }(\xi )\,d\xi \biggr) \,du \biggr)\,ds>\frac{1}{e}, \end{aligned}$$

(1.20)

where

$$ S_{\ell }(t):=Q(t) \biggl[ 1+ \int _{t}^{\sigma (t)}Q(s)\exp \biggl( \int _{t}^{\sigma (s)}Q(u)\exp \biggl( \int _{u}^{\sigma (u)}S_{\ell -1}( \xi )\,d\xi \biggr) \,du \biggr)\,ds \biggr] $$

with

$$ S_{0}(t):=Q(t) \biggl[ 1+ \int _{t}^{\sigma (t)}Q(s)\exp \biggl( \int _{t}^{\sigma (s)}Q(\omega )\exp \biggl( \lambda _{0} \int _{\omega }^{ \sigma (\omega )}Q(u)\,du \biggr)\,d\omega \biggr)\,ds \biggr], $$

where $\lambda _{0}$ is the smaller root of the transcendental equation $\lambda =e^{\beta \lambda}$.

2 Main results

2.1 DDEs

New sufficient conditions are established for the oscillation of all solutions of (E) using an iterative method. These conditions, involving limsup and liminf, significantly improve several results in the literature.

We now cite two lemmas which will be used to prove the main results. Their proofs are similar to those of Lemmas 2.1.1, 2.1.3, and 2.1.2 in [8], respectively.

Lemma 1

Let h be as in (1.6). Then

$$ \liminf_{t\rightarrow \infty } \int _{\tau (t)}^{t}P(s)\,ds= \liminf_{t\rightarrow \infty } \int _{h(t)}^{t}P(s)\,ds. $$

(2.1)

Lemma 2

Let $\alpha \in (0,1/e]$, x be an eventually positive solution of (E), and h be as in (1.6). Then

$$ \liminf_{t\rightarrow \infty }\frac{x(t)}{x(h(t))}\geq D(\alpha ) $$

(2.2)

and

$$ \liminf_{t\rightarrow \infty }\frac{x(h(t))}{x(t)}\geq \lambda _{0} , $$

(2.3)

where $\lambda _{0}$ is the smaller root of the transcendental equation $\lambda =e^{\alpha \lambda }$.

On the basis of the above lemmas, we present the following results. Without loss of generality, we deal only with eventually positive solutions of (E) (or ($E'$)) since, under our assumptions, if x is a solution, so is −x.

Theorem 1

Let $\alpha \in (0,1/e]$ and h be as in (1.6). Assume that, for some $\ell \in \mathbb{N}$,

$$ \limsup_{t\rightarrow \infty } \int _{h(t)}^{t}P(s)\exp \biggl( \int _{\tau ( s ) }^{h(t)}P(u)\exp \biggl( \int _{\tau (u)} ^{u}B_{\ell }(\xi )\,d\xi \biggr) \,du \biggr)\,ds>1, $$

(2.4)

where

$$ B_{\ell }(t):=P(t) \biggl[ 1+ \int _{\tau (t)}^{t}P(s)\exp \biggl( \int _{\tau ( s ) }^{t}P(u)\exp \biggl( \int _{\tau (u)} ^{u}B_{\ell -1}(\xi )\,d\xi \biggr) \,du \biggr)\,ds \biggr] $$

(2.5)

with

$$\begin{aligned} B_{0}(t) :=&P(t) \biggl[ 1 \\ &{}+ \int _{\tau (t)}^{t}P(s)\exp \biggl( \int _{\tau (s)}^{t}P(y)\exp \biggl( \int _{\tau (y)}^{y}P(\omega ) \exp \biggl( \lambda _{0} \int _{\tau (\omega )}^{\omega }P(u)\,du \biggr)\,d\omega \biggr)\,dy \biggr)\,ds \biggr], \end{aligned}$$

and $\lambda _{0}$ is the smaller root of the transcendental equation $\lambda =e^{\alpha \lambda }$. Then every solution of (E) oscillates.

Proof

Assume the opposite. Let x be an eventually positive solution of (E). Then there exists a $t_{1}>t_{0}$ such that $x(t)>0$ and $x( \tau _{i}(t)) >0$ for all $t\geq t_{1}$ and $1 \leq i \leq m$. Thus, by virtue of (E),

$$ x^{\prime }(t)=-\sum_{i=1}^{m} p_{i}(t)x\bigl( \tau _{i}(t)\bigr) \leq 0\quad \text{for all } t\geq t_{1}, $$

which implies that x is an eventually nonincreasing function of positive numbers.

Dividing (E) by $x( t) >0$ and integrating the resulting equality on $[ \tau (t),t ]$, we deduce that

$$ \int _{\tau (t)}^{t}\frac{x^{\prime }(u)}{x(u)}\,du=- \int _{\tau (t)}^{t} \sum_{i=1}^{m} p_{i}(u)\frac{x( \tau _{i}(u)) }{x(u)}\,du, $$

or

$$ \int _{\tau (t)}^{t}\frac{x^{\prime }(u)}{x(u)}\,du\leq - \int _{\tau (t)} ^{t} \Biggl( \sum _{i=1}^{m} p_{i}(u) \Biggr) \frac{x( \tau (u)) }{x(u)}\,du, $$

or

$$ \int _{\tau (t)}^{t}\frac{x^{\prime }(u)}{x(u)}\,du\leq - \int _{\tau (t)} ^{t}P(u)\frac{x( \tau (u)) }{x(u)}\,du. $$

Therefore,

$$ x\bigl(\tau (t)\bigr)\geq x(t)\exp \biggl( \int _{\tau (t)}^{t}P(u)\frac{x( \tau (u)) }{x(u)}\,du \biggr) . $$

(2.6)

Combining (E) and (2.6), we arrive at

$$ \begin{aligned}[b] 0 &= x^{\prime }(t)+\sum _{i=1}^{m} p_{i}(t)x\bigl( \tau _{i}(t)\bigr) \geq x^{ \prime }(t)+P(t)x\bigl( \tau (t)\bigr) \\ &\geq x^{\prime }(t)+P(t)x(t)\exp \biggl( \int _{\tau (t)}^{t}P(u)\frac{x( \tau (u)) }{x(u)}\,du \biggr) . \end{aligned} $$

(2.7)

Dividing (2.7) by $x( t) >0$ and integrating the resulting inequality on $[ \tau (t),t ]$, we obtain

$$ \int _{\tau (t)}^{t}\frac{x^{\prime }(\omega )}{x(\omega )}\,d\omega \leq - \int _{\tau (t)}^{t}P(\omega )\exp \biggl( \int _{\tau (\omega )} ^{\omega }P(u)\frac{x( \tau (u)) }{x(u)}\,du \biggr)\,d \omega $$

or

$$ x\bigl(\tau (t)\bigr)\geq x(t)\exp \biggl( \int _{\tau (t)}^{t}P(\omega )\exp \biggl( \int _{\tau (\omega )}^{\omega }P(u)\frac{x( \tau (u)) }{x(u)}\,du \biggr)\,d \omega \biggr) . $$

(2.8)

Combining (E) and (2.8), we have

$$ x^{\prime }(t)+P(t)x(t)\exp \biggl( \int _{\tau (t)}^{t}P(\omega ) \exp \biggl( \int _{\tau (\omega )}^{\omega }P(u) \frac{x( \tau (u)) }{x(u)}\,du \biggr)\,d \omega \biggr) \leq 0 . $$

(2.9)

Dividing (2.9) by $x( t) >0$ and integrating the resulting inequality on $[ \tau (s),t ]$, we get

$$ \int _{\tau (s)}^{t}\frac{x^{\prime }(y)}{x(y)}\,dy\leq - \int _{\tau (s)} ^{t}P(y)\exp \biggl( \int _{\tau (y)}^{y}P(\omega )\exp \biggl( \int _{\tau (\omega )}^{\omega }P(u)\frac{x( \tau (u)) }{x(u)}\,du \biggr)\,d \omega \biggr)\,dy $$

or

$$\begin{aligned}& x\bigl(\tau (s)\bigr) \\& \quad \geq x(t)\exp \biggl( \int _{\tau (s)}^{t}P(y)\exp \biggl( \int _{\tau (y)}^{y}P(\omega )\exp \biggl( \int _{\tau (\omega )}^{ \omega }P(u)\frac{x( \tau (u)) }{x(u)}\,du \biggr)\,d \omega \biggr)\,dy \biggr) . \end{aligned}$$

(2.10)

Integrating (E) from $\tau (t)$ to t, using (2.10), multiplying by $P(t)$, and taking into account the fact that $x^{\prime }(t)\leq -P(t)x(\tau (t))$, we conclude that

$$ \begin{aligned}[b] 0\geq{} &x^{\prime }(t) +P(t)x(t) \\ &{}+P(t)x(t) \int _{\tau (t)}^{t}P(s)\exp \biggl( \int _{\tau (s)}^{t}P(y) \\ &{}\times \exp \biggl( \int _{\tau (y)}^{y}P(\omega )\exp \biggl( \int _{\tau (\omega )}^{\omega }P(u)\frac{x( \tau (u)) }{x(u)}\,du \biggr)\,d \omega \biggr)\,dy \biggr)\,ds. \end{aligned} $$

It follows from $\tau (u)\leq h(u)$ that

$$ \begin{aligned}[b] 0\geq{}& x^{\prime }(t) +P(t)x(t) \\ &{}+P(t)x(t) \int _{\tau (t)}^{t}P(s)\exp \biggl( \int _{\tau (s)}^{t}P(y) \\ &{}\times \exp \biggl( \int _{\tau (y)}^{y}P(\omega )\exp \biggl( \int _{\tau (\omega )}^{\omega }P(u)\frac{x( h(u)) }{x(u)}\,du \biggr)\,d \omega \biggr)\,dy \biggr)\,ds. \end{aligned} $$

By virtue of (2.3), for each $\epsilon >0$ and for sufficiently large t, the last inequality becomes

$$\begin{aligned} 0 \geq& x^{\prime }(t) \\ &{}+P(t) \biggl[ 1+ \int _{\tau (t)}^{t}P(s)\exp \biggl( \int _{\tau (s)} ^{t}P(y) \\ &{}\times \exp \biggl( \int _{\tau (y)}^{y}P(\omega )\exp \biggl( ( \lambda _{0}-\epsilon ) \int _{\tau (\omega )}^{\omega }P(u)\,du \biggr)\,d\omega \biggr)\,dy \biggr)\,ds \biggr] x(t) \end{aligned}$$

or

$$ x^{\prime }(t)+B_{0}(t,\epsilon )x(t)\leq 0 $$

(2.11)

with

$$\begin{aligned} B_{0}(t,\epsilon ) :=&P(t) \biggl[ 1+ \int _{\tau (t)}^{t}P(s)\exp \biggl( \int _{\tau (s)}^{t}P(y) \\ &{}\times \exp \biggl( \int _{\tau (y)}^{y}P(\omega ) \exp \biggl( ( \lambda _{0}-\epsilon ) \int _{\tau (\omega )}^{\omega }P(u)\,du \biggr)\,d\omega \biggr)\,dy \biggr)\,ds \biggr] . \end{aligned}$$

Applying the Grönwall inequality in (2.11), we obtain

$$ x\bigl(\tau (u)\bigr)\geq x(u)\exp \biggl( \int _{\tau (u)}^{u}B_{0}(\xi ,\epsilon )\,d\xi \biggr) . $$

(2.12)

Dividing (E) by $x( t) >0$, integrating the resulting equality on $[\tau ( s),t ]$ and using (2.12), we deduce that

$$ - \int _{\tau ( s ) }^{t}\frac{x^{\prime }(u)}{x(u)}\,du \geq \int _{\tau ( s ) }^{t}P(u)\frac{x( \tau (u)) }{x(u)}\,du\geq \int _{\tau (s)}^{t}P(u)\exp \biggl( \int _{\tau (u)}^{u}B_{0}( \xi ,\epsilon )\,d\xi \biggr)\,du $$

or

$$ x\bigl(\tau ( s) \bigr)\geq x(t)\exp \biggl( \int _{\tau ( s ) }^{t}P(u) \exp \biggl( \int _{\tau (u)}^{u}B_{0}(\xi ,\epsilon )\,d\xi \biggr)\,du \biggr) . $$

(2.13)

Integrating (E) from $\tau (t)$ to t and using (2.13), we obtain

$$ x(t)-x\bigl(\tau (t)\bigr)+x(t) \int _{\tau (t)}^{t}P(s)\exp \biggl( \int _{\tau ( s ) }^{t}P(u)\exp \biggl( \int _{\tau (u)} ^{u}B_{0}(\xi ,\epsilon )\,d\xi \biggr)\,du \biggr)\,ds\leq 0. $$

Multiplying the last inequality by $P(t)$, we have

$$\begin{aligned}& P(t)x(t)-P(t)x\bigl(\tau (t)\bigr)+P(t)x(t) \int _{\tau (t)}^{t}P(s)\exp \biggl( \int _{\tau ( s ) }^{t}P(u)\exp \biggl( \int _{\tau (u)} ^{u}B_{0}(\xi ,\epsilon )\,d\xi \biggr)\,du \biggr)\,ds \\& \quad \leq 0, \end{aligned}$$

which, in view of $x^{\prime }(t)\leq -P(t)x(\tau (t))$, reduces to

$$ x^{\prime }(t)+P(t)x(t)+P(t)x(t) \int _{\tau (t)}^{t}P(s)\exp \biggl( \int _{\tau ( s ) }^{t}P(u)\exp \biggl( \int _{\tau (u)} ^{u}B_{0}(\xi ,\epsilon )\,d\xi \biggr)\,du \biggr)\,ds\leq 0. $$

Hence, for sufficiently large t,

$$ x^{\prime }(t)+P(t) \biggl[ 1+ \int _{\tau (t)}^{t}P(s)\exp \biggl( \int _{\tau ( s ) }^{t}P(u)\exp \biggl( \int _{\tau (u)} ^{u}B_{0}(\xi ,\epsilon )\,d\xi \biggr)\,du \biggr)\,ds \biggr] x(t) \leq 0 $$

or

$$ x^{\prime }(t)+B_{1}(t,\epsilon )x(t)\leq 0, $$

where

$$ B_{1}(t,\epsilon ):=P(t) \biggl[ 1+ \int _{\tau (t)}^{t}P(s)\exp \biggl( \int _{\tau ( s ) }^{t}P(u)\exp \biggl( \int _{\tau (u)} ^{u}B_{0}(\xi ,\epsilon )\,d\xi \biggr)\,du \biggr)\,ds \biggr] . $$

Following the above procedures, we can inductively construct the inequalities

$$ x^{\prime }(t)+B_{\ell }(t,\epsilon )x(t )\leq 0, \quad \ell \in \mathbb{N} , $$

where

$$ B_{\ell }(t,\epsilon ):=P(t) \biggl[ 1+ \int _{\tau (t)}^{t}P(s)\exp \biggl( \int _{\tau ( s ) }^{t}P(u)\exp \biggl( \int _{ \tau (u)}^{u}B_{\ell -1}(\xi ,\epsilon )\,d\xi \biggr)\,du \biggr)\,ds \biggr] $$

and

$$ x\bigl(\tau ( s) \bigr)\geq x\bigl(h(t)\bigr)\exp \biggl( \int _{\tau ( s ) } ^{h(t)}P(u)\exp \biggl( \int _{\tau (u)}^{u}B_{\ell }(\xi ,\epsilon )\,d\xi \biggr)\,du \biggr) . $$

(2.14)

Integrating (E) from $h(t)$ to t and using (2.14), we arrive at

$$\begin{aligned}& x(t)-x\bigl(h(t)\bigr)+x\bigl(h(t)\bigr) \int _{h(t)}^{t}P(s)\exp \biggl( \int _{\tau ( s ) }^{h(t)}P(u)\exp \biggl( \int _{\tau (u)} ^{u}B_{\ell }(\xi ,\epsilon )\,d\xi \biggr)\,du \biggr)\,ds \\& \quad \leq 0 . \end{aligned}$$

(2.15)

If we omit $x(t)>0$, then (2.15) becomes

$$ x\bigl(h(t)\bigr) \biggl[ \int _{h(t)}^{t}P(s)\exp \biggl( \int _{\tau ( s ) }^{h(t)}P(u)\exp \biggl( \int _{\tau (u)} ^{u}B_{\ell }(\xi ,\epsilon )\,d\xi \biggr)\,du \biggr)\,ds-1 \biggr] < 0 , $$

which means that

$$ \limsup_{t\rightarrow \infty } \int _{h(t)}^{t}P(s)\exp \biggl( \int _{\tau ( s ) }^{h(t)}P(u)\exp \biggl( \int _{\tau (u)} ^{u}B_{\ell }(\xi ,\epsilon )\,d\xi \biggr)\,du \biggr)\,ds\leq 1 . $$

This inequality contradicts (2.4) due to the fact that ϵ may be taken arbitrarily small. The proof is complete. □

Theorem 2

Let $\alpha \in (0,1/e]$ and h be as in (1.6). If, for some $\ell \in \mathbb{N}$,

$$ \limsup_{t\rightarrow \infty } \int _{h(t)}^{t}P(s)\exp \biggl( \int _{\tau ( s ) }^{h(t)}P(u)\exp \biggl( \int _{\tau (u)} ^{u}B_{\ell }(\xi )\,d\xi \biggr) \,du \biggr)\,ds>1-D(\alpha ), $$

(2.16)

where $B_{\ell }$ is as in (2.5), then every solution of (E) oscillates.

Proof

Let x be an eventually positive solution of (E). As in the proof of Theorem 1, (2.15) holds, that is,

$$ x(t)-x\bigl(h(t)\bigr)+x\bigl(h(t)\bigr) \int _{h(t)}^{t}P(s)\exp \biggl( \int _{\tau ( s ) }^{h(t)}P(u)\exp \biggl( \int _{\tau (u)} ^{u}B_{\ell }(\xi ,\epsilon )\,d\xi \biggr)\,du \biggr)\,ds\leq 0 , $$

which yields

$$ \int _{h(t)}^{t}P(s)\exp \biggl( \int _{\tau ( s ) }^{h(t)}P(u) \exp \biggl( \int _{\tau (u)}^{u}B_{\ell }(\xi ,\epsilon )\,d\xi \biggr)\,du \biggr)\,ds\leq 1-\frac{x(t)}{x(h(t))}, $$

and hence

$$\begin{aligned}& \limsup_{t\rightarrow \infty } \int _{h(t)}^{t}P(s)\exp \biggl( \int _{\tau ( s ) }^{h(t)}P(u)\exp \biggl( \int _{\tau (u)} ^{u}B_{\ell }(\xi ,\epsilon )\,d\xi \biggr)\,du \biggr)\,ds \\& \quad \leq 1- \liminf_{t\rightarrow \infty }\frac{x(t)}{x(h(t))}. \end{aligned}$$

(2.17)

It follows from Lemma 2 that inequality (2.2) is satisfied. So, by virtue of (2.2) and (2.17),

$$ \limsup_{t\rightarrow \infty } \int _{h(t)}^{t}P(s)\exp \biggl( \int _{\tau ( s ) }^{h(t)}P(u)\exp \biggl( \int _{\tau (u)} ^{u}B_{\ell }(\xi ,\epsilon )\,d\xi \biggr)\,du \biggr)\,ds\leq 1-D( \alpha ). $$

This inequality contradicts (2.16) due to the fact that ϵ may be taken arbitrarily small. The proof is complete. □

Theorem 3

Let $\alpha \in (0,1/e]$ and h be as in (1.6). If, for some $\ell \in \mathbb{N}$,

$$ \liminf_{t\rightarrow \infty } \int _{h(t)}^{t}P(s)\exp \biggl( \int _{\tau ( s ) }^{h(s)}P(u)\exp \biggl( \int _{\tau (u)} ^{u}B_{\ell }(\xi )\,d\xi \biggr) \,du \biggr)\,ds>\frac{1}{e}, $$

(2.18)

where $B_{\ell }$ is as in (2.5), then every solution of (E) oscillates.

Proof

As above, assume that (E) has a nonoscillatory solution x which is eventually positive. Then there exists a $t_{1}>t_{0}$ such that $x(t)>0$, $x( \tau _{i}(t)) >0$, $1\leq i\leq m$, for all $t\geq t _{1}$. Thus, by (E), we have

$$ x^{\prime }(t)=-\sum_{i=1}^{m} p_{i}(t)x\bigl( \tau _{i}(t)\bigr) \leq 0 \quad \text{for all }t\geq t_{1}, $$

which implies that x is an eventually nonincreasing function of positive numbers. Moreover, as in the proof of Theorem 1, (2.14) is fulfilled.

Dividing (E) by $x(t)$ and integrating the resulting equality from $h(t)$ to t, we deduce that

$$\begin{aligned} \ln \biggl( \frac{x(h(t))}{x(t)} \biggr) =& \int _{h(t)}^{t} \sum_{i=1}^{m} p_{i}(s)\frac{x( \tau _{i}(s)) }{x( s) }\,ds \\ \geq& \int _{h(t)}^{t} \Biggl( \sum _{i=1}^{m} p_{i}(s) \Biggr) \frac{x( \tau (s)) }{x( s) }\,ds= \int _{h(t)}^{t}P(s)\frac{x( \tau (s)) }{x( s) }\,ds \\ \geq& \int _{h(t)}^{t}P(s)\frac{x(h(s))}{x( s) }\exp \biggl( \int _{\tau ( s ) }^{h(s)}P(u)\exp \biggl( \int _{\tau (u)} ^{u}B_{\ell }(\xi ,\epsilon )\,d\xi \biggr)\,du \biggr)\,ds \\ \geq& \int _{h(t)}^{t}P(s)\exp \biggl( \int _{\tau ( s ) } ^{h(s)}P(u)\exp \biggl( \int _{\tau (u)}^{u}B_{\ell }(\xi ,\epsilon )\,d\xi \biggr)\,du \biggr)\,ds. \end{aligned}$$

(2.19)

It follows from (2.18) that there exists a constant $c>0$ such that, for all sufficiently large t,

$$ \int _{h(t)}^{t}P(s)\exp \biggl( \int _{\tau ( s ) }^{h(s)}P(u) \exp \biggl( \int _{\tau (u)}^{u}B_{\ell }(\xi )\,d\xi \biggr) \,du \biggr)\,ds\geq c>\frac{1}{e}. $$

Choose $c^{\prime }$ such that $c>c^{\prime }>1/e$. For every $\epsilon >0$ satisfying $c-\epsilon >c^{\prime }$, we get

$$ \int _{h(t)}^{t}P(s)\exp \biggl( \int _{\tau ( s ) }^{h(s)}P(u) \exp \biggl( \int _{\tau (u)}^{u}B_{\ell }(\xi ,\epsilon )\,d\xi \biggr)\,du \biggr)\,ds\geq c-\epsilon >c^{\prime }>\frac{1}{e}. $$

(2.20)

Hence, we derive from (2.19) and (2.20) that

$$ \ln \biggl( \frac{x(h(t))}{x(t)} \biggr) \geq c^{\prime }, $$

which yields

$$ \frac{x(h(t))}{x(t)}\geq e^{c^{\prime }}\geq ec^{\prime }>1, $$

and so

$$ x\bigl(h(t)\bigr)\geq \bigl(ec^{\prime }\bigr)x(t). $$

Repeating the above steps, it follows by induction that, for any positive integer k,

$$ \frac{x(h(t))}{x(t)}\geq \bigl(ec^{\prime }\bigr)^{k}\quad \text{for sufficiently large }t. $$

Since $ec^{\prime }>1$, there is a $k\in {\mathbb{N}}$ satisfying $k>2(\ln 2-\ln c^{\prime })/(1+\ln c^{\prime })$ such that, for t sufficiently large,

$$ \frac{x(h(t))}{x(t)}\geq \bigl(ec^{\prime }\bigr)^{k}> \biggl( \frac{2}{c^{ \prime }} \biggr) ^{2}. $$

(2.21)

Taking the integral on $[h(t),t]$, which is not less than $c^{\prime }$, we split the interval into two parts where integrals are not less than $c^{\prime }/2$, let $t_{m}\in (h(t),t)$ be the splitting point:

$$ \begin{aligned} & \int _{h(t)}^{t_{m}}P(s)\exp \biggl( \int _{\tau ( s ) } ^{h(s)}P(u)\exp \biggl( \int _{\tau (u)}^{u}B_{\ell }(\xi ,\epsilon )\,d\xi \biggr)\,du \biggr)\,ds\geq \frac{c^{\prime }}{2}, \\ & \int _{t_{m}}^{t}P(s)\exp \biggl( \int _{\tau ( s ) }^{h(s)}P(u) \exp \biggl( \int _{\tau (u)}^{u}B_{\ell }(\xi ,\epsilon )\,d\xi \biggr)\,du \biggr)\,ds\geq \frac{c^{\prime }}{2}. \end{aligned} $$

(2.22)

Integrating (E) from $t_{m}$ to t, we arrive at

$$ \begin{aligned} 0 &=x(t)-x(t_{m})+ \int _{t_{m}}^{t}\sum_{i=1}^{m} p_{i}(s)x\bigl(\tau _{i}(s)\bigr)\,ds \\ &\geq x(t)-x(t_{m})+ \int _{t_{m}}^{t}P(s)x\bigl(\tau (s)\bigr)\,ds \\ &\geq x(t)-x(t_{m})+x\bigl(h(t)\bigr) \int _{t_{m}}^{t}P(s)\exp \biggl( \int _{\tau ( s ) }^{h(s)}P(u)\exp \biggl( \int _{\tau (u)} ^{u}B_{\ell }(\xi ,\epsilon )\,d\xi \biggr)\,du \biggr)\,ds \\ &>-x(t_{m})+x\bigl(h(t)\bigr) \int _{t_{m}}^{t}P(s)\exp \biggl( \int _{\tau ( s ) }^{h(s)}P(u)\exp \biggl( \int _{\tau (u)} ^{u}B_{\ell }(\xi ,\epsilon )\,d\xi \biggr)\,du \biggr)\,ds. \end{aligned} $$

This, along with the second inequality in (2.22), implies that

$$ x(t_{m})>\frac{c^{\prime }}{2}x\bigl(h(t)\bigr). $$

(2.23)

Similarly, integrating (E) from $h(t)$ to $t_{m}$ and subsequently applying (2.14), we conclude that

$$ x(t_{m})-x\bigl(h(t)\bigr)+x\bigl(h(t_{m})\bigr) \int _{h(t)}^{t_{m}}P(s)\exp \biggl( \int _{\tau ( s ) }^{h(s)}P(u)\exp \biggl( \int _{\tau (u)} ^{u}B_{\ell }(\xi ,\epsilon )\,d\xi \biggr)\,du \biggr)\,ds\leq 0 . $$

If we omit $x(t_{m})>0$ in the left-hand side, then the strict inequality becomes valid:

$$ -x\bigl(h(t)\bigr)+x\bigl(h(t_{m})\bigr) \int _{h(t)}^{t_{m}}P(s)\exp \biggl( \int _{\tau ( s ) }^{h(s)}P(u)\exp \biggl( \int _{\tau (u)} ^{u}B_{\ell }(\xi ,\epsilon )\,d\xi \biggr)\,du \biggr)\,ds< 0. $$

This, along with the first inequality in (2.22), yields

$$ x\bigl(h(t)\bigr)>\frac{c^{\prime }}{2}x\bigl(h(t_{m})\bigr). $$

(2.24)

Combining inequalities (2.23) and (2.24), we obtain

$$ x\bigl(h(t_{m})\bigr)< \frac{2}{c^{\prime }}x\bigl(h(t)\bigr)< \biggl( \frac{2}{c^{\prime }} \biggr) ^{2}x(t_{m}), $$

which contradicts (2.21). This completes the proof. □

2.2 ADEs

Similar oscillation criteria can easily be derived for the (dual) advanced differential equation ($E'$). The proofs are omitted due to the fact that they are quite similar to those of the delay equation.

Theorem 4

Let $\beta \in (0,1/e]$ and ρ be as in (1.15). If, for some $\ell \in \mathbb{N}$,

$$ \limsup_{t\rightarrow \infty } \int _{t}^{\rho (t)}Q(s)\exp \biggl( \int _{\rho (t)}^{\sigma (s)}Q(u)\exp \biggl( \int _{u}^{\sigma (u)} \varPhi _{\ell }(\xi )\,d\xi \biggr)\,du \biggr)\,ds>1, $$

(2.25)

where

$$ \varPhi _{\ell }(t):=Q(t) \biggl[ 1+ \int _{t}^{\sigma (t)}Q(s)\exp \biggl( \int _{t}^{\sigma (s)}Q(u)\exp \biggl( \int _{u}^{\sigma (u)}\varPhi _{ \ell -1}(\xi )\,d\xi \biggr)\,du \biggr)\,ds \biggr] $$

(2.26)

with

$$\begin{aligned} \varPhi _{0}(t) :=&Q(t) \biggl[ 1+ \int _{t}^{\sigma (t)}Q(s)\exp \biggl( \int _{t}^{\sigma (s)}Q(y) \\ &{}\times \exp \biggl( \int _{y}^{\sigma (y)}Q(\omega ) \exp \biggl( \lambda _{0} \int _{\omega }^{\sigma (\omega )}Q(u)\,du \biggr)\,d\omega \biggr)\,dy \biggr)\,ds \biggr], \end{aligned}$$

and $\lambda _{0}$ is the smaller root of the transcendental equation $\lambda =e^{\beta \lambda }$, then every solution of ($E'$) oscillates.

Theorem 5

Let $\beta \in (0,1/e]$ and ρ be as in (1.15). If, for some $\ell \in \mathbb{N}$,

$$ \limsup_{t\rightarrow \infty } \int _{t}^{\rho (t)}Q(s)\exp \biggl( \int _{\rho (t)}^{\sigma (s)}Q(u)\exp \biggl( \int _{u}^{\sigma (u)} \varPhi _{\ell }(\xi )\,d\xi \biggr)\,du \biggr)\,ds>1-D(\beta ), $$

(2.27)

where $\varPhi _{\ell }$ is as in (2.26), then every solution of ($E'$) oscillates.

Theorem 6

Let $\beta \in (0,1/e]$ and ρ be as in (1.15). If, for some $\ell \in \mathbb{N}$,

$$ \liminf_{t\rightarrow \infty } \int _{t}^{\rho (t)}Q(s)\exp \biggl( \int _{\rho (s)}^{\sigma (s)}Q(u)\exp \biggl( \int _{u}^{\sigma (u)} \varPhi _{\ell }(\xi )\,d\xi \biggr)\,du \biggr)\,ds>\frac{1}{e}, $$

(2.28)

where $\varPhi _{\ell }$ is as in (2.26), then every solution of ($E'$) oscillates.

3 Examples

The examples provided in this section illustrate cases where the results of the present paper ensure oscillations, whereas the previously known results fail to apply in these equations. Moreover, these examples show the improvement attained by the obtained conditions over the known ones. The calculations performed have been produced in MATLAB.

Example 1

Consider the DDE

$$ x^{\prime }(t)+\frac{523}{6250}x\bigl(\tau _{1}(t)\bigr)+ \frac{523}{25{,}000}x\bigl(\tau _{2}(t)\bigr)=0 ,\quad t\geq 0, $$

(3.1)

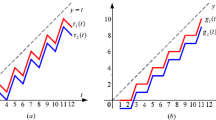
with (see Fig. 1(a))

$$ \tau _{1}(t)=\textstyle\begin{cases} -t+12k-2, & \text{if }t\in [ 6k,6k+1 ], \\ 4t-18k-7, & \text{if }t\in [ 6k+1,6k+2 ], \\ 0.5t+3k, & \text{if }t\in [ 6k+2,6k+4 ], \\ -6t+42k+26, & \text{if }t\in [ 6k+4,6k+5 ], \\ 8t-42k-44, & \text{if }t\in [ 6k+5,6k+6 ], \end{cases}\displaystyle \quad \text{and} \quad \tau _{2}(t)= \tau _{1}(t)-0.5, $$

where $k\in \mathbb{N} _{0}$ and $\mathbb{N} _{0}$ is the set containing all nonnegative integers.

Figure 1

The graphs of $\tau _{1}(t)$ and $h_{1}(t)$

By (1.6), we see (Fig. 1(b)) that

$$ h_{1}(t)=\textstyle\begin{cases} 6k-2, & \text{if }t\in [ 6k,6k+1.25 ], \\ 4t-18k-7, & \text{if }t\in [ 6k+1.25,6k+2 ], \\ 0.5t+3k, & \text{if }t\in [ 6k+2,6k+4 ], \\ 6k+2, & \text{if }t\in [ 6k+4,6k+5.75 ], \\ 8t-42k-44, & \text{if }t\in [ 6k+5.75,6k+6 ], \end{cases}\displaystyle \quad \text{and}\quad h_{2}(t)=h_{1}(t)-0.5, $$

and consequently,

$$ h(t)=\max_{1\leq i\leq 2} \bigl\{ h_{i}(t) \bigr\} =h_{1}(t) \quad \text{and} \quad \tau (t)=\max_{1\leq i\leq 2} \tau _{i}(t)=\tau _{1}(t) . $$

It is easy to see that

$$ \alpha =\liminf_{t\rightarrow \infty } \int _{\tau (t)}^{t} \sum_{i=1}^{2}p_{i}(s) \,ds=\liminf_{k\rightarrow \infty } \int _{6k+1} ^{6k+2} \biggl( \frac{523}{6250}+ \frac{523}{25{,}000} \biggr)\,ds=0.1046; $$

and therefore, the smaller root of $e^{0.1046\lambda }=\lambda$ is $\lambda _{0}=1.12486$.

Observe that the function $F_{\ell }:\mathbb{R} _{0}\rightarrow \mathbb{R} _{+}$ defined as

$$ F_{\ell }(t)= \int _{h(t)}^{t}P(s)\exp \biggl( \int _{\tau ( s ) }^{h(t)}P(u)\exp \biggl( \int _{\tau (u)} ^{u}B_{\ell }(\xi )\,d\xi \biggr) \,du \biggr)\,ds $$

attains its maximum at $t=6k+5.75$, $k\in \mathbb{N} _{0}$, for every $\ell \in \mathbb{N}$. In particular,

$$\begin{aligned} F_{1}(t =6k+5.75)= \int _{6k+2}^{6k+5.75}P(s)\exp \biggl( \int _{\tau ( s ) }^{6k+2}P(u)\exp \biggl( \int _{\tau (u)} ^{u}B_{1}(\xi )\,d\xi \biggr) \,du \biggr)\,ds \simeq 1.043, \end{aligned}$$

and thus

$$ \limsup_{t\rightarrow \infty }F_{1}(t)\simeq 1.043>1. $$

That is, condition (2.4) of Theorem 1 is satisfied for $\ell =1$, which implies that every solution of (3.1) oscillates.

Observe, however, that

$$\begin{aligned}& \limsup_{k\rightarrow \infty } \int _{6k+2}^{6k+5.75} \biggl( \frac{523}{6250}+ \frac{523}{25{,}000} \biggr)\,ds= 0.39225< 1, \\& \alpha =0.1046< \frac{1}{e}, \end{aligned}$$

and

$$\begin{aligned}& \liminf_{t\rightarrow \infty }\sum_{i=1}^{2}p_{i}(t) \bigl( t-\tau _{i}(t) \bigr) \\& \quad =\liminf_{t\rightarrow \infty } \biggl[ \frac{523}{6250} \bigl( t- \tau _{1}(t) \bigr) +\frac{523}{25{,}000} \bigl( t- \bigl( \tau _{1}(t)-0.5 \bigr) \bigr) \biggr] \\& \quad =\liminf_{t\rightarrow \infty } \biggl[ \frac{523}{5000} \bigl( t- \tau _{1}(t) \bigr) +\frac{523}{50{,}000} \biggr] \\& \quad = \liminf_{t\rightarrow \infty } \biggl[ \frac{523}{5000} \bigl( t-\tau _{1}(t) \bigr) \biggr] +\frac{523}{50{,}000} \\& \quad =\frac{523}{5000}\cdot \liminf_{t\rightarrow \infty } \bigl( t-\tau _{1}(t) \bigr) +\frac{523}{50{,}000} \\& \quad =\frac{523}{5000}\cdot 1+ \frac{523}{50{,}000}=0.11506< \frac{1}{e}. \end{aligned}$$

Note that the function $D_{r}:\mathbb{R}_{0} \rightarrow \mathbb{R} _{+}$ defined as

$$ D_{r}(t)= \int _{h(t)}^{t}\sum_{i=1}^{2}p_{i}( \zeta )a_{r}\bigl(h(t),\tau _{i}( \zeta )\bigr)\,d\zeta $$

attains its maximum at $t=6k+5.75$ and its minimum at $t=6k+2$, $k \in \mathbb{N} _{0}$, for every $r\in \mathbb{N}$. In particular,

$$\begin{aligned}& \begin{aligned} D_{1}(t =6k+5.75) ={}& \int _{6k+2}^{6k+5.75}\sum_{i=1}^{2}p_{i}( \zeta )a _{1}\bigl(6k+2,\tau _{i}(\zeta )\bigr)\,d\zeta \\ ={}& \int _{6k+2}^{6k+4} \bigl[ p_{1}(\zeta )a_{1}\bigl(6k+2,\tau _{1}(\zeta )\bigr)+p _{2}( \zeta )a_{1}\bigl(6k+2,\tau _{2}(\zeta )\bigr) \bigr]\,d\zeta \\ &{} + \int _{6k+4}^{6k+5} \bigl[ p_{1}(\zeta )a_{1}\bigl(6k+2,\tau _{1}( \zeta )\bigr)+p_{2}( \zeta )a_{1}\bigl(6k+2,\tau _{2}(\zeta )\bigr) \bigr]\,d\zeta \\ &{} + \int _{6k+5}^{6k+5.75} \bigl[ p_{1}(\zeta )a_{1}\bigl(6k+2,\tau _{1}(\zeta )\bigr)+p_{2}( \zeta )a_{1}\bigl(6k+2,\tau _{2}(\zeta )\bigr) \bigr]\,d\zeta \\ \simeq{}& 0.4803, \end{aligned} \\& \begin{aligned} D_{1}(t =6k+2) &= \int _{6k+1}^{6k+2}\sum_{i=1}^{2}p_{i}( \zeta )a_{1}\bigl(6k+1, \tau _{i}(\zeta )\bigr)\,d\zeta \\ &= \int _{6k+1}^{6k+2} \bigl[ p_{1}(\zeta )a_{1}\bigl(6k+1,\tau _{1}(\zeta )\bigr)+p_{2}( \zeta )a_{1}\bigl(6k+1,\tau _{2}(\zeta )\bigr) \bigr]\,d\zeta \\ &\simeq 0.1313 . \end{aligned} \end{aligned}$$

Hence,

$$\begin{aligned}& \limsup_{t\rightarrow \infty }D_{1}(t)\simeq 0.4803< 1, \\& \liminf_{t\rightarrow \infty }D_{1}(t)\simeq 0.1313< 1/e. \end{aligned}$$

Finally, using algorithms on MATLAB software, we obtain

$$\begin{aligned}& \limsup_{t\rightarrow \infty } \int _{h(t)}^{t}P(s)\exp \biggl( \int _{\tau ( s ) }^{h(t)}P(u)\exp \biggl( \int _{\tau (u)} ^{u}W_{1}(\xi )\,d\xi \biggr) \,du \biggr)\,ds\simeq 0.8157< 1, \\& 0.8157< 1-D(\alpha )\simeq 0.9938, \\& \liminf_{t\rightarrow \infty } \int _{h(t)}^{t}P(s)\exp \biggl( \int _{\tau ( s ) }^{h(s)}P(u)\exp \biggl( \int _{\tau (u)} ^{u}W_{1}(\xi )\,d\xi \biggr) \,du \biggr)\,ds\simeq 0.1064< \frac{1}{e} . \end{aligned}$$

That is, none of conditions (1.3)–(1.5), (1.7) and (1.8) (for $r=1$), and (1.9)–(1.11) (for $\ell =1$) is satisfied.

Comments

It is worth noticing that the improvement of condition (2.4) over the corresponding condition (1.3) is significant, approximately 165.9% when comparing the values on the left-hand side of these conditions. Meanwhile, the improvement compared to conditions (1.7) and (1.9) is very satisfactory, around 117.16% and 27.87%, respectively. In addition, observe that conditions (1.7)–(1.11) do not ensure oscillations from the first iteration. On the contrary, condition (2.4) is fulfilled from the first iteration. This means that this condition is better and more efficient, leading to oscillations much faster than conditions (1.7)–(1.11).

Example 2

Consider the ADE

$$ x^{\prime }(t)-\frac{417}{5000}x\bigl(\sigma _{1}(t)\bigr)- \frac{139}{2500}x\bigl( \sigma _{2}(t)\bigr)=0,\quad t\geq 0, $$

(3.2)

with (see Fig. 2(a))

$$ \sigma _{1}(t)=\textstyle\begin{cases} 5k+2, & \text{if }t\in [ 5k,5k+1 ], \\ 5t-20k-3, & \text{if }t\in [ 5k+1,5k+2 ], \\ -2t+15k+11, & \text{if }t\in [ 5k+2,5k+3 ], \\ 3t-10k-4, & \text{if }t\in [ 5k+3,5k+4 ], \\ -t+10k+12, & \text{if }t\in [ 5k+4,5k+5 ], \end{cases}\displaystyle \quad \text{and}\quad \sigma _{2}(t)=\sigma _{1}(t)+0.5 , $$

where $k\in \mathbb{N} _{0}$ and $\mathbb{N} _{0}$ stands for the set containing all nonnegative integers.

Figure 2

The graphs of $\sigma _{1}(t)$ and $\rho _{1}(t)$

By (1.15), we see (Fig. 2(b)) that

$$ \rho _{1}(t)=\textstyle\begin{cases} 5k+2, & \text{if }t\in [ 5k,5k+1 ], \\ 5t-20k-3, & \text{if }t\in [ 5k+1,5k+8/5 ], \\ 5k+5, & \text{if }t\in [ 5k+8/5,5k+3 ], \\ 3t-10k-4, & \text{if }t\in [ 5k+3,5k+11/3 ], \\ 5k+7, & \text{if }t\in [ 5k+11/3,5k+5 ], \end{cases}\displaystyle \quad \text{and}\quad \rho _{2}(t)=\rho _{1}(t)+0.5, $$

and consequently,

$$ \rho (t)=\min_{1\leq i\leq 2} \bigl\{ \rho _{i}(t) \bigr\} = \rho _{1}(t) \quad \text{and}\quad \sigma (t)=\min_{1\leq i\leq 2} \bigl\{ \sigma _{i}(t) \bigr\} =\sigma _{1}(t). $$

It is easy to see that

$$ \beta =\liminf_{t\rightarrow \infty } \int _{t}^{\sigma (t)}\sum_{i=1} ^{2} q_{i}(s)\,ds=\liminf_{k\rightarrow \infty } \int _{5k+1}^{5k+2} \frac{139}{1000}\,ds=0.139; $$

and therefore, the smaller root of $e^{0.139\lambda }=\lambda$ is $\lambda _{0}=1.17789$.

Observe that the function $F_{\ell }:\mathbb{R} _{0}\rightarrow \mathbb{R} _{+}$ defined as

$$ F_{\ell }(t)= \int _{t}^{\rho (t)}Q(s)\exp \biggl( \int _{\rho (t)}^{ \sigma (s)}Q(u)\exp \biggl( \int _{u}^{\sigma (u)}\varPhi _{\ell }(\xi )\,d\xi \biggr)\,du \biggr)\,ds $$

attains its maximum at $t=5k+8/5$, $k\in \mathbb{N} _{0}$, for every $\ell \in \mathbb{N}$. In particular, by using an algorithm on MATLAB software, we obtain

$$ F_{1}(t=5k+8/5)= \int _{5k+8/5}^{5k+5}Q(s)\exp \biggl( \int _{5k+2}^{ \sigma (s)}Q(u)\exp \biggl( \int _{u}^{\sigma (u)}\varPhi _{1}(\xi )\,d\xi \biggr)\,du \biggr)\,ds\simeq 0.9996, $$

and so

$$ \liminf_{t\rightarrow \infty }F_{1}(t)\simeq 0.9996>1-D(\beta ) \simeq 0.9886. $$

That is, condition (2.27) of Theorem 5 is satisfied for $\ell =1$, and therefore every solution of (3.2) oscillates.

Observe, however, that

$$\begin{aligned}& \limsup_{k\rightarrow \infty } \int _{5k+8/5}^{5k+5} \frac{139}{1000}\,ds=0.4726< 1, \\& \beta =0.139< \frac{1}{e}, \\& \begin{aligned} \liminf_{t\rightarrow \infty }\sum_{i=1}^{2}q_{i}(t) \bigl( \sigma _{i}(t)-t \bigr) &=\liminf_{t\rightarrow \infty }\sum _{i=1} ^{2}q_{i}(t) \bigl( \rho _{i}(t)-t \bigr) \\ &=\liminf_{t\rightarrow \infty } \biggl[ \frac{417}{5000} \bigl( \rho _{1}(t)-t \bigr) +\frac{139}{2500} \bigl( \rho _{1}(t)+0.5-t \bigr) \biggr] \\ &=\liminf_{t\rightarrow \infty } \bigl[ 0.139 \bigl( \rho _{1}(t)-t \bigr) +0.0278 \bigr] \\ &=\liminf_{t\rightarrow \infty } \bigl[ 0.139 \bigl( \rho _{1}(t)-t \bigr) \bigr] +0.0278 \\ &=0.139\cdot 1+0.0278=0.1668< \frac{1}{e}, \end{aligned} \\& \limsup_{t\rightarrow \infty } \int _{t}^{\rho (t)}\sum_{i=1}^{2} q _{i}(\zeta )b_{1}\bigl(\rho (t),\sigma _{i}( \zeta )\bigr)\,d\zeta \\& \quad =\limsup_{k\rightarrow \infty } \int _{5k+8/5}^{5k+5}\sum_{i=1} ^{2} q_{i}(\zeta )b_{1}\bigl(5k+5,\sigma _{i}(\zeta )\bigr)\,d\zeta \\& \quad =\limsup_{k\rightarrow \infty }\left\{\textstyle\begin{array}{l} \int _{5k+8/5}^{5k+2} \bigl[ q_{1}(\zeta )b_{1}\bigl(5k+5,\sigma _{1}(\zeta )\bigr)+q_{2}( \zeta )b_{1}\bigl(5k+5,\sigma _{2}(\zeta )\bigr) \bigr]\,d \zeta \\ \quad {}+ \int _{5k+2}^{5k+3} \bigl[ q_{1}(\zeta )b_{1}\bigl(5k+5,\sigma _{1}(\zeta )\bigr)+q _{2}(\zeta )b_{1}\bigl(5k+5,\sigma _{2}(\zeta ) \bigr) \bigr]\,d\zeta \\ \quad {}+ \int _{5k+3}^{5k+4} \bigl[ q_{1}(\zeta )b_{1}\bigl(5k+5,\sigma _{1}(\zeta )\bigr)+q _{2}(\zeta )b_{1}\bigl(5k+5,\sigma _{2}(\zeta ) \bigr) \bigr]\,d\zeta \\ \quad {}+ \int _{5k+4}^{5k+5} \bigl[ q_{1}(\zeta )b_{1}\bigl(5k+5,\sigma _{1}(\zeta )\bigr)+q _{2}(\zeta )b_{1}\bigl(5k+5,\sigma _{2}(\zeta ) \bigr) \bigr]\,d\zeta \end{array}\displaystyle \right\} \\& \quad =0.6108< 1, \end{aligned}$$

and

$$\begin{aligned}& \liminf_{t\rightarrow \infty } \int _{t}^{\rho (t)}\sum_{i=1}^{2} q _{i}(\zeta )b_{1}\bigl(\rho (t),\sigma _{i}( \zeta )\bigr)\,d\zeta \\& \quad =\liminf_{k\rightarrow \infty } \int _{5k+1}^{5k+2} \bigl[ q_{1}( \zeta )b_{1}\bigl(5k+2,\sigma _{1}(\zeta )\bigr)+q_{2}( \zeta )b_{1}\bigl(5k+2,\sigma _{2}(\zeta )\bigr) \bigr]\,d \zeta \\& \quad \simeq 0.2065< 1/e. \end{aligned}$$

That is, none of conditions (1.12)–(1.14), (1.16), and (1.17) (for $r=1$) is satisfied.

Finally, by using algorithms on MATLAB software, we see that none of conditions (1.18)–(1.20) (for $\ell =1$) is satisfied.

Remark 1

Similarly, one can present examples to illustrate the efficiency of other main results.