1 Introduction

Consider the following singularly perturbed Volterra integro-differential equation:

$$ \textstyle\begin{cases} \epsilon u'(t)+a(t)u(t)+\int _{0}^{t} k(t,s)u(s)\,ds =f(t), & t\in [0,T], \\ u(0)=u_{0}, & \end{cases} $$
(1.1)

where \(0<\epsilon \ll 1\) is the perturbation parameter. Here \(a(t)\ge \alpha >0\) for some constant α, \(f(t)\) and \(k(t,s)\) are sufficiently smooth functions, and u is the unknown function. When putting \(\epsilon =0\) in (1.1), we obtain the reduced equation

$$ a(t)u(t)+ \int _{0}^{t} k(t,s)u(s)\,ds =f(t), $$
(1.2)

which is a Volterra integral equation of the second kind. Singularly perturbed Volterra integro-differential equations arise in many physical and biological problems (see, e.g., [1,2,3,4,5,6,7]). A survey of singularly perturbed Volterra integral and integro-differential equations is provided in [8]. For singularly perturbed problems, when the perturbed parameter ϵ approaches to zero, the width of the boundary layer becomes thinner. The behavior of u in the boundary layer is hard to simulate numerically, i.e., the solution of (1.1) for the singular perturbation parameter ϵ varies very rapidly in a thin layer near \(t=0\) compared to the solution of (1.2) (see, e.g., [9, 10]). Traditional methods, such as finite difference or finite element method, do not work well for these problems because they often produce oscillatory solutions which are inaccurate when the perturbed parameter ϵ is small. The goal of this paper is to construct a robust numerical method for singularly perturbed Volterra integro-differential equations.

Numerical methods for the solution of the singularly perturbed Volterra integral and integro-differential equations include exponential finite difference method, finite difference method, implicit Runge–Kutta method, tension spline collocation method, the Petrov–Galerkin method, the spectral method, and so on. From the numerical experiments in [9], uniform convergence of the exponential finite difference method under a Shishkin mesh at nodes was almost second order. In [10], Amiraliyev and Sevgin constructed an exponentially fitted difference scheme and analyzed the first order uniform convergence property under uniform mesh in the discrete maximum norm. Cen and Li [11] studied a finite difference scheme based on trapezoidal integration under the Shishkin mesh, which is almost second-order uniformly convergent at nodes theoretically and numerically. In [12], Kauthen proved the convergence of the implicit Runge Kutta methods out of the boundary layer. Moreover, Horvat and Rogina [13] gave an analysis of the global convergence properties of a new tension spline collocation solution at nodes, i.e., \(O(h^{m-1})\) for singularly perturbed Volterra integro-differential equations and \(O(h^{m})\) for singularly perturbed Volterra integral equations.

The local discontinuous Galerkin (LDG) method proposed by Cockburn and Shu [14] has been shown to be highly stable and effective for convection-diffusion problems. Larsson, Thomée, and Wahlbin [15] applied the DG method in time to solve parabolic integro-differential equations with a weakly singular kernel and provided the error estimate. In [16], an hp-DG method was implemented to solve the Volterra integro-differential equation with a weakly singular kernel, and the exponential convergence property was investigated.

Though the DG method allows discontinuity between adjacent elements, it produces more degrees of freedom than the continuous finite element method (CFEM) and hence requires a large amount of computation. On the other hand, the standard Galerkin FEM even on layer-adapted meshes lacks stability in spite of its good convergence properties.

A coupled (LDG-CFEM) approach was introduced by Alotto [17] in the framework of rotating electrical machines. Perugia and Schötzau [18] studied the coupled method for the modeling of elliptic problems arising in electromagnetics. Roos and Zarin [19], Zarin [20] analyzed the NIPG-CFEM coupled method on the Shishkin mesh for two-dimensional convection-diffusion problems with exponentially layers or characteristic layers. Zhu and Xie [21, 22] applied a coupling of continuous finite element method and discontinuous Galerkin method to solve convection-diffusion problems. Inspired by the great success of the coupled (LDG-CFEM) method in solving elliptic equations and convection-diffusion equation, in our work we aim to derive a coupled approach of LDG and CFEM to solve the singularly perturbed Volterra integro-differential equations. The basic idea is to decompose the region into two parts. In the boundary layer, CFEM is adopted where the mesh size is comparable with ϵ, and the LDG method is used out of the boundary layer for its stabilization. The coupled method is robust with respect to the singularly perturbed parameter ϵ under layer-adapted meshes. Moreover, the 2p-order uniform superconvergence at nodes for the numerical solution \(\hat{U}_{N}\) in the \(L^{\infty }\) norm on the layer-adapted mesh is observed.

The paper is organized as follows. In Sect. 2, the coupled (LDG-CFEM) method for singularly perturbed Volterra integro-differential equations is introduced. In Sect. 3, the existence and uniqueness of the coupled solution are given. The implementation of the coupled method on the Shishkin mesh and the improved graded mesh is presented in Sect. 4. In Sect. 5, some concluding remarks are given.

2 The coupled (LDG-CFEM) method

To describe the coupled method, we first introduce the partition of the interval \(I:=[0,T]\) given by the nodal points \(0=t_{0}< t_{1}<\cdots <t _{N}=T\). Denote the cell \(I_{n}=[t_{n-1},t_{n}]\) and the step-size \(h_{n}=t_{n}-t_{n-1}\) for \(n=1,\ldots ,N\). Let

$$ \tau =\tau _{N}=\min \bigl\{ T/2,\epsilon (2p+1)\ln N\bigr\} $$

or

$$ \tau =\tau _{\epsilon }=\min \bigl\{ T/2,-\epsilon (p+1)\ln \epsilon \bigr\} , $$

and divide both intervals \((0,\tau )\) and \((\tau ,T)\) into \(N/2\) subintervals. The mesh is quasi-uniform on \((0,\tau )\) and on \((\tau ,T)\). Denote \(\mathcal{T}^{1}=\{I_{n}\}_{n=1}^{N/2}\), \(\mathcal{T}^{2}=\{I_{n}\}_{n=N/2+1}^{N}\). Define the piecewise polynomial space \(V_{N}^{1}\) and \(V_{N}^{2}\) as the space of polynomials of degree \(p\geq 1\) and \(q\geq 1\) in each cell \(I_{n}\), respectively, i.e.,

$$\begin{aligned}& V^{1}_{N}=\bigl\{ v_{1}\in H^{1}\bigl([0, \tau ]\bigr): v_{1}(0)=u_{0}, {v_{1}}|_{I _{n}} \in P^{p}(I_{n}), \forall I_{n}\in \mathcal{T}^{1}\bigr\} , \\& V^{2}_{N}=\bigl\{ v_{2}\in L^{2}\bigl([ \tau ,T]\bigr): {v_{2}}|_{I_{n}}\in P^{q}(I _{n}), \forall I_{n}\in \mathcal{T}^{2}\bigr\} . \end{aligned}$$

Multiplying (1.1) by \(v_{1}\in V_{N}^{1}\), \(v_{2}\in V_{N}^{2}\) and integrating the resultant equations in each cell \(I_{n}\) in \(\mathcal{T}^{1}\) and \(\mathcal{T}^{2}\), respectively, we obtain

$$ \begin{aligned}[b] &\epsilon \int _{I_{n}}U_{1,N}'v_{1}\,dt+ \int _{I_{n}}aU_{1,N}v_{1}\,dt + \int _{I_{n}} \int _{0}^{t} k(t,s)U_{1,N}(s)\,ds v_{1}(t)\,dt\\ &\quad = \int _{I_{n}}fv _{1}\,dt, \quad \forall v_{1} \in V_{N}^{1}, \end{aligned} $$
(2.1)

and

$$ \begin{aligned}[b] &\epsilon \int _{I_{n}}U_{2,N}'v_{2}\,dt+ \int _{I_{n}}aU_{2,N}v_{2}\,dt + \int _{I_{n}} \int _{0}^{t} k(t,s)U_{2,N}(s)\,ds v_{2}(t)\,dt\\ &\quad = \int _{I_{n}}fv _{2}\,dt, \quad \forall v_{2} \in V_{N}^{2}, \end{aligned} $$
(2.2)

respectively. Based on (2.1), the finite element method is implemented in the interval \([0,\tau ]\), that is, find \(U_{1,N} \in V_{N}^{1}\), s.t.

$$ \begin{aligned}[b] &\epsilon \int _{I_{n}}U_{1,N}'v_{1}\,dt+ \int _{I_{n}}aU_{1,N}v_{1}\,dt + \int _{I_{n}} \int _{t_{n-1}}^{t} k(t,s)U_{1,N}(s)\,ds v_{1}(t)\,dt \\ &\quad = \int _{I_{n}}fv_{1}\,dt - \int _{I_{n}} \int _{0}^{t_{n-1}} k(t,s)U_{1,N}(s)\,ds v _{1}(t)\,dt, \quad \forall v_{1}\in V_{N}^{1}. \end{aligned} $$
(2.3)

Similarly, the discontinuous Galerkin(DG) method is adopted by (2.2) in the interval \([\tau ,T]\). The DG scheme is to find \(U_{2,N}\in V_{N}^{2}\), s.t.,

$$ \begin{aligned}[b] &{-}\epsilon \int _{I_{n}}U_{2,N}v_{2}'\,dt+ \int _{I_{n}}aU_{2,N}v_{2}\,dt\\ &\qquad {} + \int _{I_{n}} \int _{t_{n-1}}^{t} k(t,s)U_{2,N}(s)\,ds v_{2}(t)\,dt+\epsilon (\hat{U}_{2,N})_{n} {(v_{2})}_{n}^{-} \\ &\quad =\epsilon (\hat{U}_{2,N})_{n-1} {(v_{2})}_{n-1}^{+} + \int _{I_{n}}fv _{2}\,dt - \int _{I_{n}} \int _{0}^{\tau } k(t,s)U_{1,N}(s)\,ds v_{2}(t)\,dt \\ &\qquad {}- \int _{I_{n}} \int _{\tau }^{t_{n-1}} k(t,s)U_{2,N}(s)\,ds v_{2}(t)\,dt, \quad \forall v_{2}\in V_{N}^{2}, \end{aligned} $$
(2.4)

where \(\hat{U}_{2,N}\) is the numerical flux, which plays an important role for the DG method.

In this article, the numerical flux \((\hat{U}_{2,N})_{j}\) is the one-sided form, i.e.,

$$ (\hat{U}_{2,N})_{j}= \textstyle\begin{cases} (U_{1,N})_{j}, & j=N/2, \\ \{U_{2,N}\}_{j}-\frac{1}{2} [U_{2,N}]_{j}=(U_{2,N})_{n}^{-}, & j=N/2+1, \ldots ,N, \end{cases} $$
(2.5)

where the average \(\{\cdot \}\) and the jump \([\cdot ]\) are defined as follows:

$$ \{u\}_{j}=\frac{u^{+}_{j}+u^{-}_{j}}{2}, \qquad [u]_{j}=u^{+}_{j}-u^{-}_{j}. $$

The combination of (2.4) and (2.5) leads to the LDG method: for \(n=N/2+1,\ldots ,N\),

$$ \begin{aligned}[b] &{-}\epsilon \int _{I_{n}}U_{2,N}v_{2}'\,dt+ \int _{I_{n}}aU_{2,N}v_{2}\,dt \\ &\qquad {}+ \int _{I_{n}} \int _{t_{n-1}}^{t} k(t,s)U_{2,N}(s)\,ds v_{2}(t)\,dt+\epsilon (U_{2,N})_{n}^{-} {(v_{2})}_{n}^{-} \\ &\quad =\epsilon (U_{2,N})_{n-1}^{-} {(v_{2})}_{n-1}^{+} + \int _{I_{n}}fv _{2}\,dt - \int _{I_{n}} \int _{0}^{\tau } k(t,s)U_{1,N}(s)\,ds v_{2}(t)\,dt \\ &\qquad {}- \int _{I_{n}} \int _{\tau }^{t_{n-1}} k(t,s)U_{2,N}(s)\,ds v_{2}(t)\,dt, \quad \forall v_{2}\in V_{N}^{2}. \end{aligned} $$
(2.6)

From the viewpoint of computation, when \(n=1\), (2.3) can be written as

$$ \begin{aligned}[b] &{-}\epsilon \int _{I_{1}}U_{1,N}v_{1}'\,dt+ \int _{I_{1}}aU_{1,N}v_{1}\,dt\\ &\qquad {} + \int _{I_{1}} \int _{0}^{t} k(t,s)U_{1,N}(s)\,ds v_{1}(t)\,dt+\epsilon (U_{1,N})_{1} (v_{1})_{1} \\ &\quad =\epsilon u_{0} (v_{1})_{1}+ \int _{I_{1}}fv_{1}\,dt, \quad \forall v_{1} \in V_{N}^{1}, \end{aligned} $$
(2.7)

where \((U_{1,N})_{1}=u_{0}\) is used. For \(n=2,\ldots ,N/2\), (2.3) becomes

$$ \begin{aligned}[b] &{-}\epsilon \int _{I_{n}}U_{1,N}'v_{1}\,dt + \int _{I_{n}}aU_{1,N}v_{1}\,dt\\ &\qquad {}+ \int _{I_{n}} \int _{t_{n-1}}^{t} k(t,s)U_{1,N}(s)\,ds v_{1}(t)\,dt +\epsilon (U_{1,N})_{n} (v_{1})_{n} \\ &\quad =\epsilon (U_{1,N})_{n-1} (v_{1})_{n-1}+ \int _{I_{n}}fv_{1}\,dt \\ &\qquad {}- \int _{I_{n}} \int _{0}^{t_{n-1}} k(t,s)U_{1,N}(s)\,ds v_{1}(t)\,dt, \quad \forall v_{1}\in V_{N}^{1}. \end{aligned} $$
(2.8)

For \(n=N/2+1\), (2.6) could be written as

$$ \begin{aligned}[b] &{-}\epsilon \int _{I_{N/2+1}}U_{2,N}v_{2}'\,dt + \int _{I_{N/2+1}}aU_{2,N}v _{2}\,dt\\ &\qquad {}+ \int _{I_{N/2+1}} \int _{\tau }^{t} k(t,s)U_{2,N}(s)\,ds v_{2}(t)\,dt+ \epsilon (U_{2,N})_{N/2+1}^{-} {(v_{2})}_{N/2+1}^{-} \\ &\quad =\epsilon (U_{1,N})_{N/2} {(v_{2})}_{N/2}^{+} + \int _{I_{N/2+1}}fv _{2}\,dt \\ &\qquad {}- \int _{I_{N/2+1}} \int _{0}^{\tau } k(t,s)U_{1,N}(s)\,ds v_{2}(t)\,dt, \quad \forall v_{2}\in V_{N}^{2}, \end{aligned} $$
(2.9)

where \((U_{2,N})_{N/2}^{-}=(U_{1,N})_{N/2}\) is used. For \(n=N/2+2\), (2.6) becomes

$$ \begin{aligned}[b] &{-}\epsilon \int _{I_{N/2+2}}U_{2,N}v_{2}'\,dt + \int _{I_{N/2+2}}aU_{2,N}v _{2}\,dt \\ &\qquad {}+ \int _{I_{N/2+2}} \int _{t_{N/2+1}}^{t} k(t,s)U_{2,N}(s)\,ds v_{2}(t)\,dt+ \epsilon (U_{2,N})_{N/2+2}^{-} {(v_{2})}_{N/2+2}^{-} \\ &\quad =\epsilon (U_{2,N})_{N/2+1}^{-} {(v_{2})}_{N/2+1}^{+} + \int _{I_{N/2+2}}fv _{2}\,dt - \int _{I_{N/2+2}} \int _{0}^{\tau } k(t,s)U_{1,N}(s)\,ds v_{2}(t)\,dt \\ &\qquad {}- \int _{I_{N/2+2}} \int _{\tau }^{t_{N/2+1}} k(t,s)U_{2,N}(s)\,ds v _{2}(t)\,dt, \quad \forall v_{2}\in V_{N}^{2}. \end{aligned} $$
(2.10)

For \(n=N/2+3,\ldots ,N\), (2.6) becomes

$$ \begin{aligned}[b] &{-}\epsilon \int _{I_{n}}U_{2,N}v_{2}'\,dt+ \int _{I_{n}}aU_{2,N}v_{2}\,dt \\ &\qquad {}+ \int _{I_{n}} \int _{t_{n-1}}^{t} k(t,s)U_{2,N}(s)\,ds v_{2}(t)\,dt+\epsilon {(U_{2,N})}_{n}^{-} {(v_{2})}_{n}^{-} \\ &\quad =\epsilon {(U_{2,N})}_{n-1}^{-} {(v_{2})}_{n-1}^{+} + \int _{I_{n}}fv _{2}\,dt - \int _{I_{n}} \int _{0}^{\tau } k(t,s)U_{1,N}(s)\,ds v_{2}(t)\,dt \\ &\qquad {}- \int _{I_{n}} \int _{\tau }^{t_{n-1}} k(t,s)U_{2,N}(s)\,ds v_{2}(t)\,dt, \quad \forall v_{2}\in V_{N}^{2}. \end{aligned} $$
(2.11)

3 The existence and uniqueness of the coupled method

The discrete Gronwall inequality plays a very important role in the existence and uniqueness analysis. According to [23], the discrete Gronwall inequality is described as follows.

Lemma 3.1

Suppose \(\omega _{n}\geq 0\), \(f_{n}\geq 0\), and \(y_{n}\geq 0\) for \(n=0,1,\ldots \) . Further, they satisfy, for \(n=1,2,\ldots ,N\),

$$ y_{n}\le f_{n}+\sum_{j=0}^{n-1} \omega _{j}y_{j}. $$

Then, for any \(N\geq 1\), we have

$$ y_{N}\le \exp \Biggl(\sum_{i=0}^{N-1} \omega _{i}\Biggr) \max_{0\leq n\leq N}f_{n}. $$

Summing up (2.3) over the first l elements with \(l=1,2,\ldots ,N/2\), we obtain, for any \(v_{1}\in V^{1}_{N}\),

$$ \begin{aligned}[b] B_{l}(U_{1},v_{1}) &\triangleq \epsilon \int _{0}^{t_{l}} U_{1}'v_{1} \,dt+ \int _{0}^{t_{l}}aU_{1}v_{1}\,dt + \int _{0}^{t_{l}} \int _{0}^{t} k(t,s)U _{1}(s)\,ds v_{1}(t)\,dt \\ &= \int _{0}^{t_{l}}fv_{1}\,dt. \end{aligned} $$
(3.1)

Equivalently, we have

$$ \begin{aligned}[b] B_{l}(U_{1},v_{1}) &\triangleq -\epsilon \int _{0}^{t_{l}} U_{1}v_{1}'\,dt+ \int _{0}^{t_{l}}aU_{1}v_{1}\,dt \\ &\quad {}+ \int _{0}^{t_{l}} \int _{0}^{t} k(t,s)U _{1}(s)\,ds v_{1}(t)\,dt+\epsilon U_{1}(t_{l})v_{1}(t_{l}) -\epsilon u_{0}v _{1}(t_{0}) \\ &= \int _{0}^{t_{l}}fv_{1}\,dt, \end{aligned} $$
(3.2)

where \(U_{1}(t_{0})=u_{0}\) is used.

Similarly, summing up (2.6) over the first l elements on the interval \([\tau ,T]\) with \(l=1,2,\ldots ,N/2\), we obtain, for any \(v_{2}\in V^{2}_{N}\),

$$ \begin{aligned}[b] B_{l}(U_{2},v_{2}) &\triangleq -\epsilon \int _{\tau }^{t_{l}} U_{2}v _{2}'\,dt+ \int _{\tau }^{t_{l}}aU_{2}v_{2}\,dt\\ &\quad {} + \int _{\tau }^{t_{l}} \int _{0}^{\tau } k(t,s)U_{1}(s)\,ds v_{2}(t)\,dt+ \int _{\tau }^{t_{l}} \int _{ \tau }^{t} k(t,s)U_{2}(s)\,ds v_{2}(t)\,dt \\ &\quad {}+\epsilon (U_{2} )^{-}_{l} (v_{2} )^{-}_{l} - \epsilon U_{1}(\tau )v_{2}^{+}(\tau ) -\epsilon \sum _{j=N/2+1} ^{l-1} (U_{2} )^{-}_{j} [v_{2}]_{j} \\ &= \int _{\tau }^{t_{l}}fv_{2}\,dt, \end{aligned} $$
(3.3)

with \([v]_{j}=v_{j}^{+}-v_{j}^{-}\), where \(U_{2}^{-}(\tau )=U_{1}( \tau )\) is used. Equivalently, we have

$$ \begin{aligned}[b] B_{l}(U_{2},v_{2}) &\triangleq \epsilon \int _{\tau }^{t_{l}} U_{2}'v _{2}\,dt+ \int _{\tau }^{t_{l}}aU_{2}v_{2}\,dt + \int _{\tau }^{t_{l}} \int _{0}^{\tau } k(t,s)U_{1}(s)\,ds v_{2}(t)\,dt \\ &\quad {}+ \int _{\tau }^{t_{l}} \int _{ \tau }^{t} k(t,s)U_{2}(s)\,ds v_{2}(t)\,dt+\epsilon \sum_{j=N/2+1}^{l-1}[U_{2}]_{j} (v_{2} )_{j}^{+} \\ &= \int _{\tau }^{t_{l}}fv_{2}\,dt, \end{aligned} $$
(3.4)

where \(U_{2}^{+}(\tau )=U_{2}^{-}(\tau )\) is used.

Lemma 3.2

For any \(v\in V^{1}_{N}\), we have the identity

$$ B_{l}(v,v)= \frac{\epsilon }{2}v^{2}(t_{l})- \frac{\epsilon }{2}u_{0} ^{2}+ \int _{0}^{t_{l}}av^{2}\,dt + \int _{0}^{t_{l}} \int _{0}^{t} k(t,s)v(s)\,ds v(t)\,dt. $$

Proof

By (3.1) and direct integration, we reach the conclusion. □

Lemma 3.3

For any \(v_{1}\in V^{1}_{N}\) and \(v_{2}\in V^{2} _{N}\), we have the identity

$$ \begin{aligned}[b] B_{l}(v_{2},v_{2}) &= \int _{\tau }^{t_{l}}av_{2}^{2}\,dt + \int _{\tau } ^{t_{l}} \int _{0}^{\tau } k(t,s)v_{1}(s)\,ds v_{2}(t)\,dt+ \int _{\tau }^{t _{l}} \int _{\tau }^{t} k(t,s)v_{2}(s)\,ds v_{2}(t)\,dt \\ &\quad {}+\frac{\epsilon }{2}\sum_{j=N/2+1}^{l-1}[v_{2}]_{j} ^{2} +\frac{\epsilon }{2} \bigl( (v_{2} )_{l}^{-} \bigr)^{2} -\frac{ \epsilon }{2}v_{1}^{2}(\tau ). \end{aligned} $$

Proof

By (3.3) and (3.4), we have, for \(U_{2}\in V^{2}_{N}\),

$$\begin{aligned}& \begin{aligned}[b] B_{l}(v_{2},v_{2}) &= -\epsilon \int _{\tau }^{t_{l}} v_{2}v_{2}'\,dt+ \int _{\tau }^{t_{l}}av_{2}^{2}\,dt\\ &\quad {} + \int _{\tau }^{t_{l}} \int _{0}^{ \tau } k(t,s)v_{1}(s)\,ds v_{2}(t)\,dt+ \int _{\tau }^{t_{l}} \int _{\tau } ^{t} k(t,s)v_{2}(s)\,ds v_{2}(t)\,dt \\ &\quad {}+\epsilon (v_{2} )^{-}_{l} (v_{2} )^{-}_{l} - \epsilon v_{1}(\tau )v_{2}^{+}(\tau ) -\epsilon \sum _{j=N/2+1} ^{l-1} (v_{2} )^{-}_{j} [v_{2}]_{j}, \end{aligned} \end{aligned}$$
(3.5)
$$\begin{aligned}& \begin{aligned}[b] B_{l}(v_{2},v_{2}) &= \epsilon \int _{\tau }^{t_{l}} v_{2}'v_{2} \,dt+ \int _{\tau }^{t_{l}}av_{2}^{2}\,dt + \int _{\tau }^{t_{l}} \int _{0}^{ \tau } k(t,s)v_{1}(s)\,ds v_{2}(t)\,dt \\ &\quad {}+ \int _{\tau }^{t_{l}} \int _{\tau } ^{t} k(t,s)v_{2}(s)\,ds v_{2}(t)\,dt+\epsilon \sum_{j=N/2+1}^{l-1}[v_{2}]_{j} (v_{2} )_{j}^{+}, \end{aligned} \end{aligned}$$
(3.6)

respectively. The summation of (3.5) and (3.6) leads to the conclusion, where \(v_{2}^{+}( \tau )=v_{1}(\tau )\) is used. □

We now address the existence and uniqueness of discrete solutions.

Theorem 3.1

Suppose that \(f(t)\), \(a(t)\) are continuous in I, and the kernel function \(k(t,s)\) is continuous in \(I\times I\) with \(a(t)\ge \alpha >0\). \(U_{1,N}\) is the CFEM solution of (2.3) and \(U_{2,N}\) is the LDG solution of (2.6). Then \(U_{1,N}\) and \(U_{2,N}\) are existent and unique.

Proof

As the dimensions of \(V_{N}^{1}\) and \(V_{N}^{2}\) are finite, we only need to prove that the solution of (2.3) is \(U_{1,N}=0\) and the solution of (2.6) is \(U_{2,N}=0\) when \(f=0\) and \(u_{0}=0\). By Lemma 3.2 and \(u_{0}=0\), we obtain, for any \(U_{1}\in V^{1}_{N}\),

$$ B_{l}(U_{1},U_{1})= \frac{\epsilon }{2}U_{1}^{2}(t_{l})+ \int _{0}^{t _{l}}aU_{1}^{2}\,dt + \int _{0}^{t_{l}} \int _{0}^{t} k(t,s)U_{1}(s)\,ds U_{1}(t)\,dt=0. $$
(3.7)

Therefore,

$$ \frac{\epsilon }{2}U_{1}^{2}(t_{l})+ \int _{0}^{t_{l}}aU_{1}^{2}\,dt=- \int _{0}^{t_{l}} \int _{0}^{t} k(t,s)U_{1}(s)\,ds U_{1}(t)\,dt. $$

When \(k(t,s)\) is bounded, i.e., \(\|k(t,s)\|_{\infty }\leq M\), we have

$$ \begin{aligned}[b]& \biggl\vert \int _{0}^{t_{l}} \int _{0}^{t} k(t,s)U_{1}(s)\,ds U_{1}(t)\,dt \biggr\vert \\ &\quad \leq \int _{0}^{t_{l}} \int _{0}^{t} \bigl\vert k(t,s) \bigr\vert \bigl\vert U_{1}(s) \bigr\vert \, ds \bigl\vert U_{1}(t) \bigr\vert \, dt \\ &\quad \leq \biggl( \int _{0}^{t_{l}}aU_{1}^{2}\,dt \biggr)^{\frac{1}{2}} \biggl( \int _{0}^{t_{l}}\frac{1}{a} \biggl( \int _{0}^{t} \bigl\vert k(t,s) \bigr\vert \bigl\vert U_{1}(s) \bigr\vert \, ds \biggr)^{2}\,dt \biggr)^{\frac{1}{2}} \\ &\quad \leq \frac{1}{2} \int _{0}^{t_{l}}aU_{1}^{2}\,dt + \frac{1}{2} \int _{0} ^{t_{l}}\frac{1}{a} \biggl( \int _{0}^{t} \bigl\vert k(t,s) \bigr\vert \bigl\vert U_{1}(s) \bigr\vert \, ds \biggr)^{2}\,dt. \end{aligned} $$
(3.8)

The combination of (3.7) and (3.8) implies

$$ \begin{aligned}[b] \int _{0}^{t_{l}} aU_{1}^{2}\,dt &\leq \int _{0}^{t_{l}}\frac{1}{a} \biggl( \int _{0}^{t} \bigl\vert k(t,s) \bigr\vert \bigl\vert U_{1}(s) \bigr\vert \, ds \biggr)^{2}\,dt \\ &\leq \frac{M ^{2}t_{l}}{\alpha } \int _{0}^{t_{l}} \int _{0}^{t} U_{1}^{2}(s)\,ds \,dt \leq \frac{M^{2}\tau }{\alpha }\sum_{i=1}^{l} \int _{I_{i}} \int _{0}^{t _{i}}U_{1}^{2}(s)\,ds \,dt. \end{aligned} $$
(3.9)

Consequently, we get

$$ \alpha \int _{0}^{t_{l}} U_{1}^{2}\,dt\le \int _{0}^{t_{l}} aU_{1}^{2}\,dt \le \frac{M^{2}\tau }{\alpha }\sum_{i=1}^{l}h_{i} \int _{0}^{t_{i}}U _{1}^{2}(t)\,dt. $$
(3.10)

Let \(y_{i}=\int _{0}^{t_{i}} U_{1}^{2}\,dt\). Then (3.10) is written as

$$ \biggl(\alpha -\frac{M^{2}\tau h_{l}}{\alpha }\biggr)y_{l}\leq \frac{M^{2}\tau }{ \alpha }\sum_{i=1}^{l-1}h_{i}y_{i}. $$
(3.11)

Set \(h=\max_{1\leq l\leq \frac{N}{2}}h_{l}\). When h is small enough s.t. \(h\leq \frac{\alpha ^{2}}{2M^{2}\tau }\), we have

$$ y_{l}\leq \frac{2M^{2}\tau }{\alpha ^{2}}\sum _{i=1}^{l-1}h_{i}y_{i} $$
(3.12)

for \(l=1,2,\ldots , N/2\). By the discrete Gronwall inequality in Lemma 3.1, we have \(y_{N/2}=0\). Thus \(U_{1}=0\).

Similarly, by Lemma 3.3, we obtain, for any \(U_{2}\in V^{2}_{N}\),

$$ \begin{aligned}[b] B_{l}(U_{2},U_{2})&= \int _{\tau }^{t_{l}}aU_{2}^{2}\,dt + \int _{\tau } ^{t_{l}} \int _{\tau }^{t} k(t,s)U_{2}(s)\,ds U_{2}(t)\,dt\\ &\quad {} + \frac{\epsilon }{2}\sum_{j=N/2+1}^{l-1}[U_{2}]_{j}^{2} +\frac{ \epsilon }{2} \bigl( (U_{2} )_{l}^{-} \bigr)^{2}\\ &=0, \end{aligned} $$
(3.13)

where \(f=0\) and \(U_{1}=0\) are used. Therefore,

$$ \int _{\tau }^{t_{l}}aU_{2}^{2}\,dt+ \frac{\epsilon }{2}\sum_{j=N/2+1} ^{l-1}[U_{2}]_{j}^{2} +\frac{\epsilon }{2} \bigl( (U_{2} )_{l} ^{-} \bigr)^{2} =- \int _{\tau }^{t_{l}} \int _{\tau }^{t} k(t,s)U_{2}(s)\,ds U _{2}(t)\,dt. $$

When \(k(t,s)\) is bounded, we have

$$ \begin{aligned}[b] &\biggl\vert \int _{\tau }^{t_{l}} \int _{\tau }^{t} k(t,s)U_{2}(s)\,ds U_{2}(t)\,dt \biggr\vert \\ &\quad \leq \int _{\tau }^{t_{l}} \int _{\tau }^{t} \bigl\vert k(t,s) \bigr\vert \bigl\vert U_{2}(s) \bigr\vert \, ds \bigl\vert U_{2}(t) \bigr\vert \, dt \\ &\quad \leq \biggl( \int _{\tau }^{t_{l}}aU_{2}^{2}\,dt \biggr)^{\frac{1}{2}} \biggl( \int _{\tau }^{t_{l}}\frac{1}{a} \biggl( \int _{0}^{t} \bigl\vert k(t,s) \bigr\vert \bigl\vert U_{2}(s) \bigr\vert \, ds \biggr)^{2}\,dt \biggr)^{\frac{1}{2}} \\ &\quad \leq \frac{1}{2} \int _{\tau }^{t_{l}}aU_{2}^{2}\,dt + \frac{1}{2} \int _{\tau }^{t_{l}}\frac{1}{a} \biggl( \int _{0}^{t} \bigl\vert k(t,s) \bigr\vert \bigl\vert U_{2}(s) \bigr\vert \, ds \biggr)^{2}\,dt. \end{aligned} $$
(3.14)

The combination of (3.13) and (3.14) implies

$$ \begin{aligned}[b] \int _{\tau }^{t_{l}} aU_{2}^{2}\,dt & \leq \int _{\tau }^{t_{l}} \frac{1}{a} \biggl( \int _{\tau }^{t} \bigl\vert k(t,s) \bigr\vert \bigl\vert U_{2}(s) \bigr\vert \, ds \biggr)^{2}\,dt \\ &\leq \frac{M^{2}t_{l}}{\alpha } \int _{\tau }^{t_{l}} \int _{\tau }^{t} U_{2}^{2}(s)\,ds \,dt \\ &\leq \frac{M^{2}T}{\alpha }\sum_{i=N/2+1}^{l} \int _{I_{i}} \int _{ \tau }^{t_{i}}U_{2}^{2}(s)\,ds \,dt. \end{aligned} $$
(3.15)

Consequently, we get

$$ \alpha \int _{\tau }^{t_{l}} U_{2}^{2}\,dt\le \int _{\tau }^{t_{l}} aU _{2}^{2}\,dt \le \frac{M^{2}T}{\alpha }\sum_{i=N/2+1}^{l}h_{i} \int _{ \tau }^{t_{i}}U_{2}^{2}(t)\,dt. $$
(3.16)

Let \(z_{i}=\int _{\tau }^{t_{i}} U_{2}^{2}\,dt\). Then (3.16) is written as

$$ \biggl(\alpha -\frac{M^{2}T h_{l}}{\alpha }\biggr)z_{l}\leq \frac{M^{2}T}{\alpha }\sum_{i=N/2+1}^{l-1}h_{i}z_{i}. $$
(3.17)

Set \(h'=\max_{\frac{N}{2}+1\leq l\leq N}h_{l}\). When \(h'\) is small enough s.t. \(h'\leq \frac{\alpha ^{2}}{2M^{2}T}\), we have

$$ z_{l}\leq \frac{2M^{2}T}{\alpha ^{2}}\sum _{i=N/2+1}^{l-1}h_{i}z_{i} $$
(3.18)

for \(l=N/2+1,2,\ldots , N\). By the discrete Gronwall inequality in Lemma 3.1, we have \(z_{N}=0\). Thus \(U_{2}=0\). □

4 Numerical experiments

Example

Consider the singularly perturbed Volterra integro-differential equation (1.1) with \(a=1\), \(k(t,s)=\exp (s)\). The corresponding exact solution is given by

$$ u(t)=\exp (t-1)+\exp { \biggl(-\frac{(1+\epsilon )}{\epsilon }t \biggr)}, \quad t\in [0,1], $$

which exhibits a boundary layer at \(t=0\) of thickness \(O(\epsilon )\), with the initial condition \(u_{0}=1+\exp (-1)\) and the right-hand side of equation (1.1) given by

$$ f(t)=(\epsilon +1)e^{t-1} -\epsilon e^{-(1+\epsilon )t/\epsilon } - \epsilon e^{-t/\epsilon } +\frac{e^{2t-1}}{2}+\epsilon -\frac{1}{2e}. $$

We implement the numerical schemes (2.3) and (2.6) in the intervals \([0,\tau ]\) and \([\tau ,1]\), respectively, to solve this example. Denote \(U_{N}=(U_{1,N},U_{2,N})\), \(\hat{U}_{N}=(U_{1,N},\hat{U}_{2,N})\). Herein we denote

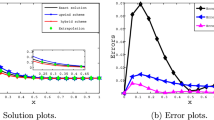
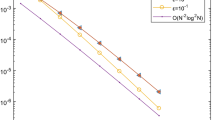
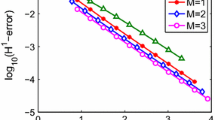
$$ \begin{aligned}[b] & \Vert u-\hat{U}_{N} \Vert _{L^{\infty }([0,1])}=\max_{0\le i\le N} \bigl\vert u(t _{i})- \hat{U}_{N}(t_{i}) \bigr\vert , \\ & \Vert u-U_{N} \Vert _{L^{2}([0,1])}= \Biggl(\sum _{n=1}^{N} \int _{I_{n}}(u-U _{N})^{2} \Biggr)^{1/2}, \\ & \Vert u-U_{1,N} \Vert _{L^{\infty }([0,\tau ])}=\max_{0\le i\le N/2} \bigl\vert u(t _{i})-U_{1,N}(t_{i}) \bigr\vert , \\ & \Vert u-U_{1,N} \Vert _{L^{2}([0,\tau ])}= \Biggl(\sum _{n=1}^{N/2} \int _{I_{n}}(u-U_{1,N})^{2} \Biggr)^{1/2}, \\ & \Vert u-\hat{U}_{2,N} \Vert _{L^{\infty }([\tau ,1])}=\max _{N/2+1\le i\le N} \bigl\vert u(t_{i})-\hat{U}_{2,N}(t_{i}) \bigr\vert , \\ & \Vert u-U_{2,N} \Vert _{L^{2}([\tau ,1])}= \Biggl(\sum _{n=N/2+1}^{N} \int _{I_{n}}(u-U_{2,N})^{2} \Biggr)^{1/2}. \end{aligned} $$

Now we observe the numerical results of the coupled approach under a Shishkin mesh, in which the intervals \([0,\tau ]\) and \([\tau ,1]\) are each divided into \(N/2\) equal subintervals. We first take \(\tau =\tau _{N}=\min \{0.5,\epsilon (2p+1)\ln N\}\). For this case, Table 1 and Table 2 show the errors of the coupled solution \(U_{N}\) in the \(L^{2}\) norm and the numerical solution \(\hat{U}_{N}\) in the \(L^{\infty }\) norm for \(\epsilon =10^{-6}\) and \(\epsilon =10^{-8}\), respectively. Taking ϵ as 10−4, 10−6, and 10−8, Fig. 1 and Fig. 2 demonstrate the convergence curve of the numerical solution \(\hat{U}_{N}\) in the \(L^{\infty }([0,1])\) norm for \(p=1\) and \(p=2\), respectively. From Table 1, Table 2, Fig. 1, and Fig. 2, we observe that under this kind of Shishkin mesh, the following error estimate holds:

$$ \Vert u-\hat{U}_{N} \Vert _{L^{\infty }([0,1])}\le C \biggl( \frac{\ln N}{N} \biggr)^{2p}, $$

where the constant C is independent of ϵ.

Figure 1
figure 1

Convergence curve, Shishkin mesh, \(\tau _{N}=\min \{0.5, \epsilon (2p+1)\ln (N+1)\}\), \(p=1\)

Full size image
Figure 2
figure 2

Convergence curve, Shishkin mesh, \(\tau _{N}=\min \{0.5, \epsilon (2p+1)\ln (N+1)\}\), \(p=2\)

Full size image
Table 1 Shishkin mesh, \(\tau _{N}=\min \{0.5,\epsilon (2p+1)\ln (N+1) \}\), \(\epsilon =10^{-6}\)
Full size table
Table 2 Shishkin mesh, \(\tau _{N}=\min \{0.5,\epsilon (2p+1)\ln (N+1) \}\), \(\epsilon =10^{-8}\)
Full size table

Then we take \(\tau =\tau _{\epsilon }=\min \{0.5,-\epsilon (p+1)\ln \epsilon \}\). For this case, Table 3 and Table 4 show the errors of the coupled solution \(U_{N}\) in the \(L^{2}\) norm and the numerical solution \(\hat{U}_{N}\) in the \(L^{\infty }\) norm for \(\epsilon =10^{-6}\) and \(\epsilon =10^{-8}\), respectively. Taking ϵ as 10−4, 10−6, and 10−8, Fig. 3 and Fig. 4 demonstrate the convergence curve of the numerical solution \(\hat{U}_{N}\) in the \(L^{\infty }([0,1])\) norm for \(p=1\) and \(p=2\), respectively. From Table 3, Table 4, Fig. 3, and Fig. 4, we observe that under this kind of Shishkin mesh, the following error estimate holds:

$$ \Vert u-\hat{U}_{N} \Vert _{L^{\infty }}\le C \biggl( \frac{\ln \epsilon ^{-1}}{N} \biggr)^{2p}, $$

where the constant C is independent of ϵ.

Figure 3
figure 3

Convergence curve, Shishkin mesh, \(\tau _{\epsilon }=\min \{0.5,- \epsilon (p+1)\ln \epsilon \}\), \(p=1\)

Full size image
Figure 4
figure 4

Convergence curve, Shishkin mesh, \(\tau _{\epsilon }=\min \{0.5,- \epsilon (p+1)\ln \epsilon \}\), \(p=2\)

Full size image
Table 3 Shishkin mesh, \(\tau _{\epsilon }=\min \{0.5,-\epsilon (p+1) \ln \epsilon \}\), \(\epsilon =10^{-6}\)
Full size table
Table 4 Shishkin mesh, \(\tau _{\epsilon }=\min \{0.5,-\epsilon (p+1) \ln \epsilon \}\), \(\epsilon =10^{-8}\)
Full size table

In the following part, we focus on the numerical results on the improved graded mesh. The first part \([0,\tau ]\) is divided into \(N/2\) non-uniform subintervals with nodes as follows:

$$ x_{j}=\tau * \bigl((j-1)/N \bigr)^{\lambda }, \quad j=1,2,\ldots ,N/2+1. $$

On the other hand, the interval \([\tau ,1]\) is partitioned into \(N/2\) equal subintervals. Apparently the Shishkin mesh is a special case of the improved graded mesh with \(\lambda =1\). By increasing the value of λ, more and more mesh points would concentrate in the neighborhood of \(t=0\), i.e., the region of boundary layer. By taking \(\lambda =2\), we will observe that the solution approximated better than the case of the Shishkin mesh.

In the case of \(\tau =\tau _{N}\) and \(\lambda =2\), Table 5 and Table 6 show the errors of the coupled solution \(U_{N}\) in the \(L^{2}\) norm and the numerical solution \(\hat{U}_{N}\) in the \(L^{\infty }\) norm for \(\epsilon =10^{-6}\) and \(\epsilon =10^{-8}\), respectively. Taking ϵ as 10−4, 10−6, and 10−8, Fig. 5 and Fig. 6 demonstrate the convergence curve of the numerical solution \(\hat{U}_{N}\) in the \(L^{\infty }([0,1])\) norm for \(p=1\) and \(p=2\), respectively. For \(\tau =\tau _{\epsilon }\) and \(\lambda =2\), Table 7 and Table 8 show the errors of the coupled solution \(U_{N}\) in the \(L^{2}\) norm and the numerical solution \(\hat{U}_{N}\) in the \(L^{\infty }\) norm for \(\epsilon =10^{-6}\) and \(\epsilon =10^{-8}\), respectively. Taking ϵ as 10−4, 10−6, and 10−8, Fig. 7 and Fig. 8 demonstrate the convergence curve of the numerical solution \(\hat{U}_{N}\) in the \(L^{\infty }([0,1])\) norm for \(p=1\) and \(p=2\), respectively. Compared with the existing numerical methods, our coupled approach is robust and has a higher order of accuracy than these older methods, i.e., the numerical solution \(\hat{U}_{N}\) in the \(L^{\infty }\) norm on the layer-adapted mesh has 2p-order uniform superconvergence.

Figure 5
figure 5

Convergence curve, improved graded mesh, \(\lambda =2\), \(\tau _{N}=\min \{0.5,\epsilon (2p+1)\ln (N+1)\}\), \(p=1\)

Full size image
Figure 6
figure 6

Convergence curve, improved graded mesh, \(\lambda =2\), \(\tau _{N}=\min \{0.5,\epsilon (2p+1)\ln (N+1)\}\), \(p=2\)

Full size image
Figure 7
figure 7

Convergence curve, improved graded mesh, \(\lambda =2\), \(\tau _{\epsilon }=\min \{0.5,-\epsilon (p+1)\ln \epsilon \}\), \(p=1\)

Full size image
Figure 8
figure 8

Convergence curve, improved graded mesh, \(\lambda =2\), \(\tau _{\epsilon }=\min \{0.5,-\epsilon (p+1)\ln \epsilon \}\), \(p=2\)

Full size image
Table 5 Improved graded mesh, \(\lambda =2\), \(\tau _{N}=\min \{0.5, \epsilon (2p+1)\ln (N+1)\}\), \(\epsilon =10^{-6}\)
Full size table
Table 6 Improved graded mesh, \(\lambda =2\), \(\tau _{N}=\min \{0.5, \epsilon (2p+1)\ln (N+1)\}\), \(\epsilon =10^{-8}\)
Full size table
Table 7 Improved graded mesh, \(\lambda =2\), \(\tau _{\epsilon }= \min \{0.5,-\epsilon (p+1)\ln \epsilon \}\), \(\epsilon =10^{-6}\)
Full size table
Table 8 Improved graded mesh, \(\lambda =2\), \(\tau _{\epsilon }= \min \{0.5,-\epsilon (p+1)\ln \epsilon \}\), \(\epsilon =10^{-8}\)
Full size table

5 Conclusions

In this paper, we focus on the coupled method for the singularly perturbed integro-differential equation (1.1), whose solution exhibits a boundary layer at \(t=0\). The existence and uniqueness of the coupled solution is provided. Based on the numerical experiment, we observe the optimal convergence rate \(p+1\) in the \(L^{2}\) norm and the uniform superconvergence rate 2p at nodes for the numerical solution \(\hat{U}_{N}\) with the one-sided flux inside the boundary layer region under layer-adapted meshes. The uniform convergence analysis of the coupled method is our future work.